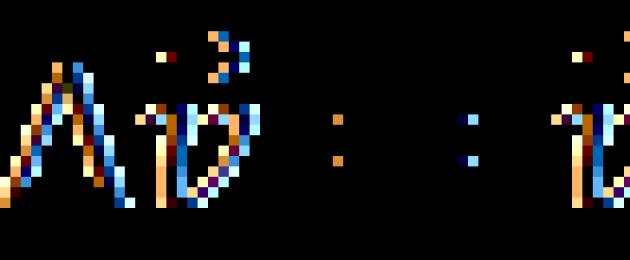Пусть на тело массой m
в течение некоторого малого промежутка времени Δt
действовала сила Под действием этой силы скорость тела изменилась на 
Следовательно, в течение времени Δt
тело двигалось с ускорением
Из основного закона динамики (второго закона Ньютона ) следует:
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения ). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с) .
Физическая величина, равная произведению силы на время ее действия, называется импульсом силы . Импульс силы также является векторной величиной.
В новых терминах второй закон Ньютона может быть сформулирован следующим образом:
И зменение импульса тела (количества движения) равно импульсу силы .
Обозначив импульс тела буквой второй закон Ньютона можно записать в виде
Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси:
Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. Рассмотрим в качестве примера одномерное движение, т. е. движение тела по одной из координатных осей (например, оси OY ). Пусть тело свободно падает с начальной скоростью υ 0 под действием силы тяжести; время падения равно t . Направим ось OY вертикально вниз. Импульс силы тяжести F т = mg за время t равен mgt . Этот импульс равен изменению импульса тела
Этот простой результат совпадает с кинематической формулой для скорости равноускоренного движения . В этом примере сила оставалась неизменной по модулю на всем интервале времени t . Если сила изменяется по величине, то в выражение для импульса силы нужно подставлять среднее значение силы F ср на промежутке времени ее действия. Рис. 1.16.1 иллюстрирует метод определения импульса силы, зависящей от времени.
Выберем на оси времени малый интервал Δt , в течение которого сила F (t ) остается практически неизменной. Импульс силы F (t ) Δt за время Δt будет равен площади заштрихованного столбика. Если всю ось времени на интервале от 0 до t разбить на малые интервалы Δt i , а затем просуммировать импульсы силы на всех интервалах Δt i , то суммарный импульс силы окажется равным площади, которую образует ступенчатая кривая с осью времени. В пределе (Δt i → 0) эта площадь равна площади, ограниченной графиком F (t ) и осью t . Этот метод определения импульса силы по графику F (t ) является общим и применим для любых законов изменения силы со временем. Математически задача сводится к интегрированию функции F (t ) на интервале .
Импульс силы, график которой представлен на рис. 1.16.1, на интервале от t 1 = 0 с до t 2 = 10 с равен:
В этом простом примере
В некоторых случаях среднюю силу F ср можно определить, если известно время ее действия и сообщенный телу импульс. Например, сильный удар футболиста по мячу массой 0,415 кг может сообщить ему скорость υ = 30 м/с. Время удара приблизительно равно 8·10 –3 с.
Импульс p , приобретенный мячом в результате удара есть:
Следовательно, средняя сила F ср, с которой нога футболиста действовала на мяч во время удара, есть:
Это очень большая сила. Она приблизительно равна весу тела массой 160 кг.
Если движение тела во время действия силы происходило по некоторой криволинейной траектории, то начальный и конечный импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса удобно использовать диаграмму импульсов
, на которой изображаются вектора и , а также вектор 
построенный по правилу параллелограмма. В качестве примера на рис. 1.16.2 изображена диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой m
налетел на стенку со скоростью под углом α к нормали (ось OX
) и отскочил от нее со скоростью под углом β. Во время контакта со стеной на мяч действовала некоторая сила направление которой совпадает с направлением вектора
При нормальном падении мяча массой m
на упругую стенку со скоростью ,после отскока мяч будет иметь скорость . Следовательно, изменение импульса мяча за время отскока равно 
В проекциях на ось OX этот результат можно записать в скалярной форме Δp x = –2m υx . Ось OX направлена от стенки (как на рис. 1.16.2), поэтому υx < 0 и Δp x > 0. Следовательно, модуль Δp изменения импульса связан с модулем υ скорости мяча соотношением Δp = 2m υ.
Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.
Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.
Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара - 30 м/с. Сила, с которой нога действовала на мяч - 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.
Изменение импульса тела
Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.
1) Во время удара на мяч действуют две силы: сила реакции опоры , сила тяжести .
Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.
Любые задачи на движущиеся тела в классической механике требуют знания концепции импульса. В данной статье рассматривается эта концепция, дается ответ на вопрос, куда направлен вектор импульса тела, а также приводится пример решения задачи.
Количество движения
Чтобы выяснить, куда направлен вектор импульса тела, следует, в первую очередь, понять его физический смысл. Впервые термин был объяснен Исааком Ньютоном, однако важно отметить, что итальянский ученый Галилео Галилей в своих работах уже использовал похожее понятие. Для характеристики движущегося объекта он ввел величину, которая называлась стремление, натиск или собственно импульс (impeto на итальянском). Заслуга же Исаака Ньютона заключается в том, что он смог связать эту характеристику с действующими на тело силами.
Итак, изначально и более правильно то, что большинство понимают под импульсом тела, называть количеством движения. Действительно, математическая формула для рассматриваемой величины пишется в виде:
Здесь m - масса тела, v¯ - его скорость. Как видно из формулы, ни о каком импульсе речь не идет, имеется лишь скорость тела и его масса, то есть количество движения.
Важно отметить, что эта формула не следует из математических доказательств или выражений. Ее возникновение в физике имеет исключительно интуитивный, бытовой характер. Так, любой человек хорошо представляет, что если муха и грузовик будут двигаться с одинаковой скоростью, то грузовик остановить гораздо тяжелее, поскольку он обладает намного большим количеством движения, чем насекомое.
Откуда возникло понятие вектор импульса тела, рассмотрено далее.
Импульс силы - причина изменения количества движения
Интуитивно введенную характеристику Ньютон смог связать со вторым законом, носящим его фамилию.
Импульс силы - это известная физическая величина, которая равна произведению приложенной внешней силы к некоторому телу на время ее действия. Воспользовавшись известным законом Ньютона и полагая, что сила от времени не зависит, можно прийти к выражению:
F¯ * Δt = m * a¯ * Δt.
Здесь Δt - время действия силы F, a - это линейное ускорение, сообщаемое силой F телу массой m. Как известно, умножение ускорения тела на промежуток времени, который оно действует, дает приращение скорости. Этот факт позволяет переписать формулу выше в несколько ином виде:
F¯ * Δt = m * Δv¯, где Δv¯= a¯ * Δt.
Правая часть равенства представляет собой изменение количества движения (см. выражение в предыдущем пункте). Тогда получится:
F¯ * Δt = Δp¯, где Δp¯ = m * Δv¯.
Таким образом, пользуясь законом Ньютона и понятием об импульсе силы, можно прийти к важному выводу: воздействие внешней силы на объект в течение некоторого времени приводит к изменению его количества движения.
Теперь становится понятным, почему количество движения принято называть импульсом, ведь его изменение совпадает с импульсом силы (слово "сила", как правило, опускают).
Векторная величина p¯
Над некоторыми величинами (F¯, v¯, a¯, p¯) стоит черта. Это означает, что речь идет о векторной характеристике. То есть количество движения так же, как и скорость, сила и ускорение, помимо абсолютной величины (модуля), описывается еще направлением.
Так как каждый вектор можно разложить на отдельные компоненты, то, пользуясь декартовой прямоугольной системой координат, можно записать следующие равенства:
1) p¯ = m * v¯;
2) p x = m * v x ; p y = m * v y ; p z = m * v z ;
3) |p¯| = √(p x 2 + p y 2 + p z 2).
Здесь 1-е выражение - это векторная форма представления количества движения, 2-й набор формул позволяет рассчитать каждую из компонентов импульса p¯, зная соответствующие компоненты скорости (индексы x, y, z говорят о проекции вектора на соответствующую ось координат). Наконец, 3-я формула позволяет вычислить длину вектора импульса (абсолютное значение величины) через его компоненты.
Куда направлен вектор импульса тела?
Рассмотрев понятие количества движения p¯ и его основные свойства, можно легко ответить на поставленный вопрос. Вектор импульса тела направлен так же, как и вектор линейной скорости. Действительно, из математики известно, что умножение вектора a¯ на число k приводит к образованию нового вектора b¯, обладающего следующими свойствами:
- его длина равна произведению числа на модуль исходного вектора, то есть |b¯| = k * |a¯|;
- он направлен так же, как исходный вектор, если k > 0, в противном случае он будет направлен противоположно a¯.
В данном случае роль вектора a¯ играет скорость v¯, импульс p¯ - это новый вектор b¯, а число k - это масса тела m. Поскольку последняя всегда является положительной (m>0), то, отвечая на вопрос: чему сонаправлен вектор импульса тела p¯, следует сказать, что он сонаправлен скорости v¯.
Вектор изменения количества движения
Интересно рассмотреть еще один похожий вопрос: куда направлен вектор изменения импульса тела, то есть Δp¯. Для ответа на него стоит использовать полученную выше формулу:
F¯ * Δt = m * Δv¯ = Δp¯.
Исходя из рассуждений в предыдущем пункте, можно сказать, что направление изменения количества движения Δp¯ совпадает с направлением вектора силы F¯ (Δt > 0) или с направлением вектора изменения скорости Δv¯ (m > 0).
Здесь важно не путать, что речь идет именно об изменении величин. В общем случае векторы p¯ и Δp¯ не совпадают, поскольку они никак не связаны друг с другом. Например, если сила F¯ будет действовать против скорости v¯ перемещения объекта, тогда p¯ и Δp¯ будут направлены в противоположные стороны.
Где важно учитывать векторный характер количества движения?
Рассмотренные выше вопросы: куда направлен вектор импульса тела и вектор его изменения, обусловлены не простым любопытством. Дело в том, что закон сохранения импульса p¯ выполняется для каждой его компоненты. То есть в наиболее полной форме он записывается так:
p x = m * v x ; p y = m * v y ; p z = m * v z .
Каждая компонента вектора p¯ сохраняет свое значение в системе взаимодействующих объектов, на которые не действуют внешние силы (Δp¯ = 0).
Как пользоваться этим законом и векторными представлениями величины p¯, чтобы решать задачи на взаимодействие (соударение) тел?
Задача с двумя шарами
На рисунке ниже изображены два шара разной массы, которые летят под разными углами к горизонтальной линии. Пусть массы шаров равны m 1 = 1 кг, m 2 = 0,5 кг, их скорости v 1 = 2 м/с, v 2 = 3 м/с. Необходимо определить направление импульса после удара шаров, полагая последний абсолютно неупругим.
Начиная решать задачу, следует записать закон неизменности количества движения в векторной форме, то есть:
p 1 ¯ + p 2 ¯ = const.
Поскольку каждая компонента импульса должна сохраняться, то нужно переписать это выражение, учитывая также, что после столкновения два шара начнут двигаться, как единый объект (абсолютно неупругий удар):
m 1 * v 1x + m 2 * v 2x = (m 1 + m 2) * u x ;
M 1 * v 1y + m 2 * v 2y = (m 1 + m 2) * u y .
Знак минус для проекции импульса первого тела на ось y появился вследствие ее направленности против выбранного вектора оси ординат (см. рис.).
Теперь нужно выразить неизвестные компоненты скорости u, а затем подставить известные значения в выражения (соответствующие проекции скоростей определяются умножением модулей векторов v 1 ¯ и v 2 ¯ на тригонометрические функции):
u x = (m 1 * v 1x + m 2 * v 2x) / (m 1 + m 2), v 1x = v 1 * cos(45 o); v 2x = v 2 * cos(30 o);
u x = (1 * 2 * 0,7071 + 0,5 * 3 * 0,866) / (1 + 0,5) = 1,8088 м/с;
u y = (-m 1 * v 1y + m 2 * v 2y) / (m 1 + m 2), v 1y = v 1 * sin(45 o); v 2y = v 2 * sin(30 o);
u y = (-1 * 2 * 0,7071 + 0,5 * 3 * 0,5) / (1 + 0,5) = -0,4428 м/с.
Это две компоненты скорости тела после удара и "слипания" шаров. Поскольку направление скорости совпадает с вектором импульса p¯, то ответить на вопрос задачи можно, если определить u¯. Угол его относительно горизонтальной оси будет равен арктангенсу отношения компонент u y и u x:
α = arctg(-0,4428 / 1,8088) = -13,756 o .
Знак минус указывает, что импульс (скорость) после удара будет направлен вниз от оси x.
Если на тело массой m за определенный промежуток времени Δ t действует сила F → , тогда следует изменение скорости тела ∆ v → = v 2 → - v 1 → . Получаем, что за время Δ t тело продолжает движение с ускорением:
a → = ∆ v → ∆ t = v 2 → - v 1 → ∆ t .
Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:
F → = m a → = m v 2 → - v 1 → ∆ t или F → ∆ t = m v 2 → - m v 1 → = m ∆ v → = ∆ m v → .
Определение 1Импульс тела , или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.
Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду (к г м / с) .
Определение 2
Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.
Импульс относят к векторным величинам. Существует еще одна формулировка определения.
Определение 3
Изменение импульса тела равняется импульсу силы.
При обозначении импульса p → второй закон Ньютона записывается как:
F → ∆ t = ∆ p → .
Данный вид позволяет формулировать второй закон Ньютона. Сила F → является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:
F x Δ t = Δ p x ; F y Δ t = Δ p y ; F z Δ t = Δ p z .
Рисунок 1 . 16 . 1 . Модель импульса тела.
Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.
Определение 4
Одномерное движение – это движение тела по одной из координатный осей.
Пример 1
На примере рассмотрим свободное падение тела с начальной скоростью v 0 под действием силы тяжести за промежуток времени t . При направлении оси O Y вертикально вниз импульс силы тяжести F т = mg , действующий за время t , равняется m g t . Такой импульс равняется изменению импульса тела:
F т t = m g t = Δ p = m (v – v 0) , откуда v = v 0 + g t .
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t . Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы F с р из временного промежутка t . Рисунок 1 . 16 . 2 показывает, каким образом определяется импульс силы, которая зависит от времени.
Рисунок 1 . 16 . 2 . Вычисление импульса силы по графику зависимости F (t)
Необходимо выбрать на временной оси интервал Δ t , видно, что сила F (t) практически неизменна. Импульс силы F (t) Δ t за промежуток времени Δ t будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δ t i на промежутке от от 0 до t , сложить импульсы всех действующих сил из этих промежутков Δ t i , тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.
Применив предел (Δ t i → 0) , можно найти площадь, которая будет ограничиваться графиком F (t) и осью t . Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F (t) из интервала [ 0 ; t ] .
Рисунок 1 . 16 . 2 показывает импульс силы, находящийся на интервале от t 1 = 0 с до t 2 = 10 .
Из формулы получим, что F с р (t 2 - t 1) = 1 2 F m a x (t 2 - t 1) = 100 Н · с = 100 к г · м / с.
То есть, из примера видно F с р = 1 2 F m a x = 10 Н.
Имеются случаи, когда определение средней силы F с р возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0 , 415 к г можно сообщить скорость, равную v = 30 м / с. Приблизительным временем удара является значение 8 · 10 – 3 с.
Тогда формула импульса приобретает вид:
p = m v = 12 , 5 к г · м / с.
Чтобы определить среднюю силу F с р во время удара, необходимо F с р = p ∆ t = 1 , 56 · 10 3 Н.
Получили очень большое значение, которое равняется телу массой 160 к г.
Когда движение происходит по криволинейной траектории, то начальное значение p 1 → и конечное
p 2 → могут быть различны по модулю и по направлению. Для определения импульса ∆ p → применяют диаграмму импульсов, где имеются векторы p 1 → и p 2 → , а ∆ p → = p 2 → - p 1 → построен по правилу параллелограмма.
Пример 2
Для примера приводится рисунок 1 . 16 . 2 , где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v 1 → налетает на поверхность под углом α к нормали и отскакивает со скоростью v 2 → с углом β . При ударе в стену мяч подвергался действию силы F → , направленной также, как и вектор ∆ p → .
Рисунок 1 . 16 . 3 . Отскакивание мяча от шероховатой стенки и диаграмма импульсов.
Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v 1 → = v → , тогда при отскоке она изменится на v 2 → = - v → . Значит, за определенный промежуток времени импульс изменится и будет равен ∆ p → = - 2 m v → . Используя проекции на О Х, результат запишется как Δ p x = – 2 m v x . Из рисунка 1 . 16 . 3 видно, что ось О Х направлена от стенки, тогда следует v x < 0 и Δ p x > 0 . Из формулы получим, что модуль Δ p связан с модулем скорости, который принимает вид Δ p = 2 m v .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Произведение массы тела на его скорость называют импульсом или мерой движения тела. Он относится к векторным величинам. Его направление сонаправлено вектору скорости тела.
Вспомним второй закон механики:
Для ускорения верно соотношение:
,
Где v0 и v - скорости тела в начале и конце некоторого временного отрезка Δt.
Перепишем второй закон следующим образом:
Векторные суммы импульсов двух тел до и после удара равны между собой.
Полезной аналогией для понимания закона сохранения импульса является денежная сделка между двумя людьми. Предположим, что у двух людей до сделки была определённая сумма. У Ивана было 1000 рублей и Петр тоже обладал 1000 рублей. Общая сумма в их карманах составляет 2000 рублей. Во время сделки Иван платит Петру 500 рублей, осуществляется передача денег. У Петра в кармане теперь 1500 руб., а у Ивана - 500. Но общая сумма в их карманах не изменилась и также составляет 2000 рублей.
Полученное выражение справедливо для любого количества тел, принадлежащих изолированной системе, и является математической формулировкой закона сохранения импульса.
Суммарный импульс N-ного количества тел, образующих изолированную систему, не меняется с течением времени.
Когда система тел подвергается воздействию нескомпенсированных внешних сил (система незамкнутая), то суммарный импульс тел этой системы изменяется с течением времени. Но справедливым остаётся закон сохранения для суммы проекций импульсов этих тел на любое направление, перпендикулярное направлению результирующей внешней силы.
Движение ракеты
Движение, которое возникает при отделении от тела его части определённой массы с некоторой скоростью, называют реактивным.
Примером реактивного движения может служить движение ракеты, находящейся на значительном удалении от Солнца и планет. В этом случае ракета не испытывает гравитационного воздействия и может считаться изолированной системой.
Ракета состоит из оболочки и топлива. Они и являются взаимодействующими телами изолированной системы. В начальный момент времени скорость ракеты равна нулю. В этот момент равен нулю и импульс системы, и оболочки, и топлива. Если включить двигатель, то топливо ракеты сгорает и превращается в высокотемпературный газ, покидающий двигатель под высоким давлением и с большой скоростью.
Обозначим массу образующегося газа mг. Будем считать, что он вылетает из сопла ракеты моментально со скоростью vг. Массу и скорость оболочки обозначим соответственно mоб и vоб.
Закон сохранения импульса даёт право записать соотношение:
Знак «минус» указывает на то, что скорость оболочки направлена в противоположную сторону от выбрасываемого газа.
Скорость оболочки пропорциональна скорости выброса газа и массе газа. И обратно пропорциональна массе оболочки.
Принцип реактивного движения позволяет рассчитывать перемещение ракет, самолётов и других тел в условиях, когда на них действуют внешние сила тяжести или сила сопротивления атмосферы. Конечно, в этом случае уравнение даёт завышенное значение скорости оболочки vоб. В реальных условиях и газ вытекает из ракеты не мгновенно, что влияет на итоговое значение vоб.
Действующие формулы, описывающее движение тела с реактивным двигателем получены русскими учёными И.В. Мещерским и К.Э. Циолковским.
