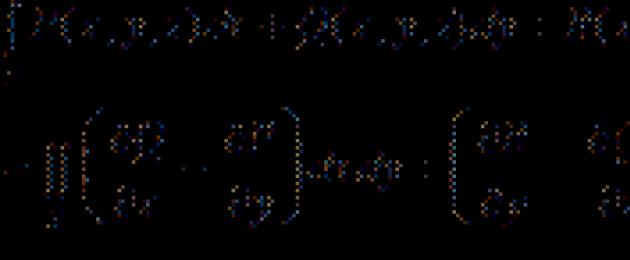Эти формулы связывают интеграл по фигуре с некоторым интегралом по границе данной фигуры.

Пусть функции непрерывны в области D ÌOxy и на ее границе Г ; область D – связная; Г – кусочно-гладкая кривая. Тогда верна формула Грина :

здесь слева стоит криволинейный интеграл I рода, справа – двойной интеграл; контур Г обходится против часовой стрелки.

Пусть Т – кусочно-гладкая ограниченная двусторонняя поверхность с кусочно-гладкой границей Г . Если функции P (x ,y ,z ), Q (x ,y ,z ), R (x ,y ,z ) и их частные производные I порядка непрерывны в точках поверхности Т и границы Г , то имеет место формула Стокса :

(2.23)

слева стоит криволинейный интеграл II рода; справа – поверхностный интеграл II рода, взятый по той стороне поверхности Т , которая остается слева при обходе кривой Г .

Если связная область W ÌOxyz ограничена кусочно-гладкой, замкнутой поверхностью Т , а функции P (x ,y ,z ), Q (x ,y ,z ), R (x ,y ,z ) и их частные производные первого порядка непрерывны в точках из W и Т , то имеет место формула Остроградского-Гаусса :

(2.24)

слева – поверхностный интеграл II рода по внешней стороне поверхности Т ; справа – тройной интеграл по области W .

Пример 1. Вычислить работу силы при обходе точки ее приложения окружности Г : , начиная от оси Ox , по часовой стрелке (рис. 2.18).

Решение. Работа равна . Применим формулу Грина (2.22), ставя знак “-” справа перед интегралом (так как обход контура – по часовой стрелке) и учитывая, что P (x ,y )=x -y , Q (x ,y )=x +y . Имеем:
,
где S D – площадь круга D : , равная . В итоге: – искомая работа силы.

Пример 2. Вычислить интеграл , если Г есть окружность в плоскости z =2, обходимая против часовой стрелки.

Решение. По формуле Стокса (2.23) исходный интеграл сведем к поверхностному интегралу по кругу Т :
T :

Итак, учитывая, что , имеем:

Последний интеграл есть двойной интеграл по кругу D ÌOxy , на который проектировался круг Т ; D : . Перейдем к полярным координатам: x =r cosj, y =r sinj, jÎ, r Î. В итоге:
.

Пример 3. Найти поток П Т пирамиды W : (рис. 2.19) в направлении внешней нормали к поверхности.

Решение. Поток равен . Применяя формулу Остроградского-Гаусса (2.24), сводим задачу к вычислению тройного интеграла по фигуре W -пирамиде:

Пример 4. Найти поток П векторного поля через полную поверхность T пирамиды W : ; (рис. 2.20), в направлении внешней нормали к поверхности.

Решение. Применим формулу Остроградского-Гаусса (2.24) , где V – объем пирамиды. Сравним с решением непосредственного вычисления потока ( – грани пирамиды).

,
так как проекция граней на плоскость Oxy имеет нулевую площадь (рис. 2.21),

Формула Остроградского - Грина

Эта формула устанавливает связь между криволинейным интегралом по замкнутому контуры С и двойным интегралом по области, ограниченной этим контуром.

Определение 1. Область D называется простой областью, если её можно разбить на канечное число областей первого типа и независимо от этого на конечное число областей второго типа.

Теорема 1. Пусть в простой области определены функции P(x,y) и Q(x,y) непрерывные вместе со своими частными производными и

Тогда имеет место формула

где С - замкнутый контур области D.

Это формула Остроградского - Грина.

Условия независимости криволинейного интеграла от пути интегрирования

Определение 1. Говорят, что замкнутая квадрируемая область D односвязна, если любую замкнутую кривую l D можно непрерывно диформировать в точку так, что все точки этой кривой принадлежали бы области D (область без “дырок” - D 1), если такое деформирование невозможно, то область назывется многосвязной (с “дырками” - D 2).

Определение 2. Если значение криволинейного интеграла по кривой АВ не зависит от вида кривой, соединяющей точки А и В, то говорят, что этот криволинейный интеграл не зависит от пути интегрирования:

Теорема 1. Пусть в замкнутой односвязной области D определены непрерывные, вместе со своими частными производными функции P(x,y) и Q(x,y). Тогда следующие 4 условия равносильны (эквивалентны):

1) криволинейный интеграл по замкнутому контуру

где С - любой замкнутый контур в D;

2) криволинейный интеграл по замкнутому контуру не зависит от пути интегрирования в области D, т.е.

3) дифференциальная форма P(x,y)dx + Q(x,y)dy является полным дифференциалом некоторой функции F в области D, т.е., что существует функция F такая, что (х,у) D имеет место равенство

dF(x,y) = P(x,y)dx + Q(x,y)dy; (3)

4) для всех точек (х,у) D будет выполняться следующее условие:

Докажем по схеме.

Докажем, что из.

Пусть дано 1), т.е. = 0 по свойству 2 §1, что = 0 (по свойству 1 §1) .

Докажем, что из.

Дано, что кр.инт. не зависит от пути интегрирования, а только от выбора начала и канца пути

Рассмотрим функцию

Пакажем, что дифференциальная форма P(x,y)dx + Q(x,y)dy является полным дифференциалом функции F(x,y), т.е. , что

Зададим частный прирост

х F (x,y)= F(х + х, у) -F (x,y)= = == =

(по свойству 3 § 1, ВВ* Оу) = = P (c,y)х (по теореме о среднем, с -const), где x

(всилу непрерывности функции Р). Получили формулу (5). Аналогично получается формула (6).

Докажем, что из.

Дана формула

dF(x,y) = P(x,y)dx + Q(x,y)dy.

Очевидно, что = Р(х,у). Тогда

По условию теоремы правые части равенств (7) и (8) непрерывные функции, то по теореме о равенстве смешанных производных будут равны и левые части, т.е.., что

Докажем, что из 41.

Выберем любой замкнутый контур из области D, который ограничивает область D 1 .

Функции P и Q удовлетворяют условиям Остроградского-Грина:

В силу равенства (4) в левой части (9) интеграл равен 0, а это значит, что и правая часть равенства равна

Замечание 1. Теорема 1. может быть сформулировано в виде трёх самостоятельных теорем

Теорема 1*. Для того, чтобы в односвязной квадрируемой области D крив.инт. не зависил от пути интегрирования чтобы выполнялось условие (.1), т.е.

Теорема 2*. Для того, чтобы в односвязной квадрируемой области D крив.инт. не зависил от пути интегрирования чтобы выполнялось условие (3):

дифференциальная форма P(x,y)dx + Q(x,y)dy является полным дифференциалом некоторой функции F в области D.

Теорема 3*. Для того, чтобы в односвязной квадрируемой области D крив.инт. не зависил от пути интегрирования чтобы выполнялось условие (4):

Замечание 2. В теореме2* область D может быть и многосвязной.

Связь между двойным интегралом по области D и криволинейным интегралом по границе L этой области устанавливает формула Остроградского – Грина, которая широко применяется в математическом анализе.

Пусть на плоскости Оху задана область D , ограниченная кривой, пересекающейся с прямыми, параллельными координатными осями не более чем в двух точках, т.е. область D – правильная.

Теорема 10.2. Если функции P (x ; y ) и Q (x ; y ) непрерывны вместе со своими частными производными ив областиD , то имеет место формула

(10.8)

где L – граница области D и интегрирование вдоль кривой L производится в положительном направлении (т.е. при движении вдоль кривой, область D остается слева).

Формула (10.8) называется формулой Остроградского – Грина.

Пусть
- уравнение дугиAnB , а
- уравнение дугиAmB (см. рис. 8). Найдем сначала
.По правилу вычисления двойного интеграла, имеем:

Или согласно формуле (10.6), Рис. 8.

Аналогично доказывается, что
(10.10)

Если из равенства (10.10) вычесть равенство (10.9), то получим формулу (10.8).

Замечание. Формула (10.8) справедлива и для произвольной области, которую можно разбить на конечное число правильных областей.

Пример 10.3. С помощью формулы Остроградского – Грина вычислить

где L – контур прямоугольника с вершинами А (3;2 ), В (6;2 ), С (6;4 ), D (3;4 ).

○ Решение: На рисунке 9 изображен контур интегрирования. Поскольку

по формуле (10.8) имеем:

10.4. Условия независимости криволинейного интеграла II рода от пути интегрирования

П
устьA (x 1 ; y 1) и B (x 2 ; y 2) – две произвольные точки односвязной области D плоскости Оху (плоскость D называется односвязной , если для любого замкнутого контура, лежащего в этой области, ограниченная им часть плоскости целиком принадлежит D (область без «дыр»)). Точки А и В можно соединить различными линиями (на рис. 10 это L 1 , L 2 и L 3). По каждой из этих кривых интеграл
имеет, вообще говоря, свое значение.

Если же его значения по всевозможным кривым AB одинаковы, то говорят, что интеграл I не зависит от вида пути интегрирования.

Рис. 10. В этом случае для интеграла I достаточно отметить лишь его начальную точку A (x 1 ; y 1 ) и его конечную точку B (x 2 ; y 2 ) пути. Записывают:

(10.11)

Каковы же условия, при которых криволинейный интеграл II рода не зависел от вида пути интегрирования?

Теорема 10.3. Для того, что бы криволинейный интеграл
не зависел от пути интегрирования в односвязной областиD , в которой функции P (x ; y ), Q (x ; y ) непрерывны вместе со своими частными производными, необходимо и достаточно, что бы в каждой точке этой области выполнялось условие=(10.12)

Докажем достаточность условия (10.12). Рассмотрим произвольный замкнутый круг AmBnA (или L ) в области D (см. рис. 11). Для него имеет место формула Остроградского – Грина (10.8) В силу условия (10.12) имеем:
, или
. Учитывая свойства криволинейного интеграла, имеем:

, т.е.

Полученное равенство означает, что криволинейный интеграл не зависит о пути интегрирования.

Рис.11. В ходе доказательства теоремы получено, что если выполняется условие =, то интеграл по замкнутому кругу равен нулю:

Верно и обратное утверждение.

Следствие 10.1. Если выполняется условие (10.12), то подынтегральное выражение является полным дифференциалом некоторой функцииu = u (x ; y ), т.е.

Тогда (см. (10.11))

Формула (10.14) называется обобщенной формулой Ньютона – Лейбница для криволинейного интеграла от полного дифференциала.

Следствие 10.2. Если подынтегральное выражение Pdx + Qdy есть полный дифференциал и путь интегрирования L замкнутый, то
.

Замечания:

В качестве начальной точки (x 0 ; y 0) обычно берут точку (0;0) – начало координат (см. пример 10.5).

= ,=,=;

Пример 10.4. Найти

Решение: Здесь P = y , Q = x , == 1. Согласно вышеприведенной теореме, интеграл не зависит от пути интегрирования. В качестве пути интегрирования можно взять отрезок прямой y = x , дугу параболы y = x 2 и т. д. или воспользоваться формулой (10.14). Так как ydx + xdy = d(xy) , то

Пример 10.5. Убедиться, что выражение представляет собой полный дифференциал функцииU (x ; y ) и найти ее.

Решение: Для того чтобы указанное выражение являлось полным дифференциалом, необходимо выполнение условий (10.12):

Условия выполнены, следовательно, А так как полный дифференциал имеет вид

,

то верны соотношения

(10.16)

Интегрируем по х первое из уравнений, считая у постоянным, при этом вместо постоянно интегрирования следует поставить
- неизвестную функцию зависящую только оту :

Подставляя полученное выражение во второе уравнение (10.16), найдем
:

Таким образом,

Отметим, что функцию U проще найти, используя формулу (10.15).

(Остроградский Михаил Васильевич (1861-1862) – русский математик,

академик Петерб. А. Н.)

(Джордж Грин (1793 – 1841) – английский математик)

Иногда эту формулу называют формулой Грина, однако, Дж. Грин предложил в 1828 году только частный случай формулы.

Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т. е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.

Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:

Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования, получим формулу для контура произвольной формы:

Эта формула называется Формулой Остроградского – Грина .

Формула Остроградского – Грина справедлива и в случае многосвязной области, т. е. области, внутри которой есть исключенные участки. В этом случае правая часть формулы будет представлять собой сумму интегралов по внешнему контуру области и интегралов по контурам всех исключенных участков, причем каждый из этих контуров интегрируется в таком направлении, чтобы область D все время оставалась по левую сторону линии обхода.

Пример. Решим пример, рассмотренный выше, воспользовавшись формулой Остроградского – Грина.

Формула Остроградского – Грина позволяет значительно упростить вычисление криволинейного интеграла.

Криволинейный интеграл не зависит от формы пути, если он вдоль всех путей, соединяющих начальную и конечную точку, имеет одну и ту же величину.

Условием независимости криволинейного интеграла от формы пути равносильно равенству нулю этого интеграла по любому замкнутому контуру, содержащему начальную и конечную точки.

Пусть π - плоскость в , - единичный вектор нормали к π, D - односвязная область на π (т.е. кусочно гладкая замкнутая без самопересечений кривая, располо­женная в D, ограничивает область, все точки которой также D ). Пусть D удовлетворяет условиям:

1) граница С области D является замкнутой кусочно гладкой кривой без особых точек;

2) на π можно выбрать такую декартову прямо­угольную систему координат, что все прямые, параллельные ко­ординатным осям, пересекают D не более чем в 2 точках.

Пусть t - С, согласованный с , т. е. положительное направление обхода кривой С t с направле­нием t С

Т1 (формула Грина). Пусть а - 1), 2), направлению непре­рывна в . Тогда справедлива формула

Справа - циркуляция век­торного поля по кривой С , слева - по­ток векторного поля через D.

Док-во. Все входящие в (1) функции непрерывны => оба интеграла . Интегралы слева и справа в (1) инвариантны относительно выбора прямоугольной системы координат, т.к. и инвариантны, элементы площади и длины дуги не зависят от выбора де­картовой системы координат => достаточно доказать (1) в какой-то одной специально выбранной системе.

Выберем декартову прямоугольную систему координат Охуz так, чтобы выполнялось условие 2), и Оz направим вдоль . Т.к векторное поле плос­кое, то =>

Для плоской области и , где l - длина дуги С , выбранная в качестве параметра, возрастание которого согласовано с направлением обхода С =>

Для доказательства формулы Грина достаточно доказать 2 равенства:

Пусть прямая, парал­лельная оси Оу, пересекает С в точках . Пусть - наименьшая и наибольшая абс­циссы точек области , кривая С 1 соединяет с , а кривая С 2 - с и , ориентированы согласованно с C => по формуле сведения двой­ного интеграла к повторному:

Аналогично вычисляется интеграл J .

З1 . Из док-ва => формулу (1) можно записать в виде (1"):

Ох"у"; а имеет координаты Р" и Q ", то

Якобиан преобразования при переходе к новой систе­ме координат по модулю = 1, параметризация с по­мощью длины дуги не связана с системой координат =>

Пусть D - односвязная область в (т. е. для кусочно гладкой замкнутой кривой C , расположенной в D, можно указать ориентируемую кусочно гладкую поверхность G , расположенную в D, имеющую границей С ), поверхность S - ее граница, удовлетворяющая условиям:

1) S - кусочно гладкая двусторонняя полная ограниченная замкнутая и без особых точек;

2) прямоугольную декартову систему координат в можно выбрать так, что для каждой из осей координат прямая, параллельная этой оси, будет пересекать S не более чем в 2 точках.

Пусть n - единичный вектор внешней нормали к S .

Т2 (формула Остроградского - Гаусса ). Пусть а - векторное поле, дифф-мое в D, удовлетво­ряющей условиям 1), 2), и такое, что производная по на­правлению непрерывна в . Тогда

Cправа - поток векторного поля через поверхность S , слева - это объемный интеграл от дивергенции вектора по области D => Объемный интеграл от дивергенции вектора по области D ра­вен потоку векторного поля через поверхность S - границу этой области.

Док-во Все входящие в (2) функции непрерывны => оба интеграла . Формула (2) инвариантна относительно выбо­ра прямоугольной системы координат, т.к. все входящие в нее величины - инварианты => достаточно доказать (2) при каком-то 1 выборе декартовой системы. Выберем декартову прямоугольную систему координат Охуz так,чтобы выполнялось условие 2) ; пусть => учитывая :

Надо док-ть:

Докажем для L, другие ан-но. Пусть D"- проекция D на плоскость Оху. Через граничные точки D" проведем пря­мые, параллельные Оz. Каждая из них пересекается с S лишь в 1 точке. Множество этих точек разделяет S на 2 части: . Ес­ли провести прямую из внут­ренней точки D" , парал­лельную Оz, то она пересечет S в 2 точках: и . и кусочно и непрерывно дифф-мые функции в D". По формуле све­дения тройного интеграла к повторному интегралу:

Воспользовались тем, что , и соотношением

справедливым, т.к. внешняя нормаль к образует тупой угол с Оz (=> ).

З2 . Из док-ва => формулу (2) мо­жно записать:

Док-во ан-но З1.

Формула Стокса.

Пусть S односвязная (т.е. кусочно гладкая замкнутая без самопересечений кривая, располо­женная на S, ограничивает мн-о, все точки которого S ) поверхность в , удовлетворяющая условиям:

1) S - кусочно гладкая двусторонняя полная ограниченная поверхность без особых точек; ее границей является замкнутый кусочно гладкий контур С ;

2) декартову систему координат можно выбрать так, чтобы S однозначно проектировалась на из 3 координатных плоскостей.

Пусть n - единичный вектор нормали к S , t - единичный век­тор касательной к C , согласованный с n, т. е. положительное направление обхода кривой С совпадает в точке приложения вектора t с направле­нием t , и если смотреть с конца , то кон­тур С ориентирован положительно (его обход против часовой стрелки).

Т (формула Стокса). Пусть а - векторное поле, непрерывно дифф-мое в некоторой окрестности поверх­ности S (т. е. на некотором открытом мн-ве в , содержа­щем S). Тогда

Или: Поток вектора через поверхность S равен циркуляции вектора а по замкнутому контуру С.

Док-во . В силу условий теоремы интегралы в (1) существуют. Формула (1) инвари­антна относительно выбора базиса => достаточно доказать при каком-то одном выборе базиса. Выберем пря­моугольную декартову систему координат Охуz так, чтобы S од­нозначно проектировалась на все три координатные плоскости. Пусть

Согласуем выбор системы координат так, чтобы вектор нор­мали образовывал острые углы с координатными осями. Учитывая выражение для в декартовой системе координат

Достаточно доказать:

S - кусочно гладкая и однозначно проектируется на Оху. Пусть D - ее проекция, Г - проекция С на плоскость Оху => дифф-мая ф-я , ко­торая задает уравнение поверх­ности S . При этом

и поверхностный интеграл по S = двойному интегралу по D . По формуле Грина* :

З1 . δ > 0 такое, что для части Ф S размера < δ (ее можно расположить в сфере радиуса δ/2) можно так выбрать декартову координатную систему, что Ф однозначно проекти­руется на все координатные плоскости. Пусть - фиксированная точка S . Проведем касательную плоскость через ,пусть - вектор единичной нормали поверхно­сти в . Выберем прямоугольную систему координат, чтобы составлял острые углы с осями. Т.к. поле нормалей непрерывно, то окрестность такая, что все нормали в точках этой окрестности обра­зуют острые углы с осями => некоторая окрестность радиуса δ/2 точки , которая однозначно проектируется на все координатные плоскости.

Можно выбрать универсаль­ное, не зависящее от число δ > 0. Пусть такого δ => для каждого можно указать часть поверхности S , размеры которой < и которая не проектируется однозначно на все координатные плоскости декартовой системы коор­динат.

Выберем в каждой точку , из полученной после­д-сти выберем послед-сть, сходящуюся к неко­торой М S . У М окрестность, однозначно проектируемая на координатные плоскости некоторой прямоугольной системы. Эта окрестность для некоторого номера п содержит часть , которая также будет однозначно проектироваться на все три координатные плоскости => противоречие с вы­бором .

Разобьем S на конечное число гладких частей , размер каждой из которых < δ, указанного выше. однозначно проектируется на все координатные плос­кости некоторой декартовой системы координат => формула Стокса верна для каждой . Просуммируем левые и пра­вые части этих формул. Интегралы по общим участкам границы берутся в противоположных направлениях и поэтому сокра­тятся => слева получим интеграл по поверхности от , а справа - интеграл по границе С от , т. е. формулу Стокса для общего случая => формулы Стокса справедлива для поверхностей, удовлетворяющих условию 1) и не удовлетворяющих, вообще говоря, условию 2).

З 2 . Формула Стокса верна для поверхностей S , допускающих разбиение с помощью кусочно гладких кривых на конечное число односвязных, обладающих свойством 1) по­верхностей. Док-во: просуммировать интегралы слева и справа в формулах Стокса для односвязных поверхностей и учесть, что интегралы по кри­вым, входящим в разбиение, берутся в разных направлениях и поэтому сократятся.

З3 . Из док-ва => формулу (1) мо­жно записать в виде (1"):

Интегралы слева и справа в (1") инвариантны, т.к. значения подынтеграль­ных выражений равны соответ­ственно и - инвариантным величинам. Форма подынтегральных выражений в формуле (1") тоже не меняется при переходе к новой системе Ох"у" z"; если в новом базисе векторное поле а имеет координаты Р" , Q " и R" , то

Якобиан преобразования при переходе к новой систе­ме координат по модулю = 1, параметризация с по­мощью длины дуги не связана с системой координат => интегралы слева и справа в (1") не меняют своего значения и формы.

*: π - плоскость в , - единичный вектор нормали к π, D - односвязная область на π. Пусть D удовлетворяет условиям: 1) граница С области D является замкнутой кусочно гладкой кривой без особых точек; 2) на π можно выбрать такую декартову прямо­угольную систему координат, что все прямые, параллельные ко­ординатным осям, пересекают D не более чем в 2 точках.

Пусть t - единичный вектор касательной к кривой С, согласованный с .

Т1 (формула Грина). Пусть а - векторное поле, дифф-мое в D, удовлетворяющей условиям 1), 2), и такое, что его производная по направлению непре­рывна в . Тогда справедлива формула