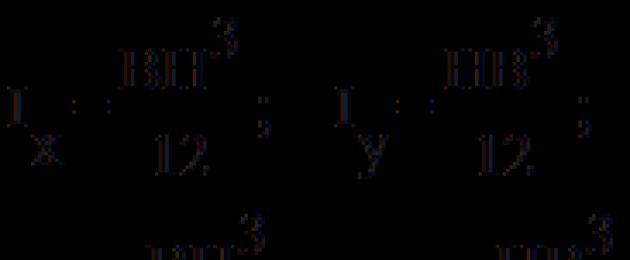Η θέση του κέντρου βάρους του ημικυκλίου. Μέθοδοι προσδιορισμού των συντεταγμένων του κέντρου βάρους

Το αποτέλεσμα των υπολογισμών εξαρτάται όχι μόνο από το εμβαδόν διατομής, επομένως, κατά την επίλυση προβλημάτων σχετικά με την αντοχή των υλικών, δεν μπορεί κανείς να κάνει χωρίς να προσδιορίσει γεωμετρικά χαρακτηριστικά των σχημάτων: στατικές, αξονικές, πολικές και φυγόκεντρες ροπές αδράνειας. Είναι επιτακτική ανάγκη να μπορείτε να προσδιορίσετε τη θέση του κέντρου βάρους της τομής (τα αναγραφόμενα γεωμετρικά χαρακτηριστικά εξαρτώνται από τη θέση του κέντρου βάρους). Επιπρόσθετα γεωμετρικά χαρακτηριστικά απλών σχημάτων: ορθογώνιο, τετράγωνο, ισοσκελές και ορθογώνια τρίγωνα, κύκλος, ημικύκλιο. Υποδεικνύεται το κέντρο βάρους και η θέση των κύριων κεντρικών αξόνων και προσδιορίζονται τα σχετικά γεωμετρικά χαρακτηριστικά, υπό την προϋπόθεση ότι το υλικό της δοκού είναι ομοιογενές.

Γεωμετρικά χαρακτηριστικά ορθογωνίου και τετραγώνου

Αξονικές ροπές αδράνειας ορθογωνίου (τετράγωνο)

Γεωμετρικά χαρακτηριστικά ορθογωνίου τριγώνου

Αξονικές ροπές αδράνειας ορθογωνίου τριγώνου

Γεωμετρικά χαρακτηριστικά ισοσκελούς τριγώνου

Αξονικές ροπές αδράνειας ισοσκελούς τριγώνου

Το κέντρο βάρους είναι το σημείο από το οποίο διέρχεται η γραμμή δράσης του προκύπτοντος των στοιχειωδών δυνάμεων βάρους. Έχει την ιδιότητα κέντρου παράλληλων δυνάμεων (Ε.Μ. Νικήτιν, § 42). Να γιατί τύποι για τον προσδιορισμό της θέσης του κέντρου βάρους διαφόρων σωμάτωνέχουν τη μορφή:
x c = (∑ G i x i) / ∑ G i ;
(1) y c = (∑ G i y i) / ∑ G i ;
z c = (∑ G i z i) / ∑ G i .

Εάν το σώμα του οποίου το κέντρο βάρους πρέπει να προσδιοριστεί μπορεί να ταυτιστεί με ένα σχήμα που αποτελείται από γραμμές (για παράδειγμα, ένα κλειστό ή ανοιχτό περίγραμμα από σύρμα, όπως στο Σχ. 173), τότε το βάρος G i κάθε τμήματος l i μπορεί να αναπαρασταθεί ως το προϊόν
G i = l i d,
όπου d είναι το σταθερό βάρος μιας μονάδας μήκους υλικού για ολόκληρο το σχήμα.

Αφού αντικατασταθούν οι τιμές l i d σε τύπους (1) αντί για G i, ο σταθερός παράγοντας d σε κάθε όρο του αριθμητή και του παρονομαστή μπορεί να αφαιρεθεί από αγκύλες (πέρα από το πρόσημο του αθροίσματος) και να μειωθεί. Ετσι, τύποι για τον προσδιορισμό των συντεταγμένων του κέντρου βάρους ενός σχήματος που αποτελείται από ευθύγραμμα τμήματα, θα λάβει τη μορφή:
x c = (∑ l i x i) / ∑ l i ;
(2) y c = (∑ l i y i) / ∑ l i ;
z c = (∑ l i z i) / ∑ l i .

Εάν το σώμα έχει τη μορφή σχήματος που αποτελείται από επίπεδα ή καμπύλες επιφάνειες διατεταγμένες με διάφορους τρόπους (Εικ. 174), τότε το βάρος κάθε επιπέδου (επιφάνειας) μπορεί να αναπαρασταθεί ως εξής:
G i = F i p,
όπου F i είναι το εμβαδόν κάθε επιφάνειας και p είναι το βάρος ανά μονάδα επιφάνειας του σχήματος.

Αφού αντικαταστήσουμε αυτή την τιμή του G i στους τύπους (1), λαμβάνουμε τύποι για τις συντεταγμένες του κέντρου βάρους ενός σχήματος που αποτελείται από περιοχές:
x c = (∑ F i x i) / ∑ F i ;
(3) y c = (∑ F i y i) / ∑ F i ;
z c = (∑ F i z i) / ∑ F i .

Εάν ένα ομοιογενές σώμα μπορεί να χωριστεί σε απλά μέρη ενός συγκεκριμένου γεωμετρικού σχήματος (Εικ. 175), τότε το βάρος κάθε μέρους
G i = V i γ,
όπου V i είναι ο όγκος κάθε μέρους και γ είναι το βάρος ανά μονάδα όγκου του σώματος.

Αφού αντικαταστήσουμε τις τιμές του G i στους τύπους (1), λαμβάνουμε τύποι για τον προσδιορισμό των συντεταγμένων του κέντρου βάρους ενός σώματος που αποτελείται από ομοιογενείς όγκους:
x c = (∑ V i x i) / ∑ V i ;
(4) y c = (∑ V i y i) / ∑ V i ;
z c = (∑ V i z i) / ∑ V i .

Κατά την επίλυση ορισμένων προβλημάτων προσδιορισμού της θέσης του κέντρου βάρους των σωμάτων, μερικές φορές είναι απαραίτητο να γνωρίζουμε πού βρίσκεται το κέντρο βάρους ενός τόξου ενός κύκλου, ενός κυκλικού τομέα ή ενός τριγώνου.

Εάν η ακτίνα του τόξου r και η κεντρική γωνία 2α που υποβάλλεται από το τόξο και εκφράζεται σε ακτίνια είναι γνωστές, τότε η θέση του κέντρου βάρους C (Εικ. 176, α) σε σχέση με το κέντρο του τόξου Ο προσδιορίζεται από ο τύπος:
(5) x c = (r sin α)/α.

Εάν δίνεται η χορδή AB=b του τόξου, τότε στον τύπο (5) μπορείτε να κάνετε την αντικατάσταση
sin α = b/(2r)
και μετά
(5a) x c = b/(2α).

Στη συγκεκριμένη περίπτωση για ένα ημικύκλιο, και οι δύο τύποι θα έχουν τη μορφή (Εικ. 176, β):
(5β) x c = OC = 2r/π = d/π.

Η θέση του κέντρου βάρους ενός κυκλικού τομέα, εάν δίνεται η ακτίνα του r (Εικ. 176, γ), προσδιορίζεται χρησιμοποιώντας τον τύπο:
(6) x c = (2r sin α)/(3α).

Εάν δοθεί η χορδή τομέα, τότε:
(6a) x c = b/(3α).

Στην ειδική περίπτωση για ένα ημικύκλιο, και οι δύο τελευταίοι τύποι θα έχουν τη μορφή (Εικ. 176, δ)
(6b) x c = OC = 4r/(3π) = 2d/(3π).

Το κέντρο βάρους της περιοχής οποιουδήποτε τριγώνου βρίσκεται από οποιαδήποτε πλευρά σε απόσταση ίση με το ένα τρίτο του αντίστοιχου ύψους.

Σε ένα ορθογώνιο τρίγωνο, το κέντρο βάρους βρίσκεται στη διασταύρωση των κάθετων που ανυψώνονται στα σκέλη από σημεία που βρίσκονται σε απόσταση του ενός τρίτου του μήκους των σκελών, μετρώντας από την κορυφή της ορθής γωνίας (Εικ. 177).

Κατά την επίλυση προβλημάτων προσδιορισμού της θέσης του κέντρου βάρους οποιουδήποτε ομοιογενούς σώματος, που αποτελείται είτε από λεπτές ράβδους (γραμμές), είτε από πλάκες (περιοχές) ή από όγκους, συνιστάται να τηρείτε την ακόλουθη σειρά:

1) σχεδιάστε ένα σώμα, η θέση του κέντρου βάρους του οποίου πρέπει να προσδιοριστεί. Δεδομένου ότι όλες οι διαστάσεις του σώματος είναι συνήθως γνωστές, πρέπει να τηρείται η κλίμακα.

2) σπάστε το σώμα σε συστατικά μέρη (τμήματα γραμμής ή περιοχές ή όγκοι), η θέση των κέντρων βάρους καθορίζεται με βάση το μέγεθος του σώματος.

3) προσδιορίστε είτε τα μήκη, είτε τις επιφάνειες ή τους όγκους των εξαρτημάτων.

4) επιλέξτε τη θέση των αξόνων συντεταγμένων.

5) προσδιορίστε τις συντεταγμένες των κέντρων βάρους των συστατικών.

6) αντικαταστήστε τις ευρεθείσες τιμές μηκών ή εμβαδών ή όγκων μεμονωμένων μερών, καθώς και τις συντεταγμένες των κέντρων βάρους τους, στους κατάλληλους τύπους και υπολογίστε τις συντεταγμένες του κέντρου βάρους ολόκληρου του σώματος.

7) χρησιμοποιώντας τις συντεταγμένες που βρέθηκαν, υποδείξτε στο σχήμα τη θέση του κέντρου βάρους του σώματος.

§ 23. Προσδιορισμός της θέσης του κέντρου βάρους σώματος που αποτελείται από λεπτές ομοιογενείς ράβδους

§ 24. Προσδιορισμός της θέσης του κέντρου βάρους μορφών που αποτελούνται από πλάκες

Στο τελευταίο πρόβλημα, καθώς και στα προβλήματα που αναφέρονται στην προηγούμενη παράγραφο, η διαίρεση των σχημάτων στα συστατικά μέρη τους δεν προκαλεί ιδιαίτερες δυσκολίες. Αλλά μερικές φορές το σχήμα έχει μια μορφή που του επιτρέπει να χωριστεί στα συστατικά μέρη του με διάφορους τρόπους, για παράδειγμα, μια λεπτή ορθογώνια πλάκα με τριγωνική εγκοπή (Εικ. 183). Κατά τον προσδιορισμό της θέσης του κέντρου βάρους μιας τέτοιας πλάκας, η περιοχή της μπορεί να χωριστεί σε τέσσερα ορθογώνια (1, 2, 3 και 4) και ένα ορθογώνιο τρίγωνο 5 - με διάφορους τρόπους. Δύο επιλογές φαίνονται στο Σχ. 183, α και β.

Ο πιο ορθολογικός τρόπος διαίρεσης ενός σχήματος στα συστατικά μέρη του είναι αυτός που παράγει τον μικρότερο αριθμό μερών. Εάν υπάρχουν εγκοπές στο σχήμα, τότε μπορούν επίσης να συμπεριληφθούν στα συστατικά μέρη του σχήματος, αλλά η περιοχή του αποκομμένου τμήματος θεωρείται αρνητική. Επομένως, αυτή η διαίρεση ονομάζεται μέθοδος αρνητικών περιοχών.

Η πλάκα στο Σχ. 183, το in χωρίζεται χρησιμοποιώντας αυτή τη μέθοδο σε δύο μόνο μέρη: ορθογώνιο 1 με το εμβαδόν ολόκληρης της πλάκας, σαν να ήταν ολόκληρο, και τρίγωνο 2 με την περιοχή, την οποία θεωρούμε αρνητική.

§ 26. Προσδιορισμός της θέσης του κέντρου βάρους ενός σώματος που αποτελείται από μέρη που έχουν απλό γεωμετρικό σχήμα

Για να λύσετε προβλήματα προσδιορισμού της θέσης του κέντρου βάρους ενός σώματος που αποτελείται από μέρη που έχουν απλό γεωμετρικό σχήμα, πρέπει να έχετε τις δεξιότητες να προσδιορίσετε τις συντεταγμένες του κέντρου βάρους μορφών που αποτελούνται από γραμμές ή περιοχές.

Κέντρα βάρους μερικών απλών γεωμετρικών σχημάτων

Για τον προσδιορισμό των κέντρων βάρους των σωμάτων με σχήματα που εμφανίζονται συχνά (τρίγωνο, κυκλικό τόξο, τομέας, τμήμα), είναι βολικό να χρησιμοποιηθούν δεδομένα αναφοράς (βλ. πίνακα).

Συντεταγμένες του κέντρου βάρους κάποιων ομοιογενών σωμάτων

№	Όνομα του σχήματος	Σχέδιο
	Τόξο κύκλου: το κέντρο βάρους ενός τόξου ομοιόμορφου κύκλου βρίσκεται στον άξονα συμμετρίας (συντεταγμένη y γ R– ακτίνα του κύκλου.
	Ομοιογενής κυκλικός τομέας y γ= 0). όπου α είναι το ήμισυ της κεντρικής γωνίας. R– ακτίνα του κύκλου.
	Τμήμα: το κέντρο βάρους βρίσκεται στον άξονα συμμετρίας (συντεταγμένη y γ= 0). όπου α είναι το ήμισυ της κεντρικής γωνίας. R– ακτίνα του κύκλου.
	Ημικύκλιο:
	Τρίγωνο: το κέντρο βάρους ενός ομοιογενούς τριγώνου βρίσκεται στο σημείο τομής των διαμέτρων του. Οπου x1, y1, x2, y2, x3, y3– συντεταγμένες των κορυφών του τριγώνου
	Κώνος: το κέντρο βάρους ενός ομοιόμορφου κυκλικού κώνου βρίσκεται στο ύψος του και βρίσκεται σε απόσταση 1/4 του ύψους από τη βάση του κώνου.
	Ημισφαίριο: το κέντρο βάρους βρίσκεται στον άξονα συμμετρίας.
	Τραπεζοειδές: - περιοχή του σχήματος.
	- περιοχή του σχήματος

Το κέντρο βάρους του αυτοκινήτου είναι ένα υπό όρους σημείο στο οποίο συγκεντρώνεται όλο το βάρος του. Η θέση του κέντρου βάρους έχει σημαντικό αντίκτυπο στον χειρισμό και τη σταθερότητα του οχήματος, κάτι που πρέπει πάντα να λαμβάνεται υπόψη από τον οδηγό. Η θέση του κέντρου βάρους σε ύψος εξαρτάται από το βάρος και τη φύση του φορτίου. Ας πούμε ότι εάν ένα επιβατικό αυτοκίνητο μεταφέρει φορτίο που βρίσκεται μόνο στο αμάξωμα, τότε το κέντρο βάρους του θα είναι πολύ χαμηλότερο από ό,τι όταν μεταφέρει φορτίο στο πορτμπαγκάζ, το οποίο βρίσκεται πάνω από την οροφή. Ωστόσο, ανεξάρτητα από τη φύση του φορτίου και την τοποθέτησή του, το κέντρο βάρους ενός φορτωμένου οχήματος θα είναι πάντα υψηλότερο από αυτό ενός οχήματος χωρίς φορτίο. Λαμβάνοντας υπόψη αυτό, η υπάρχουσα άποψη πολλών οδηγών σχετικά με την καλή ευστάθεια ενός φορτωμένου οχήματος (και ακόμη περισσότερο τη μείωση της πιθανότητας ανατροπής) δεν είναι σωστή.

Το ύψος του κέντρου βάρους του μηχανήματος επηρεάζει την ανακατανομή των κανονικών αντιδράσεων μεταξύ των τροχών κατά την επιτάχυνση και το φρενάρισμα, καθώς και όταν η μηχανή γέρνει, γεγονός που επηρεάζει τη μάζα πρόσφυσης και, κατά συνέπεια, τη μέγιστη δύναμη έλξης.

Η θέση του κέντρου βάρους του οχήματος είναι σημαντική. Χαρακτηρίζει τη σταθερότητα του μηχανήματος έναντι ανατροπής. Αυτό εμφανίζεται ξεκάθαρα σε λεωφορεία με όρθιους επιβάτες και είναι επίσης πιο σχετικό για οχήματα (οδικά τρένα) που μεταφέρουν μεγάλο φορτίο, φορτηγά και ειδικά οχήματα μεταφοράς (εναέριες πλατφόρμες, γερανοί φορτηγών κ.λπ.).

Η μαθηματική τεχνική υπολογισμού του κέντρου μάζας ανήκει στο πεδίο των μαθηματικών μαθημάτων. Εκεί, παρόμοια προβλήματα χρησιμεύουν ως καλά παραδείγματα στον ολοκληρωτικό λογισμό. Αλλά ακόμα κι αν ξέρετε πώς να ενσωματώνετε, είναι χρήσιμο να γνωρίζετε μερικά κόλπα για τον υπολογισμό της θέσης του κέντρου μάζας. Ένα τέτοιο κόλπο βασίζεται στη χρήση του λεγόμενου θεωρήματος του Πάππου, το οποίο λειτουργεί ως εξής. Αν πάρουμε κάποιο κλειστό σχήμα και σχηματίσουμε ένα άκαμπτο σώμα, περιστρέφοντας αυτό το σχήμα στο χώρο έτσι ώστε κάθε σημείο να κινείται κάθετα στο επίπεδο του σχήματος, τότε ο όγκος του σώματος που προκύπτει είναι ίσος με το γινόμενο του εμβαδού του σχήματος και την απόσταση που διανύει το κέντρο βάρους του! Φυσικά, αυτό το θεώρημα ισχύει και στην περίπτωση που ένα επίπεδο σχήμα κινείται σε ευθεία γραμμή κάθετα στο εμβαδόν του, αλλά αν το μετακινήσουμε κατά μήκος κύκλου ή κάποιου άλλου

καμπύλη, τότε αυτό έχει ως αποτέλεσμα ένα πολύ πιο ενδιαφέρον σώμα. Όταν κινείστε κατά μήκος μιας καμπύλης διαδρομής, το εσωτερικό μέρος του σχήματος κινείται λιγότερο από το εξωτερικό μέρος και αυτά τα εφέ αντισταθμίζουν το ένα το άλλο. Έτσι, αν θέλουμε να ορίσουμε? το κέντρο μάζας μιας επίπεδης φιγούρας με ομοιόμορφη πυκνότητα, τότε πρέπει να θυμάστε ότι ο όγκος που σχηματίζεται από την περιστροφή του γύρω από τον άξονα είναι ίσος με την απόσταση που διανύθηκε από το κέντρο μάζας πολλαπλασιαζόμενη με την περιοχή του σχήματος.
Για παράδειγμα, αν χρειαστεί να βρούμε το κέντρο μάζας ενός ορθογωνίου τριγώνου με βάση D και ύψος H (Εικ. 19.2), τότε αυτό γίνεται ως εξής. Φανταστείτε έναν άξονα κατά μήκος H και περιστρέψτε το τρίγωνο 360° γύρω από αυτόν τον άξονα. Αυτό μας δίνει έναν κώνο. Η απόσταση που διανύει η συντεταγμένη x του κέντρου μάζας είναι 2πx και η περιοχή της περιοχής που μετακινήθηκε, δηλαδή η περιοχή του τριγώνου, είναι l/2 HD. Το γινόμενο της απόστασης που διανύθηκε από το κέντρο μάζας και το εμβαδόν του τριγώνου είναι ίσο με τον όγκο του κώνου, δηλαδή 1/3 πD 2 H. Έτσι, (2πх) (1/2HD) = 1/3D 2 Η, ή x = D/З. Αντίστοιχα, περιστρέφοντας γύρω από το δεύτερο σκέλος ή απλώς για λόγους συμμετρίας, βρίσκουμε ότι y = H/3. Γενικά, το κέντρο μάζας οποιουδήποτε ομοιογενούς τριγώνου βρίσκεται στο σημείο τομής των τριών διαμέσου του (γραμμές που συνδέουν την κορυφή του τριγώνου με το μέσο της απέναντι πλευράς), το οποίο βρίσκεται σε απόσταση από τη βάση ίση με 1 /3 του μήκους κάθε διάμεσου.
Πώς να το δείτε; Κόψτε το τρίγωνο με γραμμές παράλληλες στη βάση σε πολλές λωρίδες. Παρατηρήστε τώρα ότι η διάμεσος χωρίζει κάθε λωρίδα στο μισό, επομένως το κέντρο μάζας πρέπει να βρίσκεται στη διάμεσο.
Ας πάρουμε τώρα ένα πιο σύνθετο σχήμα. Ας υποθέσουμε ότι πρέπει να βρούμε τη θέση του κέντρου μάζας ενός ομοιογενούς ημικυκλίου, δηλαδή ενός κύκλου κομμένου στη μέση. Πού θα είναι το κέντρο μάζας σε αυτή την περίπτωση; Για έναν πλήρη κύκλο, το κέντρο μάζας βρίσκεται στο γεωμετρικό κέντρο, αλλά για ένα ημικύκλιο είναι πιο δύσκολο να βρεθεί η θέση του. Έστω r η ακτίνα του κύκλου και x η απόσταση του κέντρου μάζας από το ευθύγραμμο όριο του ημικυκλίου. Περιστρέφοντάς το γύρω από αυτή την άκρη σαν γύρω από έναν άξονα, παίρνουμε μια μπάλα. Σε αυτήν την περίπτωση, το κέντρο μάζας διανύει απόσταση 2πx και το εμβαδόν του ημικυκλίου είναι ίσο με 1/2πr 2 (το μισό της περιοχής του κύκλου). Δεδομένου ότι ο όγκος της μπάλας είναι, φυσικά, 4πg 3 /3, τότε από εδώ βρίσκουμε

ή

Υπάρχει ένα άλλο θεώρημα του Πάππου, το οποίο είναι στην πραγματικότητα μια ειδική περίπτωση του θεωρήματος που διατυπώθηκε παραπάνω, και επομένως είναι επίσης έγκυρο. Ας υποθέσουμε ότι αντί για συμπαγές ημικύκλιο παίρνουμε ένα ημικύκλιο, για παράδειγμα ένα κομμάτι σύρμα σε μορφή ημικυκλίου με ομοιόμορφη πυκνότητα, και θέλουμε να βρούμε το κέντρο μάζας του. Αποδεικνύεται ότι η περιοχή που «σαρώνεται» από μια επίπεδη καμπύλη κατά τη διάρκεια της κίνησής της, παρόμοια με αυτή που περιγράφεται παραπάνω, είναι ίση με την απόσταση που διανύθηκε από το κέντρο μάζας πολλαπλασιαζόμενη με το μήκος αυτής της καμπύλης. (Η καμπύλη μπορεί να θεωρηθεί ως μια πολύ στενή λωρίδα και το προηγούμενο θεώρημα εφαρμόζεται σε αυτήν.)

Κέντρο βάρους κυκλικού τόξου

Το τόξο έχει άξονα συμμετρίας. Το κέντρο βάρους βρίσκεται σε αυτόν τον άξονα, δηλ. y ντο = 0 .

δλ– στοιχείο τόξου, δλ = Rdφ, R- ακτίνα του κύκλου, x = Rcosφ, L= 2αR,

Ως εκ τούτου:

Χ ντο = R(sina/α).

Κέντρο βάρους κυκλικού τομέα

Τομέας ακτίνας Rμε κεντρική γωνία 2 α έχει άξονα συμμετρίας Βόδι, όπου βρίσκεται το κέντρο βάρους.

Χωρίζουμε τον τομέα σε στοιχειώδεις τομείς, οι οποίοι μπορούν να θεωρηθούν τρίγωνα. Τα κέντρα βάρους των στοιχειωδών τομέων βρίσκονται σε ένα κυκλικό τόξο ακτίνας (2/3) R.

Το κέντρο βάρους του τομέα συμπίπτει με το κέντρο βάρους του τόξου ΑΒ:

Ημικύκλιο:

37. Κινηματική. Κινηματική ενός σημείου. Μέθοδοι προσδιορισμού της κίνησης ενός σημείου.

Κινηματική– κλάδος της μηχανικής στον οποίο μελετάται η κίνηση των υλικών σωμάτων από γεωμετρική άποψη, χωρίς να λαμβάνεται υπόψη η μάζα και οι δυνάμεις που ασκούνται σε αυτά. Τρόποι προσδιορισμού της κίνησης ενός σημείου: 1) φυσικό, 2) συντεταγμένο, 3) διανυσματικό.

Κινηματική ενός σημείου- κλάδος της κινηματικής που μελετά τη μαθηματική περιγραφή της κίνησης των υλικών σημείων. Το κύριο καθήκον της κινηματικής είναι να περιγράψει την κίνηση χρησιμοποιώντας μια μαθηματική συσκευή χωρίς να προσδιορίσει τους λόγους που προκαλούν αυτή την κίνηση.

Φυσικό sp. υποδεικνύεται η τροχιά του σημείου, ο νόμος της κίνησής του κατά μήκος αυτής της τροχιάς, η αρχή και η κατεύθυνση της συντεταγμένης του τόξου: s=f(t) – ο νόμος της κίνησης του σημείου. Για γραμμική κίνηση: x=f(t).

Συντεταγμένη sp. η θέση ενός σημείου στο χώρο καθορίζεται από τρεις συντεταγμένες, αλλαγές στις οποίες καθορίζουν τον νόμο κίνησης του σημείου: x=f 1 (t), y=f 2 (t), z=f 3 (t).

Αν η κίνηση είναι σε επίπεδο, τότε υπάρχουν δύο εξισώσεις κίνησης. Οι εξισώσεις κίνησης περιγράφουν την εξίσωση τροχιάς σε παραμετρική μορφή. Εξαιρώντας την παράμετρο t από τις εξισώσεις, λαμβάνουμε την εξίσωση τροχιάς στη συνήθη μορφή: f(x,y)=0 (για ένα επίπεδο).

Vector sp. η θέση ενός σημείου καθορίζεται από το διάνυσμα της ακτίνας του που τραβιέται από κάποιο κέντρο. Μια καμπύλη που σχεδιάζεται στο τέλος ενός διανύσματος ονομάζεται. οδογράφημααυτό το διάνυσμα. Εκείνοι. διανυσματικό οδόγραφο τροχιάς – ακτίνας.

38. Σχέση συντεταγμένης και διανύσματος, συντεταγμένων και φυσικών μεθόδων προσδιορισμού της κίνησης ενός σημείου.

ΣΧΕΣΗ ΤΗΣ ΜΕΘΟΔΟΥ ΔΙΑΝΥΣΜΑΤΟΣ ΜΕ ΤΗ ΣΥΝΤΕΤΑΓΜΕΝΗ ΚΑΙ ΦΥΣΙΚΗ ΜΕΘΟΔΟεκφράζεται με τις αναλογίες:

όπου είναι η μονάδα μονάδας της εφαπτομένης στην τροχιά σε ένα δεδομένο σημείο, κατευθυνόμενη προς την απόσταση αναφοράς, και είναι η μονάδα μονάδας της κανονικής στην τροχιά σε ένα δεδομένο σημείο, κατευθυνόμενη προς το κέντρο της καμπυλότητας (βλ. Εικ. 3) .

ΣΥΝΔΕΣΗ ΤΗΣ ΣΥΝΤΟΝΤΙΚΗΣ ΜΕΘΟΔΟΥ ΜΕ ΤΟ ΦΥΣΙΚΟ. Εξίσωση τροχιάς f(x, y)=z; Η f 1 (x, z)=y προκύπτει από τις εξισώσεις κίνησης σε μορφή συντεταγμένων εξαλείφοντας το χρόνο t. Η πρόσθετη ανάλυση των τιμών που μπορούν να λάβουν οι συντεταγμένες ενός σημείου προσδιορίζει το τμήμα της καμπύλης που είναι μια τροχιά. Για παράδειγμα, αν η κίνηση ενός σημείου δίνεται από τις εξισώσεις: x=sin t; y=sin 2 t=x 2 , τότε η τροχιά του σημείου είναι εκείνο το τμήμα της παραβολής y=x 2 για το οποίο -1≤x≤+1, 0≤x≤1. Η αρχή και η κατεύθυνση της μέτρησης της απόστασης επιλέγονται αυθαίρετα, αυτό καθορίζει περαιτέρω το πρόσημο της ταχύτητας και το μέγεθος και το πρόσημο της αρχικής απόστασης s 0 .

Ο νόμος της κίνησης καθορίζεται από την εξάρτηση:

το πρόσημο + ή - καθορίζεται ανάλογα με την αποδεκτή κατεύθυνση μέτρησης απόστασης.

Ταχύτητα σημείουείναι ένα κινηματικό μέτρο της κίνησής του, ίσο με τη χρονική παράγωγο του διανύσματος ακτίνας αυτού του σημείου στο υπό εξέταση σύστημα αναφοράς. Το διάνυσμα της ταχύτητας κατευθύνεται εφαπτομενικά στην τροχιά του σημείου προς την κατεύθυνση της κίνησης

Διάνυσμα ταχύτητας (v)είναι η απόσταση που διανύει ένα σώμα σε μια συγκεκριμένη κατεύθυνση ανά μονάδα χρόνου. Σημειώστε ότι ο ορισμός διάνυσμα ταχύτηταςμοιάζει πολύ με τον ορισμό της ταχύτητας, εκτός από μια σημαντική διαφορά: η ταχύτητα ενός σώματος δεν δείχνει την κατεύθυνση της κίνησης, αλλά το διάνυσμα της ταχύτητας ενός σώματος υποδεικνύει τόσο την ταχύτητα όσο και την κατεύθυνση της κίνησης. Επομένως, χρειάζονται δύο μεταβλητές που περιγράφουν το διάνυσμα της ταχύτητας του σώματος: ταχύτητα και κατεύθυνση. Τα φυσικά μεγέθη που έχουν τιμή και κατεύθυνση ονομάζονται διανυσματικά μεγέθη.

Διάνυσμα ταχύτηταςτο σώμα μπορεί να αλλάζει από καιρό σε καιρό. Αν αλλάξει είτε η ταχύτητα είτε η κατεύθυνσή του, αλλάζει και η ταχύτητα του σώματος. Ένα διάνυσμα σταθερής ταχύτητας υποδηλώνει μια σταθερή ταχύτητα και μια σταθερή κατεύθυνση, ενώ ο όρος σταθερή ταχύτητα υποδηλώνει μόνο μια σταθερή τιμή χωρίς να λαμβάνεται υπόψη η κατεύθυνση. Ο όρος "διάνυσμα ταχύτητας" χρησιμοποιείται συχνά εναλλακτικά με τον όρο "ταχύτητα". Και οι δύο εκφράζουν την απόσταση που διανύει ένα σώμα ανά μονάδα χρόνου

Σημειακή επιτάχυνσηείναι ένα μέτρο της μεταβολής της ταχύτητάς του, ίσο με την παράγωγο ως προς το χρόνο της ταχύτητας αυτού του σημείου ή τη δεύτερη παράγωγο του διανύσματος ακτίνας του σημείου ως προς το χρόνο. Η επιτάχυνση χαρακτηρίζει τη μεταβολή του διανύσματος της ταχύτητας σε μέγεθος και κατεύθυνση και κατευθύνεται προς την κοιλότητα της τροχιάς.

Διάνυσμα επιτάχυνσης

Αυτή είναι η αναλογία της αλλαγής της ταχύτητας προς τη χρονική περίοδο κατά την οποία συνέβη αυτή η αλλαγή. Η μέση επιτάχυνση μπορεί να προσδιοριστεί από τον τύπο:

Οπου - διάνυσμα επιτάχυνσης.

Η κατεύθυνση του διανύσματος επιτάχυνσης συμπίπτει με την κατεύθυνση της αλλαγής της ταχύτητας Δ = - 0 (εδώ 0 είναι η αρχική ταχύτητα, δηλαδή η ταχύτητα με την οποία το σώμα άρχισε να επιταχύνει).

Τη χρονική στιγμή t1 (βλ. Εικ. 1.8) το σώμα έχει ταχύτητα 0. Τη χρονική στιγμή t2 το σώμα έχει ταχύτητα . Σύμφωνα με τον κανόνα της αφαίρεσης του διανύσματος, βρίσκουμε το διάνυσμα μεταβολής της ταχύτητας Δ = - 0. Στη συνέχεια, μπορείτε να προσδιορίσετε την επιτάχυνση ως εξής: