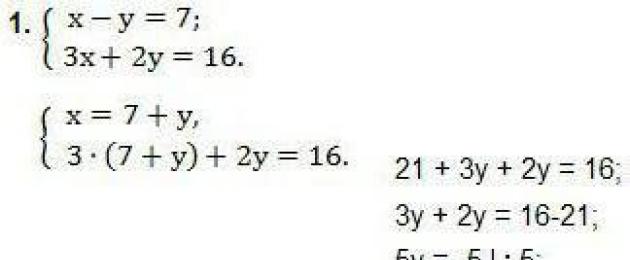Η διατήρηση του απορρήτου σας είναι σημαντική για εμάς. Για το λόγο αυτό, έχουμε αναπτύξει μια Πολιτική Απορρήτου που περιγράφει τον τρόπο με τον οποίο χρησιμοποιούμε και αποθηκεύουμε τις πληροφορίες σας. Διαβάστε τις πρακτικές απορρήτου μας και ενημερώστε μας εάν έχετε ερωτήσεις.
Συλλογή και χρήση προσωπικών πληροφοριών
Οι προσωπικές πληροφορίες αναφέρονται σε δεδομένα που μπορούν να χρησιμοποιηθούν για την αναγνώριση ή επικοινωνία με ένα συγκεκριμένο άτομο.
Ενδέχεται να σας ζητηθεί να δώσετε τα προσωπικά σας στοιχεία ανά πάσα στιγμή όταν επικοινωνήσετε μαζί μας.
Ακολουθούν ορισμένα παραδείγματα των τύπων προσωπικών πληροφοριών που ενδέχεται να συλλέγουμε και πώς μπορούμε να χρησιμοποιήσουμε αυτές τις πληροφορίες.
Ποιες προσωπικές πληροφορίες συλλέγουμε:
- Όταν υποβάλλετε ένα αίτημα στον ιστότοπο, ενδέχεται να συλλέξουμε διάφορες πληροφορίες, συμπεριλαμβανομένου του ονόματος, του αριθμού τηλεφώνου, της διεύθυνσης email σας κ.λπ.
Πώς χρησιμοποιούμε τα προσωπικά σας στοιχεία:
- Συλλέγεται από εμάς προσωπικές πληροφορίεςμας επιτρέπει να επικοινωνήσουμε μαζί σας και να σας ενημερώσουμε για μοναδικές προσφορές, προσφορές και άλλες εκδηλώσεις και επερχόμενες εκδηλώσεις.
- Από καιρό σε καιρό, ενδέχεται να χρησιμοποιήσουμε τα προσωπικά σας στοιχεία για να στείλουμε σημαντικές ειδοποιήσεις και επικοινωνίες.
- Ενδέχεται επίσης να χρησιμοποιήσουμε προσωπικές πληροφορίες για εσωτερικούς σκοπούς, όπως διεξαγωγή ελέγχων, ανάλυση δεδομένων και διάφορες έρευνες, προκειμένου να βελτιώσουμε τις υπηρεσίες που παρέχουμε και να σας παρέχουμε συστάσεις σχετικά με τις υπηρεσίες μας.
- Εάν συμμετέχετε σε κλήρωση, διαγωνισμό ή παρόμοια προσφορά, ενδέχεται να χρησιμοποιήσουμε τις πληροφορίες που παρέχετε για τη διαχείριση τέτοιων προγραμμάτων.
Αποκάλυψη πληροφοριών σε τρίτους
Δεν αποκαλύπτουμε τις πληροφορίες που λαμβάνουμε από εσάς σε τρίτους.
Εξαιρέσεις:
- Εάν είναι απαραίτητο - σύμφωνα με το νόμο, τη δικαστική διαδικασία, σε νομικές διαδικασίες και/ή βάσει δημόσιων αιτημάτων ή αιτημάτων από κυβερνητικές αρχές στην επικράτεια της Ρωσικής Ομοσπονδίας - να αποκαλύψετε τα προσωπικά σας στοιχεία. Ενδέχεται επίσης να αποκαλύψουμε πληροφορίες σχετικά με εσάς εάν κρίνουμε ότι αυτή η αποκάλυψη είναι απαραίτητη ή κατάλληλη για λόγους ασφάλειας, επιβολής του νόμου ή άλλους σκοπούς δημόσιας σημασίας.
- Σε περίπτωση αναδιοργάνωσης, συγχώνευσης ή πώλησης, ενδέχεται να μεταφέρουμε τις προσωπικές πληροφορίες που συλλέγουμε στον αντίστοιχο τρίτο διάδοχο.
Προστασία προσωπικών πληροφοριών
Λαμβάνουμε προφυλάξεις - συμπεριλαμβανομένων διοικητικών, τεχνικών και φυσικών - για την προστασία των προσωπικών σας δεδομένων από απώλεια, κλοπή και κακή χρήση, καθώς και από μη εξουσιοδοτημένη πρόσβαση, αποκάλυψη, τροποποίηση και καταστροφή.
Σεβασμός του απορρήτου σας σε εταιρικό επίπεδο
Για να διασφαλίσουμε ότι τα προσωπικά σας στοιχεία είναι ασφαλή, κοινοποιούμε τα πρότυπα απορρήτου και ασφάλειας στους υπαλλήλους μας και εφαρμόζουμε αυστηρά τις πρακτικές απορρήτου.
Τα συστήματα εξισώσεων έχουν χρησιμοποιηθεί ευρέως στην οικονομική βιομηχανία με μαθηματική μοντελοποίησηδιάφορες διαδικασίες. Για παράδειγμα, κατά την επίλυση προβλημάτων διαχείρισης και προγραμματισμού παραγωγής, διαδρομών logistics (πρόβλημα μεταφοράς) ή τοποθέτησης εξοπλισμού.
Τα συστήματα εξισώσεων χρησιμοποιούνται όχι μόνο στα μαθηματικά, αλλά και στη φυσική, τη χημεία και τη βιολογία, κατά την επίλυση προβλημάτων εύρεσης μεγέθους πληθυσμού.
Σύστημα γραμμικές εξισώσειςονομάστε δύο ή περισσότερες εξισώσεις με πολλές μεταβλητές για τις οποίες είναι απαραίτητο να βρεθεί μια κοινή λύση. Μια τέτοια ακολουθία αριθμών για την οποία όλες οι εξισώσεις γίνονται αληθινές ισότητες ή αποδεικνύουν ότι η ακολουθία δεν υπάρχει.
Γραμμική εξίσωση
Οι εξισώσεις της μορφής ax+by=c ονομάζονται γραμμικές. Οι χαρακτηρισμοί x, y είναι οι άγνωστοι των οποίων η τιμή πρέπει να βρεθεί, b, a είναι οι συντελεστές των μεταβλητών, c είναι ο ελεύθερος όρος της εξίσωσης.
Η επίλυση μιας εξίσωσης σχεδιάζοντας την θα μοιάζει με μια ευθεία γραμμή, της οποίας όλα τα σημεία είναι λύσεις του πολυωνύμου.
Είδη συστημάτων γραμμικών εξισώσεων
Τα πιο απλά παραδείγματα θεωρούνται συστήματα γραμμικών εξισώσεων με δύο μεταβλητές X και Y.
F1(x, y) = 0 και F2(x, y) = 0, όπου F1,2 είναι συναρτήσεις και (x, y) είναι μεταβλητές συνάρτησης.
Επίλυση συστήματος εξισώσεων - Αυτό σημαίνει εύρεση τιμών (x, y) στις οποίες το σύστημα μετατρέπεται σε αληθινή ισότητα ή διαπίστωση ότι οι κατάλληλες τιμές των x και y δεν υπάρχουν.
Ένα ζεύγος τιμών (x, y), γραμμένο ως συντεταγμένες ενός σημείου, ονομάζεται λύση σε ένα σύστημα γραμμικών εξισώσεων.
Εάν τα συστήματα έχουν μία κοινή λύση ή δεν υπάρχει λύση, ονομάζονται ισοδύναμα.
Ομογενή συστήματα γραμμικών εξισώσεων είναι συστήματα των οποίων η δεξιά πλευρά είναι ίση με μηδέν. Αν το δεξί μέρος μετά το πρόσημο ίσου έχει τιμή ή εκφράζεται με συνάρτηση, ένα τέτοιο σύστημα είναι ετερογενές.
Ο αριθμός των μεταβλητών μπορεί να είναι πολύ μεγαλύτερος από δύο, τότε θα πρέπει να μιλήσουμε για ένα παράδειγμα συστήματος γραμμικών εξισώσεων με τρεις ή περισσότερες μεταβλητές.
Όταν έρχονται αντιμέτωποι με συστήματα, οι μαθητές υποθέτουν ότι ο αριθμός των εξισώσεων πρέπει απαραίτητα να συμπίπτει με τον αριθμό των αγνώστων, αλλά αυτό δεν συμβαίνει. Ο αριθμός των εξισώσεων στο σύστημα δεν εξαρτάται από τις μεταβλητές μπορεί να υπάρχουν τόσες από αυτές.
Απλές και σύνθετες μέθοδοι επίλυσης συστημάτων εξισώσεων
Δεν υπάρχει γενική αναλυτική μέθοδος για την επίλυση τέτοιων συστημάτων αριθμητικές λύσεις. Το μάθημα των σχολικών μαθηματικών περιγράφει λεπτομερώς μεθόδους όπως μετάθεση, αλγεβρική πρόσθεση, αντικατάσταση, καθώς και γραφικές και μητρικές μεθόδους, λύση με τη μέθοδο Gaussian.
Το κύριο καθήκον κατά τη διδασκαλία μεθόδων λύσης είναι να διδάξετε πώς να αναλύετε σωστά το σύστημα και να βρείτε τον βέλτιστο αλγόριθμο λύσης για κάθε παράδειγμα. Το κύριο πράγμα δεν είναι να απομνημονεύσετε ένα σύστημα κανόνων και ενεργειών για κάθε μέθοδο, αλλά να κατανοήσετε τις αρχές της χρήσης μιας συγκεκριμένης μεθόδου
Η επίλυση παραδειγμάτων συστημάτων γραμμικών εξισώσεων για το πρόγραμμα σπουδών της 7ης τάξης γενικής εκπαίδευσης είναι αρκετά απλή και εξηγείται με μεγάλη λεπτομέρεια. Σε κάθε εγχειρίδιο μαθηματικών δίνεται αρκετή προσοχή σε αυτή την ενότητα. Η επίλυση παραδειγμάτων συστημάτων γραμμικών εξισώσεων με τη μέθοδο Gauss and Cramer μελετάται λεπτομερέστερα στα πρώτα χρόνια της τριτοβάθμιας εκπαίδευσης.
Επίλυση συστημάτων με τη μέθοδο της υποκατάστασης
Οι ενέργειες της μεθόδου αντικατάστασης στοχεύουν στην έκφραση της τιμής μιας μεταβλητής ως προς τη δεύτερη. Η έκφραση αντικαθίσταται στην υπόλοιπη εξίσωση και στη συνέχεια ανάγεται σε μορφή με μία μεταβλητή. Η ενέργεια επαναλαμβάνεται ανάλογα με τον αριθμό των αγνώστων στο σύστημα
Ας δώσουμε μια λύση σε ένα παράδειγμα συστήματος γραμμικών εξισώσεων της κλάσης 7 χρησιμοποιώντας τη μέθοδο αντικατάστασης:

Όπως φαίνεται από το παράδειγμα, η μεταβλητή x εκφράστηκε μέσω F(X) = 7 + Y. Η προκύπτουσα έκφραση, που αντικαταστάθηκε στη 2η εξίσωση του συστήματος στη θέση του X, βοήθησε να ληφθεί μία μεταβλητή Y στη 2η εξίσωση . Η επίλυση αυτού του παραδείγματος είναι εύκολη και σας επιτρέπει να λάβετε την τιμή Y Το τελευταίο βήμα είναι να ελέγξετε τις λαμβανόμενες τιμές.
Δεν είναι πάντα δυνατό να λυθεί ένα παράδειγμα συστήματος γραμμικών εξισώσεων με αντικατάσταση. Οι εξισώσεις μπορεί να είναι σύνθετες και η έκφραση της μεταβλητής με βάση το δεύτερο άγνωστο θα είναι πολύ δυσκίνητη για περαιτέρω υπολογισμούς. Όταν υπάρχουν περισσότερα από 3 άγνωστα στο σύστημα, η επίλυση με αντικατάσταση είναι επίσης ακατάλληλη.
Λύση παραδείγματος συστήματος γραμμικών ανομοιογενών εξισώσεων:

Λύση με αλγεβρική πρόσθεση
Κατά την αναζήτηση λύσεων σε συστήματα χρησιμοποιώντας τη μέθοδο πρόσθεσης, οι εξισώσεις προστίθενται όρο προς όρο και πολλαπλασιάζονται με διάφορους αριθμούς. Ο απώτερος στόχοςΟι μαθηματικές πράξεις είναι μια εξίσωση με μία μεταβλητή.

Η εφαρμογή αυτής της μεθόδου απαιτεί εξάσκηση και παρατήρηση. Η επίλυση ενός συστήματος γραμμικών εξισώσεων χρησιμοποιώντας τη μέθοδο πρόσθεσης όταν υπάρχουν 3 ή περισσότερες μεταβλητές δεν είναι εύκολη. Η αλγεβρική πρόσθεση είναι βολική στη χρήση όταν οι εξισώσεις περιέχουν κλάσματα και δεκαδικούς.
Αλγόριθμος λύσης:
- Πολλαπλασιάστε και τις δύο πλευρές της εξίσωσης με έναν συγκεκριμένο αριθμό. Σαν άποτέλεσμα αριθμητική δράσηένας από τους συντελεστές της μεταβλητής πρέπει να είναι ίσος με 1.
- Προσθέστε την προκύπτουσα έκφραση όρο προς όρο και βρείτε ένα από τα άγνωστα.
- Αντικαταστήστε την τιμή που προκύπτει στη 2η εξίσωση του συστήματος για να βρείτε την υπόλοιπη μεταβλητή.
Μέθοδος επίλυσης με την εισαγωγή νέας μεταβλητής
Μια νέα μεταβλητή μπορεί να εισαχθεί εάν το σύστημα απαιτεί την εύρεση λύσης για όχι περισσότερες από δύο εξισώσεις, ο αριθμός των αγνώστων δεν πρέπει επίσης να είναι μεγαλύτερος από δύο.
Η μέθοδος χρησιμοποιείται για να απλοποιήσει μία από τις εξισώσεις εισάγοντας μια νέα μεταβλητή. Η νέα εξίσωση λύνεται για το εισαγόμενο άγνωστο και η τιμή που προκύπτει χρησιμοποιείται για τον προσδιορισμό της αρχικής μεταβλητής.

Το παράδειγμα δείχνει ότι με την εισαγωγή μιας νέας μεταβλητής t, ήταν δυνατό να μειωθεί η 1η εξίσωση του συστήματος στην τυπική τετραγωνικό τριώνυμο. Μπορείτε να λύσετε ένα πολυώνυμο βρίσκοντας το διαχωριστικό.
Είναι απαραίτητο να βρούμε την τιμή του διαχωριστή χρησιμοποιώντας τον γνωστό τύπο: D = b2 - 4*a*c, όπου D είναι η επιθυμητή διάκριση, b, a, c είναι οι συντελεστές του πολυωνύμου. Στο συγκεκριμένο παράδειγμα, a=1, b=16, c=39, επομένως D=100. Εάν η διάκριση είναι μεγαλύτερη από το μηδέν, τότε υπάρχουν δύο λύσεις: t = -b±√D / 2*a, εάν η διάκριση είναι μικρότερη από μηδέν, τότε υπάρχει μία λύση: x = -b / 2*a.
Η λύση για τα συστήματα που προκύπτουν βρίσκεται με τη μέθοδο της προσθήκης.
Οπτική μέθοδος επίλυσης συστημάτων
Κατάλληλο για συστήματα 3 εξισώσεων. Η μέθοδος είναι να βασιστείτε άξονα συντεταγμένωνγραφήματα κάθε εξίσωσης που περιλαμβάνεται στο σύστημα. Οι συντεταγμένες των σημείων τομής των καμπυλών θα είναι η γενική λύση του συστήματος.
Η γραφική μέθοδος έχει μια σειρά από αποχρώσεις. Ας δούμε αρκετά παραδείγματα επίλυσης συστημάτων γραμμικών εξισώσεων με οπτικό τρόπο.

Όπως φαίνεται από το παράδειγμα, για κάθε γραμμή κατασκευάστηκαν δύο σημεία, επιλέχθηκαν αυθαίρετα οι τιμές της μεταβλητής x: 0 και 3. Με βάση τις τιμές του x, βρέθηκαν οι τιμές για το y: 3 και 0. Σημεία με συντεταγμένες (0, 3) και (3, 0) σημειώθηκαν στο γράφημα και συνδέθηκαν με μια γραμμή.
Τα βήματα πρέπει να επαναληφθούν για τη δεύτερη εξίσωση. Το σημείο τομής των ευθειών είναι η λύση του συστήματος.
Το παρακάτω παράδειγμα απαιτεί την εύρεση μιας γραφικής λύσης σε ένα σύστημα γραμμικών εξισώσεων: 0,5x-y+2=0 και 0,5x-y-1=0.

Όπως φαίνεται από το παράδειγμα, το σύστημα δεν έχει λύση, γιατί οι γραφικές παραστάσεις είναι παράλληλες και δεν τέμνονται σε όλο τους το μήκος.

Τα συστήματα από τα παραδείγματα 2 και 3 είναι παρόμοια, αλλά όταν κατασκευάζονται γίνεται προφανές ότι οι λύσεις τους είναι διαφορετικές. Θα πρέπει να θυμόμαστε ότι δεν είναι πάντα δυνατό να πούμε εάν ένα σύστημα έχει μια λύση ή όχι, είναι πάντα απαραίτητο να κατασκευαστεί ένα γράφημα.
Η μήτρα και οι ποικιλίες της
Οι πίνακες χρησιμοποιούνται για τη συνοπτική σύνταξη ενός συστήματος γραμμικών εξισώσεων. Ο πίνακας είναι ένας ειδικός τύπος πίνακα γεμάτο με αριθμούς. Το n*m έχει n - γραμμές και m - στήλες.
Ένας πίνακας είναι τετράγωνος όταν ο αριθμός των στηλών και των γραμμών είναι ίσος. Ένας πίνακας-διάνυσμα είναι ένας πίνακας μιας στήλης με έναν απεριόριστο δυνατό αριθμό σειρών. Ένας πίνακας με μονάδες κατά μήκος μιας από τις διαγωνίους και άλλα μηδενικά στοιχεία ονομάζεται ταυτότητα.
Ένας αντίστροφος πίνακας είναι ένας πίνακας, όταν πολλαπλασιάζεται με τον οποίο ο αρχικός μετατρέπεται σε μοναδιαίο πίνακα, υπάρχει μόνο για τον αρχικό τετράγωνο.
Κανόνες μετατροπής συστήματος εξισώσεων σε πίνακα
Σε σχέση με συστήματα εξισώσεων, οι συντελεστές και οι ελεύθεροι όροι των εξισώσεων γράφονται ως αριθμοί μήτρας.
Μια γραμμή πίνακα λέγεται ότι είναι μη μηδενική εάν τουλάχιστον ένα στοιχείο της γραμμής δεν είναι μηδέν. Επομένως, εάν σε κάποια από τις εξισώσεις ο αριθμός των μεταβλητών διαφέρει, τότε είναι απαραίτητο να εισαγάγετε μηδέν στη θέση του αγνώστου που λείπει.
Οι στήλες του πίνακα πρέπει να αντιστοιχούν αυστηρά στις μεταβλητές. Αυτό σημαίνει ότι οι συντελεστές της μεταβλητής x μπορούν να γραφτούν μόνο σε μία στήλη, για παράδειγμα η πρώτη, ο συντελεστής του αγνώστου y - μόνο στη δεύτερη.
Κατά τον πολλαπλασιασμό ενός πίνακα, όλα τα στοιχεία του πίνακα πολλαπλασιάζονται διαδοχικά με έναν αριθμό.
Επιλογές για την εύρεση του αντίστροφου πίνακα
Ο τύπος για την εύρεση του αντίστροφου πίνακα είναι αρκετά απλός: K -1 = 1 / |K|, όπου K -1 είναι ο αντίστροφος πίνακας και |K| είναι η ορίζουσα του πίνακα. |Κ| δεν πρέπει να είναι ίσο με μηδέν, τότε το σύστημα έχει μια λύση.
Η ορίζουσα υπολογίζεται εύκολα για έναν πίνακα δύο προς δύο, απλά πρέπει να πολλαπλασιάσετε τα διαγώνια στοιχεία μεταξύ τους. Για την επιλογή "τρία επί τρία", υπάρχει ένας τύπος |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Μπορείτε να χρησιμοποιήσετε τον τύπο ή μπορείτε να θυμηθείτε ότι πρέπει να πάρετε ένα στοιχείο από κάθε γραμμή και κάθε στήλη, έτσι ώστε οι αριθμοί των στηλών και των σειρών των στοιχείων να μην επαναλαμβάνονται στην εργασία.
Επίλυση παραδειγμάτων συστημάτων γραμμικών εξισώσεων με τη μέθοδο του πίνακα
Η μέθοδος μήτρας για την εύρεση λύσης σάς επιτρέπει να μειώσετε τις περίπλοκες εγγραφές κατά την επίλυση συστημάτων με μεγάλο αριθμό μεταβλητών και εξισώσεων.

Στο παράδειγμα, ένα nm είναι οι συντελεστές των εξισώσεων, ο πίνακας είναι ένα διάνυσμα x n είναι μεταβλητές και b n είναι ελεύθεροι όροι.


Επίλυση συστημάτων με τη μέθοδο Gaussian
Στα ανώτερα μαθηματικά, η μέθοδος Gauss μελετάται μαζί με τη μέθοδο Cramer και η διαδικασία εύρεσης λύσεων σε συστήματα ονομάζεται μέθοδος λύσης Gauss-Cramer. Αυτές οι μέθοδοι χρησιμοποιούνται για την εύρεση μεταβλητών συστημάτων με μεγάλο αριθμό γραμμικών εξισώσεων.
Η μέθοδος Gauss μοιάζει πολύ με λύσεις με υποκατάσταση και αλγεβρική πρόσθεση, αλλά είναι πιο συστηματική. Στο σχολικό μάθημα η λύση με τη μέθοδο Gauss χρησιμοποιείται για συστήματα 3 και 4 εξισώσεων. Ο σκοπός της μεθόδου είναι να αναγάγει το σύστημα στη μορφή ενός ανεστραμμένου τραπεζοειδούς. Με αλγεβρικοί μετασχηματισμοίκαι αντικαταστάσεις, η τιμή μιας μεταβλητής βρίσκεται σε μία από τις εξισώσεις του συστήματος. Η δεύτερη εξίσωση είναι μια παράσταση με 2 άγνωστα, ενώ τα 3 και 4 είναι, αντίστοιχα, με 3 και 4 μεταβλητές.
Αφού φέρει το σύστημα στην περιγραφόμενη μορφή, η περαιτέρω λύση ανάγεται στη διαδοχική αντικατάσταση γνωστών μεταβλητών στις εξισώσεις του συστήματος.
ΣΕ σχολικά εγχειρίδιαγια τον βαθμό 7, ένα παράδειγμα λύσης με τη μέθοδο Gaussian περιγράφεται ως εξής:

Όπως φαίνεται από το παράδειγμα, στο βήμα (3) προέκυψαν δύο εξισώσεις: 3x 3 -2x 4 =11 και 3x 3 +2x 4 =7. Η επίλυση οποιασδήποτε από τις εξισώσεις θα σας επιτρέψει να βρείτε μία από τις μεταβλητές x n.

Το θεώρημα 5, το οποίο αναφέρεται στο κείμενο, δηλώνει ότι εάν μια από τις εξισώσεις του συστήματος αντικατασταθεί από μια ισοδύναμη, τότε το σύστημα που προκύπτει θα είναι επίσης ισοδύναμο με το αρχικό.
Η μέθοδος Gauss είναι δύσκολο να κατανοηθεί από τους μαθητές Λύκειο, αλλά είναι ένας από τους πιο ενδιαφέροντες τρόπους για την ανάπτυξη της εφευρετικότητας των παιδιών που είναι εγγεγραμμένα σε προχωρημένα προγράμματα εκμάθησης στα μαθήματα μαθηματικών και φυσικής.
Για ευκολία καταγραφής, οι υπολογισμοί συνήθως γίνονται ως εξής:

Οι συντελεστές των εξισώσεων και οι ελεύθεροι όροι γράφονται με τη μορφή πίνακα, όπου κάθε σειρά του πίνακα αντιστοιχεί σε μία από τις εξισώσεις του συστήματος. χωρίζει την αριστερή πλευρά της εξίσωσης από τη δεξιά. Οι λατινικοί αριθμοί δείχνουν τους αριθμούς των εξισώσεων στο σύστημα.
Πρώτα, σημειώστε τη μήτρα με την οποία θα εργαστείτε και μετά όλες τις ενέργειες που πραγματοποιήθηκαν με μία από τις σειρές. Ο πίνακας που προκύπτει γράφεται μετά το σύμβολο "βέλος" και οι απαραίτητες αλγεβρικές πράξεις συνεχίζονται μέχρι να επιτευχθεί το αποτέλεσμα.
Το αποτέλεσμα θα πρέπει να είναι ένας πίνακας στον οποίο μία από τις διαγώνιες είναι ίση με 1 και όλοι οι άλλοι συντελεστές είναι ίσοι με μηδέν, δηλαδή ο πίνακας μειώνεται σε μορφή μονάδας. Δεν πρέπει να ξεχνάμε να κάνουμε υπολογισμούς με αριθμούς και στις δύο πλευρές της εξίσωσης.
Αυτή η μέθοδος εγγραφής είναι λιγότερο επαχθής και σας επιτρέπει να μην αποσπάτε την προσοχή αναφέροντας πολλά άγνωστα.
Η δωρεάν χρήση οποιασδήποτε μεθόδου λύσης απαιτεί προσοχή και κάποια εμπειρία. Δεν είναι όλες οι μέθοδοι εφαρμοσμένου χαρακτήρα. Ορισμένες μέθοδοι εύρεσης λύσεων είναι πιο προτιμητέες σε έναν συγκεκριμένο τομέα της ανθρώπινης δραστηριότητας, ενώ άλλες υπάρχουν για εκπαιδευτικούς σκοπούς.
2. Μέθοδος αλγεβρικής πρόσθεσης.
3. Μέθοδος εισαγωγής νέας μεταβλητής (μέθοδος αντικατάστασης μεταβλητής).
Ορισμός:Ένα σύστημα εξισώσεων αναφέρεται σε πολλές εξισώσεις για μία ή περισσότερες μεταβλητές που πρέπει να εκτελεστούν ταυτόχρονα, δηλ. με τις ίδιες τιμές των μεταβλητών για όλες τις εξισώσεις. Οι εξισώσεις στο σύστημα συνδυάζονται με ένα σύμβολο συστήματος - ένα σγουρό στήριγμα.
Παράδειγμα 1:
- ένα σύστημα δύο εξισώσεων με δύο μεταβλητές ΧΚαι y.
Η λύση στο σύστημα είναι οι ρίζες. Όταν αυτές οι τιμές αντικατασταθούν, οι εξισώσεις γίνονται αληθινές ταυτότητες:
Επίλυση συστημάτων γραμμικών εξισώσεων.
Η πιο κοινή μέθοδος για την επίλυση ενός συστήματος είναι η μέθοδος αντικατάστασης.
Μέθοδος αντικατάστασης.
Η μέθοδος αντικατάστασης για την επίλυση συστημάτων εξισώσεων είναι η έκφραση μιας μεταβλητής από μια εξίσωση του συστήματος με όρους άλλων, και η αντικατάσταση αυτής της έκφρασης στις υπόλοιπες εξισώσεις του συστήματος αντί της εκφρασμένης μεταβλητής.
Παράδειγμα 2:
Λύστε το σύστημα των εξισώσεων:
Λύση:
Δίνεται ένα σύστημα εξισώσεων και πρέπει να λυθεί με τη μέθοδο της αντικατάστασης.
Ας εκφράσουμε τη μεταβλητή yαπό τη δεύτερη εξίσωση του συστήματος.
Σχόλιο:"Εκφράστε μια μεταβλητή" σημαίνει μετατροπή της ισότητας έτσι ώστε αυτή η μεταβλητή να παραμένει στα αριστερά του πρόσημου ίσου με συντελεστή 1, και όλοι οι άλλοι όροι να εισέρχονται σε σωστη πλευραισότητα.
Δεύτερη εξίσωση του συστήματος:
Ας φύγουμε μόνο αριστερά y:
Και ας αντικαταστήσουμε (από εδώ προέρχεται το όνομα της μεθόδου) στην πρώτη εξίσωση αντί για στοη έκφραση με την οποία ισούται, δηλ. .
Πρώτη εξίσωση:
Ας αντικαταστήσουμε: ![]()
Ας λύσουμε αυτή τη συνηθισμένη τετραγωνική εξίσωση. Για όσους έχουν ξεχάσει πώς να το κάνουν αυτό, υπάρχει ένα άρθρο Επίλυση τετραγωνικών εξισώσεων. . 
Άρα οι μεταβλητές τιμές Χβρέθηκαν.
Ας αντικαταστήσουμε αυτές τις τιμές στην έκφραση για τη μεταβλητή y. Εδώ υπάρχουν δύο έννοιες Χ, δηλ. για καθένα από αυτά θα πρέπει να βρείτε μια τιμή y .
1) Αφήστε
Το αντικαθιστούμε στην έκφραση.
2) Αφήστε
Το αντικαθιστούμε στην έκφραση.
Όλα μπορούν να απαντηθούν:
Σχόλιο:Σε αυτή την περίπτωση, η απάντηση θα πρέπει να γράφεται σε ζευγάρια για να μην μπερδεύεται ποια τιμή της μεταβλητής y αντιστοιχεί σε ποια τιμή της μεταβλητής x.
Απάντηση:
Σχόλιο:Στο παράδειγμα 1, μόνο ένα ζεύγος υποδεικνύεται ως λύση στο σύστημα, δηλ. αυτό το ζεύγος είναι μια λύση στο σύστημα, αλλά όχι ολοκληρωμένη. Επομένως, πώς να λύσετε μια εξίσωση ή ένα σύστημα σημαίνει να υποδείξετε τη λύση και να δείξετε ότι δεν υπάρχουν άλλες λύσεις. Και εδώ είναι ένα άλλο ζευγάρι.
Ας επισημοποιήσουμε τη λύση σε αυτό το σύστημα σε σχολικό στυλ:
Σχόλιο:Το σύμβολο "" σημαίνει "ισοδύναμο", δηλ. το επόμενο σύστημα ή έκφραση είναι ισοδύναμο με το προηγούμενο.
Η χρήση των εξισώσεων είναι ευρέως διαδεδομένη στη ζωή μας. Χρησιμοποιούνται σε πολλούς υπολογισμούς, κατασκευές κατασκευών ακόμα και σε αθλήματα. Ο άνθρωπος χρησιμοποιούσε εξισώσεις στην αρχαιότητα, και από τότε η χρήση τους έχει αυξηθεί. Η μέθοδος αντικατάστασης σας επιτρέπει να επιλύετε εύκολα συστήματα γραμμικών εξισώσεων οποιασδήποτε πολυπλοκότητας. Η ουσία της μεθόδου είναι ότι, χρησιμοποιώντας την πρώτη έκφραση του συστήματος, εκφράζουμε το "y" και στη συνέχεια αντικαθιστούμε την έκφραση που προκύπτει στη δεύτερη εξίσωση του συστήματος αντί για "y". Δεδομένου ότι η εξίσωση περιέχει ήδη όχι δύο άγνωστα, αλλά μόνο ένα, μπορούμε εύκολα να βρούμε την τιμή αυτής της μεταβλητής και στη συνέχεια να τη χρησιμοποιήσουμε για να προσδιορίσουμε την τιμή της δεύτερης.
Ας υποθέσουμε ότι μας δίνεται ένα σύστημα γραμμικών εξισώσεων της ακόλουθης μορφής:
\[\αριστερά\(\αρχή(μήτρα) 3x-y-10=0\\ x+4y-12=0 \end(μήτρας)\δεξιά.\]
Ας εκφραστούμε \
\[\αριστερά\(\αρχή(μήτρα) 3x-10=y\\ x+4y-12=0 \end(μήτρας)\δεξιά.\]
Ας αντικαταστήσουμε την έκφραση που προκύπτει στην εξίσωση 2:
\[\αριστερά\(\αρχή(μήτρα) y=3x-10\\ x+4(3x-10)-12=0 \end(μήτρα)\δεξιά.\]
Ας απλοποιήσουμε και ας λύσουμε την εξίσωση ανοίγοντας αγκύλες και λαμβάνοντας υπόψη τους κανόνες μεταφοράς όρων:
Τώρα ξέρουμε την τιμή \ Ας το χρησιμοποιήσουμε για να βρούμε την τιμή \
Απάντηση: \[(4;2).\]
Πού μπορώ να λύσω ένα σύστημα εξισώσεων online χρησιμοποιώντας τη μέθοδο αντικατάστασης;
Μπορείτε να λύσετε το σύστημα εξισώσεων στην ιστοσελίδα μας. Ένας δωρεάν διαδικτυακός λύτης θα σας επιτρέψει να λύσετε την εξίσωση online οποιαδήποτεπολυπλοκότητα σε δευτερόλεπτα. Το μόνο που χρειάζεται να κάνετε είναι απλώς να εισαγάγετε τα δεδομένα σας στο πρόγραμμα επίλυσης. Μπορείτε επίσης να μάθετε πώς να λύσετε την εξίσωση στον ιστότοπό μας. Και αν εξακολουθείτε να έχετε ερωτήσεις, μπορείτε να τις ρωτήσετε στην ομάδα μας VKontakte.
1 . ΠΛΗΡΕΣ ΟΝΟΜΑ. δάσκαλοι: ____Tkachuk Natalya Petrovna _________________________________________________________________________________________________
2. Τάξη: _8 Ημερομηνία: .11.03________Θέμα_-μαθηματικά, μάθημα Νο 71 σύμφωνα με το πρόγραμμα:
3. Θέμα μαθήματος Επίλυση συστημάτων με αντικατάσταση 4 . Η θέση και ο ρόλος του μαθήματος στο υπό μελέτη θέμα :. Μάθημα για την εμπέδωση της γνώσης. Ο σκοπός του μαθήματος :
Εκπαιδευτικά: ανάπτυξη γνώσεων επίλυσης συστημάτων εξισώσεων με τη μέθοδο της υποκατάστασης. Γνωρίζω/καταλαβαίνω: αν τα γραφήματα έχουν κοινά σημεία, τότε το σύστημα έχει λύσεις. Εάν τα γραφήματα δεν έχουν κοινά σημεία, τότε το σύστημα δεν έχει λύσεις. αλγόριθμος για την επίλυση συστημάτων εξισώσεων.Εχω την δυνατότητα να επίλυση συστημάτων με αντικατάσταση Προώθηση της ανάπτυξης δεξιοτήτων για την εφαρμογή της αποκτηθείσας γνώσης σε μη τυποποιημένες (τυποποιημένες) συνθήκεςΑναπτυξιακή: Να προωθήσει την ανάπτυξη των δεξιοτήτων των μαθητών για γενίκευση της αποκτηθείσας γνώσης, διεξαγωγή ανάλυσης, σύνθεσης, συγκρίσεων και εξαγωγής των απαραίτητων συμπερασμάτων. Να προωθήσει την ανάπτυξη δεξιοτήτων για την εφαρμογή της αποκτηθείσας γνώσης σε μη τυποποιημένες και τυπικές συνθήκες.Εκπαιδευτικός: Προωθήστε την ανάπτυξη μιας δημιουργικής στάσης απέναντι εκπαιδευτικές δραστηριότητες
Χαρακτηριστικά των σταδίων του μαθήματος
ΔραστηριότηταΦοιτητές
Αυτοδιάθεση.
Ενεργοποιήστε τη γνωστική δραστηριότητα
Λύστε το σύστημα
προφορικός
Μετωπικός
Χαιρετισμός μαθητών. εκτελώντας. Δημιουργία κατάστασης ετοιμότητας για το μάθημα, επιτυχία στο επερχόμενο μάθημα.
Ελέγξτε την ετοιμότητα για το μάθημα.
2. Επικαιροποίηση γνώσεων.
Προσδιορίστε την ποιότητα και το επίπεδο κατάκτησης των γνώσεων και των δεξιοτήτων που αποκτήθηκαν σε προηγούμενα μαθήματα σχετικά με το θέμα
Μάθετε εάν ένα ζεύγος αριθμών είναι λύση στο σύστημα. x=5 y=9
Ποιες πράξεις μπορούν να γίνουν με εξισώσεις;
(Πολλαπλασιάστε και τις δύο πλευρές της εξίσωσης με τον ίδιο αριθμό, διαιρέστε με έναν αριθμό όχι ίσο με το μηδέν...)
Ομαδική δουλειά
Μετωπικός. Guppovaya - ανάλυση αλγορίθμων για την επίλυση προβλημάτων.
Κάνει βασικές ερωτήσεις όταν χρειάζεται.
Απαντούν στις ερωτήσεις που τέθηκαν.
3.Στάση μαθησιακό έργο, στόχοι μαθήματος.
Σχηματισμός
και ανάπτυξη δεξιοτήτων
ορίζουν και διατυπώνουν
πρόβλημα, στόχος και θέμα
να μελετήσει τις γραμμές
Πώς να λύσετε ένα σύστημα εξισώσεων με πρόσθεση, με αντικατάσταση.
Ποια μέθοδος είναι κατάλληλη να χρησιμοποιηθεί κατά την επίλυση. αυτό το σύστημα;
Ομαδική δουλειά.
Ατομο.
Μετωπικός.
Τι βήματα κάναμε για να μάθουμε την τιμή αγοράς;
Τι θέμα θα μελετήσουμε;
Μιλούν ανοιχτά.
4. Στάδιο ενημέρωσης γνώσεων για το θέμα
Να προωθήσει την ανάπτυξη δεξιοτήτων διάκρισης και σύγκρισης γραμμών. Παρέχετε συνθήκες για την ανάπτυξη δεξιοτήτων για να εκφράσετε τις σκέψεις σας με ικανοποίηση, καθαρότητα και ακρίβεια.
№ 621
Μάθετε τις σχετικές θέσεις των γραμμών
2x+0,5y= 1,2 και x- 4y=0
Είναι δυνατόν να προσδιοριστεί εάν οι ευθείες τέμνονται ή όχι από τους συντελεστές τους;
2. δημιουργήστε εξισώσεις ευθειών που είναι παράλληλες μεταξύ τους.
Εργασία με μαθητή
Εργαστείτε σε ζευγάρια με αυτοέλεγχο
Μετωπικό, ατομικό. εργαστήριο επίλυσης προβλημάτων
Κάνει βασικές ερωτήσεις όταν χρειάζεται. Σχεδιάζει παραλληλισμούς με προηγουμένως μελετημένο υλικό.
Παρέχει κίνητρο για την ολοκλήρωση των προτεινόμενων εργασιών.
Οδηγεί τους μαθητές στο συμπέρασμα για την ύπαρξη τύπων.
Λύστε προβλήματα, απαντήστε σε ερωτήσεις του δασκάλου, εάν χρειάζεται, κάντε την άσκηση σε ένα τετράδιο.
Να σχολιάζετε, να αναλύετε εναλλάξ, να εντοπίζετε λόγους και λύσεις.
5.Εργαστείτε ανεξάρτητα
εφαρμογή της αποκτηθείσας γνώσης. Επικαιροποίηση γνώσεων και δεξιοτήτων στην επίλυση προβλημάτων.
Σχηματισμός και ανάπτυξη δεξιοτήτων ανάγνωσης αριθμών Σχεδιασμός των δραστηριοτήτων σας για την επίλυση μιας δεδομένης εργασίας, παρακολούθηση του ληφθέντος αποτελέσματος, διόρθωση του ληφθέντος αποτελέσματος, αυτορρύθμιση
1 var -
2 var
Ανεξάρτητη εργασία. Έλεγχος του γείτονά σας.
"καταιγισμός ιδεών",
Παρακολουθεί την εκτέλεση των εργασιών.
Παρέχει: ατομικό έλεγχο. επιλεκτικός έλεγχος.
Σας ενθαρρύνει να εκφράσετε τη γνώμη σας.
Λύνω προβλήματα. Πραγματοποιήστε: αυτοαξιολόγηση, αμοιβαία επαλήθευση. παρέχει μια προκαταρκτική αξιολόγηση.
6. Αξιολόγηση μαθήματος, αυτοαξιολόγηση.
Διαμόρφωση και ανάπτυξη της ικανότητας ανάλυσης και κατανόησης των επιτευγμάτων κάποιου.
Η ικανότητα προσδιορισμού του επιπέδου γνώσης του εκπαιδευτικού υλικού.
Αξιολόγηση ενδιάμεσων αποτελεσμάτων και αυτορρύθμιση για αύξηση κινήτρων για εκπαιδευτικές δραστηριότητες
Αξιολόγηση σε κάθε στάδιο
1. Μπορείτε να γράψετε γραμμικές εξισώσεις;
2. Μπορείτε να προσδιορίσετε αν τέμνονται ή όχι;
3. Γνωρίζετε αλγόριθμο για την επίλυση συστημάτων εξισώσεων;
4. ποιες μεθόδους γνωρίζετε για την επίλυση συστημάτων εξισώσεων;
Ομαδική δουλειά.
Ομαδική και ατομική...
Σας ενθαρρύνει να εκφράσετε τη γνώμη σας.
Πραγματοποιήστε: αυτοαξιολόγηση και αξιολόγηση φίλου.
7. Περίληψη μαθήματος. Εργασία για το σπίτι.
Η ικανότητα συσχέτισης στόχων και αποτελεσμάτων των δικών του δραστηριοτήτων. Διατήρηση υγιούς πνεύματος ανταγωνισμού για τη διατήρηση των κινήτρων για εκπαιδευτικές δραστηριότητες. συμμετοχή στη συλλογική συζήτηση των προβλημάτων.
σελ. 4.4 Νο. 623
Ομαδική δουλειά.
Μετωπική - Προσδιορισμός και διατύπωση γνωστικού στόχου, προβληματισμός για μεθόδους και συνθήκες δράσης
Ανάλυση και σύνθεση αντικειμένων
Σας ενθαρρύνει να εκφράσετε τη γνώμη σας.
Δίνει ένα σχόλιο για εργασία για το σπίτι; εργασία για αναζήτηση χαρακτηριστικών στο κείμενο...
Τα παιδιά συμμετέχουν στη συζήτηση, αναλύουν, συζητούν. Σκεφθείτε και καταγράψτε τα επιτεύγματά τους.
Σήμερα στην τάξη έμαθα...
Σήμερα στην τάξη έμαθα...
- Σε επαφή με 0
- Google+ 0
- Εντάξει 0
- Facebook 0