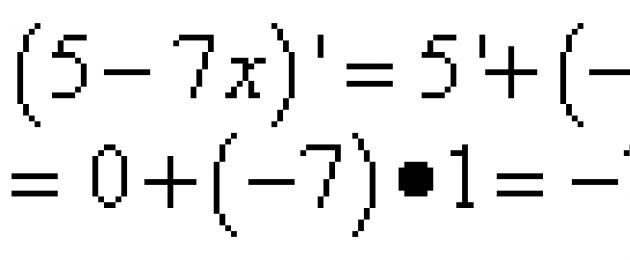Η παράγωγος της συνάρτησης y είναι η ρίζα του x. Να βρείτε την παράγωγο: αλγόριθμος και παραδείγματα λύσεων

Η λειτουργία εύρεσης της παραγώγου ονομάζεται διαφοροποίηση.

Ως αποτέλεσμα της επίλυσης προβλημάτων εύρεσης παραγώγων των απλούστερων (και όχι πολύ απλών) συναρτήσεων ορίζοντας την παράγωγο ως το όριο του λόγου της αύξησης προς την αύξηση του επιχειρήματος, εμφανίστηκε ένας πίνακας παραγώγων και επακριβώς καθορισμένοι κανόνες διαφοροποίησης . Οι πρώτοι που εργάστηκαν στον τομέα της εύρεσης παραγώγων ήταν ο Isaac Newton (1643-1727) και ο Gottfried Wilhelm Leibniz (1646-1716).

Επομένως, στην εποχή μας, για να βρείτε την παράγωγο οποιασδήποτε συνάρτησης, δεν χρειάζεται να υπολογίσετε το προαναφερθέν όριο του λόγου της αύξησης της συνάρτησης προς την αύξηση του ορίσματος, αλλά χρειάζεται μόνο να χρησιμοποιήσετε τον πίνακα τα παράγωγα και οι κανόνες διαφοροποίησης. Ο παρακάτω αλγόριθμος είναι κατάλληλος για την εύρεση της παραγώγου.

Για να βρείτε την παράγωγο, χρειάζεστε μια έκφραση κάτω από το πρώτο σύμβολο αναλύει τις απλές λειτουργίες σε στοιχείακαι καθορίστε ποιες ενέργειες (προϊόν, άθροισμα, πηλίκο)αυτές οι λειτουργίες σχετίζονται. Στη συνέχεια, βρίσκουμε τις παραγώγους των στοιχειωδών συναρτήσεων στον πίνακα των παραγώγων και τους τύπους για τις παραγώγους του γινομένου, του αθροίσματος και του πηλίκου - στους κανόνες διαφοροποίησης. Ο πίνακας παραγώγων και οι κανόνες διαφοροποίησης δίνονται μετά τα δύο πρώτα παραδείγματα.

Παράδειγμα 1.Να βρείτε την παράγωγο μιας συνάρτησης

Λύση. Από τους κανόνες διαφοροποίησης διαπιστώνουμε ότι η παράγωγος ενός αθροίσματος συναρτήσεων είναι το άθροισμα των παραγώγων συναρτήσεων, δηλ.

Από τον πίνακα των παραγώγων διαπιστώνουμε ότι η παράγωγος του «x» ισούται με ένα, και η παράγωγος του ημιτόνου ίση με το συνημίτονο. Αντικαθιστούμε αυτές τις τιμές στο άθροισμα των παραγώγων και βρίσκουμε την παράγωγο που απαιτείται από την συνθήκη του προβλήματος:

Παράδειγμα 2.Να βρείτε την παράγωγο μιας συνάρτησης

Λύση. Διαφοροποιούμε ως παράγωγο ενός αθροίσματος στο οποίο ο δεύτερος όρος έχει σταθερό παράγοντα μπορεί να αφαιρεθεί από το πρόσημο της παραγώγου:

Εάν εξακολουθούν να προκύπτουν ερωτήσεις σχετικά με το από πού προέρχεται κάτι, συνήθως ξεκαθαρίζονται αφού εξοικειωθείτε με τον πίνακα των παραγώγων και τους απλούστερους κανόνες διαφοροποίησης. Προχωράμε σε αυτούς αυτή τη στιγμή.

Πίνακας παραγώγων απλών συναρτήσεων

1. Παράγωγος σταθεράς (αριθμός). Οποιοσδήποτε αριθμός (1, 2, 5, 200...) που βρίσκεται στην παράσταση συνάρτησης. Πάντα ίσο με μηδέν. Αυτό είναι πολύ σημαντικό να το θυμάστε, καθώς απαιτείται πολύ συχνά
2. Παράγωγος της ανεξάρτητης μεταβλητής. Τις περισσότερες φορές "Χ". Πάντα ίσο με ένα. Αυτό είναι επίσης σημαντικό να το θυμάστε για μεγάλο χρονικό διάστημα
3. Παράγωγο πτυχίου. Κατά την επίλυση προβλημάτων, πρέπει να μετατρέψετε τις μη τετραγωνικές ρίζες σε δυνάμεις.
4. Παράγωγος μεταβλητής στην ισχύ -1
5. Παράγωγο τετραγωνικής ρίζας
6. Παράγωγο ημιτόνου
7. Παράγωγο συνημίτονου
8. Παράγωγος εφαπτομένης
9. Παράγωγο συνεφαπτομένης
10. Παράγωγο αρσινίου
11. Παράγωγο συνημιτόνου τόξου
12. Παράγωγο του arctangent
13. Παράγωγο συνεφαπτομένης τόξου
14. Παράγωγος του φυσικού λογάριθμου
15. Παράγωγος λογαριθμικής συνάρτησης
16. Παράγωγος του εκθέτη
17. Παράγωγος εκθετικής συνάρτησης

Κανόνες διαφοροποίησης

1. Παράγωγο αθροίσματος ή διαφοράς
2. Παράγωγο του προϊόντος
2α. Παράγωγο έκφρασης πολλαπλασιαζόμενο με σταθερό παράγοντα
3. Παράγωγος του πηλίκου
4. Παράγωγος μιγαδικής συνάρτησης

Κανόνας 1.Εάν οι λειτουργίες

είναι διαφοροποιήσιμες σε κάποιο σημείο, τότε οι συναρτήσεις είναι διαφοροποιήσιμες στο ίδιο σημείο

και

εκείνοι. η παράγωγος ενός αλγεβρικού αθροίσματος συναρτήσεων ισούται με το αλγεβρικό άθροισμα των παραγώγων αυτών των συναρτήσεων.

Συνέπεια. Αν δύο διαφοροποιήσιμες συναρτήσεις διαφέρουν κατά σταθερό όρο, τότε οι παράγωγοί τους είναι ίσες, δηλ.

Κανόνας 2.Εάν οι λειτουργίες

είναι διαφοροποιήσιμα σε κάποιο σημείο, τότε το προϊόν τους είναι διαφοροποιήσιμο στο ίδιο σημείο

και

εκείνοι. Η παράγωγος του γινομένου δύο συναρτήσεων είναι ίση με το άθροισμα των γινομένων καθεμιάς από αυτές τις συναρτήσεις και την παράγωγο της άλλης.

Συμπέρασμα 1. Ο σταθερός παράγοντας μπορεί να αφαιρεθεί από το πρόσημο της παραγώγου:

Συμπέρασμα 2. Η παράγωγος του γινομένου πολλών διαφοροποιήσιμων συναρτήσεων είναι ίση με το άθροισμα των γινομένων της παραγώγου κάθε παράγοντα και όλων των άλλων.

Για παράδειγμα, για τρεις πολλαπλασιαστές:

Κανόνας 3.Εάν οι λειτουργίες

διαφοροποιήσιμο σε κάποιο σημείο Και , τότε σε αυτό το σημείο το πηλίκο τους είναι και διαφοροποιήσιμοu/v και

εκείνοι. η παράγωγος του πηλίκου δύο συναρτήσεων είναι ίση με ένα κλάσμα, ο αριθμητής του οποίου είναι η διαφορά μεταξύ των γινομένων του παρονομαστή και της παραγώγου του αριθμητή και του αριθμητή και της παραγώγου του παρονομαστή, και ο παρονομαστής είναι το τετράγωνο του ο πρώην αριθμητής.

Πού να αναζητήσετε πράγματα σε άλλες σελίδες

Όταν βρίσκουμε την παράγωγο ενός προϊόντος και ένα πηλίκο σε πραγματικά προβλήματα, είναι πάντα απαραίτητο να εφαρμόζουμε πολλούς κανόνες διαφοροποίησης ταυτόχρονα, επομένως περισσότερα παραδείγματαγια αυτά τα παράγωγα - στο άρθρο"Παράγωγο του γινομένου και πηλίκο συναρτήσεων".

Σχόλιο.Δεν πρέπει να συγχέετε μια σταθερά (δηλαδή έναν αριθμό) ως όρο σε άθροισμα και ως σταθερό παράγοντα! Στην περίπτωση ενός όρου, η παράγωγός του ισούται με μηδέν και σε περίπτωση σταθερού παράγοντα, βγαίνει από το πρόσημο των παραγώγων. Αυτό είναι ένα τυπικό σφάλμα που παρουσιάζεται στις αρχικό στάδιομελετώντας παραγώγους, αλλά καθώς λύνουμε πολλά μονομερή και διμερή παραδείγματα μέσος μαθητήςδεν κάνει πλέον αυτό το λάθος.

Και αν, όταν διαφοροποιείτε ένα προϊόν ή ένα πηλίκο, έχετε έναν όρο u"v, στο οποίο u- ένας αριθμός, για παράδειγμα, 2 ή 5, δηλαδή μια σταθερά, τότε η παράγωγος αυτού του αριθμού θα είναι ίση με μηδέν και, επομένως, ολόκληρος ο όρος θα είναι ίσος με μηδέν (αυτή η περίπτωση συζητείται στο παράδειγμα 10).

Ένα άλλο συνηθισμένο λάθος είναι η μηχανική επίλυση της παραγώγου μιας σύνθετης συνάρτησης ως παραγώγου μιας απλής συνάρτησης. Να γιατί παράγωγο μιγαδικής συνάρτησηςαφιερώνεται ένα ξεχωριστό άρθρο. Πρώτα όμως θα μάθουμε να βρίσκουμε παράγωγα απλές λειτουργίες.

Στην πορεία, δεν μπορείτε να κάνετε χωρίς να μεταμορφώσετε εκφράσεις. Για να το κάνετε αυτό, ίσως χρειαστεί να ανοίξετε το εγχειρίδιο σε νέα παράθυρα. Δράσεις με δυνάμεις και ρίζεςΚαι Πράξεις με κλάσματα .

Αν αναζητάτε λύσεις σε παραγώγους κλασμάτων με δυνάμεις και ρίζες, δηλαδή όταν η συνάρτηση μοιάζει με , μετά ακολουθήστε το μάθημα «Παράγωγος αθροισμάτων κλασμάτων με δυνάμεις και ρίζες».

Εάν έχετε μια εργασία όπως , τότε θα πάρετε το μάθημα «Παράγωγα απλών τριγωνομετρικών συναρτήσεων».

Παραδείγματα βήμα προς βήμα - πώς να βρείτε την παράγωγο

Παράδειγμα 3.Να βρείτε την παράγωγο μιας συνάρτησης

Λύση. Ορίζουμε τα μέρη της παράστασης συνάρτησης: ολόκληρη η παράσταση αντιπροσωπεύει ένα προϊόν και οι συντελεστές της είναι αθροίσματα, στο δεύτερο από τα οποία ένας από τους όρους περιέχει έναν σταθερό παράγοντα. Εφαρμόζουμε τον κανόνα διαφοροποίησης προϊόντος: η παράγωγος του γινομένου δύο συναρτήσεων είναι ίση με το άθροισμα των γινομένων καθεμιάς από αυτές τις συναρτήσεις από την παράγωγο της άλλης:

Στη συνέχεια, εφαρμόζουμε τον κανόνα της διαφοροποίησης του αθροίσματος: η παράγωγος του αλγεβρικού αθροίσματος των συναρτήσεων είναι ίση με το αλγεβρικό άθροισμα των παραγώγων αυτών των συναρτήσεων. Στην περίπτωσή μας, σε κάθε άθροισμα ο δεύτερος όρος έχει πρόσημο μείον. Σε κάθε άθροισμα βλέπουμε και μια ανεξάρτητη μεταβλητή, της οποίας η παράγωγος είναι ίση με ένα, και μια σταθερά (αριθμός), η παράγωγος της οποίας είναι ίση με μηδέν. Έτσι, το "Χ" μετατρέπεται σε ένα και το μείον 5 μετατρέπεται σε μηδέν. Στη δεύτερη παράσταση, το "x" πολλαπλασιάζεται επί 2, άρα πολλαπλασιάζουμε δύο με την ίδια μονάδα με την παράγωγο του "x". Λαμβάνουμε τις ακόλουθες τιμές παραγώγων:

Αντικαθιστούμε τις παραγώγους που βρέθηκαν στο άθροισμα των γινομένων και λαμβάνουμε την παράγωγο ολόκληρης της συνάρτησης που απαιτείται από την συνθήκη του προβλήματος:

Και μπορείτε να ελέγξετε τη λύση στο πρόβλημα της παραγώγου στο.

Παράδειγμα 4.Να βρείτε την παράγωγο μιας συνάρτησης

Λύση. Απαιτείται να βρούμε την παράγωγο του πηλίκου. Εφαρμόζουμε τον τύπο για τη διαφοροποίηση του πηλίκου: η παράγωγος του πηλίκου δύο συναρτήσεων είναι ίση με ένα κλάσμα, ο αριθμητής του οποίου είναι η διαφορά μεταξύ των γινομένων του παρονομαστή και της παραγώγου του αριθμητή και του αριθμητή και της παραγώγου του παρονομαστής, και ο παρονομαστής είναι το τετράγωνο του προηγούμενου αριθμητή. Παίρνουμε:

Έχουμε ήδη βρει την παράγωγο των παραγόντων στον αριθμητή στο παράδειγμα 2. Ας μην ξεχνάμε επίσης ότι το γινόμενο, που είναι ο δεύτερος παράγοντας στον αριθμητή στο τρέχον παράδειγμα, λαμβάνεται με πρόσημο μείον:

Αν ψάχνετε για λύσεις σε προβλήματα στα οποία πρέπει να βρείτε την παράγωγο μιας συνάρτησης, όπου υπάρχει ένας συνεχής σωρός από ρίζες και δυνάμεις, όπως, για παράδειγμα, , τότε καλώς ήρθατε στην τάξη "Παράγωγο αθροισμάτων κλασμάτων με δυνάμεις και ρίζες" .

Εάν χρειάζεται να μάθετε περισσότερα για τις παραγώγους των ημιτόνων, των συνημιτόνων, των εφαπτομένων και άλλων τριγωνομετρικές συναρτήσεις, δηλαδή όταν μοιάζει η συνάρτηση , τότε ένα μάθημα για εσάς "Παράγωγα απλών τριγωνομετρικών συναρτήσεων" .

Παράδειγμα 5.Να βρείτε την παράγωγο μιας συνάρτησης

Λύση. Σε αυτή τη συνάρτηση βλέπουμε ένα γινόμενο, ένας από τους παράγοντες του οποίου είναι η τετραγωνική ρίζα της ανεξάρτητης μεταβλητής, την παράγωγο της οποίας εξοικειωθήκαμε στον πίνακα των παραγώγων. Χρησιμοποιώντας τον κανόνα για τη διαφοροποίηση του γινομένου και της πινακοποιημένης τιμής της παραγώγου της τετραγωνικής ρίζας, παίρνουμε:

Μπορείτε να ελέγξετε τη λύση στο πρόβλημα της παραγώγου στο διαδικτυακή αριθμομηχανή παραγώγων .

Παράδειγμα 6.Να βρείτε την παράγωγο μιας συνάρτησης

Λύση. Σε αυτή τη συνάρτηση βλέπουμε ένα πηλίκο του οποίου το μέρισμα είναι η τετραγωνική ρίζα της ανεξάρτητης μεταβλητής. Χρησιμοποιώντας τον κανόνα διαφοροποίησης των πηλίκων, που επαναλάβαμε και εφαρμόσαμε στο παράδειγμα 4, και την πινακοποιημένη τιμή της παραγώγου της τετραγωνικής ρίζας, παίρνουμε:

Για να απαλλαγείτε από ένα κλάσμα στον αριθμητή, πολλαπλασιάστε τον αριθμητή και τον παρονομαστή με .

1. Γενική περίπτωση του τύπου για την παράγωγο ρίζας αυθαίρετου βαθμού- ένα κλάσμα στον αριθμητή του οποίου υπάρχει ένας και στον παρονομαστή ένας αριθμός ίσος με τη δύναμη της ρίζας για την οποία υπολογίστηκε η παράγωγος, πολλαπλασιαζόμενος με τη ρίζα της ίδιας δύναμης, η ριζική έκφραση του οποίου είναι μεταβλητή σε η ισχύς της ρίζας για την οποία υπολογίστηκε η παράγωγος, μειωμένη κατά ένα
2. Παράγωγο τετραγωνικής ρίζας- είναι μια ειδική περίπτωση του προηγούμενου τύπου. Παράγωγο της τετραγωνικής ρίζας του xείναι ένα κλάσμα του οποίου ο αριθμητής είναι ένας και ο παρονομαστής είναι δύο φορές η τετραγωνική ρίζα του x
3. Παράγωγο κυβικής ρίζας, Επίσης ειδική περίπτωσηγενικός τύπος. Το παράγωγο μιας κυβικής ρίζας είναι ένα διαιρούμενο με τρεις κυβικές ρίζες x στο τετράγωνο.

Ακολουθούν μετασχηματισμοί που εξηγούν γιατί οι τύποι για την εύρεση των παραγώγων τετραγωνικών και κυβικών ριζών είναι ακριβώς οι ίδιοι με αυτούς που φαίνονται στο σχήμα.

Φυσικά, δεν χρειάζεται να θυμάστε καθόλου αυτούς τους τύπους, αν λάβετε υπόψη ότι η εξαγωγή της ρίζας μιας παραγώγου ισχύος είναι το ίδιο με το να αυξήσετε ένα κλάσμα του οποίου ο παρονομαστής είναι ίσος με την ίδια ισχύ. Στη συνέχεια, η εύρεση της παραγώγου της ρίζας ανάγεται στην εφαρμογή του τύπου για την εύρεση της παραγώγου της ισχύος του αντίστοιχου κλάσματος.

Παράγωγο μεταβλητής κάτω από τετραγωνική ρίζα

(√x)" = 1 / (2√x)ή 1/2 x -1/2

Εξήγηση:
(√x)" = (x 1/2)"

Η τετραγωνική ρίζα είναι ακριβώς η ίδια λειτουργία με την αύξηση στη δύναμη του 1/2,Αυτό σημαίνει ότι για να βρείτε την παράγωγο μιας ρίζας, μπορείτε να εφαρμόσετε τον τύπο από τον κανόνα για την εύρεση της παραγώγου μιας μεταβλητής σε αυθαίρετο βαθμό:

(x 1/2)" = 1/2 x -1/2 = 1 / (2√x)

Παράγωγο κυβικής ρίζας (παράγωγο τρίτης ρίζας)

Το παράγωγο μιας κυβικής ρίζας βρίσκεται χρησιμοποιώντας ακριβώς την ίδια αρχή με την τετραγωνική ρίζα.

Φανταστείτε την κυβική ρίζα ως δύναμη 1/3 και βρείτε την παράγωγο σε σχέση με γενικοί κανόνεςΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ-διάκριση. Ο σύντομος τύπος φαίνεται στην παραπάνω εικόνα και παρακάτω είναι μια εξήγηση του γιατί συμβαίνει αυτό.

Η ισχύς -2/3 προκύπτει αφαιρώντας το ένα από το 1/3

Λειτουργίες σύνθετου τύπουδεν ταιριάζουν πάντα με τον ορισμό μιας σύνθετης συνάρτησης. Αν υπάρχει συνάρτηση της μορφής y = sin x - (2 - 3) · a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, τότε δεν μπορεί να θεωρηθεί σύνθετη, σε αντίθεση με το y = sin 2 x.

Αυτό το άρθρο θα δείξει την έννοια μιας σύνθετης συνάρτησης και τον προσδιορισμό της. Ας δουλέψουμε με τύπους για την εύρεση της παραγώγου με παραδείγματα λύσεων στο συμπέρασμα. Η χρήση του πίνακα παραγώγων και των κανόνων διαφοροποίησης μειώνει σημαντικά τον χρόνο εύρεσης του παραγώγου.

Βασικοί ορισμοί

Ορισμός 1

Μια σύνθετη συνάρτηση είναι αυτή της οποίας το όρισμα είναι επίσης συνάρτηση.

Αυτό συμβολίζεται ως εξής: f (g (x)). Έχουμε ότι η συνάρτηση g (x) θεωρείται όρισμα f (g (x)).

Ορισμός 2

Αν υπάρχει συνάρτηση f και είναι συνεφαπτομένη, τότε g(x) = ln x είναι η φυσική συνάρτηση λογάριθμου. Διαπιστώνουμε ότι η μιγαδική συνάρτηση f (g (x)) θα γραφτεί ως arctg(lnx). Ή μια συνάρτηση f, η οποία είναι μια συνάρτηση αυξημένη στην 4η δύναμη, όπου g (x) = x 2 + 2 x - 3 θεωρείται μια ολόκληρη ορθολογική συνάρτηση, λαμβάνουμε ότι f (g (x)) = (x 2 + 2 x - 3) 4 .

Προφανώς το g(x) μπορεί να είναι σύνθετο. Από το παράδειγμα y = sin 2 x + 1 x 3 - 5 είναι σαφές ότι η τιμή του g έχει την κυβική ρίζα του κλάσματος. Αυτή η έκφραση μπορεί να συμβολιστεί ως y = f (f 1 (f 2 (x))). Από όπου έχουμε ότι η f είναι ημιτονοειδής συνάρτηση και η f 1 είναι μια συνάρτηση που βρίσκεται κάτω από την τετραγωνική ρίζα, η f 2 (x) = 2 x + 1 x 3 - 5 είναι μια κλασματική ορθολογική συνάρτηση.

Ορισμός 3

Ο βαθμός φωλιάς καθορίζεται από οποιαδήποτε φυσικός αριθμόςκαι γράφεται ως y = f (f 1 (f 2 (f 3 (... (f n (x)))))) .

Ορισμός 4

Η έννοια της σύνθεσης συνάρτησης αναφέρεται στον αριθμό των ένθετων συναρτήσεων σύμφωνα με τις συνθήκες του προβλήματος. Για να λύσετε, χρησιμοποιήστε τον τύπο για την εύρεση της παραγώγου μιας μιγαδικής συνάρτησης της μορφής

(f (g (x))) " = f " (g (x)) g " (x)

Παραδείγματα

Παράδειγμα 1

Να βρείτε την παράγωγο μιγαδικής συνάρτησης της μορφής y = (2 x + 1) 2.

Λύση

Η συνθήκη δείχνει ότι η f είναι συνάρτηση τετραγωνισμού και η g(x) = 2 x + 1 θεωρείται γραμμική συνάρτηση.

Ας εφαρμόσουμε τον τύπο της παραγώγου για μια σύνθετη συνάρτηση και ας γράψουμε:

f " (g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g " (x) = (2 x + 1) " = (2 x) " + 1 " = 2 x " + 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) " = f " (g (x)) g " (x) = 2 (2 x + 1) 2 = 8 x + 4

Είναι απαραίτητο να βρεθεί η παράγωγος με μια απλοποιημένη αρχική μορφή της συνάρτησης. Παίρνουμε:

y = (2 x + 1) 2 = 4 x 2 + 4 x + 1

Από εδώ το έχουμε

y " = (4 x 2 + 4 x + 1) " = (4 x 2) " + (4 x) " + 1 " = 4 (x 2) " + 4 (x) " + 0 = = 4 · 2 · x 2 - 1 + 4 · 1 · x 1 - 1 = 8 x + 4

Τα αποτελέσματα ήταν τα ίδια.

Κατά την επίλυση προβλημάτων αυτού του τύπου, είναι σημαντικό να κατανοήσουμε πού θα βρίσκεται η συνάρτηση της μορφής f και g (x).

Παράδειγμα 2

Θα πρέπει να βρείτε τις παραγώγους των μιγαδικών συναρτήσεων της μορφής y = sin 2 x και y = sin x 2.

Λύση

Ο πρώτος συμβολισμός συνάρτησης λέει ότι η f είναι η συνάρτηση τετραγωνισμού και η g(x) είναι η ημιτονοειδής συνάρτηση. Τότε το καταλαβαίνουμε

y " = (αμαρτία 2 x) " = 2 αμαρτία 2 - 1 x (αμαρτία x) " = 2 αμαρτία x συν x

Η δεύτερη καταχώριση δείχνει ότι η f είναι μια ημιτονοειδής συνάρτηση και η g(x) = x 2 υποδηλώνει μια συνάρτηση ισχύος. Από αυτό προκύπτει ότι γράφουμε το γινόμενο μιας μιγαδικής συνάρτησης ως

y " = (sin x 2) " = cos (x 2) (x 2) " = cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)

Ο τύπος για την παράγωγο y = f (f 1 (f 2 (f 3 (. . . (f n (x))))) θα γραφεί ως y " = f " (f 1 (f 2 (f 3 (. . )) )) · . . . fn "(x)

Παράδειγμα 3

Να βρείτε την παράγωγο της συνάρτησης y = sin (ln 3 a r c t g (2 x)).

Λύση

Αυτό το παράδειγμα δείχνει τη δυσκολία γραφής και προσδιορισμού της θέσης των συναρτήσεων. Τότε y = f (f 1 (f 2 (f 3 (f 4 (x))))) δηλώνει όπου f , f 1 , f 2 , f 3 , f 4 (x) είναι η ημιτονοειδής συνάρτηση, η συνάρτηση ανύψωσης έως 3 μοίρες, συνάρτηση με λογάριθμο και βάση e, εφαπτομενική και γραμμική συνάρτηση.

Από τον τύπο για τον ορισμό μιας μιγαδικής συνάρτησης έχουμε ότι

y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2 " (f 3 (f 4 (x)) f 3 " (f 4 (x)) f 4 " (x)

Παίρνουμε αυτό που πρέπει να βρούμε

1. f " (f 1 (f 2 (f 3 (f 4 (x))))) ως η παράγωγος του ημιτόνου σύμφωνα με τον πίνακα των παραγώγων, στη συνέχεια f " (f 1 (f 2 (f 3 (f 4 ( x)))) ) = cos (ln 3 a r c t g (2 x)) .
2. f 1 "(f 2 (f 3 (f 4 (x)))) ως παράγωγο λειτουργία ισχύος, μετά f 1 "(f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 a r c t g (2 x) = 3 ln 2 a r c t g (2 x).
3. f 2 " (f 3 (f 4 (x))) ως λογαριθμική παράγωγος, μετά f 2" (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
4. f 3 " (f 4 (x)) ως η παράγωγος της εφαπτομένης, μετά f 3" (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. Όταν βρίσκετε την παράγωγο f 4 (x) = 2 x, αφαιρέστε το 2 από το πρόσημο της παραγώγου χρησιμοποιώντας τον τύπο για την παράγωγο μιας συνάρτησης ισχύος με εκθέτη ίσο με 1, στη συνέχεια f 4 " (x) = (2 x) " = 2 x " = 2 · 1 · x 1 - 1 = 2 .

Συνδυάζουμε τα ενδιάμεσα αποτελέσματα και το παίρνουμε

y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2 " (f 3 (f 4 (x)) f 3 " (f 4 (x)) f 4 " (x) = = cos (ln 3 a r c t g (2 x)) 3 ln 2 a r c t g (2 x) 1 a r c t g (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 a r c t g (2 x)) ln 2 a r c t g (2 x) a r c t g (2 x) (1 + 4 x 2)

Η ανάλυση τέτοιων λειτουργιών θυμίζει κούκλες που φωλιάζουν. Οι κανόνες διαφοροποίησης δεν μπορούν πάντα να εφαρμόζονται ρητά χρησιμοποιώντας έναν πίνακα παραγώγων. Συχνά χρειάζεται να χρησιμοποιήσετε έναν τύπο για την εύρεση παραγώγων μιγαδικών συναρτήσεων.

Υπάρχουν κάποιες διαφορές μεταξύ σύνθετης εμφάνισης και πολύπλοκων λειτουργιών. Με σαφή ικανότητα διάκρισης αυτού, η εύρεση παραγώγων θα είναι ιδιαίτερα εύκολη.

Παράδειγμα 4

Πρέπει να ληφθεί υπόψη στο casting παρόμοιο παράδειγμα. Αν υπάρχει συνάρτηση της μορφής y = t g 2 x + 3 t g x + 1, τότε μπορεί να θεωρηθεί ως σύνθετη συνάρτηση της μορφής g (x) = t g x, f (g) = g 2 + 3 g + 1 . Προφανώς, είναι απαραίτητο να χρησιμοποιηθεί ο τύπος για μια σύνθετη παράγωγο:

f " (g (x)) = (g 2 (x) + 3 g (x) + 1) " = (g 2 (x)) " + (3 g (x)) " + 1 " = = 2 · g 2 - 1 (x) + 3 g " (x) + 0 = 2 g (x) + 3 1 g 1 - 1 (x) = = 2 g (x) + 3 = 2 t g x + 3 ; g " (x) = (t g x) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 t g x + 3 ) · 1 cos 2 x = 2 t g x + 3 cos 2 x

Μια συνάρτηση της μορφής y = t g x 2 + 3 t g x + 1 δεν θεωρείται σύνθετη, αφού έχει το άθροισμα των t g x 2, 3 t g x και 1. Ωστόσο, η t g x 2 θεωρείται σύνθετη συνάρτηση, τότε λαμβάνουμε μια συνάρτηση ισχύος της μορφής g (x) = x 2 και f, η οποία είναι εφαπτομένη. Για να το κάνετε αυτό, διαφοροποιήστε κατά ποσό. Το καταλαβαίνουμε

y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + (3 t g x) " + 1 " = = (t g x 2) " + 3 (t g x) " + 0 = (t g x 2) " + 3 cos 2 x

Ας προχωρήσουμε στην εύρεση της παραγώγου μιας μιγαδικής συνάρτησης (t g x 2) ":

f " (g (x)) = (t g (g (x))) " = 1 cos 2 g (x) = 1 cos 2 (x 2) g " (x) = (x 2) " = 2 x 2 - 1 = 2 x ⇒ (t g x 2) " = f " (g (x)) g " (x) = 2 x cos 2 (x 2)

Παίρνουμε ότι y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Οι συναρτήσεις ενός μιγαδικού τύπου μπορούν να συμπεριληφθούν σε μιγαδικές συναρτήσεις και οι ίδιες οι σύνθετες συναρτήσεις μπορούν να είναι συστατικά συναρτήσεων μιγαδικού τύπου.

Παράδειγμα 5

Για παράδειγμα, θεωρήστε μια σύνθετη συνάρτηση της μορφής y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Αυτή η συνάρτηση μπορεί να αναπαρασταθεί ως y = f (g (x)), όπου η τιμή της f είναι συνάρτηση του λογάριθμου βάσης 3 και η g (x) θεωρείται το άθροισμα δύο συναρτήσεων της μορφής h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 και k (x) = ln 2 x · (x 2 + 1) . Προφανώς, y = f (h (x) + k (x)).

Θεωρήστε τη συνάρτηση h(x). Αυτή είναι η αναλογία l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 προς m (x) = e x 2 + 3 3

Έχουμε ότι l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) είναι το άθροισμα δύο συναρτήσεων n (x) = x 2 + 7 και p ( x) = 3 cos 3 (2 x + 1) , όπου p (x) = 3 p 1 (p 2 (p 3 (x))) είναι μια σύνθετη συνάρτηση με αριθμητικό συντελεστή 3, και η p 1 είναι μια συνάρτηση κύβου, p 2 με συνημίτονο, p 3 (x) = 2 x + 1 από μια γραμμική συνάρτηση.

Βρήκαμε ότι m (x) = e x 2 + 3 3 = q (x) + r (x) είναι το άθροισμα δύο συναρτήσεων q (x) = e x 2 και r (x) = 3 3, όπου q (x) = q 1 (q 2 (x)) είναι μιγαδική συνάρτηση, q 1 είναι συνάρτηση με εκθετική, q 2 (x) = x 2 είναι συνάρτηση ισχύος.

Αυτό δείχνει ότι h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)

Όταν μετακινούμαστε σε μια παράσταση της μορφής k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x), είναι σαφές ότι η συνάρτηση παρουσιάζεται με τη μορφή μιγαδικού s ( x) = ln 2 x = s 1 ( s 2 (x)) με ορθολογικό ακέραιο t (x) = x 2 + 1, όπου s 1 είναι τετραγωνισμένη συνάρτηση και s 2 (x) = ln x είναι λογαριθμική με βάση ε.

Συνεπάγεται ότι η παράσταση θα πάρει τη μορφή k (x) = s (x) · t (x) = s 1 (s 2 (x)) · t (x).

Τότε το καταλαβαίνουμε

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) = = f n (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Με βάση τις δομές της συνάρτησης, έγινε σαφές πώς και ποιοι τύποι πρέπει να χρησιμοποιούνται για την απλοποίηση της έκφρασης κατά τη διαφοροποίησή της. Για να εξοικειωθούμε με τέτοια προβλήματα και για την έννοια της επίλυσής τους, είναι απαραίτητο να στραφούμε στο σημείο της διαφοροποίησης μιας συνάρτησης, δηλαδή στην εύρεση της παραγώγου της.

Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter

Παραγωγή του τύπου για την παράγωγο συνάρτησης ισχύος (x στη δύναμη του α). Θεωρούνται παράγωγα από ρίζες του x. Τύπος για την παράγωγο συνάρτησης ισχύος υψηλότερης τάξης. Παραδείγματα υπολογισμού παραγώγων.

Περιεχόμενο

Δείτε επίσης: Συνάρτηση ισχύος και ρίζες, τύποι και γράφημα
Γραφήματα συναρτήσεων ισχύος

Βασικοί τύποι

Η παράγωγος του x στη δύναμη του a είναι ίση με a επί x στη δύναμη ενός μείον ένα:
(1) .

Η παράγωγος της νης ρίζας του x στη mth δύναμη είναι:
(2) .

Παραγωγή του τύπου για την παράγωγο συνάρτησης ισχύος

Περίπτωση x > 0

Θεωρήστε μια συνάρτηση ισχύος της μεταβλητής x με εκθέτη a:
(3) .
Εδώ το a είναι ένας αυθαίρετος πραγματικός αριθμός. Ας εξετάσουμε πρώτα την περίπτωση.

Για να βρούμε την παράγωγο της συνάρτησης (3), χρησιμοποιούμε τις ιδιότητες μιας συνάρτησης ισχύος και τη μετατρέπουμε στην ακόλουθη μορφή:
.

Τώρα βρίσκουμε την παράγωγο χρησιμοποιώντας:
;
.
Εδώ .

Η φόρμουλα (1) έχει αποδειχθεί.

Παραγωγή του τύπου για την παράγωγο ρίζας βαθμού n του x στον βαθμό m

Τώρα θεωρήστε μια συνάρτηση που είναι η ρίζα της παρακάτω φόρμας:
(4) .

Για να βρούμε την παράγωγο, μετατρέπουμε τη ρίζα σε συνάρτηση ισχύος:
.
Συγκρίνοντας με τον τύπο (3) βλέπουμε ότι
.
Επειτα
.

Χρησιμοποιώντας τον τύπο (1) βρίσκουμε την παράγωγο:
(1) ;
;
(2) .

Στην πράξη, δεν χρειάζεται να απομνημονεύσετε τον τύπο (2). Είναι πολύ πιο βολικό να μετατρέψετε πρώτα τις ρίζες σε συναρτήσεις ισχύος και, στη συνέχεια, να βρείτε τα παράγωγά τους χρησιμοποιώντας τον τύπο (1) (δείτε παραδείγματα στο τέλος της σελίδας).

Περίπτωση x = 0

Αν , τότε η συνάρτηση ισχύος ορίζεται για την τιμή της μεταβλητής x = 0 . Ας βρούμε την παράγωγο της συνάρτησης (3) στο x = 0 . Για να γίνει αυτό, χρησιμοποιούμε τον ορισμό μιας παραγώγου:
.

Ας αντικαταστήσουμε το x = 0 :
.
Στην περίπτωση αυτή, ως παράγωγος εννοούμε το δεξιό όριο για το οποίο .

Βρήκαμε λοιπόν:
.
Από αυτό είναι σαφές ότι για , .
Στο , .
Στο , .
Αυτό το αποτέλεσμα προκύπτει επίσης από τον τύπο (1):
(1) .
Επομένως, ο τύπος (1) ισχύει και για x = 0 .

Περίπτωση x< 0

Εξετάστε ξανά τη συνάρτηση (3):
(3) .
Για ορισμένες τιμές της σταθεράς a, ορίζεται και για αρνητικές τιμές της μεταβλητής x. Δηλαδή, έστω a είναι ένας ρητός αριθμός. Τότε μπορεί να αναπαρασταθεί ως μη αναγώγιμο κλάσμα:
,
όπου m και n είναι ακέραιοι που δεν έχουν κοινό διαιρέτη.

Εάν το n είναι περιττό, τότε η συνάρτηση ισχύος ορίζεται επίσης για τις αρνητικές τιμές της μεταβλητής x. Για παράδειγμα, όταν n = 3 και m = 1 έχουμε την κυβική ρίζα του x:
.
Ορίζεται επίσης για αρνητικές τιμές της μεταβλητής x.

Ας βρούμε την παράγωγο της συνάρτησης ισχύος (3) για και για λογικές τιμές της σταθεράς a για την οποία ορίζεται. Για να γίνει αυτό, ας αναπαραστήσουμε το x στην ακόλουθη μορφή:
.
Επειτα ,
.
Βρίσκουμε την παράγωγο τοποθετώντας τη σταθερά έξω από το πρόσημο της παραγώγου και εφαρμόζοντας τον κανόνα για τη διαφοροποίηση μιας μιγαδικής συνάρτησης:

.
Εδώ . Αλλά
.
Από τότε
.
Επειτα
.
Δηλαδή, ο τύπος (1) ισχύει και για:
(1) .

Παράγωγα υψηλότερης τάξης

Ας βρούμε τώρα παραγώγους υψηλότερης τάξης της συνάρτησης ισχύος
(3) .
Έχουμε ήδη βρει την παράγωγο πρώτης τάξης:
.

Παίρνοντας τη σταθερά a έξω από το πρόσημο της παραγώγου, βρίσκουμε την παράγωγο δεύτερης τάξης:
.
Ομοίως, βρίσκουμε παράγωγα τρίτης και τέταρτης τάξης:
;

.

Από αυτό είναι σαφές ότι παράγωγο αυθαίρετης νης τάξηςέχει την εξής μορφή:
.

σημειώσε ότι αν ο α είναι φυσικός αριθμός, τότε η ντη παράγωγος είναι σταθερή:
.
Τότε όλες οι επόμενες παράγωγοι είναι ίσες με μηδέν:
,
στο .

Παραδείγματα υπολογισμού παραγώγων

Παράδειγμα

Βρείτε την παράγωγο της συνάρτησης:
.

Ας μετατρέψουμε τις ρίζες σε δυνάμεις:
;
.
Τότε η αρχική συνάρτηση παίρνει τη μορφή:
.

Εύρεση παραγώγων δυνάμεων:
;
.
Η παράγωγος της σταθεράς είναι μηδέν:
.

Οδηγίες

Πριν βρείτε την παράγωγο της ρίζας, δώστε προσοχή στις άλλες συναρτήσεις που υπάρχουν στο παράδειγμα που λύνεται. Εάν το πρόβλημα έχει πολλές ριζικές εκφράσεις, τότε χρησιμοποιήστε τον ακόλουθο κανόνα για να βρείτε την παράγωγο της τετραγωνικής ρίζας:

(√x)" = 1 / 2√x.

Και για να βρείτε το παράγωγο της κυβικής ρίζας, χρησιμοποιήστε τον τύπο:

(³√х)" = 1 / 3(³√х)²,

όπου ³√x δηλώνει την κυβική ρίζα του x.

Εάν, που προορίζεται για διαφοροποίηση, υπάρχει μια μεταβλητή στο κλασματικό , τότε μετατρέψτε τη ρίζα σε συνάρτηση ισχύος με τον κατάλληλο εκθέτη. Για μια τετραγωνική ρίζα θα είναι δύναμη ½ και για μια κυβική ρίζα θα είναι ⅓:

√x = x^½,
³√х = x ^ ⅓,

όπου το ^ δηλώνει εκθετικότητα.

Για να βρείτε την παράγωγο μιας συνάρτησης ισχύος γενικά και x^1, x^⅓ ειδικότερα, χρησιμοποιήστε τον ακόλουθο κανόνα:

(x^n)" = n * x^(n-1).

Για το παράγωγο μιας ρίζας, αυτή η σχέση συνεπάγεται:

(x^½)" = ½ x ^ (-½) και
(x^⅓)" = ⅓ x ^ (-⅔).

Έχοντας διαφοροποιήσει τα πάντα, δείτε προσεκτικά το υπόλοιπο παράδειγμα. Εάν έχετε μια πολύ δυσκίνητη έκφραση στην απάντησή σας, τότε μπορείτε πιθανώς να την απλοποιήσετε. Η πλειοψηφία σχολικά παραδείγματασυντίθεται με τέτοιο τρόπο ώστε το αποτέλεσμα να είναι ένας μικρός αριθμός ή μια συμπαγής έκφραση.

Σε πολλά προβλήματα παραγώγων, οι ρίζες (τετράγωνο και κύβος) βρίσκονται μαζί με άλλες συναρτήσεις. Για να βρείτε το παράγωγο της ρίζας σε αυτήν την περίπτωση, χρησιμοποιήστε τους ακόλουθους κανόνες:
η παράγωγος μιας σταθεράς (σταθερός αριθμός, C) ισούται με μηδέν: C" = 0;
ο σταθερός παράγοντας αφαιρείται από το παράγωγο πρόσημο: (k*f)" = k * (f)" (f είναι μια αυθαίρετη συνάρτηση).
η παράγωγος του αθροίσματος πολλών συναρτήσεων είναι ίση με το άθροισμα των παραγώγων: (f + g)" = (f)" + (g)";
η παράγωγος του γινομένου δύο συναρτήσεων ισούται με... όχι, όχι το γινόμενο των παραγώγων, αλλά η ακόλουθη έκφραση: (fg)" = (f)"g + f (g)";
η παράγωγος του πηλίκου επίσης δεν είναι ίση με το πηλίκο των παραγώγων, αλλά βρίσκεται σύμφωνα με τον ακόλουθο κανόνα: (f/g)" = ((f)"g – f(g)") / g².

Σημείωση

Σε αυτή τη σελίδα θα μπορείτε να υπολογίσετε την παράγωγο μιας συνάρτησης online, λαμβάνοντας αναλυτική λύσηκαθήκοντα. Η λύση των παραγώγων μιας συνάρτησης γίνεται χρησιμοποιώντας τους κανόνες διαφοροποίησης που μαθαίνουν οι μαθητές στο μάθημα μαθηματική ανάλυσηΣτο ινστιτούτο. Για να βρείτε την παράγωγο μιας συνάρτησης, πρέπει να εισαγάγετε τη συνάρτηση για διαφοροποίηση στο πεδίο "Function" σύμφωνα με τους κανόνες εισαγωγής δεδομένων.

Χρήσιμες συμβουλές

Η παράγωγος μιας συνάρτησης είναι το όριο του λόγου της αύξησης μιας συνάρτησης προς την αύξηση του ορίσματος όταν η αύξηση του ορίσματος τείνει στο μηδέν: Το μαθηματικό νόημα αυτού του ορισμού δεν είναι πολύ εύκολο να κατανοηθεί, αφού σε ένα σχολείο μάθημα άλγεβρας η έννοια του ορίου μιας συνάρτησης είτε δεν μελετάται καθόλου είτε μελετάται πολύ επιφανειακά. Αλλά για να μάθετε πώς να βρίσκετε παράγωγα διαφόρων συναρτήσεων, αυτό δεν είναι απαραίτητο.

Πηγές:

• παράγωγο της ρίζας του x