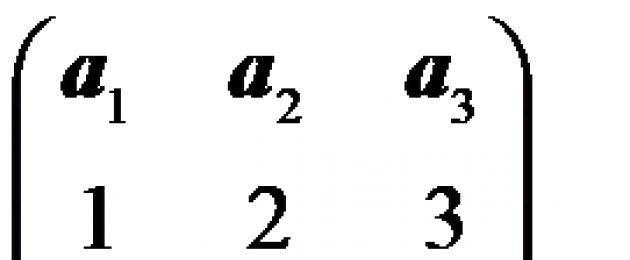Πώς να ελέγξετε εάν τα διανύσματα εξαρτώνται γραμμικά. Γραμμική εξάρτηση και γραμμική ανεξαρτησία διανυσμάτων

Γραμμική εξάρτηση διανυσμάτων

Κατά την επίλυση διαφόρων προβλημάτων, κατά κανόνα, δεν πρέπει να ασχοληθεί κανείς με ένα διάνυσμα, αλλά με ένα ορισμένο σύνολο διανυσμάτων της ίδιας διάστασης. Τέτοια αδρανή ονομάζονται σύστημα διανυσμάτωνκαι δηλώνουν

Ορισμός.Γραμμικός συνδυασμός διανυσμάτωνονομάζεται διάνυσμα της μορφής

όπου υπάρχουν πραγματικοί αριθμοί. Ένα διάνυσμα λέγεται επίσης ότι εκφράζεται γραμμικά ως διανύσματα ή αποσυντίθεται σε αυτά τα διανύσματα.

Για παράδειγμα, ας δοθούν τρία διανύσματα: , , . Ο γραμμικός συνδυασμός τους με τους συντελεστές 2, 3 και 4, αντίστοιχα, είναι το διάνυσμα

Ορισμός.Το σύνολο όλων των δυνατών γραμμικών συνδυασμών ενός συστήματος διανυσμάτων ονομάζεται γραμμικό εύρος αυτού του συστήματος.

Ορισμός.Ένα σύστημα μη μηδενικών διανυσμάτων ονομάζεται γραμμικά εξαρτώμενη, εάν υπάρχουν αριθμοί που δεν είναι ταυτόχρονα ίσοι με μηδέν, έτσι ώστε ο γραμμικός συνδυασμός ενός δεδομένου συστήματος με τους υποδεικνυόμενους αριθμούς να είναι ίσος με το μηδενικό διάνυσμα:

Εάν η τελευταία ισότητα για ένα δεδομένο σύστημα διανυσμάτων είναι δυνατή μόνο για , τότε αυτό το σύστημα διανυσμάτων ονομάζεται γραμμικά ανεξάρτητη.

Για παράδειγμα, ένα σύστημα δύο διανυσμάτων είναι γραμμικά ανεξάρτητο. σύστημα δύο διανυσμάτων και εξαρτάται γραμμικά, αφού .

Έστω το σύστημα των διανυσμάτων (19) γραμμικά εξαρτώμενο. Ας επιλέξουμε τον όρο στο άθροισμα (20) στον οποίο είναι ο συντελεστής και ας τον εκφράσουμε με τους υπόλοιπους όρους:

Όπως φαίνεται από αυτή την ισότητα, ένα από τα διανύσματα του γραμμικά εξαρτημένου συστήματος (19) αποδείχθηκε ότι εκφράζεται ως προς άλλα διανύσματα αυτού του συστήματος (ή επεκτείνεται ως προς τα υπόλοιπα διανύσματά του).

Ιδιότητες ενός γραμμικά εξαρτώμενου διανυσματικού συστήματος

1. Ένα σύστημα που αποτελείται από ένα μη μηδενικό διάνυσμα είναι γραμμικά ανεξάρτητο.

2. Ένα σύστημα που περιέχει μηδενικό διάνυσμα είναι πάντα γραμμικά εξαρτημένο.

3. Ένα σύστημα που περιέχει περισσότερα από ένα διανύσματα εξαρτάται γραμμικά εάν και μόνο εάν τα διανύσματά του περιέχουν τουλάχιστον ένα διάνυσμα που εκφράζεται γραμμικά ως προς τα άλλα.

Η γεωμετρική σημασία μιας γραμμικής σχέσης στην περίπτωση των δισδιάστατων διανυσμάτων σε ένα επίπεδο: όταν ένα διάνυσμα εκφράζεται μέσω ενός άλλου, έχουμε, δηλ. Αυτά τα διανύσματα είναι συγγραμμικά, ή το ίδιο, που βρίσκονται σε παράλληλες ευθείες.

Στη χωρική περίπτωση γραμμικής εξάρτησης τριών διανυσμάτων, είναι παράλληλα σε ένα επίπεδο, δηλ. ομοεπίπεδη. Αρκεί να «διορθωθούν» τα μήκη αυτών των διανυσμάτων με τους αντίστοιχους παράγοντες, ώστε ο ένας από αυτούς να γίνει το άθροισμα των άλλων δύο ή να εκφραστεί μέσω αυτών.

Θεώρημα.Στο διάστημα, κάθε σύστημα που περιέχει διανύσματα εξαρτάται γραμμικά από το .

Παράδειγμα.Μάθετε εάν τα διανύσματα εξαρτώνται γραμμικά.

Λύση. Ας κάνουμε μια διανυσματική ισότητα. Γράφοντας σε διανυσματική μορφή στήλης, παίρνουμε

Έτσι, το πρόβλημα περιορίστηκε στην επίλυση του συστήματος

Ας λύσουμε το σύστημα χρησιμοποιώντας τη μέθοδο Gauss:

Ως αποτέλεσμα, παίρνουμε ένα σύστημα εξισώσεων:

που έχει άπειρο αριθμό λύσεων, μεταξύ των οποίων είναι βέβαιο ότι υπάρχει μία μη μηδενική, επομένως, τα διανύσματα εξαρτώνται γραμμικά.

Αφήνω μεγάλοείναι ένας αυθαίρετος γραμμικός χώρος, α Εγώ Î ΜΕΓΑΛΟ,- τα στοιχεία του (διανύσματα).

Ορισμός 3.3.1.Εκφραση , Οπου , - αυθαίρετοι πραγματικοί αριθμοί, που ονομάζονται γραμμικός συνδυασμός φορείςα 1, α 2,…, α n.

Αν το διάνυσμα R = , μετά το λένε αυτό R αποσυντίθεται σε διανύσματαα 1, α 2,…, α n.

Ορισμός 3.3.2.Ένας γραμμικός συνδυασμός διανυσμάτων ονομάζεται μη τετριμμένο, εάν μεταξύ των αριθμών υπάρχει τουλάχιστον ένας μη μηδενικός. Διαφορετικά, ονομάζεται ο γραμμικός συνδυασμός ασήμαντος.

Ορισμός 3.3.3 . Διανύσματα a 1 , a 2 ,…, a nονομάζονται γραμμικά εξαρτώμενα εάν υπάρχει ένας μη τετριμμένος γραμμικός συνδυασμός τους τέτοιος ώστε

= 0 .

Ορισμός 3.3.4. Διανύσματα a 1 ,a 2 ,…, a nονομάζονται γραμμικά ανεξάρτητα αν η ισότητα = 0 είναι δυνατή μόνο στην περίπτωση που όλοι οι αριθμοί μεγάλο 1, μεγάλο 2,…, l nείναι ταυτόχρονα ίσα με μηδέν.

Σημειώστε ότι οποιοδήποτε μη μηδενικό στοιχείο a 1 μπορεί να θεωρηθεί ως γραμμικά ανεξάρτητο σύστημα, αφού η ισότητα μεγάλοα 1 = 0 δυνατό μόνο αν μεγάλο= 0.

Θεώρημα 3.3.1.Απαραίτητη και επαρκής συνθήκη για τη γραμμική εξάρτηση a 1 , a 2 ,…, a nείναι η δυνατότητα αποσύνθεσης τουλάχιστον ενός από αυτά τα στοιχεία στα υπόλοιπα.

Απόδειξη. Ανάγκη. Έστω τα στοιχεία a 1 , a 2 ,…, a nγραμμικά εξαρτώμενη. Αυτό σημαίνει ότι = 0 , και τουλάχιστον έναν από τους αριθμούς μεγάλο 1, μεγάλο 2,…, l nδιαφορετικό από το μηδέν. Αφήστε για βεβαιότητα μεγάλο 1 ¹ 0. Τότε

δηλαδή το στοιχείο a 1 αποσυντίθεται σε στοιχεία a 2 , a 3 , …, a n.

Επάρκεια. Έστω το στοιχείο a 1 να αποσυντεθεί σε στοιχεία a 2 , a 3 , …, a n, δηλαδή α 1 = . Τότε = 0 , επομένως, υπάρχει ένας μη τετριμμένος γραμμικός συνδυασμός διανυσμάτων a 1 , a 2 ,…, a n, ίσος 0 , άρα εξαρτώνται γραμμικά .

Θεώρημα 3.3.2. Αν τουλάχιστον ένα από τα στοιχεία a 1 , a 2 ,…, a nμηδέν, τότε αυτά τα διανύσματα εξαρτώνται γραμμικά.

Απόδειξη . Αφήνω ένα n= 0 , τότε = 0 , που σημαίνει τη γραμμική εξάρτηση αυτών των στοιχείων.

Θεώρημα 3.3.3. Αν μεταξύ n διανυσμάτων οποιοδήποτε p (σελ< n) векторов линейно зависимы, то и все n элементов линейно зависимы.

Απόδειξη. Έστω, για βεβαιότητα, τα στοιχεία a 1 , a 2 ,…, a Πγραμμικά εξαρτώμενη. Αυτό σημαίνει ότι υπάρχει ένας μη τετριμμένος γραμμικός συνδυασμός τέτοιος ώστε = 0 . Η καθορισμένη ισότητα θα διατηρηθεί εάν προσθέσουμε το στοιχείο και στα δύο μέρη του. Επειτα + = 0 , και τουλάχιστον έναν από τους αριθμούς μεγάλο 1, μεγάλο 2,…, λπδιαφορετικό από το μηδέν. Επομένως, τα διανύσματα a 1 , a 2 ,…, a nεξαρτώνται γραμμικά.

Συμπέρασμα 3.3.1.Αν n στοιχεία είναι γραμμικά ανεξάρτητα, τότε οποιοδήποτε k από αυτά είναι γραμμικά ανεξάρτητα (k< n).

Θεώρημα 3.3.4. Αν οι φορείςα 1, α 2,…, α n- 1 είναι γραμμικά ανεξάρτητα, και τα στοιχείαα 1, α 2,…, α n- 1, α Τα n εξαρτώνται γραμμικά, τότε το διάνυσμαένα Το n μπορεί να επεκταθεί σε διανύσματαα 1, α 2,…, α n- 1 .

Απόδειξη.Εφόσον από την προϋπόθεση a 1 , a 2 ,…, ένα n- 1, α n εξαρτώνται γραμμικά, τότε υπάρχει ένας μη τετριμμένος γραμμικός συνδυασμός τους = 0 , και (διαφορετικά, τα διανύσματα a 1 , a 2 ,…, a θα αποδειχθούν γραμμικά εξαρτώμενα n- 1). Αλλά μετά το διάνυσμα

Q.E.D.

Εργασία 1.Μάθετε εάν το σύστημα των διανυσμάτων είναι γραμμικά ανεξάρτητο. Το σύστημα των διανυσμάτων θα καθοριστεί από τον πίνακα του συστήματος, οι στήλες του οποίου αποτελούνται από τις συντεταγμένες των διανυσμάτων.

.

Λύση.Αφήστε τον γραμμικό συνδυασμό ίσο με μηδέν. Έχοντας γράψει αυτή την ισότητα σε συντεταγμένες, λαμβάνουμε το ακόλουθο σύστημα εξισώσεων:

.

Ένα τέτοιο σύστημα εξισώσεων ονομάζεται τριγωνικό. Έχει μόνο μία λύση . Επομένως, τα διανύσματα γραμμικά ανεξάρτητη.

Εργασία 2.Μάθετε εάν το σύστημα των διανυσμάτων είναι γραμμικά ανεξάρτητο.

.

Λύση.Διανύσματα γραμμικά ανεξάρτητο (βλ. πρόβλημα 1). Ας αποδείξουμε ότι το διάνυσμα είναι ένας γραμμικός συνδυασμός διανυσμάτων . Διανυσματικοί συντελεστές επέκτασης καθορίζονται από το σύστημα των εξισώσεων

.

Αυτό το σύστημα, όπως ένα τριγωνικό, έχει μια μοναδική λύση.

Επομένως, το σύστημα των διανυσμάτων γραμμικά εξαρτώμενος.

Σχόλιο. Καλούνται πίνακες του ίδιου τύπου όπως στο Πρόβλημα 1 τριγωνικός και στο πρόβλημα 2 - κλιμακωτό τριγωνικό . Το ζήτημα της γραμμικής εξάρτησης ενός συστήματος διανυσμάτων επιλύεται εύκολα εάν ο πίνακας που αποτελείται από τις συντεταγμένες αυτών των διανυσμάτων είναι τριγωνικός σταδιακά. Εάν η μήτρα δεν έχει ειδική μορφή, τότε χρησιμοποιήστε στοιχειώδεις μετατροπές συμβολοσειρών , διατηρώντας τις γραμμικές σχέσεις μεταξύ των στηλών, μπορεί να μειωθεί σε τριγωνική μορφή.

Μετατροπές στοιχειωδών συμβολοσειρώνπίνακες (EPS) οι ακόλουθες πράξεις σε έναν πίνακα ονομάζονται:

1) αναδιάταξη των χορδών.

2) πολλαπλασιασμός μιας συμβολοσειράς με έναν μη μηδενικό αριθμό.

3) προσθέτοντας μια άλλη συμβολοσειρά σε μια συμβολοσειρά, πολλαπλασιασμένη με έναν αυθαίρετο αριθμό.

Εργασία 3.Βρείτε το μέγιστο γραμμικά ανεξάρτητο υποσύστημα και υπολογίστε την κατάταξη του συστήματος των διανυσμάτων

.

Λύση.Ας μειώσουμε τη μήτρα του συστήματος χρησιμοποιώντας το EPS σε βηματική τριγωνική μορφή. Για να εξηγήσουμε τη διαδικασία, συμβολίζουμε τη γραμμή με τον αριθμό του πίνακα που θα μετασχηματιστεί με το σύμβολο . Η στήλη μετά το βέλος υποδεικνύει τις ενέργειες στις σειρές του πίνακα που μετατρέπεται και που πρέπει να εκτελεστούν για να ληφθούν οι σειρές του νέου πίνακα.

.

Προφανώς, οι δύο πρώτες στήλες του προκύπτοντος πίνακα είναι γραμμικά ανεξάρτητες, η τρίτη στήλη είναι ο γραμμικός συνδυασμός τους και η τέταρτη δεν εξαρτάται από τις δύο πρώτες. Διανύσματα ονομάζονται βασικά. Αποτελούν ένα μέγιστο γραμμικά ανεξάρτητο υποσύστημα του συστήματος , και η κατάταξη του συστήματος είναι τρεις.

Βάση, συντεταγμένες

Εργασία 4.Βρείτε τη βάση και τις συντεταγμένες των διανυσμάτων σε αυτή τη βάση στο σύνολο των γεωμετρικών διανυσμάτων των οποίων οι συντεταγμένες ικανοποιούν τη συνθήκη .

Λύση. Το σετ είναι ένα αεροπλάνο που διέρχεται από την αρχή. Μια αυθαίρετη βάση σε ένα επίπεδο αποτελείται από δύο μη γραμμικά διανύσματα. Οι συντεταγμένες των διανυσμάτων στην επιλεγμένη βάση καθορίζονται με την επίλυση του αντίστοιχου συστήματος γραμμικών εξισώσεων.

Υπάρχει ένας άλλος τρόπος για να λύσετε αυτό το πρόβλημα, όταν μπορείτε να βρείτε τη βάση χρησιμοποιώντας τις συντεταγμένες.

Συντεταγμένες Οι χώροι δεν είναι συντεταγμένες στο επίπεδο, αφού σχετίζονται με τη σχέση , δηλαδή δεν είναι ανεξάρτητα. Οι ανεξάρτητες μεταβλητές και (ονομάζονται ελεύθερες) ορίζουν μοναδικά ένα διάνυσμα στο επίπεδο και, επομένως, μπορούν να επιλεγούν ως συντεταγμένες στο . Στη συνέχεια η βάση αποτελείται από διανύσματα που βρίσκονται μέσα και αντιστοιχούν σε σύνολα ελεύθερων μεταβλητών Και , αυτό είναι .

Εργασία 5.Βρείτε τη βάση και τις συντεταγμένες των διανυσμάτων σε αυτή τη βάση στο σύνολο όλων των διανυσμάτων στο χώρο των οποίων οι περιττές συντεταγμένες είναι ίσες μεταξύ τους.

Λύση. Ας επιλέξουμε, όπως και στο προηγούμενο πρόβλημα, συντεταγμένες στο χώρο.

Επειδή , στη συνέχεια δωρεάν μεταβλητές καθορίζουν μοναδικά το διάνυσμα από και επομένως είναι συντεταγμένες. Η αντίστοιχη βάση αποτελείται από διανύσματα.

Εργασία 6.Βρείτε τη βάση και τις συντεταγμένες των διανυσμάτων σε αυτή τη βάση στο σύνολο όλων των πινάκων της φόρμας , Οπου – αυθαίρετοι αριθμοί.

Λύση. Κάθε μήτρα από μπορεί να αναπαρασταθεί μοναδικά με τη μορφή:

Αυτή η σχέση είναι η επέκταση του διανύσματος από ως προς τη βάση
με συντεταγμένες .

Εργασία 7.Να βρείτε τη διάσταση και τη βάση της γραμμικής γάστρας ενός συστήματος διανυσμάτων

.

Λύση.Χρησιμοποιώντας το EPS, μετατρέπουμε τη μήτρα από τις συντεταγμένες των διανυσμάτων του συστήματος σε μια τριγωνική μορφή βήματος.

.

Στήλες οι τελευταίοι πίνακες είναι γραμμικά ανεξάρτητοι και οι στήλες εκφράζεται γραμμικά μέσα από αυτά. Επομένως, τα διανύσματα αποτελούν βάση , Και .

Σχόλιο. Βάση σε επιλέγεται διφορούμενα. Για παράδειγμα, διανύσματα αποτελούν επίσης βάση .

Ορισμός. Γραμμικός συνδυασμός διανυσμάτων a 1 , ..., a n με συντελεστές x 1 , ..., x n ονομάζεται διάνυσμα

x 1 a 1 + ... + x n a n .

ασήμαντος, αν όλοι οι συντελεστές x 1 , ..., x n είναι ίσοι με μηδέν.

Ορισμός. Ο γραμμικός συνδυασμός x 1 a 1 + ... + x n a n ονομάζεται μη τετριμμένο, αν τουλάχιστον ένας από τους συντελεστές x 1, ..., x n δεν είναι ίσος με μηδέν.

γραμμικά ανεξάρτητη, εάν δεν υπάρχει κανένας μη τετριμμένος συνδυασμός αυτών των διανυσμάτων ίσος με το μηδενικό διάνυσμα.

Δηλαδή, τα διανύσματα a 1, ..., a n είναι γραμμικά ανεξάρτητα αν x 1 a 1 + ... + x n a n = 0 αν και μόνο αν x 1 = 0, ..., x n = 0.

Ορισμός. Τα διανύσματα a 1, ..., a n λέγονται γραμμικά εξαρτώμενη, εάν υπάρχει ένας μη τετριμμένος συνδυασμός αυτών των διανυσμάτων ίσος με το μηδενικό διάνυσμα.

Ιδιότητες γραμμικά εξαρτημένων διανυσμάτων:

Για 2 και τρισδιάστατα διανύσματα.

Δύο γραμμικά εξαρτώμενα διανύσματα είναι συγγραμμικά. (Τα συγγραμμικά διανύσματα εξαρτώνται γραμμικά.)

Για τρισδιάστατα διανύσματα.

Τρία γραμμικά εξαρτώμενα διανύσματα είναι συνεπίπεδα. (Τρία συνεπίπεδα διανύσματα εξαρτώνται γραμμικά.)

• Για διανύσματα ν-διάστατων.

  Τα n + 1 διανύσματα εξαρτώνται πάντα γραμμικά.

Παραδείγματα προβλημάτων γραμμικής εξάρτησης και γραμμικής ανεξαρτησίας διανυσμάτων:

Παράδειγμα 1. Ελέγξτε εάν τα διανύσματα a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) είναι γραμμικά ανεξάρτητα .

Λύση:

Τα διανύσματα θα εξαρτώνται γραμμικά, αφού η διάσταση των διανυσμάτων είναι μικρότερη από τον αριθμό των διανυσμάτων.

Παράδειγμα 2. Ελέγξτε εάν τα διανύσματα a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) είναι γραμμικά ανεξάρτητα.

Λύση:

	x 1 + x 2 = 0
	x 1 + 2x 2 - x 3 = 0
	x 1 + x 3 = 0

	1	1	0	0		~
	1	2	-1	0
	1	0	1	0

~		1	1	0	0		~		1	1	0	0		~
		1 - 1	2 - 1	-1 - 0	0 - 0				0	1	-1	0
		1 - 1	0 - 1	1 - 0	0 - 0				0	-1	1	0

αφαιρέστε το δεύτερο από την πρώτη γραμμή. προσθέστε μια δεύτερη γραμμή στην τρίτη γραμμή:

~		1 - 0	1 - 1	0 - (-1)	0 - 0		~		1	0	1	0
		0	1	-1	0				0	1	-1	0
		0 + 0	-1 + 1	1 + (-1)	0 + 0				0	0	0	0

Αυτή η λύση δείχνει ότι το σύστημα έχει πολλές λύσεις, δηλαδή υπάρχει ένας μη μηδενικός συνδυασμός τιμών των αριθμών x 1, x 2, x 3 έτσι ώστε ο γραμμικός συνδυασμός των διανυσμάτων a, b, c να είναι ίσος με το μηδενικό διάνυσμα, για παράδειγμα:

Α + β + γ = 0

που σημαίνει ότι τα διανύσματα a, b, c εξαρτώνται γραμμικά.

Απάντηση:Τα διανύσματα a, b, c εξαρτώνται γραμμικά.

Παράδειγμα 3. Ελέγξτε εάν τα διανύσματα a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) είναι γραμμικά ανεξάρτητα.

Λύση:Ας βρούμε τις τιμές των συντελεστών στους οποίους ο γραμμικός συνδυασμός αυτών των διανυσμάτων θα είναι ίσος με το μηδενικό διάνυσμα.

x 1 a + x 2 b + x 3 c 1 = 0

Αυτή η διανυσματική εξίσωση μπορεί να γραφτεί ως σύστημα γραμμικών εξισώσεων

	x 1 + x 2 = 0
	x 1 + 2x 2 - x 3 = 0
	x 1 + 2x 3 = 0

Ας λύσουμε αυτό το σύστημα χρησιμοποιώντας τη μέθοδο Gauss

	1	1	0	0		~
	1	2	-1	0
	1	0	2	0

αφαιρέστε την πρώτη από τη δεύτερη γραμμή. αφαιρέστε την πρώτη από την τρίτη γραμμή:

~		1	1	0	0		~		1	1	0	0		~
		1 - 1	2 - 1	-1 - 0	0 - 0				0	1	-1	0
		1 - 1	0 - 1	2 - 0	0 - 0				0	-1	2	0

αφαιρέστε το δεύτερο από την πρώτη γραμμή. προσθέστε ένα δεύτερο στην τρίτη γραμμή.

Παρουσιάστηκε από εμάς γραμμικές πράξεις σε διανύσματακαθιστούν δυνατή τη δημιουργία διαφόρων εκφράσεων για διανυσματικές ποσότητεςκαι να τα μετατρέψετε χρησιμοποιώντας τις ιδιότητες που έχουν οριστεί για αυτές τις πράξεις.

Με βάση ένα δεδομένο σύνολο διανυσμάτων a 1, ..., a n, μπορείτε να δημιουργήσετε μια έκφραση της μορφής

όπου τα 1, ... και n είναι αυθαίρετοι πραγματικοί αριθμοί. Αυτή η έκφραση ονομάζεται γραμμικός συνδυασμός διανυσμάτων a 1, ..., a n. Οι αριθμοί α i, i = 1, n, αντιπροσωπεύουν συντελεστές γραμμικού συνδυασμού. Ένα σύνολο διανυσμάτων ονομάζεται επίσης σύστημα διανυσμάτων.

Σε σχέση με την εισαγόμενη έννοια ενός γραμμικού συνδυασμού διανυσμάτων, προκύπτει το πρόβλημα της περιγραφής ενός συνόλου διανυσμάτων που μπορούν να γραφτούν ως γραμμικός συνδυασμός ενός δεδομένου συστήματος διανυσμάτων a 1, ..., a n. Επιπλέον, υπάρχουν φυσικά ερωτήματα σχετικά με τις συνθήκες υπό τις οποίες υπάρχει μια αναπαράσταση ενός διανύσματος με τη μορφή γραμμικού συνδυασμού και σχετικά με τη μοναδικότητα μιας τέτοιας αναπαράστασης.

Ορισμός 2.1.Τα διανύσματα a 1, ..., και n ονομάζονται γραμμικά εξαρτώμενη, αν υπάρχει ένα σύνολο συντελεστών α 1 , ... , α n τέτοιο ώστε

α 1 a 1 + ... + α n а n = 0 (2.2)

και τουλάχιστον ένας από αυτούς τους συντελεστές είναι μη μηδενικός. Εάν το καθορισμένο σύνολο συντελεστών δεν υπάρχει, τότε καλούνται τα διανύσματα γραμμικά ανεξάρτητη.

Αν α 1 = ... = α n = 0, τότε, προφανώς, α 1 a 1 + ... + α n a n = 0. Έχοντας αυτό υπόψη, μπορούμε να πούμε το εξής: διανύσματα a 1, ..., και Τα n είναι γραμμικά ανεξάρτητα αν από την ισότητα (2.2) προκύπτει ότι όλοι οι συντελεστές α 1 , ... , α n είναι ίσοι με μηδέν.

Το παρακάτω θεώρημα εξηγεί γιατί η νέα έννοια ονομάζεται όρος «εξάρτηση» (ή «ανεξαρτησία») και παρέχει ένα απλό κριτήριο για τη γραμμική εξάρτηση.

Θεώρημα 2.1.Για να είναι γραμμικά εξαρτημένα τα διανύσματα a 1, ..., και n, n > 1, είναι απαραίτητο και αρκετό ένα από αυτά να είναι γραμμικός συνδυασμός των άλλων.

◄ Αναγκαιότητα. Ας υποθέσουμε ότι τα διανύσματα a 1, ..., και n εξαρτώνται γραμμικά. Σύμφωνα με τον ορισμό 2.1 της γραμμικής εξάρτησης, στην ισότητα (2.2) στα αριστερά υπάρχει τουλάχιστον ένας μη μηδενικός συντελεστής, για παράδειγμα α 1. Αφήνοντας τον πρώτο όρο στην αριστερή πλευρά της ισότητας, μετακινούμε τους υπόλοιπους στη δεξιά πλευρά, αλλάζοντας τα πρόσημά τους, ως συνήθως. Διαιρώντας την προκύπτουσα ισότητα με α 1, παίρνουμε

a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n /α 1 ⋅ a n

εκείνοι. αναπαράσταση του διανύσματος a 1 ως γραμμικός συνδυασμός των υπόλοιπων διανυσμάτων a 2, ..., a n.

Επάρκεια. Έστω, για παράδειγμα, το πρώτο διάνυσμα a 1 μπορεί να αναπαρασταθεί ως ένας γραμμικός συνδυασμός των υπόλοιπων διανυσμάτων: a 1 = β 2 a 2 + ... + β n a n. Μεταφέροντας όλους τους όρους από τη δεξιά πλευρά στην αριστερή, παίρνουμε ένα 1 - β 2 a 2 - ... - β n a n = 0, δηλ. ένας γραμμικός συνδυασμός διανυσμάτων a 1, ..., a n με συντελεστές α 1 = 1, α 2 = - β 2, ..., α n = - β n, ίσοι με μηδενικό διάνυσμα.Σε αυτόν τον γραμμικό συνδυασμό, δεν είναι όλοι οι συντελεστές μηδέν. Σύμφωνα με τον ορισμό 2.1, τα διανύσματα a 1, ..., και n εξαρτώνται γραμμικά.

Ο ορισμός και το κριτήριο για τη γραμμική εξάρτηση διατυπώνονται έτσι ώστε να υποδηλώνουν την παρουσία δύο ή περισσότερων διανυσμάτων. Ωστόσο, μπορούμε επίσης να μιλήσουμε για γραμμική εξάρτηση ενός διανύσματος. Για να πραγματοποιήσετε αυτή τη δυνατότητα, αντί για "τα διανύσματα εξαρτώνται γραμμικά", πρέπει να πείτε "το σύστημα των διανυσμάτων εξαρτάται γραμμικά". Είναι εύκολο να δούμε ότι η έκφραση "ένα σύστημα ενός διανύσματος εξαρτάται γραμμικά" σημαίνει ότι αυτό το μεμονωμένο διάνυσμα είναι μηδέν (σε έναν γραμμικό συνδυασμό υπάρχει μόνο ένας συντελεστής και δεν πρέπει να είναι ίσος με μηδέν).

Η έννοια της γραμμικής εξάρτησης έχει μια απλή γεωμετρική ερμηνεία. Οι ακόλουθες τρεις δηλώσεις διευκρινίζουν αυτήν την ερμηνεία.

Θεώρημα 2.2.Δύο διανύσματα εξαρτώνται γραμμικά αν και μόνο αν εξαρτώνται συγγραμμική.

◄ Αν τα διανύσματα a και b είναι γραμμικά εξαρτημένα, τότε το ένα από αυτά, για παράδειγμα το a, εκφράζεται μέσω του άλλου, δηλ. a = λb για κάποιο πραγματικό αριθμό λ. Σύμφωνα με τον ορισμό 1.7 έργαδιανύσματα ανά αριθμό, τα διανύσματα a και b είναι συγγραμμικά.

Έστω τώρα τα διανύσματα a και b συγγραμμικά. Αν και τα δύο είναι μηδέν, τότε είναι προφανές ότι είναι γραμμικά εξαρτώμενα, αφού οποιοσδήποτε γραμμικός συνδυασμός τους είναι ίσος με το μηδενικό διάνυσμα. Έστω ένα από αυτά τα διανύσματα να μην είναι ίσο με 0, για παράδειγμα το διάνυσμα b. Ας συμβολίσουμε με λ τον λόγο των διανυσματικών μηκών: λ = |a|/|b|. Τα συγγραμμικά διανύσματα μπορούν να είναι μονοκατευθυντικήή αντίθετα κατευθυνόμενη. Στην τελευταία περίπτωση, αλλάζουμε το πρόσημο του λ. Στη συνέχεια, ελέγχοντας τον Ορισμό 1.7, είμαστε πεπεισμένοι ότι a = λb. Σύμφωνα με το Θεώρημα 2.1, τα διανύσματα a και b εξαρτώνται γραμμικά.

Παρατήρηση 2.1.Στην περίπτωση δύο διανυσμάτων, λαμβάνοντας υπόψη το κριτήριο της γραμμικής εξάρτησης, το αποδεδειγμένο θεώρημα μπορεί να αναδιατυπωθεί ως εξής: δύο διανύσματα είναι συγγραμμικά εάν και μόνο εάν το ένα από αυτά παριστάνεται ως γινόμενο του άλλου με έναν αριθμό. Αυτό είναι ένα βολικό κριτήριο για τη συγγραμμικότητα δύο διανυσμάτων.

Θεώρημα 2.3.Τρία διανύσματα εξαρτώνται γραμμικά αν και μόνο αν εξαρτώνται ομοεπίπεδη.

◄ Αν τρία διανύσματα a, b, c εξαρτώνται γραμμικά, τότε, σύμφωνα με το Θεώρημα 2.1, ένα από αυτά, για παράδειγμα a, είναι γραμμικός συνδυασμός των άλλων: a = βb + γс. Ας συνδυάσουμε τις απαρχές των διανυσμάτων b και c στο σημείο Α. Τότε τα διανύσματα βb, γσ θα έχουν κοινή αρχή στο σημείο Α και κατά μήκος σύμφωνα με τον κανόνα του παραλληλογράμμου, το άθροισμά τους είναιεκείνοι. το διάνυσμα a θα είναι ένα διάνυσμα με αρχή Α και το τέλος, που είναι η κορυφή ενός παραλληλογράμμου που βασίζεται σε διανύσματα συνιστωσών. Έτσι, όλα τα διανύσματα βρίσκονται στο ίδιο επίπεδο, δηλαδή σε ομοεπίπεδα.

Έστω τα διανύσματα a, b, c συνεπίπεδα. Εάν ένα από αυτά τα διανύσματα είναι μηδέν, τότε είναι προφανές ότι θα είναι ένας γραμμικός συνδυασμός των άλλων. Αρκεί να ληφθούν όλοι οι συντελεστές ενός γραμμικού συνδυασμού ίσοι με μηδέν. Επομένως, μπορούμε να υποθέσουμε ότι και τα τρία διανύσματα δεν είναι μηδενικά. Σύμφωνος ξεκίνησεαυτών των διανυσμάτων σε κοινό σημείο Ο. Έστω τα άκρα τους τα σημεία Α, Β, Γ, αντίστοιχα (Εικ. 2.1). Μέσω του σημείου Γ σχεδιάζουμε ευθείες παράλληλες σε ευθείες που διέρχονται από ζεύγη σημείων Ο, Α και Ο, Β. Ορίζοντας τα σημεία τομής ως Α" και Β", παίρνουμε ένα παραλληλόγραμμο ΟΑ"CB", επομένως, OC" = ΟΑ" + OB". Διάνυσμα OA" και το μη μηδενικό διάνυσμα a = OA είναι συγγραμμικά, και επομένως το πρώτο από αυτά μπορεί να ληφθεί πολλαπλασιάζοντας το δεύτερο με έναν πραγματικό αριθμό α:OA" = αOA. Ομοίως, OB" = βOB, β ∈ R. Ως αποτέλεσμα, λαμβάνουμε ότι OC" = α OA. + βOB, δηλαδή το διάνυσμα c είναι ένας γραμμικός συνδυασμός των διανυσμάτων a και b. Σύμφωνα με το Θεώρημα 2.1, τα διανύσματα a, b, c εξαρτώνται γραμμικά.

Θεώρημα 2.4.Οποιαδήποτε τέσσερα διανύσματα εξαρτώνται γραμμικά.

◄ Πραγματοποιούμε την απόδειξη σύμφωνα με το ίδιο σχήμα όπως στο Θεώρημα 2.3. Θεωρήστε αυθαίρετα τέσσερα διανύσματα a, b, c και d. Εάν ένα από τα τέσσερα διανύσματα είναι μηδέν, ή μεταξύ αυτών υπάρχουν δύο συγγραμμικά διανύσματα ή τρία από τα τέσσερα διανύσματα είναι συνεπίπεδα, τότε αυτά τα τέσσερα διανύσματα είναι γραμμικά εξαρτημένα. Για παράδειγμα, εάν τα διανύσματα a και b είναι συγγραμμικά, τότε μπορούμε να κάνουμε τον γραμμικό συνδυασμό τους αa + βb = 0 με μη μηδενικούς συντελεστές και στη συνέχεια να προσθέσουμε τα υπόλοιπα δύο διανύσματα σε αυτόν τον συνδυασμό, λαμβάνοντας μηδενικά ως συντελεστές. Λαμβάνουμε έναν γραμμικό συνδυασμό τεσσάρων διανυσμάτων ίσο με 0, στα οποία υπάρχουν μη μηδενικοί συντελεστές.

Έτσι, μπορούμε να υποθέσουμε ότι μεταξύ των τεσσάρων επιλεγμένων διανυσμάτων, κανένα διάνυσμα δεν είναι μηδέν, κανένα δύο δεν είναι συγγραμμικό και κανένα τρία δεν είναι συνεπίπεδα. Ας επιλέξουμε ως κοινή αρχή το σημείο O. Τότε τα άκρα των διανυσμάτων a, b, c, d θα είναι κάποια σημεία A, B, C, D (Εικ. 2.2). Μέσω του σημείου Δ σχεδιάζουμε τρία επίπεδα παράλληλα με τα επίπεδα OBC, OCA, OAB και έστω Α", Β", Γ" τα σημεία τομής αυτών των επιπέδων με τις ευθείες ΟΑ, ΟΒ, ΟΣ αντίστοιχα. Λαμβάνουμε ένα παραλληλεπίπεδο OA" C "B" C" B"DA", και τα διανύσματα a, b, c βρίσκονται στις άκρες του που αναδύονται από την κορυφή O. Εφόσον το τετράπλευρο OC"DC" είναι παραλληλόγραμμο, τότε OD = OC" + OC "Με τη σειρά του, το τμήμα OC" είναι ένα παραλληλόγραμμο OA"C"B", άρα OC" = OA" + OB" και OD = OA" + OB" + OC".

Παραμένει να σημειωθεί ότι τα ζεύγη των διανυσμάτων OA ≠ 0 και OA" , OB ≠ 0 και OB" , OC ≠ 0 και OC" είναι συγγραμμικά και, επομένως, είναι δυνατό να επιλεγούν οι συντελεστές α, β, γ έτσι ώστε OA" = αOA , OB" = βOB και OC" = γOC. Τελικά παίρνουμε OD = αOA + βOB + γOC. Κατά συνέπεια, το διάνυσμα OD εκφράζεται ως προς τα άλλα τρία διανύσματα, και τα τέσσερα διανύσματα, σύμφωνα με το Θεώρημα 2.1, εξαρτώνται γραμμικά.