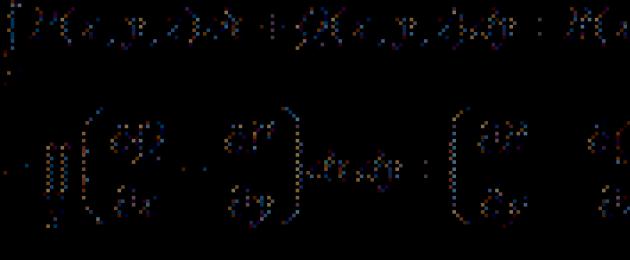Αυτοί οι τύποι συνδέουν το ολοκλήρωμα πάνω από ένα σχήμα με κάποιο ολοκλήρωμα πάνω από το όριο ενός δεδομένου σχήματος.

Αφήστε τις συναρτήσεις να είναι συνεχείς στον τομέα ρεÌ Oxyκαι στα σύνορά της σολ; περιοχή ρε– συνδεδεμένο σολ– τμηματικά ομαλή καμπύλη. Τότε αλήθεια Η φόρμουλα του Γκριν:

Εδώ στα αριστερά είναι ένα καμπυλόγραμμο ολοκλήρωμα του πρώτου είδους, στα δεξιά είναι ένα διπλό ολοκλήρωμα. κύκλωμα σολπηγαίνει αριστερόστροφα.

Αφήνω Τ– τμηματικά λεία οριοθετημένη επιφάνεια δύο όψεων με τμηματικά λείο όριο σολ. Εάν οι λειτουργίες Π(Χ,y,z), Q(Χ,y,z), R(Χ,y,z) και οι μερικές παράγωγοί τους πρώτης τάξης είναι συνεχείς σε σημεία της επιφάνειας Τκαι σύνορα σολ, τότε συμβαίνει Φόρμουλα Stokes:

(2.23)

στα αριστερά είναι ένα καμπυλόγραμμο ολοκλήρωμα του δεύτερου είδους. στα δεξιά – ολοκλήρωμα επιφάνειας του δεύτερου είδους, που λαμβάνεται κατά μήκος αυτής της πλευράς της επιφάνειας Τ, το οποίο παραμένει προς τα αριστερά κατά τη διέλευση της καμπύλης σολ.

Εάν μια συνδεδεμένη περιοχή WÌ Oxyzπεριορίζεται από μια τμηματικά λεία, κλειστή επιφάνεια Τκαι τις λειτουργίες Π(Χ,y,z), Q(Χ,y,z), R(Χ,y,z) και οι μερικές παράγωγοί τους πρώτης τάξης είναι συνεχείς σε σημεία από WΚαι Τ, τότε συμβαίνει Ο τύπος Ostrogradsky-Gauss:

(2.24)

στα αριστερά – επιφάνεια αναπόσπαστο του δεύτερου είδους πάνω από την εξωτερική πλευρά της επιφάνειας Τ; στα δεξιά – τριπλό ολοκλήρωμα στην περιοχή W.

Παράδειγμα 1.Υπολογίστε το έργο που έκανε η δύναμη όταν διασχίζει το σημείο εφαρμογής του του κύκλου σολ: , ξεκινώντας από τον άξονα Βόδι, δεξιόστροφα (Εικ. 2.18).

Λύση.Η εργασία ισούται με . Ας εφαρμόσουμε τον τύπο του Green (2.22), τοποθετώντας το σύμβολο «-» στα δεξιά πριν από το ολοκλήρωμα (καθώς το κύκλωμα διασχίζεται δεξιόστροφα) και λαμβάνοντας υπόψη ότι Π(Χ,y)=Χ-y, Q(Χ,y)=Χ+y. Εχουμε:
,
Οπου Σ Δ- περιοχή ενός κύκλου ρε: , ίσο με . Ως αποτέλεσμα: – το απαιτούμενο έργο δύναμης.

Παράδειγμα 2.Υπολογίστε ολοκλήρωμα , Αν σολυπάρχει ένας κύκλος στο αεροπλάνο z=2, γυρίζοντας αριστερόστροφα.

Λύση.Χρησιμοποιώντας τον τύπο Stokes (2.23), ανάγουμε το αρχικό ολοκλήρωμα στο επιφανειακό ολοκλήρωμα σε έναν κύκλο Τ:
Τ:

Λοιπόν, με δεδομένο αυτό, έχουμε:

Το τελευταίο ολοκλήρωμα είναι ένα διπλό ολοκλήρωμα πάνω από έναν κύκλο ρεÌ Oxy, πάνω στο οποίο προβαλλόταν ο κύκλος Τ; ρε: . Ας προχωρήσουμε στις πολικές συντεταγμένες: Χ=r cosj, y=r sinj, jÎ, rΟ. Τελικά:
.

Παράδειγμα 3.Εύρεση ροής Π Τπυραμίδες W: (Εικ. 2.19) προς την κατεύθυνση του εξωτερικού κάθετου προς την επιφάνεια.

Λύση.Η ροή είναι . Εφαρμόζοντας τον τύπο Ostrogradsky-Gauss (2.24), ανάγουμε το πρόβλημα στον υπολογισμό του τριπλού ολοκληρώματος πάνω από το σχήμα W-πυραμίδα:

Παράδειγμα 4.Εύρεση ροής Πδιανυσματικό πεδίο μέσω πλήρη επιφάνεια Τπυραμίδες W: ; (Εικ. 2.20), στην κατεύθυνση του εξωτερικού κάθετου προς την επιφάνεια.

Λύση.Ας εφαρμόσουμε τον τύπο Ostrogradsky-Gauss (2.24), όπου V– όγκος της πυραμίδας. Ας κάνουμε σύγκριση με τη λύση του άμεσου υπολογισμού της ροής ( – όψεις της πυραμίδας).

,
αφού η προβολή των προσώπων στο επίπεδο Oxyέχει μηδενικό εμβαδόν (Εικ. 2.21),

Φόρμουλα Ostrogradsky-Green

Αυτός ο τύπος δημιουργεί μια σύνδεση μεταξύ του καμπυλόγραμμου ολοκληρώματος σε ένα κλειστό περίγραμμα C και του διπλού ολοκληρώματος στην περιοχή που περιορίζεται από αυτό το περίγραμμα.

Ορισμός 1. Μια περιοχή Δ ονομάζεται απλή περιοχή εάν μπορεί να χωριστεί σε πεπερασμένο αριθμό περιοχών του πρώτου τύπου και, ανεξάρτητα από αυτό, σε πεπερασμένο αριθμό περιοχών του δεύτερου τύπου.

Θεώρημα 1. Έστω οι συναρτήσεις P(x,y) και Q(x,y) να ορίζονται σε ένα απλό πεδίο ορισμού και να είναι συνεχείς μαζί με τις μερικές παραγώγους τους και

Τότε ισχύει ο τύπος

όπου C είναι το κλειστό περίγραμμα της περιοχής D.

Αυτή είναι η φόρμουλα Ostrogradsky-Green.

Προϋποθέσεις για την ανεξαρτησία ενός καμπυλόγραμμου ολοκληρώματος από την πορεία της ολοκλήρωσης

Ορισμός 1. Μια κλειστή τετραγωνισμένη περιοχή D λέγεται ότι είναι απλά συνδεδεμένη εάν οποιαδήποτε κλειστή καμπύλη l D μπορεί να παραμορφώνεται συνεχώς σε ένα σημείο έτσι ώστε όλα τα σημεία αυτής της καμπύλης να ανήκουν στην περιοχή D (περιοχή χωρίς «οπές» - D 1) , εάν μια τέτοια παραμόρφωση είναι αδύνατη, τότε η περιοχή ονομάζεται πολλαπλασιασμένη σύνδεση (με "τρύπες" - D 2).

Ορισμός 2. Εάν η τιμή ενός ολοκληρώματος καμπύλης κατά μήκος μιας καμπύλης ΑΒ δεν εξαρτάται από τον τύπο της καμπύλης που συνδέει τα σημεία Α και Β, τότε αυτό το ολοκλήρωμα καμπύλης λέγεται ότι είναι ανεξάρτητο από τη διαδρομή ολοκλήρωσης:

Θεώρημα 1. Έστω οι συνεχείς συναρτήσεις P(x,y) και Q(x,y) να οριστούν σε ένα κλειστό απλά συνδεδεμένο πεδίο D, μαζί με τις μερικές παραγώγους τους. Τότε οι ακόλουθες 4 συνθήκες είναι ισοδύναμες:

1) καμπυλόγραμμο ολοκλήρωμα σε κλειστό βρόχο

όπου C είναι οποιοσδήποτε κλειστός βρόχος στο D.

2) το καμπυλόγραμμο ολοκλήρωμα σε έναν κλειστό βρόχο δεν εξαρτάται από τη διαδρομή ολοκλήρωσης στην περιοχή D, δηλ.

3) η διαφορική μορφή P(x,y)dx + Q(x,y)dy είναι πλήρες διαφορικόκάποια συνάρτηση F στο πεδίο ορισμού D, δηλ. ότι υπάρχει μια συνάρτηση F τέτοια ώστε (x,y) D να ισχύει η ισότητα

dF(x,y) = P(x,y)dx + Q(x,y)dy; (3)

4) για όλα τα σημεία (x,y) D θα ικανοποιηθεί η ακόλουθη συνθήκη:

Ας το αποδείξουμε χρησιμοποιώντας το διάγραμμα.

Ας το αποδείξουμε από.

Έστω 1 να δοθεί), δηλ. = 0 από την ιδιότητα 2 §1, που = 0 (από την ιδιότητα 1 §1) .

Ας το αποδείξουμε από.

Δίνεται ότι cr.int. δεν εξαρτάται από το μονοπάτι της ολοκλήρωσης, αλλά μόνο από την επιλογή της αρχής και του τέλους του μονοπατιού

Εξετάστε τη συνάρτηση

Ας δείξουμε ότι η διαφορική μορφή P(x,y)dx + Q(x,y)dy είναι το πλήρες διαφορικό της συνάρτησης F(x,y), δηλ. , Τι

Ας ορίσουμε την ιδιωτική ανάπτυξη

x F (x,y)= F(x + x, y) -F (x,y)= = == =

(από την ιδιότητα 3 της § 1, BB* Oy) = = P (c,y)x (από το θεώρημα μέσης τιμής, c -const), όπου x

(λόγω της συνέχειας της συνάρτησης P). Λάβαμε τον τύπο (5). Ο τύπος (6) λαμβάνεται παρομοίως.

Ας το αποδείξουμε από.

Δίνεται ο τύπος

dF(x,y) = P(x,y)dx + Q(x,y)dy.

Προφανώς = P(x,y). Επειτα

Σύμφωνα με τις συνθήκες του θεωρήματος, οι δεξιές πλευρές των ισοτήτων (7) και (8) είναι συνεχείς συναρτήσεις, τότε, με το θεώρημα για την ισότητα των μικτών παραγώγων, οι αριστερές πλευρές θα είναι επίσης ίσες, δηλ. ότι

Ας αποδείξουμε ότι από τα 41.

Ας επιλέξουμε οποιοδήποτε κλειστό περίγραμμα από την περιοχή D που οριοθετεί την περιοχή D 1 .

Οι συναρτήσεις P και Q ικανοποιούν τις συνθήκες Ostrogradsky-Green:

Δυνάμει της ισότητας (4), στην αριστερή πλευρά του (9) το ολοκλήρωμα είναι ίσο με 0, πράγμα που σημαίνει ότι η δεξιά πλευρά της ισότητας είναι επίσης ίση με

Παρατήρηση 1. Το θεώρημα 1 μπορεί να διατυπωθεί με τη μορφή τριών ανεξάρτητων θεωρημάτων

Θεώρημα 1*. Προκειμένου ένας απλά συνδεδεμένος τετραγωνιζόμενος τομέας D να έχει καμπύλη int. δεν εξαρτιόταν από το μονοπάτι της ολοκλήρωσης οπότε ικανοποιείται η συνθήκη (.1), δηλ.

Θεώρημα 2*. Προκειμένου ένας απλά συνδεδεμένος τετραγωνιζόμενος τομέας D να έχει καμπύλη int. δεν εξαρτιόταν από το μονοπάτι της ολοκλήρωσης, έτσι ώστε η συνθήκη (3) να ικανοποιείται:

η διαφορική μορφή P(x,y)dx + Q(x,y)dy είναι η συνολική διαφορά κάποιας συνάρτησης F στο πεδίο ορισμού D.

Θεώρημα 3*. Προκειμένου ένας απλά συνδεδεμένος τετραγωνιζόμενος τομέας D να έχει καμπύλη int. δεν εξαρτιόταν από το μονοπάτι της ολοκλήρωσης, έτσι ώστε η συνθήκη (4) να ικανοποιείται:

Παρατήρηση 2. Στο Θεώρημα 2*, ο τομέας D μπορεί επίσης να πολλαπλασιαστεί.

Σχέση μεταξύ διπλού ολοκληρώματος σε έναν τομέα ρεκαι ένα καμπυλόγραμμο ολοκλήρωμα πάνω από το όριο μεγάλοΑυτή η περιοχή καθορίζεται από τον τύπο Ostrogradsky–Green, ο οποίος χρησιμοποιείται ευρέως στη μαθηματική ανάλυση.

Αφήστε στο αεροπλάνο Ωχούκαθορισμένη περιοχή ρε, που οριοθετείται από μια καμπύλη που τέμνει ευθείες γραμμές παράλληλες προς τους άξονες συντεταγμένων σε όχι περισσότερα από δύο σημεία, δηλ. περιοχή ρε- σωστός.

Θεώρημα 10.2.Εάν οι λειτουργίες Π(Χ; y) Και Q(Χ; y) είναι συνεχείς μαζί με τις μερικές παράγωγές τους Και στην περιοχή ρε, τότε ισχύει ο τύπος

(10.8)

Οπου μεγάλο– όριο περιοχής ρεκαι ολοκλήρωση κατά μήκος της καμπύλης μεγάλοπαράγεται προς τη θετική κατεύθυνση (δηλαδή όταν κινείται κατά μήκος μιας καμπύλης, η περιοχή ρεπαραμένει στα αριστερά).

Ο τύπος (10.8) ονομάζεται τύπος Ostrogradsky–Green.

Π Ust
- εξίσωση τόξου AnB, ΕΝΑ
- εξίσωση τόξου AmB(βλ. Εικ. 8). Ας βρούμε πρώτα
.Σύμφωνα με τον κανόνα για τον υπολογισμό του διπλού ολοκληρώματος έχουμε:

Ή σύμφωνα με τον τύπο (10.6), Εικ. 8.

Ομοίως, αποδεικνύεται ότι
(10.10)

Αν αφαιρέσουμε την ισότητα (10,9) από την ισότητα (10,10), παίρνουμε τον τύπο (10,8).

Σχόλιο.Ο τύπος (10.8) ισχύει επίσης για μια αυθαίρετη περιοχή, η οποία μπορεί να διαιρεθεί σε έναν πεπερασμένο αριθμό κανονικών περιοχών.

Παράδειγμα 10.3.Χρησιμοποιώντας τον τύπο Ostrogradsky–Green, υπολογίστε

Οπου μεγάλο– περίγραμμα ορθογωνίου με κορυφές ΕΝΑ(3;2 ), ΣΕ(6;2 ), ΜΕ(6;4 ), ρε(3;4 ).

○ Λύση:Το σχήμα 9 δείχνει τον βρόχο ολοκλήρωσης. Επειδή η

σύμφωνα με τον τύπο (10.8) έχουμε:

10.4. Προϋποθέσεις για την ανεξαρτησία ενός καμπυλόγραμμου ολοκληρώματος δεύτερου είδους από την οδό ολοκλήρωσης

Π
Ust ΕΝΑ(Χ 1 ; y 1) και σι(Χ 2 ; y 2) – δύο αυθαίρετα σημεία μιας απλώς συνδεδεμένης περιοχής ρεεπίπεδο Ωχού(επίπεδο ρεπου ονομάζεται απλά συνδεδεμένο , εάν για οποιοδήποτε κλειστό περίγραμμα βρίσκεται σε αυτήν την περιοχή, το τμήμα του επιπέδου που περιορίζεται από αυτό ανήκει εξ ολοκλήρου ρε(περιοχή χωρίς «τρύπες»)). Πόντοι ΕΝΑΚαι ΣΕμπορεί να συνδεθεί με διαφορετικές γραμμές (στο Σχ. 10 αυτό είναι μεγάλο 1 , μεγάλο 2 και μεγάλο 3). Για καθεμία από αυτές τις καμπύλες το ολοκλήρωμα
Σε γενικές γραμμές, έχει τη δική του σημασία.

Εάν οι τιμές του σύμφωνα με όλες τις πιθανές καμπύλες ΑΒείναι τα ίδια, τότε λέμε ότι το ολοκλήρωμα Εγώδεν εξαρτάται από τον τύπο της διαδρομής ολοκλήρωσης.

Ρύζι. 10. Στην περίπτωση αυτή για το ολοκλήρωμα Εγώαρκεί να σημειωθεί μόνο η αφετηρία του ΕΝΑ(Χ 1 ; y 1 ) και το τελικό σημείο του σι(Χ 2 ; y 2 ) τρόπους. Σημειωσε:

(10.11)

Ποιες είναι οι συνθήκες υπό τις οποίες ένα καμπυλόγραμμο ολοκλήρωμα δεύτερου είδους δεν εξαρτιόταν από τον τύπο της διαδρομής ολοκλήρωσης;

Θεώρημα 10.3.Για το καμπυλόγραμμο ολοκλήρωμα
δεν εξαρτιόταν από τη διαδρομή ενσωμάτωσης σε έναν απλά συνδεδεμένο τομέα ρε, στο οποίο οι συναρτήσεις Π(Χ; y), Q(Χ; y) είναι συνεχείς μαζί με τις μερικές παράγωγές τους, είναι απαραίτητο και επαρκές η συνθήκη να ικανοποιείται σε κάθε σημείο αυτής της περιοχής =(10.12)

Ας αποδείξουμε την επάρκεια της συνθήκης (10.12). Σκεφτείτε έναν αυθαίρετο κλειστό κύκλο AmBnA(ή μεγάλο) στην περιοχή ρε(βλ. Εικ. 11). Για αυτό, ισχύει ο τύπος Ostrogradsky–Green (10.8) Βάσει της συνθήκης (10.12), έχουμε:
, ή
. Λαμβάνοντας υπόψη τις ιδιότητες του καμπυλόγραμμου ολοκληρώματος, έχουμε:

, δηλ.

Η προκύπτουσα ισότητα σημαίνει ότι το καμπυλόγραμμο ολοκλήρωμα δεν εξαρτάται από την πορεία της ολοκλήρωσης.

Εικ. 11. Κατά την απόδειξη του θεωρήματος, προέκυψε ότι εάν η συνθήκη ικανοποιείται =, τότε το ολοκλήρωμα σε έναν κλειστό κύκλο είναι ίσο με μηδέν:

Το αντίστροφο είναι επίσης αλήθεια.

Συμπέρασμα 10.1.Εάν η συνθήκη (10.12) ικανοποιείται, τότε το ολοκλήρωμα είναι το συνολικό διαφορικό κάποιας συνάρτησης u = u(Χ; y), δηλ.

Στη συνέχεια (βλέπε (10.11))

Ο τύπος (10.14) ονομάζεται γενικευμένος τύπος Newton–Leibniz για το καμπυλόγραμμο ολοκλήρωμα του συνολικού διαφορικού.

Συμπέρασμα 10.2.Αν το ολοκλήρωμα Pdx + Qdyυπάρχει μια συνολική διαφορά και μια πορεία ολοκλήρωσης μεγάλοέκλεισε, λοιπόν
.

Σημειώσεις:

Ως αφετηρία ( Χ 0 ; y 0) συνήθως παίρνει το σημείο (0;0) - την αρχή των συντεταγμένων (βλ. παράδειγμα 10.5).

= ,=,=;

Παράδειγμα 10.4.Εύρημα

Λύση:Εδώ Π = y, Q = Χ, == 1. Σύμφωνα με το παραπάνω θεώρημα, το ολοκλήρωμα δεν εξαρτάται από τη διαδρομή της ολοκλήρωσης. Ως μονοπάτι ολοκλήρωσης, μπορούμε να πάρουμε ένα ευθύγραμμο τμήμα y = Χ, τόξο παραβολής y = Χ 2, κ.λπ. ή χρησιμοποιήστε τον τύπο (10.14). Επειδή ydx + xdy = d(xy), Οτι

Παράδειγμα 10.5.Βεβαιωθείτε ότι η έκφραση είναι το πλήρες διαφορικό της συνάρτησης U (Χ; y) και βρες την.

Λύση:Προκειμένου η υποδεικνυόμενη έκφραση να είναι πλήρης διαφορική, πρέπει να πληρούνται οι προϋποθέσεις (10.12):

Συντρέχουν λοιπόν οι προϋποθέσεις Και αφού η συνολική διαφορική έχει τη μορφή

,

τότε οι σχέσεις είναι σωστές

(10.16)

Ενσωματώνουμε από Χτην πρώτη από τις εξισώσεις, λαμβάνοντας υπόψη στοσταθερό, και αντί για σταθερή ολοκλήρωση θα πρέπει να βάλει κανείς
- μια άγνωστη λειτουργία που εξαρτάται μόνο από στο:

Αντικαθιστώντας την έκφραση που προκύπτει στη δεύτερη εξίσωση (10.16), βρίσκουμε
:

Ετσι,

Σημειώστε ότι η συνάρτηση Uείναι ευκολότερο να το βρείτε χρησιμοποιώντας τον τύπο (10.15).

(Ostrogradsky Mikhail Vasilievich (1861-1862) - Ρώσος μαθηματικός,

Ακαδημαϊκός Πετρούπολη ΕΝΑ.)

(George Green (1793 – 1841) – Άγγλος μαθηματικός)

Μερικές φορές αυτός ο τύπος ονομάζεται τύπος του Green, ωστόσο, ο J. Green πρότεινε το 1828 μόνο μια ειδική περίπτωση του τύπου.

Ο τύπος Ostrogradsky-Green δημιουργεί μια σύνδεση μεταξύ του καμπυλόγραμμου ολοκληρώματος και του διπλού ολοκληρώματος, δηλαδή δίνει μια έκφραση για το ολοκλήρωμα σε ένα κλειστό περίγραμμα μέσω του διπλού ολοκληρώματος στην περιοχή που περιορίζεται από αυτό το περίγραμμα.

Εάν το κλειστό περίγραμμα έχει τη μορφή που φαίνεται στο σχήμα, τότε το ολοκλήρωμα της καμπύλης κατά μήκος του περιγράμματος L μπορεί να γραφτεί ως:

Εάν τα τμήματα AB και CD του περιγράμματος ληφθούν ως αυθαίρετες καμπύλες, τότε, αφού πραγματοποιήσουμε παρόμοιους μετασχηματισμούς, λαμβάνουμε έναν τύπο για ένα περίγραμμα αυθαίρετου σχήματος:

Αυτός ο τύπος ονομάζεται Ostrogradsky–Green formula.

Ο τύπος Ostrogradsky-Green ισχύει επίσης στην περίπτωση μιας πολλαπλασιαζόμενης περιοχής, δηλαδή μιας περιοχής εντός της οποίας υπάρχουν εξαιρούμενες περιοχές. Σε αυτήν την περίπτωση, η δεξιά πλευρά του τύπου θα είναι το άθροισμα των ολοκληρωμάτων κατά μήκος του εξωτερικού περιγράμματος της περιοχής και των ολοκληρωμάτων κατά μήκος των περιγραμμάτων όλων των εξαιρούμενων τμημάτων, και καθένα από αυτά τα περιγράμματα είναι ενσωματωμένο σε τέτοια κατεύθυνση ώστε η περιοχή D παραμένει στην αριστερή πλευρά της γραμμής παράκαμψης ανά πάσα στιγμή.

Παράδειγμα.Ας λύσουμε το παράδειγμα που συζητήθηκε παραπάνω χρησιμοποιώντας τον τύπο Ostrogradsky–Green.

Ο τύπος Ostrogradsky–Green σάς επιτρέπει να απλοποιήσετε σημαντικά τον υπολογισμό του καμπυλόγραμμου ολοκληρώματος.

Το ολοκλήρωμα γραμμής δεν εξαρτάται από το σχήμα της διαδρομής εάν έχει την ίδια τιμή σε όλες τις διαδρομές που συνδέουν τα σημεία έναρξης και λήξης.

Η προϋπόθεση για την ανεξαρτησία ενός καμπυλόγραμμου ολοκληρώματος από το σχήμα της διαδρομής είναι ισοδύναμη με την ισότητα προς το μηδέν αυτού του ολοκληρώματος κατά μήκος οποιουδήποτε κλειστού περιγράμματος που περιέχει τα σημεία έναρξης και λήξης.

Έστω π το επίπεδο στο , είναι το μοναδιαίο κανονικό διάνυσμα στο π, ΡΕ-απλά συνδεδεμένος τομέας στο π (δηλαδή μια τμηματικά ομαλή κλειστή καμπύλη χωρίς αυτοτομές που βρίσκονται σε ΡΕ,οριοθετεί μια περιοχή όλα τα σημεία της οποίας επίσης ρε). Αφήνω ρεπληροί τις προϋποθέσεις:

1) σύνορα ΜΕπεριοχή ρεείναι μια κλειστή τμηματικά ομαλή καμπύλη χωρίς μοναδικά σημεία.

2) στο π μπορεί κανείς να επιλέξει ένα καρτεσιανό ορθογώνιο σύστημα συντεταγμένων έτσι ώστε όλες οι ευθείες παράλληλες προς τους άξονες συντεταγμένων να τέμνονται ρεόχι περισσότερο από 2 βαθμούς.

Αφήνω t- ΜΕ,συνεπής με, δηλ., τη θετική κατεύθυνση διέλευσης της καμπύλης ΜΕ tμε κατεύθυνση t ΜΕ

T1 (τύπος του Green). ΑφήνωΕΝΑ - 1), 2), η κατεύθυνση είναι συνεχής μέσα . Τότε ο τύπος είναι έγκυρος

Στα δεξιά - διανυσματική κυκλοφορία πεδίουκατά μήκος της καμπύλης ΜΕ, στα αριστερά - διέρχεται το διανυσματικό πεδίο ΡΕ.

Έγγρ.Όλες οι συναρτήσεις που περιλαμβάνονται στο (1) είναι συνεχείς => και τα δύο ολοκληρώματα. Το αριστερό και το δεξί ολοκληρώματα στο (1) είναι αμετάβλητα ως προς την επιλογή ενός ορθογώνιου συστήματος συντεταγμένων, αφού και αμετάβλητο, τα στοιχεία του εμβαδού και του μήκους τόξου δεν εξαρτώνται από την επιλογή του καρτεσιανού συστήματος συντεταγμένων => αρκεί να αποδειχθεί το (1) σε ένα ειδικά επιλεγμένο σύστημα.

Ας επιλέξουμε καρτεσιανό ορθογώνιο σύστημασυντεταγμένες Ωχζώστε να πληρούται η προϋπόθεση 2) ​​και Οζας κατευθύνουμε μαζί. Εφόσον το διανυσματικό πεδίο είναι επίπεδο, τότε =>

Για μια επίπεδη περιοχή και , όπου μεγάλο- μήκος τόξου ΜΕ, επιλέχθηκε ως παράμετρος της οποίας η αύξηση είναι συνεπής με την κατεύθυνση διέλευσης ΜΕ =>

Για να αποδείξουμε τον τύπο του Green, αρκεί να αποδείξουμε 2 ισότητες:

Αφήστε μια ευθεία παράλληλη προς τον άξονα OU,σταυρούς ΜΕσε σημεία . Αφήνω - μικρότερη και μεγαλύτερη τετμημένη σημείων σε μια περιοχή, καμπύλη ΜΕ 1 συνδέεται με , και η καμπύλη ΜΕ 2 - с και , προσανατολίζονται σε συμφωνία με το C => σύμφωνα με τον τύπο για την αναγωγή ενός διπλού ολοκληρώματος σε επαναλαμβανόμενο:

Το ολοκλήρωμα υπολογίζεται με παρόμοιο τρόπο J.

Ζ1. Από το έγγραφο => ο τύπος (1) μπορεί να γραφτεί με τη μορφή (1"):

Ω "υ"? ΕΝΑέχει συντεταγμένες R"Και Q", Οτι

Ο μετασχηματισμός Jacobian κατά τη μετάβαση σε ένα νέο σύστημα συντεταγμένων modulo = 1, η παραμετροποίηση χρησιμοποιώντας μήκος τόξου δεν σχετίζεται με το σύστημα συντεταγμένων =>

Αφήνω ΡΕ-απλά συνδεδεμένος τομέας σε (δηλαδή για μια τμηματικά ομαλή κλειστή καμπύλη ντο, που βρίσκεται στην ΡΕ,μπορεί κανείς να καθορίσει μια προσανατολιζόμενη τμηματικά λεία επιφάνεια σολ, που βρίσκεται στην ΡΕ,έχοντας σύνορα ΜΕ), επιφάνεια ΜΙΚΡΟ-το όριο του που πληροί τις προϋποθέσεις:

1) μικρό- τμηματικά λεία αμφίπλευρη πλήρης οριοθετημένη κλειστή και χωρίς μοναδικά σημεία.

2) μπορεί να επιλεγεί ένα ορθογώνιο καρτεσιανό σύστημα συντεταγμένων έτσι ώστε για κάθε έναν από τους άξονες συντεταγμένων να τέμνεται μια ευθεία παράλληλη προς αυτόν τον άξονα μικρόόχι περισσότερο από 2 βαθμούς.

Αφήνω n- μοναδιαίο διάνυσμα εξωτερικού κανονικού προς μικρό.

T2 ( Ο τύπος Ostrogradsky - Gauss ). ΑφήνωΕΝΑείναι ένα διανυσματικό πεδίο, διαφορά στο D, που ικανοποιεί τις συνθήκες 1), 2), και τέτοια ώστε το παράγωγο σε σχέση με η κατεύθυνση είναι συνεχής μέσα . Επειτα

Σωστά - διανυσματική ροή πεδίουμέσα από την επιφάνεια μικρό, στα αριστερά είναι το ολοκλήρωμα όγκου της απόκλισης του διανύσματος στην περιοχή D => Το ολοκλήρωμα όγκου της απόκλισης ενός διανύσματος στην περιοχή D είναι ίσο με τη ροή του διανυσματικού πεδίου μέσω της επιφάνειας S - το όριο αυτής της περιοχής.

ΕγγραφοΌλες οι συναρτήσεις που περιλαμβάνονται στο (2) είναι συνεχείς => και τα δύο ολοκληρώματα. Ο τύπος (2) είναι αμετάβλητος ως προς την επιλογή ενός ορθογώνιου συστήματος συντεταγμένων, επειδή όλες οι ποσότητες που περιλαμβάνονται σε αυτό είναι αμετάβλητες => αρκεί να αποδείξουμε το (2) με καμιά 1 επιλογή του καρτεσιανού συστήματος. Ας επιλέξουμε ένα καρτεσιανό ορθογώνιο σύστημα συντεταγμένων Ωχζώστε να πληρούται η προϋπόθεση 2). ας => δεδομένο :

Απαιτείται έγγραφο:

Ας αποδείξουμε για ΜΕΓΑΛΟ,άλλοι αν-όχι. Αφήνω ΡΕ"-προβολή ρεστο αεροπλάνο Ωχ.Μέσω οριακών σημείων ΡΕ"ας τραβήξουμε παράλληλες γραμμές Οζ.Κάθε ένα από αυτά διασταυρώνεται με μικρόμόνο σε 1 βαθμό. Το σύνολο αυτών των σημείων χωρίζει μικρόσε 2 μέρη: . Εάν σχεδιάσετε μια ευθεία γραμμή από ένα εσωτερικό σημείο ΡΕ"παράλληλο Οζ,τότε θα περάσει μικρόστα 2 σημεία: Και . και τμηματικά και συνεχώς διαφορετικές λειτουργίες σε ΡΕ".Σύμφωνα με τον τύπο για την αναγωγή ενός τριπλού ολοκληρώματος σε επαναλαμβανόμενο ολοκλήρωμα:

Χρησιμοποιήσαμε το γεγονός ότι και τη σχέση

δίκαιο, γιατί η εξωτερική κανονική προς σχηματίζει αμβλεία γωνία με Οζ(=> ).

Ζ2. Από το έγγραφο => τύπος (2) μπορεί να γραφτεί:

Έγγραφο Ζ1.

Φόρμουλα Stokes.

Αφήνω μικρόαπλά συνδεδεμένο (δηλαδή μια τμηματικά ομαλή κλειστή καμπύλη χωρίς αυτοτομές που βρίσκονται επάνω ΜΙΚΡΟ,περιορίζει ένα σύνολο, όλα τα σημεία του οποίου μικρό) επιφάνεια μέσα , πληρούν τις προϋποθέσεις:

1) μικρό- τμηματικά λεία αμφίπλευρη πλήρης οριοθετημένη επιφάνεια χωρίς ειδικά σημεία. το όριό του είναι ένα κλειστό τμηματικά ομαλό περίγραμμα ΜΕ;

2) το καρτεσιανό σύστημα συντεταγμένων μπορεί να επιλεγεί έτσι ώστε μικρόπροβλήθηκε μοναδικά σε 3 επίπεδα συντεταγμένων.

Αφήνω n- μονάδα κανονικό διάνυσμα προς μικρό, t- μονάδα διάνυσμα που εφάπτεται σε ντο, σύμφωνος με n,δηλαδή τη θετική κατεύθυνση της διάβασης της καμπύλης ΜΕσυμπίπτει στο σημείο εφαρμογής του διανύσματος tμε κατεύθυνση t, και αν κοιτάξετε από το τέλος, τότε το περίγραμμα ΜΕπροσανατολίζεται θετικά (γυρίζει αριστερόστροφα).

T (φόρμουλα Stokes). ΑφήνωΕΝΑ - διανυσματικό πεδίο, διαφέρει συνεχώς σε κάποια γειτονιά της επιφάνειας S(δηλαδή σε κάποιο ανοιχτό σετ , που περιέχει S). Επειτα

Ή: Διάνυσμα ροής μέσω της επιφάνειας S ισούται με την κυκλοφορία του διανύσματοςΕΝΑ κατά μήκος ενός κλειστού κυκλώματος Γ.

Εγγραφο. Λόγω των συνθηκών του θεωρήματος, τα ολοκληρώματα στο (1) υπάρχουν. Ο τύπος (1) είναι αμετάβλητος ως προς την επιλογή της βάσης => αρκεί να το αποδείξουμε για οποιαδήποτε επιλογή βάσης. Ας επιλέξουμε ένα ορθογώνιο καρτεσιανό σύστημα συντεταγμένων Ωχζέτσι ώστε μικρόσχεδιάστηκε σίγουρα και για τα τρία αεροπλάνα συντεταγμένων. Αφήνω

Ας συντονίσουμε την επιλογή του συστήματος συντεταγμένων έτσι ώστε το κανονικό διάνυσμα να σχηματίζει οξείες γωνίες με τους άξονες συντεταγμένων. Δίνεται μια έκφραση για στο καρτεσιανό σύστημα συντεταγμένων

Αρκεί να αποδείξουμε:

μικρό- τμηματικά ομαλή και μοναδικά προβαλλόμενη επάνω Ωχ.Αφήνω ΡΕ-προβολή του, G - προβολή ΜΕστο αεροπλάνο Ohu => diff-may f-i, που καθορίζει την εξίσωση της επιφάνειας μικρό. Εν

και επιφάνεια ενσωματωμένη μικρό = διπλό ολοκλήρωμαΜε ρε. Σύμφωνα με τον τύπο του Green*:

Ζ1. δ > 0 τέτοια ώστε για εξαρτήματαφά μέγεθος S< δ (μπορεί να βρίσκεται σε μια σφαίρα ακτίνας δ/2) μπορεί κανείς να επιλέξει ένα καρτεσιανό σύστημα συντεταγμένων έτσι ώστεφά προβάλλεται μοναδικά σε όλα τα επίπεδα συντεταγμένων.Αφήνω - σταθερό σημείο μικρό. Ας σχεδιάσουμε ένα εφαπτόμενο επίπεδο διαμέσου του , έστω το μοναδιαίο κανονικό διάνυσμα της επιφάνειας μέσα . Ας επιλέξουμε ένα ορθογώνιο σύστημα συντεταγμένων ώστε να κάνει οξείες γωνίες με τους άξονες. Επειδή το πεδίο των κανονικών είναι συνεχές, τότε η γειτονιά είναι τέτοια που όλα τα κανονικά σε σημεία αυτής της γειτονιάς σχηματίζουν οξείες γωνίες με τους άξονες => κάποια γειτονιά ακτίνας δ/2 του σημείου , που προβάλλει μοναδικά σε όλα τα επίπεδα συντεταγμένων.

Μπορείτε να επιλέξετε έναν καθολικό αριθμό που δεν εξαρτάται από τον αριθμό δ > 0. Έστω τέτοιο δ => για καθένα μπορείτε να καθορίσετε ένα μέρος της επιφάνειας μικρό, των οποίων οι διαστάσεις< и которая не проектируется однозначно на все координатные плоскости декартовой системы коор­динат.

Ας επιλέξουμε σε κάθε σημείο , από την λαμβανόμενη συνέπεια επιλέγουμε μια ακολουθία που συγκλίνει σε κάποια Μ μικρό. U Μμια γειτονιά που προβάλλεται μοναδικά στα επίπεδα συντεταγμένων ενός συγκεκριμένου ορθογώνιου συστήματος. Αυτή η γειτονιά είναι για κάποιο αριθμό Ππεριέχει ένα τμήμα που θα προβάλλει επίσης μοναδικά και στα τρία επίπεδα συντεταγμένων => μια αντίφαση με την επιλογή.

Ας το αναλύσουμε μικρόσε έναν πεπερασμένο αριθμό λείων τμημάτων, το μέγεθος καθενός από τα οποία είναι< δ, указанного выше. однозначно проектируется на все координатные плос­кости некоторой декартовой системы координат =>Ο τύπος του Στόουκς ισχύει για τον καθένα. Ας συνοψίσουμε την αριστερή και τη δεξιά πλευρά αυτών των τύπων. Ολοκληρώματα σε κοινά τμήματα του ορίου λαμβάνονται σε αντίθετες κατευθύνσεις και επομένως ακυρώνουμε => στα αριστερά λαμβάνουμε το ολοκλήρωμα πάνω από την επιφάνεια του και στα δεξιά - το ολοκλήρωμα πάνω από το όριο ΜΕαπό , δηλ. ο τύπος Stokes για τη γενική περίπτωση => ο τύπος Stokes ισχύει για επιφάνειες που ικανοποιούν την συνθήκη 1) και δεν πληρούν, γενικά, τη συνθήκη 2).

Ζ 2. Η φόρμουλα Stokes ισχύει για επιφάνειες μικρό, επιτρέποντας τη διαίρεση χρησιμοποιώντας τμηματικές ομαλές καμπύλες σε έναν πεπερασμένο αριθμό απλά συνδεδεμένων επιφανειών που έχουν την ιδιότητα 1) επιφάνειες. Έγγραφο: αθροίστε τα ολοκληρώματα αριστερά και δεξιά στους τύπους Stokes για απλά συνδεδεμένες επιφάνειες και λάβετε υπόψη ότι τα ολοκληρώματα κατά μήκος των καμπυλών που περιλαμβάνονται στο διαμέρισμα λαμβάνονται σε διαφορετικές κατευθύνσεις και επομένως ακυρώνονται.

Ζ3. Από το έγγραφο => ο τύπος (1) μπορεί να γραφτεί με τη μορφή (1"):

Τα ολοκληρώματα αριστερά και δεξιά στο (1") είναι αμετάβλητα, αφού οι τιμές των ολοκληρωμάτων είναι ίσες με και - αμετάβλητες ποσότητες, αντίστοιχα. Η μορφή των ολοκληρωμάτων στον τύπο (1") επίσης δεν αλλάζει κατά τη μετακίνηση προς την νέο σύστημα Ox"y"z";εάν στη νέα βάση το διανυσματικό πεδίο ΕΝΑέχει συντεταγμένες R", Q" Και R", Οτι

Το Jacobian του μετασχηματισμού κατά τη μετάβαση σε ένα νέο σύστημα συντεταγμένων modulo = 1, η παραμετροποίηση χρησιμοποιώντας μήκος τόξου δεν σχετίζεται με το σύστημα συντεταγμένων => τα ολοκληρώματα αριστερά και δεξιά στο (1") δεν αλλάζουν την τιμή και το σχήμα τους.

*: π - επίπεδο σε , - μοναδιαίο διάνυσμα κανονικό στο π, ΡΕ-απλά συνδεδεμένη περιοχή στο π . Αφήνω ρεικανοποιεί τις προϋποθέσεις: 1) όριο ΜΕπεριοχή ρεείναι μια κλειστή τμηματικά ομαλή καμπύλη χωρίς μοναδικά σημεία. 2) στο π μπορεί κανείς να επιλέξει ένα καρτεσιανό ορθογώνιο σύστημα συντεταγμένων έτσι ώστε όλες οι ευθείες παράλληλες προς τους άξονες συντεταγμένων να τέμνονται ρεόχι περισσότερο από 2 βαθμούς.

Αφήνω t-μοναδιαίο διάνυσμα της εφαπτομένης στην καμπύλη ΜΕ,σύμφωνος με .

T1 (τύπος του Green). ΑφήνωΕΝΑ - διανυσματικό πεδίο διαφορά στο D που ικανοποιεί τις συνθήκες 1), 2), και τέτοια ώστε το παράγωγό του σε σχέση με η κατεύθυνση είναι συνεχής μέσα . Τότε ο τύπος είναι έγκυρος