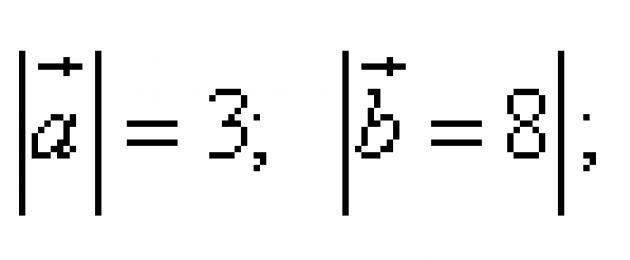Εάν στο πρόβλημα τόσο τα μήκη των διανυσμάτων όσο και η μεταξύ τους γωνία παρουσιάζονται «σε μια ασημένια πιατέλα», τότε η κατάσταση του προβλήματος και η λύση του μοιάζουν με αυτό:
Παράδειγμα 1.Δίνονται διανύσματα. Βρείτε το βαθμωτό γινόμενο των διανυσμάτων εάν τα μήκη τους και η μεταξύ τους γωνία αντιπροσωπεύονται από τις ακόλουθες τιμές:
Ένας άλλος ορισμός είναι επίσης έγκυρος, εντελώς ισοδύναμος με τον ορισμό 1.
Ορισμός 2. Το βαθμωτό γινόμενο των διανυσμάτων είναι ένας αριθμός (βαθμωτός) ίσος με το γινόμενο του μήκους ενός από αυτά τα διανύσματα και την προβολή ενός άλλου διανύσματος στον άξονα που καθορίζεται από το πρώτο από αυτά τα διανύσματα. Φόρμουλα σύμφωνα με τον ορισμό 2:
Θα λύσουμε το πρόβλημα χρησιμοποιώντας αυτόν τον τύπο μετά το επόμενο σημαντικό θεωρητικό σημείο.
Ορισμός του βαθμωτού γινόμενου των διανυσμάτων ως προς τις συντεταγμένες
Ο ίδιος αριθμός μπορεί να ληφθεί εάν στα διανύσματα που πολλαπλασιάζονται δοθούν οι συντεταγμένες τους.
Ορισμός 3.Το γινόμενο με τελείες των διανυσμάτων είναι ένας αριθμός ίσος με το άθροισμα των κατά ζεύγη γινομένων των αντίστοιχων συντεταγμένων τους.
Στην επιφάνεια
Αν δύο διανύσματα και στο επίπεδο ορίζονται από τα δύο τους Καρτεσιανές ορθογώνιες συντεταγμένες
τότε το κλιμακωτό γινόμενο αυτών των διανυσμάτων είναι ίσο με το άθροισμα των κατά ζεύγη γινομένων των αντίστοιχων συντεταγμένων τους:
.
Παράδειγμα 2.Να βρείτε την αριθμητική τιμή της προβολής του διανύσματος στον παράλληλο προς το διάνυσμα άξονα.
Λύση. Βρίσκουμε το βαθμωτό γινόμενο των διανυσμάτων προσθέτοντας τα κατά ζεύγη γινόμενα των συντεταγμένων τους:
Τώρα πρέπει να εξισώσουμε το προκύπτον βαθμωτό γινόμενο με το γινόμενο του μήκους του διανύσματος και την προβολή του διανύσματος σε έναν άξονα παράλληλο προς το διάνυσμα (σύμφωνα με τον τύπο).
Βρίσκουμε το μήκος του διανύσματος ως τετραγωνική ρίζα του αθροίσματος των τετραγώνων των συντεταγμένων του:
.
Δημιουργούμε μια εξίσωση και τη λύνουμε:
Απάντηση. Η απαιτούμενη αριθμητική τιμή είναι μείον 8.
Στο διάστημα
Αν δύο διανύσματα και στον χώρο ορίζονται από τις τρεις καρτεσιανές ορθογώνιες συντεταγμένες τους
,
τότε το κλιμακωτό γινόμενο αυτών των διανυσμάτων είναι επίσης ίσο με το άθροισμα των κατά ζεύγη γινομένων των αντίστοιχων συντεταγμένων τους, μόνο που υπάρχουν ήδη τρεις συντεταγμένες:
.
Το έργο της εύρεσης του κλιμακωτού γινομένου με τη χρήση της μεθόδου που εξετάζεται είναι μετά την ανάλυση των ιδιοτήτων του κλιμακωτού προϊόντος. Επειδή στο πρόβλημα θα πρέπει να προσδιορίσετε ποια γωνία σχηματίζουν τα πολλαπλασιασμένα διανύσματα.
Ιδιότητες του βαθμωτού γινομένου των διανυσμάτων
Αλγεβρικές ιδιότητες
1. (ανταλλακτική ιδιότητα: η αντιστροφή των θέσεων των πολλαπλασιασμένων διανυσμάτων δεν αλλάζει την τιμή του κλιμακωτού γινόμενου τους).
2. 
(συνειρμική ιδιότητα σε σχέση με έναν αριθμητικό παράγοντα: το κλιμακωτό γινόμενο ενός διανύσματος πολλαπλασιασμένο με έναν ορισμένο παράγοντα και ενός άλλου διανύσματος είναι ίσο με το κλιμακωτό γινόμενο αυτών των διανυσμάτων πολλαπλασιασμένο με τον ίδιο παράγοντα).
3. 
(κατανεμητική ιδιότητα σε σχέση με το άθροισμα των διανυσμάτων: το κλιμακωτό γινόμενο του αθροίσματος δύο διανυσμάτων από το τρίτο διάνυσμα είναι ίσο με το άθροισμα των κλιμακωτών γινομένων του πρώτου διανύσματος από το τρίτο διάνυσμα και του δεύτερου διανύσματος από το τρίτο διάνυσμα).
4. (κλιμακωτό τετράγωνο του διανύσματος μεγαλύτερο από μηδέν), αν είναι μη μηδενικό διάνυσμα και, αν είναι μηδενικό διάνυσμα.
Γεωμετρικές ιδιότητες
Στους ορισμούς της υπό μελέτη πράξης έχουμε ήδη θίξει την έννοια της γωνίας μεταξύ δύο διανυσμάτων. Ήρθε η ώρα να ξεκαθαρίσουμε αυτή την έννοια.
Στο παραπάνω σχήμα μπορείτε να δείτε δύο διανύσματα που φέρονται σε μια κοινή αρχή. Και το πρώτο πράγμα που πρέπει να προσέξετε είναι ότι υπάρχουν δύο γωνίες μεταξύ αυτών των διανυσμάτων - φ 1 Και φ 2 . Ποια από αυτές τις γωνίες εμφανίζεται στους ορισμούς και τις ιδιότητες του βαθμωτού γινομένου των διανυσμάτων; Το άθροισμα των εξεταζόμενων γωνιών είναι 2 π και επομένως τα συνημίτονα αυτών των γωνιών είναι ίσα. Ο ορισμός του γινόμενου κουκκίδων περιλαμβάνει μόνο το συνημίτονο της γωνίας και όχι την τιμή της έκφρασής του. Αλλά οι ιδιότητες λαμβάνουν υπόψη μόνο μία γωνία. Και αυτή είναι η μία από τις δύο γωνίες που δεν υπερβαίνει π , δηλαδή 180 μοίρες. Στο σχήμα αυτή η γωνία υποδεικνύεται ως φ 1 .
1. Καλούνται δύο διανύσματα ορθογώνιο Και η γωνία μεταξύ αυτών των διανυσμάτων είναι ευθεία (90 μοίρες ή π /2), εάν το κλιμακωτό γινόμενο αυτών των διανυσμάτων είναι μηδέν :
.
Η ορθογωνία στη διανυσματική άλγεβρα είναι η καθετότητα δύο διανυσμάτων.
2. Απαρτίζουν δύο μη μηδενικά διανύσματα αιχμηρή γωνία (από 0 έως 90 μοίρες, ή, που είναι το ίδιο - λιγότερο π το προϊόν κουκκίδας είναι θετικό .
3. Απαρτίζουν δύο μη μηδενικά διανύσματα αμβλεία γωνία (από 90 έως 180 μοίρες, ή, το ίδιο - περισσότερο π /2) εάν και μόνο εάν αυτοί το προϊόν κουκκίδας είναι αρνητικό .
Παράδειγμα 3.Οι συντεταγμένες δίνονται από τα διανύσματα:
.
Υπολογίστε τα βαθμωτά γινόμενα όλων των ζευγών δεδομένων διανυσμάτων. Ποια γωνία (οξεία, ορθή, αμβλεία) σχηματίζουν αυτά τα ζεύγη διανυσμάτων;
Λύση. Θα υπολογίσουμε προσθέτοντας τα γινόμενα των αντίστοιχων συντεταγμένων.
Πήραμε αρνητικό αριθμό, οπότε τα διανύσματα σχηματίζουν αμβλεία γωνία.
Πήραμε θετικό αριθμό, οπότε τα διανύσματα σχηματίζουν οξεία γωνία.
Πήραμε μηδέν, άρα τα διανύσματα σχηματίζουν ορθή γωνία.
Πήραμε θετικό αριθμό, οπότε τα διανύσματα σχηματίζουν οξεία γωνία.
.
Πήραμε θετικό αριθμό, οπότε τα διανύσματα σχηματίζουν οξεία γωνία.
Για αυτοέλεγχο μπορείτε να χρησιμοποιήσετε online αριθμομηχανή Το γινόμενο κουκίδων των διανυσμάτων και του συνημιτόνου της μεταξύ τους γωνίας .
Παράδειγμα 4.Δίνοντας τα μήκη δύο διανυσμάτων και τη γωνία μεταξύ τους:
.
Να προσδιορίσετε σε ποια τιμή του αριθμού τα διανύσματα και είναι ορθογώνια (κάθετα).
Λύση. Ας πολλαπλασιάσουμε τα διανύσματα χρησιμοποιώντας τον κανόνα για τον πολλαπλασιασμό πολυωνύμων:
Τώρα ας υπολογίσουμε κάθε όρο:
.
Ας δημιουργήσουμε μια εξίσωση (το γινόμενο είναι ίσο με μηδέν), ας προσθέσουμε παρόμοιους όρους και λύνουμε την εξίσωση:
Απάντηση: πήραμε την αξία λ = 1,8, στο οποίο τα διανύσματα είναι ορθογώνια.
Παράδειγμα 5.Να αποδείξετε ότι το διάνυσμα 
ορθογώνιο (κάθετο) στο διάνυσμα
Λύση. Για να ελέγξουμε την ορθογωνικότητα, πολλαπλασιάζουμε τα διανύσματα και ως πολυώνυμα, αντικαθιστώντας την έκφραση που δίνεται στη δήλωση προβλήματος:
.
Για να γίνει αυτό, πρέπει να πολλαπλασιάσετε κάθε όρο (όρος) του πρώτου πολυωνύμου με κάθε όρο του δεύτερου και να προσθέσετε τα προκύπτοντα γινόμενα:
.
Στο αποτέλεσμα που προκύπτει, το κλάσμα μειώνεται κατά. Προκύπτει το ακόλουθο αποτέλεσμα:
Συμπέρασμα: ως αποτέλεσμα πολλαπλασιασμού έχουμε μηδέν, επομένως, αποδεικνύεται η ορθογωνικότητα (καθετότητα) των διανυσμάτων.
Λύστε το πρόβλημα μόνοι σας και μετά δείτε τη λύση
Παράδειγμα 6.Τα μήκη των διανυσμάτων και δίνονται, και η γωνία μεταξύ αυτών των διανυσμάτων είναι π /4. Προσδιορίστε σε ποια τιμή μ διανύσματα και είναι αμοιβαία κάθετα.
Για αυτοέλεγχο μπορείτε να χρησιμοποιήσετε online αριθμομηχανή Το γινόμενο κουκίδων των διανυσμάτων και του συνημιτόνου της μεταξύ τους γωνίας .
Αναπαράσταση μήτρας του γινομένου κουκίδων των διανυσμάτων και του γινόμενου διανυσμάτων ν-διάστατων
Μερικές φορές είναι πλεονεκτικό για τη σαφήνεια να αναπαριστούν δύο πολλαπλασιασμένα διανύσματα με τη μορφή πινάκων. Στη συνέχεια, το πρώτο διάνυσμα αντιπροσωπεύεται ως πίνακας γραμμής και το δεύτερο - ως πίνακας στήλης:
Τότε το βαθμωτό γινόμενο των διανυσμάτων θα είναι το γινόμενο αυτών των πινάκων :
Το αποτέλεσμα είναι το ίδιο με αυτό που προκύπτει με τη μέθοδο που έχουμε ήδη εξετάσει. Πήραμε έναν μοναδικό αριθμό και το γινόμενο ενός πίνακα σειρών από έναν πίνακα στήλης είναι επίσης ένας απλός αριθμός.
Είναι βολικό να αναπαραστήσουμε το γινόμενο αφηρημένων ν-διαστάσεων διανυσμάτων σε μορφή μήτρας. Έτσι, το γινόμενο δύο τετραδιάστατων διανυσμάτων θα είναι το γινόμενο ενός πίνακα σειρών με τέσσερα στοιχεία από έναν πίνακα στήλης επίσης με τέσσερα στοιχεία, το γινόμενο δύο πενταδιάστατων διανυσμάτων θα είναι το γινόμενο ενός πίνακα σειρών με πέντε στοιχεία κατά έναν πίνακα στήλης επίσης με πέντε στοιχεία, και ούτω καθεξής.
Παράδειγμα 7.Βρείτε κλιμακωτά γινόμενα ζευγών διανυσμάτων
,
χρησιμοποιώντας αναπαράσταση μήτρας.
Λύση. Το πρώτο ζεύγος διανυσμάτων. Αντιπροσωπεύουμε το πρώτο διάνυσμα ως πίνακα γραμμής και το δεύτερο ως πίνακα στήλης. Βρίσκουμε το βαθμωτό γινόμενο αυτών των διανυσμάτων ως το γινόμενο ενός πίνακα σειρών και ενός πίνακα στηλών:
Ομοίως αντιπροσωπεύουμε το δεύτερο ζεύγος και βρίσκουμε:
Όπως μπορείτε να δείτε, τα αποτελέσματα ήταν τα ίδια με τα ίδια ζεύγη από το παράδειγμα 2.
Γωνία μεταξύ δύο διανυσμάτων
Η εξαγωγή του τύπου για το συνημίτονο της γωνίας μεταξύ δύο διανυσμάτων είναι πολύ όμορφη και συνοπτική.
Για να εκφράσετε το γινόμενο κουκίδων των διανυσμάτων
(1)
σε μορφή συντεταγμένων, βρίσκουμε πρώτα το βαθμωτό γινόμενο των μοναδιαίων διανυσμάτων. Το κλιμακωτό γινόμενο ενός διανύσματος με τον εαυτό του εξ ορισμού:
Αυτό που γράφεται στον παραπάνω τύπο σημαίνει: το κλιμακωτό γινόμενο ενός διανύσματος με τον εαυτό του είναι ίσο με το τετράγωνο του μήκους του. Το συνημίτονο του μηδέν είναι ίσο με ένα, άρα το τετράγωνο κάθε μονάδας θα είναι ίσο με ένα:
Δεδομένου ότι οι φορείς
είναι κατά ζεύγη κάθετες, τότε τα κατά ζεύγη γινόμενα των μοναδιαίων διανυσμάτων θα είναι ίσα με μηδέν:
Τώρα ας εκτελέσουμε τον πολλαπλασιασμό των διανυσματικών πολυωνύμων:
Αντικαθιστούμε τις τιμές των αντίστοιχων βαθμωτών γινομένων των μοναδιαίων διανυσμάτων στη δεξιά πλευρά της ισότητας:
Λαμβάνουμε τον τύπο για το συνημίτονο της γωνίας μεταξύ δύο διανυσμάτων:
Παράδειγμα 8.Δίνονται τρεις βαθμοί ΕΝΑ(1;1;1), σι(2;2;1), ντο(2;1;2).
Βρείτε τη γωνία.
Λύση. Εύρεση των συντεταγμένων των διανυσμάτων:
,
.
Χρησιμοποιώντας τον τύπο συνημιτόνου γωνίας παίρνουμε:
Ως εκ τούτου, .
Για αυτοέλεγχο μπορείτε να χρησιμοποιήσετε online αριθμομηχανή Το γινόμενο κουκίδων των διανυσμάτων και του συνημιτόνου της μεταξύ τους γωνίας .
Παράδειγμα 9.Δίνονται δύο διανύσματα
Βρείτε το άθροισμα, τη διαφορά, το μήκος, το γινόμενο κουκίδων και τη γωνία μεταξύ τους.
2.Διαφορά
Ορισμός 1
Το κλιμακωτό γινόμενο των διανυσμάτων είναι ένας αριθμός ίσος με το γινόμενο των dynes αυτών των διανυσμάτων και το συνημίτονο της μεταξύ τους γωνίας.
Ο συμβολισμός για το γινόμενο των διανυσμάτων a → και b → έχει τη μορφή a → , b → . Ας το μετατρέψουμε στον τύπο:
a → , b → = a → · b → · cos a → , b → ^ . a → και b → δηλώνουν τα μήκη των διανυσμάτων, a → , b → ^ - ορισμός της γωνίας μεταξύ των δεδομένων διανυσμάτων. Εάν τουλάχιστον ένα διάνυσμα είναι μηδέν, δηλαδή έχει τιμή 0, τότε το αποτέλεσμα θα είναι ίσο με μηδέν, a → , b → = 0
Πολλαπλασιάζοντας ένα διάνυσμα από μόνο του, παίρνουμε το τετράγωνο του μήκους του:
a → , b → = a → b → cos a → , a → ^ = a → 2 cos 0 = a → 2
Ορισμός 2
Ο βαθμωτός πολλαπλασιασμός ενός διανύσματος από μόνος του ονομάζεται βαθμωτό τετράγωνο.
Υπολογίζεται με τον τύπο:
a → , b → = a → · b → · cos a → , b → ^ .
Ο συμβολισμός a → , b → = a → · b → · cos a → , b → ^ = a → · n p a → b → = b → · n p b → a → δείχνει ότι n p b → a → είναι η αριθμητική προβολή του a → σε b → , n p a → a → - προβολή του b → σε a →, αντίστοιχα.
Ας διατυπώσουμε τον ορισμό ενός προϊόντος για δύο διανύσματα:
Το κλιμακωτό γινόμενο δύο διανυσμάτων a → κατά b → ονομάζεται γινόμενο του μήκους του διανύσματος a → με την προβολή b → με τη φορά του a → ή το γινόμενο του μήκους b → με την προβολή a →, αντίστοιχα.
Το προϊόν με τελείες σε συντεταγμένες
Το κλιμακωτό γινόμενο μπορεί να υπολογιστεί μέσω των συντεταγμένων των διανυσμάτων σε ένα δεδομένο επίπεδο ή στο διάστημα.
Το κλιμακωτό γινόμενο δύο διανυσμάτων σε ένα επίπεδο, σε τρισδιάστατο χώρο, ονομάζεται το άθροισμα των συντεταγμένων των δεδομένων διανυσμάτων a → και b →.
Όταν υπολογίζετε το κλιμακωτό γινόμενο δεδομένων διανυσμάτων a → = (a x , a y) , b → = (b x , b y) στο επίπεδο στο καρτεσιανό σύστημα, χρησιμοποιήστε:
a → , b → = a x b x + a y b y,
για τρισδιάστατο χώρο ισχύει η έκφραση:
a → , b → = a x · b x + a y · b y + a z · b z .
Στην πραγματικότητα, αυτός είναι ο τρίτος ορισμός του βαθμωτού προϊόντος.
Ας το αποδείξουμε.
Αποδεικτικά στοιχεία 1
Για να το αποδείξουμε, χρησιμοποιούμε a → , b → = a → · b → · cos a → , b → ^ = a x · b x + a y · b y για διανύσματα a → = (a x , a y) , b → = (b x , β υ) στο καρτεσιανό σύστημα.
Τα διανύσματα πρέπει να παραμεριστούν
O A → = a → = a x , a y και O B → = b → = b x , b y .
Τότε το μήκος του διανύσματος A B → θα είναι ίσο με A B → = O B → - O A → = b → - a → = (b x - a x , b y - a y) .
Θεωρήστε το τρίγωνο O A B .
A B 2 = O A 2 + O B 2 - 2 · O A · O B · cos (∠ A O B) είναι σωστό με βάση το θεώρημα συνημιτόνου.
Σύμφωνα με την συνθήκη, είναι σαφές ότι O A = a → , O B = b → , A B = b → - a → , ∠ A O B = a → , b → ^ , που σημαίνει ότι γράφουμε τον τύπο για την εύρεση της γωνίας μεταξύ των διανυσμάτων διαφορετικά
b → - a → 2 = a → 2 + b → 2 - 2 · a → · b → · cos (a → , b → ^) .
Τότε από τον πρώτο ορισμό προκύπτει ότι b → - a → 2 = a → 2 + b → 2 - 2 · (a → , b →) , που σημαίνει (a → , b →) = 1 2 · (a → 2 + b → 2 - b → - a → 2) .
Εφαρμόζοντας τον τύπο για τον υπολογισμό του μήκους των διανυσμάτων, παίρνουμε:
a → , b → = 1 2 · ((a 2 x + a y 2) 2 + (b 2 x + b y 2) 2 - ((b x - a x) 2 + (b y - a y) 2) 2) = = 1 2 (a 2 x + a 2 y + b 2 x + b 2 y - (b x - a x) 2 - (b y - a y) 2) = = a x b x + a y b y
Ας αποδείξουμε τις ισότητες:
(a → , b →) = a → b → cos (a → , b → ^) = = a x b x + a y b y + a z b z
– αντίστοιχα για διανύσματα τρισδιάστατου χώρου.
Το κλιμακωτό γινόμενο διανυσμάτων με συντεταγμένες λέει ότι το βαθμωτό τετράγωνο ενός διανύσματος είναι ίσο με το άθροισμα των τετραγώνων των συντεταγμένων του στο χώρο και στο επίπεδο, αντίστοιχα. a → = (a x , a y , a z) , b → = (b x , b y , b z) και (a → , a →) = a x 2 + a y 2 .
Το προϊόν Dot και οι ιδιότητές του
Υπάρχουν ιδιότητες του προϊόντος με κουκκίδες που ισχύουν για τα a → , b → και c → :
- commutativity (a → , b →) = (b → , a →) ;
- κατανομή (a → + b → , c →) = (a → , c →) + (b → , c →) , (a → + b → , c →) = (a → , b →) + (a → , γ →) ;
- συνδυαστική ιδιότητα (λ · a → , b →) = λ · (a → , b →), (a → , λ · b →) = λ · (a → , b →), λ - οποιοσδήποτε αριθμός;
- Το κλιμακωτό τετράγωνο είναι πάντα μεγαλύτερο από το μηδέν (a → , a →) ≥ 0, όπου (a → , a →) = 0 στην περίπτωση που a → μηδέν.
Οι ιδιότητες είναι εξηγήσιμες χάρη στον ορισμό του βαθμωτού γινομένου στο επίπεδο και τις ιδιότητες της πρόσθεσης και του πολλαπλασιασμού των πραγματικών αριθμών.
Να αποδείξετε τη μεταθετική ιδιότητα (a → , b →) = (b → , a →) . Από τον ορισμό έχουμε ότι (a → , b →) = a y · b y + a y · b y και (b → , a →) = b x · a x + b y · a y .
Με την ιδιότητα της ανταλλαξιμότητας, οι ισότητες a x · b x = b x · a x και a y · b y = b y · a y είναι αληθείς, που σημαίνει a x · b x + a y · b y = b x · a x + b y · a y .
Έπεται ότι (a → , b →) = (b → , a →) . Q.E.D.
Η διανομή ισχύει για οποιονδήποτε αριθμό:
(a (1) → + a (2) → + . . . + a (n) → , b →) = (a (1) → , b →) + (a (2) → , b →) + . . . + (a (n) → , b →)
και (a → , b (1) → + b (2) → + . . + b (n) →) = (a → , b (1) →) + (a → , b (2) →) + . . . + (a → , b → (n)) ,
άρα έχουμε
(a (1) → + a (2) → + . . . + a (n) → , b (1) → + b (2) → + . . . + b (m) →) = = (a ( 1) → , b (1) →) + (a (1) → , b (2) →) + . . . + (a (1) → , b (m) →) + + (a (2) → , b (1) →) + (a (2) → , b (2) →) + . . . + (a (2) → , b (m) →) + . . . + + (a (n) → , b (1) →) + (a (n) → , b (2) →) + . . . + (a (n) → , b (m) →)
Το προϊόν με κουκκίδες με παραδείγματα και λύσεις
Οποιοδήποτε πρόβλημα αυτού του είδους επιλύεται χρησιμοποιώντας τις ιδιότητες και τους τύπους που σχετίζονται με το βαθμωτό γινόμενο:
- (a → , b →) = a → · b → · cos (a → , b → ^) ;
- (a → , b →) = a → · n p a → b → = b → · n p b → a → ;
- (a → , b →) = a x · b x + a y · b y ή (a → , b →) = a x · b x + a y · b y + a z · b z ;
- (a → , a →) = a → 2 .
Ας δούμε μερικά παραδείγματα λύσεων.
Παράδειγμα 2
Το μήκος του a → είναι 3, το μήκος του b → είναι 7. Βρείτε το γινόμενο με τελείες αν η γωνία είναι 60 μοίρες.
Λύση
Κατά συνθήκη, έχουμε όλα τα δεδομένα, επομένως τα υπολογίζουμε χρησιμοποιώντας τον τύπο:
(a → , b →) = a → b → cos (a → , b → ^) = 3 7 cos 60 ° = 3 7 1 2 = 21 2
Απάντηση: (a → , b →) = 21 2 .
Παράδειγμα 3
Δίνονται διανύσματα a → = (1 , - 1 , 2 - 3) , b → = (0 , 2 , 2 + 3) . Τι είναι το βαθμωτό προϊόν;
Λύση
Αυτό το παράδειγμα εξετάζει τον τύπο για τον υπολογισμό των συντεταγμένων, καθώς προσδιορίζονται στη δήλωση προβλήματος:
(a → , b →) = a x · b x + a y · b y + a z · b z = = 1 · 0 + (- 1) · 2 + (2 + 3) · (2 + 3) = = 0 - 2 + ( 2 - 9) = - 9
Απάντηση: (a → , b →) = - 9
Παράδειγμα 4
Βρείτε το βαθμωτό γινόμενο των A B → και A C →. Τα σημεία A (1, - 3), B (5, 4), C (1, 1) δίνονται στο επίπεδο συντεταγμένων.
Λύση
Αρχικά, υπολογίζονται οι συντεταγμένες των διανυσμάτων, αφού κατά συνθήκη δίνονται οι συντεταγμένες των σημείων:
A B → = (5 - 1, 4 - (- 3)) = (4, 7) A C → = (1 - 1, 1 - (- 3)) = (0, 4)
Αντικαθιστώντας τον τύπο χρησιμοποιώντας συντεταγμένες, παίρνουμε:
(A B →, A C →) = 4 0 + 7 4 = 0 + 28 = 28.
Απάντηση: (A B → , A C →) = 28 .
Παράδειγμα 5
Δίνονται διανύσματα a → = 7 · m → + 3 · n → και b → = 5 · m → + 8 · n → , βρείτε το γινόμενο τους. m → ίσον 3 και n → ίσον 2 μονάδες, είναι κάθετες.
Λύση
(a → , b →) = (7 m → + 3 n → , 5 m → + 8 n →) . Εφαρμόζοντας την ιδιότητα διανομής, παίρνουμε:
(7 m → + 3 n →, 5 m → + 8 n →) = = (7 m →, 5 m →) + (7 m →, 8 n →) + (3 n → , 5 m →) + ( 3 n → , 8 n →)
Βγάζουμε τον συντελεστή από το πρόσημο του προϊόντος και παίρνουμε:
(7 m → , 5 m →) + (7 m → , 8 n →) + (3 n → , 5 m →) + (3 n → , 8 n →) = = 7 · 5 · (m → , m →) + 7 · 8 · (m → , n →) + 3 · 5 · (n → , m →) + 3 · 8 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →)
Με την ιδιότητα της ανταλλαγής μετασχηματίζουμε:
35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (m → , n →) + 24 · (n → , n →) = = 35 · (m → , m →) + 71 · (m → , n → ) + 24 · (n → , n →)
Ως αποτέλεσμα παίρνουμε:
(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →).
Τώρα εφαρμόζουμε τον τύπο για το βαθμωτό γινόμενο με τη γωνία που καθορίζεται από την συνθήκη:
(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →) = = 35 · m → 2 + 71 · m → · n → · cos (m → , n → ^) + 24 · n → 2 = 35 · 3 2 + 71 · 3 · 2 · cos π 2 + 24 · 2 2 = 411 .
Απάντηση: (a → , b →) = 411
Αν υπάρχει αριθμητική προβολή.
Παράδειγμα 6
Βρείτε το βαθμωτό γινόμενο των a → και b →. Το διάνυσμα a → έχει συντεταγμένες a → = (9, 3, - 3), προβολή b → με συντεταγμένες (- 3, - 1, 1).
Λύση
Κατά συνθήκη, τα διανύσματα a → και η προβολή b → κατευθύνονται αντίθετα, επειδή a → = - 1 3 · n p a → b → → , που σημαίνει ότι η προβολή b → αντιστοιχεί στο μήκος n p a → b → → , και με το « -" σημάδι:
n p a → b → → = - n p a → b → → = - (- 3) 2 + (- 1) 2 + 1 2 = - 11 ,
Αντικαθιστώντας τον τύπο, παίρνουμε την έκφραση:
(a → , b →) = a → · n p a → b → → = 9 2 + 3 2 + (- 3) 2 · (- 11) = - 33 .
Απάντηση: (a → , b →) = - 33 .
Προβλήματα με ένα γνωστό βαθμωτό γινόμενο, όπου είναι απαραίτητο να βρεθεί το μήκος ενός διανύσματος ή μιας αριθμητικής προβολής.
Παράδειγμα 7
Ποια τιμή πρέπει να πάρει το λ για ένα δεδομένο βαθμωτό γινόμενο a → = (1, 0, λ + 1) και b → = (λ, 1, λ) θα είναι ίση με -1.
Λύση
Από τον τύπο είναι σαφές ότι είναι απαραίτητο να βρεθεί το άθροισμα των γινομένων των συντεταγμένων:
(a → , b →) = 1 λ + 0 1 + (λ + 1) λ = λ 2 + 2 λ .
Δίνεται έχουμε (a → , b →) = - 1 .
Για να βρούμε το λ, υπολογίζουμε την εξίσωση:
λ 2 + 2 · λ = - 1, επομένως λ = - 1.
Απάντηση: λ = - 1.
Φυσική έννοια του βαθμωτού προϊόντος
Η μηχανική εξετάζει την εφαρμογή του προϊόντος κουκίδων.
Όταν το A λειτουργεί με σταθερή δύναμη F → ένα κινούμενο σώμα από ένα σημείο M στο N, μπορείτε να βρείτε το γινόμενο των μηκών των διανυσμάτων F → και M N → με το συνημίτονο της μεταξύ τους γωνίας, που σημαίνει ότι το έργο είναι ίσο στο γινόμενο των διανυσμάτων δύναμης και μετατόπισης:
A = (F → , M N →) .
Παράδειγμα 8
Η κίνηση ενός υλικού σημείου κατά 3 μέτρα υπό την επίδραση δύναμης ίσης με 5 Nton κατευθύνεται υπό γωνία 45 μοιρών σε σχέση με τον άξονα. Βρες ένα.
Λύση
Εφόσον το έργο είναι το γινόμενο του διανύσματος δύναμης και της μετατόπισης, σημαίνει ότι με βάση τη συνθήκη F → = 5, S → = 3, (F →, S → ^) = 45 °, λαμβάνουμε A = (F →, S →) = F → · S → · cos (F → , S → ^) = 5 · 3 · cos (45 °) = 15 2 2 .
Απάντηση: A = 15 2 2 .
Παράδειγμα 9
Ένα υλικό σημείο, που κινείται από το M (2, - 1, - 3) στο N (5, 3 λ - 2, 4) υπό τη δύναμη F → = (3, 1, 2), λειτούργησε ίσο με 13 J. Υπολογίστε το μήκος της κίνησης.
Λύση
Για δεδομένες διανυσματικές συντεταγμένες M N → έχουμε M N → = (5 - 2, 3 λ - 2 - (- 1) , 4 - (- 3)) = (3, 3 λ - 1, 7) .
Χρησιμοποιώντας τον τύπο για την εύρεση εργασίας με διανύσματα F → = (3, 1, 2) και M N → = (3, 3 λ - 1, 7), λαμβάνουμε A = (F ⇒, M N →) = 3 3 + 1 ( 3 λ - 1) + 2 7 = 22 + 3 λ.
Σύμφωνα με την συνθήκη, δίνεται ότι A = 13 J, που σημαίνει 22 + 3 λ = 13. Αυτό σημαίνει λ = - 3, που σημαίνει M N → = (3, 3 λ - 1, 7) = (3, - 10, 7).
Για να βρείτε το μήκος της κίνησης M N →, εφαρμόστε τον τύπο και αντικαταστήστε τις τιμές:
M N → = 3 2 + (- 10) 2 + 7 2 = 158.
Απάντηση: 158.
Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter
Κλιμακωτό γινόμενο διανυσμάτων (εφεξής καλούμενο SP). Αγαπητοί φίλοι και φίλες! Η εξέταση των μαθηματικών περιλαμβάνει μια ομάδα προβλημάτων επίλυσης διανυσμάτων. Έχουμε ήδη εξετάσει ορισμένα προβλήματα. Μπορείτε να τα δείτε στην κατηγορία "Διανύσματα". Γενικά, η θεωρία των διανυσμάτων δεν είναι περίπλοκη, το κύριο πράγμα είναι να τη μελετήσουμε με συνέπεια. Οι υπολογισμοί και οι πράξεις με διανύσματα στο μάθημα των σχολικών μαθηματικών είναι απλοί, οι τύποι δεν είναι περίπλοκοι. Ρίξε μια ματιά στο. Σε αυτό το άρθρο θα αναλύσουμε προβλήματα στο SP των διανυσμάτων (που περιλαμβάνονται στην Εξέταση Ενιαίας Πολιτείας). Τώρα «βύθιση» στη θεωρία:
H Για να βρείτε τις συντεταγμένες ενός διανύσματος, πρέπει να αφαιρέσετε από τις συντεταγμένες του τέλους τουτις αντίστοιχες συντεταγμένες της προέλευσής του
Και επιπλέον:
*Το διανυσματικό μήκος (μέτρο) προσδιορίζεται ως εξής:
Αυτές οι φόρμουλες πρέπει να θυμόμαστε!!!
Ας δείξουμε τη γωνία μεταξύ των διανυσμάτων:
Είναι σαφές ότι μπορεί να κυμαίνεται από 0 έως 180 0(ή σε ακτίνια από 0 έως Pi).
Μπορούμε να βγάλουμε κάποια συμπεράσματα σχετικά με το πρόσημο του βαθμωτού γινομένου. Τα μήκη των διανυσμάτων έχουν θετική τιμή, αυτό είναι προφανές. Αυτό σημαίνει ότι το πρόσημο του βαθμωτού γινομένου εξαρτάται από την τιμή του συνημιτόνου της γωνίας μεταξύ των διανυσμάτων.
Πιθανές περιπτώσεις:
1. Εάν η γωνία μεταξύ των διανυσμάτων είναι οξεία (από 0 0 έως 90 0), τότε το συνημίτονο της γωνίας θα έχει θετική τιμή.
2. Εάν η γωνία μεταξύ των διανυσμάτων είναι αμβλεία (από 90 0 έως 180 0), τότε το συνημίτονο της γωνίας θα έχει αρνητική τιμή.
*Στις μηδέν μοίρες, όταν δηλαδή τα διανύσματα έχουν την ίδια φορά, το συνημίτονο είναι ίσο με ένα και, κατά συνέπεια, το αποτέλεσμα θα είναι θετικό.
Στο 180 o, δηλαδή όταν τα διανύσματα έχουν αντίθετες κατευθύνσεις, το συνημίτονο είναι ίσο με μείον ένα,και ανάλογα το αποτέλεσμα θα είναι αρνητικό.
Τώρα το ΣΗΜΑΝΤΙΚΟ ΣΗΜΕΙΟ!
Στο 90 o, δηλαδή όταν τα διανύσματα είναι κάθετα μεταξύ τους, το συνημίτονο είναι ίσο με μηδέν και επομένως το SP είναι ίσο με μηδέν. Αυτό το γεγονός (συνέπεια, συμπέρασμα) χρησιμοποιείται για την επίλυση πολλών προβλημάτων όπου μιλάμε για τη σχετική θέση των διανυσμάτων, συμπεριλαμβανομένων των προβλημάτων που περιλαμβάνονται στην ανοιχτή τράπεζα μαθηματικών εργασιών.
Ας διατυπώσουμε τη δήλωση: το βαθμωτό γινόμενο είναι ίσο με μηδέν αν και μόνο αν αυτά τα διανύσματα βρίσκονται σε κάθετες ευθείες.
Έτσι, οι τύποι για διανύσματα SP:
Εάν είναι γνωστές οι συντεταγμένες των διανυσμάτων ή οι συντεταγμένες των σημείων της αρχής και του άκρου τους, τότε μπορούμε πάντα να βρούμε τη γωνία μεταξύ των διανυσμάτων:
Ας εξετάσουμε τα καθήκοντα:
27724 Να βρείτε το βαθμωτό γινόμενο των διανυσμάτων a και b.
Μπορούμε να βρούμε το βαθμωτό γινόμενο των διανυσμάτων χρησιμοποιώντας έναν από τους δύο τύπους:
Η γωνία μεταξύ των διανυσμάτων είναι άγνωστη, αλλά μπορούμε εύκολα να βρούμε τις συντεταγμένες των διανυσμάτων και στη συνέχεια να χρησιμοποιήσουμε τον πρώτο τύπο. Εφόσον οι απαρχές και των δύο διανυσμάτων συμπίπτουν με την αρχή των συντεταγμένων, οι συντεταγμένες αυτών των διανυσμάτων είναι ίσες με τις συντεταγμένες των άκρων τους, δηλαδή
Πώς να βρείτε τις συντεταγμένες ενός διανύσματος περιγράφεται στο.
Υπολογίζουμε:
Απάντηση: 40
Ας βρούμε τις συντεταγμένες των διανυσμάτων και ας χρησιμοποιήσουμε τον τύπο:
Για να βρούμε τις συντεταγμένες ενός διανύσματος, είναι απαραίτητο να αφαιρέσουμε τις αντίστοιχες συντεταγμένες της αρχής του από τις συντεταγμένες του τέλους του διανύσματος, που σημαίνει
Υπολογίζουμε το βαθμωτό γινόμενο:
Απάντηση: 40
Να βρείτε τη γωνία μεταξύ των διανυσμάτων α και β. Δώστε την απάντησή σας σε μοίρες.
Έστω οι συντεταγμένες των διανυσμάτων να έχουν τη μορφή:
Για να βρούμε τη γωνία μεταξύ των διανυσμάτων, χρησιμοποιούμε τον τύπο για το βαθμωτό γινόμενο των διανυσμάτων:
Συνημίτονο της γωνίας μεταξύ των διανυσμάτων:
Ως εκ τούτου:
Οι συντεταγμένες αυτών των διανυσμάτων είναι ίσες:
Ας τα αντικαταστήσουμε στον τύπο:
Η γωνία μεταξύ των διανυσμάτων είναι 45 μοίρες.
Απάντηση: 45
): ⟨a | b ⟩ (\displaystyle \langle a|b\rangle )
Στην απλούστερη περίπτωση του συνηθισμένου χώρου, το βαθμωτό γινόμενο μη μηδενικών διανυσμάτων και b (\displaystyle \mathbf (β) )ορίζεται ως το γινόμενο των μηκών αυτών των διανυσμάτων κατά συνημίτονογωνία μεταξύ τους:
(α , β) = | α | | β | cos (θ) (\displaystyle (\mathbf (a) ,\mathbf (b))=|\mathbf (a) ||\mathbf (b) |\cos(\theta))Ισοδύναμος ορισμός: το κλιμακωτό γινόμενο είναι το γινόμενο του μήκους προβολέςτο πρώτο διάνυσμα στο δεύτερο και το μήκος του δεύτερου διανύσματος (βλ. σχήμα). Εάν τουλάχιστον ένα από τα διανύσματα είναι μηδέν, τότε το γινόμενο θεωρείται ίσο με μηδέν.
Η έννοια ενός κλιμακωτού προϊόντος έχει επίσης μεγάλο αριθμό γενικεύσεων για διάφορα διανυσματικοί χώροι, δηλαδή για σύνολα διανυσμάτων με τις πράξεις πρόσθεσης και πολλαπλασιασμού με βαθμωτούς. Ο γεωμετρικός ορισμός του βαθμωτού γινομένου που δίνεται παραπάνω είναι γενικά ακατάλληλος, αφού δεν είναι σαφές τι εννοείται με τα μήκη των διανυσμάτων και το μέγεθος της γωνίας μεταξύ τους. Ως εκ τούτου, στα σύγχρονα μαθηματικά, χρησιμοποιείται η αντίθετη προσέγγιση: το βαθμωτό γινόμενο προσδιορίζεται αξιωματικά και μέσω αυτού - μήκη και γωνίες. Συγκεκριμένα, το βαθμωτό γινόμενο ορίζεται για σύνθετα διανύσματα , πολυδιάστατοΚαι άπειρων διαστάσεων χώροι, V τανυστική άλγεβρα.
Το κλιμακωτό προϊόν και οι γενικεύσεις του παίζουν εξαιρετικά σημαντικό ρόλο διανυσματική άλγεβρα , θεωρία ποικιλίας, μηχανική και φυσική. Για παράδειγμα, έργο δύναμηςκατά τη μηχανική κίνηση ισούται με το κλιμακωτό γινόμενο του διανύσματος δύναμης και του διανύσματος μετατόπισης.
Ορισμός
Ορισμός στον Ευκλείδειο χώρο
ΣΕ n (\displaystyle n)-διαστατικός πραγματικός Ευκλείδειος χώρος, τα διανύσματα ορίζονται από τις συντεταγμένες - σύνολά τους n (\displaystyle n)πραγματικοί αριθμοί σε ορθοκανονική βάση. Μπορείτε να ορίσετε το βαθμωτό γινόμενο των διανυσμάτων ως εξής:
(a , b) = a 1 b 1 + a 2 b 2 + a 3 b 3 + ⋯ + a n b n (\displaystyle (\mathbf (a) ,\mathbf (b))=a_(1)b_(1)+ a_(2)b_(2)+a_(3)b_(3)+\dots +a_(n)b_(n))Ο έλεγχος δείχνει ότι και τα τρία αξιώματα ικανοποιούνται.
Για παράδειγμα, το βαθμωτό γινόμενο των διανυσμάτων ( 1 , 3 , − 5 ) (\displaystyle \(1,3,-5\))Και ( 4 , − 2 , − 1 ) (\displaystyle \(4,-2,-1\))θα υπολογιστεί ως εξής:
( 1 , 3 , − 5 ) ⋅ ( 4 , − 2 , − 1 ) = 1 ⋅ 4 + 3 ⋅ (− 2) + (− 5) ⋅ (− 1) = 4 − 6 + 5 = 3. (\ στυλ εμφάνισης (\begin(στοίχιση)\ \(1,3,-5\)\cdot \(4,-2,-1\)&=1\cdot 4+3\cdot (-2)+(-5) \cdot (-1)\\&=4-6+5\\&=3.\end(στοίχιση)))Για σύνθετα διανύσματα a = ( a 1 , a 2 ... a n ) , b = ( b 1 , b 2 ... b n ) (\displaystyle \mathbf (a) =\(a_(1),a_(2)\dots a_(n)\ ),\mathbf (b) =\(b_(1),b_(2)\dots b_(n)\))ας ορίσουμε παρόμοια:
(a , b) = ∑ k = 1 n a k b k ¯ = a 1 b 1 ¯ + a 2 b 2 ¯ + ⋯ + a n b n ¯ (\displaystyle (\mathbf (a) ,\mathbf (b))=\sum _( k=1)^(n)a_(k)(\overline (b_(k)))=a_(1)(\overline (b_(1)))+a_(2)(\overline (b_(2) ))+\cdots +a_(n)(\overline (b_(n)))).Παράδειγμα (για n = 2 (\displaystyle n=2)): ( 1 + i , 2 ) ⋅ ( 2 + i , i ) = (1 + i) ⋅ (2 + i ¯) + 2 ⋅ i ¯ = (1 + i) ⋅ (2 − i) + 2 ⋅ (− i) = 3 − i . (\displaystyle \(1+i,2\)\cdot \(2+i,i\)=(1+i)\cdot ((\overline (2+i)))+2\cdot (\overline ( i))=(1+i)\cdot (2-i)+2\cdot (-i)=3-i.)
Σχετικοί ορισμοί
Στη σύγχρονη αξιωματική προσέγγιση, ήδη με βάση την έννοια του βαθμωτού γινομένου των διανυσμάτων, εισάγονται οι ακόλουθες παράγωγες έννοιες:
Μήκοςδιάνυσμα, το οποίο συνήθως νοείται ως το Ευκλείδειο του κανόνας :
| α | = (a , a) (\displaystyle |\mathbf (a) |=(\sqrt ((\mathbf (a) ,\mathbf (a)))))(ο όρος "μήκος" χρησιμοποιείται συνήθως σε διανύσματα πεπερασμένων διαστάσεων, αλλά στην περίπτωση υπολογισμού του μήκους μιας καμπύλης διαδρομής χρησιμοποιείται συχνά στην περίπτωση χώρων άπειρων διαστάσεων).
|
Για οποιαδήποτε στοιχεία a , b (\displaystyle \mathbf (a) ,\mathbf (b))διανυσματικός χώρος με βαθμωτό γινόμενο ισχύει η ακόλουθη ανισότητα: | (α , β) | 2 ⩽ (a , a) (b , b) (\displaystyle \vert (\mathbf (a) ,\mathbf (b))\vert ^(2)\leqslant (\mathbf (a) ,\mathbf (a) )(\mathbf (b) ,\mathbf (β))) |
Σε περίπτωση που ο χώρος είναι ψευδοευκλείδειος, η έννοια της γωνίας ορίζεται μόνο για διανύσματα που δεν περιέχουν ισότροπες γραμμές μέσα στον τομέα που σχηματίζεται από τα διανύσματα. Η ίδια η γωνία εισάγεται ως αριθμός, υπερβολικό συνημίτονοπου είναι ίσος με τον λόγο του συντελεστή του βαθμωτού γινομένου αυτών των διανυσμάτων προς το γινόμενο των μηκών τους (νόρμες):
| (α , β) | = | α | | β | ch φ . (\displaystyle |(\mathbf (a) ,\mathbf (b))|=|\mathbf (a) ||\mathbf (b) |\όνομα χειριστή (ch) \varphi .)- Ορθογώνιο(κάθετα) είναι διανύσματα των οποίων το βαθμωτό γινόμενο είναι ίσο με μηδέν. Αυτός ο ορισμός ισχύει για οποιουσδήποτε χώρους με θετικό καθορισμένο βαθμωτό γινόμενο. Για παράδειγμα, ορθογώνια πολυώνυμαείναι στην πραγματικότητα ορθογώνια (με την έννοια αυτού του ορισμού) μεταξύ τους σε κάποιο χώρο Hilbert.
- Ένας χώρος (πραγματικός ή σύνθετος) με θετικό οριστικό βαθμωτό γινόμενο ονομάζεται χώρος προ Χίλμπερτ.
- Σε αυτή την περίπτωση, ονομάζεται επίσης ένας πεπερασμένων διαστάσεων πραγματικός χώρος με θετικό οριστικό βαθμωτό γινόμενο Ευκλείδειοςκαι σύνθετο - ερημίτης ή ενιαίοςχώρος.
- Η περίπτωση που το κλιμακωτό γινόμενο δεν είναι πρόσημο-ορισμένο οδηγεί στο λεγόμενο. διαστήματα με αόριστη μετρική. Το κλιμακωτό γινόμενο σε τέτοιους χώρους δεν δημιουργεί πλέον κανόνα (και συνήθως εισάγεται επιπλέον). Ένας πεπερασμένος-διάστατος πραγματικός χώρος με απροσδιόριστη μετρική ονομάζεται ψευδοευκλείδειος(η πιο σημαντική ειδική περίπτωση ενός τέτοιου χώρου είναι Χώρος Minkowski). Μεταξύ των απεριόριστων διαστάσεων χώρων με απροσδιόριστη μετρική, οι χώροι Pontryagin και οι χώροι Kerin παίζουν σημαντικό ρόλο.
Ιδιότητες
- Θεώρημα συνημιτονίουπροκύπτει εύκολα χρησιμοποιώντας το προϊόν κουκίδων: | B C | 2 = B C → 2 = (A C → − A B →) 2 = ⟨ A C → − A B → , A C → − A B → ⟩ = A C → 2 + A B → 2 − 2 ⟨ A C → , A B → ⟩ = | Α Β | 2 + | A C | 2 − 2 | Α Β | | A C | cos A ^ (\displaystyle |BC|^(2)=(\vec (BC))^(2)=((\vec (AC))-(\vec (AB)))^(2)=\ langle (\vec (AC))-(\vec (AB)),(\vec (AC))-(\vec (AB))\rangle =(\vec (AC))^(2)+(\vec (AB))^(2)-2\langle (\vec (AC)),(\vec (AB))\rangle =|AB|^(2)+|AC|^(2)-2|AB| |AC|\cos (\καπέλο (A)))
- Εκτίμηση της γωνίας μεταξύ των διανυσμάτων: στον τύπο (α , β) = | α | ⋅ | β | ⋅ cos ∠ (a , b) (\displaystyle (\mathbf (\mathbf (a) ) ,\mathbf (b))=|\mathbf (a) |\cdot |\mathbf (b) |\cdot \cos \γωνία ((\mathbf (a) ,\mathbf (β))))το πρόσημο καθορίζεται μόνο από το συνημίτονο της γωνίας (οι κανόνες των διανυσμάτων είναι πάντα θετικοί). Επομένως, το κλιμακωτό γινόμενο > 0 εάν η γωνία μεταξύ των διανυσμάτων είναι οξεία, και< 0, если угол между векторами тупой.
- Προβολή ενός διανύσματος στην κατεύθυνση που ορίζεται από το μοναδιαίο διάνυσμα e (\displaystyle \mathbf (e) ): a e = (a , e) = | α | | e | cos ∠ (a , e) = | α | cos ∠ (a , e) (\displaystyle a_(e)=(\mathbf (a) ,\mathbf (e))=|\mathbf (a) ||\mathbf (e) |\cos \angle (( \mathbf (a) ,\mathbf (e)))=|\mathbf (a) |\cos \angle ((\mathbf (a) ,\mathbf (e)))), επειδή | e | = 1. (\displaystyle |\mathbf (e) |=1.)
- Εμβαδόν παραλληλογράμμου που εκτείνεται από δύο διανύσματα a (\displaystyle \mathbf (a)\ )Και b (\displaystyle \mathbf (b)\ ), είναι ίσο
- Σε επαφή με 0
- Google+ 0
- Εντάξει 0
- Facebook 0
