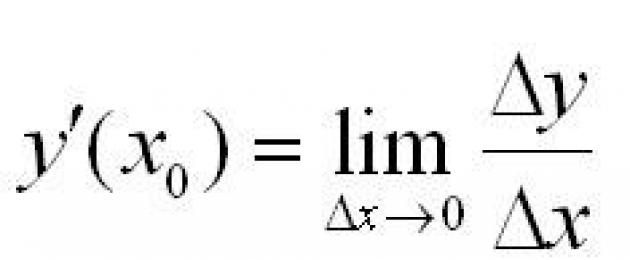Η επίλυση φυσικών προβλημάτων ή παραδειγμάτων στα μαθηματικά είναι εντελώς αδύνατη χωρίς γνώση της παραγώγου και των μεθόδων υπολογισμού της. Η παράγωγος είναι μια από τις πιο σημαντικές έννοιες στη μαθηματική ανάλυση. Αποφασίσαμε να αφιερώσουμε το σημερινό άρθρο σε αυτό το θεμελιώδες θέμα. Τι είναι η παράγωγος, ποια η φυσική και γεωμετρική της σημασία, πώς υπολογίζεται η παράγωγος μιας συνάρτησης; Όλες αυτές οι ερωτήσεις μπορούν να συνδυαστούν σε μία: πώς να κατανοήσουμε την παράγωγο;

Γεωμετρική και φυσική σημασία της παραγώγου

Ας υπάρχει μια συνάρτηση f(x) , καθορίζεται σε ένα ορισμένο διάστημα (α, β) . Τα σημεία x και x0 ανήκουν σε αυτό το διάστημα. Όταν το x αλλάζει, αλλάζει και η ίδια η συνάρτηση. Αλλαγή του επιχειρήματος - η διαφορά στις τιμές του x-x0 . Αυτή η διαφορά γράφεται ως δέλτα χ και ονομάζεται προσαύξηση ορίσματος. Μια αλλαγή ή αύξηση μιας συνάρτησης είναι η διαφορά μεταξύ των τιμών μιας συνάρτησης σε δύο σημεία. Ορισμός παραγώγου:

Η παράγωγος μιας συνάρτησης σε ένα σημείο είναι το όριο του λόγου της αύξησης της συνάρτησης σε ένα δεδομένο σημείο προς την αύξηση του ορίσματος όταν το τελευταίο τείνει στο μηδέν.

Διαφορετικά μπορεί να γραφτεί ως εξής:

Τι νόημα έχει να βρεις ένα τέτοιο όριο; Και να τι είναι:

η παράγωγος μιας συνάρτησης σε ένα σημείο είναι ίση με την εφαπτομένη της γωνίας μεταξύ του άξονα OX και της εφαπτομένης στη γραφική παράσταση της συνάρτησης σε ένα δεδομένο σημείο.

Φυσική σημασία του παραγώγου: η παράγωγος της διαδρομής ως προς το χρόνο είναι ίση με την ταχύτητα της ευθύγραμμης κίνησης.

Πράγματι, από τα σχολικά χρόνια όλοι γνωρίζουν ότι η ταχύτητα είναι μια ιδιαίτερη διαδρομή x=f(t) και του χρόνου t . Μέση ταχύτητα για μια συγκεκριμένη χρονική περίοδο:

Για να μάθετε την ταχύτητα κίνησης σε μια χρονική στιγμή t0 πρέπει να υπολογίσετε το όριο:

Κανόνας πρώτος: ορίστε μια σταθερά

Η σταθερά μπορεί να αφαιρεθεί από το παράγωγο πρόσημο. Επιπλέον, αυτό πρέπει να γίνει. Όταν λύνετε παραδείγματα στα μαθηματικά, πάρτε το ως κανόνα - Εάν μπορείτε να απλοποιήσετε μια έκφραση, φροντίστε να την απλοποιήσετε .

Παράδειγμα. Ας υπολογίσουμε την παράγωγο:

Κανόνας δεύτερος: παράγωγος του αθροίσματος των συναρτήσεων

Η παράγωγος του αθροίσματος δύο συναρτήσεων είναι ίση με το άθροισμα των παραγώγων αυτών των συναρτήσεων. Το ίδιο ισχύει και για την παράγωγο της διαφοράς των συναρτήσεων.

Δεν θα δώσουμε μια απόδειξη αυτού του θεωρήματος, αλλά θα εξετάσουμε μάλλον ένα πρακτικό παράδειγμα.

Βρείτε την παράγωγο της συνάρτησης:

Κανόνας τρίτος: παράγωγος του γινομένου των συναρτήσεων

Η παράγωγος του γινομένου δύο διαφοροποιήσιμων συναρτήσεων υπολογίζεται με τον τύπο:

Παράδειγμα: βρείτε την παράγωγο μιας συνάρτησης:

Λύση:

Είναι σημαντικό να μιλήσουμε για τον υπολογισμό των παραγώγων μιγαδικών συναρτήσεων εδώ. Η παράγωγος μιας μιγαδικής συνάρτησης είναι ίση με το γινόμενο της παραγώγου αυτής της συνάρτησης ως προς το ενδιάμεσο όρισμα και την παράγωγο του ενδιάμεσου ορίσματος ως προς την ανεξάρτητη μεταβλητή.

Στο παραπάνω παράδειγμα συναντάμε την έκφραση:

Σε αυτήν την περίπτωση, το ενδιάμεσο όρισμα είναι 8x στην πέμπτη δύναμη. Για να υπολογίσουμε την παράγωγο μιας τέτοιας έκφρασης, υπολογίζουμε πρώτα την παράγωγο της εξωτερικής συνάρτησης σε σχέση με το ενδιάμεσο όρισμα και στη συνέχεια πολλαπλασιάζουμε με την παράγωγο του ίδιου του ενδιάμεσου ορίσματος σε σχέση με την ανεξάρτητη μεταβλητή.

Κανόνας τέταρτος: παράγωγος του πηλίκου δύο συναρτήσεων

Τύπος για τον προσδιορισμό της παραγώγου του πηλίκου δύο συναρτήσεων:

Προσπαθήσαμε να μιλήσουμε για παράγωγα για ομοιώματα από την αρχή. Αυτό το θέμα δεν είναι τόσο απλό όσο φαίνεται, γι' αυτό προειδοποιήστε: υπάρχουν συχνά παγίδες στα παραδείγματα, επομένως να είστε προσεκτικοί κατά τον υπολογισμό των παραγώγων.

Για οποιεσδήποτε ερωτήσεις σχετικά με αυτό και άλλα θέματα, μπορείτε να επικοινωνήσετε με την υπηρεσία σπουδαστών. Σε σύντομο χρονικό διάστημα, θα σας βοηθήσουμε να λύσετε το πιο δύσκολο τεστ και να κατανοήσετε τις εργασίες, ακόμα κι αν δεν έχετε κάνει ποτέ στο παρελθόν υπολογισμούς παραγώγων.

Οι μερικές παράγωγοι μιας συνάρτησης πολλών μεταβλητών είναι συναρτήσεις των ίδιων μεταβλητών. Αυτές οι συναρτήσεις, με τη σειρά τους, μπορούν να έχουν μερικές παραγώγους, τις οποίες θα ονομάσουμε δευτερεύουσες μερικές παράγωγες (ή μερικές παράγωγες δεύτερης τάξης) της αρχικής συνάρτησης.

Για παράδειγμα, μια συνάρτηση δύο μεταβλητών έχει τέσσερις μερικές παραγώγους δεύτερης τάξης, οι οποίες ορίζονται και συμβολίζονται ως εξής:

Μια συνάρτηση τριών μεταβλητών έχει εννέα μερικές παραγώγους δεύτερης τάξης:

Οι επιμέρους παράγωγοι τρίτης και ανώτερης τάξης μιας συνάρτησης πολλών μεταβλητών ορίζονται και συμβολίζονται ομοίως: η μερική παράγωγος της τάξης μιας συνάρτησης πολλών μεταβλητών είναι η μερική παράγωγος της πρώτης τάξης της μερικής παραγώγου της τάξης της ίδιας λειτουργία.

Για παράδειγμα, η μερική παράγωγος τρίτης τάξης μιας συνάρτησης είναι η μερική παράγωγος πρώτης τάξης σε σχέση με το y της μερικής παραγώγου δεύτερης τάξης

Μια μερική παράγωγος δεύτερης ή υψηλότερης τάξης που λαμβάνεται σε σχέση με πολλές διαφορετικές μεταβλητές ονομάζεται μικτή μερική παράγωγος.

Για παράδειγμα, μερικά παράγωγα

είναι μικτές μερικές παράγωγοι συνάρτησης δύο μεταβλητών.

Παράδειγμα. Βρείτε μικτές μερικές παραγώγους δεύτερης τάξης μιας συνάρτησης

Λύση. Εύρεση μερικών παραγώγων πρώτης τάξης

Στη συνέχεια βρίσκουμε τις μικτές μερικές παράγωγες δεύτερης τάξης

Βλέπουμε ότι οι μικτές επιμέρους παράγωγοι που διαφέρουν μεταξύ τους μόνο ως προς τη σειρά διαφοροποίησης, δηλαδή την ακολουθία στην οποία πραγματοποιείται η διαφοροποίηση σε σχέση με διάφορες μεταβλητές, αποδείχθηκε ότι είναι πανομοιότυπα ίσες. Αυτό το αποτέλεσμα δεν είναι τυχαίο. Όσον αφορά τις μικτές μερικές παραγώγους, ισχύει το ακόλουθο θεώρημα, το οποίο δεχόμαστε χωρίς απόδειξη.

Μερικές παράγωγοι συνάρτησης δύο μεταβλητών.
Έννοια και παραδείγματα λύσεων

Σε αυτό το μάθημα θα συνεχίσουμε τη γνωριμία μας με τη συνάρτηση δύο μεταβλητών και θα εξετάσουμε ίσως την πιο κοινή θεματική εργασία - εύρεση επιμέρους παράγωγοι πρώτης και δεύτερης τάξης, καθώς και το ολικό διαφορικό της συνάρτησης. Οι φοιτητές μερικής φοίτησης, κατά κανόνα, συναντούν μερική παράγωγα στο 1ο έτος στο 2ο εξάμηνο. Επιπλέον, σύμφωνα με τις παρατηρήσεις μου, το έργο της εύρεσης μερικών παραγώγων εμφανίζεται σχεδόν πάντα στην εξέταση.

Για να μελετήσετε αποτελεσματικά το παρακάτω υλικό, εσείς απαραίτητηνα είναι σε θέση να βρίσκει λίγο πολύ με σιγουριά «συνήθεις» παραγώγους συναρτήσεων μιας μεταβλητής. Μπορείτε να μάθετε πώς να χειρίζεστε σωστά τα παράγωγα στα μαθήματα Πώς να βρείτε το παράγωγο;Και Παράγωγος μιγαδικής συνάρτησης. Θα χρειαστούμε επίσης έναν πίνακα παραγώγων στοιχειωδών συναρτήσεων και κανόνων διαφοροποίησης, είναι πιο βολικό εάν είναι διαθέσιμος σε έντυπη μορφή. Μπορείτε να λάβετε υλικό αναφοράς στη σελίδα Μαθηματικοί τύποι και πίνακες.

Ας επαναλάβουμε γρήγορα την έννοια της συνάρτησης δύο μεταβλητών, θα προσπαθήσω να περιοριστώ στο ελάχιστο. Μια συνάρτηση δύο μεταβλητών συνήθως γράφεται ως , με τις μεταβλητές να καλούνται ανεξάρτητες μεταβλητέςή επιχειρήματα.

Παράδειγμα: – συνάρτηση δύο μεταβλητών.

Μερικές φορές χρησιμοποιείται ο συμβολισμός. Υπάρχουν επίσης εργασίες όπου χρησιμοποιείται το γράμμα αντί για ένα γράμμα.

Από γεωμετρική άποψη, μια συνάρτηση δύο μεταβλητών αναπαριστά τις περισσότερες φορές μια επιφάνεια σε τρισδιάστατο χώρο (επίπεδο, κύλινδρος, σφαίρα, παραβολοειδές, υπερβολοειδές κ.λπ.). Αλλά, στην πραγματικότητα, αυτή είναι πιο αναλυτική γεωμετρία και στην ατζέντα μας είναι η μαθηματική ανάλυση, την οποία ο καθηγητής μου στο πανεπιστήμιο δεν με άφησε ποτέ να διαγράψω και είναι το «δυνατό μου σημείο».

Ας προχωρήσουμε στο ζήτημα της εύρεσης μερικών παραγώγων πρώτης και δεύτερης τάξης. Έχω μερικά καλά νέα για όσους έχουν πιει μερικά φλιτζάνια καφέ και συντονίζονται σε κάποιο απίστευτα δύσκολο υλικό: οι μερικές παράγωγοι είναι σχεδόν ίδιες με τις «συνήθεις» παράγωγες μιας συνάρτησης μιας μεταβλητής.

Για τις μερικές παραγώγους ισχύουν όλοι οι κανόνες διαφοροποίησης και ο πίνακας παραγώγων στοιχειωδών συναρτήσεων. Υπάρχουν μόνο μερικές μικρές διαφορές, τις οποίες θα μάθουμε τώρα:

...ναι, παρεμπιπτόντως, για αυτό το θέμα δημιούργησα μικρό βιβλίο pdf, που θα σας επιτρέψει να «μπείτε στα δόντια σας» μέσα σε λίγες μόνο ώρες. Αλλά χρησιμοποιώντας τον ιστότοπο, σίγουρα θα έχετε το ίδιο αποτέλεσμα - ίσως λίγο πιο αργά:

Παράδειγμα 1

Να βρείτε τις μερικές παραγώγους πρώτης και δεύτερης τάξης της συνάρτησης

Αρχικά, ας βρούμε τις μερικές παραγώγους πρώτης τάξης. Υπάρχουν δύο από αυτούς.

Ονομασίες:
ή – μερική παράγωγος σε σχέση με το "x"
ή – μερικό παράγωγο σε σχέση με το "y"

Ας ξεκινήσουμε με . Όταν βρίσκουμε τη μερική παράγωγο ως προς το "x", η μεταβλητή θεωρείται σταθερή (σταθερός αριθμός).

Σχόλια για τις ενέργειες που πραγματοποιήθηκαν:

(1) Το πρώτο πράγμα που κάνουμε όταν βρίσκουμε τη μερική παράγωγο είναι να συμπεράνουμε όλαλειτουργία σε αγκύλες κάτω από τον αστάρι με δείκτη.

Προσοχή, σημαντικό!ΔΕΝ ΧΑΝΟΥΜΕ συνδρομητές κατά τη διαδικασία λύσης. Σε αυτήν την περίπτωση, αν σχεδιάσετε ένα "εγκεφαλικό επεισόδιο" κάπου χωρίς , τότε ο δάσκαλος, τουλάχιστον, μπορεί να το βάλει δίπλα στην εργασία (να δαγκώσει αμέσως μέρος του σημείου για απροσεξία).

(2) Χρησιμοποιούμε τους κανόνες διαφοροποίησης , . Για ένα απλό παράδειγμα όπως αυτό, και οι δύο κανόνες μπορούν εύκολα να εφαρμοστούν σε ένα βήμα. Προσοχή στον πρώτο όρο: αφού θεωρείται σταθερά και οποιαδήποτε σταθερά μπορεί να αφαιρεθεί από το παράγωγο πρόσημο, μετά το βάζουμε εκτός παρένθεσης. Δηλαδή, σε αυτή την κατάσταση δεν είναι καλύτερο από έναν συνηθισμένο αριθμό. Ας δούμε τώρα τον τρίτο όρο: εδώ, αντίθετα, δεν υπάρχει τίποτα να βγάλουμε. Δεδομένου ότι είναι μια σταθερά, είναι επίσης μια σταθερά, και από αυτή την άποψη δεν είναι καλύτερο από τον τελευταίο όρο - "επτά".

(3) Χρησιμοποιούμε παράγωγα σε πίνακα και .

(4) Ας απλοποιήσουμε ή, όπως μου αρέσει να λέω, ας «τσιμπήσουμε» την απάντηση.

Τώρα . Όταν βρούμε τη μερική παράγωγο ως προς το «y», τότε τη μεταβλητήθεωρείται σταθερά (σταθερός αριθμός).

(1) Χρησιμοποιούμε τους ίδιους κανόνες διαφοροποίησης , . Στον πρώτο όρο βγάζουμε τη σταθερά από το πρόσημο της παραγώγου, στον δεύτερο όρο δεν μπορούμε να βγάλουμε τίποτα αφού είναι ήδη σταθερά.

(2) Χρησιμοποιούμε τον πίνακα παραγώγων στοιχειωδών συναρτήσεων. Ας αλλάξουμε νοερά όλα τα «Χ» στον πίνακα σε «Εγώ». Δηλαδή, αυτός ο πίνακας ισχύει εξίσου για (και μάλιστα σχεδόν για οποιοδήποτε γράμμα). Συγκεκριμένα, οι τύποι που χρησιμοποιούμε μοιάζουν με αυτό: και .

Ποια είναι η έννοια των μερικών παραγώγων;

Στην ουσία, τα μερικά παράγωγα 1ης τάξης μοιάζουν «συνηθισμένο» παράγωγο:

- Αυτό λειτουργίες, που χαρακτηρίζουν ρυθμός αλλαγήςλειτουργεί προς την κατεύθυνση των αξόνων και, αντίστοιχα. Έτσι, για παράδειγμα, η συνάρτηση χαρακτηρίζει την απότομη «ανύψωση» και «πλαγιές» επιφάνειεςπρος την κατεύθυνση του άξονα της τετμημένης, και η συνάρτηση μας λέει για το «ανάγλυφο» της ίδιας επιφάνειας προς την κατεύθυνση του άξονα τεταγμένης.

! Σημείωση : εδώ εννοούμε οδηγίες που παράλληλοάξονες συντεταγμένων.

Για λόγους καλύτερης κατανόησης, ας εξετάσουμε ένα συγκεκριμένο σημείο στο επίπεδο και ας υπολογίσουμε την τιμή της συνάρτησης («ύψος») σε αυτό:
– και τώρα φανταστείτε ότι είστε εδώ (ΕΠΙΦΑΝΕΙΑ).

Ας υπολογίσουμε τη μερική παράγωγο ως προς το "x" σε ένα δεδομένο σημείο:

Το αρνητικό πρόσημο της παραγώγου «Χ» μας λέει για μειώνεταιλειτουργεί σε σημείο προς την κατεύθυνση του άξονα της τετμημένης. Αν κάνουμε δηλαδή ένα μικρό, μικρό (απειροελάχιστος)βήμα προς την άκρη του άξονα (παράλληλα με αυτόν τον άξονα), τότε θα κατεβούμε την κλίση της επιφάνειας.

Τώρα ανακαλύπτουμε τη φύση του "εδάφους" προς την κατεύθυνση του άξονα τεταγμένων:

Η παράγωγος ως προς το «y» είναι θετική, επομένως, σε ένα σημείο προς την κατεύθυνση του άξονα η συνάρτηση αυξάνει. Για να το πω απλά, εδώ περιμένουμε μια ανηφόρα.

Επιπλέον, η μερική παράγωγος σε ένα σημείο χαρακτηρίζει ρυθμός αλλαγήςλειτουργεί προς την αντίστοιχη κατεύθυνση. Όσο μεγαλύτερη είναι η τιμή που προκύπτει modulo– όσο πιο απότομη είναι η επιφάνεια και αντίστροφα, όσο πιο κοντά στο μηδέν, τόσο πιο επίπεδη είναι η επιφάνεια. Έτσι, στο παράδειγμά μας, η "κλίση" προς την κατεύθυνση του άξονα της τετμημένης είναι πιο απότομη από το "βουνό" προς την κατεύθυνση του άξονα τεταγμένης.

Αλλά αυτά ήταν δύο ιδιωτικά μονοπάτια. Είναι ξεκάθαρο ότι από το σημείο στο οποίο βρισκόμαστε, (και γενικά από οποιοδήποτε σημείο σε μια δεδομένη επιφάνεια)μπορούμε να κινηθούμε προς κάποια άλλη κατεύθυνση. Έτσι, υπάρχει ενδιαφέρον για τη δημιουργία ενός γενικού «χάρτη πλοήγησης» που θα μας ενημερώνει για το «τοπίο» της επιφάνειας αν είναι δυνατόνσε κάθε σημείο τομέα ορισμού αυτής της συνάρτησηςσε όλα τα διαθέσιμα μονοπάτια. Θα μιλήσω για αυτό και άλλα ενδιαφέροντα πράγματα σε ένα από τα παρακάτω μαθήματα, αλλά προς το παρόν ας επιστρέψουμε στην τεχνική πλευρά του θέματος.

Ας συστηματοποιήσουμε τους στοιχειώδεις εφαρμοσμένους κανόνες:

1) Όταν διαφοροποιούμε ως προς το , η μεταβλητή θεωρείται σταθερά.

2) Όταν η διαφοροποίηση πραγματοποιείται σύμφωνα με, τότε θεωρείται σταθερά.

3) Οι κανόνες και ο πίνακας παραγώγων στοιχειωδών συναρτήσεων ισχύουν και ισχύουν για οποιαδήποτε μεταβλητή (ή οποιαδήποτε άλλη) με την οποία πραγματοποιείται η διαφοροποίηση.

Βήμα δυο. Βρίσκουμε μερικές παραγώγους δεύτερης τάξης. Είναι τέσσερις από αυτούς.

Ονομασίες:
ή – δεύτερη παράγωγος ως προς το “x”
ή – δεύτερη παράγωγος ως προς το «Y»
ή - μικτόςπαράγωγο του "x by igr"
ή - μικτόςπαράγωγο του "Y"

Δεν υπάρχουν προβλήματα με τη δεύτερη παράγωγο. Με απλά λόγια, η δεύτερη παράγωγος είναι η παράγωγος της πρώτης παραγώγου.

Για ευκολία, θα ξαναγράψω τα μερικά παράγωγα πρώτης τάξης που έχουν ήδη βρεθεί:

Αρχικά, ας βρούμε μικτές παραγώγους:

Όπως μπορείτε να δείτε, όλα είναι απλά: παίρνουμε τη μερική παράγωγο και τη διαφοροποιούμε ξανά, αλλά σε αυτήν την περίπτωση - αυτή τη φορά σύμφωνα με το "Y".

Επίσης:

Σε πρακτικά παραδείγματα, μπορείτε να εστιάσετε στην ακόλουθη ισότητα:

Έτσι, μέσω μικτών παραγώγων δεύτερης τάξης είναι πολύ βολικό να ελέγξουμε αν βρήκαμε σωστά τις μερικές παραγώγους πρώτης τάξης.

Βρείτε τη δεύτερη παράγωγο ως προς το «x».
Καμία εφεύρεση, ας το πάρουμε και διαφοροποιήστε το ξανά με "x":

Επίσης:

Θα πρέπει να σημειωθεί ότι κατά την εύρεση, πρέπει να δείξετε αυξημένη προσοχή, αφού δεν υπάρχουν θαυματουργές ισότητες για την επαλήθευση τους.

Οι δεύτερες παράγωγοι βρίσκουν επίσης ευρείες πρακτικές εφαρμογές, ειδικότερα, χρησιμοποιούνται στο πρόβλημα της εύρεσης άκρα μιας συνάρτησης δύο μεταβλητών. Όλα όμως έχουν τον χρόνο τους:

Παράδειγμα 2

Υπολογίστε τις επιμέρους παραγώγους πρώτης τάξης της συνάρτησης στο σημείο. Βρείτε παράγωγα δεύτερης τάξης.

Αυτό είναι ένα παράδειγμα για να λύσετε μόνοι σας (απαντήσεις στο τέλος του μαθήματος). Εάν δυσκολεύεστε να διαφοροποιήσετε τις ρίζες, επιστρέψτε στο μάθημα Πώς να βρείτε το παράγωγο;Σε γενικές γραμμές, πολύ σύντομα θα μάθετε να βρίσκετε τέτοια παράγωγα "εν κινήσει".

Ας γίνουμε καλύτεροι σε πιο σύνθετα παραδείγματα:

Παράδειγμα 3

Ελεγξε εκείνο . Καταγράψτε τη συνολική διαφορά πρώτης τάξης.

Λύση: Βρείτε τις μερικές παραγώγους πρώτης τάξης:

Προσοχή στον δείκτη: , δίπλα στο «Χ» δεν απαγορεύεται να γράψετε σε παρένθεση ότι είναι σταθερά. Αυτή η σημείωση μπορεί να είναι πολύ χρήσιμη για αρχάριους για να διευκολύνει την πλοήγηση στη λύση.

Περαιτέρω σχόλια:

(1) Μετακινούμε όλες τις σταθερές πέρα ​​από το πρόσημο της παραγώγου. Σε αυτή την περίπτωση, και , και, επομένως, το γινόμενο τους θεωρείται σταθερός αριθμός.

(2) Μην ξεχνάτε πώς να διαφοροποιείτε σωστά τις ρίζες.

(1) Βγάζουμε όλες τις σταθερές από το πρόσημο της παραγώγου σε αυτή την περίπτωση, η σταθερά είναι .

(2) Κάτω από τον πρώτο έχουμε το γινόμενο δύο συναρτήσεων, επομένως, πρέπει να χρησιμοποιήσουμε τον κανόνα για τη διαφοροποίηση του προϊόντος .

(3) Μην ξεχνάτε ότι αυτή είναι μια σύνθετη συνάρτηση (αν και η πιο απλή από τις σύνθετες). Χρησιμοποιούμε τον αντίστοιχο κανόνα: .

Τώρα βρίσκουμε μικτές παραγώγους δεύτερης τάξης:

Αυτό σημαίνει ότι όλοι οι υπολογισμοί έγιναν σωστά.

Ας γράψουμε τη συνολική διαφορά. Στο πλαίσιο της εργασίας που εξετάζουμε, δεν έχει νόημα να πούμε ποια είναι η συνολική διαφορά μιας συνάρτησης δύο μεταβλητών. Είναι σημαντικό ότι αυτή η πολύ διαφορά χρειάζεται πολύ συχνά να καταγράφεται σε πρακτικά προβλήματα.

Συνολικό διαφορικό πρώτης τάξηςΗ συνάρτηση δύο μεταβλητών έχει τη μορφή:

Σε αυτήν την περίπτωση:

Δηλαδή, πρέπει απλώς να αντικαταστήσετε ανόητα τις ήδη βρεθείτε μερικές παραγώγους πρώτης τάξης στον τύπο. Σε αυτήν και σε παρόμοιες περιπτώσεις, είναι καλύτερο να γράφετε διαφορικά πρόσημα σε αριθμητές:

Και σύμφωνα με επανειλημμένα αιτήματα αναγνωστών, πλήρες διαφορικό δεύτερης τάξης.

Μοιάζει με αυτό:

Ας βρούμε ΠΡΟΣΕΚΤΙΚΑ τις παράγωγες «μονογράμματος» της 2ης τάξης:

και γράψτε το "τέρας", "κολλώντας" προσεκτικά τα τετράγωνα, το γινόμενο και μην ξεχάσετε να διπλασιάσετε τη μικτή παράγωγο:

Είναι εντάξει, αν κάτι φαίνεται δύσκολο, μπορείτε πάντα να επιστρέψετε στα παράγωγα αργότερα, αφού καταλάβετε την τεχνική διαφοροποίησης:

Παράδειγμα 4

Να βρείτε μερικές παραγώγους πρώτης τάξης μιας συνάρτησης . Ελεγξε εκείνο . Καταγράψτε τη συνολική διαφορά πρώτης τάξης.

Ας δούμε μια σειρά από παραδείγματα με σύνθετες συναρτήσεις:

Παράδειγμα 5

Βρείτε τις μερικές παραγώγους πρώτης τάξης της συνάρτησης.

Λύση:

Παράδειγμα 6

Να βρείτε μερικές παραγώγους πρώτης τάξης μιας συνάρτησης .
Καταγράψτε τη συνολική διαφορά.

Αυτό είναι ένα παράδειγμα για να λύσετε μόνοι σας (απάντηση στο τέλος του μαθήματος). Δεν θα σας δώσω μια ολοκληρωμένη λύση γιατί είναι αρκετά απλή.

Αρκετά συχνά, όλοι οι παραπάνω κανόνες εφαρμόζονται συνδυαστικά.

Παράδειγμα 7

Να βρείτε μερικές παραγώγους πρώτης τάξης μιας συνάρτησης .

(1) Χρησιμοποιούμε τον κανόνα για τη διαφοροποίηση του αθροίσματος

(2) Ο πρώτος όρος σε αυτή την περίπτωση θεωρείται σταθερός, αφού δεν υπάρχει τίποτα στην έκφραση που να εξαρτάται από το "x" - μόνο "y". Ξέρετε, είναι πάντα ωραίο όταν ένα κλάσμα μπορεί να μετατραπεί σε μηδέν). Για τον δεύτερο όρο εφαρμόζουμε τον κανόνα διαφοροποίησης προϊόντων. Παρεμπιπτόντως, υπό αυτή την έννοια, τίποτα δεν θα είχε αλλάξει αν είχε δοθεί μια συνάρτηση - το σημαντικό είναι ότι εδώ προϊόν δύο συναρτήσεων, ΚΑΘΕ ένα από τα οποία εξαρτάται από "Χ", και επομένως, πρέπει να χρησιμοποιήσετε τον κανόνα διαφοροποίησης προϊόντων. Για τον τρίτο όρο εφαρμόζουμε τον κανόνα της διαφοροποίησης μιας σύνθετης συνάρτησης.

(1) Ο πρώτος όρος και στον αριθμητή και στον παρονομαστή περιέχει ένα "Y", επομένως, πρέπει να χρησιμοποιήσετε τον κανόνα για τη διαφοροποίηση των πηλίκων: . Ο δεύτερος όρος εξαρτάται ΜΟΝΟ από το «x», που σημαίνει ότι θεωρείται σταθερά και μετατρέπεται στο μηδέν. Για τον τρίτο όρο χρησιμοποιούμε τον κανόνα για τη διαφοροποίηση μιας σύνθετης συνάρτησης.

Για όσους αναγνώστες έφτασαν με θάρρος σχεδόν στο τέλος του μαθήματος, θα σας πω ένα παλιό αστείο του Μεχμάτοφ για ανακούφιση:

Μια μέρα, ένα κακό παράγωγο εμφανίστηκε στον χώρο των συναρτήσεων και άρχισε να διαφοροποιεί τους πάντες. Όλες οι λειτουργίες είναι διάσπαρτες προς όλες τις κατευθύνσεις, κανείς δεν θέλει να μεταμορφωθεί! Και μόνο μία λειτουργία δεν ξεφεύγει. Το παράγωγο την πλησιάζει και τη ρωτά:

- Γιατί δεν φεύγεις μακριά μου;

- Χα. Αλλά δεν με νοιάζει, γιατί είμαι "e to the power of X" και δεν θα μου κάνετε τίποτα!

Στο οποίο το κακό παράγωγο με ένα ύπουλο χαμόγελο απαντά:

- Εδώ κάνετε λάθος, θα σας διαφοροποιήσω με το "Y", άρα θα πρέπει να είστε μηδέν.

Όποιος κατάλαβε το αστείο έχει κατακτήσει τα παράγωγα, τουλάχιστον στο επίπεδο «Γ»).

Παράδειγμα 8

Να βρείτε μερικές παραγώγους πρώτης τάξης μιας συνάρτησης .

Αυτό είναι ένα παράδειγμα για να το λύσετε μόνοι σας. Η πλήρης λύση και το παράδειγμα του προβλήματος βρίσκονται στο τέλος του μαθήματος.

Λοιπόν, αυτό είναι σχεδόν όλο. Τέλος, δεν μπορώ παρά να παρακαλέσω τους λάτρεις των μαθηματικών με ένα ακόμη παράδειγμα. Δεν πρόκειται καν για ερασιτέχνες, ο καθένας έχει διαφορετικό επίπεδο μαθηματικής προετοιμασίας - υπάρχουν άνθρωποι (και όχι τόσο σπάνιοι) που τους αρέσει να ανταγωνίζονται πιο δύσκολες εργασίες. Αν και, το τελευταίο παράδειγμα σε αυτό το μάθημα δεν είναι τόσο περίπλοκο όσο είναι δυσκίνητο από υπολογιστική άποψη.

Σε αυτό το μάθημα θα εξοικειωθούμε με την έννοια της συνάρτησης δύο μεταβλητών και επίσης θα εξετάσουμε λεπτομερώς την πιο κοινή εργασία - την εύρεση μερικώς παράγωγαπρώτης και δεύτερης τάξης, πλήρες διαφορικό μιας συνάρτησης.

Για να μελετήσετε αποτελεσματικά το παρακάτω υλικό, εσείς απαραίτητηνα είναι σε θέση να βρει λίγο πολύ με σιγουριά «συνήθεις» παραγώγους συναρτήσεων μιας μεταβλητής. Μπορείτε να μάθετε πώς να χειρίζεστε σωστά τα παράγωγα στα μαθήματα Πώς να βρείτε το παράγωγο; και Παράγωγος μιγαδικής συνάρτησης. Θα χρειαστούμε επίσης έναν πίνακα παραγώγων στοιχειωδών συναρτήσεων και κανόνων διαφοροποίησης, είναι πιο βολικό εάν είναι διαθέσιμος σε έντυπη μορφή.

Ας ξεκινήσουμε με την ίδια την έννοια της συνάρτησης δύο μεταβλητών, θα προσπαθήσουμε να περιοριστούμε στο ελάχιστο της θεωρίας, αφού ο ιστότοπος έχει πρακτικό προσανατολισμό. Μια συνάρτηση δύο μεταβλητών συνήθως γράφεται ως , με τις μεταβλητές να καλούνται ανεξάρτητες μεταβλητέςή επιχειρήματα.

Παράδειγμα: - συνάρτηση δύο μεταβλητών.

Μερικές φορές χρησιμοποιείται ο συμβολισμός. Υπάρχουν επίσης εργασίες όπου χρησιμοποιείται το γράμμα αντί για ένα γράμμα.

Είναι χρήσιμο να γνωρίζουμε τη γεωμετρική σημασία των συναρτήσεων. Μια συνάρτηση μιας μεταβλητής αντιστοιχεί σε μια συγκεκριμένη γραμμή σε ένα επίπεδο, για παράδειγμα, τη γνωστή σχολική παραβολή. Οποιαδήποτε συνάρτηση δύο μεταβλητών από γεωμετρική άποψη αντιπροσωπεύει μια επιφάνεια σε τρισδιάστατο χώρο (επίπεδα, κύλινδροι, μπάλες, παραβολοειδή κ.λπ.). Αλλά, στην πραγματικότητα, αυτό είναι ήδη αναλυτική γεωμετρία και η μαθηματική ανάλυση είναι στην ατζέντα μας.

Ας προχωρήσουμε στο ζήτημα της εύρεσης μερικών παραγώγων πρώτης και δεύτερης τάξης. Έχω μερικά καλά νέα για όσους έχουν πιει μερικά φλιτζάνια καφέ και συντονίζονται σε κάποιο απίστευτα δύσκολο υλικό: οι μερικές παράγωγοι είναι σχεδόν ίδιες με τις «συνήθεις» παράγωγες μιας συνάρτησης μιας μεταβλητής.

Για τις μερικές παραγώγους ισχύουν όλοι οι κανόνες διαφοροποίησης και ο πίνακας παραγώγων στοιχειωδών συναρτήσεων. Υπάρχουν μόνο μερικές μικρές διαφορές, στις οποίες θα φτάσουμε σε λίγο.

Παράδειγμα 1

Να βρείτε τις μερικές παραγώγους πρώτης και δεύτερης τάξης της συνάρτησης

Αρχικά, ας βρούμε τις μερικές παραγώγους πρώτης τάξης. Υπάρχουν δύο από αυτούς.

Ονομασίες:

Ή - μερική παράγωγος σε σχέση με το "x"

Ή - μερική παράγωγος σε σχέση με το "y"

Ας ξεκινήσουμε με .

Σπουδαίος! Όταν βρούμε τη μερική παράγωγο ως προς το «x», τότε τη μεταβλητή θεωρείται σταθερά (σταθερός αριθμός).

Ας αποφασίσουμε. Σε αυτό το μάθημα θα παρέχουμε αμέσως την πλήρη λύση και θα δώσουμε σχόλια παρακάτω.

Σχόλια για τις ενέργειες που πραγματοποιήθηκαν:

(1) Το πρώτο πράγμα που κάνουμε όταν βρίσκουμε τη μερική παράγωγο είναι να συμπεράνουμε όλαλειτουργία σε αγκύλες κάτω από τον αστάρι με δείκτη.

Προσοχή, σημαντικό!ΔΕΝ ΧΑΝΟΥΜΕ συνδρομητές κατά τη διαδικασία λύσης. Σε αυτήν την περίπτωση, εάν σχεδιάσετε ένα "εγκεφαλικό επεισόδιο" κάπου χωρίς , τότε ο δάσκαλος, τουλάχιστον, μπορεί να το βάλει δίπλα στην εργασία (να δαγκώσει αμέσως μέρος του σημείου για απροσεξία).

(2) Χρησιμοποιούμε τους κανόνες διαφοροποίησης ; . Για ένα απλό παράδειγμα όπως αυτό, και οι δύο κανόνες μπορούν εύκολα να εφαρμοστούν σε ένα βήμα. Προσοχή στον πρώτο όρο: αφού θεωρείται σταθερά και οποιαδήποτε σταθερά μπορεί να αφαιρεθεί από το παράγωγο πρόσημο, μετά το βάζουμε εκτός παρένθεσης. Δηλαδή, σε αυτή την κατάσταση δεν είναι καλύτερο από έναν συνηθισμένο αριθμό. Ας δούμε τώρα τον τρίτο όρο: εδώ, αντίθετα, δεν υπάρχει τίποτα να βγάλουμε. Δεδομένου ότι είναι μια σταθερά, είναι επίσης μια σταθερά, και από αυτή την άποψη δεν είναι καλύτερο από τον τελευταίο όρο - "επτά".

(2) Χρησιμοποιούμε τον πίνακα παραγώγων στοιχειωδών συναρτήσεων. Ας αλλάξουμε νοερά όλα τα «Χ» στον πίνακα σε «Εγώ». Δηλαδή, αυτός ο πίνακας ισχύει εξίσου (και γενικά για οποιοδήποτε γράμμα).Σε αυτήν την περίπτωση, οι τύποι που χρησιμοποιούμε είναι: και .

Έτσι, βρίσκονται οι μερικές παράγωγοι πρώτης τάξης

Οι μερικές παράγωγοι χρησιμοποιούνται σε προβλήματα που αφορούν συναρτήσεις πολλών μεταβλητών. Οι κανόνες εύρεσης είναι ακριβώς οι ίδιοι με τις συναρτήσεις μιας μεταβλητής, με τη μόνη διαφορά ότι μία από τις μεταβλητές πρέπει να θεωρείται σταθερή (σταθερός αριθμός) τη στιγμή της διαφοροποίησης.

Τύπος

Οι μερικές παράγωγοι για μια συνάρτηση δύο μεταβλητών $ z(x,y) $ γράφονται με την ακόλουθη μορφή $ z"_x, z"_y $ και βρίσκονται χρησιμοποιώντας τους τύπους:

Μερικά παράγωγα πρώτης τάξης

$$ z"_x = \frac(\μερικό z)(\μερικό x) $$

$$ z"_y = \frac(\μερικό z)(\μερικό y) $$

Μερικά παράγωγα δεύτερης τάξης

$$ z""_(xx) = \frac(\μερική^2 z)(\μερική x \μερική x) $$

$$ z""_(yy) = \frac(\μερικό^2 z)(\μερικό y \μερικό y) $$

Μικτό παράγωγο

$$ z""_(xy) = \frac(\μερική^2 z)(\μερική x \μερική y) $$

$$ z""_(yx) = \frac(\μερική^2 z)(\μερική y \μερική x) $$

Μερική παράγωγος μιγαδικής συνάρτησης

α) Έστω $ z (t) = f(x(t), y(t)) $, τότε η παράγωγος μιας μιγαδικής συνάρτησης προσδιορίζεται από τον τύπο:

$$ \frac(dz)(dt) = \frac(\μερικό z)(\μερικό x) \cdot \frac(dx)(dt) + \frac(\μερικό z)(\μερικό y) \cdot \frac (dy)(dt)$$

β) Έστω $ z (u,v) = z(x(u,v),y(u,v)) $, τότε οι μερικές παράγωγοι της συνάρτησης βρίσκονται από τον τύπο:

$$ \frac(\μερικό z)(\μερικό u) = \frac(\μερικό z)(\μερικό x) \cdot \frac(\μερικό x)(\μερικό u) + \frac(\μερικό z)( \μερικό y) \cdot \frac(\μερικό y)(\μερικό u) $$

$$ \frac(\μερικό z)(\μερικό v) = \frac(\μερικό z)(\μερικό x) \cdot \frac(\μερικό x)(\μερικό v) + \frac(\μερικό z)( \μερικό y) \cdot \frac(\μερικό y)(\μερικό v) $$

Μερικές παράγωγοι μιας άρρητης συνάρτησης

α) Έστω $ F(x,y(x)) = 0 $, μετά $$ \frac(dy)(dx) = -\frac(f"_x)(f"_y) $$

β) Έστω $ F(x,y,z)=0 $, μετά $$ z"_x = - \frac(F"_x)(F"_z); z"_y = - \frac(F"_y)( F"_z) $$

Παραδείγματα λύσεων

Παράδειγμα 1

Εύρεση μερικών παραγώγων πρώτης τάξης $ z (x,y) = x^2 - y^2 + 4xy + 10 $

Λύση

Για να βρούμε τη μερική παράγωγο σε σχέση με το $ x $, θα θεωρήσουμε ότι το $ y $ είναι μια σταθερή τιμή (αριθμός): $$ z"_x = (x^2-y^2+4xy+10)"_x = 2x - 0 + 4y + 0 = 2x+4y $$ Για να βρούμε τη μερική παράγωγο μιας συνάρτησης σε σχέση με το $y$, ορίζουμε το $y$ με μια σταθερά: $$ z"_y = (x^2-y^2+4xy+10)"_y = -2y+4x $$ Εάν δεν μπορείτε να λύσετε το πρόβλημά σας, στείλτε το σε εμάς. Θα δώσουμε λεπτομερή λύση. Θα μπορείτε να δείτε την πρόοδο του υπολογισμού και να λάβετε πληροφορίες. Αυτό θα σας βοηθήσει να πάρετε τον βαθμό σας από τον δάσκαλό σας έγκαιρα!

Απάντηση

$$ z"_x = 2x+4y; z"_y = -2y+4x $$

Παράδειγμα 2

Βρείτε τις μερικές παραγώγους της συνάρτησης δεύτερης τάξης $ z = e^(xy) $

Λύση

Πρώτα πρέπει να βρείτε τα πρώτα παράγωγα και μετά γνωρίζοντάς τα μπορείτε να βρείτε τα παράγωγα δεύτερης τάξης. Έστω σταθερά το $y$: $$ z"_x = (e^(xy))"_x = e^(xy) \cdot (xy)"_x = ye^(xy) $$ Ας ορίσουμε τώρα το $ x $ ως σταθερή τιμή: $$ z"_y = (e^(xy))"_y = e^(xy) \cdot (xy)"_y = xe^(xy) $$ Γνωρίζοντας τα πρώτα παράγωγα, βρίσκουμε ομοίως και τα δεύτερα. Ορίστε το $y$ σε μια σταθερά: $$ z""_(xx) = (z"_x)"_x = (ye^(xy))"_x = (y)"_x e^(xy) + y(e^(xy))"_x = 0 + ye^(xy)\cdot (xy)"_x = y^2e^(xy) $$ Ορίζουμε το $ x $ σε μια σταθερά: $$ z""_(yy) = (z"_y)"_y = (xe^(xy))"_y = (x)"_y e^(xy) + x(e^(xy))"_y = 0 + x^2e^(xy) = x^2e^(xy) $$ Τώρα το μόνο που μένει είναι να βρεθεί η μικτή παράγωγος. Μπορείτε να διαφοροποιήσετε το $ z"_x $ κατά $ y $, και μπορείτε να διαφοροποιήσετε το $ z"_y $ με το $ x $, αφού από το θεώρημα $ z""_(xy) = z""_(yx) $ $$ z""_(xy) = (z"_x)"_y = (ye^(xy))"_y = (y)"_y e^(xy) + y (e^(xy))"_y = ye^(xy)\cdot (xy)"_y = yxe^(xy) $$

Απάντηση

$$ z"_x = ye^(xy); z"_y = xe^(xy); z""_(xy) = yxe^(xy) $$

Παράδειγμα 4

Έστω $ 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ να ορίσει την άρρητη συνάρτηση $ F(x,y,z) = 0 $. Βρείτε μερικές παραγώγους πρώτης τάξης.

Λύση

Γράφουμε τη συνάρτηση με τη μορφή: $ F(x,y,z) = 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ και βρίσκουμε τις παραγώγους: $$ z"_x (y,z - const) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_x = 3 x^2 z - 4 $$ $$ z"_y (x,y - const) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_y = 3z^2 $$

Απάντηση

$$ z"_x = 3x^2 z - 4; z"_y = 3z^2; $$