Μάθημα και παρουσίαση με θέμα: "Ιδιότητες συνάρτησης. Αύξηση και μείωση συναρτήσεων"
Πρόσθετα υλικά
Αγαπητοί χρήστες, μην ξεχάσετε να αφήσετε τα σχόλια, τις κριτικές, τις επιθυμίες σας! Όλα τα υλικά έχουν ελεγχθεί από ένα πρόγραμμα προστασίας από ιούς.
Εκπαιδευτικά βοηθήματα και προσομοιωτές στο ηλεκτρονικό κατάστημα Integral για την 9η τάξη
Διαδραστικό εγχειρίδιο για την 9η τάξη "Κανόνες και ασκήσεις στη γεωμετρία"
Ηλεκτρονικό εγχειρίδιο «Εννοητή Γεωμετρία» για τις τάξεις 7-9
Παιδιά, συνεχίζουμε να μελετάμε αριθμητικές συναρτήσεις. Σήμερα θα επικεντρωθούμε σε ένα θέμα όπως οι ιδιότητες συνάρτησης. Οι συναρτήσεις έχουν πολλές ιδιότητες. Θυμηθείτε ποιες ιδιότητες μελετήσαμε πρόσφατα. Σωστά, ο τομέας ορισμού και ο τομέας των τιμών, είναι μια από τις βασικές ιδιότητες. Μην τα ξεχνάτε ποτέ και να θυμάστε ότι μια συνάρτηση έχει πάντα αυτές τις ιδιότητες.
Σε αυτή την ενότητα, θα ορίσουμε ορισμένες ιδιότητες των συναρτήσεων. Συνιστώ να ακολουθήσετε τη σειρά με την οποία θα τα προσδιορίσουμε κατά την επίλυση προβλημάτων.
Λειτουργία αύξησης και μείωσης
Η πρώτη ιδιότητα που θα ορίσουμε είναι η αύξουσα και φθίνουσα συνάρτηση.
Μια συνάρτηση λέγεται ότι αυξάνεται στο σύνολο X⊂D(f) εάν για οποιαδήποτε x1 και x2 έτσι ώστε x1< x2 - выполняется неравенство f(x1) < f(x2). То есть большему значению аргумента, соответствует большее значение функции.Μια συνάρτηση λέγεται ότι είναι φθίνουσα στο σύνολο X⊂D(f) εάν για οποιαδήποτε x1 και x2 τέτοια ώστε x1< x2 - выполняется неравенство f(x1)>f(x2). Δηλαδή, μια μεγαλύτερη τιμή του ορίσματος αντιστοιχεί σε μια μικρότερη τιμή της συνάρτησης.
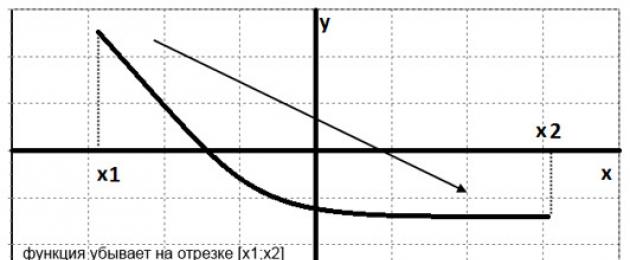
Οι έννοιες της «αύξησης» και της «μείωσης» μιας συνάρτησης είναι πολύ εύκολα κατανοητές αν κοιτάξετε προσεκτικά τα γραφήματα της συνάρτησης. Για μια αύξουσα συνάρτηση: φαίνεται να ανεβαίνουμε έναν λόφο, για μια φθίνουσα συνάρτηση, κατεβαίνουμε ανάλογα. Η γενική άποψη των συναρτήσεων αύξησης και μείωσης παρουσιάζεται στα παρακάτω γραφήματα.

Οι συναρτήσεις αύξησης και μείωσης ονομάζονται γενικά μονοτονία.Δηλαδή, το καθήκον μας είναι να βρούμε τα διαστήματα μείωσης και αύξησης της συνάρτησης. Στη γενική περίπτωση, αυτό διατυπώνεται ως εξής: βρείτε διαστήματα μονοτονίας ή εξετάστε μια συνάρτηση για μονοτονία.
Εξετάστε τη μονοτονία της συνάρτησης $y=3x+2$.
Λύση: Ας ελέγξουμε τη συνάρτηση για οποιαδήποτε x1 και x2 και ας x1< x2.
$f(x1)=3x1+2$
$f(x2)=3x2+2$
Από τότε, x1< x2, то f(x1) < f(x2), т. е. большему значению аргумента, соответствует большее значение функции.
Περιορισμένη λειτουργία
Μια συνάρτηση $y=f(x)$ λέγεται ότι οριοθετείται από κάτω στο σύνολο X⊂D(f) εάν υπάρχει ένας αριθμός a τέτοιος ώστε για οποιοδήποτε χϵΧ ισχύει η ανισότητα f(x)< a.
Μια συνάρτηση $y=f(x)$ λέγεται ότι οριοθετείται από πάνω στο σύνολο X⊂D(f) εάν υπάρχει ένας αριθμός a τέτοιος ώστε για οποιοδήποτε χϵΧ ισχύει η ανισότητα f(x)< a.
Εάν το διάστημα X δεν έχει καθοριστεί, τότε η συνάρτηση θεωρείται ότι περιορίζεται σε ολόκληρο τον τομέα ορισμού. Μια συνάρτηση που είναι οριοθετημένη τόσο πάνω όσο και κάτω ονομάζεται περιορισμένη.
Ο περιορισμός της συνάρτησης είναι εύκολο να διαβαστεί από το γράφημα. Είναι δυνατό να τραβήξετε κάποια ευθεία γραμμή
$у=а$, και αν η συνάρτηση είναι υψηλότερη από αυτή τη γραμμή, τότε περιορίζεται από κάτω. Αν παρακάτω, τότε ανάλογα παραπάνω. Παρακάτω είναι ένα γράφημα μιας συνάρτησης που οριοθετείται παρακάτω. Παιδιά, προσπαθήστε να σχεδιάσετε μόνοι σας ένα γράφημα μιας περιορισμένης συνάρτησης.

Εξετάστε το όριο της συνάρτησης $y=\sqrt(16-x^2)$.
Λύση: Η τετραγωνική ρίζα ενός συγκεκριμένου αριθμού είναι μεγαλύτερη ή ίση με το μηδέν. Προφανώς, η συνάρτησή μας είναι επίσης μεγαλύτερη ή ίση με το μηδέν, δηλαδή οριοθετημένη από κάτω.
Μπορούμε μόνο να εξαγάγουμε την τετραγωνική ρίζα από έναν μη αρνητικό αριθμό και μετά $16-x^2≥0$.
Η λύση στην ανισότητά μας θα είναι το διάστημα [-4;4]. Σε αυτό το τμήμα $16-x^2≤16$ ή $\sqrt(16-x^2)≤4$, αλλά αυτό σημαίνει όριο από πάνω.
Απάντηση: η συνάρτησή μας περιορίζεται σε δύο ευθείες $y=0$ και $y=4$.
Υψηλότερη και Χαμηλότερη Αξία
Η μικρότερη τιμή της συνάρτησης y= f(x) στο σύνολο X⊂D(f) είναι κάποιος αριθμός m έτσι ώστε:
β) Για κάθε χϵΧ ισχύει το $f(x)≥f(x0)$.
Η μεγαλύτερη τιμή της συνάρτησης y=f(x) στο σύνολο X⊂D(f) είναι κάποιος αριθμός m τέτοιος ώστε:
α) Υπάρχει κάποια x0 τέτοια που $f(x0)=m$.
β) Για κάθε χϵΧ ισχύει το $f(x)≤f(x0)$.
Οι μεγαλύτερες και οι μικρότερες τιμές συνήθως συμβολίζονται με y max. και το όνομα y .
Οι έννοιες της οριοθέτησης και της μεγαλύτερης με τη μικρότερη τιμή μιας συνάρτησης συνδέονται στενά. Οι παρακάτω δηλώσεις είναι αληθείς:
α) Εάν υπάρχει μια ελάχιστη τιμή για μια συνάρτηση, τότε αυτή οριοθετείται παρακάτω.
β) Εάν υπάρχει μια μέγιστη τιμή για μια συνάρτηση, τότε αυτή περιορίζεται παραπάνω.
γ) Εάν η συνάρτηση δεν είναι οριοθετημένη παραπάνω, τότε η μεγαλύτερη τιμή δεν υπάρχει.
δ) Εάν η συνάρτηση δεν είναι οριοθετημένη παρακάτω, τότε η μικρότερη τιμή δεν υπάρχει.
Βρείτε τη μεγαλύτερη και τη μικρότερη τιμή της συνάρτησης $y=\sqrt(9-4x^2+16x)$.
Λύση: $f(x)=y=\sqrt(9-4x^2+16x)=\sqrt(9-(x-4)^2+16)=\sqrt(25-(x-4)^2 )≤5$.
Για $х=4$ $f(4)=5$, για όλες τις άλλες τιμές η συνάρτηση παίρνει μικρότερες τιμές ή δεν υπάρχει, δηλαδή αυτή είναι η μεγαλύτερη τιμή της συνάρτησης.
Εξ ορισμού: $9-4x^2+16x≥0$. Ας βρούμε τις ρίζες του τετραγωνικού τριωνύμου $(2x+1)(2x-9)≥0$. Σε $x=-0,5$ και $x=4,5$ η συνάρτηση εξαφανίζεται σε όλα τα άλλα σημεία είναι μεγαλύτερη από το μηδέν. Τότε, εξ ορισμού, η μικρότερη τιμή της συνάρτησης είναι ίση με μηδέν.
Απάντηση: y μέγ. =5 και y όνομα. =0.
Παιδιά, μελετήσαμε και την έννοια της κυρτότητας μιας συνάρτησης. Κατά την επίλυση ορισμένων προβλημάτων, μπορεί να χρειαστούμε αυτήν την ιδιότητα. Αυτή η ιδιότητα προσδιορίζεται επίσης εύκολα χρησιμοποιώντας γραφήματα.
Μια συνάρτηση είναι κυρτή προς τα κάτω εάν συνδέονται δύο σημεία στο γράφημα της αρχικής συνάρτησης και η γραφική παράσταση της συνάρτησης βρίσκεται κάτω από τη γραμμή σύνδεσης των σημείων.
Μια συνάρτηση είναι κυρτή προς τα πάνω αν συνδέονται δύο σημεία στο γράφημα της αρχικής συνάρτησης και η γραφική παράσταση της συνάρτησης βρίσκεται πάνω από τη γραμμή σύνδεσης των σημείων.

Μια συνάρτηση είναι συνεχής αν το γράφημα της συνάρτησής μας δεν έχει διακοπές, για παράδειγμα, όπως το γράφημα της παραπάνω συνάρτησης.
Εάν πρέπει να βρείτε τις ιδιότητες μιας συνάρτησης, τότε η ακολουθία αναζήτησης των ιδιοτήτων είναι η εξής:
α) Τομέας ορισμού.
β) Μονοτονία.
γ) Περιορισμός.
δ) Η μεγαλύτερη και η μικρότερη τιμή.
δ) Συνέχεια.
ε) Εύρος τιμών.
Βρείτε τις ιδιότητες της συνάρτησης $y=-2x+5$.
Λύση.
α) Τομέας ορισμού D(y)=(-∞;+∞).
β) Μονοτονία. Ας ελέγξουμε για τυχόν τιμές x1 και x2 και αφήστε το x1< x2.
$f(x1)=-2x1+2$.
$f(x2)=-2x2+2$.
Από x1< x2, то f(x1) < f(x2), то есть большему значению аргумента, соответствует меньшее значение функции. Функция убывает.
γ) Περιορισμός. Προφανώς η λειτουργία δεν είναι περιορισμένη.
δ) Η μεγαλύτερη και η μικρότερη τιμή. Εφόσον η συνάρτηση είναι απεριόριστη, δεν υπάρχει μέγιστη ή ελάχιστη τιμή.
δ) Συνέχεια. Η γραφική παράσταση της συνάρτησής μας δεν έχει διακοπές, τότε η συνάρτηση είναι συνεχής.
ε) Εύρος τιμών. E(y)=(-∞;+∞).
Προβλήματα στις ιδιότητες μιας συνάρτησης για ανεξάρτητη λύση
Εύρεση ιδιοτήτων συνάρτησης:α) $y=2x+7$,
β) $y=3x^2$,
γ) $y=\frac(4)(x)$.
Η έννοια της συνάρτησης. Περιορισμένες δυνατότητες.
Ορισμός συνάρτησης: Αν κάθε αριθμός x από το σύνολο των αριθμών D σχετίζεται με έναν μόνο αριθμό y, τότε λένε ότι δίνεται μια συνάρτηση f στο σύνολο D και γράφουν y= f(x), όπου x ονομάζεται ανεξάρτητη μεταβλητή ή όρισμα αυτής της συνάρτησης και το σύνολο D είναι το πεδίο ορισμού αυτής της συνάρτησης.
Περιορισμένες και απεριόριστες λειτουργίες.Η συνάρτηση καλείται περιορισμένος, εάν υπάρχει τόσο θετικός αριθμός Μτι | φά(Χ) | Μγια όλες τις αξίες Χ.Εάν δεν υπάρχει τέτοιος αριθμός, τότε η συνάρτηση είναι απεριόριστος.
ΠΑΡΑΔΕΙΓΜΑΤΑ.
Λειτουργίες ζυγές, περιττές, μονοτονικές.
Ζυγές και περιττές συναρτήσεις.Αν για οποιοδήποτε xαπό τον τομέα ορισμού της συνάρτησης ισχύει το εξής: φά(- Χ) = φά (Χ), τότε καλείται η συνάρτηση ακόμη και; αν συμβεί: φά(- Χ) = - φά (Χ), τότε καλείται η συνάρτηση Περιττός. Γράφημα άρτιας συνάρτησης συμμετρικά ως προς τον άξονα Υ(Εικ. 5), μια γραφική παράσταση μιας περιττής συνάρτησης συμμετρικό περίπου προέλευση(Εικ. 6).
Μονοτονική λειτουργία.Εάν για οποιεσδήποτε δύο τιμές του ορίσματος Χ 1 και Χ 2 της συνθήκης Χ 2 >Χ 1 ακολουθεί φά(Χ 2 ) >φά(Χ 1), μετά η συνάρτηση φά(Χ) που ονομάζεται αυξανόμενη; αν για κανένα Χ 1 και Χ 2 της συνθήκης Χ 2 >Χ 1 ακολουθεί φά(Χ 2 ) <φά(Χ 1 ), μετά η συνάρτηση φά(Χ) λέγεται μειώνεται. Μια συνάρτηση που μόνο αυξάνεται ή μόνο μειώνεται ονομάζεται μονότονος.
3. Ακολουθίες αριθμών. Ορισμός και παραδείγματα.
Θα πούμε ότι η μεταβλητή ΧΥπάρχει διατεταγμένη μεταβλητή, αν είναι γνωστό το εμβαδόν της αλλαγής του και για καθεμία από τις δύο τιμές του μπορεί κανείς να πει ποια είναι η προηγούμενη και ποια η επόμενη. Μια ειδική περίπτωση μιας παραγγελθείσας μεταβλητής ποσότητας είναι μια μεταβλητή ποσότητα της οποίας οι τιμές σχηματίζονται ακολουθία αριθμών x 1 , x 2 ,…, x n ,…Για τέτοιες τιμές στο Εγώ< j, i, j Î N , έννοια x iθεωρείται προγενέστερο, και x j– επακόλουθη, ανεξάρτητα από το ποια από αυτές τις τιμές είναι μεγαλύτερη. Έτσι, μια ακολουθία αριθμών είναι μια μεταβλητή της οποίας οι διαδοχικές τιμές μπορούν να επαναριθμηθούν. Θα συμβολίσουμε μια αριθμητική ακολουθία με . Οι επιμέρους αριθμοί μιας ακολουθίας ονομάζονται της στοιχεία.
Για παράδειγμα, η αριθμητική ακολουθία σχηματίζεται από τις ακόλουθες ποσότητες:
3. , όπου Ενα δ– σταθεροί αριθμοί.
Όριο ακολουθίας αριθμών.
Αριθμός έναπου ονομάζεται όριοακολουθίες Χ = {x n), αν για έναν αυθαίρετο προκαθορισμένο αυθαίρετα μικρό θετικό αριθμό ε υπάρχει ένας τέτοιος φυσικός αριθμός Νπου μπροστά σε όλους n>Nη ανισότητα |x n - a|< ε.
Εάν ο αριθμός έναυπάρχει όριο ακολουθίας Χ = {x n), μετά το λένε αυτό x nαγωνίζεται για ένα, και γράψε.
Για να διατυπώσουμε αυτόν τον ορισμό με γεωμετρικούς όρους, εισάγουμε την ακόλουθη έννοια. Γειτονιά σημείου x 0ονομάζεται αυθαίρετο διάστημα ( α, β), που περιέχει αυτό το σημείο μέσα του. Συχνά θεωρείται η γειτονιά ενός σημείου x 0, για το οποίο x 0είναι η μέση, λοιπόν x 0που ονομάζεται κέντρογειτονιά και η αξία ( σι–ένα)/2 – ακτίνα κύκλουγειτονιά.
Λοιπόν, ας μάθουμε τι σημαίνει γεωμετρικά η έννοια του ορίου μιας αριθμητικής ακολουθίας. Για να γίνει αυτό, γράφουμε την τελευταία ανισότητα από τον ορισμό ως Αυτή η ανισότητα σημαίνει ότι όλα τα στοιχεία της ακολουθίας με αριθμούς n>Nπρέπει να βρίσκεται στο διάστημα (a – ε; a + ε).
Επομένως, ένας σταθερός αριθμός έναυπάρχει ένα όριο στην ακολουθία αριθμών ( x n), εάν για οποιαδήποτε μικρή γειτονιά με κέντρο στο σημείο έναακτίνα ε (ε είναι η γειτονιά του σημείου ένα) υπάρχει ένα τέτοιο στοιχείο της ακολουθίας με αριθμό Νότι όλα τα επόμενα στοιχεία είναι αριθμημένα n>Nθα βρίσκεται σε αυτήν την περιοχή.
Παραδείγματα.
1. Έστω η μεταβλητή Χπαίρνει τιμές διαδοχικά
Ας αποδείξουμε ότι το όριο αυτής της ακολουθίας αριθμών είναι ίσο με 1. Πάρτε έναν αυθαίρετο θετικό αριθμό ε. Πρέπει να βρούμε έναν τέτοιο φυσικό αριθμό Νπου μπροστά σε όλους n>Nη ανισότητα ισχύει | x n - 1| < ε. Действительно, т.к.
τότε να ικανοποιηθεί η σχέση |x n - a|< ε достаточно, чтобы или . Поэтому, взяв в качестве Νκάθε φυσικός αριθμός που ικανοποιεί την ανίσωση, παίρνουμε αυτό που χρειαζόμαστε. Αν λοιπόν πάρουμε, για παράδειγμα, τότε, βάζοντας Ν= 6, για όλους n>6 θα έχουμε .
2. Χρησιμοποιώντας τον ορισμό του ορίου μιας αριθμητικής ακολουθίας, να αποδείξετε ότι .
Ας πάρουμε ένα αυθαίρετο ε > 0. Σκεφτείτε Τότε , εάν ή , δηλ. . Επομένως, επιλέγουμε οποιοδήποτε φυσικό αριθμό που ικανοποιεί την ανίσωση.
Παραδείγματα.
3. Ας εξετάσουμε. Στο x→1ο αριθμητής του κλάσματος τείνει στο 1, και ο παρονομαστής τείνει στο 0. Επειδή όμως, δηλ. είναι απειροελάχιστη συνάρτηση στο x→ 1, λοιπόν
Θεώρημα 4.Ας δοθούν τρεις συναρτήσεις f(x), u(x)Και v(x), ικανοποιώντας τις ανισότητες u (x)≤f(x)≤ v(x). Εάν οι λειτουργίες u(x)Και v(x)έχουν το ίδιο όριο στο x→a(ή x→∞), μετά η συνάρτηση f(x)τείνει στο ίδιο όριο, δηλ. Αν
Θεώρημα 5.Αν στο x→a(ή x→∞) λειτουργία y=f(x)δέχεται μη αρνητικές τιμές y≥0και ταυτόχρονα τείνει στο όριο σι, τότε αυτό το όριο δεν μπορεί να είναι αρνητικό: b≥0.
Απόδειξη. Θα πραγματοποιήσουμε την απόδειξη με αντίφαση. Ας το προσποιηθούμε σι<0 , Επειτα |y – b|≥|b|και, επομένως, ο συντελεστής διαφοράς δεν τείνει στο μηδέν όταν x→a. Αλλά στη συνέχεια yδεν αγγίζει το όριο σιστο x→a, που έρχεται σε αντίθεση με τις προϋποθέσεις του θεωρήματος.
Θεώρημα 6.Αν δύο λειτουργίες f(x)Και g(x)για όλες τις τιμές του επιχειρήματος Χικανοποιούν την ανισότητα f(x)≥ g(x)και έχουν όρια, τότε ισχύει η ανισότητα β≥ γ.
Απόδειξη.Σύμφωνα με τις προϋποθέσεις του θεωρήματος f(x)-g(x) ≥0, επομένως, από το Θεώρημα 5, ή .
6. Γνωστοποίηση αβεβαιότητας (0/0), ∞ -∞
ΕΓΩ.Αβεβαιότητα.
Κατά την παραγοντοποίηση του αριθμητή, χρησιμοποιήσαμε τον κανόνα της διαίρεσης ενός πολυωνύμου με ένα πολυώνυμο με μια "γωνία". Από τον αριθμό Χ=1 είναι η ρίζα του πολυωνύμου x 3 – 6x 2 + 11Χ– 6, τότε κατά τη διαίρεση παίρνουμε
7. Όριο ακολουθίας . Η έννοια του φυσικού λογάριθμου.
ΤΟ ΔΕΥΤΕΡΟ ΣΗΜΑΝΤΙΚΟ ΟΡΙΟ
Παραδείγματα:
Λογάριθμος προς βάση μι (μι- ένας υπερβατικός αριθμός περίπου ίσος με 2,718281828...) ονομάζεται φυσικός λογάριθμος. Φυσικός λογάριθμος ενός αριθμού Χσυμβολίζεται ln Χ. Οι φυσικοί λογάριθμοι χρησιμοποιούνται ευρέως στα μαθηματικά, τη φυσική και τους μηχανικούς υπολογισμούς.
Οι λογάριθμοι χρησιμοποιούνται ευρέως
βάση, που ονομάζεται φυσική. Οι φυσικοί λογάριθμοι υποδεικνύονται με το σύμβολο
Η έννοια του ορίου μιας συνάρτησης.
Η έννοια της συνέχειας μιας συνάρτησης σχετίζεται άμεσα με την έννοια του ορίου μιας συνάρτησης.
Ένας αριθμός Α ονομάζεται όριο μιας συνάρτησης f σε ένα σημείο α, το όριο ενός συνόλου Ε, εάν για οποιαδήποτε γειτονιά V(A) του σημείου Α, υπάρχει μια τρυπημένη γειτονιά του σημείου a τέτοια ώστε η εικόνα του κάτω από η αντιστοίχιση f είναι ένα υποσύνολο της δεδομένης γειτονιάς V(A) του σημείου Α.
Το όριο μιας συνάρτησης f σε ένα σημείο a, ένα όριο για το σύνολο Ε, συμβολίζεται ως εξής: ή, εάν η αναφορά του συνόλου Ε μπορεί να παραλειφθεί.
Δεδομένου ότι κάθε γειτονιά μπορεί να συσχετιστεί με τη δική της κανονική (συμμετρική) γειτονιά, ο ορισμός του ορίου μπορεί να διατυπωθεί στη γλώσσα -δ όπως συνηθίζεται στη μαθηματική ανάλυση:
Το όριο μιας συνάρτησης σε ένα σημείο f σε ένα σημείο α, το όριο του συνόλου Ε, σχετίζεται άμεσα με το όριο της ακολουθίας.
Θα εξετάσουμε όλες τις πιθανές ακολουθίες σημείων του συνόλου Ε που έχουν ως όριο το σημείο α και τις αντίστοιχες ακολουθίες τιμών συνάρτησης στα σημεία της ακολουθίας. Εάν υπάρχει ένα όριο μιας συνάρτησης f στο σημείο a, τότε αυτό το όριο θα είναι το όριο κάθε ακολουθίας.
Το αντίστροφο ισχύει επίσης: εάν όλες οι ακολουθίες συγκλίνουν στην ίδια τιμή, τότε η συνάρτηση έχει ένα όριο ίσο με αυτήν την τιμή.
ΤΟ ΠΡΩΤΟ ΣΗΜΑΝΤΙΚΟ ΟΡΙΟ
Η λειτουργία δεν ορίζεται πότε Χ=0, αφού ο αριθμητής και ο παρονομαστής του κλάσματος γίνονται μηδέν. Το γράφημα της συνάρτησης φαίνεται στο σχήμα.
Ωστόσο, είναι δυνατό να βρεθεί το όριο αυτής της συνάρτησης στο Χ→0.
Ας δώσουμε μια απόδειξη του γραπτού τύπου. Θεωρήστε έναν κύκλο ακτίνας 1 και υποθέστε ότι η γωνία α, εκφρασμένη σε ακτίνια, περιέχεται εντός 0< α < π/2. (Так как четная функция и ее значения не изменяются при изменении знака α, то достаточно рассмотреть случай, когда α >0.) Από το σχήμα είναι σαφές ότι
SΔOAC .
Αφού οι υποδεικνυόμενες περιοχές είναι αντίστοιχα ίσες
SΔOAC=0,5∙O.C.∙Ο.Α.∙αμαρτία α= 0,5 σινα, S αίρεση. OAC = 0,5∙O.C. 2 ∙α=0,5α, SΔOBC=0,5∙O.C.∙π.Χ.= 0,5 tgα.
Ως εκ τούτου,
αμαρτία α< α < tg α.
Ας διαιρέσουμε όλους τους όρους της ανισότητας με το sin α > 0: .
Αλλά . Επομένως, με βάση το Θεώρημα 4 για τα όρια, συμπεραίνουμε ότι ο παραγόμενος τύπος ονομάζεται πρώτο αξιοσημείωτο όριο.
Έτσι, το πρώτο αξιοσημείωτο όριο χρησιμεύει για να αποκαλύψει την αβεβαιότητα. Σημειώστε ότι ο προκύπτων τύπος δεν πρέπει να συγχέεται με τα όρια Παραδείγματα.
11.Όριο και τα σχετικά όριά του.
ΤΟ ΔΕΥΤΕΡΟ ΣΗΜΑΝΤΙΚΟ ΟΡΙΟ
Το δεύτερο αξιοσημείωτο όριο χρησιμεύει για να αποκαλύψει την αβεβαιότητα του 1 ∞ και μοιάζει με αυτό:
Ας δώσουμε προσοχή στο γεγονός ότι στον τύπο για το δεύτερο αξιοσημείωτο όριο, ο εκθέτης πρέπει να περιέχει μια έκφραση αντίστροφη από αυτήν που προστίθεται στη μονάδα στη βάση (καθώς σε αυτή την περίπτωση είναι δυνατή η εισαγωγή μιας αλλαγής μεταβλητών και μειώστε το επιθυμητό όριο στο δεύτερο αξιοσημείωτο όριο)
Παραδείγματα.
1. Λειτουργία f(x)=(Χ-1) Το 2 είναι απειροελάχιστο στο Χ→1, αφού (βλ. σχήμα).
2. Λειτουργία f(x)= tg Χ– απειροελάχιστο στο Χ→0.
3. f(x)= log(1+ Χ) – απειροελάχιστο στο Χ→0.
4. f(x) = 1/Χ– απειροελάχιστο στο Χ→∞.
Ας δημιουργήσουμε την ακόλουθη σημαντική σχέση:
Θεώρημα.Εάν η συνάρτηση y=f(x)αντιπροσωπεύσιμο με x→aως άθροισμα ενός σταθερού αριθμού σικαι απειροελάχιστο μέγεθος α(x): f (x)=b+ α(x)Οτι .
Αντίθετα, αν , τότε f (x)=b+α(x), Οπου τσεκούρι)– απειροελάχιστο στο x→a.
Απόδειξη.
1. Ας αποδείξουμε το πρώτο μέρος της δήλωσης. Από την ισότητα f(x)=b+α(x)πρέπει |f(x) – b|=| α|. Αλλά από τότε τσεκούρι)είναι απειροελάχιστο, τότε για το αυθαίρετο ε υπάρχει δ – μια γειτονιά του σημείου ένα,μπροστά σε όλους Χαπό το οποίο, αξίες τσεκούρι)ικανοποιήσει τη σχέση |α(x)|< ε. Επειτα |f(x) – b|< ε. Και αυτό σημαίνει ότι.
2. Αν , τότε για οποιαδήποτε ε >0 για όλα Χαπό κάποια δ – γειτονιά ενός σημείου έναθα |f(x) – b|< ε. Αν όμως υποδηλώσουμε f(x) – b= α, Οτι |α(x)|< ε, που σημαίνει ότι ένα– απειροελάχιστο.
Ας εξετάσουμε τις βασικές ιδιότητες των απειροελάχιστων συναρτήσεων.
Θεώρημα 1.Το αλγεβρικό άθροισμα δύο, τριών και γενικά οποιουδήποτε πεπερασμένου αριθμού απειροελάχιστων είναι απειροελάχιστη συνάρτηση.
Απόδειξη. Ας δώσουμε μια απόδειξη για δύο όρους. Αφήνω f(x)=α(x)+β(x), πού και . Πρέπει να αποδείξουμε ότι για κάθε αυθαίρετο μικρό ε > 0 βρέθηκαν δ> 0, έτσι ώστε για Χ, ικανοποιώντας την ανισότητα |x – α|<δ , εκτελέστηκε |f(x)|< ε.
Λοιπόν, ας διορθώσουμε έναν αυθαίρετο αριθμό ε > 0. Αφού σύμφωνα με τις προϋποθέσεις του θεωρήματος α(x)είναι απειροελάχιστη συνάρτηση, τότε υπάρχει τέτοια δ 1 > 0, που είναι |x – a|< δ 1 έχουμε |α(x)|< ε / 2. Ομοίως, από τότε β(x)είναι απειροελάχιστο, τότε υπάρχει τέτοιο δ 2 > 0, που είναι |x – a|< δ 2 έχουμε | β(x)|< ε / 2.
Ας πάρουμε δ=min(δ 1 , δ2 } .Στη συνέχεια στην περιοχή του σημείου έναακτίνα κύκλου δ καθεμία από τις ανισότητες θα ικανοποιηθεί |α(x)|< ε / 2 και | β(x)|< ε / 2. Επομένως, σε αυτή τη γειτονιά θα υπάρχουν
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
εκείνοι. |f(x)|< ε, που είναι αυτό που έπρεπε να αποδειχθεί.
Θεώρημα 2.Προϊόν μιας απειροελάχιστης συνάρτησης τσεκούρι)για περιορισμένη λειτουργία f(x)στο x→a(ή πότε x→∞) είναι μια απειροελάχιστη συνάρτηση.
Απόδειξη. Από τη λειτουργία f(x)είναι περιορισμένη, τότε υπάρχει αριθμός Μέτσι ώστε για όλες τις αξίες Χαπό κάποια γειτονιά ενός σημείου a|f(x)|≤M.Επιπλέον, από τότε τσεκούρι)είναι απειροελάχιστη συνάρτηση στο x→a, τότε για αυθαίρετο ε > 0 υπάρχει μια γειτονιά του σημείου ένα, στην οποία θα ισχύει η ανισότητα |α(x)|< ε /Μ. Στη συνέχεια στη μικρότερη από αυτές τις γειτονιές έχουμε | αf|< ε /Μ= ε. Και αυτό σημαίνει ότι αφ– απειροελάχιστο. Για την περίσταση x→∞η απόδειξη γίνεται με παρόμοιο τρόπο.
Από το αποδεδειγμένο θεώρημα προκύπτει:
Συμπέρασμα 1.Αν και , τότε
Συμπέρασμα 2.Αν c= const, τότε .
Θεώρημα 3.Λόγος απειροελάχιστης συνάρτησης α(x)ανά λειτουργία f(x), το όριο του οποίου είναι διαφορετικό από το μηδέν, είναι μια απειροελάχιστη συνάρτηση.
Απόδειξη. Αφήστε . Μετά 1 /f(x)υπάρχει περιορισμένη λειτουργία. Επομένως, ένα κλάσμα είναι το γινόμενο μιας απειροελάχιστης συνάρτησης και μιας περιορισμένης συνάρτησης, δηλ. η συνάρτηση είναι απειροελάχιστη.
Παραδείγματα.
1. Είναι σαφές ότι όταν x→+∞λειτουργία y=x 2 +Το 1 είναι απείρως μεγάλο. Αλλά τότε, σύμφωνα με το θεώρημα που διατυπώθηκε παραπάνω, η συνάρτηση είναι απειροελάχιστη στο x→+∞, δηλ. .
Το θεώρημα της αντίστροφης μπορεί επίσης να αποδειχθεί.
Θεώρημα 2.Εάν η συνάρτηση f(x)- απειροελάχιστο στο x→a(ή x→∞)και δεν εξαφανίζεται, λοιπόν y= 1/f(x)είναι μια απείρως μεγάλη συνάρτηση.
Εκτελέστε την απόδειξη του θεωρήματος μόνοι σας.
Παραδείγματα.
3. , αφού οι συναρτήσεις και είναι απειροελάχιστες στο x→+∞, λοιπόν, καθώς το άθροισμα των απειροελάχιστων συναρτήσεων είναι απειροελάχιστη συνάρτηση. Μια συνάρτηση είναι το άθροισμα ενός σταθερού αριθμού και μιας απειροελάχιστης συνάρτησης. Συνεπώς, με το Θεώρημα 1 για απειροελάχιστες συναρτήσεις λαμβάνουμε την απαιτούμενη ισότητα.
Έτσι, οι απλούστερες ιδιότητες των απειροελάχιστων και απείρως μεγάλων συναρτήσεων μπορούν να γραφτούν χρησιμοποιώντας τις ακόλουθες σχέσεις υπό όρους: ΕΝΑ≠ 0
13. Απειροελάχιστες συναρτήσεις ίδιας τάξης, ισοδύναμες απειροελάχιστες.
Απειροελάχιστες συναρτήσεις και ονομάζονται απειροελάχιστες ίδιας τάξης μικρότητας αν , δηλώνουν . Και τέλος, αν δεν υπάρχει, τότε οι απειροελάχιστες συναρτήσεις είναι ασύγκριτες.
ΠΑΡΑΔΕΙΓΜΑ 2. Σύγκριση απειροελάχιστων συναρτήσεων
Ισοδύναμες απειροελάχιστες συναρτήσεις.
Αν , τότε καλούνται απειροελάχιστες συναρτήσεις ισοδύναμος, δηλώνουν ~ .
Τοπικά ισοδύναμες συναρτήσεις:
Όταν αν
Κάποιες ισοδυναμίες(στο):
Μονόπλευρα όρια.
Μέχρι στιγμής έχουμε σκεφτεί να προσδιορίσουμε το όριο μιας συνάρτησης όταν x→aμε αυθαίρετο τρόπο, δηλ. το όριο της συνάρτησης δεν εξαρτιόταν από το πώς βρισκόταν Χπρος ένα, αριστερά ή δεξιά του ένα. Ωστόσο, είναι αρκετά συνηθισμένο να βρίσκουμε συναρτήσεις που δεν έχουν όριο υπό αυτήν την προϋπόθεση, αλλά έχουν ένα όριο εάν x→a, παραμένοντας στη μία πλευρά του ΕΝΑ, αριστερά ή δεξιά (βλ. εικόνα). Ως εκ τούτου, εισάγονται οι έννοιες των μονόπλευρων ορίων.
Αν f(x)τείνει στο όριο σιστο Χτείνουν σε έναν ορισμένο αριθμό έναΈτσι Χδέχεται μόνο τιμές μικρότερες από ένα, μετά γράφουν και τηλεφωνούν όριο της συνάρτησης f(x) στο σημείο α στα αριστερά.
Ο αριθμός λοιπόν σιονομάζεται όριο της συνάρτησης y=f(x)στο x→aστα αριστερά, αν οποιοσδήποτε θετικός αριθμός ε είναι, υπάρχει ένας τέτοιος αριθμός δ (μικρότερος ένα
Ομοίως, αν x→aκαι παίρνει μεγάλες αξίες ένα, μετά γράφουν και τηλεφωνούν σιόριο της συνάρτησης στο σημείο ΕΝΑστα δεξιά. Εκείνοι. αριθμός σιπου ονομάζεται όριο της συνάρτησης y=f(x) ως x→a στα δεξιά, αν οποιοσδήποτε θετικός αριθμός ε είναι, υπάρχει ένας τέτοιος αριθμός δ (μεγαλύτερος ΕΝΑ) ότι η ανισότητα ισχύει για όλους.
Σημειώστε ότι αν τα όρια στα αριστερά και δεξιά στο σημείο έναγια λειτουργία f(x)δεν συμπίπτουν, τότε η συνάρτηση δεν έχει όριο (δύο όψεων) στο σημείο ΕΝΑ.
Παραδείγματα.
1. Εξετάστε τη συνάρτηση y=f(x), ορίζεται στο τμήμα ως εξής
Ας βρούμε τα όρια της συνάρτησης f(x)στο x→ 3. Προφανώς, και
Με άλλα λόγια, για κάθε αυθαίρετα μικρό αριθμό έψιλον, υπάρχει ένας αριθμός δέλτα ανάλογα με το έψιλον έτσι ώστε από το γεγονός ότι για κάθε x που ικανοποιεί την ανισότητα προκύπτει ότι οι διαφορές στις τιμές της συνάρτησης σε αυτά τα σημεία θα είναι αυθαίρετα μικρό.
Κριτήριο για τη συνέχεια μιας συνάρτησης σε ένα σημείο:
Λειτουργίαθα συνεχήςστο σημείο Α αν και μόνο αν είναι συνεχές στο σημείο Α και στα δεξιά και στα αριστερά, δηλαδή, ώστε στο σημείο Α να υπάρχουν δύο μονόπλευρα όρια, να είναι ίσα μεταξύ τους και ίσα με την τιμή του η συνάρτηση στο σημείο Α.
Ορισμός 2: Η λειτουργία είναι συνεχήςσε ένα σύνολο εάν είναι συνεχές σε όλα τα σημεία αυτού του συνόλου.
Παράγωγος συνάρτησης σε σημείο
Ας οριστεί η ντάνα σε μια γειτονιά. Ας σκεφτούμε
Εάν υπάρχει αυτό το όριο, τότε καλείται παράγωγος της συνάρτησης f στο σημείο .
Παράγωγος συνάρτησης– το όριο του λόγου της αύξησης της συνάρτησης προς την αύξηση του ορίσματος, όταν το όρισμα αυξάνεται.
Η πράξη του υπολογισμού ή της εύρεσης της παραγώγου σε ένα σημείο ονομάζεται ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ-διάκριση .
Κανόνες διαφοροποίησης.
Παράγωγολειτουργίες f(x)στο σημείο x=x 0ονομάζεται λόγος της αύξησης μιας συνάρτησης σε αυτό το σημείο προς την αύξηση του ορίσματος, καθώς το τελευταίο τείνει στο μηδέν Η εύρεση της παραγώγου ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ-διάκριση. Η παράγωγος μιας συνάρτησης υπολογίζεται σύμφωνα με τον γενικό κανόνα της διαφοροποίησης: Ας υποδηλώσουμε f(x) = u, g(x) = v- συναρτήσεις διαφοροποιήσιμες σε ένα σημείο Χ. Βασικοί κανόνες διαφοροποίησης 1) (η παράγωγος ενός αθροίσματος είναι ίση με το άθροισμα των παραγώγων του) 2) (από εδώ, συγκεκριμένα, προκύπτει ότι η παράγωγος του γινομένου μιας συνάρτησης και μιας σταθεράς είναι ίση με το γινόμενο της παραγώγου αυτής συνάρτηση και η σταθερά) 3) Παράγωγος πηλίκου: , αν g 0 4) Παράγωγος μιγαδικής συνάρτησης: 5) Εάν η συνάρτηση καθορίζεται παραμετρικά: , τότε
Παραδείγματα.
1. y = ΧΤο a είναι μια συνάρτηση ισχύος με αυθαίρετο εκθέτη.
Σιωπηρή λειτουργία
Αν μια συνάρτηση δίνεται από την εξίσωση y=ƒ(x), επιλύεται ως προς το y, τότε η συνάρτηση δίνεται σε ρητή μορφή (ρητη συνάρτηση).
Κάτω από άρρητη εργασίαΟι συναρτήσεις κατανοούν τον ορισμό μιας συνάρτησης με τη μορφή εξίσωσης F(x;y)=0, που δεν επιλύεται ως προς το y.
Οποιαδήποτε ρητά δεδομένη συνάρτηση y=ƒ (x) μπορεί να γραφτεί όπως σιωπηρά δίνεται από την εξίσωση ƒ(x)-y=0, αλλά όχι το αντίστροφο.
Δεν είναι πάντα εύκολο, και μερικές φορές αδύνατο, να λυθεί μια εξίσωση για το y (για παράδειγμα, y+2x+cozy-1=0 ή 2 y -x+y=0).
Εάν η άρρητη συνάρτηση δίνεται από την εξίσωση F(x; y) = 0, τότε για να βρεθεί η παράγωγος του y ως προς το x δεν χρειάζεται να επιλυθεί η εξίσωση ως προς το y: αρκεί να διαφοροποιήσουμε αυτή την εξίσωση ως προς το x, ενώ θεωρούμε το y ως συνάρτηση του x,και στη συνέχεια λύστε την εξίσωση που προκύπτει για το y."
Η παράγωγος μιας άρρητης συνάρτησης εκφράζεται με το όρισμα x και τη συνάρτηση y.
Παράδειγμα:
Να βρείτε την παράγωγο της συνάρτησης y, που δίνεται από την εξίσωση x 3 + y 3 -3xy = 0.
Λύση: Η συνάρτηση y καθορίζεται σιωπηρά. Διαφοροποιούμε ως προς το x την ισότητα x 3 + y 3 -3xy = 0. Από τη σχέση που προκύπτει
3x 2 +3y 2 y"-3(1 y+x y")=0
έπεται ότι y 2 y"-xy"=y-x 2, δηλ. y"=(y-x 2)/(y 2 -x).
Παράγωγα υψηλότερης τάξης
Είναι σαφές ότι το παράγωγο
λειτουργίες y=f(x)υπάρχει επίσης μια λειτουργία από Χ:
y" =f " (x)
Εάν η συνάρτηση f" (x)είναι διαφοροποιήσιμη, τότε η παράγωγός της συμβολίζεται με το σύμβολο y"" =f "" (x) xεις διπλούν.
Η παράγωγος της δεύτερης παραγώγου, δηλ. λειτουργίες y""=f""(x), που ονομάζεται τρίτη παράγωγος της συνάρτησης y=f(x)ή παράγωγος της συνάρτησης f(x) τρίτης τάξηςκαι υποδεικνύεται με τα σύμβολα
Καθόλου n-i παράγωγο ή παράγωγο nσυνάρτηση ης τάξης y=f(x)υποδεικνύεται με σύμβολα
Φιλ Λάιμπνιτς:
Ας υποθέσουμε ότι οι συναρτήσεις και είναι διαφοροποιήσιμες μαζί με τις παραγώγους τους μέχρι την nη τάξη συμπεριλαμβανομένων. Εφαρμόζοντας τον κανόνα για τη διαφοροποίηση του γινομένου δύο συναρτήσεων, παίρνουμε
Ας συγκρίνουμε αυτές τις εκφράσεις με τις δυνάμεις του διωνύμου:
Ο κανόνας αντιστοιχίας είναι εντυπωσιακός: για να αποκτήσετε έναν τύπο για την παράγωγο 1ης, 2ης ή 3ης τάξης του γινομένου των συναρτήσεων και , πρέπει να αντικαταστήσετε τις δυνάμεις και στην έκφραση για (όπου n= 1,2,3) παράγωγα των αντίστοιχων παραγγελιών. Επιπλέον, μηδενικές δυνάμεις ποσοτήτων και θα πρέπει να αντικατασταθούν από παράγωγα μηδενικής τάξης, δηλαδή από αυτές τις συναρτήσεις και:
Γενικεύοντας αυτόν τον κανόνα στην περίπτωση των παραγώγων αυθαίρετης τάξης n, παίρνουμε Ο τύπος του Leibniz,
πού είναι οι διωνυμικοί συντελεστές:
Θεώρημα Rolle.
Αυτό το θεώρημα καθιστά δυνατή την εύρεση κρίσιμων σημείων και στη συνέχεια, χρησιμοποιώντας επαρκείς συνθήκες, την εξέταση της συνάρτησης για ακρότατα.
Έστω 1) η f(x) καθορισμένη και συνεχής σε κάποιο κλειστό διάστημα. 2) υπάρχει μια πεπερασμένη παράγωγος, τουλάχιστον στο ανοιχτό διάστημα (a;b). 3) στα άκρα του διαστήματος f-i παίρνει ίσες τιμές f(a) = f(b). Τότε μεταξύ των σημείων a και b υπάρχει ένα σημείο c τέτοιο ώστε η παράγωγος σε αυτό το σημείο θα είναι = 0.
Σύμφωνα με το θεώρημα για την ιδιότητα των συναρτήσεων που είναι συνεχείς σε ένα διάστημα, η συνάρτηση f(x) παίρνει τις μέγιστες και ελάχιστες τιμές της σε αυτό το διάστημα.
f(x 1) = M – max, f(x 2) = m – min; x 1 ;x 2 О
1) Έστω M = m, δηλ. m £ f(x) £ Μ
Το Þ f(x) θα λάβει σταθερές τιμές στο διάστημα από το a έως το b και Þ η παράγωγός του θα είναι ίση με μηδέν. f’(x)=0
2) Έστω M>m
Επειδή Σύμφωνα με τις συνθήκες του θεωρήματος, η f(a) = f(b) Þ θα λάβει τη μικρότερη ή τη μεγαλύτερη τιμή του όχι στα άκρα του τμήματος, αλλά το Þ θα πάρει M ή m στο εσωτερικό σημείο αυτού του τμήματος. Τότε, με το θεώρημα του Fermat, f’(c)=0.
Θεώρημα Lagrange.
Τύπος πεπερασμένης αύξησηςή Θεώρημα μέσης τιμής του Lagrangeδηλώνει ότι αν μια συνάρτηση φάείναι συνεχής στο διάστημα [ ένα;σι] και διαφοροποιήσιμο στο διάστημα ( ένα;σι), τότε υπάρχει ένα σημείο τέτοιο που
Θεώρημα Cauchy.
Εάν οι συναρτήσεις f(x) και g(x) είναι συνεχείς στο διάστημα και διαφοροποιήσιμες στο διάστημα (a, b) και g¢(x) ¹ 0 στο διάστημα (a, b), τότε υπάρχει τουλάχιστον ένα σημείο ε, α< e < b, такая, что
Εκείνοι. ο λόγος των αυξήσεων των συναρτήσεων σε ένα δεδομένο τμήμα είναι ίσος με τον λόγο των παραγώγων στο σημείο e. Παραδείγματα επίλυσης προβλημάτων μάθημα διαλέξεων Υπολογισμός του όγκου ενός σώματος από γνωστές περιοχές των παράλληλων τομών του Ολοκληρωμένος λογισμός
Παραδείγματα μαθημάτωνΗλεκτρολόγος Μηχανικός
Για να αποδείξουμε αυτό το θεώρημα, με την πρώτη ματιά είναι πολύ βολικό να χρησιμοποιήσουμε το θεώρημα του Lagrange. Γράψτε έναν τύπο πεπερασμένης διαφοράς για κάθε συνάρτηση και στη συνέχεια διαιρέστε τις μεταξύ τους. Ωστόσο, αυτή η ιδέα είναι λανθασμένη, γιατί Το σημείο ε για κάθε συνάρτηση είναι γενικά διαφορετικό. Φυσικά, σε ορισμένες ειδικές περιπτώσεις αυτό το σημείο του διαστήματος μπορεί να αποδειχθεί το ίδιο και για τις δύο συναρτήσεις, αλλά αυτό είναι μια πολύ σπάνια σύμπτωση και όχι κανόνας και επομένως δεν μπορεί να χρησιμοποιηθεί για την απόδειξη του θεωρήματος.
Απόδειξη. Εξετάστε τη συνάρτηση βοηθού
Ως x→x 0, η τιμή του c τείνει επίσης στο x 0. Ας πάμε στο όριο στην προηγούμενη ισότητα:
Επειδή , Οτι .
Να γιατί
(το όριο του λόγου δύο απειροελάχιστων είναι ίσο με το όριο του λόγου των παραγώγων τους, αν υπάρχει το δεύτερο)
Κανόνας του L'Hopital, στο ∞/∞.
Παρακαλώ σημειώστε: όλοι οι ορισμοί περιλαμβάνουν ένα αριθμητικό σύνολο X, το οποίο είναι μέρος του τομέα της συνάρτησης: X με D(f). Στην πράξη, τις περισσότερες φορές υπάρχουν περιπτώσεις όπου το Χ είναι ένα αριθμητικό διάστημα (τμήμα, διάστημα, ακτίνα κ.λπ.).
Ορισμός 1.
Μια συνάρτηση y = f(x) λέγεται ότι αυξάνεται σε ένα σύνολο X με D(f) εάν για οποιαδήποτε δύο σημεία x 1 και x 2 του συνόλου X έτσι ώστε x 1< х 2 , выполняется неравенство f(х 1 < f(х 2).
Ορισμός 2.
Μια συνάρτηση y = f(x) λέγεται ότι είναι φθίνουσα σε ένα σύνολο X με D(f) εάν για οποιαδήποτε δύο σημεία x 1 και x 2 του συνόλου X έτσι ώστε x 1< х 2 , функции выполняется неравенство f(x 1) >f(x 2).
Στην πράξη, είναι πιο βολικό να χρησιμοποιείτε τις ακόλουθες διατυπώσεις: μια συνάρτηση αυξάνεται εάν μια μεγαλύτερη τιμή του ορίσματος αντιστοιχεί σε μια μεγαλύτερη τιμή της συνάρτησης. μια συνάρτηση μειώνεται εάν μια μεγαλύτερη τιμή του ορίσματος αντιστοιχεί σε μια μικρότερη τιμή της συνάρτησης.
Στην 7η και 8η τάξη χρησιμοποιήσαμε την ακόλουθη γεωμετρική ερμηνεία των εννοιών της αύξησης ή της μείωσης μιας συνάρτησης: κινούμενοι κατά μήκος του γραφήματος μιας αυξανόμενης συνάρτησης από αριστερά προς τα δεξιά, φαίνεται να σκαρφαλώνουμε σε ένα λόφο (Εικ. 55). κινούμενοι κατά μήκος της γραφικής παράστασης μιας φθίνουσας συνάρτησης από αριστερά προς τα δεξιά, είναι σαν να κατεβαίνουμε έναν λόφο (Εικ. 56).
Συνήθως οι όροι "αύξηση συνάρτηση", "φθίνουσα συνάρτηση" συνδυάζονται με τη γενική ονομασία μονοτονική συνάρτηση και η μελέτη μιας συνάρτησης για αύξηση ή μείωση ονομάζεται μελέτη μιας συνάρτησης για μονοτονία.
Ας σημειώσουμε μια ακόμη περίσταση: εάν μια συνάρτηση αυξάνεται (ή μειώνεται) στο φυσικό της πεδίο ορισμού, τότε συνήθως λέμε ότι η συνάρτηση αυξάνεται (ή μειώνεται) - χωρίς να υποδεικνύεται το αριθμητικό σύνολο X.
Παράδειγμα 1.
Εξετάστε τη συνάρτηση για μονοτονία:
ΕΝΑ) y = x 3 + 2; β) y = 5 - 2x.
Λύση:
α) Πάρτε αυθαίρετες τιμές του ορίσματος x 1 και x 2 και έστω x 1<х 2 . Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:

Η τελευταία ανισότητα σημαίνει ότι f(x 1)< f(х 2). Итак, из х 1 < х 2 следует f{х 1) < f(х 2), а это означает, что заданная функция возрастает (на всей числовой прямой).
Άρα από x 1< х 2 следует f(х 1) >f(x 2), που σημαίνει ότι η δεδομένη συνάρτηση είναι φθίνουσα (σε ολόκληρη την αριθμητική γραμμή).
Ορισμός 3.
Μια συνάρτηση y - f(x) λέγεται ότι οριοθετείται από κάτω σε ένα σύνολο X με D(f) εάν όλες οι τιμές της συνάρτησης στο σύνολο X είναι μεγαλύτερες από έναν ορισμένο αριθμό (με άλλα λόγια, εάν υπάρχει έναν αριθμό m τέτοιο ώστε για οποιαδήποτε τιμή x є X η ανίσωση f( x) >m).
Ορισμός 4.
Μια συνάρτηση y = f(x) λέγεται ότι οριοθετείται από πάνω σε ένα σύνολο X με D(f) εάν όλες οι τιμές της συνάρτησης είναι μικρότερες από έναν ορισμένο αριθμό (με άλλα λόγια, εάν υπάρχει ένας αριθμός M π.χ. ότι για οποιαδήποτε τιμή x є X ισχύει η ανισότητα f(x).< М).
Εάν το σύνολο X δεν προσδιορίζεται, τότε εννοείται ότι μιλάμε για τη συνάρτηση που οριοθετείται από κάτω ή από πάνω σε ολόκληρο το πεδίο ορισμού.
Αν μια συνάρτηση είναι οριοθετημένη τόσο από κάτω όσο και από πάνω, τότε ονομάζεται περιορισμένη.
Η οριοθέτηση μιας συνάρτησης διαβάζεται εύκολα από το γράφημά της: εάν μια συνάρτηση οριοθετείται από κάτω, τότε η γραφική παράσταση της βρίσκεται εξ ολοκλήρου πάνω από μια συγκεκριμένη οριζόντια γραμμή y = m (Εικ. 57). αν μια συνάρτηση είναι οριοθετημένη από πάνω, τότε η γραφική παράσταση της βρίσκεται εξ ολοκλήρου κάτω από κάποια οριζόντια γραμμή y = M (Εικ. 58).

Παράδειγμα 2.Εξετάστε το όριο μιας συνάρτησης
Λύση.Αφενός, η ανισότητα είναι αρκετά εμφανής (με τον ορισμό της τετραγωνικής ρίζας, αυτό σημαίνει ότι η συνάρτηση οριοθετείται παρακάτω. Από την άλλη, έχουμε και επομένως
Αυτό σημαίνει ότι η συνάρτηση είναι άνω όριο. Τώρα κοιτάξτε το γράφημα της δεδομένης συνάρτησης (Εικ. 52 από την προηγούμενη παράγραφο). Ο περιορισμός της συνάρτησης τόσο πάνω όσο και κάτω μπορεί να διαβαστεί αρκετά εύκολα από το γράφημα.
Ορισμός 5.
Ο αριθμός m ονομάζεται η μικρότερη τιμή της συνάρτησης y = f(x) στο σύνολο X C D(f) αν:
1) στο X υπάρχει ένα σημείο x 0 τέτοιο ώστε f(x 0) = m;
2) για όλα τα x από το X ισχύει η ανισότητα m>f(x 0).
Ορισμός 6.
Ο αριθμός M ονομάζεται η μεγαλύτερη τιμή της συνάρτησης y = f(x) στο σύνολο X C D(f), εάν:
1) στο X υπάρχει ένα σημείο x 0 τέτοιο ώστε f(x 0) = M;
2) για όλα τα x από το X την ανισότητα
Σημειώσαμε τη μικρότερη τιμή μιας συνάρτησης τόσο στην 7η όσο και στην 8η τάξη με το σύμβολο y και τη μεγαλύτερη με το σύμβολο y.
Εάν το σύνολο X δεν προσδιορίζεται, τότε υποτίθεται ότι μιλάμε για την εύρεση της μικρότερης ή μεγαλύτερης τιμής της συνάρτησης σε ολόκληρο το πεδίο ορισμού.
Οι ακόλουθες χρήσιμες δηλώσεις είναι αρκετά προφανείς:
1) Εάν μια συνάρτηση έχει Y, τότε είναι φραγμένη παρακάτω.
2) Αν μια συνάρτηση έχει Υ, τότε είναι φραγμένη παραπάνω.
3) Εάν η συνάρτηση δεν περιορίζεται παρακάτω, τότε το Y δεν υπάρχει.
4) Εάν η συνάρτηση δεν είναι περιορισμένη παραπάνω, τότε το Υ δεν υπάρχει.
Παράδειγμα 3.
Βρείτε τις μικρότερες και μεγαλύτερες τιμές μιας συνάρτησης
Λύση.
Είναι αρκετά προφανές, ειδικά αν χρησιμοποιήσετε το γράφημα συνάρτησης (Εικ. 52), ότι = 0 (η συνάρτηση φτάνει αυτή την τιμή στα σημεία x = -3 και x = 3), a = 3 (η συνάρτηση φτάνει σε αυτήν την τιμή στο x = 0.
Στην 7η και 8η τάξη αναφέραμε δύο ακόμη ιδιότητες συναρτήσεων. Η πρώτη ονομαζόταν ιδιότητα κυρτότητας μιας συνάρτησης. Μια συνάρτηση θεωρείται ότι είναι κυρτή προς τα κάτω σε ένα διάστημα Χ αν, συνδέοντας οποιαδήποτε δύο σημεία της γραφικής της παράστασης (με τετμημένες από το Χ) με ένα ευθύγραμμο τμήμα, διαπιστώσουμε ότι το αντίστοιχο τμήμα της γραφικής παράστασης βρίσκεται κάτω από το σχεδιασμένο τμήμα (Εικ. 59). Συνέχεια Μια συνάρτηση είναι κυρτή προς τα πάνω σε ένα διάστημα Χ αν, συνδέοντας οποιαδήποτε δύο σημεία της γραφικής της παράστασης (με τετμημένα από το Χ) της συνάρτησης με ένα ευθύγραμμο τμήμα, βρούμε ότι το αντίστοιχο τμήμα της γραφικής παράστασης βρίσκεται πάνω από το σχεδιασμένο τμήμα ( Εικ. 60).

Η δεύτερη ιδιότητα - η συνέχεια μιας συνάρτησης στο διάστημα Χ - σημαίνει ότι η γραφική παράσταση της συνάρτησης στο διάστημα Χ είναι συνεχής, δηλ. δεν έχει τρυπήματα ή άλματα.
Σχόλιο.
Στην πραγματικότητα, στα μαθηματικά όλα είναι, όπως λένε, «ακριβώς το αντίθετο»: το γράφημα μιας συνάρτησης απεικονίζεται ως μια συμπαγής γραμμή (χωρίς τρυπήματα ή άλματα) μόνο όταν αποδειχθεί η συνέχεια της συνάρτησης. Αλλά ένας επίσημος ορισμός της συνέχειας μιας συνάρτησης, ο οποίος είναι αρκετά περίπλοκος και λεπτός, δεν είναι ακόμη μέσα στις δυνατότητές μας. Το ίδιο μπορεί να ειπωθεί για την κυρτότητα μιας συνάρτησης. Όταν συζητάμε αυτές τις δύο ιδιότητες των συναρτήσεων, θα συνεχίσουμε να βασιζόμαστε σε οπτικές και διαισθητικές έννοιες.
Τώρα ας αναθεωρήσουμε τις γνώσεις μας. Θυμούμενοι τις συναρτήσεις που μελετήσαμε στην 7η και 8η τάξη, ας διευκρινίσουμε πώς μοιάζουν τα γραφήματα τους και ας απαριθμήσουμε τις ιδιότητες της συνάρτησης, τηρώντας μια συγκεκριμένη σειρά, για παράδειγμα: τομέας ορισμού. μονότονη ομιλία; περιορισμός; , ; συνέχεια; εύρος; κυρτός.
Στη συνέχεια, θα εμφανιστούν νέες ιδιότητες συναρτήσεων και η λίστα των ιδιοτήτων θα αλλάξει ανάλογα.
1. Σταθερή συνάρτηση y = C
Η γραφική παράσταση της συνάρτησης y = C φαίνεται στο Σχ. 61 - ευθεία γραμμή, παράλληλη προς τον άξονα x. Αυτό είναι τόσο μη ενδιαφέρον χαρακτηριστικό που δεν έχει νόημα να απαριθμήσουμε τις ιδιότητές του.

Η γραφική παράσταση της συνάρτησης y = kx + m είναι ευθεία γραμμή (Εικ. 62, 63).

Ιδιότητες της συνάρτησης y = kx + m:
1) ![]()
2) αυξάνεται εάν k > 0 (Εικ. 62), μειώνεται εάν k< 0 (рис. 63);
4) δεν υπάρχει ούτε η μεγαλύτερη ούτε η μικρότερη τιμή.
5) η συνάρτηση είναι συνεχής.
6) ![]()
7) δεν έχει νόημα να μιλάμε για κυρτότητα.
Η γραφική παράσταση της συνάρτησης y = kx 2 είναι μια παραβολή με κορυφή στην αρχή και με κλάδους στραμμένους προς τα πάνω αν k > O (Εικ. 64) και προς τα κάτω αν k< 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.

Ιδιότητες της συνάρτησης y - kx 2:
Για την περίπτωση k> 0 (Εικ. 64):
1) D(f) = (-oo,+oo);
4) = δεν υπάρχει.
5) συνεχής?
6) E(f) = η συνάρτηση μειώνεται και στο διάστημα μειώνεται στην ακτίνα.
7) κυρτό προς τα πάνω.
Η γραφική παράσταση της συνάρτησης y = f(x) απεικονίζεται σημείο προς σημείο. Όσο περισσότερα σημεία της φόρμας (x; f(x)) πάρουμε, τόσο πιο ακριβής θα έχουμε μια ιδέα για το γράφημα. Εάν λάβετε πολλά από αυτά τα σημεία, τότε θα έχετε μια πιο ολοκληρωμένη εικόνα του γραφήματος. Σε αυτήν την περίπτωση, η διαίσθηση μας λέει ότι το γράφημα πρέπει να απεικονίζεται ως μια συμπαγής γραμμή (στην περίπτωση αυτή, με τη μορφή παραβολής). Και μετά, διαβάζοντας το γράφημα, βγάζουμε συμπεράσματα για τη συνέχεια της συνάρτησης, για την κυρτότητά της προς τα κάτω ή προς τα πάνω, για το εύρος τιμών της συνάρτησης. Πρέπει να καταλάβετε ότι από τις αναφερόμενες επτά ιδιότητες, μόνο οι ιδιότητες 1), 2), 3), 4) είναι «νόμιμες» - «νόμιμες» με την έννοια ότι μπορούμε να τις δικαιολογήσουμε κάνοντας αναφορά σε ακριβείς ορισμούς. Έχουμε μόνο οπτικές και διαισθητικές ιδέες για τις υπόλοιπες ιδιότητες. Παρεμπιπτόντως, δεν υπάρχει τίποτα κακό σε αυτό. Από την ιστορία της ανάπτυξης των μαθηματικών είναι γνωστό ότι η ανθρωπότητα συχνά και για μεγάλο χρονικό διάστημα χρησιμοποιούσε διάφορες ιδιότητες ορισμένων αντικειμένων, χωρίς να γνωρίζει τους ακριβείς ορισμούς. Τότε, όταν μπορούσαν να διατυπωθούν τέτοιοι ορισμοί, όλα μπήκαν στη θέση τους. ![]()
Η γραφική παράσταση της συνάρτησης είναι υπερβολή, οι άξονες συντεταγμένων χρησιμεύουν ως ασύμπτωτες της υπερβολής (Εικ. 66, 67).

1) D(f) = (-00,0)1U (0,+oo);
2) αν k > 0, τότε η συνάρτηση μειώνεται στην ανοιχτή ακτίνα (-oo, 0) και στην ανοιχτή ακτίνα (0, +oo) (Εικ. 66). αν να< 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) δεν περιορίζεται ούτε από κάτω ούτε από πάνω.
4) δεν υπάρχει ούτε η μικρότερη ούτε η μεγαλύτερη τιμή.
5) η συνάρτηση είναι συνεχής στην ανοιχτή ακτίνα (-oo, 0) και στην ανοιχτή ακτίνα (0, +oo).
6) E(f) = (-oo,0) U (0,+oo);
7) αν k > 0, τότε η συνάρτηση είναι κυρτή προς τα πάνω στο x< 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х >0, δηλ. στην ανοιχτή δοκό (0, +oo) (Εικ. 66). Αν να< 0, то функция выпукла вверх при х >O και κυρτό προς τα κάτω στο x< О (рис. 67).
Η γραφική παράσταση της συνάρτησης είναι κλάδος παραβολής (Εικ. 68). Ιδιότητες λειτουργίας:
1) D(f) = αυξάνεται στην ακτίνα (σύνολο Α), στη συνέχεια σε αυτήν θα περιοριστεί τόσο πάνω όσο και κάτω.
Πράγματι, για να δείξουμε ότι οριοθετείται από πάνω, πρέπει να εξετάσουμε το κατηγόρημα
και να δείξετε ότι υπάρχει (υπάρχει) τέτοιο M που για όλα τα x που λαμβάνονται στο διάστημα [–2;1], θα είναι αληθές
Η εύρεση ενός τέτοιου Μ δεν είναι δύσκολη. Μπορούμε να υποθέσουμε M = 7, ο ποσοτικός ύπαρξης περιλαμβάνει την εύρεση τουλάχιστον μιας τιμής του M. Η παρουσία ενός τέτοιου M επιβεβαιώνει το γεγονός ότι η συνάρτηση στο διάστημα [–2;1] οριοθετείται από πάνω.
Για να αποδείξουμε ότι οριοθετείται από κάτω, πρέπει να εξετάσουμε το κατηγόρημα
Η τιμή του M που διασφαλίζει την αλήθεια ενός δεδομένου κατηγορήματος είναι, για παράδειγμα, M = –100.
Μπορεί να αποδειχθεί ότι η συνάρτηση θα είναι επίσης περιορισμένη σε συντελεστή: για όλα τα x από το διάστημα [–2;1], οι τιμές της συνάρτησης συμπίπτουν με τις τιμές του , έτσι όπως M μπορούμε να πάρουμε, για για παράδειγμα, η προηγούμενη τιμή M = 7.
Ας δείξουμε ότι η ίδια συνάρτηση, αλλά στο διάστημα, θα είναι απεριόριστη, δηλαδή
Για να δείξετε ότι υπάρχει τέτοιο x, εξετάστε τη δήλωση
Αναζητώντας τις απαιτούμενες τιμές του x μεταξύ των θετικών τιμών του επιχειρήματος, λαμβάνουμε
Αυτό σημαίνει ότι ανεξάρτητα από το θετικό M που πάρουμε, οι τιμές του x εξασφαλίζουν την εκπλήρωση της ανισότητας
προκύπτουν από τη σχέση .
Θεωρώντας μια συνάρτηση σε ολόκληρο τον πραγματικό άξονα, μπορεί να φανεί ότι είναι απεριόριστη σε απόλυτη τιμή.
Πράγματι, από την ανισότητα
Δηλαδή, όσο μεγάλο κι αν είναι το θετικό M, ή θα εξασφαλίσει την εκπλήρωση της ανισότητας .
ΑΚΡΑΙΑ ΛΕΙΤΟΥΡΓΙΑ.
Η συνάρτηση έχει στο σημείο Με τοπικό μέγιστο (ελάχιστο), εάν υπάρχει τέτοια γειτονιά αυτού του σημείου που για Χ¹ Με από αυτή τη γειτονιά ισχύει η ανισότητα
ειδικά ότι το ακραίο σημείο μπορεί να είναι μόνο ένα εσωτερικό σημείο του διαστήματος και το f(x) σε αυτό πρέπει απαραίτητα να οριστεί. Πιθανές περιπτώσεις απουσίας άκρου φαίνονται στο Σχ. 8.8.
Εάν μια συνάρτηση αυξάνεται (μειώνεται) σε ένα συγκεκριμένο διάστημα και μειώνεται (αυξάνεται) σε ένα συγκεκριμένο διάστημα, τότε το σημείο Με είναι ένα τοπικό μέγιστο (ελάχιστο) σημείο.
Απουσία μέγιστου της συνάρτησης f(x) στο σημείο Με μπορεί να διατυπωθεί ως εξής:
_______________________
Η f(x) έχει μέγιστο στο σημείο c
Αυτό σημαίνει ότι αν το σημείο c δεν είναι τοπικό μέγιστο σημείο, τότε όποια και αν είναι η γειτονιά που περιλαμβάνει το σημείο c ως εσωτερικό, θα υπάρχει τουλάχιστον μία τιμή x όχι ίση με c για την οποία . Έτσι, εάν δεν υπάρχει μέγιστο στο σημείο c, τότε σε αυτό το σημείο μπορεί να μην υπάρχει καθόλου άκρο ή μπορεί να είναι ένα ελάχιστο σημείο (Εικ. 8.9).
Η έννοια του ακραίου δίνει μια συγκριτική εκτίμηση της τιμής μιας συνάρτησης σε οποιοδήποτε σημείο σε σχέση με τις κοντινές. Μια παρόμοια σύγκριση τιμών συνάρτησης μπορεί να πραγματοποιηθεί για όλα τα σημεία ενός συγκεκριμένου διαστήματος.
Η ΜΕΓΙΣΤΗ (ΜΙΚΡΟΤΕΡΗ) τιμή μιας συνάρτησης σε ένα σύνολο είναι η τιμή της σε ένα σημείο από αυτό το σύνολο έτσι ώστε – στο . Η μεγαλύτερη τιμή της συνάρτησης επιτυγχάνεται στο εσωτερικό σημείο του τμήματος και η μικρότερη – στο αριστερό άκρο του.
Για να προσδιορίσετε τη μεγαλύτερη (μικρότερη) τιμή μιας συνάρτησης που καθορίζεται σε ένα διάστημα, είναι απαραίτητο να επιλέξετε τον μεγαλύτερο (μικρότερο) αριθμό μεταξύ όλων των τιμών των μέγιστων (ελάχιστων) της, καθώς και των τιμών που γίνονται δεκτές στα άκρα του διαστήματος. Αυτή θα είναι η μεγαλύτερη (μικρότερη) τιμή της συνάρτησης. Αυτός ο κανόνας θα διευκρινιστεί αργότερα.
Το πρόβλημα της εύρεσης της μεγαλύτερης και της μικρότερης τιμής μιας συνάρτησης σε ένα ανοιχτό διάστημα δεν είναι πάντα εύκολο να λυθεί. Για παράδειγμα, η συνάρτηση
στο διάστημα (Εικ. 8.11) δεν τα έχει.
Ας βεβαιωθούμε, για παράδειγμα, ότι αυτή η συνάρτηση δεν έχει τη μεγαλύτερη σημασία. Στην πραγματικότητα, λαμβάνοντας υπόψη τη μονοτονία της συνάρτησης, μπορεί να υποστηριχθεί ότι ανεξάρτητα από το πόσο κοντά θέσουμε τις τιμές του x στα αριστερά της μονάδας, θα υπάρχουν άλλα x στα οποία οι τιμές της συνάρτησης θα να είναι μεγαλύτερη από τις τιμές του στα δεδομένα σταθερά σημεία, αλλά ακόμα μικρότερη από ένα.
1) Τομέας συνάρτησης και εύρος συναρτήσεων.
Ο τομέας μιας συνάρτησης είναι το σύνολο όλων των έγκυρων έγκυρων τιμών ορίσματος Χ(μεταβλητός Χ), για την οποία η συνάρτηση y = f(x)προσδιορίζεται. Το εύρος μιας συνάρτησης είναι το σύνολο όλων των πραγματικών τιμών y, το οποίο αποδέχεται η συνάρτηση.
Στα στοιχειώδη μαθηματικά, οι συναρτήσεις μελετώνται μόνο στο σύνολο των πραγματικών αριθμών.
2) Συναρτήσεις μηδενικά.
Η συνάρτηση μηδέν είναι η τιμή του ορίσματος στο οποίο η τιμή της συνάρτησης είναι ίση με μηδέν.
3) Διαστήματα σταθερού πρόσημου μιας συνάρτησης.
Τα διαστήματα σταθερού πρόσημου μιας συνάρτησης είναι σύνολα τιμών ορισμάτων στα οποία οι τιμές της συνάρτησης είναι μόνο θετικές ή μόνο αρνητικές.
4) Μονοτονία της συνάρτησης.
Μια αυξανόμενη συνάρτηση (σε ένα ορισμένο διάστημα) είναι μια συνάρτηση στην οποία μια μεγαλύτερη τιμή του ορίσματος από αυτό το διάστημα αντιστοιχεί σε μια μεγαλύτερη τιμή της συνάρτησης.
Μια φθίνουσα συνάρτηση (σε ένα ορισμένο διάστημα) είναι μια συνάρτηση στην οποία μια μεγαλύτερη τιμή του ορίσματος από αυτό το διάστημα αντιστοιχεί σε μια μικρότερη τιμή της συνάρτησης.
5) Ζυγή (περιττή) συνάρτηση.
Μια άρτια συνάρτηση είναι μια συνάρτηση της οποίας το πεδίο ορισμού είναι συμμετρικό ως προς την αρχή και για οποιαδήποτε Χαπό το πεδίο ορισμού την ισότητα f(-x) = f(x). Η γραφική παράσταση μιας άρτιας συνάρτησης είναι συμμετρική ως προς την τεταγμένη.
Μια περιττή συνάρτηση είναι μια συνάρτηση της οποίας το πεδίο ορισμού είναι συμμετρικό ως προς την αρχή και για οποιαδήποτε Χαπό τον τομέα του ορισμού η ισότητα είναι αληθής f(-x) = - f(x). Η γραφική παράσταση μιας περιττής συνάρτησης είναι συμμετρική ως προς την προέλευση.
6) Περιορισμένες και απεριόριστες λειτουργίες.
Μια συνάρτηση ονομάζεται δεσμευμένη αν υπάρχει θετικός αριθμός M τέτοιος ώστε |f(x)| ≤ M για όλες τις τιμές του x. Εάν δεν υπάρχει τέτοιος αριθμός, τότε η συνάρτηση είναι απεριόριστη.
7) Περιοδικότητα της συνάρτησης.
Μια συνάρτηση f(x) είναι περιοδική εάν υπάρχει ένας μη μηδενικός αριθμός Τ τέτοιος ώστε για οποιοδήποτε x από το πεδίο ορισμού της συνάρτησης ισχύει το εξής: f(x+T) = f(x). Αυτός ο μικρότερος αριθμός ονομάζεται περίοδος της συνάρτησης. Όλες οι τριγωνομετρικές συναρτήσεις είναι περιοδικές. (Τριγωνομετρικοί τύποι).
19. Βασικές στοιχειώδεις συναρτήσεις, οι ιδιότητες και οι γραφικές παραστάσεις τους. Εφαρμογή συναρτήσεων στα οικονομικά.
Βασικές στοιχειώδεις λειτουργίες. Οι ιδιότητες και τα γραφήματα τους
1. Γραμμική συνάρτηση.
Γραμμική συνάρτηση ονομάζεται συνάρτηση της μορφής , όπου x είναι μεταβλητή, a και b είναι πραγματικοί αριθμοί.
Αριθμός ΕΝΑπου ονομάζεται κλίση της ευθείας, είναι ίση με την εφαπτομένη της γωνίας κλίσης αυτής της ευθείας στη θετική κατεύθυνση του άξονα x. Η γραφική παράσταση μιας γραμμικής συνάρτησης είναι μια ευθεία γραμμή. Ορίζεται από δύο σημεία.
Ιδιότητες μιας Γραμμικής συνάρτησης
1. Τομέας ορισμού - το σύνολο όλων των πραγματικών αριθμών: D(y)=R
2. Το σύνολο των τιμών είναι το σύνολο όλων των πραγματικών αριθμών: E(y)=R
3. Η συνάρτηση παίρνει μηδενική τιμή όταν ή.
4. Η συνάρτηση αυξάνεται (μειώνεται) σε ολόκληρο το πεδίο ορισμού.
5. Μια γραμμική συνάρτηση είναι συνεχής σε όλο το πεδίο ορισμού, διαφοροποιήσιμη και .
2. Τετραγωνική συνάρτηση.
Μια συνάρτηση της μορφής, όπου x είναι μια μεταβλητή, οι συντελεστές a, b, c είναι πραγματικοί αριθμοί, ονομάζεται τετραγωνικός
Πιθανότητα α, β, γπροσδιορίστε τη θέση του γραφήματος στο επίπεδο συντεταγμένων
Ο συντελεστής α καθορίζει την κατεύθυνση των κλάδων. Η γραφική παράσταση μιας τετραγωνικής συνάρτησης είναι παραβολή. Οι συντεταγμένες της κορυφής της παραβολής βρίσκονται χρησιμοποιώντας τους τύπους:
Ιδιότητες λειτουργίας:
2. Ένα σύνολο τιμών για ένα από τα διαστήματα: ή.
3. Η συνάρτηση παίρνει μηδενικές τιμές όταν ![]() , όπου η διάκριση υπολογίζεται με τον τύπο:.
, όπου η διάκριση υπολογίζεται με τον τύπο:.
4. Η συνάρτηση είναι συνεχής σε όλο το πεδίο ορισμού και η παράγωγος της συνάρτησης ισούται με .
- Σε επαφή με 0
- Google+ 0
- Εντάξει 0
- Facebook 0