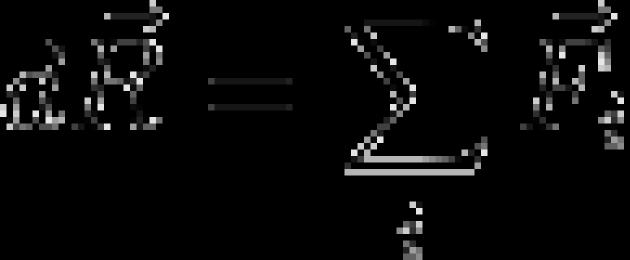Ο νόμος για την αλλαγή της ορμής ενός σημείου. Αλλαγή της ορμής ενός μηχανικού συστήματος

Θέα:αυτό το άρθρο έχει διαβαστεί 14066 φορές

Pdf Επιλογή γλώσσας... Ρωσικά Ουκρανικά Αγγλικά

Σύντομη επισκόπηση

Ολόκληρο το υλικό κατεβάζεται παραπάνω, αφού επιλέξετε τη γλώσσα

Ποσότητα κίνησης

Ορμή ενός υλικού σημείου - διανυσματική ποσότητα ίση με το γινόμενο της μάζας ενός σημείου και του διανύσματος της ταχύτητάς του.

Η μονάδα μέτρησης της ορμής είναι (kg m/s).

Ποσότητα κίνησης μηχανικό σύστημα - διανυσματική ποσότητα ίση με γεωμετρικό άθροισμα(κύριο διάνυσμα) της ορμής ενός μηχανικού συστήματος ισούται με το γινόμενο της μάζας ολόκληρου του συστήματος και την ταχύτητα του κέντρου μάζας του.

Όταν ένα σώμα (ή σύστημα) κινείται έτσι ώστε το κέντρο μάζας του να είναι ακίνητο, τότε το μέγεθος της κίνησης του σώματος είναι ίσο με μηδέν (για παράδειγμα, περιστροφή του σώματος γύρω από σταθερού άξοναπερνώντας από το κέντρο μάζας του σώματος).

Στην περίπτωση σύνθετης κίνησης, το μέγεθος της κίνησης του συστήματος δεν θα χαρακτηρίζει το περιστροφικό τμήμα της κίνησης όταν περιστρέφεται γύρω από το κέντρο μάζας. Δηλαδή, το μέγεθος της κίνησης χαρακτηρίζει μόνο τη μεταφορική κίνηση του συστήματος (μαζί με το κέντρο μάζας).

Δύναμη ώθησης

Η ώθηση μιας δύναμης χαρακτηρίζει τη δράση μιας δύναμης σε μια ορισμένη χρονική περίοδο.

Επιβολή ώθησης σε πεπερασμένο χρονικό διάστημα ορίζεται ως το ολοκληρωτικό άθροισμα των αντίστοιχων στοιχειωδών παλμών.

Θεώρημα για τη μεταβολή της ορμής ενός υλικού σημείου

(σε διαφορικές μορφές μι ):

Η χρονική παράγωγος της ορμής ενός υλικού σημείου είναι ίση με το γεωμετρικό άθροισμα των δυνάμεων που ασκούνται στα σημεία.

(V αναπόσπαστη μορφή ):

Η μεταβολή της ορμής ενός υλικού σημείου σε μια ορισμένη χρονική περίοδο είναι ίση με το γεωμετρικό άθροισμα των παλμών των δυνάμεων που εφαρμόζονται στο σημείο κατά τη διάρκεια αυτής της χρονικής περιόδου.

Θεώρημα για τη μεταβολή της ορμής ενός μηχανικού συστήματος

(σε διαφορική μορφή ):

Η παράγωγος ως προς το χρόνο της ορμής του συστήματος είναι ίση με το γεωμετρικό άθροισμα όλων εξωτερικές δυνάμεις, ενεργώντας στο σύστημα.

(σε ολοκληρωμένη μορφή ):

Η μεταβολή της ορμής ενός συστήματος σε μια ορισμένη χρονική περίοδο είναι ίση με το γεωμετρικό άθροισμα των παλμών των εξωτερικών δυνάμεων που δρουν στο σύστημα κατά τη διάρκεια αυτής της χρονικής περιόδου.

Το θεώρημα επιτρέπει σε κάποιον να αποκλείσει προφανώς άγνωστες εσωτερικές δυνάμεις από την εξέταση.

Το θεώρημα για τη μεταβολή της ορμής ενός μηχανικού συστήματος και το θεώρημα για την κίνηση του κέντρου μάζας είναι δύο διαφορετικές μορφές του ίδιου θεωρήματος.

Νόμος διατήρησης της ορμής ενός συστήματος

1. Αν το άθροισμα όλων των εξωτερικών δυνάμεων που δρουν στο σύστημα είναι ίσο με μηδέν, τότε το διάνυσμα της ορμής του συστήματος θα είναι σταθερό ως προς την κατεύθυνση και το μέγεθος.
2. Εάν το άθροισμα των προβολών όλων των ενεργών εξωτερικών δυνάμεων σε οποιονδήποτε αυθαίρετο άξονα είναι ίσο με μηδέν, τότε η προβολή της ορμής σε αυτόν τον άξονα είναι σταθερή τιμή.

συμπεράσματα:

1. Οι νόμοι διατήρησης δείχνουν ότι οι εσωτερικές δυνάμεις δεν μπορούν να αλλάξουν τη συνολική ποσότητα κίνησης του συστήματος.
2. Το θεώρημα για τη μεταβολή της ορμής ενός μηχανικού συστήματος δεν χαρακτηρίζει την περιστροφική κίνηση ενός μηχανικού συστήματος, αλλά μόνο τη μεταφορική.

Δίνεται ένα παράδειγμα: Προσδιορίστε την ορμή ενός δίσκου ορισμένης μάζας εάν είναι γνωστά η γωνιακή του ταχύτητα και το μέγεθός του.

Παράδειγμα υπολογισμού ενός οδοντωτού τροχού
Ένα παράδειγμα υπολογισμού ενός γραναζιού στροφείου. Η επιλογή του υλικού, ο υπολογισμός των επιτρεπόμενων τάσεων, ο υπολογισμός της επαφής και της αντοχής σε κάμψη έχουν πραγματοποιηθεί.

Ένα παράδειγμα επίλυσης προβλήματος κάμψης δοκού
Στο παράδειγμα, κατασκευάζονται διαγράμματα διατμητικές δυνάμειςκαι ροπές κάμψης, βρέθηκε επικίνδυνο τμήμα και επιλέχθηκε δοκός Ι. Το πρόβλημα ανέλυσε την κατασκευή των διαγραμμάτων χρησιμοποιώντας διαφορικές εξαρτήσεις, που πραγματοποιήθηκε συγκριτική ανάλυσηδιαφορετικές διατομές της δοκού.

Ένα παράδειγμα επίλυσης προβλήματος στρέψης άξονα
Ο στόχος είναι να δοκιμαστεί η αντοχή ενός χαλύβδινου άξονα σε δεδομένη διάμετρο, υλικό και επιτρεπόμενη τάση. Κατά την επίλυση κατασκευάζονται διαγράμματα ροπών, διατμητικές τάσεις και γωνίες συστροφής. Το βάρος του ίδιου του άξονα δεν λαμβάνεται υπόψη

Ένα παράδειγμα επίλυσης προβλήματος τάσης-συμπίεσης ράβδου
Ο στόχος είναι η δοκιμή της αντοχής μιας χαλύβδινης ράβδου σε καθορισμένες επιτρεπόμενες τάσεις. Κατά την επίλυση κατασκευάζονται διαγράμματα διαμήκων δυνάμεων, κανονικών τάσεων και μετατοπίσεων. Το ίδιο το βάρος της ράβδου δεν λαμβάνεται υπόψη

Εφαρμογή του θεωρήματος διατήρησης της κινητικής ενέργειας
Ένα παράδειγμα επίλυσης ενός προβλήματος χρησιμοποιώντας το θεώρημα για τη διατήρηση της κινητικής ενέργειας ενός μηχανικού συστήματος

Προσδιορισμός της ταχύτητας και της επιτάχυνσης ενός σημείου χρησιμοποιώντας δεδομένες εξισώσεις κίνησης
Ένα παράδειγμα επίλυσης ενός προβλήματος για τον προσδιορισμό της ταχύτητας και της επιτάχυνσης ενός σημείου χρησιμοποιώντας δεδομένες εξισώσεις κίνησης

Προσδιορισμός ταχυτήτων και επιταχύνσεων σημείων άκαμπτου σώματος κατά την επίπεδη παράλληλη κίνηση
Παράδειγμα επίλυσης προβλήματος για τον προσδιορισμό των ταχυτήτων και των επιταχύνσεων των σημείων στερεόςσε επίπεδο-παράλληλη κίνηση

Προσδιορισμός δυνάμεων στις ράβδους ενός επίπεδου ζευκτού
Ένα παράδειγμα επίλυσης του προβλήματος του προσδιορισμού των δυνάμεων στις ράβδους ενός επίπεδου ζευκτού χρησιμοποιώντας τη μέθοδο Ritter και τη μέθοδο κοπής κόμβων

Εφαρμογή του θεωρήματος για τη μεταβολή της γωνιακής ορμής
Ένα παράδειγμα επίλυσης ενός προβλήματος χρησιμοποιώντας το θεώρημα της αλλαγής κινητική στιγμήγια τον προσδιορισμό της γωνιακής ταχύτητας ενός σώματος που περιστρέφεται γύρω από έναν σταθερό άξονα.

Το σύστημα που συζητείται στο θεώρημα μπορεί να είναι οποιοδήποτε μηχανικό σύστημα που αποτελείται από οποιαδήποτε σώματα.

Δήλωση του θεωρήματος

Η ποσότητα κίνησης (παλμική) ενός μηχανικού συστήματος είναι μια ποσότητα ίση με το άθροισμα των ποσοτήτων κίνησης (παλμών) όλων των σωμάτων που περιλαμβάνονται στο σύστημα. Η ώθηση των εξωτερικών δυνάμεων που δρουν στα σώματα του συστήματος είναι το άθροισμα των παλμών όλων των εξωτερικών δυνάμεων που δρουν στα σώματα του συστήματος.

( kg m/s)

Λέει το θεώρημα για την αλλαγή της ορμής ενός συστήματος

Η μεταβολή της ορμής του συστήματος σε μια ορισμένη χρονική περίοδο είναι ίση με την ώθηση των εξωτερικών δυνάμεων που δρουν στο σύστημα κατά την ίδια χρονική περίοδο.

Νόμος διατήρησης της ορμής ενός συστήματος

Αν το άθροισμα όλων των εξωτερικών δυνάμεων που δρουν στο σύστημα είναι μηδέν, τότε το μέγεθος της κίνησης (ορμή) του συστήματος είναι σταθερό μέγεθος.

, λαμβάνουμε την έκφραση του θεωρήματος για τη μεταβολή της ορμής του συστήματος σε διαφορική μορφή:

Έχοντας ενσωματώσει και τις δύο πλευρές της προκύπτουσας ισότητας σε μια αυθαίρετα χρονική περίοδο μεταξύ ορισμένων και , λαμβάνουμε την έκφραση του θεωρήματος για τη μεταβολή της ορμής του συστήματος σε ολοκληρωμένη μορφή:

Νόμος διατήρησης της ορμής (Νόμος διατήρησης της ορμής) δηλώνει ότι το διανυσματικό άθροισμα των παλμών όλων των σωμάτων του συστήματος είναι σταθερή τιμή εάν το διανυσματικό άθροισμα των εξωτερικών δυνάμεων που δρουν στο σύστημα είναι ίσο με μηδέν.

(ροπή ορμής m 2 kg s −1)

Θεώρημα για τη μεταβολή της γωνιακής ορμής σε σχέση με το κέντρο

η χρονική παράγωγος της ροπής της ορμής (κινητική ροπή) ενός υλικού σημείου σε σχέση με οποιοδήποτε σταθερό κέντρο είναι ίση με τη στιγμή της δύναμης που ασκείται στο σημείο σε σχέση με το ίδιο κέντρο.

dk 0 /dt = M 0 (φά ) .

Θεώρημα για τη μεταβολή της γωνιακής ορμής σε σχέση με έναν άξονα

η χρονική παράγωγος της ροπής της ορμής (κινητική ροπή) ενός υλικού σημείου σε σχέση με οποιονδήποτε σταθερό άξονα είναι ίση με τη ροπή της δύναμης που ασκείται σε αυτό το σημείο σε σχέση με τον ίδιο άξονα.

dk x /dt = M x (φά ); dk y /dt = M y (φά ); dk z /dt = M z (φά ) .

Ας αναλογιστούμε υλικό σημείο Μ μάζα m , που κινείται υπό την επίδραση της δύναμης φά (Εικόνα 3.1). Ας γράψουμε και ας κατασκευάσουμε το διάνυσμα της γωνιακής ορμής (κινητική ορμή) Μ 0 υλικό σημείο σε σχέση με το κέντρο Ο :

Ας διαφοροποιήσουμε την έκφραση για τη γωνιακή ορμή (κινητική ροπή κ 0) κατά χρόνο:

Επειδή Δρ /dt = V , μετά το διανυσματικό γινόμενο V ⊗ m ⋅ V (συγγραμμικά διανύσματα V Και m ⋅ V ) ισούται με μηδέν. Συγχρόνως δ(μ ⋅ V) /dt = F σύμφωνα με το θεώρημα για την ορμή ενός υλικού σημείου. Επομένως το καταλαβαίνουμε

dk 0 /dt = r ⊗φά , (3.3)

Οπου r ⊗φά = Μ 0 (φά ) – διάνυσμα-ροπή δύναμης φά σε σχέση με ένα σταθερό κέντρο Ο . Διάνυσμα κ 0 ⊥ αεροπλάνο ( r , m ⊗V ), και το διάνυσμα Μ 0 (φά ) ⊥ αεροπλάνο ( r ,φά ), επιτέλους έχουμε

dk 0 /dt = M 0 (φά ) . (3.4)

Η εξίσωση (3.4) εκφράζει το θεώρημα σχετικά με τη μεταβολή της γωνιακής ορμής (γωνιακή ορμή) ενός υλικού σημείου σε σχέση με το κέντρο: η χρονική παράγωγος της ροπής της ορμής (κινητική ροπή) ενός υλικού σημείου σε σχέση με οποιοδήποτε σταθερό κέντρο είναι ίση με τη στιγμή της δύναμης που ασκείται στο σημείο σε σχέση με το ίδιο κέντρο.

Προβάλλοντας την ισότητα (3.4) στους άξονες των καρτεσιανών συντεταγμένων, λαμβάνουμε

dk x /dt = M x (φά ); dk y /dt = M y (φά ); dk z /dt = M z (φά ) . (3.5)

Οι ισότητες (3.5) εκφράζουν το θεώρημα για τη μεταβολή της γωνιακής ορμής (κινητική ορμή) ενός υλικού σημείου σε σχέση με τον άξονα: η χρονική παράγωγος της ροπής της ορμής (κινητική ροπή) ενός υλικού σημείου σε σχέση με οποιονδήποτε σταθερό άξονα είναι ίση με τη ροπή της δύναμης που ασκείται σε αυτό το σημείο σε σχέση με τον ίδιο άξονα.

Ας εξετάσουμε τις συνέπειες που ακολουθούν από τα θεωρήματα (3.4) και (3.5).

Συμπέρασμα 1.Ας εξετάσουμε την περίπτωση όταν η δύναμη φά καθ' όλη τη διάρκεια της κίνησης του σημείου διέρχεται από το ακίνητο κέντρο Ο (περίπτωση κεντρικής δύναμης), δηλ. Οταν Μ 0 (φά ) = 0. Τότε από το Θεώρημα (3.4) προκύπτει ότι κ 0 = συνθ ,

εκείνοι. στην περίπτωση μιας κεντρικής δύναμης, η γωνιακή ορμή (κινητική ροπή) ενός υλικού σημείου σε σχέση με το κέντρο αυτής της δύναμης παραμένει σταθερή σε μέγεθος και κατεύθυνση (Εικόνα 3.2).

Εικόνα 3.2

Από την κατάσταση κ 0 = συνθ έπεται ότι η τροχιά ενός κινούμενου σημείου είναι μια επίπεδη καμπύλη, το επίπεδο της οποίας διέρχεται από το κέντρο αυτής της δύναμης.

Συμπέρασμα 2.Αφήνω Μ z (φά ) = 0, δηλ. δύναμη διασχίζει τον άξονα z ή παράλληλα με αυτό. Στην περίπτωση αυτή, όπως φαίνεται από την τρίτη των εξισώσεων (3.5), κ z = συνθ ,

εκείνοι. αν η ροπή της δύναμης που ασκείται σε ένα σημείο σε σχέση με οποιονδήποτε σταθερό άξονα είναι πάντα μηδέν, τότε η γωνιακή ορμή (κινητική ροπή) του σημείου σε σχέση με αυτόν τον άξονα παραμένει σταθερή.

Απόδειξη του θεωρήματος της μεταβολής της ορμής

Αφήστε το σύστημα να αποτελείται από υλικά σημεία με μάζες και επιταχύνσεις. Διαχωρίζουμε όλες τις δυνάμεις που δρουν στα σώματα του συστήματος σε δύο τύπους:

Οι εξωτερικές δυνάμεις είναι δυνάμεις που δρουν από σώματα που δεν περιλαμβάνονται στο υπό εξέταση σύστημα. Το αποτέλεσμα των εξωτερικών δυνάμεων που δρουν σε ένα υλικό σημείο με αριθμό εγώας υποδηλώσουμε

Οι εσωτερικές δυνάμεις είναι οι δυνάμεις με τις οποίες αλληλεπιδρούν μεταξύ τους τα σώματα του ίδιου του συστήματος. Η δύναμη με την οποία στο σημείο με τον αριθμό εγώισχύει το σημείο με τον αριθμό κ, θα υποδηλώσουμε , και τη δύναμη της επιρροής εγώτο σημείο στο κτο σημείο - . Προφανώς, πότε, τότε

Χρησιμοποιώντας την εισαγόμενη σημείωση, γράφουμε τον δεύτερο νόμο του Νεύτωνα για κάθε ένα από τα υπό εξέταση υλικά σημεία στη μορφή

Λαμβάνοντας υπόψη ότι και αθροίζοντας όλες τις εξισώσεις του δεύτερου νόμου του Νεύτωνα, παίρνουμε:

Η έκφραση αντιπροσωπεύει το άθροισμα όλων των εσωτερικών δυνάμεων που δρουν στο σύστημα. Σύμφωνα με τον τρίτο νόμο του Νεύτωνα, σε αυτό το άθροισμα, κάθε δύναμη αντιστοιχεί σε μια δύναμη τέτοια που, επομένως, ισχύει Εφόσον ολόκληρο το άθροισμα αποτελείται από τέτοια ζεύγη, το ίδιο το άθροισμα είναι μηδέν. Έτσι, μπορούμε να γράψουμε

Χρησιμοποιώντας τον συμβολισμό για την ορμή του συστήματος, παίρνουμε

Εισάγοντας υπόψη τη μεταβολή της ορμής των εξωτερικών δυνάμεων , λαμβάνουμε την έκφραση του θεωρήματος για τη μεταβολή της ορμής του συστήματος σε διαφορική μορφή:

Έτσι, καθεμία από τις τελευταίες εξισώσεις που ελήφθησαν μας επιτρέπει να δηλώσουμε: μια αλλαγή στην ορμή του συστήματος συμβαίνει μόνο ως αποτέλεσμα της δράσης εξωτερικών δυνάμεων και οι εσωτερικές δυνάμεις δεν μπορούν να επηρεάσουν αυτήν την τιμή.

Έχοντας ενσωματώσει και τις δύο πλευρές της προκύπτουσας ισότητας σε ένα αυθαίρετα λαμβανόμενο χρονικό διάστημα μεταξύ μερικών και , λαμβάνουμε την έκφραση του θεωρήματος για την αλλαγή της ορμής του συστήματος σε ακέραια μορφή:

όπου και είναι οι τιμές της ποσότητας κίνησης του συστήματος σε χρονικές στιγμές και, αντίστοιχα, και είναι η ώθηση εξωτερικών δυνάμεων σε μια χρονική περίοδο. Σύμφωνα με όσα ειπώθηκαν προηγουμένως και τις εισαγόμενες σημειώσεις,

Αφήστε ένα υλικό σημείο να κινηθεί υπό την επίδραση δύναμης φά. Απαιτείται ο προσδιορισμός της κίνησης αυτού του σημείου σε σχέση με το κινούμενο σύστημα Oxyz Ο 1 x 1 y 1 z 1 .

(βλ. σύνθετη κίνηση υλικού σημείου), που κινείται με γνωστό τρόπο σε σχέση με ακίνητο σύστημα

Βασική εξίσωση δυναμικής σε ακίνητο σύστημα

Ας γράψουμε την απόλυτη επιτάχυνση ενός σημείου χρησιμοποιώντας το θεώρημα Coriolis Οπου ένακοιλιακούς

Οπου – απόλυτη επιτάχυνση.σχετ

Οπου – σχετική επιτάχυνση.μονοπάτι

Οπου – φορητή επιτάχυνση.πυρήνας

– Επιτάχυνση Coriolis.

Ας ξαναγράψουμε το (25) λαμβάνοντας υπόψη το (26)
Ας εισάγουμε τη σημειογραφία
- φορητή δύναμη αδράνειας,

Η βασική εξίσωση της δυναμικής για τη μελέτη της σχετικής κίνησης (28) γράφεται με τον ίδιο τρόπο όπως και για την απόλυτη κίνηση, μόνο οι δυνάμεις αδράνειας μεταφοράς και Coriolis πρέπει να προστεθούν στις δυνάμεις που δρουν σε ένα σημείο.

Γενικά θεωρήματα για τη δυναμική ενός υλικού σημείου

Κατά την επίλυση πολλών προβλημάτων, μπορείτε να χρησιμοποιήσετε προκατασκευασμένα κενά που λαμβάνονται με βάση τον δεύτερο νόμο του Νεύτωνα. Τέτοιες μέθοδοι επίλυσης προβλημάτων συνδυάζονται σε αυτήν την ενότητα.

Θεώρημα για τη μεταβολή της ορμής ενός υλικού σημείου

Ας παρουσιάσουμε τα ακόλουθα δυναμικά χαρακτηριστικά:

1. Ορμή ενός υλικού σημείου– διανυσματική ποσότητα ίση με το γινόμενο της μάζας ενός σημείου και του διανύσματος της ταχύτητάς του

. (29)

2. Δύναμη παρόρμηση

Στοιχειώδης ώθηση δύναμης– διανυσματική ποσότητα ίση με το γινόμενο του διανύσματος δύναμης και ένα στοιχειώδες χρονικό διάστημα

(30).

Τότε πλήρης ώθηση

. (31)

Στο φά=const που παίρνουμε μικρό=Ft.

Η συνολική ώθηση για μια πεπερασμένη χρονική περίοδο μπορεί να υπολογιστεί μόνο σε δύο περιπτώσεις, όταν η δύναμη που ασκεί σε ένα σημείο είναι σταθερή ή εξαρτάται από το χρόνο. Σε άλλες περιπτώσεις, είναι απαραίτητο να εκφραστεί η δύναμη σε συνάρτηση με το χρόνο.

Η ισότητα των διαστάσεων της ώθησης (29) και της ορμής (30) μας επιτρέπει να δημιουργήσουμε μια ποσοτική σχέση μεταξύ τους.

Ας εξετάσουμε την κίνηση ενός υλικού σημείου Μ κάτω από τη δράση αυθαίρετη δύναμη φάσε μια αυθαίρετη τροχιά.

ΓΙΑ UD:
. (32)

Διαχωρίζουμε τις μεταβλητές στην (32) και ολοκληρώνουμε

. (33)

Ως αποτέλεσμα, λαμβάνοντας υπόψη το (31), λαμβάνουμε

. (34)

Η εξίσωση (34) εκφράζει το ακόλουθο θεώρημα.

Θεώρημα: Η μεταβολή της ορμής ενός υλικού σημείου σε μια ορισμένη χρονική περίοδο είναι ίση με την ώθηση της δύναμης που ασκεί το σημείο στο ίδιο χρονικό διάστημα.

Κατά την επίλυση προβλημάτων, η εξίσωση (34) πρέπει να προβάλλεται στους άξονες συντεταγμένων

Αυτό το θεώρημα είναι βολικό να χρησιμοποιηθεί όταν μεταξύ των δεδομένων και άγνωστων μεγεθών υπάρχει η μάζα ενός σημείου, η αρχική και τελική του ταχύτητα, οι δυνάμεις και ο χρόνος κίνησης.

Θεώρημα για τη μεταβολή της γωνιακής ορμής ενός υλικού σημείου

Μ
στιγμή της ορμής ενός υλικού σημείουσε σχέση με το κέντρο ισούται με το γινόμενο του συντελεστή ορμής του σημείου και του ώμου, δηλ. η μικρότερη απόσταση (κάθετη) από το κέντρο προς τη γραμμή που συμπίπτει με το διάνυσμα της ταχύτητας

, (36)

. (37)

Η σχέση μεταξύ της ροπής της δύναμης (αιτία) και της ροπής της ορμής (αποτέλεσμα) καθορίζεται από το ακόλουθο θεώρημα.

Έστω σημείο Μ μιας δεδομένης μάζας mκινείται υπό την επίδραση της δύναμης φά.

,
,

, (38)

. (39)

Ας υπολογίσουμε την παράγωγο του (39)

. (40)

Συνδυάζοντας το (40) και το (38), παίρνουμε τελικά

. (41)

Η εξίσωση (41) εκφράζει το ακόλουθο θεώρημα.

Θεώρημα: Η χρονική παράγωγος του διανύσματος γωνιακής ορμής ενός υλικού σημείου σε σχέση με κάποιο κέντρο είναι ίση με τη ροπή της δύναμης που ασκεί το σημείο σε σχέση με το ίδιο κέντρο.

Κατά την επίλυση προβλημάτων, η εξίσωση (41) πρέπει να προβάλλεται στους άξονες συντεταγμένων

Στις εξισώσεις (42), οι ροπές ορμής και δύναμης υπολογίζονται σε σχέση με τους άξονες συντεταγμένων.

Από το (41) προκύπτει νόμος διατήρησης της γωνιακής ορμής (νόμος Κέπλερ).

Εάν η ροπή της δύναμης που ασκείται σε ένα υλικό σημείο σε σχέση με κάποιο κέντρο είναι μηδέν, τότε η γωνιακή ορμή του σημείου σε σχέση με αυτό το κέντρο διατηρεί το μέγεθος και την κατεύθυνσή της.

Αν
, Αυτό
.

Το θεώρημα και ο νόμος διατήρησης χρησιμοποιούνται σε προβλήματα που περιλαμβάνουν καμπυλόγραμμη κίνηση, ειδικά υπό τη δράση κεντρικών δυνάμεων.

Ας εξετάσουμε ένα σύστημα που αποτελείται από υλικά σημεία. Ας συνθέσουμε για αυτό το σύστημα διαφορικές εξισώσειςκινήσεις (13) και αθροίστε τις ανά όρο. Μετά παίρνουμε

Το τελευταίο άθροισμα, λόγω της ιδιότητας των εσωτερικών δυνάμεων, είναι ίσο με μηδέν. Εκτός,

Επιτέλους βρίσκουμε

Η εξίσωση (20) εκφράζει το θεώρημα για τη μεταβολή της ορμής του συστήματος σε διαφορική μορφή: η χρονική παράγωγος της ορμής του συστήματος είναι ίση με το γεωμετρικό άθροισμα όλων των εξωτερικών δυνάμεων που δρουν στο σύστημα. Σε προβολές για άξονες συντεταγμένωνθα:

Ας βρούμε μια άλλη έκφραση για το θεώρημα. Έστω τη στιγμή του χρόνου το μέγεθος της κίνησης του συστήματος είναι ίσο και τη στιγμή γίνεται ίσο με . Στη συνέχεια, πολλαπλασιάζοντας και τις δύο πλευρές της ισότητας (20) και ολοκληρώνοντας, παίρνουμε

αφού τα ολοκληρώματα στα δεξιά δίνουν ωθήσεις εξωτερικών δυνάμεων.

Η εξίσωση (21) εκφράζει το θεώρημα για τη μεταβολή της ορμής του συστήματος σε ολοκληρωμένη μορφή: η μεταβολή της ορμής του συστήματος σε μια ορισμένη χρονική περίοδο είναι ίση με το άθροισμα των παλμών που δρουν στο σύστημα εξωτερικών δυνάμεων. την ίδια χρονική περίοδο.

Σε προβολές σε άξονες συντεταγμένων θα υπάρχουν:

Ας επισημάνουμε τη σύνδεση μεταξύ του αποδεδειγμένου θεωρήματος και του θεωρήματος για την κίνηση του κέντρου μάζας. Αφού, λοιπόν, αντικαθιστούμε αυτήν την τιμή με την ισότητα (20) και λαμβάνοντας υπόψη ότι λαμβάνουμε , δηλαδή την εξίσωση (16).

Κατά συνέπεια, το θεώρημα για την κίνηση του κέντρου μάζας και το θεώρημα για τη μεταβολή της ορμής του συστήματος είναι ουσιαστικά δύο διαφορετικά σχήματατο ίδιο θεώρημα. Σε περιπτώσεις όπου μελετάται η κίνηση ενός άκαμπτου σώματος (ή συστήματος σωμάτων), οποιαδήποτε από αυτές τις μορφές μπορεί να χρησιμοποιηθεί εξίσου και η εξίσωση (16) είναι συνήθως πιο βολική στη χρήση. Για ένα συνεχές μέσο (υγρό, αέριο), όταν λύνουν προβλήματα, συνήθως χρησιμοποιούν το θεώρημα της μεταβολής της ορμής του συστήματος. Αυτό το θεώρημα έχει επίσης σημαντικές εφαρμογές στη θεωρία της κρούσης (βλ. Κεφάλαιο XXXI) και στη μελέτη της κίνησης πίδακα (βλ. § 114).

Διαφορική εξίσωση κίνησης υλικού σημείου υπό την επίδραση δύναμης φάμπορεί να αναπαρασταθεί στην ακόλουθη διανυσματική μορφή:

Από τη μάζα ενός σημείου mγίνεται αποδεκτή ως σταθερή, τότε μπορεί να εισαχθεί κάτω από το παράγωγο πρόσημο. Τότε

Ο τύπος (1) εκφράζει το θεώρημα για τη μεταβολή της ορμής ενός σημείου σε διαφορική μορφή: η πρώτη παράγωγος ως προς το χρόνο της ορμής ενός σημείου είναι ίση με τη δύναμη που ασκεί στο σημείο.

Σε προβολές στους άξονες συντεταγμένων (1) μπορεί να αναπαρασταθεί ως

Αν και οι δύο πλευρές (1) πολλαπλασιαστούν επί dt, τότε παίρνουμε μια άλλη μορφή του ίδιου θεωρήματος - το θεώρημα ορμής σε διαφορική μορφή:

εκείνοι. το διαφορικό της ορμής ενός σημείου είναι ίσο με τη στοιχειώδη ώθηση της δύναμης που ασκεί στο σημείο.

Προβάλλοντας και τα δύο μέρη του (2) στους άξονες συντεταγμένων, λαμβάνουμε

Ενσωματώνοντας και τα δύο μέρη του (2) από το μηδέν στο t (Εικ. 1), έχουμε

πού είναι η ταχύτητα του σημείου αυτή τη στιγμή t; - ταχύτητα σε t = 0;

μικρό- παρόρμηση δύναμης με την πάροδο του χρόνου t.

Μια έκφραση στη μορφή (3) ονομάζεται συχνά θεώρημα ορμής σε πεπερασμένη (ή ολοκληρωτική) μορφή: η μεταβολή της ορμής ενός σημείου σε οποιαδήποτε χρονική περίοδο είναι ίση με την ώθηση της δύναμης για την ίδια χρονική περίοδο.

Σε προβολές σε άξονες συντεταγμένων, αυτό το θεώρημα μπορεί να αναπαρασταθεί με την ακόλουθη μορφή:

Για ένα υλικό σημείο, το θεώρημα για την αλλαγή της ορμής σε οποιαδήποτε από τις μορφές ουσιαστικά δεν διαφέρει από τις διαφορικές εξισώσεις κίνησης ενός σημείου.

Θεώρημα για τη μεταβολή της ορμής ενός συστήματος

Η ποσότητα κίνησης του συστήματος θα ονομάζεται διανυσματική ποσότητα Q, ίσο με το γεωμετρικό άθροισμα (κύριο διάνυσμα) των ποσών κίνησης όλων των σημείων του συστήματος.

Σκεφτείτε ένα σύστημα που αποτελείται από n υλικά σημεία. Ας συνθέσουμε διαφορικές εξισώσεις κίνησης για αυτό το σύστημα και ας τις προσθέσουμε ανά όρο. Τότε παίρνουμε:

Το τελευταίο άθροισμα, λόγω της ιδιότητας των εσωτερικών δυνάμεων, είναι ίσο με μηδέν. Εκτός,

Τελικά βρίσκουμε:

Η εξίσωση (4) εκφράζει το θεώρημα για τη μεταβολή της ορμής του συστήματος σε διαφορική μορφή: η χρονική παράγωγος της ορμής του συστήματος είναι ίση με το γεωμετρικό άθροισμα όλων των εξωτερικών δυνάμεων που δρουν στο σύστημα.

Ας βρούμε μια άλλη έκφραση για το θεώρημα. Αφήστε τη στιγμή t= 0 το μέγεθος της κίνησης του συστήματος είναι Q 0, και τη στιγμή του χρόνου t 1γίνεται ίσος Ε 1.Στη συνέχεια, πολλαπλασιάζοντας και τις δύο πλευρές της ισότητας (4) επί dtκαι ενσωματώνοντας, παίρνουμε:

Ή πού:

(S- ώθηση δύναμης)

αφού τα ολοκληρώματα στα δεξιά δίνουν ωθήσεις εξωτερικών δυνάμεων,

Η εξίσωση (5) εκφράζει το θεώρημα για τη μεταβολή της ορμής του συστήματος σε ολοκληρωμένη μορφή: η μεταβολή της ορμής του συστήματος σε μια ορισμένη χρονική περίοδο είναι ίση με το άθροισμα των παλμών των εξωτερικών δυνάμεων που δρουν στο σύστημα κατά την ίδια χρονική περίοδο.

Σε προβολές στους άξονες συντεταγμένων θα έχουμε:

Νόμος διατήρησης της ορμής

Από το θεώρημα της μεταβολής της ορμής ενός συστήματος, μπορούν να προκύψουν τα ακόλουθα σημαντικά συμπεράσματα:

1. Έστω το άθροισμα όλων των εξωτερικών δυνάμεων που δρουν στο σύστημα ίσο με μηδέν:

Τότε από την εξίσωση (4) προκύπτει ότι στην περίπτωση αυτή Q = συνεχ.

Ετσι, αν το άθροισμα όλων των εξωτερικών δυνάμεων που δρουν στο σύστημα είναι ίσο με μηδέν, τότε το διάνυσμα της ορμής του συστήματος θα είναι σταθερό σε μέγεθος και κατεύθυνση.

2. 01 Έστω οι εξωτερικές δυνάμεις που δρουν στο σύστημα τέτοιες ώστε το άθροισμα των προβολών τους σε κάποιον άξονα (για παράδειγμα Ox) να είναι ίσο με μηδέν:

Τότε από τις εξισώσεις (4`) προκύπτει ότι στην περίπτωση αυτή Q = συνεχ.

Ετσι, αν το άθροισμα των προβολών όλων των ενεργών εξωτερικών δυνάμεων σε οποιονδήποτε άξονα είναι ίσο με μηδέν, τότε η προβολή της ποσότητας κίνησης του συστήματος σε αυτόν τον άξονα είναι σταθερή τιμή.

Αυτά τα αποτελέσματα εκφράζουν νόμος διατήρησης της ορμής ενός συστήματος.Από αυτά προκύπτει ότι οι εσωτερικές δυνάμεις δεν μπορούν να αλλάξουν τη συνολική ποσότητα κίνησης του συστήματος.

Ας δούμε μερικά παραδείγματα:

· Φαινόμενο για την επιστροφή του ρολού. Αν θεωρήσουμε το τουφέκι και τη σφαίρα ως ένα σύστημα, τότε η πίεση των αερίων σκόνης κατά τη διάρκεια μιας βολής θα είναι μια εσωτερική δύναμη. Αυτή η δύναμη δεν μπορεί να αλλάξει τη συνολική ορμή του συστήματος. Αλλά δεδομένου ότι τα αέρια σκόνης, που δρουν στη σφαίρα, της προσδίδουν μια συγκεκριμένη ποσότητα κίνησης που κατευθύνεται προς τα εμπρός, πρέπει ταυτόχρονα να προσδώσουν στο τουφέκι την ίδια ποσότητα κίνησης αντίστροφη κατεύθυνση. Αυτό θα κάνει το τουφέκι να κινηθεί προς τα πίσω, δηλ. η λεγόμενη επιστροφή. Παρόμοιο φαινόμενο συμβαίνει κατά την πυροδότηση όπλου (rollback).

· Λειτουργία της προπέλας (προπέλα). Η προπέλα μεταδίδει κίνηση σε μια ορισμένη μάζα αέρα (ή νερού) κατά μήκος του άξονα της προπέλας, ρίχνοντας αυτή τη μάζα πίσω. Αν θεωρήσουμε την εκτοξευόμενη μάζα και το αεροσκάφος (ή το πλοίο) ως ένα σύστημα, τότε οι δυνάμεις αλληλεπίδρασης μεταξύ της προπέλας και του περιβάλλοντος, ως εσωτερικές, δεν μπορούν να αλλάξουν τη συνολική ποσότητα κίνησης αυτού του συστήματος. Επομένως, όταν μια μάζα αέρα (νερού) εκτινάσσεται προς τα πίσω, το αεροσκάφος (ή το πλοίο) λαμβάνει μια αντίστοιχη ταχύτητα προς τα εμπρός τέτοια ώστε το συνολικό ποσό κίνησης του υπό εξέταση συστήματος παραμένει ίσο με μηδέν, αφού ήταν μηδέν πριν ξεκινήσει η κίνηση .

Παρόμοιο αποτέλεσμα επιτυγχάνεται με τη δράση κουπιών ή τροχών με κουπιά.

· R e c t i v e Πρόωση Σε έναν πύραυλο (πύραυλο), τα αέρια προϊόντα της καύσης του καυσίμου εκτινάσσονται με μεγάλη ταχύτητα από την οπή στην ουρά του πυραύλου (από το ακροφύσιο του κινητήρα τζετ). Οι δυνάμεις πίεσης που δρουν σε αυτή την περίπτωση θα είναι εσωτερικές δυνάμεις και δεν μπορούν να αλλάξουν τη συνολική ορμή του συστήματος αερίων πυραύλων-σκόνης. Όμως, δεδομένου ότι τα αέρια που διαφεύγουν έχουν μια συγκεκριμένη ποσότητα κίνησης που κατευθύνεται προς τα πίσω, ο πύραυλος λαμβάνει μια αντίστοιχη ταχύτητα προς τα εμπρός.

Θεώρημα ροπών γύρω από άξονα.

Εξετάστε το υλικό σημείο μάζας m, που κινείται υπό την επίδραση της δύναμης φά. Ας βρούμε γι' αυτό τη σχέση μεταξύ της ροπής των διανυσμάτων mVΚαι φάσε σχέση με κάποιο σταθερό άξονα Ζ.

m z (F) = xF - yF (7)

Ομοίως για την αξία m(mV), εάν αφαιρεθεί mθα είναι εκτός παρένθεσης

m z (mV) = m(xV - yV)(7`)

Λαμβάνοντας τις παράγωγες ως προς το χρόνο και από τις δύο πλευρές αυτής της ισότητας, βρίσκουμε

Στη δεξιά πλευρά της παράστασης που προκύπτει, η πρώτη αγκύλη είναι ίση με 0, αφού dx/dt=V και dу/dt = V, η δεύτερη αγκύλη σύμφωνα με τον τύπο (7) είναι ίση με

mz(F), αφού σύμφωνα με τον βασικό νόμο της δυναμικής:

Επιτέλους θα έχουμε (8)

Η εξίσωση που προκύπτει εκφράζει το θεώρημα των ροπών γύρω από τον άξονα: η χρονική παράγωγος της ροπής ορμής ενός σημείου σε σχέση με οποιονδήποτε άξονα είναι ίση με τη ροπή δρούσα δύναμηπερίπου στον ίδιο άξονα.Ένα παρόμοιο θεώρημα ισχύει για στιγμές για οποιοδήποτε κέντρο Ο.