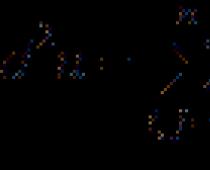Προσθήκη μήτραςΤο $ A $ και το $ B $ είναι μια αριθμητική πράξη, ως αποτέλεσμα της οποίας θα πρέπει να ληφθεί ο πίνακας $ C $, κάθε στοιχείο του οποίου είναι ίσο με το άθροισμα των αντίστοιχων στοιχείων των πινάκων που προστίθενται:
$$ c_(ij) = a_(ij) + b_(ij) $$
Περισσότερες λεπτομέρειες Ο τύπος για την προσθήκη δύο πινάκων μοιάζει με αυτό:
$$ A + B = \begin(pmatrix) a_(11) & a_(12) & a_(13) \\ a_(21) & a_(22) & a_(23) \\ a_(31) & a_( 32) & a_(33) \end(pmatrix) + \begin(pmatrix) b_(11) & b_(12) & b_(13) \\ b_(21) & b_(22) & b_(23) \\ b_(31) & b_(32) & b_(33) \end(pmatrix) = $$
$$ = \begin(pmatrix) a_(11) + b_(11) & a_(12)+b_(12) & a_(13)+b_(13) \\ a_(21)+b_(21) & a_ (22)+b_(22) & a_(23)+b_(23) \\ a_(31)+b_(31) & a_(32)+b_(32) & a_(33)+b_(33) \ end(pmatrix) = C$$
Λάβετε υπόψη ότι μπορείτε να προσθέσετε και να αφαιρέσετε μόνο πίνακες της ίδιας διάστασης. Με το άθροισμα ή τη διαφορά, το αποτέλεσμα θα είναι ένας πίνακας $ C $ της ίδιας διάστασης με τους όρους (αφαιρούμενους) των πινάκων $ A $ και $ B $. Εάν οι πίνακες $ A $ και $ B $ διαφέρουν μεταξύ τους σε μέγεθος, τότε η προσθήκη (αφαίρεση) τέτοιων πινάκων θα είναι σφάλμα!
Ο τύπος προσθέτει πίνακες 3 επί 3, πράγμα που σημαίνει ότι το αποτέλεσμα πρέπει να είναι ένας πίνακας 3 επί 3.
Αφαίρεση πινάκωνεντελώς παρόμοιο με τον αλγόριθμο πρόσθεσης, μόνο με πρόσημο μείον. Κάθε στοιχείο του απαιτούμενου πίνακα $C$ προκύπτει αφαιρώντας τα αντίστοιχα στοιχεία των πινάκων $A$ και $B$:
$$ c_(ij) = a_(ij) - b_(ij) $$
Ας γράψουμε τα αναλυτικά τύπος για την αφαίρεση δύο πινάκων:
$$ A - B = \begin(pmatrix) a_(11) & a_(12) & a_(13) \\ a_(21) & a_(22) & a_(23) \\ a_(31) & a_( 32) & a_(33) \end(pmatrix) - \begin(pmatrix) b_(11) & b_(12) & b_(13) \\ b_(21) & b_(22) & b_(23) \\ b_(31) & b_(32) & b_(33) \end(pmatrix) = $$
$$ = \begin(pmatrix) a_(11) - b_(11) & a_(12)-b_(12) & a_(13)-b_(13) \\ a_(21)-b_(21) & a_ (22)-b_(22) & a_(23)-b_(23) \\ a_(31)-b_(31) & a_(32)-b_(32) & a_(33)-b_(33) \ end(pmatrix) = C$$
Αξίζει επίσης να σημειωθεί ότι δεν μπορείτε να προσθέσετε και να αφαιρέσετε πίνακες με συνηθισμένους αριθμούς, καθώς και με ορισμένα άλλα στοιχεία
Θα είναι χρήσιμο να γνωρίζουμε τις ιδιότητες της πρόσθεσης (αφαίρεσης) για περαιτέρω λύσεις σε προβλήματα με πίνακες.
Σκηνικά θέατρου
- Εάν οι πίνακες $ A,B,C $ έχουν το ίδιο μέγεθος, τότε η ιδιότητα συσχέτισης ισχύει για αυτούς: $$ A + (B + C) = (A + B) + C $$
- Για κάθε πίνακα υπάρχει ένας μηδενικός πίνακας, που συμβολίζεται $ O $, μετά την πρόσθεση (αφαίρεση) με τον οποίο ο αρχικός πίνακας δεν αλλάζει: $$ A \pm O = A $$
- Για κάθε μη μηδενικό πίνακα $ A $ υπάρχει ένας αντίθετος πίνακας $ (-A) $ του οποίου το άθροισμα εξαφανίζεται: $ $ A + (-A) = 0 $ $
- Κατά την προσθήκη (αφαίρεση) πινάκων, επιτρέπεται η ιδιότητα της ανταλλαξιμότητας, δηλαδή, οι πίνακες $ A $ και $ B $ μπορούν να αντικατασταθούν: $$ A + B = B + A $$ $$ A - B = B - A $$
Παραδείγματα λύσεων
| Παράδειγμα 1 |
|
Δίνονται πίνακες $ A = \begin(pmatrix) 2&3 \\ -1& 4 \end(pmatrix) $ και $ B = \begin(pmatrix) 1&-3 \\ 2&5 \end(pmatrix) $. Εκτελέστε πρόσθεση πινάκων και μετά αφαίρεση. |
| Διάλυμα |
|
Πρώτα απ 'όλα, ελέγχουμε τους πίνακες για διάσταση. Ο πίνακας $ A $ έχει διάσταση $ 2 \ φορές 2 $, ο δεύτερος πίνακας $ B $ έχει διάσταση $ 2 \ φορές 2 $. Αυτό σημαίνει ότι με αυτούς τους πίνακες είναι δυνατό να πραγματοποιηθεί μια κοινή πράξη πρόσθεσης και αφαίρεσης. Θυμηθείτε ότι για το άθροισμα είναι απαραίτητο να πραγματοποιηθεί κατά ζεύγη πρόσθεση των αντίστοιχων στοιχείων των πινάκων $ A \text( και ) B $. $$ A + B = \begin(pmatrix) 2&3 \\ -1& 4 \end(pmatrix) + \begin(pmatrix) 1&-3 \\ 2&5 \end(pmatrix) = $$ $$ = \begin(pmatrix) 2 + 1 & 3 + (-3) \\ -1 + 2 & 4 + 5 \end(pmatrix) = \begin(pmatrix) 3 & 0 \\ 1 & 9 \end( pmatrix)$$ Ομοίως με το άθροισμα, βρίσκουμε τη διαφορά των πινάκων αντικαθιστώντας το πρόσημο «συν» με ένα «μείον»: $$ A - B = \begin(pmatrix) 2&3 \\ -1& 4 \end(pmatrix) + \begin(pmatrix) 1&-3 \\ 2&5 \end(pmatrix) = $$ $$ = \begin(pmatrix) 2 - 1 & 3 - (-3) \\ -1 - 2 & 4 - 5 \end(pmatrix) = \begin(pmatrix) 1 & 6 \\ -3 & -1 \ end(pmatrix)$$ Εάν δεν μπορείτε να λύσετε το πρόβλημά σας, στείλτε το σε εμάς. Θα δώσουμε λεπτομερή λύση. Θα μπορείτε να δείτε την πρόοδο του υπολογισμού και να λάβετε πληροφορίες. Αυτό θα σας βοηθήσει να πάρετε τον βαθμό σας από τον δάσκαλό σας έγκαιρα! |
| Απάντηση |
|
$$ A + B = \begin(pmatrix) 3 & 0 \\ 1 & 9 \end(pmatrix); A - B = \begin(pmatrix) 1 & 6 \\ -3 & -1 \end(pmatrix) $$ |
Στο άρθρο: «Πρόσθεση και αφαίρεση πινάκων» δόθηκαν ορισμοί, κανόνες, σχόλια, ιδιότητες πράξεων και πρακτικά παραδείγματα λύσεων.
Ορισμός.Προϊόν δύο πινάκων ΕΝΑΚαι ΣΕονομάζεται μήτρα ΜΕ, το στοιχείο του οποίου βρίσκεται στη διασταύρωση εγώη γραμμή και ιη στήλη, ίσο με το άθροισμα των γινομένων των στοιχείων εγώη σειρά του πίνακα ΕΝΑστα αντίστοιχα (κατά σειρά) στοιχεία ιη στήλη μήτρας ΣΕ.
Από αυτόν τον ορισμό ακολουθεί ο τύπος του στοιχείου μήτρας ντο:
Προϊόν μήτρας ΕΝΑστη μήτρα ΣΕσυμβολίζεται με ΑΒ.
Παράδειγμα 1.Βρείτε το γινόμενο δύο πινάκων ΕΝΑΚαι σι, Αν
![]() ,
,
 .
.
Διάλυμα. Είναι βολικό να βρείτε το γινόμενο δύο πινάκων ΕΝΑΚαι ΣΕγράψτε όπως στο Σχ. 2:

Στο διάγραμμα, τα γκρι βέλη υποδεικνύουν ποιες σειρές του πίνακα είναι στοιχεία ΕΝΑστα στοιχεία ποιας στήλης του πίνακα ΣΕπρέπει να πολλαπλασιαστεί για να ληφθούν στοιχεία μήτρας ΜΕ, και οι γραμμές είναι τα χρώματα του στοιχείου μήτρας ντοσυνδέονται τα αντίστοιχα στοιχεία μήτρας ΕΝΑΚαι σι, των οποίων τα προϊόντα προστίθενται για να ληφθεί ένα στοιχείο μήτρας ντο.
Ως αποτέλεσμα, λαμβάνουμε τα στοιχεία του προϊόντος μήτρας:
Τώρα έχουμε τα πάντα για να γράψουμε το γινόμενο δύο πινάκων:
![]() .
.
Προϊόν δύο πινάκων ΑΒέχει νόημα μόνο εάν ο αριθμός των στηλών του πίνακα ΕΝΑσυμπίπτει με τον αριθμό των σειρών του πίνακα ΣΕ.
Αυτή η σημαντική λειτουργία θα είναι πιο εύκολο να θυμάστε εάν χρησιμοποιείτε πιο συχνά τις ακόλουθες υπενθυμίσεις:
Υπάρχει ένα άλλο σημαντικό χαρακτηριστικό του γινομένου των πινάκων σε σχέση με τον αριθμό των γραμμών και στηλών:
Στο γινόμενο των πινάκων ΑΒο αριθμός των σειρών είναι ίσος με τον αριθμό των σειρών του πίνακα ΕΝΑ, και ο αριθμός των στηλών είναι ίσος με τον αριθμό των στηλών μήτρας ΣΕ .
Παράδειγμα 2.Βρείτε τον αριθμό των γραμμών και στηλών ενός πίνακα ντο, που είναι το γινόμενο δύο πινάκων ΕΝΑΚαι σιοι ακόλουθες διαστάσεις:
α) 2 Χ 10 και 10 Χ 5.
β) 10 Χ 2 και 2 Χ 5;
Παράδειγμα 3.Βρείτε το γινόμενο των πινάκων ΕΝΑΚαι σι, Εάν:
 .
.
ΕΝΑ σι- 2. Επομένως, η διάσταση του πίνακα ντο = ΑΒ- 2 Χ 2.
Υπολογισμός στοιχείων μήτρας ντο = ΑΒ.

Βρέθηκε γινόμενο πινάκων: .
Μπορείτε να ελέγξετε τη λύση σε αυτό και άλλα παρόμοια προβλήματα στη διεύθυνση ηλεκτρονικός υπολογιστής προϊόντων matrix .
Παράδειγμα 5.Βρείτε το γινόμενο των πινάκων ΕΝΑΚαι σι, Εάν:
 .
.
Διάλυμα. Αριθμός σειρών στον πίνακα ΕΝΑ- 2, αριθμός στηλών στον πίνακα σι ντο = ΑΒ- 2 Χ 1.
Υπολογισμός στοιχείων μήτρας ντο = ΑΒ.
![]()
Το γινόμενο των πινάκων θα γραφεί ως πίνακας στήλης: .
Μπορείτε να ελέγξετε τη λύση σε αυτό και άλλα παρόμοια προβλήματα στη διεύθυνση ηλεκτρονικός υπολογιστής προϊόντων matrix .
Παράδειγμα 6.Βρείτε το γινόμενο των πινάκων ΕΝΑΚαι σι, Εάν:
 .
.
Διάλυμα. Αριθμός σειρών στον πίνακα ΕΝΑ- 3, αριθμός στηλών στον πίνακα σι- 3. Επομένως, η διάσταση του πίνακα ντο = ΑΒ- 3 Χ 3.
Υπολογισμός στοιχείων μήτρας ντο = ΑΒ.
Το προϊόν που βρέθηκε των πινάκων:  .
.
Μπορείτε να ελέγξετε τη λύση σε αυτό και άλλα παρόμοια προβλήματα στη διεύθυνση ηλεκτρονικός υπολογιστής προϊόντων matrix .
Παράδειγμα 7.Βρείτε το γινόμενο των πινάκων ΕΝΑΚαι σι, Εάν:
 .
.
Διάλυμα. Αριθμός σειρών στον πίνακα ΕΝΑ- 1, αριθμός στηλών στον πίνακα σι- 1. Επομένως, η διάσταση του πίνακα ντο = ΑΒ- 1 Χ 1.
Υπολογισμός του στοιχείου μήτρας ντο = ΑΒ.
Το γινόμενο των πινάκων είναι ένας πίνακας ενός στοιχείου: .
Μπορείτε να ελέγξετε τη λύση σε αυτό και άλλα παρόμοια προβλήματα στη διεύθυνση ηλεκτρονικός υπολογιστής προϊόντων matrix .
Η εφαρμογή λογισμικού του γινομένου δύο πινάκων σε C++ συζητείται στο αντίστοιχο άρθρο στο μπλοκ «Υπολογιστές και προγραμματισμός».
Εκτίμηση μήτραςΗ εκθετικότητα πίνακα ορίζεται ως ο πολλαπλασιασμός ενός πίνακα με τον ίδιο πίνακα. Δεδομένου ότι ένα γινόμενο πινάκων υπάρχει μόνο όταν ο αριθμός των στηλών του πρώτου πίνακα συμπίπτει με τον αριθμό των γραμμών του δεύτερου πίνακα, μόνο οι τετράγωνοι πίνακες μπορούν να αυξηθούν σε ισχύ. nη δύναμη ενός πίνακα πολλαπλασιάζοντας τον πίνακα με τον εαυτό του nμια φορά:

Παράδειγμα 8.Δίνεται μια μήτρα. Εύρημα ΕΝΑ² και ΕΝΑ³ .


Βρείτε μόνοι σας το προϊόν μήτρας και μετά δείτε τη λύση
Παράδειγμα 9.Δίνεται μια μήτρα ![]()
Να βρείτε το γινόμενο του δεδομένου πίνακα και του μετατιθέμενου πίνακα, το γινόμενο του μετατιθέμενου πίνακα και του δεδομένου πίνακα.
Ιδιότητες του γινομένου δύο πινάκωνΙδιοκτησία 1. Το γινόμενο οποιουδήποτε πίνακα Α και του πίνακα ταυτότητας Ε της αντίστοιχης σειράς, τόσο στα δεξιά όσο και στα αριστερά, συμπίπτει με τον πίνακα Α, δηλ. ΑΕ = ΕΑ = Α.
Με άλλα λόγια, ο ρόλος του μοναδιαίου πίνακα στον πολλαπλασιασμό του πίνακα είναι ο ίδιος με τον ρόλο των μονάδων στον πολλαπλασιασμό αριθμών.
Παράδειγμα 10.Βεβαιωθείτε ότι η ιδιότητα 1 είναι αληθής βρίσκοντας τα προϊόντα του πίνακα
![]()
στον πίνακα ταυτότητας δεξιά και αριστερά.
Διάλυμα. Από τη μήτρα ΕΝΑπεριέχει τρεις στήλες, τότε πρέπει να βρείτε το προϊόν ΑΕ, Πού
 -
-
μήτρα ταυτότητας τρίτης τάξης. Ας βρούμε τα στοιχεία του έργου ΜΕ = ΑΕ :
Αποδεικνύεται ότι ΑΕ = ΕΝΑ .
Τώρα ας βρούμε το προϊόν EA, Πού μιείναι ένας πίνακας ταυτότητας δεύτερης τάξης, αφού ο πίνακας Α περιέχει δύο σειρές. Ας βρούμε τα στοιχεία του έργου ΜΕ = EA :
![]()
Προσθήκη μήτρας:
Αφαίρεση και πρόσθεση πινάκωνανάγεται στις αντίστοιχες πράξεις στα στοιχεία τους. Λειτουργία προσθήκης μήτραςεισήχθη μόνο για μήτρεςτο ίδιο μέγεθος, δηλαδή για μήτρες, όπου ο αριθμός των γραμμών και των στηλών είναι αντίστοιχα ίσος. Άθροισμα πινάκωνΤα Α και Β λέγονται μήτραΓ, του οποίου τα στοιχεία είναι ίσα με το άθροισμα των αντίστοιχων στοιχείων. C = A + B c ij = a ij + b ij Ορίζεται ομοίως διαφορά μήτρας.
Πολλαπλασιάζοντας έναν πίνακα με έναν αριθμό:
Πράξη πολλαπλασιασμού (διαίρεσης) μήτραςοποιουδήποτε μεγέθους με έναν αυθαίρετο αριθμό ανάγεται στον πολλαπλασιασμό (διαίρεση) κάθε στοιχείου μήτρεςγια αυτόν τον αριθμό. Προϊόν μήτραςΚαι ο αριθμός k ονομάζεται μήτραΒ, έτσι ώστε
b ij = k × a ij . B = k × A b ij = k × a ij . Μήτρα- A = (-1) × A λέγεται το αντίθετο μήτραΕΝΑ.
Ιδιότητες πρόσθεσης πινάκων και πολλαπλασιασμού ενός πίνακα με έναν αριθμό:
Πράξεις προσθήκης μήτραςΚαι πολλαπλασιασμός μήτραςσε έναν αριθμό έχουν τις ακόλουθες ιδιότητες: 1. A + B = B + A; 2. A + (B + C) = (A + B) + C; 3. A + 0 = A; 4. A - A = 0; 5. 1 × A = A; 6. α × (Α + Β) = αΑ + αΒ; 7. (α + β) × Α = αΑ + βΑ; 8. α × (βΑ) = (αβ) × Α; , όπου τα Α, Β και Γ είναι πίνακες, τα α και β είναι αριθμοί.
Πολλαπλασιασμός μήτρας (Γιόν μήτρας):
Λειτουργία πολλαπλασιασμού δύο πινάκωνκαταχωρείται μόνο για την περίπτωση που ο αριθμός των στηλών του πρώτου μήτρεςίσο με τον αριθμό των γραμμών του δεύτερου μήτρες. Προϊόν μήτραςΚαι m×n σε μήτραΣε n×p, καλείται μήτραΜε m×p τέτοιο ώστε με ik = a i1 × b 1k + a i2 × b 2k + ... + a σε × b nk , δηλ., βρίσκεται το άθροισμα των γινομένων των στοιχείων της i-ης σειράς μήτρεςΚαι στα αντίστοιχα στοιχεία της jης στήλης μήτρεςΒ. Αν μήτρεςΤα Α και Β είναι τετράγωνα ίδιου μεγέθους, τότε τα γινόμενα ΑΒ και ΒΑ υπάρχουν πάντα. Είναι εύκολο να δείξουμε ότι A × E = E × A = A, όπου το A είναι τετράγωνο μήτρα, E - μονάδα μήτρατο ίδιο μέγεθος.

Ιδιότητες πολλαπλασιασμού πίνακα:
Πολλαπλασιασμός πίνακαόχι ανταλλακτική, δηλ. AB ≠ BA ακόμα και αν ορίζονται και τα δύο προϊόντα. Ωστόσο, εάν για κανένα μήτρεςη σχέση ΑΒ=ΒΑ ικανοποιείται, τότε τέτοια μήτρεςονομάζονται ανταλλακτική. Το πιο χαρακτηριστικό παράδειγμα είναι ένα single μήτρα, που μετακινείται με οποιοδήποτε άλλο μήτρατο ίδιο μέγεθος. Μόνο τα τετράγωνα μπορούν να είναι μεταβλητά μήτρεςτης ίδιας τάξης. Α × Ε = Ε × Α = Α
Πολλαπλασιασμός πίνακαέχει τις ακόλουθες ιδιότητες: 1. A × (B × C) = (A × B) × C; 2. A × (B + C) = AB + AC; 3. (A + B) × C = AC + BC; 4. α × (ΑΒ) = (αΑ) × Β; 5. A × 0 = 0; 0 × A = 0; 6. (AB) T = B T A T; 7. (ABC) T = C T V T A T; 8. (Α + Β) Τ = Α Τ + Β Τ;

2. Ορίζουσες 2ης και 3ης τάξης. Ιδιότητες προσδιοριστικών παραγόντων.
Καθοριστική μήτραδεύτερη τάξη, ή καθοριστικόςδεύτερη σειρά είναι ένας αριθμός που υπολογίζεται από τον τύπο:

Καθοριστική μήτρατρίτης τάξης, ή καθοριστικόςτρίτη τάξη είναι ένας αριθμός που υπολογίζεται από τον τύπο:

Αυτός ο αριθμός αντιπροσωπεύει ένα αλγεβρικό άθροισμα που αποτελείται από έξι όρους. Κάθε όρος περιέχει ακριβώς ένα στοιχείο από κάθε γραμμή και κάθε στήλη μήτρες. Κάθε όρος αποτελείται από το γινόμενο τριών παραγόντων.

Σημάδια με τα οποία τα μέλη ορίζουσα του πίνακαπεριλαμβάνονται στον τύπο βρίσκοντας την ορίζουσα του πίνακαΗ τρίτη τάξη μπορεί να προσδιοριστεί χρησιμοποιώντας το δεδομένο σχήμα, το οποίο ονομάζεται κανόνας τριγώνων ή κανόνας Sarrus. Οι τρεις πρώτοι όροι λαμβάνονται με πρόσημο συν και προσδιορίζονται από το αριστερό σχήμα και οι επόμενοι τρεις όροι λαμβάνονται με αρνητικό πρόσημο και προσδιορίζονται από το δεξί σχήμα.
Προσδιορίστε τον αριθμό των όρων που θέλετε να βρείτε ορίζουσα του πίνακα, σε αλγεβρικό άθροισμα, μπορείτε να υπολογίσετε το παραγοντικό: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6
Ιδιότητες προσδιοριστικών πινάκων
Ιδιότητες προσδιοριστικών πινάκων:
Ιδιοκτησία #1:
Καθοριστική μήτραδεν θα αλλάξει εάν οι σειρές της αντικατασταθούν με στήλες, κάθε γραμμή με μια στήλη με τον ίδιο αριθμό και αντίστροφα (Μεταφορά). |Α| = |Α| Τ
Συνέπεια:
Στήλες και γραμμές ορίζουσα του πίνακαείναι ίσες, επομένως, οι ιδιότητες που είναι εγγενείς στις γραμμές πληρούνται και για τις στήλες.
Ιδιοκτησία #2:
Κατά την αναδιάταξη 2 σειρών ή στηλών ορίζουσα μήτραςθα αλλάξει το πρόσημο στο αντίθετο, διατηρώντας την απόλυτη τιμή, δηλαδή:

Ιδιοκτησία #3:
Καθοριστική μήτραέχοντας δύο ίδιες σειρές ισούται με μηδέν.
Ιδιοκτησία #4:
Κοινός παράγοντας στοιχείων οποιασδήποτε σειράς ορίζουσα του πίνακαμπορεί να ληφθεί ως σημάδι καθοριστικός.

Συμπεράσματα από τα ακίνητα Νο. 3 και Νο. 4:
Εάν όλα τα στοιχεία μιας συγκεκριμένης σειράς (γραμμή ή στήλη) είναι ανάλογα με τα αντίστοιχα στοιχεία μιας παράλληλης σειράς, τότε ορίζουσα μήτραςίσο με μηδέν.
Ιδιοκτησία #5:
ορίζουσα του πίνακαείναι ίσα με μηδέν, λοιπόν ορίζουσα μήτραςίσο με μηδέν.
Ιδιοκτησία #6:
Αν όλα τα στοιχεία μιας γραμμής ή στήλης καθοριστικόςπαρουσιάζεται ως άθροισμα 2 όρων, λοιπόν καθοριστικός μήτρεςμπορεί να αναπαρασταθεί ως το άθροισμα του 2 καθοριστικέςσύμφωνα με τον τύπο:

Ιδιοκτησία #7:
Εάν σε οποιαδήποτε γραμμή (ή στήλη) καθοριστικόςπροσθέστε τα αντίστοιχα στοιχεία μιας άλλης γραμμής (ή στήλης), πολλαπλασιαζόμενα με τον ίδιο αριθμό, στη συνέχεια ορίζουσα μήτραςδεν θα αλλάξει την αξία του.

Παράδειγμα χρήσης ιδιοτήτων για υπολογισμό ορίζουσα του πίνακα:

1ο έτος, ανώτερα μαθηματικά, σπουδές μήτρεςκαι βασικές ενέργειες πάνω τους. Εδώ συστηματοποιούμε τις βασικές πράξεις που μπορούν να εκτελεστούν με πίνακες. Από πού να ξεκινήσετε την εξοικείωση με τους πίνακες; Φυσικά, από τα πιο απλά πράγματα - ορισμούς, βασικές έννοιες και απλές πράξεις. Σας διαβεβαιώνουμε ότι οι πίνακες θα γίνουν κατανοητοί από όλους όσοι τους αφιερώνουν έστω λίγο χρόνο!
Ορισμός Matrix
Μήτραείναι ένας ορθογώνιος πίνακας στοιχείων. Λοιπόν, με απλά λόγια - ένας πίνακας αριθμών.
Συνήθως, οι πίνακες σημειώνονται με κεφαλαία λατινικά γράμματα. Για παράδειγμα, μήτρα ΕΝΑ , μήτρα σι και ούτω καθεξής. Οι πίνακες μπορούν να είναι διαφορετικών μεγεθών: ορθογώνιοι, τετράγωνοι και υπάρχουν επίσης πίνακες σειρών και στηλών που ονομάζονται διανύσματα. Το μέγεθος του πίνακα καθορίζεται από τον αριθμό των γραμμών και στηλών. Για παράδειγμα, ας γράψουμε μια ορθογώνια μήτρα μεγέθους m επί n , Πού m – αριθμός γραμμών και n – αριθμός στηλών.

Στοιχεία για τα οποία i=j (a11, a22, .. ) σχηματίζουν την κύρια διαγώνιο του πίνακα και ονομάζονται διαγώνιοι.
Τι μπορείτε να κάνετε με τους πίνακες; Προσθήκη/Αφαίρεση, πολλαπλασιάστε με έναν αριθμό, πολλαπλασιάζονται μεταξύ τους, μεταθέτω. Τώρα για όλες αυτές τις βασικές πράξεις σε πίνακες με τη σειρά.
Πράξεις πρόσθεσης και αφαίρεσης πίνακα
Ας σας προειδοποιήσουμε αμέσως ότι μπορείτε να προσθέσετε μόνο πίνακες ίδιου μεγέθους. Το αποτέλεσμα θα είναι μια μήτρα του ίδιου μεγέθους. Η προσθήκη (ή η αφαίρεση) πινάκων είναι απλή - απλά πρέπει να προσθέσετε τα αντίστοιχα στοιχεία τους . Ας δώσουμε ένα παράδειγμα. Ας εκτελέσουμε την πρόσθεση δύο πινάκων Α και Β μεγέθους δύο προς δύο.

Η αφαίρεση γίνεται κατ' αναλογία, μόνο με το αντίθετο πρόσημο.
Οποιοσδήποτε πίνακας μπορεί να πολλαπλασιαστεί με έναν αυθαίρετο αριθμό. Για να γίνει αυτό πρέπει να πολλαπλασιάσετε κάθε στοιχείο του με αυτόν τον αριθμό. Για παράδειγμα, ας πολλαπλασιάσουμε τον πίνακα A από το πρώτο παράδειγμα με τον αριθμό 5:

Λειτουργία πολλαπλασιασμού μήτρας
Δεν μπορούν να πολλαπλασιαστούν όλοι οι πίνακες μαζί. Για παράδειγμα, έχουμε δύο πίνακες - Α και Β. Μπορούν να πολλαπλασιαστούν ο ένας με τον άλλο μόνο εάν ο αριθμός των στηλών του πίνακα Α είναι ίσος με τον αριθμό των σειρών του πίνακα Β. Σε αυτήν την περίπτωση κάθε στοιχείο του πίνακα που προκύπτει, που βρίσκεται στην i-η σειρά και στην j-η στήλη, θα είναι ίσο με το άθροισμα των γινομένων των αντίστοιχων στοιχείων στην i-η σειρά του πρώτου παράγοντα και της j-ης στήλης του το δεύτερο. Για να κατανοήσουμε αυτόν τον αλγόριθμο, ας γράψουμε πώς πολλαπλασιάζονται δύο τετραγωνικοί πίνακες:

Και ένα παράδειγμα με πραγματικούς αριθμούς. Ας πολλαπλασιάσουμε τους πίνακες:

Λειτουργία μεταφοράς μήτρας
Η μεταφορά πίνακα είναι μια πράξη όπου οι αντίστοιχες γραμμές και στήλες ανταλλάσσονται. Για παράδειγμα, ας μεταφέρουμε τον πίνακα A από το πρώτο παράδειγμα:

Καθοριστική μήτρα
Ορίζουσα, ή ορίζουσα, είναι μια από τις βασικές έννοιες της γραμμικής άλγεβρας. Μια φορά κι έναν καιρό, οι άνθρωποι έβγαζαν γραμμικές εξισώσεις και μετά από αυτές έπρεπε να καταλήξουν σε μια ορίζουσα. Στο τέλος, είναι στο χέρι σας να τα αντιμετωπίσετε όλα αυτά, οπότε, η τελευταία ώθηση!
Η ορίζουσα είναι ένα αριθμητικό χαρακτηριστικό ενός τετραγωνικού πίνακα, που απαιτείται για την επίλυση πολλών προβλημάτων.
Για να υπολογίσετε την ορίζουσα του απλούστερου τετραγωνικού πίνακα, πρέπει να υπολογίσετε τη διαφορά μεταξύ των γινομένων των στοιχείων της κύριας και της δευτερεύουσας διαγωνίου.
Η ορίζουσα ενός πίνακα πρώτης τάξης, δηλαδή που αποτελείται από ένα στοιχείο, είναι ίση με αυτό το στοιχείο.
Τι γίνεται αν η μήτρα είναι τρία επί τρία; Αυτό είναι πιο δύσκολο, αλλά μπορείτε να το διαχειριστείτε.
Για έναν τέτοιο πίνακα, η τιμή της ορίζουσας είναι ίση με το άθροισμα των γινομένων των στοιχείων της κύριας διαγωνίου και των γινομένων των στοιχείων που βρίσκονται στα τρίγωνα με όψη παράλληλη προς την κύρια διαγώνιο, από την οποία το γινόμενο της αφαιρούνται στοιχεία της δευτερεύουσας διαγωνίου και το γινόμενο των στοιχείων που βρίσκονται στα τρίγωνα με την όψη της παράλληλης δευτερεύουσας διαγωνίου.
Ευτυχώς, στην πράξη είναι σπάνια απαραίτητος ο υπολογισμός των καθοριστικών παραγόντων πινάκων μεγάλων μεγεθών.
Εδώ εξετάσαμε τις βασικές πράξεις σε πίνακες. Φυσικά, στην πραγματική ζωή μπορεί να μην συναντήσετε ποτέ ούτε έναν υπαινιγμό ενός συστήματος εξισώσεων μήτρας ή, αντίθετα, μπορεί να συναντήσετε πολύ πιο περίπλοκες περιπτώσεις όταν πρέπει πραγματικά να βάλετε τα μυαλά σας. Για τέτοιες περιπτώσεις υπάρχουν επαγγελματικές φοιτητικές υπηρεσίες. Ζητήστε βοήθεια, λάβετε μια υψηλής ποιότητας και λεπτομερή λύση, απολαύστε ακαδημαϊκή επιτυχία και ελεύθερο χρόνο.
Ορισμός 1Το γινόμενο πίνακα (C = AB) είναι μια πράξη μόνο για τους αντιστοιχισμένους πίνακες A και B, στους οποίους ο αριθμός των στηλών του πίνακα A είναι ίσος με τον αριθμό των σειρών του πίνακα B:
C ⏟ m × n = A ⏟ m × p × B ⏟ p × n
Παράδειγμα 1
Δεδομένοι πίνακες:
- A = a (i j) διαστάσεων m × n;
- B = b (i j) διαστάσεων p × n
Πίνακας C, τα στοιχεία c i j του οποίου υπολογίζονται χρησιμοποιώντας τον ακόλουθο τύπο:
c i j = a i 1 × b 1 j + a i 2 × b 2 j + . . . + a i p × b p j , i = 1 , . . . m, j = 1, . . . m
Παράδειγμα 2
Ας υπολογίσουμε τα γινόμενα ΑΒ=ΒΑ:
A = 1 2 1 0 1 2 , B = 1 0 0 1 1 1
Λύση χρησιμοποιώντας τον κανόνα πολλαπλασιασμού του πίνακα:
A ⏟ 2 × 3 × B ⏟ 3 × 2 = 1 2 1 0 1 2 × 1 0 0 1 1 1 = 1 × 1 + 2 × 0 + 1 × 1 1 × 0 + 2 × 1 + 1 × 1 0 × 1 + 1 × 0 + 2 × 1 0 × 0 + 1 × 1 + 2 × 1 = = 2 3 2 3 ⏟ 2 × 2
B ⏟ 3 × 2 × A ⏟ 2 × 3 = 1 0 0 1 1 1 × 1 2 1 0 1 2 = 1 × 1 + 0 × 0 1 × 2 + 0 × 1 1 × 1 + 0 × 2 0 × 1 + 1 × 0 0 × 2 + 1 × 1 0 × 1 + 1 × 2 1 × 1 + 1 × 0 1 × 2 + 1 × 1 1 × 1 + 1 × 2 = 1 2 1 0 1 2 1 3 3 ⏟ 3×3
Βρίσκονται το γινόμενο A B και BA A, αλλά είναι πίνακες διαφορετικών μεγεθών: το A B δεν είναι ίσο με το BA A.
Ιδιότητες πολλαπλασιασμού πινάκων
Ιδιότητες πολλαπλασιασμού πίνακα:
- (A B) C = A (B C) - συσχετισμός πολλαπλασιασμού πίνακα.
- A (B + C) = A B + A C - κατανομή πολλαπλασιασμού.
- (A + B) C = A C + B C - κατανομή πολλαπλασιασμού.
- λ (A B) = (λ A) B
Ας ελέγξουμε την ιδιότητα Νο. 1: (A B) C = A (B C) :
(A × B) × A = 1 2 3 4 × 5 6 7 8 × 1 0 0 2 = 19 22 43 50 × 1 0 0 2 = 19 44 43 100,
A (B × C) = 1 2 3 4 × 5 6 7 8 1 0 0 2 = 1 2 3 4 × 5 12 7 16 = 19 44 43 100.
Παράδειγμα 2
Ας ελέγξουμε την ιδιότητα Νο. 2: A (B + C) = A B + A C:
A × (B + C) = 1 2 3 4 × 5 6 7 8 + 1 0 0 2 = 1 2 3 4 × 6 6 7 10 = 20 26 46 58,
A B + A C = 1 2 3 4 × 5 6 7 8 + 1 2 3 4 × 1 0 0 2 = 19 22 43 50 + 1 4 3 8 = 20 26 46 58.
Προϊόν τριών πινάκων
Το γινόμενο τριών πινάκων A B C υπολογίζεται με 2 τρόπους:
- Βρείτε το A B και πολλαπλασιάστε με το C: (A B) C;
- ή να βρείτε πρώτα το B C και μετά να πολλαπλασιάσετε το A (B C).
Πολλαπλασιάστε πίνακες με 2 τρόπους:
4 3 7 5 × - 28 93 38 - 126 × 7 3 2 1
Αλγόριθμος ενεργειών:
- Βρείτε το γινόμενο 2 πινάκων.
- και μετά βρείτε ξανά το γινόμενο 2 πινάκων.
1). A B = 4 3 7 5 × - 28 93 38 - 126 = 4 (- 28) + 3 × 38 4 × 93 + 3 (- 126) 7 (- 28) + 5 × 38 7 × 93 + 5 (- 126 ) = 2 - 6 - 6 21
2). A B C = (A B) C = 2 - 6 - 6 21 7 3 2 1 = 2 × 7 - 6 × 2 2 × 3 - 6 × 1 - 6 × 7 + 21 × 2 - 6 × 3 + 21 × 1 = 2 0 0 3 .
Χρησιμοποιούμε τον τύπο A B C = (A B) C:
1). B C = - 28 93 38 - 126 7 3 2 1 = - 28 × 7 + 93 × 2 - 28 × 3 + 93 × 1 38 × 7 - 126 × 2 38 × 3 - 126 × 1 = 2 - 14 - 1
2). A B C = (A B) C = 7 3 2 1 - 10 9 14 - 12 = 4 (- 10) + 3 × 14 4 × 9 + 3 (- 12) 7 (- 10) + 5 × 14 7 × 9 + 5 (- 12) = 2 0 0 3
Απάντηση: 4 3 7 5 - 28 93 38 - 126 7 3 2 1 = 2 0 0 3
Πολλαπλασιάζοντας έναν πίνακα με έναν αριθμό
Ορισμός 2Το γινόμενο του πίνακα A με τον αριθμό k είναι ο πίνακας B = A k ίδιου μεγέθους, ο οποίος προκύπτει από τον αρχικό πολλαπλασιάζοντας όλα τα στοιχεία του με έναν δεδομένο αριθμό:
b i, j = k × a i, j
Ιδιότητες πολλαπλασιασμού ενός πίνακα με έναν αριθμό:
- 1 × Α = Α
- 0 × A = μηδενικός πίνακας
- k (A + B) = k A + k B
- (k + n) A = k A + n Α
- (k × n) × A = k (n × A)
Ας βρούμε το γινόμενο του πίνακα A = 4 2 9 0 επί 5.
5 A = 5 4 2 9 0 5 × 4 5 × 2 5 × 9 5 × 0 = 20 10 45 0
Πολλαπλασιάζοντας έναν πίνακα με ένα διάνυσμα
Ορισμός 3Για να βρείτε το γινόμενο ενός πίνακα και ενός διανύσματος, πρέπει να πολλαπλασιάσετε χρησιμοποιώντας τον κανόνα «γραμμή προς στήλη»:
- Εάν πολλαπλασιάσετε έναν πίνακα με ένα διάνυσμα στήλης, ο αριθμός των στηλών στον πίνακα πρέπει να ταιριάζει με τον αριθμό των γραμμών στο διάνυσμα στήλης.
- Το αποτέλεσμα του πολλαπλασιασμού ενός διανύσματος στήλης είναι μόνο ένα διάνυσμα στήλης:
A B = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a m 1 a m 2 ⋯ a m n b 1 b 2 ⋯ b 1 n = a 11 × 1 b 1 × b + a 1 n × b n a 21 × b 1 + a 22 × b 2 + ⋯ + a 2 n × b n ⋯ ⋯ ⋯ ⋯ a m 1 × b 1 + a m 2 × b 2 + ⋯ + a m n × b n = c 1 μ
- αν πολλαπλασιάσετε έναν πίνακα με ένα διάνυσμα γραμμής, τότε ο πολλαπλασιαζόμενος πίνακας πρέπει να είναι αποκλειστικά διάνυσμα στήλης και ο αριθμός των στηλών πρέπει να ταιριάζει με τον αριθμό των στηλών στο διάνυσμα γραμμής:
A B = a a ⋯ a b b ⋯ b = a 1 × b 1 a 1 × b 2 ⋯ a 1 × b n a 2 × b 1 a 2 × b 2 ⋯ a 2 × b n ⋯ ⋯ ⋯ ⋯ a n × b a n × b n = c 11 c 12 ⋯ c 1 n c 21 c 22 ⋯ c 2 n ⋯ ⋯ ⋯ ⋯ c n 1 c n 2 ⋯ c n n
Παράδειγμα 5
Ας βρούμε το γινόμενο του πίνακα Α και του διανύσματος της στήλης Β:
A B = 2 4 0 - 2 1 3 - 1 0 1 1 2 - 1 = 2 × 1 + 4 × 2 + 0 × (- 1) - 2 × 1 + 1 × 2 + 3 × (- 1) - 1 × 1 + 0 × 2 + 1 × (- 1) = 2 + 8 + 0 - 2 + 2 - 3 - 1 + 0 - 1 = 10 - 3 - 2
Παράδειγμα 6
Ας βρούμε το γινόμενο του πίνακα Α και του διανύσματος γραμμής Β:
A = 3 2 0 - 1, B = - 1 1 0 2
A B = 3 2 0 1 × - 1 1 0 2 = 3 × (- 1) 3 × 1 3 × 0 3 × 2 2 × (- 1) 2 × 1 2 × 0 2 × 2 0 × (- 1) 0 × 1 0 × 0 0 × 2 1 × (- 1) 1 × 1 1 × 0 1 × 2 = - 3 3 0 6 - 2 2 0 4 0 0 0 0 - 1 1 0 2
Απάντηση: A B = - 3 3 0 6 - 2 2 0 4 0 0 0 0 - 1 1 0 2
Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter
- VKontakte 0
- Google+ 0
- ΕΝΤΑΞΕΙ 0
- Facebook 0