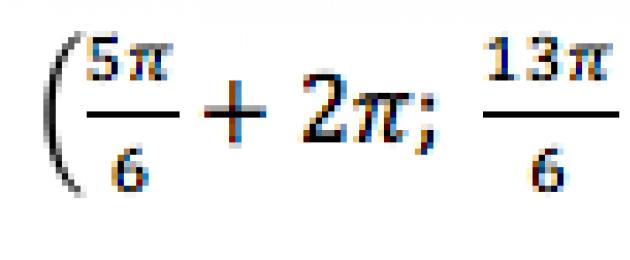Έργο Άλγεβρας «Επίλυση τριγωνομετρικών ανισώσεων» Ολοκληρώθηκε από μαθήτρια της τάξης 10 «Β» Kazachkova Yulia Επιβλέπων: καθηγήτρια μαθηματικών Kochakova N.N.
Στόχος Ενοποίηση της ύλης στο θέμα «Επίλυση τριγωνομετρικών ανισώσεων» και δημιουργία υπενθύμισης για την προετοιμασία των μαθητών για την επερχόμενη εξέταση.
Στόχοι: Συνοψίστε το υλικό για αυτό το θέμα. Συστηματοποίηση των πληροφοριών που λαμβάνονται. Εξετάστε αυτό το θέμα στην Ενιαία Κρατική Εξέταση.
Συνάφεια Η συνάφεια του θέματος που επέλεξα έγκειται στο γεγονός ότι οι εργασίες για το θέμα «Επίλυση τριγωνομετρικών ανισοτήτων» περιλαμβάνονται στις εργασίες της Ενιαίας Κρατικής Εξέτασης.
Τριγωνομετρικές ανισώσεις Μια ανισότητα είναι μια σχέση που συνδέει δύο αριθμούς ή παραστάσεις μέσω ενός από τα σημεία: (μεγαλύτερο από); ≥ (μεγαλύτερο ή ίσο με). Μια τριγωνομετρική ανισότητα είναι μια ανισότητα που περιέχει τριγωνομετρικές συναρτήσεις.
Τριγωνομετρικές ανισώσεις Η λύση των ανισώσεων που περιέχουν τριγωνομετρικές συναρτήσεις ανάγεται, κατά κανόνα, στη λύση των απλούστερων ανισώσεων της μορφής: sin x>a, sin x α, συν χ α, tg x a,ctg x
Αλγόριθμος επίλυσης τριγωνομετρικών ανισώσεων Στον άξονα που αντιστοιχεί σε μια δεδομένη τριγωνομετρική συνάρτηση, σημειώστε τη δεδομένη αριθμητική τιμή αυτής της συνάρτησης. Σχεδιάστε μια γραμμή στο σημειωμένο σημείο που τέμνει τον κύκλο της μονάδας. Επιλέξτε τα σημεία τομής μιας ευθείας και ενός κύκλου, λαμβάνοντας υπόψη το αυστηρό ή μη αυστηρό πρόσημο της ανισότητας. Επιλέξτε το τόξο του κύκλου στο οποίο βρίσκονται οι λύσεις της ανισότητας. Προσδιορίστε τις τιμές των γωνιών στο αρχικό και τελικά σημείατόξα ενός κύκλου. Να γράψετε τη λύση της ανίσωσης λαμβάνοντας υπόψη την περιοδικότητα της δεδομένης τριγωνομετρικής συνάρτησης.
Τύποι επίλυσης τριγωνομετρικών ανισώσεων sinx >a; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx ένα; x (- arccos a + 2πn· arccos a + 2πn). cosxένα; x (arctg a + πn ; + πn). tgx ένα; x (πn ; arctan + πn). ctgx
Γραφική λύση βασικών τριγωνομετρικών ανισώσεων sinx >a
Γραφική λύση βασικών τριγωνομετρικών ανισώσεων sinx Γραφική λύση βασικών τριγωνομετρικών ανισώσεων cosx >a Γραφική λύση βασικών τριγωνομετρικών ανισώσεων συνχ Γραφική λύση βασικών τριγωνομετρικών ανισώσεων tgx >a Γραφική λύση βασικών τριγωνομετρικών ανισώσεων tgx Γραφική λύση βασικών τριγωνομετρικών ανισώσεων ctgx >a
Οι ανισότητες είναι σχέσεις της μορφής a › b, όπου a και b είναι εκφράσεις που περιέχουν τουλάχιστον μία μεταβλητή. Οι ανισότητες μπορεί να είναι αυστηρές - ‹, › και μη αυστηρές - ≥, ≤.
Οι τριγωνομετρικές ανισότητες είναι εκφράσεις της μορφής: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, στις οποίες η F(x) αντιπροσωπεύεται από μία ή περισσότερες τριγωνομετρικές συναρτήσεις .
Ένα παράδειγμα της απλούστερης τριγωνομετρικής ανισότητας είναι: sin x ‹ 1/2. Είναι σύνηθες να επιλύονται τέτοια προβλήματα γραφικά, έχουν αναπτυχθεί δύο μέθοδοι.
Μέθοδος 1 - Επίλυση ανισώσεων με τη γραφική παράσταση μιας συνάρτησης
Για να βρείτε ένα διάστημα που να ικανοποιεί τις συνθήκες ανισότητα sin x ‹ 1/2, πρέπει να εκτελέσετε τα ακόλουθα βήματα:
- Επί άξονα συντεταγμένωνκατασκευάστε ένα ημιτονοειδές y = sin x.
- Στον ίδιο άξονα, σχεδιάστε μια γραφική παράσταση του αριθμητικού ορίσματος της ανίσωσης, δηλαδή μια ευθεία γραμμή που διέρχεται από το σημείο ½ της τεταγμένης OY.
- Σημειώστε τα σημεία τομής των δύο γραφημάτων.
- Σκιάστε το τμήμα που είναι η λύση στο παράδειγμα.
Όταν υπάρχουν αυστηρά σημάδια σε μια έκφραση, τα σημεία τομής δεν είναι λύσεις. Επειδή η μικρότερη θετική περίοδος ενός ημιτονοειδούς είναι 2π, γράφουμε την απάντηση ως εξής:
Εάν τα σημάδια της έκφρασης δεν είναι αυστηρά, τότε το διάστημα επίλυσης πρέπει να περικλείεται σε αγκύλες - . Η απάντηση στο πρόβλημα μπορεί επίσης να γραφτεί ως η ακόλουθη ανισότητα: 
Μέθοδος 2 - Επίλυση τριγωνομετρικών ανισώσεων χρησιμοποιώντας τον μοναδιαίο κύκλο
Τέτοια προβλήματα μπορούν εύκολα να λυθούν χρησιμοποιώντας τριγωνομετρικός κύκλος. Ο αλγόριθμος για την εύρεση απαντήσεων είναι πολύ απλός:
- Πρώτα πρέπει να σχεδιάσετε έναν κύκλο μονάδας.
- Στη συνέχεια, πρέπει να σημειώσετε την τιμή της συνάρτησης τόξου του ορίσματος της δεξιάς πλευράς της ανισότητας στο τόξο του κύκλου.
- Είναι απαραίτητο να σχεδιάσουμε μια ευθεία γραμμή που διέρχεται από την τιμή της συνάρτησης τόξου παράλληλη προς τον άξονα της τετμημένης (OX).
- Μετά από αυτό, το μόνο που μένει είναι να επιλέξετε το τόξο ενός κύκλου, το οποίο είναι το σύνολο των λύσεων στην τριγωνομετρική ανισότητα.
- Γράψτε την απάντηση στην απαιτούμενη μορφή.
Ας αναλύσουμε τα στάδια της λύσης χρησιμοποιώντας το παράδειγμα της ανισότητας sin x › 1/2. Τα σημεία α και β σημειώνονται στον κύκλο - τιμές
Τα σημεία του τόξου που βρίσκονται πάνω από το α και το β είναι το διάστημα για την επίλυση της δεδομένης ανισότητας.
Εάν πρέπει να λύσετε ένα παράδειγμα για το cos, τότε το τόξο απάντησης θα βρίσκεται συμμετρικά προς τον άξονα OX, όχι OY. Μπορείτε να εξετάσετε τη διαφορά μεταξύ των διαστημάτων λύσης για το sin και το cos στα παρακάτω διαγράμματα του κειμένου.
Οι γραφικές λύσεις για τις εφαπτομενικές και συνεφαπτομενικές ανισότητες θα διαφέρουν τόσο από το ημίτονο όσο και από το συνημίτονο. Αυτό οφείλεται στις ιδιότητες των συναρτήσεων.
Η τοξοεφαπτομένη είναι εφαπτομένη σε έναν τριγωνομετρικό κύκλο και η ελάχιστη θετική περίοδος και για τις δύο συναρτήσεις είναι π. Για να χρησιμοποιήσετε γρήγορα και σωστά τη δεύτερη μέθοδο, πρέπει να θυμάστε σε ποιον άξονα απεικονίζονται οι τιμές sin, cos, tg και ctg.
Η εφαπτομένη είναι παράλληλη με τον άξονα OY. Αν σχεδιάσουμε την τιμή του αρκτανίου a στον μοναδιαίο κύκλο, τότε το δεύτερο απαιτούμενο σημείο θα βρίσκεται στο διαγώνιο τέταρτο. Γωνίες
Είναι σημεία διακοπής για τη συνάρτηση, αφού το γράφημα τείνει προς αυτά, αλλά δεν τα φτάνει ποτέ.
Στην περίπτωση της συνεφαπτομένης, η εφαπτομένη είναι παράλληλη προς τον άξονα ΟΧ και η συνάρτηση διακόπτεται στα σημεία π και 2π.
Μιγαδικές τριγωνομετρικές ανισώσεις
Εάν το όρισμα της συνάρτησης ανισότητας αντιπροσωπεύεται όχι μόνο από μια μεταβλητή, αλλά από μια ολόκληρη παράσταση που περιέχει έναν άγνωστο, τότε μιλάμε ήδη για σύνθετη ανισότητα. Η διαδικασία και η διαδικασία επίλυσής του διαφέρουν κάπως από τις μεθόδους που περιγράφονται παραπάνω. Ας υποθέσουμε ότι πρέπει να βρούμε μια λύση στην ακόλουθη ανισότητα:
Η γραφική λύση περιλαμβάνει την κατασκευή ενός συνηθισμένου ημιτονοειδούς y = sin x χρησιμοποιώντας αυθαίρετα επιλεγμένες τιμές του x. Ας υπολογίσουμε έναν πίνακα με συντεταγμένες για τα σημεία ελέγχου του γραφήματος:
Το αποτέλεσμα πρέπει να είναι μια όμορφη καμπύλη.
Για να διευκολύνουμε την εύρεση λύσης, ας αντικαταστήσουμε το όρισμα σύνθετης συνάρτησης
Η τομή δύο γραφημάτων μας επιτρέπει να προσδιορίσουμε την περιοχή των επιθυμητών τιμών στην οποία ικανοποιείται η συνθήκη ανισότητας.
Το τμήμα που βρέθηκε είναι μια λύση για τη μεταβλητή t:
Ωστόσο, ο στόχος της εργασίας είναι να βρει όλες τις πιθανές παραλλαγές του αγνώστου x:
Η επίλυση της διπλής ανισότητας είναι αρκετά απλή, πρέπει να μετακινήσετε το π/3 στα ακραία μέρη της εξίσωσης και να εκτελέσετε τους απαιτούμενους υπολογισμούς:
Απάντηση στην εργασίαθα μοιάζει με το διάστημα για την αυστηρή ανισότητα:
Τέτοια προβλήματα θα απαιτήσουν την εμπειρία και την επιδεξιότητα των μαθητών στο χειρισμό τριγωνομετρικών συναρτήσεων. Όσο περισσότερες εκπαιδευτικές εργασίες λυθούν κατά τη διαδικασία προετοιμασίας, τόσο πιο εύκολα και γρήγορα ο μαθητής θα βρει την απάντηση στην ερώτηση. Ερώτηση Ενιαίας Κρατικής Εξέτασηςδοκιμή.
Επίλυση απλών τριγωνομετρικών εξισώσεων
Αρχικά, ας θυμηθούμε τους τύπους για την επίλυση των απλούστερων τριγωνομετρικών εξισώσεων.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Επίλυση απλών τριγωνομετρικών ανισώσεων.
Για να λύσουμε τις απλούστερες τριγωνομετρικές ανισώσεις, πρέπει πρώτα να λύσουμε την αντίστοιχη εξίσωση και στη συνέχεια, χρησιμοποιώντας έναν τριγωνομετρικό κύκλο, να βρούμε μια λύση στην ανισότητα. Ας εξετάσουμε λύσεις στις απλούστερες τριγωνομετρικές ανισώσεις χρησιμοποιώντας παραδείγματα.
Παράδειγμα 1
$sinx\ge \frac(1)(2)$
Ας βρούμε μια λύσητριγωνομετρική ανισότητα $sinx=\frac(1)(2)$
\ \
Εικόνα 1. Λύση της ανισότητας $sinx\ge \frac(1)(2)$.
Εφόσον η ανισότητα έχει πρόσημο «μεγαλύτερο ή ίσο με», η λύση βρίσκεται στο πάνω τόξο του κύκλου (σε σχέση με τη λύση της εξίσωσης).
Απάντηση: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.
Παράδειγμα 2
Ας βρούμε τη λύση της τριγωνομετρικής ανισότητας $cosx=\frac(\sqrt(3))(2)$
\ \
Ας σημειώσουμε τη λύση στον τριγωνομετρικό κύκλο
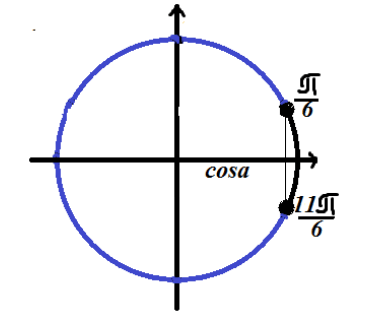
Δεδομένου ότι η ανισότητα έχει πρόσημο «λιγότερο από», η λύση βρίσκεται στο τόξο ενός κύκλου που βρίσκεται στα αριστερά (σε σχέση με τη λύση της εξίσωσης).
Απάντηση: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.
Παράδειγμα 3
$tgx\le \frac(\sqrt(3))(3)$
Ας βρούμε τη λύση στην τριγωνομετρική ανισότητα $tgx=\frac(\sqrt(3))(3)$
\ \
Εδώ χρειαζόμαστε επίσης έναν τομέα ορισμού. Όπως θυμόμαστε, η εφαπτομένη συνάρτηση $x\ne \frac(\pi )(2)+\pi n,n\in Z$
Ας σημειώσουμε τη λύση στον τριγωνομετρικό κύκλο
Εικόνα 3. Λύση της ανισότητας $tgx\le \frac(\sqrt(3))(3)$.
Εφόσον η ανισότητα έχει πρόσημο «λιγότερο από ή ίσο», η λύση βρίσκεται στα κυκλικά τόξα που σημειώνονται με μπλε χρώμα στο Σχήμα 3.
Απάντηση:$\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \αριστερά (\frac(\pi )(2)+2\pi n,\δεξιά.\αριστερά.\frac(7\pi )(6)+2\pi n\δεξιά]$
Παράδειγμα 4
Ας βρούμε τη λύση της τριγωνομετρικής ανισότητας $ctgx=\sqrt(3)$
\ \
Εδώ χρειαζόμαστε επίσης έναν τομέα ορισμού. Όπως θυμόμαστε, η εφαπτομένη συνάρτηση $x\ne \pi n,n\σε Z$
Ας σημειώσουμε τη λύση στον τριγωνομετρικό κύκλο
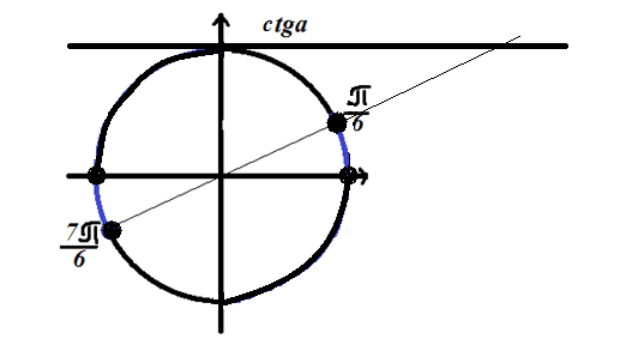
Εικόνα 4. Λύση της ανισότητας $ctgx\le \sqrt(3)$.
Εφόσον η ανισότητα έχει πρόσημο "μεγαλύτερο από", η λύση βρίσκεται στα κυκλικά τόξα που σημειώνονται με μπλε χρώμα στο Σχήμα 4.
Απάντηση:$\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\δεξιά)$
Υπουργείο Παιδείας της Δημοκρατίας της Λευκορωσίας
Εκπαιδευτικό ίδρυμα
«Κρατικό Πανεπιστήμιο Γκόμελ
πήρε το όνομά του από τον Francysk Skaryna"
Μαθηματική Σχολή
Τμήμα Άλγεβρας και Γεωμετρίας
Δεκτός για άμυνα
Κεφάλι Τμήμα Shemetkov L.A.
Τριγωνομετρικές εξισώσειςκαι ανισότητες
Εργασία μαθήματος
Εκτελεστής διαθήκης:
μαθητής της ομάδας Μ-51
ΕΚ. Γκόρσκι
Επιστημονικός υπεύθυνος Ph.D.-M.Sc.,
Ανώτερος Λέκτορας
V.G. Σαφόνοφ
Gomel 2008
ΕΙΣΑΓΩΓΗ
ΒΑΣΙΚΕΣ ΜΕΘΟΔΟΙ ΛΥΣΗΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ
Παραγοντοποίηση
Επίλυση εξισώσεων μετατρέποντας το γινόμενο τριγωνομετρικών συναρτήσεων σε άθροισμα
Επίλυση εξισώσεων χρησιμοποιώντας τύπους τριπλού ορίσματος
Πολλαπλασιασμός με κάποια τριγωνομετρική συνάρτηση
ΜΗ ΤΥΠΟΙ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΑΝΙΣΟΤΗΤΕΣ
ΕΠΙΛΟΓΗ ΡΙΖΩΝ
ΚΑΘΗΚΟΝΤΑ ΓΙΑ ΑΝΕΞΑΡΤΗΤΗ ΛΥΣΗ
ΣΥΜΠΕΡΑΣΜΑ
ΚΑΤΑΛΟΓΟΣ ΧΡΗΣΙΜΟΠΟΙΗΜΕΝΩΝ ΠΗΓΩΝ
Στην αρχαιότητα, η τριγωνομετρία προέκυψε σε σχέση με τις ανάγκες της αστρονομίας, της τοπογραφίας και της κατασκευής, δηλαδή ήταν καθαρά γεωμετρικής φύσης και αντιπροσωπευόταν κυρίως<<исчисление хорд>>. Με τον καιρό, κάποιες αναλυτικές στιγμές άρχισαν να παρεμβάλλονται σε αυτό. Στο πρώτο μισό του 18ου αιώνα σημειώθηκε μια απότομη αλλαγή, μετά την οποία η τριγωνομετρία πήρε μια νέα κατεύθυνση και στράφηκε προς μαθηματική ανάλυση. Ήταν εκείνη τη στιγμή που οι τριγωνομετρικές σχέσεις άρχισαν να θεωρούνται ως συναρτήσεις.
Οι τριγωνομετρικές εξισώσεις είναι ένα από τα πιο δύσκολα θέματα σε ένα σχολικό μάθημα μαθηματικών. Οι τριγωνομετρικές εξισώσεις προκύπτουν κατά την επίλυση προβλημάτων στην επιπεδομετρία, τη στερεομετρία, την αστρονομία, τη φυσική και άλλα πεδία. Οι τριγωνομετρικές εξισώσεις και οι ανισότητες βρίσκονται μεταξύ των κεντρικών εργασιών δοκιμών κάθε χρόνο.
Η πιο σημαντική διαφορά μεταξύ τριγωνομετρικών και αλγεβρικών εξισώσεων είναι ότι οι αλγεβρικές εξισώσεις έχουν πεπερασμένο αριθμό ριζών, ενώ οι τριγωνομετρικές εξισώσεις --- άπειρος, γεγονός που περιπλέκει πολύ την επιλογή των ριζών. Ένα άλλο ειδικό χαρακτηριστικό των τριγωνομετρικών εξισώσεων είναι η μη μοναδική μορφή γραφής της απάντησης.
Η παρούσα διατριβή είναι αφιερωμένη σε μεθόδους επίλυσης τριγωνομετρικών εξισώσεων και ανισώσεων.
Η διπλωματική εργασία αποτελείται από 6 ενότητες.
Η πρώτη ενότητα παρέχει βασικές θεωρητικές πληροφορίες: ορισμός και ιδιότητες τριγωνομετρικών και αντίστροφων τριγωνομετρικών συναρτήσεων. πίνακας τιμών τριγωνομετρικών συναρτήσεων για ορισμένα ορίσματα. έκφραση τριγωνομετρικών συναρτήσεων σε σχέση με άλλες τριγωνομετρικές συναρτήσεις, κάτι που είναι πολύ σημαντικό για τον μετασχηματισμό τριγωνομετρικών παραστάσεων, ειδικά εκείνων που περιέχουν αντίστροφες τριγωνομετρικές συναρτήσεις. εκτός από τους βασικούς τριγωνομετρικούς τύπους, πολύ γνωστούς από σχολικό μάθημα, δίνονται τύποι που απλοποιούν εκφράσεις που περιέχουν αντίστροφες τριγωνομετρικές συναρτήσεις.
Η δεύτερη ενότητα περιγράφει τις βασικές μεθόδους επίλυσης τριγωνομετρικών εξισώσεων. Εξετάζονται η λύση στοιχειωδών τριγωνομετρικών εξισώσεων, η μέθοδος παραγοντοποίησης και μέθοδοι αναγωγής τριγωνομετρικών εξισώσεων σε αλγεβρικές. Λόγω του γεγονότος ότι οι λύσεις σε τριγωνομετρικές εξισώσεις μπορούν να γραφτούν με πολλούς τρόπους και η μορφή αυτών των λύσεων δεν επιτρέπει σε κάποιον να προσδιορίσει αμέσως εάν αυτές οι λύσεις είναι ίδιες ή διαφορετικές, κάτι που μπορεί<<сбить с толку>> κατά την επίλυση δοκιμών, εξετάζεται το γενικό σχήμα για την επίλυση τριγωνομετρικών εξισώσεων και εξετάζεται λεπτομερώς ο μετασχηματισμός ομάδων γενικών λύσεων τριγωνομετρικών εξισώσεων.
Στην τρίτη ενότητα εξετάζονται οι μη τυπικές τριγωνομετρικές εξισώσεις, οι λύσεις των οποίων βασίζονται στη συναρτησιακή προσέγγιση.
Η τέταρτη ενότητα πραγματεύεται τις τριγωνομετρικές ανισότητες. Οι μέθοδοι επίλυσης στοιχειωδών τριγωνομετρικών ανισώσεων, τόσο στον μοναδιαίο κύκλο όσο και με τη γραφική μέθοδο, συζητούνται λεπτομερώς. Περιγράφεται η διαδικασία επίλυσης μη στοιχειωδών τριγωνομετρικών ανισώσεων μέσω στοιχειωδών ανισώσεων και η μέθοδος των διαστημάτων, ήδη γνωστή στους μαθητές του σχολείου.
Η πέμπτη ενότητα παρουσιάζει τα περισσότερα δύσκολα καθήκοντα: όταν είναι απαραίτητο όχι μόνο να λύσουμε μια τριγωνομετρική εξίσωση, αλλά και να επιλέξουμε ρίζες από τις ρίζες που βρέθηκαν που ικανοποιούν κάποια συνθήκη. Αυτή η ενότητα παρέχει λύσεις σε τυπικές εργασίες επιλογής ρίζας. Δίνονται οι απαραίτητες θεωρητικές πληροφορίες για την επιλογή ριζών: διαίρεση ενός συνόλου ακεραίων σε ασύνδετα υποσύνολα, επίλυση εξισώσεων σε ακέραιους αριθμούς (διαφαντικό).
Η έκτη ενότητα παρουσιάζει εργασίες για ανεξάρτητη λύση, που παρουσιάζονται σε μορφή τεστ. Οι 20 δοκιμαστικές εργασίες περιέχουν τις πιο δύσκολες εργασίες που μπορεί να συναντήσετε κατά τη διάρκεια των κεντρικών δοκιμών.
Στοιχειώδεις τριγωνομετρικές εξισώσεις
Οι στοιχειώδεις τριγωνομετρικές εξισώσεις είναι εξισώσεις της μορφής , όπου --- μία από τις τριγωνομετρικές συναρτήσεις: , , , .
Οι στοιχειώδεις τριγωνομετρικές εξισώσεις έχουν άπειρο αριθμό ριζών. Για παράδειγμα, οι ακόλουθες τιμές ικανοποιούν την εξίσωση: , , , κ.λπ. Γενικός τύποςκατά μήκος της οποίας βρίσκονται όλες οι ρίζες της εξίσωσης, όπου , είναι:
Εδώ μπορεί να πάρει οποιεσδήποτε ακέραιες τιμές, καθεμία από αυτές αντιστοιχεί σε μια συγκεκριμένη ρίζα της εξίσωσης. σε αυτόν τον τύπο (καθώς και σε άλλους τύπους με τους οποίους λύνονται στοιχειώδεις τριγωνομετρικές εξισώσεις) ονομάζονται παράμετρος. Συνήθως γράφουν , τονίζοντας έτσι ότι η παράμετρος μπορεί να δεχθεί οποιεσδήποτε ακέραιες τιμές.
Οι λύσεις της εξίσωσης , όπου , βρίσκονται από τον τύπο
Η εξίσωση λύνεται χρησιμοποιώντας τον τύπο
και η εξίσωση είναι από τον τύπο
Ας σημειώσουμε ιδιαίτερα ορισμένες ειδικές περιπτώσεις στοιχειωδών τριγωνομετρικών εξισώσεων, όταν η λύση μπορεί να γραφτεί χωρίς τη χρήση γενικών τύπων:
Κατά την επίλυση τριγωνομετρικών εξισώσεων σημαντικός ρόλοςπαίζει την περίοδο των τριγωνομετρικών συναρτήσεων. Επομένως, παρουσιάζουμε δύο χρήσιμα θεωρήματα:
Θεώρημα Αν --- η κύρια περίοδος της συνάρτησης, τότε ο αριθμός είναι η κύρια περίοδος της συνάρτησης.
Οι περίοδοι των συναρτήσεων και λέγεται ότι είναι συγκρίσιμες εάν υπάρχουν ακέραιοι αριθμοίΚαι λοιπόν .
Θεώρημα Αν οι περιοδικές συναρτήσεις και , έχουν ανάλογη και , τότε έχουν μια κοινή περίοδο, που είναι η περίοδος των συναρτήσεων , , .
Το θεώρημα δηλώνει ποια είναι η περίοδος της συνάρτησης , , , και δεν είναι απαραίτητα η κύρια περίοδος. Για παράδειγμα, η κύρια περίοδος των συναρτήσεων και --- , και η κύρια περίοδος του προϊόντος τους --- .
Εισαγωγή ενός βοηθητικού ορίσματος
Με τον τυπικό τρόπο μετασχηματισμού εκφράσεων της φόρμας 
είναι η ακόλουθη τεχνική: ας --- γωνία, που δίνονται από τις ισότητες 
, 
. Για οποιαδήποτε, μια τέτοια γωνία υπάρχει. Ετσι . Εάν , ή , , , σε άλλες περιπτώσεις.
Σχέδιο επίλυσης τριγωνομετρικών εξισώσεων
Το βασικό σχήμα που θα ακολουθήσουμε κατά την επίλυση τριγωνομετρικών εξισώσεων είναι το εξής:
η επίλυση μιας δεδομένης εξίσωσης ανάγεται στην επίλυση στοιχειωδών εξισώσεων. Λύσεις --- μετατροπές, παραγοντοποίηση, αντικατάσταση αγνώστων. Η κατευθυντήρια αρχή είναι να μην χάσεις τις ρίζες σου. Αυτό σημαίνει ότι όταν μεταβαίνουμε στην επόμενη εξίσωση (ες), δεν φοβόμαστε την εμφάνιση επιπλέον (εξωτερικών) ριζών, αλλά νοιαζόμαστε μόνο ότι κάθε επόμενη εξίσωση της «αλυσίδας» μας (ή ένα σύνολο εξισώσεων στην περίπτωση διακλάδωσης ) είναι συνέπεια του προηγούμενου. Ενας από πιθανές μεθόδουςΗ επιλογή root είναι ένας έλεγχος. Ας σημειώσουμε αμέσως ότι στην περίπτωση των τριγωνομετρικών εξισώσεων, οι δυσκολίες που σχετίζονται με την επιλογή ριζών και τον έλεγχο, κατά κανόνα, αυξάνονται απότομα σε σύγκριση με τις αλγεβρικές εξισώσεις. Εξάλλου, πρέπει να ελέγξουμε σειρές που αποτελούνται από άπειρο αριθμό όρων.
Ιδιαίτερη αναφορά πρέπει να γίνει στην αντικατάσταση αγνώστων κατά την επίλυση τριγωνομετρικών εξισώσεων. Στις περισσότερες περιπτώσεις, μετά την απαραίτητη αντικατάσταση, αποδεικνύεται αλγεβρική εξίσωση. Επιπλέον, οι εξισώσεις δεν είναι τόσο σπάνιες που, αν και είναι τριγωνομετρικές εμφάνιση, ουσιαστικά δεν είναι, αφού μετά το πρώτο βήμα --- αντικαταστάσειςοι μεταβλητές --- μετατρέπονται σε αλγεβρικές και η επιστροφή στην τριγωνομετρία συμβαίνει μόνο στο στάδιο της επίλυσης στοιχειωδών τριγωνομετρικών εξισώσεων.
Ας σας υπενθυμίσουμε για άλλη μια φορά: η αντικατάσταση του αγνώστου πρέπει να γίνει με την πρώτη ευκαιρία, η εξίσωση που προκύπτει μετά την αντικατάσταση πρέπει να λυθεί μέχρι το τέλος, συμπεριλαμβανομένου του σταδίου επιλογής των ριζών και μόνο στη συνέχεια να επιστρέψει στο αρχικό άγνωστο.
Ένα από τα χαρακτηριστικά των τριγωνομετρικών εξισώσεων είναι ότι η απάντηση σε πολλές περιπτώσεις μπορεί να γραφτεί διαφορετικοί τρόποι. Ακόμα και για να λύσουμε την εξίσωση 
η απάντηση μπορεί να γραφτεί ως εξής:
1) με τη μορφή δύο σειρών: 
, , ;
2) σε τυπική μορφή, που είναι συνδυασμός της παραπάνω σειράς: , ;
3) επειδή 
, τότε η απάντηση μπορεί να γραφτεί στη φόρμα 
, . (Σε αυτό που ακολουθεί, η παρουσία της παραμέτρου , , ή στην εγγραφή απόκρισης σημαίνει αυτόματα ότι αυτή η παράμετρος δέχεται όλες τις πιθανές ακέραιες τιμές. Θα καθοριστούν εξαιρέσεις.)
Προφανώς, οι τρεις περιπτώσεις που παρατίθενται δεν εξαντλούν όλες τις δυνατότητες γραφής της απάντησης στην εξίσωση που εξετάζουμε (είναι άπειρες).
Για παράδειγμα, όταν η ισότητα είναι αληθινή 
. Επομένως, στις δύο πρώτες περιπτώσεις, εάν , μπορούμε να αντικαταστήσουμε με .
Συνήθως η απάντηση γράφεται με βάση το σημείο 2. Είναι χρήσιμο να θυμάστε την ακόλουθη σύσταση: εάν η εργασία δεν τελειώσει με την επίλυση της εξίσωσης, είναι ακόμα απαραίτητο να διεξαχθεί έρευνα και να επιλέξετε ρίζες, τότε η πιο βολική μορφή καταγραφής υποδεικνύεται στο σημείο 1. (Μια παρόμοια σύσταση θα πρέπει να δοθεί για την εξίσωση.)
Ας εξετάσουμε ένα παράδειγμα που δείχνει τα όσα ειπώθηκαν.
Παράδειγμα Λύστε την εξίσωση.
Λύση.Ο πιο προφανής τρόπος είναι ο παρακάτω. Αυτή η εξίσωση χωρίζεται σε δύο: και . Λύνοντας καθένα από αυτά και συνδυάζοντας τις απαντήσεις που ελήφθησαν, βρίσκουμε .
Ενας άλλος τρόπος.Από τότε, αντικαθιστώντας και χρησιμοποιώντας τους τύπους για τη μείωση του βαθμού. Μετά από μικρές μετατροπές φτάνουμε , από πού 
.
Με την πρώτη ματιά, η δεύτερη φόρμουλα δεν έχει ιδιαίτερα πλεονεκτήματα σε σχέση με την πρώτη. Ωστόσο, αν πάρουμε, για παράδειγμα, τότε αποδεικνύεται ότι, δηλ. η εξίσωση έχει λύση, ενώ η πρώτη μέθοδος μας οδηγεί στην απάντηση 
. «Δείτε» και αποδείξτε την ισότητα 
Όχι και τόσο εύκολο.
Απάντηση. .
Μετατροπή και συνδυασμός ομάδων γενικών λύσεων τριγωνομετρικών εξισώσεων
θα εξετάσουμε αριθμητική πρόοδος, που εκτείνεται ατελείωτα και προς τις δύο κατευθύνσεις. Τα μέλη αυτής της προόδου μπορούν να χωριστούν σε δύο ομάδες μελών, που βρίσκονται δεξιά και αριστερά ενός συγκεκριμένου μέλους που ονομάζεται κεντρικό ή μηδενικό μέλος της προόδου.
Καθορίζοντας έναν από τους όρους μιας άπειρης προόδου με έναν αριθμό μηδέν, θα πρέπει να πραγματοποιήσουμε διπλή αρίθμηση για όλους τους υπόλοιπους όρους: θετικός για όρους που βρίσκονται στα δεξιά και αρνητικός για όρους που βρίσκονται στα αριστερά του μηδενός.
Γενικά, αν η διαφορά της προόδου είναι ο μηδενικός όρος, ο τύπος για οποιονδήποτε (ο) όρο μιας άπειρης αριθμητικής προόδου είναι:
Μετασχηματισμοί τύπου για οποιονδήποτε όρο μιας άπειρης αριθμητικής προόδου
1. Αν προσθέσετε ή αφαιρέσετε τη διαφορά της προόδου στον μηδενικό όρο, τότε η πρόοδος δεν θα αλλάξει, αλλά θα μετακινηθεί μόνο ο μηδενικός όρος, δηλ. Η αρίθμηση των μελών θα αλλάξει.
2. Αν ο συντελεστής στο μεταβλητόςπολλαπλασιαζόμενο επί , τότε αυτό θα οδηγήσει μόνο σε αναδιάταξη της δεξιάς και της αριστερής ομάδας μελών.
3. Αν διαδοχικοί όροι άπειρης προόδου
για παράδειγμα, , , ..., , κάντε τους κεντρικούς όρους των προόδων με την ίδια διαφορά ίσο με:
τότε μια πρόοδος και μια σειρά προόδους εκφράζουν τους ίδιους αριθμούς.
Παράδειγμα Η σειρά μπορεί να αντικατασταθεί από τις ακόλουθες τρεις σειρές: , , .
4. Εάν άπειρες προόδους με την ίδια διαφορά έχουν ως κεντρικούς όρους αριθμούς που σχηματίζουν αριθμητική πρόοδο με διαφορά, τότε αυτές οι σειρές μπορούν να αντικατασταθούν από μία πρόοδο με διαφορά και με έναν κεντρικό όρο ίσο με οποιονδήποτε από τους κεντρικούς όρους αυτών των προόδων, δηλ. Αν
τότε αυτές οι προόδους συνδυάζονται σε μία:
Παράδειγμα
Και τα δύο συνδυάζονται σε μια ομάδα 
.
Για να μετατραπούν οι ομάδες που έχουν κοινές λύσεις σε ομάδες που δεν έχουν κοινές λύσεις, αυτές οι ομάδες αποσυντίθενται σε ομάδες με κοινή περίοδο και στη συνέχεια προσπαθούν να ενώσουν τις ομάδες που προκύπτουν, εξαιρουμένων των επαναλαμβανόμενων.
Παραγοντοποίηση
Η μέθοδος παραγοντοποίησης είναι η εξής: αν
τότε κάθε λύση της εξίσωσης
είναι η λύση ενός συνόλου εξισώσεων
Η αντίστροφη πρόταση είναι, σε γενικές γραμμές, ψευδής: δεν είναι κάθε λύση του πληθυσμού λύση της εξίσωσης. Αυτό εξηγείται από το γεγονός ότι λύσεις σε μεμονωμένες εξισώσεις μπορεί να μην περιλαμβάνονται στον τομέα ορισμού της συνάρτησης.
Παράδειγμα Λύστε την εξίσωση.
Λύση.Χρησιμοποιώντας τη βασική τριγωνομετρική ταυτότητα, αναπαριστάνουμε την εξίσωση στη μορφή
Απάντηση.
; 
.
Μετατροπή του αθροίσματος των τριγωνομετρικών συναρτήσεων σε γινόμενο
Παράδειγμα
Λύστε την εξίσωση 
.
Λύση.Εφαρμόζοντας τον τύπο, παίρνουμε την ισοδύναμη εξίσωση
Απάντηση. .
Παράδειγμα Λύστε την εξίσωση.
Λύση.Σε αυτήν την περίπτωση, πριν εφαρμόσετε τους τύπους για το άθροισμα των τριγωνομετρικών συναρτήσεων, θα πρέπει να χρησιμοποιήσετε τον τύπο αναγωγής 
. Ως αποτέλεσμα, παίρνουμε την ισοδύναμη εξίσωση
Απάντηση.
, 
.
Επίλυση εξισώσεων μετατρέποντας το γινόμενο τριγωνομετρικών συναρτήσεων σε άθροισμα
Κατά την επίλυση ενός αριθμού εξισώσεων, χρησιμοποιούνται τύποι.
Παράδειγμα Λύστε την εξίσωση
Λύση.
Απάντηση. , .
Παράδειγμα Λύστε την εξίσωση.
Λύση.Εφαρμόζοντας τον τύπο, παίρνουμε μια ισοδύναμη εξίσωση:
Απάντηση. .
Επίλυση εξισώσεων με χρήση τύπων αναγωγής
Για την επίλυση μεγάλου εύρους τριγωνομετρικών εξισώσεων ρόλος κλειδίπαίζουν τύποι.
Παράδειγμα Λύστε την εξίσωση.
Λύση.Εφαρμόζοντας τον τύπο, παίρνουμε μια ισοδύναμη εξίσωση.
Απάντηση. ; .
Επίλυση εξισώσεων χρησιμοποιώντας τύπους τριπλού ορίσματος
Παράδειγμα Λύστε την εξίσωση.
Λύση.Εφαρμόζοντας τον τύπο, παίρνουμε την εξίσωση
Απάντηση. ; .
Παράδειγμα
Λύστε την εξίσωση 
.
Λύση.Εφαρμόζοντας τους τύπους για τη μείωση του πτυχίου παίρνουμε: 
. Με την εφαρμογή παίρνουμε:
Απάντηση. ; .
Ισότητα ομώνυμων τριγωνομετρικών συναρτήσεων
Παράδειγμα Λύστε την εξίσωση.
Λύση.
Απάντηση. , .
Παράδειγμα
Λύστε την εξίσωση 
.
Λύση.Ας μετατρέψουμε την εξίσωση.
Απάντηση. .
Παράδειγμα Είναι γνωστό ότι και ικανοποιούν την εξίσωση
Βρείτε το ποσό.
Λύση.Από την εξίσωση προκύπτει ότι
Απάντηση. .
Ας εξετάσουμε τα αθροίσματα της φόρμας
Αυτά τα ποσά μπορούν να μετατραπούν σε γινόμενο πολλαπλασιάζοντας και διαιρώντας τα με, τότε παίρνουμε
Αυτή η τεχνική μπορεί να χρησιμοποιηθεί για την επίλυση ορισμένων τριγωνομετρικών εξισώσεων, αλλά θα πρέπει να ληφθεί υπόψη ότι ως αποτέλεσμα μπορεί να εμφανιστούν ξένες ρίζες. Ας συνοψίσουμε αυτούς τους τύπους:
Παράδειγμα Λύστε την εξίσωση.
Λύση.Μπορεί να φανεί ότι το σύνολο είναι μια λύση στην αρχική εξίσωση. Επομένως, ο πολλαπλασιασμός της αριστερής και της δεξιάς πλευράς της εξίσωσης με δεν θα οδηγήσει στην εμφάνιση επιπλέον ριζών.
Εχουμε 
.
Απάντηση. ; .
Παράδειγμα Λύστε την εξίσωση.
Λύση.Ας πολλαπλασιάσουμε την αριστερή και τη δεξιά πλευρά της εξίσωσης με και ας εφαρμόσουμε τους τύπους για τη μετατροπή του γινομένου των τριγωνομετρικών συναρτήσεων σε άθροισμα, παίρνουμε
Αυτή η εξίσωση είναι ισοδύναμη με το συνδυασμό δύο εξισώσεων και , όπου και .
Εφόσον οι ρίζες της εξίσωσης δεν είναι οι ρίζες της εξίσωσης, θα πρέπει να εξαιρέσουμε το . Αυτό σημαίνει ότι στο σύνολο είναι απαραίτητο να εξαιρεθούν .
Απάντηση.Και , .
Παράδειγμα
Λύστε την εξίσωση 
.
Λύση.Ας μετατρέψουμε την έκφραση:
Η εξίσωση θα γραφτεί ως εξής:
Απάντηση. .
Αναγωγή τριγωνομετρικών εξισώσεων σε αλγεβρικές
Ανάγεται σε τετράγωνο
Αν η εξίσωση είναι της μορφής
τότε η αντικατάσταση το οδηγεί στο τετράγωνο, αφού 
() Και.
Αν αντί του όρου υπάρχει , τότε η απαιτούμενη αντικατάσταση θα είναι .
Η εξίσωση
κατεβαίνει σε τετραγωνική εξίσωση
παρουσίαση ως 
. Είναι εύκολο να ελεγχθεί αυτό για το οποίο , δεν είναι ρίζες της εξίσωσης, και κάνοντας την αντικατάσταση, η εξίσωση ανάγεται σε τετραγωνική.
Παράδειγμα Λύστε την εξίσωση.
Λύση.Ας το μετακινήσουμε στην αριστερή πλευρά, ας το αντικαταστήσουμε με , και ας το εκφράσουμε μέσω και .
Μετά από απλοποιήσεις παίρνουμε: . Διαιρέστε όρο προς όρο και κάντε την αντικατάσταση:
Επιστρέφοντας στο , βρίσκουμε 
.
Εξισώσεις ομοιογενείς ως προς ,
Θεωρήστε μια εξίσωση της μορφής
Οπου , , , ..., , --- ισχύειαριθμοί. Σε κάθε όρο στην αριστερή πλευρά της εξίσωσης, οι μοίρες των μονοωνύμων είναι ίσες, δηλαδή το άθροισμα των βαθμών του ημιτόνου και του συνημιτόνου είναι ίδιο και ίσο. Αυτή η εξίσωση ονομάζεται ομοιογενήςσε σχέση με και , και ο αριθμός ονομάζεται δείκτης ομοιογένειας .
Είναι σαφές ότι αν , τότε η εξίσωση θα έχει τη μορφή:
οι λύσεις των οποίων είναι οι τιμές στις οποίες , δηλ. οι αριθμοί , . Η δεύτερη εξίσωση γραμμένη σε αγκύλες είναι επίσης ομοιογενής, αλλά οι μοίρες είναι 1 χαμηλότερες.
Αν , τότε αυτοί οι αριθμοί δεν είναι οι ρίζες της εξίσωσης.
Όταν παίρνουμε: , και η αριστερή πλευρά της εξίσωσης (1) παίρνει την τιμή .
Έτσι, για , και , επομένως μπορούμε να διαιρέσουμε και τις δύο πλευρές της εξίσωσης με . Ως αποτέλεσμα, παίρνουμε την εξίσωση:
το οποίο, με αντικατάσταση, μπορεί εύκολα να αναχθεί σε αλγεβρικό:
Ομογενείς εξισώσεις με δείκτη ομοιογένειας 1. Όταν έχουμε την εξίσωση .
Αν , τότε αυτή η εξίσωση είναι ισοδύναμη με την εξίσωση , , από όπου , .
Παράδειγμα Λύστε την εξίσωση.
Λύση.Αυτή η εξίσωση είναι ομοιογενής πρώτου βαθμού. Διαιρούμε και τα δύο μέρη παίρνουμε: , , , .
Απάντηση. .
Παράδειγμα Όταν φτάσουμε ομοιογενής εξίσωσηείδος
Λύση.
Αν , τότε διαιρούμε και τις δύο πλευρές της εξίσωσης με , παίρνουμε την εξίσωση 
, το οποίο μπορεί εύκολα να μειωθεί σε τετράγωνο με αντικατάσταση: 
. Αν 
, τότε η εξίσωση έχει πραγματικές ρίζες , . Η αρχική εξίσωση θα έχει δύο ομάδες λύσεων: , , .
Αν 
, τότε η εξίσωση δεν έχει λύσεις.
Παράδειγμα Λύστε την εξίσωση.
Λύση.Αυτή η εξίσωση ομοιογενής δεύτερηβαθμούς. Διαιρούμε και τις δύο πλευρές της εξίσωσης με , παίρνουμε: . Ας , λοιπόν , , . , , ; .
Απάντηση.
.
Η εξίσωση ανάγεται σε μια εξίσωση της μορφής
Για να γίνει αυτό, αρκεί να χρησιμοποιήσετε την ταυτότητα 
Συγκεκριμένα, η εξίσωση ανάγεται σε ομοιογενή αν την αντικαταστήσουμε με 
, τότε παίρνουμε μια ισοδύναμη εξίσωση:
Παράδειγμα Λύστε την εξίσωση.
Λύση.Ας μετατρέψουμε την εξίσωση σε ομοιογενή:
Ας διαιρέσουμε και τις δύο πλευρές της εξίσωσης με 
, παίρνουμε την εξίσωση:
Έστω, τότε ερχόμαστε στην τετραγωνική εξίσωση: 
, , 
, 
, .
Απάντηση.
.
Παράδειγμα Λύστε την εξίσωση.
Λύση.Ας τετραγωνίσουμε και τις δύο πλευρές της εξίσωσης, λαμβάνοντας υπόψη ότι έχουν θετικές τιμές: , ,
Ας είναι, τότε παίρνουμε 
, , .
Απάντηση. .
Εξισώσεις που λύνονται με χρήση ταυτοτήτων 
Είναι χρήσιμο να γνωρίζετε τους ακόλουθους τύπους:
Παράδειγμα Λύστε την εξίσωση.
Λύση.Χρησιμοποιώντας, παίρνουμε
Απάντηση.
Δεν προσφέρουμε τους ίδιους τους τύπους, αλλά μια μέθοδο εξαγωγής τους:
ως εκ τούτου,
Ομοίως,.
Παράδειγμα
Λύστε την εξίσωση 
.
Λύση.Ας μετατρέψουμε την έκφραση:
Η εξίσωση θα γραφτεί ως εξής:
Με την αποδοχή, λαμβάνουμε. , . Ως εκ τούτου
Απάντηση. .
Καθολική τριγωνομετρική αντικατάσταση
Τριγωνομετρική εξίσωση της φόρμας
Οπου --- ορθολογικόμια συνάρτηση με τη βοήθεια τύπων - , καθώς και με τη βοήθεια τύπων - μπορεί να μειωθεί σε ορθολογική εξίσωσησε σχέση με τα ορίσματα , , , , μετά από τα οποία η εξίσωση μπορεί να αναχθεί σε μια αλγεβρική ορθολογική εξίσωση σε σχέση με τη χρήση των τύπων καθολικής τριγωνομετρικής υποκατάστασης
Θα πρέπει να σημειωθεί ότι η χρήση τύπων μπορεί να οδηγήσει σε στένωση του OD της αρχικής εξίσωσης, καθώς δεν ορίζεται στα σημεία, επομένως σε τέτοιες περιπτώσεις είναι απαραίτητο να ελεγχθεί εάν οι γωνίες είναι οι ρίζες της αρχικής εξίσωσης .
Παράδειγμα Λύστε την εξίσωση.
Λύση.Σύμφωνα με τις συνθήκες της εργασίας. Εφαρμόζοντας τους τύπους και κάνοντας την αντικατάσταση, παίρνουμε
από πού και επομένως .
Εξισώσεις της φόρμας
Εξισώσεις της μορφής , όπου --- πολυώνυμο, επιλύονται χρησιμοποιώντας αντικαταστάσεις αγνώστων
Παράδειγμα Λύστε την εξίσωση.
Λύση.Κάνοντας την αντικατάσταση και λαμβάνοντας υπόψη ότι , παίρνουμε
που , . --- εξωτερικόςρίζα, γιατί . Ρίζες της εξίσωσης 
είναι .
Χρήση περιορισμών χαρακτηριστικών
Στην πρακτική της κεντρικής δοκιμής, δεν είναι τόσο σπάνιο να συναντήσουμε εξισώσεις των οποίων η λύση βασίζεται στις περιορισμένες συναρτήσεις και . Για παράδειγμα:
Παράδειγμα Λύστε την εξίσωση.
Λύση.Αφού , , τότε η αριστερή πλευρά δεν υπερβαίνει και ισούται με , αν
Για να βρούμε τιμές που ικανοποιούν και τις δύο εξισώσεις, προχωράμε ως εξής. Ας λύσουμε ένα από αυτά και, στη συνέχεια, μεταξύ των τιμών που βρέθηκαν θα επιλέξουμε αυτές που ικανοποιούν τις άλλες.
Ας ξεκινήσουμε με το δεύτερο: , . Επειτα , 
.
Είναι σαφές ότι μόνο για ζυγούς αριθμούς θα υπάρχουν .
Απάντηση. .
Μια άλλη ιδέα υλοποιείται λύνοντας την ακόλουθη εξίσωση:
Παράδειγμα
Λύστε την εξίσωση 
.
Λύση.Ας χρησιμοποιήσουμε το ακίνητο εκθετικη συναρτηση: , 
.
Προσθέτοντας αυτές τις ανισότητες ανά όρο έχουμε:
Επομένως, η αριστερή πλευρά αυτής της εξίσωσης είναι ίση εάν και μόνο εάν ικανοποιούνται δύο ισότητες:
δηλαδή μπορεί να πάρει τις τιμές , , , ή μπορεί να πάρει τις τιμές , .
Απάντηση. , .
Παράδειγμα
Λύστε την εξίσωση 
.
Λύση., . Ως εκ τούτου, 
.
Απάντηση. .
Παράδειγμα Λύστε την εξίσωση
Λύση.Ας υποδηλώσουμε , τότε από τον ορισμό της αντίστροφης τριγωνομετρικής συνάρτησης έχουμε 
Και 
.
Αφού, τότε η ανισότητα προκύπτει από την εξίσωση, δηλ. . Αφού και , τότε και . Ωστόσο, γι' αυτό.
Αν και, τότε. Αφού προηγουμένως είχε διαπιστωθεί ότι , τότε .
Απάντηση. , .
Παράδειγμα Λύστε την εξίσωση
Λύση.Περιοχή αποδεκτές τιμέςοι εξισώσεις είναι .
Πρώτα δείχνουμε ότι η συνάρτηση
Για οποιοδήποτε, μπορεί να πάρει μόνο θετικές τιμές.
Ας φανταστούμε τη συνάρτηση ως εξής: .
Αφού , τότε λαμβάνει χώρα, δηλ. 
.
Επομένως, για να αποδειχθεί η ανισότητα, είναι απαραίτητο να δείξουμε ότι 
. Για το σκοπό αυτό, ας κύβουμε λοιπόν και τις δύο πλευρές αυτής της ανισότητας
Η αριθμητική ανισότητα που προκύπτει δείχνει ότι . Αν λάβουμε επίσης υπόψη ότι , τότε η αριστερή πλευρά της εξίσωσης είναι μη αρνητική.
Ας δούμε τώρα τη δεξιά πλευρά της εξίσωσης.
Επειδή 
, Οτι
Ωστόσο, είναι γνωστό ότι 
. Από αυτό προκύπτει ότι, δηλ. δεξί μέροςη εξίσωση δεν υπερβαίνει το . Είχε αποδειχθεί προηγουμένως ότι η αριστερή πλευρά της εξίσωσης είναι μη αρνητική, επομένως η ισότητα μπορεί να συμβεί μόνο εάν και οι δύο πλευρές είναι ίσες, και αυτό είναι δυνατό μόνο εάν .
Απάντηση. .
Παράδειγμα Λύστε την εξίσωση
Λύση.Ας υποδηλώσουμε και 
. Εφαρμόζοντας την ανισότητα Cauchy-Bunyakovsky, λαμβάνουμε . Από αυτό προκύπτει ότι 
. Από την άλλη, υπάρχει 
. Επομένως, η εξίσωση δεν έχει ρίζες.
Απάντηση. .
Παράδειγμα Λύστε την εξίσωση:
Λύση.Ας ξαναγράψουμε την εξίσωση ως εξής:
Απάντηση. .
Λειτουργικές μέθοδοι επίλυσης τριγωνομετρικών και συνδυασμένων εξισώσεων
Δεν μπορεί κάθε εξίσωση ως αποτέλεσμα μετασχηματισμών να αναχθεί σε μια εξίσωση μιας ή άλλης τυπικής μορφής, για την οποία υπάρχει μια συγκεκριμένη μέθοδος επίλυσης. Σε τέτοιες περιπτώσεις, αποδεικνύεται χρήσιμο να χρησιμοποιηθούν τέτοιες ιδιότητες συναρτήσεων όπως μονοτονία, περιορισμός, ισοτιμία, περιοδικότητα κ.λπ. Έτσι, εάν μια από τις συναρτήσεις μειωθεί και η δεύτερη αυξηθεί στο διάστημα, τότε εάν η εξίσωση έχει root σε αυτό το διάστημα, αυτή η ρίζα είναι μοναδική και, για παράδειγμα, μπορεί να βρεθεί με επιλογή. Αν η συνάρτηση είναι οριοθετημένη πάνω, και , και η συνάρτηση είναι περιορισμένη από κάτω, και , τότε η εξίσωση είναι ισοδύναμη με το σύστημα των εξισώσεων
Παράδειγμα Λύστε την εξίσωση
Λύση.Ας μετατρέψουμε την αρχική εξίσωση στη μορφή
και να το λύσετε ως τετραγωνικό σε σχέση με το . Τότε παίρνουμε,
Ας λύσουμε την πρώτη εξίσωση του πληθυσμού. Λαμβάνοντας υπόψη την περιορισμένη φύση της συνάρτησης, καταλήγουμε στο συμπέρασμα ότι η εξίσωση μπορεί να έχει μόνο ρίζα στο τμήμα. Σε αυτό το διάστημα η συνάρτηση αυξάνεται και η συνάρτηση 
μειώνεται. Επομένως, αν αυτή η εξίσωση έχει ρίζα, τότε είναι μοναδική. Βρίσκουμε με επιλογή.
Απάντηση. .
Παράδειγμα Λύστε την εξίσωση
Λύση.Αφήστε και 
, τότε η αρχική εξίσωση μπορεί να γραφτεί ως συναρτησιακή εξίσωση. Εφόσον η συνάρτηση είναι περιττή, τότε . Σε αυτή την περίπτωση, παίρνουμε την εξίσωση.
Εφόσον , και είναι μονότονη στις , η εξίσωση είναι ισοδύναμη με την εξίσωση, δηλ. 
, που έχει μία μόνο ρίζα.
Απάντηση. .
Παράδειγμα
Λύστε την εξίσωση 
.
Λύση.Με βάση το θεώρημα για την παράγωγο μιας μιγαδικής συνάρτησης, είναι σαφές ότι η συνάρτηση 
φθίνουσα (συνάρτηση μείωση, αύξηση, μείωση). Από αυτό είναι σαφές ότι η συνάρτηση 
ορίζεται στις , φθίνουσα. Να γιατί δεδομένη εξίσωσηέχει το πολύ μία ρίζα. Επειδή 
, Οτι
Απάντηση. .
Παράδειγμα Λύστε την εξίσωση.
Λύση.Ας εξετάσουμε την εξίσωση σε τρία διαστήματα.
α) Αφήστε . Τότε σε αυτό το σύνολο η αρχική εξίσωση είναι ισοδύναμη με την εξίσωση . Το οποίο δεν έχει λύσεις στο διάστημα, γιατί 
, , ΕΝΑ . Στο διάστημα, η αρχική εξίσωση επίσης δεν έχει ρίζες, γιατί 
, ΕΝΑ .
β) Αφήστε . Τότε σε αυτό το σύνολο η αρχική εξίσωση είναι ισοδύναμη με την εξίσωση
των οποίων οι ρίζες στο διάστημα είναι οι αριθμοί , , , .
γ) Αφήστε . Τότε σε αυτό το σύνολο η αρχική εξίσωση είναι ισοδύναμη με την εξίσωση
Το οποίο δεν έχει λύσεις στο διάστημα, γιατί , και . Στο διάστημα, η εξίσωση επίσης δεν έχει λύσεις, γιατί , , ΕΝΑ .
Απάντηση. , , , .
Μέθοδος συμμετρίας
Η μέθοδος συμμετρίας είναι βολική στη χρήση όταν η διατύπωση της εργασίας απαιτεί τη μοναδική λύση μιας εξίσωσης, ανισότητας, συστήματος κ.λπ. ή ακριβής ένδειξη του αριθμού των λύσεων. Σε αυτήν την περίπτωση, θα πρέπει να εντοπιστεί οποιαδήποτε συμμετρία των παραστάσεων.
Είναι επίσης απαραίτητο να ληφθεί υπόψη η ποικιλία των διαφορετικών πιθανών τύπων συμμετρίας.
Εξίσου σημαντική είναι η αυστηρή τήρηση των λογικών σταδίων στο συλλογισμό με συμμετρία.
Τυπικά, η συμμετρία επιτρέπει σε κάποιον να εδραιωθεί μόνο τις απαραίτητες προϋποθέσεις, και στη συνέχεια απαιτείται έλεγχος της επάρκειάς τους.
Παράδειγμα Βρείτε όλες τις τιμές της παραμέτρου για την οποία η εξίσωση έχει μια μοναδική λύση.
Λύση.Σημειώστε ότι --- ακόμη καισυναρτήσεις, άρα η αριστερή πλευρά της εξίσωσης είναι άρτια συνάρτηση.
Οπότε αν --- λύσηεξισώσεις, δηλαδή και τη λύση της εξίσωσης. Αν --- το μόνο πράγμαλύση της εξίσωσης, λοιπόν απαραίτητη , .
Θα επιλέξουμε δυνατόντιμές, απαιτώντας να είναι η ρίζα της εξίσωσης.
Ας σημειώσουμε αμέσως ότι άλλες τιμές δεν μπορούν να ικανοποιήσουν τις συνθήκες του προβλήματος.
Αλλά δεν είναι ακόμη γνωστό εάν όλοι όσοι επιλέχθηκαν όντως ικανοποιούν τις προϋποθέσεις του προβλήματος.
Επάρκεια.
1), η εξίσωση θα πάρει τη μορφή 
.
2), η εξίσωση θα έχει τη μορφή:
Είναι προφανές ότι, για όλους και 
. Επομένως, η τελευταία εξίσωση είναι ισοδύναμη με το σύστημα:
Έτσι, αποδείξαμε ότι για , η εξίσωση έχει μια μοναδική λύση.
Απάντηση. .
Λύση με εξερεύνηση συναρτήσεων
Παράδειγμα Να αποδείξετε ότι όλες οι λύσεις της εξίσωσης
Ολόκληροι αριθμοί.
Λύση.Η κύρια περίοδος της αρχικής εξίσωσης είναι . Επομένως, εξετάζουμε πρώτα αυτήν την εξίσωση στο διάστημα.
Ας μετατρέψουμε την εξίσωση στη μορφή:
Χρησιμοποιώντας έναν μικροϋπολογιστή παίρνουμε:
Αν , τότε από τις προηγούμενες ισότητες παίρνουμε:
Έχοντας λύσει την εξίσωση που προκύπτει, παίρνουμε: .
Οι υπολογισμοί που πραγματοποιήθηκαν καθιστούν δυνατό να υποθέσουμε ότι οι ρίζες της εξίσωσης που ανήκει στο τμήμα είναι , και .
Ο άμεσος έλεγχος επιβεβαιώνει αυτή την υπόθεση. Έτσι, έχει αποδειχθεί ότι οι ρίζες της εξίσωσης είναι μόνο ακέραιοι , .
Παράδειγμα
Λύστε την εξίσωση 
.
Λύση.Ας βρούμε την κύρια περίοδο της εξίσωσης. Η συνάρτηση έχει μια βασική περίοδο ίση με . Η κύρια περίοδος της λειτουργίας είναι . Το ελάχιστο κοινό πολλαπλάσιο του και είναι ίσο με . Επομένως, η κύρια περίοδος της εξίσωσης είναι . Αφήστε .
Προφανώς, είναι μια λύση της εξίσωσης. Στο μεσοδιάστημα. Η συνάρτηση είναι αρνητική. Επομένως, άλλες ρίζες της εξίσωσης θα πρέπει να αναζητηθούν μόνο στα διαστήματα x και .
Χρησιμοποιώντας έναν μικροϋπολογιστή, βρίσκουμε πρώτα τις κατά προσέγγιση τιμές των ριζών της εξίσωσης. Για να γίνει αυτό, συντάσσουμε έναν πίνακα τιμών συναρτήσεων 
στα διαστήματα και ? δηλαδή στα διαστήματα και .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
Από τον πίνακα διακρίνονται εύκολα οι ακόλουθες υποθέσεις: οι ρίζες της εξίσωσης που ανήκει στο τμήμα είναι οι αριθμοί: ; ; . Ο άμεσος έλεγχος επιβεβαιώνει αυτή την υπόθεση.
Απάντηση.
; 
; .
Επίλυση τριγωνομετρικών ανισώσεων χρησιμοποιώντας τον μοναδιαίο κύκλο
Κατά την επίλυση τριγωνομετρικών ανισοτήτων της μορφής , όπου είναι μία από τις τριγωνομετρικές συναρτήσεις, είναι βολικό να χρησιμοποιήσετε τριγωνομετρικός κύκλοςγια να παρουσιάσετε με μεγαλύτερη σαφήνεια τις λύσεις της ανισότητας και να γράψετε την απάντηση. Η κύρια μέθοδος για την επίλυση τριγωνομετρικών ανισώσεων είναι η αναγωγή τους στις απλούστερες ανισώσεις του τύπου. Ας δούμε ένα παράδειγμα για το πώς να λύσουμε τέτοιες ανισότητες.
Παράδειγμα Λύστε την ανισότητα.
Λύση.Ας σχεδιάσουμε έναν τριγωνομετρικό κύκλο και ας σημειώσουμε πάνω του τα σημεία για τα οποία η τεταγμένη υπερβαίνει το .
Η λύση σε αυτή την ανισότητα θα είναι . Είναι επίσης σαφές ότι εάν ένας συγκεκριμένος αριθμός διαφέρει από οποιονδήποτε αριθμό από το καθορισμένο διάστημα κατά , τότε δεν θα είναι επίσης μικρότερος από . Επομένως, χρειάζεται απλώς να προσθέσετε στα άκρα του τμήματος της εύρεσης λύσης. Τέλος, διαπιστώνουμε ότι οι λύσεις στην αρχική ανισότητα θα είναι όλες 
.
Απάντηση.
.
Για την επίλυση ανισώσεων με εφαπτομένη και συνεφαπτομένη, είναι χρήσιμη η έννοια μιας γραμμής εφαπτομένων και συνεφαπτομένων. Αυτές είναι οι ευθείες γραμμές και, αντίστοιχα (στο Σχήμα (1) και (2)), που εφάπτονται στον τριγωνομετρικό κύκλο.
Είναι εύκολο να δούμε ότι αν κατασκευάσουμε μια ακτίνα με την αρχή της στην αρχή των συντεταγμένων, κάνοντας μια γωνία με τη θετική κατεύθυνση του άξονα της τετμημένης, τότε το μήκος του τμήματος από το σημείο έως το σημείο τομής αυτής της ακτίνας με η εφαπτομένη είναι ακριβώς ίση με την εφαπτομένη της γωνίας που κάνει αυτή η ακτίνα με τον άξονα της τετμημένης. Μια παρόμοια παρατήρηση συμβαίνει για την συνεφαπτομένη.
Παράδειγμα Λύστε την ανισότητα.
Λύση.Ας υποδηλώσουμε , τότε η ανισότητα θα πάρει την απλούστερη μορφή: . Ας θεωρήσουμε ένα διάστημα μήκους ίσο με τη μικρότερη θετική περίοδο (LPP) της εφαπτομένης. Σε αυτό το τμήμα, χρησιμοποιώντας την ευθεία των εφαπτομένων, καθορίζουμε ότι . Ας θυμηθούμε τώρα τι πρέπει να προστεθεί από τη λειτουργία του NPP. Ετσι, 
. Επιστρέφοντας στη μεταβλητή, λαμβάνουμε ότι.
Απάντηση.
.
Είναι βολικό να λύνουμε ανισώσεις με αντίστροφες τριγωνομετρικές συναρτήσεις χρησιμοποιώντας γραφήματα αντίστροφων τριγωνομετρικών συναρτήσεων. Ας δείξουμε πώς γίνεται αυτό με ένα παράδειγμα.
Επίλυση τριγωνομετρικών ανισώσεων γραφικά
Σημειώστε ότι εάν --- περιοδικήσυνάρτηση, τότε για να λυθεί η ανίσωση είναι απαραίτητο να βρεθεί η λύση της σε ένα τμήμα του οποίου το μήκος είναι ίσο με την περίοδο της συνάρτησης. Όλες οι λύσεις στην αρχική ανισότητα θα αποτελούνται από τις τιμές που βρέθηκαν, καθώς και όλες εκείνες που διαφέρουν από αυτές που βρέθηκαν κατά οποιονδήποτε ακέραιο αριθμό περιόδων της συνάρτησης.
Ας εξετάσουμε τη λύση της ανισότητας ().
Αφού , τότε η ανισότητα δεν έχει λύσεις. Αν , τότε το σύνολο των λύσεων στην ανισότητα --- ένα μάτσοόλους τους πραγματικούς αριθμούς.
Αφήστε . Η συνάρτηση ημιτόνου έχει τη μικρότερη θετική περίοδο, επομένως η ανισότητα μπορεί να λυθεί πρώτα σε ένα τμήμα μήκους, για παράδειγμα, στο τμήμα. Κατασκευάζουμε γραφήματα συναρτήσεων και (). δίνονται από ανισότητες της μορφής: και, από όπου,
Στην εργασία αυτή εξετάστηκαν μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων και ανισώσεων, τόσο απλών όσο και σε επίπεδο Ολυμπιάδας. Εξετάστηκαν οι κύριες μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων και ανισώσεων και, επιπλέον, ως συγκεκριμένες --- χαρακτηριστικό γνώρισμαμόνο για τριγωνομετρικές εξισώσεις και ανισώσεις, και γενικές λειτουργικές μεθόδους για την επίλυση εξισώσεων και ανισώσεων όπως εφαρμόζονται σε τριγωνομετρικές εξισώσεις.
Η διατριβή παρέχει βασικές θεωρητικές πληροφορίες: ορισμός και ιδιότητες τριγωνομετρικών και αντίστροφων τριγωνομετρικών συναρτήσεων. έκφραση τριγωνομετρικών συναρτήσεων σε σχέση με άλλες τριγωνομετρικές συναρτήσεις, κάτι που είναι πολύ σημαντικό για τον μετασχηματισμό τριγωνομετρικών παραστάσεων, ειδικά εκείνων που περιέχουν αντίστροφες τριγωνομετρικές συναρτήσεις. Εκτός από τους βασικούς τριγωνομετρικούς τύπους, πολύ γνωστούς από το σχολικό μάθημα, δίνονται τύποι που απλοποιούν εκφράσεις που περιέχουν αντίστροφες τριγωνομετρικές συναρτήσεις. Εξετάζονται η λύση στοιχειωδών τριγωνομετρικών εξισώσεων, η μέθοδος παραγοντοποίησης και μέθοδοι αναγωγής τριγωνομετρικών εξισώσεων σε αλγεβρικές. Λόγω του γεγονότος ότι οι λύσεις σε τριγωνομετρικές εξισώσεις μπορούν να γραφτούν με πολλούς τρόπους και η μορφή αυτών των λύσεων δεν επιτρέπει σε κάποιον να προσδιορίσει αμέσως εάν αυτές οι λύσεις είναι ίδιες ή διαφορετικές, εξετάζεται ένα γενικό σχήμα για την επίλυση τριγωνομετρικών εξισώσεων και ο μετασχηματισμός ομάδων γενικών λύσεων τριγωνομετρικών εξισώσεων εξετάζεται αναλυτικά. Οι μέθοδοι επίλυσης στοιχειωδών τριγωνομετρικών ανισώσεων, τόσο στον μοναδιαίο κύκλο όσο και με τη γραφική μέθοδο, εξετάζονται λεπτομερώς. Περιγράφεται η διαδικασία επίλυσης μη στοιχειωδών τριγωνομετρικών ανισώσεων μέσω στοιχειωδών ανισώσεων και η μέθοδος των διαστημάτων, ήδη γνωστή στους μαθητές του σχολείου. Δίνονται λύσεις σε τυπικές εργασίες για την επιλογή ριζών. Δίνονται οι απαραίτητες θεωρητικές πληροφορίες για την επιλογή ριζών: διαίρεση ενός συνόλου ακεραίων σε ασύνδετα υποσύνολα, επίλυση εξισώσεων σε ακέραιους αριθμούς (διαφαντικό).
Τα αποτελέσματα αυτής της διατριβής μπορούν να χρησιμοποιηθούν ως εκπαιδευτικό υλικόκατά την προετοιμασία των μαθημάτων και διατριβές, κατά τη σύνταξη μαθημάτων επιλογής για μαθητές, η εργασία μπορεί επίσης να χρησιμοποιηθεί για την προετοιμασία των μαθητών για εισαγωγικές εξετάσεις και κεντρικές δοκιμές.
Vygodsky Ya.Ya., Εγχειρίδιο στοιχειωδών μαθηματικών. /Vygodsky Ya.Ya. --- Μ.: Nauka, 1970.
Igudisman O., Μαθηματικά στην προφορική εξέταση / Igudisman O. --- M.: Iris Press, Rolf, 2001.
Azarov A.I., equations/Azarov A.I., Gladun O.M., Fedosenko V.S. --- Μν.: Trivium, 1994.
Litvinenko V.N., Εργαστήριο για τα στοιχειώδη μαθηματικά / Litvinenko V.N.: Εκπαίδευση, 1991.
Sharygin I.F., Προαιρετικό μάθημα στα μαθηματικά: επίλυση προβλημάτων / Sharygin I.F., Golubev V.I. --- Μ.: Εκπαίδευση, 1991.
Bardushkin V., Τριγωνομετρικές εξισώσεις. Επιλογή ρίζας/Β. Bardushkin, A. Prokofiev.// Mathematics, No. 12, 2005 p. 23--27.
Vasilevsky A.B., Tasks for εξωσχολικές δραστηριότητεςστα μαθηματικά/Vasilevsky A.B. --- Μν.: Λαϊκός Ασβέτα. 1988. --- 176 σελ.
Sapunov P. I., Μετασχηματισμός και ένωση ομάδων γενικών λύσεων τριγωνομετρικών εξισώσεων / Sapunov P. I. // Μαθηματική εκπαίδευση, τεύχος αρ. 3, 1935.
Borodin P., Τριγωνομετρία. Υλικά εισαγωγικές εξετάσειςστο Κρατικό Πανεπιστήμιο της Μόσχας [κείμενο]/P Borodin, V. Galkin, V. Panferov, I. Sergeev, V. Tarasov // Mathematics No. 1, 2005 p. 36--48.
Samusenko A.V., Μαθηματικά: Κοινά λάθηαιτούντες: Εγχειρίδιο αναφοράς/Samusenko A.V., Kazachenok V.V. --- Mn.: Higher School, 1991.
Azarov A.I., Λειτουργικές και γραφικές μέθοδοι για την επίλυση προβλημάτων εξέτασης / Azarov A.I., Barvenov S.A., --- Mn.: Aversev, 2004.
- Σε επαφή με 0
- Google+ 0
- Εντάξει 0
- Facebook 0
