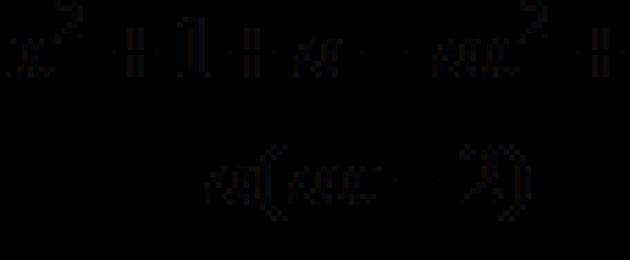Παραδείγματα συστημάτων εξισώσεων με παράμετρο. Επίλυση συστημάτων γραμμικών εξισώσεων με παραμέτρους

Μερικές φορές στις εξισώσεις, ορισμένοι συντελεστές δεν δίνονται με συγκεκριμένες αριθμητικές τιμές, αλλά υποδεικνύονται με γράμματα.

Παράδειγμα: τσεκούρι+β=γ.

Σε αυτή την εξίσωση Χ– άγνωστο, α, β, γ– συντελεστές που μπορούν να λάβουν διαφορετικές αριθμητικές τιμές. Οι συντελεστές που καθορίζονται με αυτόν τον τρόπο καλούνται Παράμετροι.

Μια εξίσωση με παραμέτρους ορίζει πολλές εξισώσεις (για όλες τις πιθανές τιμές παραμέτρων).

Παράδειγμα: –5 Χ+10=– 1;

Χ+4y= 0;

–102–1000y=; και τα λοιπά.

Αυτές είναι όλες οι εξισώσεις που καθορίζονται από την εξίσωση με τις παραμέτρους τσεκούρι+β=γ.

Η επίλυση μιας εξίσωσης με παραμέτρους σημαίνει:

1. Υποδείξτε σε ποιες τιμές παραμέτρων έχει ρίζες η εξίσωση και πόσες υπάρχουν για διαφορετικές τιμές παραμέτρων.

2. Βρείτε όλες τις εκφράσεις για τις ρίζες και υποδείξτε για καθεμία από αυτές τις τιμές παραμέτρων στις οποίες αυτή η έκφραση καθορίζει τη ρίζα της εξίσωσης.

Ας στραφούμε στην ήδη δοθείσα εξίσωση με τις παραμέτρους τσεκούρι+β=γκαι θα το λύσουμε.

Αν ΕΝΑ¹0, στη συνέχεια https://pandia.ru/text/80/014/images/image002_67.gif" width="63" height="41">;

στο a=0Και b=c, x– οποιοσδήποτε πραγματικός αριθμός.

στο a=0Και σι¹ ντο,η εξίσωση δεν έχει ρίζες.

Στη διαδικασία επίλυσης αυτής της εξίσωσης, απομονώσαμε την τιμή της παραμέτρου a=0, στην οποία συμβαίνει μια ποιοτική αλλαγή στην εξίσωση, θα ονομάσουμε περαιτέρω αυτή την τιμή της παραμέτρου «έλεγχος». Ανάλογα με το είδος της εξίσωσης που έχουμε, οι τιμές "ελέγχου" της παραμέτρου βρίσκονται διαφορετικά. Ας δούμε διαφορετικούς τύπους εξισώσεων και ας υποδείξουμε πώς να βρούμε τις τιμές "ελέγχου" της παραμέτρου.

I. Γραμμικές εξισώσεις με παράμετρο και εξισώσεις ανάγουσες σε γραμμικές

Σε τέτοιες εξισώσεις, οι τιμές "ελέγχου" των παραμέτρων, κατά κανόνα, είναι οι τιμές που κάνουν τους συντελεστές στο μηδέν Χ.

Παράδειγμα 1. : 2ΕΝΑ(ΕΝΑ–2)x=a– 2

1. Οι τιμές "Control" είναι τιμές που ικανοποιούν την προϋπόθεση:

2ΕΝΑ(ΕΝΑ–2)=0

Ας λύσουμε αυτήν την εξίσωση για τη μεταβλητή ΕΝΑ.

2α= 0 ή ΕΝΑ–2= 0, από όπου α= 0, α= 2.

2. Ας λύσουμε την αρχική εξίσωση για τις τιμές «ελέγχου» της παραμέτρου.

Στο α= 0 έχουμε 0× x=– 2, αλλά αυτό δεν ισχύει για οποιεσδήποτε πραγματικές τιμές Χ, δηλαδή σε αυτή την περίπτωση η εξίσωση δεν έχει ρίζες.

Στο α= 2 έχουμε 0× x= 0, αυτό ισχύει για οποιαδήποτε τιμή Χ, που σημαίνει ότι η ρίζα της εξίσωσης είναι οποιοσδήποτε πραγματικός αριθμός Χ.

3. Ας λύσουμε την αρχική εξίσωση στην περίπτωση όταν ΕΝΑ¹ 0 και ΕΝΑ¹ 2 μετά 2 ΕΝΑ(ΕΝΑ–2)¹ 0 και οι δύο πλευρές της εξίσωσης μπορούν να διαιρεθούν με το 2 ΕΝΑ(ΕΝΑ–2), παίρνουμε:

Επειδή ΕΝΑ¹ 2, τότε το κλάσμα μπορεί να μειωθεί κατά ( ΕΝΑ–2), τότε έχουμε .

Απάντηση:στο α= 0, χωρίς ρίζες.

στο α= 2, ρίζα – οποιοσδήποτε πραγματικός αριθμός.

στο ΕΝΑ¹ 0, ΕΝΑ¹ 2, .

Μπορεί κανείς να φανταστεί έναν αλγόριθμο για την επίλυση αυτού του τύπου εξίσωσης.

1. Προσδιορίστε τις τιμές "ελέγχου" της παραμέτρου.

2. Λύστε την εξίσωση για Χ, σε τιμές παραμέτρων ελέγχου.

3. Λύστε την εξίσωση για Χ, σε τιμές διαφορετικές από τις τιμές «ελέγχου».

4. Γράψτε την απάντηση στη φόρμα:

Απάντηση: 1) για τις τιμές των παραμέτρων..., η εξίσωση έχει ρίζες...;

2) για τις τιμές των παραμέτρων..., η εξίσωση έχει ρίζες...;

3) για τις τιμές της παραμέτρου..., η εξίσωση δεν έχει ρίζες.

Παράδειγμα 2. Επίλυση εξίσωσης με παράμετρο

(ΕΝΑ 2–2ΕΝΑ+1)x=a 2+2ΕΝΑ- 3

1. Βρείτε τις τιμές ελέγχου της παραμέτρου

ΕΝΑ 2–2ΕΝΑ+1=0 Û ( ΕΝΑ–1)2=0 Û ΕΝΑ=1

2. Λύστε την εξίσωση για α= 1

0× x=(1+2×1–3) Û 0× x= 0 Þ Χ– οποιοδήποτε πραγματικό αριθμό.

3. Λύστε την εξίσωση για ΕΝΑ¹ 1

ΕΝΑ 2–2ΕΝΑ+1¹ 0 Þ https://pandia.ru/text/80/014/images/image006_39.gif" width="115" height="45 src=">

επειδή ΕΝΑ¹ 1, το κλάσμα μπορεί να μειωθεί

https://pandia.ru/text/80/014/images/image007_35.gif" width="64" height="41 src=">.

Παράδειγμα 3. Επίλυση εξίσωσης με παράμετρο

https://pandia.ru/text/80/014/images/image009_29.gif" width="72" height="41 src=">.

4. Απάντηση: 1) στο α= 2, χωρίς ρίζες.

2) πότε ΕΝΑ¹ 0,ΕΝΑ¹ 2, ;

3) πότε α=Η εξίσωση 0 δεν έχει νόημα.

Παράδειγμα 4. Επίλυση εξίσωσης με παράμετρο

https://pandia.ru/text/80/014/images/image011_28.gif" width="135" height="45 src=">

https://pandia.ru/text/80/014/images/image013_25.gif" width="175" height="45 src=">

επειδή Χ¹ 0 και ΕΝΑ¹ – 2, η εξίσωση είναι ισοδύναμη με την εξίσωση

(ΕΝΑ+3)x= 2ΕΝΑ–1

βρείτε τις τιμές ελέγχου της παραμέτρου

ΕΝΑ+3= 0 Þ α=– 3.

2. Λύστε την εξίσωση για α=– 3.

0× x=– 7

σε οποιαδήποτε Χδεν υπάρχει ισότητα

3. Λύστε την εξίσωση για ΕΝΑ¹ – 3, α+ 3¹ 0.

https://pandia.ru/text/80/014/images/image015_21.gif" width="69" height="41 src="> Û ,

Επομένως, για να έχει νόημα η εξίσωση https://pandia.ru/text/80/014/images/image016_21.gif" width="40" height="41 src=">, δεν υπάρχουν ρίζες.

2) πότε ΕΝΑ¹ – 2, ΕΝΑ¹ – 3, , .

II. Τετραγωνικές εξισώσεις με παράμετρο και εξισώσεις ανάγουσες σε δευτεροβάθμιες

Σε τέτοιες εξισώσεις, οι τιμές της παραμέτρου που κάνουν τον συντελεστή στο μηδέν μηδέν συνήθως λαμβάνονται ως "έλεγχος" Χ 2, αφού σε αυτή την περίπτωση η εξίσωση γίνεται γραμμική, όπως και η τιμή της παραμέτρου, που κάνει τη διάκριση της εξίσωσης να εξαφανίζεται, αφού ο αριθμός των πραγματικών ριζών της τετραγωνικής εξίσωσης εξαρτάται από την τιμή της διακρίνουσας.

Παράδειγμα 5. Επίλυση εξίσωσης με παράμετρο

(ΕΝΑ–1)Χ 2+2(2ΕΝΑ+1)Χ+(4ΕΝΑ+3)= 0

1. Ας βρούμε τις τιμές της παραμέτρου που κάνουν τον συντελεστή στο μηδέν Χ

ΕΝΑ- 1=0 Û α= 1

2. Λύστε την εξίσωση για α= 1

0× Χ 2+2 (2×1+1) Χ+4×1+3=0 Û 6 Χ+7=0 Û .

3. Βρείτε τις τιμές παραμέτρων που εξαφανίζουν τη διάκριση της εξίσωσης

ρε=(2(2ΕΝΑ+1))2–4(ΕΝΑ–1)(4ΕΝΑ+3)=(4ΕΝΑ+1)2–(4ΕΝΑ–4)(4ΕΝΑ+3)=4(5ΕΝΑ+4)

4(5ΕΝΑ+4)=0 Û .

4. Ας λύσουμε την εξίσωση για το , στην περίπτωση αυτή η εξίσωση θα έχει μία πραγματική ρίζα

https://pandia.ru/text/80/014/images/image021_15.gif" width="133" height="41"> Û

9Χ 2+6Χ+1=0 Û (3 Χ+1)2=0 Û https://pandia.ru/text/80/014/images/image023_15.gif" width="51" height="41 src=">. Σε αυτήν την περίπτωση ρε<0, поэтому уравнение действительных корней не имеет.

6. Λύστε την εξίσωση για ΕΝΑΝο. 1, https://pandia.ru/text/80/014/images/image025_12.gif" width="341" height="49 src=">

7. Απάντηση: 1) με https://pandia.ru/text/80/014/images/image022_14.gif" width="51" height="41 src=">;

2) πότε α= 1, ;

3) για , δεν υπάρχουν πραγματικές ρίζες.

4) στο και ΕΝΑΝο. 1, https://pandia.ru/text/80/014/images/image027_10.gif" width="144" height="44 src=">

1. Αφού ΕΝΑείναι στον παρονομαστή του κλάσματος, τότε η εξίσωση έχει νόημα μόνο όταν ΕΝΑ#0. Ο παρονομαστής περιέχει επίσης τις εκφράσεις a2x– 2ΕΝΑκαι 2- Ω, το οποίο πρέπει επίσης να είναι μη μηδενικό

a2x– 2ΕΝΑ¹0 Û ΕΝΑ(Ω–2)¹0 Û ΕΝΑ¹0, Ω–2¹0 Û ΕΝΑ¹0, ;

2–Ω¹0 Û https://pandia.ru/text/80/014/images/image028_9.gif" width="41" height="41 src=">.

2. Λύστε την εξίσωση για ΕΝΑ¹0, https://pandia.ru/text/80/014/images/image029_9.gif" width="169" height="47 src="> Û Û

(1–ΕΝΑ)Χ 2+2Χ+1+ΕΝΑ=0 ...................(*)

3. Ας βρούμε τις τιμές των παραμέτρων που κάνουν τον συντελεστή στο μηδέν Χ 2

1–ΕΝΑ=0 Û ΕΝΑ=1

4. Λύστε την εξίσωση (*) για ΕΝΑ=1

0× Χ 2+2Χ+2=0 Û 2 x=– 2 Û x=–1

Ας ελέγξουμε αμέσως αν ταιριάζει Χαπό https://pandia.ru/text/80/014/images/image032_8.gif" width="72" height="41 src=">, που σημαίνει ότι όταν ΕΝΑ=1, x=– 1.

Στόχος:

• επαναλαμβανόμενα συστήματα επίλυσης γραμμικών εξισώσεων με δύο μεταβλητές
• ορίστε ένα σύστημα γραμμικών εξισώσεων με παραμέτρους
• θα σας διδάξει πώς να λύσετε συστήματα γραμμικών εξισώσεων με παραμέτρους.

Κατά τη διάρκεια των μαθημάτων

1. Οργάνωση χρόνου
2. Επανάληψη
3. Επεξήγηση νέου θέματος
4. Ενοποίηση
5. Περίληψη μαθήματος
6. Εργασία για το σπίτι

2. Επανάληψη:

I. Γραμμική εξίσωση με μία μεταβλητή:

1. Ορίστε μια γραμμική εξίσωση με μία μεταβλητή

[Μια εξίσωση της μορφής ax=b, όπου x είναι μια μεταβλητή, a και b είναι κάποιοι αριθμοί, ονομάζεται γραμμική εξίσωση με μία μεταβλητή]

2. Πόσες ρίζες μπορεί να έχει μια γραμμική εξίσωση;

[- Αν a=0, b0, τότε η εξίσωση δεν έχει λύσεις, x

Αν a=0, b=0, τότε x R

Αν a0, τότε η εξίσωση έχει μια μοναδική λύση, x =

3. Μάθετε πόσες ρίζες έχει η εξίσωση (σύμφωνα με τις επιλογές)

II. Γραμμική εξίσωση με 2 μεταβλητές και σύστημα γραμμικών εξισώσεων με 2 μεταβλητές.

1. Ορίστε μια γραμμική εξίσωση σε δύο μεταβλητές. Δώσε ένα παράδειγμα.

[Μια γραμμική εξίσωση με δύο μεταβλητές είναι μια εξίσωση της μορφής ax + by = c, όπου x και y είναι μεταβλητές, a, b και c είναι κάποιοι αριθμοί. Για παράδειγμα, x-y=5]

2. Τι ονομάζεται επίλυση εξίσωσης με δύο μεταβλητές;

[Μια λύση σε μια εξίσωση με δύο μεταβλητές είναι ένα ζεύγος τιμών μεταβλητών που μετατρέπει την εξίσωση σε πραγματική ισότητα.]

3. Είναι το ζεύγος τιμών των μεταβλητών x = 7, y = 3 λύση της εξίσωσης 2x + y = 17;

4. Πώς ονομάζεται η γραφική παράσταση μιας εξίσωσης σε δύο μεταβλητές;

[Η γραφική παράσταση μιας εξίσωσης με δύο μεταβλητές είναι το σύνολο όλων των σημείων στο επίπεδο συντεταγμένων των οποίων οι συντεταγμένες είναι λύσεις αυτής της εξίσωσης.]

5. Βρείτε ποια είναι η γραφική παράσταση της εξίσωσης:

[Ας εκφράσουμε τη μεταβλητή y έως x: y=-1,5x+3

Ο τύπος y=-1,5x+3 είναι μια γραμμική συνάρτηση, η γραφική παράσταση της οποίας είναι ευθεία γραμμή. Εφόσον οι εξισώσεις 3x+2y=6 και y=-1,5x+3 είναι ισοδύναμες, αυτή η γραμμή είναι επίσης γραφική παράσταση της εξίσωσης 3x+2y=6]

6. Ποια είναι η γραφική παράσταση της εξίσωσης ax+bу=c με τις μεταβλητές x και y, όπου a0 ή b0;

[Η γραφική παράσταση μιας γραμμικής εξίσωσης με δύο μεταβλητές στην οποία τουλάχιστον ένας από τους συντελεστές των μεταβλητών δεν είναι μηδέν είναι ευθεία γραμμή.]

7. Τι ονομάζεται επίλυση συστήματος εξισώσεων με δύο μεταβλητές;

[Μια λύση σε ένα σύστημα εξισώσεων με δύο μεταβλητές είναι ένα ζεύγος τιμών μεταβλητών που μετατρέπει κάθε εξίσωση του συστήματος σε αληθινή ισότητα]

8. Τι σημαίνει επίλυση συστήματος εξισώσεων;

[Για να λύσετε ένα σύστημα εξισώσεων σημαίνει να βρείτε όλες τις λύσεις του ή να αποδείξετε ότι δεν υπάρχουν λύσεις.]

9. Μάθετε αν ένα τέτοιο σύστημα έχει πάντα λύσεις και, αν ναι, πόσες (γραφικά).

10. Πόσες λύσεις μπορεί να έχει ένα σύστημα δύο γραμμικών εξισώσεων με δύο μεταβλητές;

[Η μόνη λύση είναι αν οι ευθείες τέμνονται. δεν έχει λύσεις αν οι ευθείες είναι παράλληλες. άπειρα πολλά αν συμπίπτουν οι γραμμές]

11. Ποια εξίσωση ορίζει συνήθως μια ευθεία γραμμή;

12. Δημιουργήστε μια σύνδεση μεταξύ των συντελεστών γωνίας και των ελεύθερων όρων:

Επιλογή Ι: y=-x+2 y= -x-3, k 1 = k 2 , b 1 b 2, χωρίς διαλύματα;

Επιλογή II: y=-x+8 y=2x-1, k 1 k 2 , ένα διάλυμα;

Επιλογή III: y=-x-1 y=-x-1, k 1 = k 2, b 1 = b 2, πολλές λύσεις.

Συμπέρασμα:

1. Εάν οι γωνιακοί συντελεστές των γραμμών που είναι γραφήματα αυτών των συναρτήσεων είναι διαφορετικοί, τότε αυτές οι γραμμές τέμνονται και το σύστημα έχει μια μοναδική λύση.
2. Αν οι γωνιακοί συντελεστές των ευθειών είναι ίδιοι και τα σημεία τομής με τον άξονα y είναι διαφορετικά, τότε οι ευθείες είναι παράλληλες και το σύστημα δεν έχει λύσεις.
3. Αν οι γωνιακοί συντελεστές και τα σημεία τομής με τον άξονα y είναι ίδια, τότε οι ευθείες συμπίπτουν και το σύστημα έχει άπειρες λύσεις.

Στον πίνακα υπάρχει ένας πίνακας που συμπληρώνουν σταδιακά ο δάσκαλος και οι μαθητές.

III. Επεξήγηση νέου θέματος.

Ορισμός: Σύστημα προβολής

• A 1 x+B 1 y=C
• A 2 x+B 2 y=C 2

όπου A 1, A 2, B 1, B 2, C 1 C 2 είναι εκφράσεις ανάλογα με τις παραμέτρους, και x και y είναι άγνωστες, ονομάζεται σύστημα δύο γραμμικών αλγεβρικών εξισώσεων με δύο άγνωστους στις παραμέτρους.

Είναι δυνατές οι ακόλουθες περιπτώσεις:

1) Εάν , τότε το σύστημα έχει μια μοναδική λύση

2) Εάν , τότε το σύστημα δεν έχει λύσεις

3) Αν , τότε το σύστημα έχει άπειρες λύσεις.

IV. Ενοποίηση

Παράδειγμα 1.

Σε ποιες τιμές της παραμέτρου a κάνει το σύστημα

• 2x - 3y = 7
• ah - 6y = 14

α) έχει άπειρο αριθμό λύσεων.

β) έχει μια μοναδική λύση

Απάντηση:

α) αν a=4, τότε το σύστημα έχει άπειρο αριθμό λύσεων.

β) εάν α4, τότε υπάρχει μόνο μία λύση.

Παράδειγμα 2.

Λύστε το σύστημα των εξισώσεων

• x+(m+1)y=1
• x+2y=n

Λύση: α) , δηλ. για το m1 το σύστημα έχει μια μοναδική λύση.

β), δηλ. για m=1 (2=m+1) και n1 το αρχικό σύστημα δεν έχει λύσεις

γ) , για m=1 και n=1 το σύστημα έχει άπειρες λύσεις.

Απάντηση: α) αν m=1 και n1, τότε δεν υπάρχουν λύσεις

β) m=1 και n=1, τότε η λύση είναι ένα άπειρο σύνολο

• y - οποιοδήποτε
• x=n-2y

γ) αν m1 και n είναι οποιαδήποτε, τότε

Παράδειγμα 3.

• akh-3ау=2а+3
• x+ay=1

Λύση: Από την εξίσωση II βρίσκουμε x = 1-αy και αντικαθιστούμε την εξίσωση I σε εξίσωση

α(1-αυ)-3ау=2а+3

a-a 2 y-3ау=2а+3

A 2 y-3ау=а+3

A(a+3)y=a+3

Πιθανές περιπτώσεις:

1) a=0. Τότε η εξίσωση μοιάζει με 0*y=3 [y]

Επομένως, για a=0 το σύστημα δεν έχει λύσεις

2) α=-3. Τότε 0*y=0.

Επομένως, y. Σε αυτή την περίπτωση x=1-ау=1+3у

3) a0 και a-3. Τότε y=-, x=1-a(-=1+1=2

Απάντηση:

1) αν a=0, τότε (x; y)

2) αν a=-3, τότε x=1+3y, y

3) αν α0 και a?-3, μετά x=2, y=-

Ας εξετάσουμε τη δεύτερη μέθοδο επίλυσης του συστήματος (1).

Ας λύσουμε το σύστημα (1) χρησιμοποιώντας τη μέθοδο της αλγεβρικής πρόσθεσης: πρώτα, πολλαπλασιάζουμε την πρώτη εξίσωση του συστήματος με B 2, τη δεύτερη με B 1 και προσθέτουμε αυτές τις εξισώσεις όρο προς όρο, εξαλείφοντας έτσι τη μεταβλητή y:

Επειδή A 1 B 2 -A 2 B 1 0, μετά x =

Τώρα ας εξαλείψουμε τη μεταβλητή x. Για να το κάνετε αυτό, πολλαπλασιάστε την πρώτη εξίσωση του συστήματος (1) με A 2 και τη δεύτερη με A 1 και προσθέστε και τις δύο εξισώσεις κατά όρο:

• A 1 A 2 x +A 2 B 1 y=A 2 C 1
• -A 1 A 2 x-A 1 B 2 y=-A 1 C 2
• y(A 2 B 1 -A 1 B 2) = A 2 C 1 -A 1 C 2

επειδή A 2 B 1 -A 1 B 2 0 y =

Για ευκολία επίλυσης του συστήματος (1), εισάγουμε τον ακόλουθο συμβολισμό:

- κύριος καθοριστικός παράγοντας

Τώρα η λύση στο σύστημα (1) μπορεί να γραφτεί χρησιμοποιώντας ορίζουσες:

Οι τύποι που δίνονται ονομάζονται τύποι του Cramer.

Αν , τότε το σύστημα (1) έχει μια μοναδική λύση: x=; y=

Εάν , ή , τότε το σύστημα (1) δεν έχει λύσεις

Αν , , , , τότε το σύστημα (1) έχει άπειρο αριθμό λύσεων.

Σε αυτή την περίπτωση, το σύστημα πρέπει να διερευνηθεί περαιτέρω. Σε αυτή την περίπτωση, κατά κανόνα, ανάγεται σε μία γραμμική εξίσωση. Σε αυτήν την περίπτωση, είναι συχνά βολικό να μελετήσουμε το σύστημα με τον ακόλουθο τρόπο: λύνοντας την εξίσωση, βρίσκουμε συγκεκριμένες τιμές των παραμέτρων ή εκφράζουμε μία από τις παραμέτρους ως προς τις άλλες και αντικαθιστούμε αυτές τις τιμές παραμέτρων σε το σύστημα. Τότε παίρνουμε ένα σύστημα με συγκεκριμένους αριθμητικούς συντελεστές ή με μικρότερο αριθμό παραμέτρων, που πρέπει να μελετηθούν.

Εάν οι συντελεστές A 1 , A 2 , B 1 , B 2 του συστήματος εξαρτώνται από πολλές παραμέτρους, τότε είναι βολικό να μελετήσετε το σύστημα χρησιμοποιώντας καθοριστικούς παράγοντες του συστήματος.

Παράδειγμα 4.

Για όλες τις τιμές της παραμέτρου α, λύστε το σύστημα εξισώσεων

• (a+5)x+(2a+3)y=3a+2
• (3a+10)x+(5a+6)y=2a+4

Λύση: Ας βρούμε την ορίζουσα του συστήματος:

= (a+5)(5a+6) – (3a+10) (2a+3)= 5a 2 +31a+30-6a 2 -29a-30=-a 2 +2a=a(2-a)

= (3a+2) (5a+6) –(2a+4)(2a+3)=15a 2 +28a+12-4a 2 -14a-12=11a 2 +14a=a(11a+14)

=(a+5) (2a+4)-(3a+10)(3a+2)=2a 2 +14a+20-9a 2 -36a-20=-7a 2 -22a=-a(7a+22)

Ας λύσουμε ένα σύστημα εξισώσεων με μια παράμετρο (A. Larin, επιλογή 98)

Βρείτε όλες τις τιμές της παραμέτρου, για καθεμία από τις οποίες το σύστημα

έχει ακριβώς μια λύση.

Ας ρίξουμε μια πιο προσεκτική ματιά στο σύστημα. Στην πρώτη εξίσωση του συστήματος, η αριστερή πλευρά είναι , και η δεξιά πλευρά δεν εξαρτάται από την παράμετρο. Δηλαδή, μπορούμε να θεωρήσουμε αυτή την εξίσωση ως εξίσωση της συνάρτησης

και μπορούμε να σχεδιάσουμε αυτή τη συνάρτηση.

Δεύτερη εξίσωση του συστήματος

εξαρτάται από την παράμετρο και επιλέγοντας ένα πλήρες τετράγωνο στην αριστερή πλευρά της εξίσωσης, παίρνουμε την εξίσωση ενός κύκλου.

Επομένως, είναι λογικό να σχεδιάσουμε γραφήματα κάθε εξίσωσης και να δούμε σε ποια τιμή της παραμέτρου αυτά τα γραφήματα έχουν ένα σημείο τομής.

Ας ξεκινήσουμε με την πρώτη εξίσωση. Αρχικά, ας ανοίξουμε τις ενότητες. Για να γίνει αυτό, εξισώνουμε κάθε υποαρθρωτή έκφραση με μηδέν για να βρούμε τα σημεία στα οποία αλλάζει το πρόσημο.

Η πρώτη υπομονάδα έκφραση αλλάζει πρόσημο στο , η δεύτερη - στο .

Ας σχεδιάσουμε αυτά τα σημεία στη γραμμή συντεταγμένων και ας βρούμε τα πρόσημα κάθε υπομονάδας έκφρασης σε κάθε διάστημα:

Σημειώστε ότι η εξίσωση για και δεν έχει νόημα, οπότε τρυπάμε αυτά τα σημεία.

Τώρα ας επεκτείνουμε τις ενότητες σε κάθε διάστημα. (Θυμηθείτε: εάν η υπο-αρθρωτή έκφραση είναι μεγαλύτερη ή ίση με μηδέν, τότε επεκτείνουμε τη μονάδα με το ίδιο πρόσημο και αν είναι μικρότερη από μηδέν, τότε με το αντίθετο πρόσημο.)

Και οι δύο υποαρθρωτές εκφράσεις είναι αρνητικές, επομένως, επεκτείνουμε και τις δύο ενότητες με το αντίθετο πρόσημο:

Όταν δηλαδή η αρχική συνάρτηση έχει τη μορφή

Σε αυτό το διάστημα, η πρώτη υπο-αρθρωτή έκφραση είναι αρνητική και η δεύτερη είναι θετική, επομένως παίρνουμε:

- η συνάρτηση δεν υπάρχει σε αυτό το διάστημα.

3. title="x>2">!}

Σε αυτό το διάστημα, και οι δύο υπομονάδες εκφράσεις είναι θετικές, επεκτείνουμε και τις δύο ενότητες με το ίδιο πρόσημο. Παίρνουμε:

Δηλαδή με title="x>2"> исходная функция имеет вид !}

Έτσι, πήραμε το γράφημα της συνάρτησης

Ας δούμε τώρα τη δεύτερη εξίσωση:

Ας επιλέξουμε ένα πλήρες τετράγωνο στην αριστερή πλευρά της εξίσωσης για να το κάνουμε αυτό, προσθέτουμε τον αριθμό 4 και στις δύο πλευρές της εξίσωσης:

Για μια συγκεκριμένη τιμή της παραμέτρου, η γραφική παράσταση αυτής της εξίσωσης είναι ένας κύκλος με κέντρο σε ένα σημείο με συντεταγμένες, η ακτίνα του οποίου είναι 5. Για διαφορετικές τιμές, έχουμε μια σειρά από κύκλους:

Θα μετακινήσουμε τον κύκλο από κάτω προς τα πάνω μέχρι να αγγίξει την αριστερή πλευρά του γραφήματος της πρώτης συνάρτησης. Στην εικόνα αυτός ο κύκλος είναι κόκκινος. Το κέντρο αυτού του κύκλου είναι το σημείο, οι συντεταγμένες του είναι (-2;-3). Επιπλέον, όταν κινείται προς τα πάνω, ο κύκλος έχει ένα σημείο τομής με την αριστερή πλευρά του γραφήματος συνάρτησης, δηλαδή το σύστημα έχει μια μοναδική λύση.

Συνεχίζουμε να μετακινούμε τον κύκλο προς τα πάνω μέχρι να αγγίξει τη δεξιά πλευρά του γραφήματος της πρώτης συνάρτησης. Αυτό θα συμβεί όταν το κέντρο του κύκλου βρίσκεται στο σημείο με συντεταγμένες (-2;0) - στο σχήμα αυτός ο κύκλος είναι μπλε.

Όταν κινείται προς τα πάνω, ο κύκλος θα τέμνει τόσο το αριστερό όσο και το δεξί μέρος του γραφήματος της πρώτης συνάρτησης, δηλαδή ο κύκλος θα έχει δύο σημεία τομής με το γράφημα της πρώτης συνάρτησης και το σύστημα θα έχει δύο λύσεις. Αυτή η κατάσταση συνεχίζεται έως ότου το κέντρο του κύκλου βρίσκεται στο σημείο με συντεταγμένες (-2; 5) - αυτός ο κύκλος είναι πράσινος. Σε αυτό το σημείο ο κύκλος αγγίζει την αριστερή πλευρά του γραφήματος και τέμνει τη δεξιά. Δηλαδή το σύστημα έχει μία λύση.

Έτσι, το σύστημα έχει μια μοναδική λύση όταν(-3;0], εάν οι τιμές της παραμέτρου α είναι περισσότερες από μία, τότε η εξίσωση θα έχει δύο ρίζες.

Έχετε ακόμα ερωτήσεις; Δεν ξέρετε πώς να λύσετε εξισώσεις με μια παράμετρο;
Για να λάβετε βοήθεια από έναν δάσκαλο -.
Το πρώτο μάθημα είναι δωρεάν!

blog.site, κατά την πλήρη ή μερική αντιγραφή υλικού, απαιτείται σύνδεσμος στην αρχική πηγή.

1. Συστήματα γραμμικών εξισώσεων με παράμετρο

Τα συστήματα γραμμικών εξισώσεων με μια παράμετρο επιλύονται με τις ίδιες βασικές μεθόδους με τα συνηθισμένα συστήματα εξισώσεων: τη μέθοδο αντικατάστασης, τη μέθοδο προσθήκης εξισώσεων και τη γραφική μέθοδο. Η γνώση της γραφικής ερμηνείας των γραμμικών συστημάτων καθιστά εύκολη την απάντηση στο ερώτημα σχετικά με τον αριθμό των ριζών και την ύπαρξή τους.

Παράδειγμα 1.

Βρείτε όλες τις τιμές για την παράμετρο α για την οποία το σύστημα εξισώσεων δεν έχει λύσεις.

(x + (a 2 – 3)y = a,
(x + y = 2.

Λύση.

Ας δούμε διάφορους τρόπους επίλυσης αυτής της εργασίας.

1 τρόπος.Χρησιμοποιούμε την ιδιότητα: το σύστημα δεν έχει λύσεις εάν η αναλογία των συντελεστών μπροστά από το x είναι ίση με την αναλογία των συντελεστών μπροστά από το y, αλλά όχι ίση με την αναλογία των ελεύθερων όρων (a/a 1 = b /b 1 ≠ c/c 1). Τότε έχουμε:

1/1 = (a 2 – 3)/1 ≠ a/2 ή σύστημα

(και 2 – 3 = 1,
(α ≠ 2.

Από την πρώτη εξίσωση a 2 = 4, λοιπόν, λαμβάνοντας υπόψη την συνθήκη ότι a ≠ 2, παίρνουμε την απάντηση.

Απάντηση: a = -2.

Μέθοδος 2.Λύνουμε με τη μέθοδο αντικατάστασης.

(2 – y + (a 2 – 3)y = a,
(x = 2 – y,

((a 2 – 3)y – y = a – 2,
(x = 2 – y.

Αφού αφαιρέσουμε τον κοινό παράγοντα y από αγκύλες στην πρώτη εξίσωση, παίρνουμε:

((a 2 – 4)y = a – 2,
(x = 2 – y.

Το σύστημα δεν έχει λύσεις αν η πρώτη εξίσωση δεν έχει λύσεις, δηλαδή

(και 2 – 4 = 0,
(α – 2 ≠ 0.

Προφανώς, a = ±2, αλλά λαμβάνοντας υπόψη τη δεύτερη συνθήκη, η απάντηση έρχεται μόνο με αρνητική απάντηση.

Απάντηση: a = -2.

Παράδειγμα 2.

Βρείτε όλες τις τιμές για την παράμετρο α για την οποία το σύστημα εξισώσεων έχει άπειρο αριθμό λύσεων.

(8x + ay = 2,
(ax + 2y = 1.

Λύση.

Σύμφωνα με την ιδιότητα, αν ο λόγος των συντελεστών των x και y είναι ο ίδιος και είναι ίσος με τον λόγο των ελεύθερων μελών του συστήματος, τότε έχει άπειρο αριθμό λύσεων (δηλ. a/a 1 = b/ b 1 = c/c 1). Επομένως 8/a = a/2 = 2/1. Λύνοντας καθεμία από τις εξισώσεις που προκύπτουν, βρίσκουμε ότι a = 4 είναι η απάντηση σε αυτό το παράδειγμα.

Απάντηση:α = 4.

2. Συστήματα ορθολογικών εξισώσεων με παράμετρο

Παράδειγμα 3.

(3|x| + y = 2,
(|x| + 2y = α.

Λύση.

Ας πολλαπλασιάσουμε την πρώτη εξίσωση του συστήματος επί 2:

(6|x| + 2y = 4,
(|x| + 2y = α.

Αφαιρώντας τη δεύτερη εξίσωση από την πρώτη, παίρνουμε 5|x| = 4 – α. Αυτή η εξίσωση θα έχει μια μοναδική λύση για a = 4. Σε άλλες περιπτώσεις, αυτή η εξίσωση θα έχει δύο λύσεις (για ένα< 4) или ни одного (при а > 4).

Απάντηση: α = 4.

Παράδειγμα 4.

Βρείτε όλες τις τιμές της παραμέτρου a για τις οποίες το σύστημα εξισώσεων έχει μοναδική λύση.

(x + y = a,
(y – x 2 = 1.

Λύση.

Θα λύσουμε αυτό το σύστημα χρησιμοποιώντας τη γραφική μέθοδο. Έτσι, η γραφική παράσταση της δεύτερης εξίσωσης του συστήματος είναι μια παραβολή υψωμένη κατά μήκος του άξονα Oy προς τα πάνω κατά μία μονάδα τμήματος. Η πρώτη εξίσωση καθορίζει ένα σύνολο γραμμών παράλληλων στην ευθεία y = -x (εικόνα 1). Από το σχήμα φαίνεται καθαρά ότι το σύστημα έχει λύση αν η ευθεία y = -x + a εφάπτεται στην παραβολή σε σημείο με συντεταγμένες (-0,5, 1,25). Αντικαθιστώντας αυτές τις συντεταγμένες στην ευθεία εξίσωση αντί των x και y, βρίσκουμε την τιμή της παραμέτρου a:

1,25 = 0,5 + a;

Απάντηση: a = 0,75.

Παράδειγμα 5.

Χρησιμοποιώντας τη μέθοδο αντικατάστασης, μάθετε σε ποια τιμή της παραμέτρου a, το σύστημα έχει μια μοναδική λύση.

(ax – y = a + 1,
(ax + (a + 2)y = 2.

Λύση.

Από την πρώτη εξίσωση εκφράζουμε το y και το αντικαθιστούμε στη δεύτερη:

(y = τσεκούρι – a – 1,
(ax + (a + 2)(ax – a – 1) = 2.

Ας ανάγουμε τη δεύτερη εξίσωση στη μορφή kx = b, η οποία θα έχει μοναδική λύση για k ≠ 0. Έχουμε:

ax + a 2 x – a 2 – a + 2ax – 2a – 2 = 2;

a 2 x + 3ax = 2 + a 2 + 3a + 2.

Αντιπροσωπεύουμε το τετράγωνο τριώνυμο a 2 + 3a + 2 ως γινόμενο αγκύλων

(a + 2)(a + 1), και στα αριστερά βγάζουμε x από αγκύλες:

(a 2 + 3a)x = 2 + (a + 2)(a + 1).

Προφανώς, ένα 2 + 3a δεν πρέπει να είναι ίσο με μηδέν, επομένως,

a 2 + 3a ≠ 0, a(a + 3) ≠ 0, που σημαίνει a ≠ 0 και ≠ -3.

Απάντηση: a ≠ 0; ≠ -3.

Παράδειγμα 6.

Χρησιμοποιώντας τη μέθοδο γραφικής λύσης, προσδιορίστε σε ποια τιμή της παραμέτρου a το σύστημα έχει μια μοναδική λύση.

(x 2 + y 2 = 9,
(y – |x| = α.

Λύση.

Με βάση τη συνθήκη, κατασκευάζουμε έναν κύκλο με κέντρο στην αρχή και ακτίνα 3 μονάδων τμημάτων αυτό καθορίζεται από την πρώτη εξίσωση του συστήματος

x 2 + y 2 = 9. Η δεύτερη εξίσωση του συστήματος (y = |x| + a) είναι μια διακεκομμένη γραμμή. Με τη χρήση Σχήμα 2Εξετάζουμε όλες τις πιθανές περιπτώσεις θέσης του σε σχέση με τον κύκλο. Είναι εύκολο να δούμε ότι a = 3.

Απάντηση: α = 3.

Έχετε ακόμα ερωτήσεις; Δεν ξέρετε πώς να λύσετε συστήματα εξισώσεων;
Για να λάβετε βοήθεια από έναν δάσκαλο -.
Το πρώτο μάθημα είναι δωρεάν!

blog.site, κατά την πλήρη ή μερική αντιγραφή υλικού, απαιτείται σύνδεσμος στην αρχική πηγή.