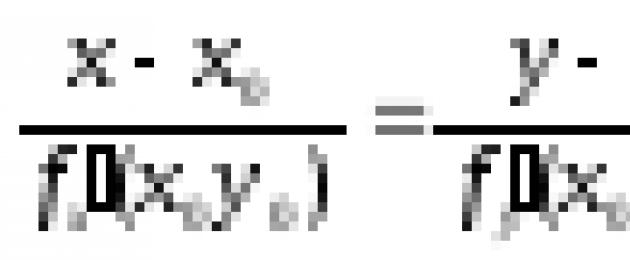Πλήρες διαφορικό. Γεωμετρική σημασία του ολικού διαφορικού

Εφαπτόμενο επίπεδο και κάθετο στην επιφάνεια.

εφαπτομενικό επίπεδο

Έστω N και N 0 σημεία αυτής της επιφάνειας. Ας σχεδιάσουμε μια ευθεία γραμμή NN 0. Το επίπεδο που διέρχεται από το σημείο N 0 ονομάζεται εφαπτομενικό επίπεδοστην επιφάνεια εάν η γωνία μεταξύ του τέμνοντος NN 0 και αυτού του επιπέδου τείνει στο μηδέν, όταν η απόσταση NN 0 τείνει στο μηδέν.

Ορισμός. Κανονικόςστην επιφάνεια στο σημείο N 0 είναι μια ευθεία γραμμή που διέρχεται από το σημείο N 0 κάθετο στο εφαπτόμενο επίπεδο σε αυτήν την επιφάνεια.

Σε οποιοδήποτε σημείο η επιφάνεια έχει είτε μόνο ένα εφαπτόμενο επίπεδο είτε δεν το έχει καθόλου.

Αν η επιφάνεια δίνεται από την εξίσωση z = f(x, y), όπου f(x, y) είναι μια συνάρτηση διαφοροποιήσιμη στο σημείο M 0 (x 0, y 0), το εφαπτομενικό επίπεδο στο σημείο N 0 ( x 0,y 0, ( x 0 ,y 0)) υπάρχει και έχει την εξίσωση:

Η εξίσωση του κανονικού προς την επιφάνεια σε αυτό το σημείο είναι:

Γεωμετρική αίσθηση πλήρες διαφορικόσυνάρτηση δύο μεταβλητών f(x, y) στο σημείο (x 0, y 0) είναι η αύξηση της εφαρμογής (συντεταγμένες z) του εφαπτομένου επιπέδου στην επιφάνεια όταν κινείται από το σημείο (x 0, y 0) στο το σημείο (x 0 +x, y 0 +у).

Όπως μπορείτε να δείτε, η γεωμετρική σημασία του ολικού διαφορικού μιας συνάρτησης δύο μεταβλητών είναι ένα χωρικό ανάλογο της γεωμετρικής σημασίας του διαφορικού μιας συνάρτησης μιας μεταβλητής.

Παράδειγμα.Να βρείτε τις εξισώσεις του εφαπτομένου επιπέδου και κάθετου στην επιφάνεια

στο σημείο Μ(1, 1, 1).

Εξίσωση εφαπτομενικού επιπέδου:

Κανονική εξίσωση:

20.4. Κατά προσέγγιση υπολογισμοί με χρήση συνολικών διαφορών.

Έστω η συνάρτηση f(x, y) διαφορίσιμη στο σημείο (x, y). Ας βρούμε τη συνολική αύξηση αυτής της συνάρτησης:

Αν αντικαταστήσουμε την έκφραση σε αυτόν τον τύπο

τότε παίρνουμε έναν κατά προσέγγιση τύπο:

Παράδειγμα.Υπολογίστε περίπου την τιμή με βάση την τιμή της συνάρτησης σε x = 1, y = 2, z = 1.

Από τη δεδομένη παράσταση προσδιορίζουμε x = 1,04 – 1 = 0,04, y = 1,99 – 2 = -0,01,

z = 1,02 – 1 = 0,02.

Ας βρούμε την τιμή της συνάρτησης u(x, y, z) =

Εύρεση μερικών παραγώγων:

Το συνολικό διαφορικό της συνάρτησης u ισούται με:

Η ακριβής τιμή αυτής της έκφρασης είναι 1,049275225687319176.

20.5. Μερικά παράγωγα υψηλότερων τάξεων.

Εάν μια συνάρτηση f(x, y) οριστεί σε κάποιο πεδίο D, τότε οι μερικές παράγωγοί της θα οριστούν επίσης στον ίδιο τομέα ή μέρος αυτού.

Θα ονομάσουμε αυτά τα παράγωγα μερικών παραγώγων πρώτης τάξης.

Οι παράγωγοι αυτών των συναρτήσεων θα είναι επί μέρους παράγωγα δεύτερης τάξης.

Συνεχίζοντας να διαφοροποιούμε τις προκύπτουσες ισότητες, λαμβάνουμε μερικές παραγώγους υψηλότερων τάξεων.

Ορισμός. Μερικά παράγωγα της μορφής και τα λοιπά. λέγονται μικτά παράγωγα.

Θεώρημα. Αν η συνάρτηση f(x, y) και οι μερικές παράγωγοί της είναι καθορισμένες και συνεχείς στο σημείο M(x, y) και στη γειτονιά της, τότε ισχύει η ακόλουθη σχέση:

Εκείνοι. τα μερικά παράγωγα υψηλότερων τάξεων δεν εξαρτώνται από τη σειρά διαφοροποίησης.

Οι διαφορές υψηλότερης τάξης ορίζονται με παρόμοιο τρόπο.

…………………

Εδώ το n είναι η συμβολική ισχύς της παραγώγου, η οποία αντικαθίσταται από την πραγματική δύναμη μετά την αύξηση της έκφρασης σε αγκύλες σε αυτήν.

Η γεωμετρική σημασία του ολικού διαφορικού μιας συνάρτησης δύο μεταβλητών f(x, y) στο σημείο (x 0, y 0) είναι η αύξηση της εφαρμογής (συντεταγμένες z) του εφαπτομένου επιπέδου στην επιφάνεια όταν κινείται από το σημείο (x 0, y 0) στο σημείο (x 0 + Dх, у 0 +Dу).

Μερικά παράγωγα υψηλότερων τάξεων. :Εάν μια συνάρτηση f(x, y) οριστεί σε κάποιο πεδίο D, τότε οι μερικές παράγωγοί της θα οριστούν επίσης στον ίδιο τομέα ή μέρος αυτού. Αυτά τα παράγωγα θα τα ονομάσουμε μερικές παράγωγα πρώτης τάξης.

Οι παράγωγοι αυτών των συναρτήσεων θα είναι μερικές παράγωγοι δεύτερης τάξης.

Συνεχίζοντας να διαφοροποιούμε τις προκύπτουσες ισότητες, λαμβάνουμε μερικές παραγώγους υψηλότερων τάξεων. Ορισμός.Μερικά παράγωγα της μορφής και τα λοιπά. ονομάζονται μικτά παράγωγα. Θεώρημα Schwartz:

Εάν μερικά παράγωγα υψηλότερων τάξεων f.m.p. είναι συνεχείς, τότε οι μικτές παράγωγοι ίδιας τάξης διαφέρουν μόνο ως προς τη σειρά διαφοροποίησης = μεταξύ τους.

14. Εξίσωση εφαπτομενικού επιπέδου και κανονικής επιφάνειας!

Ορισμός. Κανονικόςστην επιφάνεια στο σημείο N 0 είναι μια ευθεία γραμμή που διέρχεται από το σημείο N 0 κάθετο στο εφαπτόμενο επίπεδο σε αυτήν την επιφάνεια.

Σε οποιοδήποτε σημείο η επιφάνεια έχει είτε μόνο ένα εφαπτόμενο επίπεδο είτε δεν το έχει καθόλου.

Εάν η επιφάνεια δίνεται από την εξίσωση z = f(x, y), όπου f(x, y) είναι μια συνάρτηση διαφοροποιήσιμη στο σημείο M 0 (x 0, y 0), εφαπτομενικό επίπεδοστο σημείο N 0 (x 0 ,y 0, (x 0 ,y 0)) υπάρχει και έχει την εξίσωση:

Εξίσωση της κανονικής προς την επιφάνεια σε αυτό το σημείο:

Γεωμετρική αίσθησηη συνολική διαφορά μιας συνάρτησης δύο μεταβλητών f(x, y) στο σημείο (x 0, y 0) είναι η αύξηση της εφαρμογής (συντεταγμένες z) του εφαπτομένου επιπέδου στην επιφάνεια όταν κινείται από το σημείο (x 0 , y 0) στο σημείο (x 0 + Dx, y 0 +Dу).

16. Κλιμακωτό πεδίο και τα χαρακτηριστικά του.

Εάν κάθε σημείο του χώρου συσχετίζεται με μια κλιμακωτή ποσότητα, τότε προκύπτει ένα βαθμωτό πεδίο (για παράδειγμα, ένα πεδίο θερμοκρασίας, ένα πεδίο ηλεκτρικό δυναμικό). Αν εισάγονται καρτεσιανές συντεταγμένες, τότε δηλώνουν και ή Το πεδίο μπορεί να είναι επίπεδο εάν είναι κεντρικό (σφαιρικό) αν κυλινδρικό αν

Επίπεδες επιφάνειες και γραμμές: Οι ιδιότητες των βαθμωτών πεδίων μπορούν να μελετηθούν οπτικά χρησιμοποιώντας επίπεδες επιφάνειες. Πρόκειται για επιφάνειες στο χώρο στις οποίες παίρνει σταθερή τιμή. Η εξίσωσή τους είναι: . Σε ένα επίπεδο βαθμωτό πεδίο, οι γραμμές επιπέδου είναι καμπύλες στις οποίες το πεδίο παίρνει μια σταθερή τιμή: Σε ορισμένες περιπτώσεις, οι οριζόντιες γραμμές μπορεί να εκφυλιστούν σε σημεία και οι επίπεδες επιφάνειες σε σημεία και καμπύλες.

Κατευθυντική παράγωγος και κλίση βαθμωτού πεδίου:

Έστω το μοναδιαίο διάνυσμα με συντεταγμένες ένα βαθμωτό πεδίο. Η κατευθυντική παράγωγος χαρακτηρίζει την αλλαγή στο πεδίο σε μια δεδομένη κατεύθυνση και υπολογίζεται χρησιμοποιώντας τον τύπο Η κατευθυντική παράγωγος είναι κλιμακωτό προϊόνδιάνυσμα και διάνυσμα με συντεταγμένες , που ονομάζεται κλίση της συνάρτησης και συμβολίζεται από , όπου η γωνία μεταξύ και , τότε το διάνυσμα δείχνει την κατεύθυνση της ταχύτερης αύξησης στο πεδίο και ο συντελεστής του είναι ίσος με την παράγωγο προς αυτή την κατεύθυνση. Δεδομένου ότι τα συστατικά της διαβάθμισης είναι μερικώς παράγωγα, δεν είναι δύσκολο να αποκτηθούν οι ακόλουθες ιδιότητες της διαβάθμισης:

17. Extrema of f.m.p. Τοπικό άκρο f.m.p., απαραίτητες και επαρκείς προϋποθέσεις για την ύπαρξή της. Η μεγαλύτερη και η μικρότερη τιμή του f.m.p. σε περιορισμένο κλειστό χώρο.

Έστω η συνάρτηση z = ƒ(x;y) σε κάποιο πεδίο ορισμού D, σημείο N(x0;y0)

Ένα σημείο (x0;y0) ονομάζεται μέγιστο σημείο της συνάρτησης z=ƒ(x;y) αν υπάρχει d-γειτονιά του σημείου (x0;y0) τέτοια ώστε για κάθε σημείο (x;y) διαφορετική από (xo;yo), από αυτή τη γειτονιά ισχύει η ανισότητα ƒ(x;y).<ƒ(хо;уо). Аналогично определяется точка минимума функции: для всех точек (х; у), отличных от (х0;у0), из d-окрестности точки (хо;уо) выполняется неравенство: ƒ(х;у)>ƒ(x0;y0). Η τιμή της συνάρτησης στο σημείο μέγιστου (ελάχιστο) ονομάζεται μέγιστο (ελάχιστο) της συνάρτησης. Το μέγιστο και το ελάχιστο μιας συνάρτησης ονομάζονται άκρα της. Σημειώστε ότι, εξ ορισμού, το ακραίο σημείο της συνάρτησης βρίσκεται εντός του τομέα ορισμού της συνάρτησης. Το μέγιστο και το ελάχιστο έχουν τοπικό (τοπικό) χαρακτήρα: η τιμή της συνάρτησης στο σημείο (x0; y0) συγκρίνεται με τις τιμές της σε σημεία αρκετά κοντά στο (x0; y0). Στην περιοχή D, μια συνάρτηση μπορεί να έχει πολλά άκρα ή κανένα.

Απαραίτητες(1) και επαρκείς(2) προϋποθέσεις ύπαρξης:

(1) Αν στο σημείο N(x0;y0) η διαφοροποιήσιμη συνάρτηση z=ƒ(x;y) έχει άκρο, τότε οι μερικές παράγωγοί της σε αυτό το σημείο είναι ίσες με μηδέν: ƒ"x(x0;y0)=0, ƒ" y(x0;y0)=0. Σχόλιο. Μια συνάρτηση μπορεί να έχει ακρότατο σε σημεία όπου δεν υπάρχει τουλάχιστον μία από τις μερικές παραγώγους. Το σημείο στο οποίο οι μερικές παράγωγοι πρώτης τάξης της συνάρτησης z ≈ ƒ(x; y) είναι ίσες με μηδέν, δηλαδή f"x=0, f"y=0, ονομάζεται ακίνητο σημείο της συνάρτησης z.

Τα ακίνητα σημεία και τα σημεία στα οποία δεν υπάρχει τουλάχιστον μία μερική παράγωγος ονομάζονται κρίσιμα σημεία

(2) Έστω η συνάρτηση ƒ(x;y) σε ένα ακίνητο σημείο (xo; y) και κάποια από τη γειτονιά της έχουν συνεχείς μερικές παραγώγους μέχρι τη δεύτερη τάξη συμπεριλαμβανομένων. Ας υπολογίσουμε στο σημείο (x0;y0) τις τιμές A=f""xx(x0;y0), B=ƒ""xy(x0;y0), C=ƒ""yy(x0;y0) . Ας υποδηλώσουμε Επειτα:

1. αν Δ > 0, τότε η συνάρτηση ƒ(x;y) στο σημείο (x0;y0) έχει άκρο: μέγιστο αν Α< 0; минимум, если А > 0;

2. αν Δ< 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.

3. Στην περίπτωση Δ = 0, μπορεί να υπάρχει ή να μην υπάρχει ακρότατο στο σημείο (x0;y0). Χρειάζεται περισσότερη έρευνα.

$E \υποσύνολο \mathbb(R)^(n)$. Λένε ότι το $f$ έχει τοπικό μέγιστοστο σημείο $x_(0) \σε E$, αν υπάρχει μια γειτονιά $U$ του σημείου $x_(0)$ τέτοια ώστε για όλα τα $x \in U$ η ανισότητα $f\left(x\right ) \leqslant f είναι ικανοποιημένη \left(x_(0)\right)$.

Το τοπικό μέγιστο ονομάζεται αυστηρός , εάν η γειτονιά $U$ μπορεί να επιλεγεί έτσι ώστε για όλα τα $x \σε U$ διαφορετικά από τα $x_(0)$ να υπάρχει $f\left(x\right)< f\left(x_{0}\right)$.

Ορισμός
Έστω $f$ πραγματική λειτουργίαστο ανοιχτό σύνολο $E \subset \mathbb(R)^(n)$. Λένε ότι έχει $f$ τοπικό ελάχιστοστο σημείο $x_(0) \σε E$, αν υπάρχει μια γειτονιά $U$ του σημείου $x_(0)$ τέτοια ώστε για όλα τα $x \in U$ η ανισότητα $f\left(x\right ) \geqslant f είναι ικανοποιημένη \left(x_(0)\right)$.

Ένα τοπικό ελάχιστο ονομάζεται αυστηρό εάν μπορεί να επιλεγεί μια γειτονιά $U$ έτσι ώστε για όλα τα $x \in U$ διαφορετική από $x_(0)$ να υπάρχει $f\left(x\right) > f\left(x_ ( 0)\δεξιά)$.

Το τοπικό άκρο συνδυάζει τις έννοιες του τοπικού ελάχιστου και του τοπικού μέγιστου.

Θεώρημα ( απαραίτητη προϋπόθεσηάκρο της διαφοροποιήσιμης συνάρτησης)
Έστω η $f$ μια πραγματική συνάρτηση στο ανοιχτό σύνολο $E \subset \mathbb(R)^(n)$. Εάν στο σημείο $x_(0) \στο E$ η συνάρτηση $f$ έχει τοπικό άκρο σε αυτό το σημείο, τότε $$\text(d)f\left(x_(0)\right)=0.$$ Ίσο με μηδέν διαφορικό ισοδυναμεί με το γεγονός ότι όλα είναι ίσα με μηδέν, δηλ. $$\displaystyle\frac(\partial f)(\partial x_(i))\left(x_(0)\right)=0.$$

Στη μονοδιάστατη περίπτωση αυτό είναι – . Ας συμβολίσουμε $\phi \left(t\right) = f \left(x_(0)+th\right)$, όπου το $h$ είναι ένα αυθαίρετο διάνυσμα. Η συνάρτηση $\phi$ ορίζεται για τιμές $t$ που είναι αρκετά μικρές σε απόλυτη τιμή. Επιπλέον, είναι διαφοροποιήσιμο σε σχέση με , και $(\phi)’ \left(t\right) = \text(d)f \left(x_(0)+th\right)h$.
Έστω το $f$ να έχει ένα τοπικό μέγιστο στο σημείο x $0$. Αυτό σημαίνει ότι η συνάρτηση $\phi$ στο $t = 0$ έχει ένα τοπικό μέγιστο και, σύμφωνα με το θεώρημα του Fermat, $(\phi)’ \left(0\right)=0$.
Έτσι, πήραμε ότι $df \left(x_(0)\right) = 0$, δηλ. Η συνάρτηση $f$ στο σημείο $x_(0)$ είναι ίση με μηδέν σε οποιοδήποτε διάνυσμα $h$.

Ορισμός
Σημεία στα οποία η διαφορά είναι μηδέν, δηλ. εκείνες στις οποίες όλες οι επιμέρους παράγωγοι είναι ίσες με μηδέν λέγονται ακίνητες. Κρίσιμα σημείαΟι συναρτήσεις $f$ είναι εκείνα τα σημεία στα οποία η $f$ δεν είναι διαφοροποιήσιμη ή ισούται με μηδέν. Εάν το σημείο είναι ακίνητο, τότε δεν προκύπτει από αυτό ότι η συνάρτηση έχει ακρότατο σε αυτό το σημείο.

Παράδειγμα 1.
Έστω $f \left(x,y\right)=x^(3)+y^(3)$. Τότε $\displaystyle\frac(\partial f)(\partial x) = 3 \cdot x^(2)$,$\displaystyle\frac(\partial f)(\partial y) = 3 \cdot y^(2 )$, οπότε το $\left(0,0\right)$ είναι ένα ακίνητο σημείο, αλλά η συνάρτηση δεν έχει ακρότατο σε αυτό το σημείο. Πράγματι, $f \left(0,0\right) = 0$, αλλά είναι εύκολο να δούμε ότι σε οποιαδήποτε γειτονιά του σημείου $\left(0,0\right)$ η συνάρτηση παίρνει θετικές και αρνητικές τιμές.

Παράδειγμα 2.
Η συνάρτηση $f \left(x,y\right) = x^(2) − y^(2)$ έχει ένα ακίνητο σημείο στην αρχή της, αλλά είναι σαφές ότι δεν υπάρχει άκρο σε αυτό το σημείο.

Θεώρημα ( επαρκής κατάστασηακραίο).
Έστω η συνάρτηση $f$ δύο φορές συνεχώς διαφοροποιήσιμη στο ανοιχτό σύνολο $E \subset \mathbb(R)^(n)$. Έστω $x_(0) \σε E$ ένα σταθερό σημείο και $$\displaystyle Q_(x_(0)) \left(h\right) \equiv \sum_(i=1)^n \sum_(j=1 ) ^n \frac(\partial^(2) f)(\partial x_(i) \partial x_(j)) \left(x_(0)\right)h^(i)h^(j).$ $ Τότε

αν $Q_(x_(0))$ – , τότε η συνάρτηση $f$ στο σημείο $x_(0)$ έχει ένα τοπικό άκρο, δηλαδή, ένα ελάχιστο εάν η φόρμα είναι θετική οριστική, και ένα μέγιστο εάν η φόρμα είναι αρνητική οριστική?
αν η τετραγωνική μορφή $Q_(x_(0))$ δεν έχει οριστεί, τότε η συνάρτηση $f$ στο σημείο $x_(0)$ δεν έχει ακρότατο.

Ας χρησιμοποιήσουμε την επέκταση σύμφωνα με τον τύπο Taylor (12.7 σελ. 292). Λαμβάνοντας υπόψη ότι οι μερικές παράγωγοι πρώτης τάξης στο σημείο $x_(0)$ είναι ίσες με μηδέν, λαμβάνουμε $$\displaystyle f \left(x_(0)+h\right)−f \left(x_(0)\ δεξιά) = \ frac(1)(2) \sum_(i=1)^n \sum_(j=1)^n \frac(\partial^(2) f)(\μερική x_(i) \μερική x_ (j)) \left(x_(0)+\theta h\right)h^(i)h^(j),$$ όπου $0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0$ και $\epsilon \left(h\right) \rightarrow 0$ για $h \rightarrow 0$, μετά δεξί μέροςθα είναι θετικό για οποιοδήποτε διάνυσμα $h$ αρκετά μικρού μήκους.
Έτσι, καταλήξαμε στο συμπέρασμα ότι σε μια συγκεκριμένη γειτονιά του σημείου $x_(0)$ ισχύει η ανισότητα $f \left(x\right) >f \left(x_(0)\right)$ αν μόνο $ x \neq x_ (0)$ (βάζουμε $x=x_(0)+h$\δεξιά). Αυτό σημαίνει ότι στο σημείο $x_(0)$ η συνάρτηση έχει ένα αυστηρό τοπικό ελάχιστο, και έτσι αποδεικνύεται το πρώτο μέρος του θεωρήματός μας.
Ας υποθέσουμε τώρα ότι το $Q_(x_(0))$ είναι αόριστος τύπος. Στη συνέχεια, υπάρχουν διανύσματα $h_(1)$, $h_(2)$ τέτοια ώστε $Q_(x_(0)) \left(h_(1)\right)=\lambda_(1)>0$, $Q_ ( x_(0)) \left(h_(2)\right)= \lambda_(2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>$0. Τότε παίρνουμε $$f \left(x_(0)+th_(1)\right)−f \left(x_(0)\right) = \frac(1)(2) \left[ t^(2) \ lambda_(1) + t^(2) |h_(1)|^(2) \epsilon \left(th_(1)\right) \right] = \frac(1)(2) t^(2) \ αριστερά[ \lambda_(1) + |h_(1)|^(2) \epsilon \left(th_(1)\right) \right].$$ Για αρκετά μικρό $t>0$, το δεξί η πλευρά είναι θετική. Αυτό σημαίνει ότι σε οποιαδήποτε γειτονιά του σημείου $x_(0)$ η συνάρτηση $f$ παίρνει τιμές $f \left(x\right)$ μεγαλύτερες από $f \left(x_(0)\right)$.
Ομοίως, βρίσκουμε ότι σε οποιαδήποτε γειτονιά του σημείου $x_(0)$ η συνάρτηση $f$ παίρνει τιμές μικρότερες από $f \left(x_(0)\right)$. Αυτό, μαζί με το προηγούμενο, σημαίνει ότι στο σημείο $x_(0)$ η συνάρτηση $f$ δεν έχει ακρότατο.

Ας σκεφτούμε ειδική περίπτωσηαυτού του θεωρήματος για μια συνάρτηση $f \left(x,y\right)$ δύο μεταβλητών που ορίζονται σε μια συγκεκριμένη γειτονιά του σημείου $\left(x_(0),y_(0)\right)$ και έχουν συνεχή μερική παράγωγα του πρώτου σε αυτή τη γειτονιά και δεύτερες τάξεις. Ας υποθέσουμε ότι το $\left(x_(0),y_(0)\right)$ είναι ένα ακίνητο σημείο και δηλώνει το $$\displaystyle a_(11)= \frac(\partial^(2) f)(\partial x ^ (2)) \left(x_(0) ,y_(0)\right), a_(12)=\frac(\partial^(2) f)(\partial x \partial y) \left(x_( 0 ), y_(0)\right), a_(22)=\frac(\partial^(2) f)(\partial y^(2)) \left(x_(0), y_(0)\right ) .$$ Τότε το προηγούμενο θεώρημα παίρνει την ακόλουθη μορφή.

Θεώρημα
Έστω $\Delta=a_(11) \cdot a_(22) − a_(12)^2$. Επειτα:

αν $\Delta>0$, τότε η συνάρτηση $f$ έχει ένα τοπικό άκρο στο σημείο $\left(x_(0),y_(0)\right)$, δηλαδή ένα ελάχιστο αν $a_(11)> 0$ , και μέγιστο εάν $a_(11)<0$;
αν $\Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.

Παραδείγματα επίλυσης προβλημάτων

Αλγόριθμος για την εύρεση του άκρου μιας συνάρτησης πολλών μεταβλητών:

Εύρεση σταθερών σημείων.
Βρείτε το διαφορικό 2ης τάξης σε όλα τα ακίνητα σημεία
Χρησιμοποιώντας την επαρκή συνθήκη για το άκρο μιας συνάρτησης πολλών μεταβλητών, θεωρούμε τη διαφορά 2ης τάξης σε κάθε ακίνητο σημείο

Διερευνήστε τη συνάρτηση για το άκρο $f \left(x,y\right) = x^(3) + 8 \cdot y^(3) + 18 \cdot x — 30 \cdot y$.
Λύση
Ας βρούμε τα μερικά παράγωγα 1ης τάξης: $$\displaystyle \frac(\partial f)(\partial x)=3 \cdot x^(2) - 6 \cdot y;$$ $$\displaystyle \frac(\partial f)(\partial y)=24 \cdot y^(2) — 6 \cdot x.$$ Ας συνθέσουμε και λύσουμε το σύστημα: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x) = 0\\\frac(\μερική f)(\μερική y)= 0\end(περιπτώσεις) \Δεξί βέλος \αρχή(περιπτώσεις)3 \cdot x^(2) - 6 \cdot y= 0\\24 \cdot y^(2) — 6 \cdot x = 0\end(περιπτώσεις) \Rightarrow \begin(περιπτώσεις)x^(2) — 2 \cdot y= 0\\4 \cdot y^(2) — x = 0 \end(περιπτώσεις)$$ Από τη 2η εξίσωση εκφράζουμε $x=4 \cdot y^(2)$ - αντικαταστήστε την στην 1η εξίσωση: $$\displaystyle \left(4 \cdot y^(2) \right )^(2)-2 \cdot y=0$$ $$16 \cdot y^(4) — 2 \cdot y = 0$$ $$8 \cdot y^(4) — y = 0$$ $ $y \left(8 \cdot y^(3) -1\right)=0$$ Ως αποτέλεσμα, λαμβάνονται 2 σταθερά σημεία:
1) $y=0 \Δεξί βέλος x = 0, M_(1) = \αριστερά(0, 0\δεξιά)$;
2) $\displaystyle 8 \cdot y^(3) -1=0 \Rightarrow y^(3)=\frac(1)(8) \Rightarrow y = \frac(1)(2) \Rightarrow x=1 , M_(2) = \left(\frac(1)(2), 1\right)$
Ας ελέγξουμε αν ικανοποιείται η επαρκής προϋπόθεση για ένα ακραίο:
$$\displaystyle \frac(\partial^(2) f)(\partial x^(2))=6 \cdot x; \frac(\partial^(2) f)(\partial x \partial y)=-6; \frac(\partial^(2) f)(\partial y^(2))=48 \cdot y$$
1) Για το σημείο $M_(1)= \αριστερά(0,0\δεξιά)$:
$$\displaystyle A_(1)=\frac(\partial^(2) f)(\partial x^(2)) \left(0,0\right)=0; B_(1)=\frac(\partial^(2) f)(\partial x \partial y) \left(0,0\right)=-6; C_(1)=\frac(\partial^(2) f)(\partial y^(2)) \left(0,0\right)=0;$$
$A_(1) \cdot B_(1) — C_(1)^(2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) Για το σημείο $M_(2)$:
$$\displaystyle A_(2)=\frac(\partial^(2) f)(\partial x^(2)) \left(1,\frac(1)(2)\right)=6; B_(2)=\frac(\μερική^(2) f)(\μερική x \μερική y) \left(1,\frac(1)(2)\right)=-6; C_(2)=\frac(\μερική^(2) f)(\μερική y^(2)) \left(1,\frac(1)(2)\right)=24;$$
$A_(2) \cdot B_(2) — C_(2)^(2) = 108>0$, που σημαίνει ότι στο σημείο $M_(2)$ υπάρχει ένα άκρο, και αφού $A_(2)> 0$, τότε αυτό είναι το ελάχιστο.
Απάντηση: Το σημείο $\displaystyle M_(2)\left(1,\frac(1)(2)\right)$ είναι το ελάχιστο σημείο της συνάρτησης $f$.
Διερευνήστε τη συνάρτηση για το άκρο $f=y^(2) + 2 \cdot x \cdot y - 4 \cdot x - 2 \cdot y - 3$.
Λύση
Ας βρούμε σταθερά σημεία: $$\displaystyle \frac(\partial f)(\partial x)=2 \cdot y - 4;$$ $$\displaystyle \frac(\partial f)(\partial y)=2 \ cdot y + 2 \cdot x — 2,$$
Ας συνθέσουμε και λύσουμε το σύστημα: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x)= 0\\\frac(\partial f)(\partial y)= 0\end(cases = x = 1\end(περιπτώσεις) \Δεξί βέλος x = -1$$
Το $M_(0) \left(-1, 2\right)$ είναι ένα ακίνητο σημείο.
Ας ελέγξουμε αν πληρούται η επαρκής προϋπόθεση για το άκρο: $$\displaystyle A=\frac(\partial^(2) f)(\partial x^(2)) \left(-1,2\right)=0 ; B=\frac(\partial^(2) f)(\partial x \partial y) \left(-1,2\right)=2; C=\frac(\partial^(2) f)(\partial y^(2)) \left(-1,2\right)=2;$$
$A \cdot B — C^(2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Απάντηση: δεν υπάρχουν ακρότητες.

Χρονικό όριο: 0

Πλοήγηση (μόνο αριθμοί εργασίας)

Ολοκληρώθηκαν 0 από 4 εργασίες

Πληροφορίες

Κάντε αυτό το κουίζ για να ελέγξετε τις γνώσεις σας για το θέμα που μόλις διαβάσατε: Τοπικό άκρο συναρτήσεων πολλαπλών μεταβλητών.

Έχετε κάνει ήδη το τεστ στο παρελθόν. Δεν μπορείς να το ξαναρχίσεις.

Δοκιμαστική φόρτωση...

Πρέπει να συνδεθείτε ή να εγγραφείτε για να ξεκινήσετε τη δοκιμή.

Πρέπει να ολοκληρώσετε τις ακόλουθες δοκιμές για να ξεκινήσετε αυτό:

Αποτελέσματα

Σωστές απαντήσεις: 0 από 4

Ο χρόνος σου:

Ο χρόνος τελείωσε

Σημειώσατε 0 στους 0 βαθμούς (0)

Το αποτέλεσμά σας έχει καταγραφεί στον πίνακα κατάταξης

Με απάντηση
Με σήμα προβολής

Εργασία 1 από 4

1 .

Αριθμός πόντων: 1

Διερευνήστε τη συνάρτηση $f$ για ακρότατα: $f=e^(x+y)(x^(2)-2 \cdot y^(2))$

σωστά

Λανθασμένος

Εργασία 2 από 4

2 .
Αριθμός πόντων: 1
Η συνάρτηση $f = 4 + \sqrt((x^(2)+y^(2))^(2))$ έχει ακρότατο

σωστά

Για μια συνάρτηση μιας μεταβλητής y = φά(Χ) στο σημείο Χ 0 η γεωμετρική σημασία του διαφορικού σημαίνει την αύξηση της τεταγμένης της εφαπτομένης που σύρεται στη γραφική παράσταση της συνάρτησης στο σημείο με την τετμημένη Χ 0 όταν μετακινείστε σε ένα σημείο Χ 0 +  Χ. Και η διαφορά μιας συνάρτησης δύο μεταβλητών από αυτή την άποψη είναι μια αύξηση δακτυλώσειςεφαπτομένη γραμμή επίπεδοτραβηγμένη στην επιφάνεια που δίνεται από την εξίσωση z = φά(Χ, y) , στο σημείο Μ 0 (Χ 0 , y 0 ) όταν μετακινείστε σε ένα σημείο Μ(Χ 0 +  Χ, y 0 +  y). Ας ορίσουμε ένα εφαπτόμενο επίπεδο σε μια συγκεκριμένη επιφάνεια:

Df . Αεροπλάνο που διέρχεται από ένα σημείο R 0 επιφάνειες μικρό, που ονομάζεται εφαπτομενικό επίπεδοσε ένα δεδομένο σημείο, εάν η γωνία μεταξύ αυτού του επιπέδου και μιας τομής που διέρχεται από δύο σημεία R 0 Και R(οποιοδήποτε σημείο στην επιφάνεια μικρό) , τείνει στο μηδέν όταν το σημείο Rτείνει κατά μήκος αυτής της επιφάνειας σε ένα σημείο R 0 .

Αφήστε την επιφάνεια μικρόδίνεται από την εξίσωση z = φά(Χ, y). Τότε μπορεί να φανεί ότι αυτή η επιφάνεια έχει στο σημείο Π 0 (Χ 0 , y 0 , z 0 ) εφαπτομενικό επίπεδο αν και μόνο αν η συνάρτηση z = φά(Χ, y) είναι διαφοροποιήσιμο σε αυτό το σημείο. Στην περίπτωση αυτή, το εφαπτομενικό επίπεδο δίνεται από την εξίσωση:

z – z 0 = +
(6).

§5. Κατευθυντική παράγωγος, κλίση συνάρτησης.

Μερικές παράγωγες συναρτήσεις y= φά(Χ 1 , Χ 2 .. Χ n ) κατά μεταβλητές Χ 1 , Χ 2 . . . Χ nεκφράζουν το ρυθμό μεταβολής μιας συνάρτησης προς την κατεύθυνση των αξόνων συντεταγμένων. Για παράδειγμα, είναι ο ρυθμός μεταβολής της συνάρτησης κατά Χ 1 – δηλαδή, υποτίθεται ότι ένα σημείο που ανήκει στο πεδίο ορισμού της συνάρτησης κινείται μόνο παράλληλα προς τον άξονα OH 1 , και όλες οι άλλες συντεταγμένες παραμένουν αμετάβλητες. Ωστόσο, μπορεί να υποτεθεί ότι η συνάρτηση μπορεί επίσης να αλλάξει σε κάποια άλλη κατεύθυνση που δεν συμπίπτει με την κατεύθυνση κανενός από τους άξονες.

Θεωρήστε μια συνάρτηση τριών μεταβλητών: u= φά(Χ, y, z).

Ας διορθώσουμε το θέμα Μ 0 (Χ 0 , y 0 , z 0 ) και κάποια κατευθυνόμενη ευθεία (άξονας) μεγάλο, περνώντας από αυτό το σημείο. Αφήνω Μ(Χ, y, z) - αυθαίρετο σημείο αυτής της ευθείας και Μ 0 Μ- απόσταση από Μ 0 πριν Μ.

u = φά (Χ, y, z) – φά(Χ 0 , y 0 , z 0 ) – αύξηση της συνάρτησης σε ένα σημείο Μ 0 .

Ας βρούμε τον λόγο της αύξησης της συνάρτησης προς το μήκος του διανύσματος
:

Df . Παράγωγος συνάρτησης u = φά (Χ, y, z) προς μεγάλο στο σημείο Μ 0 ονομάζεται όριο του λόγου της αύξησης μιας συνάρτησης προς το μήκος του διανύσματος Μ 0 Μκαθώς το τελευταίο τείνει στο 0 (ή, που είναι το ίδιο πράγμα, με το ΜΠρος την Μ 0 ):

(1)

Αυτή η παράγωγος χαρακτηρίζει τον ρυθμό μεταβολής της συνάρτησης στο σημείο Μ 0 στην κατεύθυνση μεγάλο.

Αφήστε τον άξονα μεγάλο (διάνυσμα Μ 0 Μ) μορφές με τσεκούρια ΒΟΔΙ, OY, ΟΖγωνίες
αντίστοιχα.

Ας συμβολίσουμε x-x 0 =
;

y - y 0 =
;

z - z 0 =
.

Στη συνέχεια το διάνυσμα Μ 0 M = (Χ - Χ 0 , y - y 0 , z - z 0 )=
και τα συνημίτονα κατεύθυνσής του:

;

(4).

(4) – τύπος για τον υπολογισμό της κατευθυντικής παραγώγου.

Θεωρήστε ένα διάνυσμα του οποίου οι συντεταγμένες είναι οι μερικές παράγωγοι της συνάρτησης u= φά(Χ, y, z) στο σημείο Μ 0 :

grad u - κλίση συνάρτησης u= φά(Χ, y, z) στο σημείο Μ(Χ, y, z)

Ιδιότητες κλίσης:

συμπέρασμα: μήκος της κλίσης της συνάρτησης u= φά(Χ, y, z) – είναι η πιο δυνατή τιμή σε αυτό το σημείο Μ(Χ, y, z) και την κατεύθυνση του διανύσματος grad uσυμπίπτει με την κατεύθυνση του διανύσματος που αφήνει το σημείο Μ, κατά μήκος του οποίου η συνάρτηση αλλάζει πιο γρήγορα. Δηλαδή την κατεύθυνση της κλίσης της συνάρτησης grad u - είναι η κατεύθυνση της ταχύτερης αύξησης της συνάρτησης.

ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΑΡΤΗΣΕΩΝ ΑΡΚΕΤΩΝ ΜΕΤΑΒΛΗΤΩΝ.

Βασικές έννοιες και ορισμοί.

Όταν εξετάζουμε συναρτήσεις πολλών μεταβλητών, θα περιοριστούμε σε μια λεπτομερή περιγραφή των συναρτήσεων δύο μεταβλητών, καθώς όλα τα αποτελέσματα που λαμβάνονται θα ισχύουν για συναρτήσεις αυθαίρετου αριθμού μεταβλητών.

Εάν κάθε ζεύγος αριθμών (x, y) ανεξάρτητα ο ένας από τον άλλο από ένα συγκεκριμένο σύνολο, σύμφωνα με κάποιον κανόνα, σχετίζεται με μία ή περισσότερες τιμές της μεταβλητής z, τότε η μεταβλητή z ονομάζεται συνάρτηση δύο μεταβλητών.

Αν ένα ζεύγος αριθμών (x, y) αντιστοιχεί σε μία τιμή z, τότε καλείται η συνάρτηση ξεκάθαρος, και αν περισσότερα από ένα, τότε - πολυσημασιολογικός.

Τομέας ορισμούσυνάρτηση z είναι το σύνολο των ζευγών (x, y) για τα οποία υπάρχει η συνάρτηση z.

Γειτονιά ενός σημείου M 0 (x 0, y 0) της ακτίνας r είναι το σύνολο όλων των σημείων (x, y) που ικανοποιούν τη συνθήκη.

Ο αριθμός Α ονομάζεται όριοσυνάρτηση f(x, y) καθώς το σημείο M(x, y) τείνει προς το σημείο M 0 (x 0, y 0), αν για κάθε αριθμό e > 0 υπάρχει ένας αριθμός r > 0 τέτοιος ώστε για οποιοδήποτε σημείο M (x, y), για το οποίο ισχύει η συνθήκη

η συνθήκη είναι επίσης αληθής .

Σημειωσε:

Έστω το σημείο M 0 (x 0, y 0) στο πεδίο ορισμού της συνάρτησης f(x, y). Τότε καλείται η συνάρτηση z = f(x, y). συνεχήςστο σημείο M 0 (x 0, y 0), αν

(1)

και το σημείο M(x, y) τείνει προς το σημείο M 0 (x 0, y 0) με αυθαίρετο τρόπο.

Εάν σε οποιοδήποτε σημείο η συνθήκη (1) δεν ικανοποιείται, τότε αυτό το σημείο καλείται σημείο διακοπήςσυναρτήσεις f(x, y). Αυτό μπορεί να συμβαίνει στις ακόλουθες περιπτώσεις:

1) Η συνάρτηση z = f(x, y) δεν ορίζεται στο σημείο M 0 (x 0, y 0).

2) Δεν υπάρχει όριο.

3) Αυτό το όριο υπάρχει, αλλά δεν είναι ίσο με f(x 0 , y 0).

Ιδιότητες συναρτήσεων πολλών μεταβλητών που σχετίζονται με τη συνέχειά τους.

Ιδιοκτησία.Εάν η συνάρτηση f(x, y, ...) είναι ορισμένη και συνεχής σε ένα κλειστό και περιορισμένο πεδίο ορισμού D, τότε σε αυτό το πεδίο υπάρχουν τουλάχιστονένα σημείο

N(x 0 , y 0 , …), έτσι ώστε για τα υπόλοιπα σημεία η ανισότητα να είναι αληθής

f(x 0 , y 0 , …) ³ f(x, y, …)

καθώς και το σημείο N 1 (x 01, y 01, ...), έτσι ώστε για όλα τα άλλα σημεία η ανισότητα να είναι αληθής

f(x 01 , y 01 , …) £ f(x, y, …)

τότε f(x 0 , y 0 , …) = M – υψηλότερη τιμήσυναρτήσεις και f(x 01 , y 01 , ...) = m – μικρότερη τιμήσυναρτήσεις f(x, y,…) στον τομέα D.

Μια συνεχής συνάρτηση σε ένα κλειστό και οριοθετημένο πεδίο D φτάνει τουλάχιστον μία φορά υψηλότερη τιμήκαι κάποτε το μικρότερο.

Ιδιοκτησία.Εάν η συνάρτηση f(x, y, …) ορίζεται και είναι συνεχής σε ένα κλειστό οριοθετημένο πεδίο D, και τα M και m είναι, αντίστοιχα, οι μεγαλύτερες και μικρότερες τιμές της συνάρτησης σε αυτόν τον τομέα, τότε για οποιοδήποτε σημείο m О υπάρχει ένα σημείο

N 0 (x 0 , y 0 , …) έτσι ώστε f(x 0 , y 0 , …) = m.

Με απλά λόγια, συνεχής λειτουργίαδέχεται τα πάντα στην περιοχή Δ ενδιάμεσες τιμέςμεταξύ M και m. Συνέπεια αυτής της ιδιότητας μπορεί να είναι το συμπέρασμα ότι αν οι αριθμοί M και m έχουν διαφορετικά πρόσημα, τότε στον τομέα D η συνάρτηση εξαφανίζεται τουλάχιστον μία φορά.

Ιδιοκτησία.Συνάρτηση f(x, y, …), συνεχής σε ένα κλειστό οριοθετημένο πεδίο D, περιορισμένοςσε αυτήν την περιοχή, εάν υπάρχει ένας αριθμός K τέτοιος ώστε για όλα τα σημεία της περιοχής η ανισότητα να είναι αληθής .

Ιδιοκτησία.Εάν μια συνάρτηση f(x, y, …) ορίζεται και είναι συνεχής σε ένα κλειστό όριο πεδίου D, τότε ομοιόμορφα συνεχήςστην περιοχή αυτή, δηλ. Για οποιονδηποτε θετικός αριθμόςε υπάρχει ένας αριθμός D > 0 τέτοιος ώστε για οποιαδήποτε δύο σημεία (x 1, y 1) και (x 2, y 2) της περιοχής που βρίσκεται σε απόσταση μικρότερη από το D, ισχύει η ανισότητα

2. Μερικά παράγωγα. Μερικά παράγωγα υψηλότερων τάξεων.

Έστω μια συνάρτηση z = f(x, y) σε κάποιο πεδίο ορισμού. Ας πάρουμε ένα αυθαίρετο σημείο M(x, y) και βάλουμε την αύξηση Dx στη μεταβλητή x. Τότε ονομάζεται η ποσότητα D x z = f(x + Dx, y) – f(x, y) μερική αύξηση της συνάρτησης σε x.

Μπορείτε να γράψετε

Τότε λέγεται μερική παράγωγοσυναρτήσεις z = f(x, y) σε x.

Ονομασία:

Η μερική παράγωγος μιας συνάρτησης ως προς το y προσδιορίζεται ομοίως.

Γεωμετρική αίσθησηη μερική παράγωγος (ας πούμε) είναι η εφαπτομένη της γωνίας κλίσης της εφαπτομένης που χαράσσεται στο σημείο N 0 (x 0, y 0, z 0) στο τμήμα της επιφάνειας κατά το επίπεδο y = y 0.

Θα ονομάσουμε αυτά τα παράγωγα μερικών παραγώγων πρώτης τάξης.

Οι παράγωγοι αυτών των συναρτήσεων θα είναι επί μέρους παράγωγα δεύτερης τάξης.

Συνεχίζοντας να διαφοροποιούμε τις προκύπτουσες ισότητες, λαμβάνουμε μερικές παραγώγους υψηλότερων τάξεων.

Μερικά παράγωγα της μορφής και τα λοιπά. λέγονται μικτά παράγωγα.

Εκείνοι. τα μερικά παράγωγα υψηλότερων τάξεων δεν εξαρτώνται από τη σειρά διαφοροποίησης.

Οι διαφορές υψηλότερης τάξης ορίζονται με παρόμοιο τρόπο.

…………………

Πλήρες διαφορικό. Γεωμετρική σημασίαπλήρες διαφορικό. Εφαπτόμενο επίπεδο και κάθετο στην επιφάνεια.

Η έκφραση ονομάζεται πλήρης αύξησησυναρτήσεις f(x, y) σε κάποιο σημείο (x, y), όπου το 1 και το 2 είναι απειροελάχιστες συναρτήσεις για Dх ® 0 και Dу ® 0, αντίστοιχα.

Πλήρες διαφορικόσυνάρτηση z = f(x, y) ονομάζεται το κύριο γραμμικό μέρος ως προς το Dx και το Dу της αύξησης της συνάρτησης Dz στο σημείο (x, y).

Για μια συνάρτηση ενός αυθαίρετου αριθμού μεταβλητών:

Παράδειγμα 3.1. Βρείτε το πλήρες διαφορικό της συνάρτησης.

Σύνολο:0
Σε επαφή με 0
Google+ 0
Εντάξει 0
Facebook 0