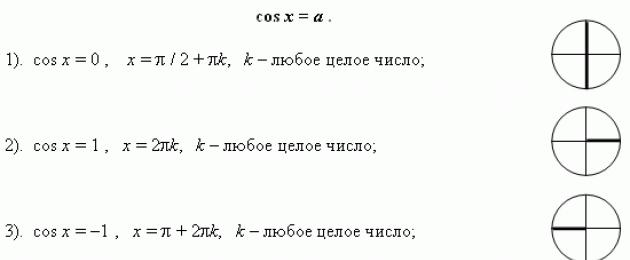Ο απλούστερος πίνακας τριγωνομετρικών εξισώσεων. Τριγωνομετρικές εξισώσεις - τύποι, λύσεις, παραδείγματα

Τριγωνομετρικές εξισώσεις .

Οι απλούστερες τριγωνομετρικές εξισώσεις .

Μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων.

Τριγωνομετρικές εξισώσεις. Μια εξίσωση που περιέχει ένα άγνωστο κάτω λέγεται το πρόσημο της τριγωνομετρικής συνάρτησης τριγωνομετρική.

Οι απλούστερες τριγωνομετρικές εξισώσεις.

Μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων. Η επίλυση μιας τριγωνομετρικής εξίσωσης αποτελείται από δύο στάδια: μετασχηματισμός εξίσωσηςγια να το πάρεις πιο απλότύπου (βλ. παραπάνω) και λύσητο πιο απλό που προκύπτει τριγωνομετρική εξίσωση.Υπάρχουν επτά βασικές μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων.

1. Αλγεβρική μέθοδος. Αυτή η μέθοδος είναι γνωστή σε εμάς από την άλγεβρα.

(μέθοδος αντικατάστασης και αντικατάστασης μεταβλητής).

2. Παραγοντοποίηση. Ας δούμε αυτή τη μέθοδο με παραδείγματα.

Παράδειγμα 1. Λύστε την εξίσωση:αμαρτία Χ+κος Χ = 1 .

Λύση Ας μετακινήσουμε όλους τους όρους της εξίσωσης προς τα αριστερά:

Αμαρτία Χ+κος Χ – 1 = 0 ,

Ας μετασχηματίσουμε και παραγοντοποιήσουμε την έκφραση

Η αριστερή πλευρά της εξίσωσης:

Παράδειγμα 2. Λύστε την εξίσωση: cos 2 Χ+ αμαρτία Χ cos Χ = 1.

Λύση: cos 2 Χ+ αμαρτία Χ cos Χ– αμαρτία 2 Χ– cos 2 Χ = 0 ,

Αμαρτία Χ cos Χ– αμαρτία 2 Χ = 0 ,

Αμαρτία Χ· (κοσ Χ– αμαρτία Χ ) = 0 ,

Παράδειγμα 3. Λύστε την εξίσωση: cos 2 Χ– συν 8 Χ+ cos 6 Χ = 1.

Λύση: cos 2 Χ+ cos 6 Χ= 1 + συν 8 Χ,

2 ως 4 Χ cos 2 Χ= 2κοσ² 4 Χ ,

Cos 4 Χ · (συν 2 Χ– cos 4 Χ) = 0 ,

Cos 4 Χ · 2 αμαρτία 3 Χαμαρτία Χ = 0 ,

1). συν 4 Χ= 0, 2). αμαρτία 3 Χ= 0, 3). αμαρτία Χ = 0 ,

3.

Οδηγει σε ομοιογενής εξίσωση. Η εξίσωση που ονομάζεται ομοιογενής από Σχετικά με αμαρτίαΚαι cos , Αν όλα αυτά όρους του ίδιου βαθμού σε σχέση με αμαρτίαΚαι cosίδια γωνία. Για να λύσετε μια ομοιογενή εξίσωση, πρέπει: ΕΝΑ) μετακινήστε όλα τα μέλη του στην αριστερή πλευρά. σι) βάλτε όλους τους κοινούς παράγοντες εκτός παρενθέσεων. V) εξισώνουν όλους τους παράγοντες και τις αγκύλες με μηδέν. σολ) παρενθέσεις ίσες με μηδέν δίνουν ομοιογενής εξίσωση μικρότερου βαθμού, η οποία πρέπει να χωριστεί σε cos(ή αμαρτία) στο ανώτερο πτυχίο? ρε) λύστε το αποτέλεσμα αλγεβρική εξίσωσησχετικάβυρσοδέψω . ΠΑΡΑΔΕΙΓΜΑ Λύστε την εξίσωση: 3αμαρτία 2 Χ+ 4 αμαρτία Χ cos Χ+ 5 κοσ 2 Χ = 2. Λύση: 3 sin 2 Χ+ 4 αμαρτία Χ cos Χ+ 5 co 2 Χ= 2 αμαρτία 2 Χ+ 2 συν 2 Χ , Αμαρτία 2 Χ+ 4 αμαρτία Χ cos Χ+ 3 co 2 Χ = 0 , Μαύρισμα 2 Χ+ 4 μαύρισμα Χ + 3 = 0 , από εδώ y 2 + 4y +3 = 0 , Οι ρίζες αυτής της εξίσωσης είναι:y 1 = - 1, y 2 = - 3, επομένως 1) μαύρισμα Χ= –1, 2) μαύρισμα Χ = –3,

4. Μετάβαση στη μισή γωνία. Ας δούμε αυτή τη μέθοδο χρησιμοποιώντας ένα παράδειγμα:

ΠΑΡΑΔΕΙΓΜΑ Λύστε την εξίσωση: 3αμαρτία Χ– 5 κοσ Χ = 7.

Λύση: 6 αμαρτία ( Χ/ 2) cos ( Χ/ 2) – 5 cos² ( Χ/ 2) + 5 αμαρτία² ( Χ/ 2) =

7 αμαρτία² ( Χ/ 2) + 7 cos² ( Χ/ 2) ,

2 αμαρτία² ( Χ/ 2) – 6 αμαρτία ( Χ/ 2) cos ( Χ/ 2) + 12 cos² ( Χ/ 2) = 0 ,

μαύρισμα² ( Χ/ 2) – 3 μαύρισμα ( Χ/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Εισαγωγή βοηθητικής γωνίας. Θεωρήστε μια εξίσωση της μορφής:

ένααμαρτία Χ + σι cos Χ = ντο ,

Οπου ένα, σι, ντο– συντελεστές·Χ– άγνωστο.

Τώρα οι συντελεστές της εξίσωσης έχουν τις ιδιότητες του ημιτόνου και του συνημιτόνου, και συγκεκριμένα: συντελεστής (απόλυτη τιμή) του καθενός

Τάξη: 10

«Οι εξισώσεις θα διαρκέσουν για πάντα».

Α. Αϊνστάιν

Στόχοι μαθήματος:

• Εκπαιδευτικός:
  • εμβάθυνση της κατανόησης των μεθόδων για την επίλυση τριγωνομετρικών εξισώσεων.
  • να αναπτύξουν τις δεξιότητες διάκρισης και σωστής επιλογής μεθόδων επίλυσης τριγωνομετρικών εξισώσεων.
• Εκπαιδευτικός:
  • καλλιέργεια γνωστικού ενδιαφέροντος για την εκπαιδευτική διαδικασία·
  • ανάπτυξη της ικανότητας ανάλυσης μιας δεδομένης εργασίας.
  • συμβάλλουν στη βελτίωση του ψυχολογικού κλίματος στην τάξη.
• Αναπτυξιακή:
  • να προωθήσει την ανάπτυξη της ικανότητας της ανεξάρτητης απόκτησης γνώσεων·
  • να προωθήσουν την ικανότητα των μαθητών να υποστηρίζουν την άποψή τους·

Εξοπλισμός:αφίσα με βασικούς τριγωνομετρικούς τύπους, υπολογιστής, προβολέας, οθόνη.

1 μάθημα

Ι. Επικαιροποίηση γνώσεων αναφοράς

Λύστε τις εξισώσεις προφορικά:

1) cosx = 1;
2) 2 cosx = 1;
3) cosx = –;
4) sin2x = 0;
5) sinx = –;
6) sinx = ;
7) tgx = ;
8) cos 2 x – sin 2 x = 0

1) x = 2k;
2) x = ± + 2k;
3) x =± + 2k;
4) x = k;
5) x = (–1) + k;
6) x = (–1) + 2k;
7) x = + k;
8) x = + k; στον Ζ.

II. Εκμάθηση νέου υλικού

– Σήμερα θα δούμε πιο σύνθετα τριγωνομετρικές εξισώσεις. Ας δούμε 10 τρόπους επίλυσής τους. Στη συνέχεια θα γίνουν δύο μαθήματα για ενοποίηση, και για το επόμενο μάθημα θα γίνει τεστ. Στο περίπτερο "For Lesson" υπάρχουν αναρτημένες εργασίες που είναι παρόμοιες με αυτές που θα είναι στο τεστ, πρέπει να τις λύσετε πριν από τη δοκιμή. (Την ημέρα πριν από τη δοκιμή, αναρτήστε τις λύσεις σε αυτές τις εργασίες στο περίπτερο).

Λοιπόν, ας προχωρήσουμε στην εξέταση τρόπων επίλυσης τριγωνομετρικών εξισώσεων. Μερικές από αυτές τις μεθόδους πιθανότατα θα σας φαίνονται δύσκολες, ενώ άλλες θα σας φαίνονται εύκολες, γιατί... Γνωρίζετε ήδη κάποιες τεχνικές για την επίλυση εξισώσεων.

Τέσσερις μαθητές στην τάξη έλαβαν μια ατομική εργασία: να κατανοήσουν και να σας δείξουν 4 τρόπους επίλυσης τριγωνομετρικών εξισώσεων.

(Οι μαθητές που μιλούν έχουν προετοιμάσει διαφάνειες εκ των προτέρων. Η υπόλοιπη τάξη καταγράφει τα κύρια βήματα για την επίλυση εξισώσεων σε ένα τετράδιο.)

1 μαθητής: 1 τρόπος. Επίλυση εξισώσεων με παραγοντοποίηση

αμαρτία 4χ = 3 συν 2χ

Για να λύσουμε την εξίσωση, χρησιμοποιούμε τον τύπο ημιτονοειδούς διπλής γωνίας sin 2 = 2 sin cos
2 αμαρτία 2x cos 2x – 3 cos 2x = 0,
cos 2x (2 sin 2x – 3) = 0. Το γινόμενο αυτών των παραγόντων είναι ίσο με μηδέν αν τουλάχιστον ένας από τους παράγοντες είναι ίσος με μηδέν.

2x = + k, k Z ή sin 2x = 1,5 – δεν υπάρχουν λύσεις, γιατί | αμαρτία| 1
x = + k; στον Ζ.
Απάντηση: x = + k, k Z.

2 μαθητής. Μέθοδος 2. Επίλυση εξισώσεων μετατρέποντας το άθροισμα ή τη διαφορά τριγωνομετρικών συναρτήσεων σε γινόμενο

cos 3x + sin 2x – sin 4x = 0.

Για να λύσουμε την εξίσωση, χρησιμοποιούμε τον τύπο sin– sin = 2 sin сos

cos 3x + 2 sin cos = 0,

сos 3x – 2 sin x cos 3x = 0,

cos 3x (1 – 2 sinx) = 0. Η εξίσωση που προκύπτει είναι ισοδύναμη με ένα σύνολο δύο εξισώσεων:

Το σύνολο των λύσεων της δεύτερης εξίσωσης περιλαμβάνεται πλήρως στο σύνολο των λύσεων της πρώτης εξίσωσης. Που σημαίνει

Απάντηση:

3 μαθητής. 3 τρόπος. Επίλυση εξισώσεων μετατρέποντας το γινόμενο τριγωνομετρικών συναρτήσεων σε άθροισμα

αμαρτία 5χ συν 3χ = αμαρτία 6χ συν2χ.

Για να λύσουμε την εξίσωση, χρησιμοποιούμε τον τύπο

Απάντηση:

4 μαθητής. 4 τρόπος. Επίλυση εξισώσεων που ανάγονται σε δευτεροβάθμιες εξισώσεις

3 sin x – 2 cos 2 x = 0,
3 αμαρτία x – 2 (1 – αμαρτία 2 x) = 0,
2 αμαρτία 2 x + 3 αμαρτία x – 2 = 0,

Έστω sin x = t, όπου | t |. Παίρνουμε τετραγωνική εξίσωση 2t 2 + 3t – 2 = 0,

D = 9 + 16 = 25.

Ετσι . δεν ικανοποιεί την προϋπόθεση | t |.

Άρα αμαρτία x = . Να γιατί .

Απάντηση:

III. Εμπέδωση όσων μάθαμε από το σχολικό βιβλίο του A. N. Kolmogorov

1. Αρ. 164 (α), 167 (α) (τετραγωνική εξίσωση)
2. Αρ. 168 (α) (παραγοντοποίηση)
3. Αρ. 174 (α) (μετατροπή ποσού σε γινόμενο)
4. (μετατροπή προϊόντος σε άθροισμα)

(Στο τέλος του μαθήματος, δείξτε τη λύση αυτών των εξισώσεων στην οθόνη για επαλήθευση)

№ 164 (ΕΝΑ)

2 αμαρτία 2 x + αμαρτία x – 1 = 0.
Έστω sin x = t, | t | 1. Στη συνέχεια
2 t 2 + t – 1 = 0, t = – 1, t= . Οπου

Απάντηση: - .

№ 167 (ΕΝΑ)

3 tg 2 x + 2 tg x – 1 = 0.

Έστω tg x = 1, τότε παίρνουμε την εξίσωση 3 t 2 + 2 t – 1 = 0.

Απάντηση:

№ 168 (ΕΝΑ)

Απάντηση:

№ 174 (ΕΝΑ)

Λύστε την εξίσωση:

Απάντηση:

Μάθημα 2 (μάθημα-διάλεξη)

IV. Εκμάθηση νέου υλικού(συνέχιση)

– Λοιπόν, ας συνεχίσουμε να μελετάμε τρόπους επίλυσης τριγωνομετρικών εξισώσεων.

5 τρόπος. Επίλυση ομοιογενών τριγωνομετρικών εξισώσεων

Εξισώσεις της φόρμας a sin x + b cos x = 0, όπου a και b είναι κάποιοι αριθμοί, ονομάζονται ομοιογενείς εξισώσεις πρώτου βαθμού ως προς το sin x ή το cos x.

Θεωρήστε την εξίσωση

sin x – cos x = 0. Ας διαιρέσουμε και τις δύο πλευρές της εξίσωσης με το cos x. Αυτό μπορεί να γίνει δεν θα συμβεί απώλεια ρίζας, επειδή , Αν cos x = 0,Οτι αμαρτία x = 0. Αλλά αυτό έρχεται σε αντίθεση με τη βασική τριγωνομετρική ταυτότητα αμαρτία 2 x+cos 2 x = 1.

Παίρνουμε μαύρισμα x – 1 = 0.

μαύρισμα x = 1,

Εξισώσεις της φόρμας όπως λέμε 2 x + bcos 2 x + c sin x cos x = 0,Οπου α, β, γ -μερικοί αριθμοί ονομάζονται ομοιογενείς εξισώσεις δεύτερου βαθμού ως προς το sin x ή το cos x.

Θεωρήστε την εξίσωση

sin 2 x – 3 sin x cos x + 2 cos 2 = 0. Ας διαιρέσουμε και τις δύο πλευρές της εξίσωσης με το cos x, και η ρίζα δεν θα χαθεί, γιατί cos x =Το 0 δεν είναι η ρίζα αυτής της εξίσωσης.

tg 2 x – 3tg x + 2 = 0.

Έστω tg x = t. D = 9 – 8 = 1.

Επομένως, tg x = 2 ή tg x = 1.

Ως αποτέλεσμα, x = αρκτάν 2 + , x =

Απάντηση: arctg 2 + ,

Εξετάστε μια άλλη εξίσωση: 3 sin 2 x – 3 sin x cos x + 4 cos 2 x = 2.
Ας μεταμορφωθούμε σωστη πλευραεξισώσεις με τη μορφή 2 = 2 · 1 = 2 · (sin 2 x + cos 2 x). Τότε παίρνουμε:
3sin 2 x – 3sin x cos x + 4cos 2 x = 2 (sin 2 x + cos 2 x),
3sin 2 x – 3sin x cos x + 4cos 2 x – 2sin 2 x – 2 cos 2 x = 0,
sin 2 x – 3sin x cos x + 2cos 2 x = 0. (Πήραμε τη 2η εξίσωση, την οποία έχουμε ήδη αναλύσει).

Απάντηση: arctan 2 + k,

6 τρόπος. Επίλυση Γραμμικών Τριγωνομετρικών Εξισώσεων

Μια γραμμική τριγωνομετρική εξίσωση είναι μια εξίσωση της μορφής a αμαρτία x + b cos x = c, όπου a, b, c είναι κάποιοι αριθμοί.

Θεωρήστε την εξίσωση sin x + cos x= – 1.
Ας ξαναγράψουμε την εξίσωση ως εξής:

Λαμβάνοντας υπόψη αυτό και, παίρνουμε:

Απάντηση:

7 τρόπος. Παρουσιάζοντας ένα επιπλέον επιχείρημα

Εκφραση a cos x + b sin xμπορεί να μετατραπεί:

(έχουμε ήδη χρησιμοποιήσει αυτόν τον μετασχηματισμό κατά την απλοποίηση τριγωνομετρικών παραστάσεων)

Ας εισαγάγουμε ένα επιπλέον επιχείρημα - η γωνία είναι τέτοια που

Επειτα

Θεωρήστε την εξίσωση: 3 sinx + 4 cosx = 1. =

Εργασία για το σπίτι:Νο. 164 -170 (c, d).

Μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων.

Η επίλυση μιας τριγωνομετρικής εξίσωσης αποτελείται από δύο στάδια: μετασχηματισμός εξίσωσηςγια να το πάρεις πιο απλότύπου (βλ. παραπάνω) και λύσητο πιο απλό που προκύπτει τριγωνομετρική εξίσωση.Υπάρχουν επτά βασικές μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων.

1. Αλγεβρική μέθοδος.

(μέθοδος αντικατάστασης και αντικατάστασης μεταβλητής).

2. Παραγοντοποίηση.

Παράδειγμα 1. Λύστε την εξίσωση:αμαρτία Χ+κος Χ = 1 .

Λύση Ας μετακινήσουμε όλους τους όρους της εξίσωσης προς τα αριστερά:

Αμαρτία Χ+κος Χ – 1 = 0 ,

Ας μετασχηματίσουμε και παραγοντοποιήσουμε την έκφραση

Η αριστερή πλευρά της εξίσωσης:

Παράδειγμα 2. Λύστε την εξίσωση: cos 2 Χ+ αμαρτία Χ cos Χ = 1.

Λύση: cos 2 Χ+ αμαρτία Χ cos Χ– αμαρτία 2 Χ– cos 2 Χ = 0 ,

Αμαρτία Χ cos Χ– αμαρτία 2 Χ = 0 ,

Αμαρτία Χ· (κοσ Χ– αμαρτία Χ ) = 0 ,

Παράδειγμα 3. Λύστε την εξίσωση: cos 2 Χ– συν 8 Χ+ cos 6 Χ = 1.

Λύση: cos 2 Χ+ cos 6 Χ= 1 + συν 8 Χ,

2 ως 4 Χ cos 2 Χ= 2κοσ² 4 Χ ,

Cos 4 Χ · (συν 2 Χ– cos 4 Χ) = 0 ,

Cos 4 Χ · 2 αμαρτία 3 Χαμαρτία Χ = 0 ,

1). συν 4 Χ= 0, 2). αμαρτία 3 Χ= 0, 3). αμαρτία Χ = 0 ,

3. Μείωση σε ομοιογενής εξίσωση. Η εξίσωση που ονομάζεται ομοιογενής από Σχετικά με αμαρτίαΚαι cos , Αν όλα αυτά όρους του ίδιου βαθμού σε σχέση με αμαρτίαΚαι cosίδια γωνία. Για να λύσετε μια ομοιογενή εξίσωση, πρέπει: ΕΝΑ) μετακινήστε όλα τα μέλη του στην αριστερή πλευρά. σι) βγάλτε τα όλα κοινούς παράγοντεςπέρα από αγκύλες? V) εξισώνουν όλους τους παράγοντες και τις αγκύλες με μηδέν. σολ) παρενθέσεις ίσες με μηδέν δίνουν ομοιογενής εξίσωση μικρότερου βαθμού, η οποία πρέπει να χωριστεί σε cos(ή αμαρτία) στο ανώτερο πτυχίο? ρε) λύστε την αλγεβρική εξίσωση που προκύπτει γιαβυρσοδέψω . αμαρτία 2 Χ+ 4 αμαρτία Χ cos Χ+ 5 κοσ 2 Χ = 2. Λύση: 3 sin 2 Χ+ 4 αμαρτία Χ cos Χ+ 5 co 2 Χ= 2 αμαρτία 2 Χ+ 2 συν 2 Χ , Αμαρτία 2 Χ+ 4 αμαρτία Χ cos Χ+ 3 co 2 Χ = 0 , Μαύρισμα 2 Χ+ 4 μαύρισμα Χ + 3 = 0 , από εδώ y 2 + 4y +3 = 0 , Οι ρίζες αυτής της εξίσωσης είναι:y 1 = - 1, y 2 = - 3, επομένως 1) μαύρισμα Χ= –1, 2) μαύρισμα Χ = –3,

4. Μετάβαση στη μισή γωνία.

Ας δούμε αυτή τη μέθοδο χρησιμοποιώντας ένα παράδειγμα:

ΠΑΡΑΔΕΙΓΜΑ Λύστε την εξίσωση: 3αμαρτία Χ– 5 κοσ Χ = 7.

Λύση: 6 αμαρτία ( Χ/ 2) cos ( Χ/ 2) – 5 cos² ( Χ/ 2) + 5 αμαρτία² ( Χ/ 2) =

7 αμαρτία² ( Χ/ 2) + 7 cos² ( Χ/ 2) ,

2 αμαρτία² ( Χ/ 2) – 6 αμαρτία ( Χ/ 2) cos ( Χ/ 2) + 12 cos² ( Χ/ 2) = 0 ,

μαύρισμα² ( Χ/ 2) – 3 μαύρισμα ( Χ/ 2) + 6 = 0 ,

. . . . . . . . . .

5. Εισαγωγή βοηθητικής γωνίας.

Θεωρήστε μια εξίσωση της μορφής:

ένααμαρτία Χ + σι cos Χ = ντο ,

Οπου ένα, σι, ντο– συντελεστές·Χ– άγνωστο.

Τώρα οι συντελεστές της εξίσωσης έχουν τις ιδιότητες του ημιτόνου και του συνημιτόνου, και συγκεκριμένα: συντελεστής (απόλυτη τιμή) του καθενός εκ των οποίων όχι περισσότερα από 1, και το άθροισμα των τετραγώνων τους είναι 1. Τότε μπορούμε να υποδηλώσουμε τους αναλόγως Πως cos and sin (εδώ - τα λεγόμενα βοηθητική γωνία), Καιπάρτε την εξίσωσή μας

Μπορείτε να παραγγείλετε αναλυτική λύσητο καθήκον σου!!!

Μια ισότητα που περιέχει έναν άγνωστο κάτω από το πρόσημο μιας τριγωνομετρικής συνάρτησης («sin x, cos x, tan x» ή «ctg x») ονομάζεται τριγωνομετρική εξίσωση και είναι οι τύποι τους που θα εξετάσουμε περαιτέρω.

Οι απλούστερες εξισώσεις είναι «sin x=a, cos x=a, tg x=a, ctg x=a», όπου «x» είναι η γωνία που πρέπει να βρεθεί, «a» είναι οποιοσδήποτε αριθμός. Ας γράψουμε τους τύπους ρίζας για καθένα από αυτά.

1. Εξίσωση `sin x=a`.

Για το `|a|>1` δεν έχει λύσεις.

Όταν `|α| Το \leq 1` έχει άπειρο αριθμό λύσεων.

Τύπος ρίζας: `x=(-1)^n arcsin a + \pi n, n \in Z`

2. Εξίσωση `cos x=a`

Για `|a|>1` - όπως στην περίπτωση του ημιτονοειδούς, δεν έχει λύσεις μεταξύ των πραγματικών αριθμών.

Όταν `|α| Το \leq 1` έχει άπειρο αριθμό λύσεων.

Τύπος ρίζας: `x=\pm arccos a + 2\pi n, n \in Z`

Ειδικές περιπτώσεις για ημίτονο και συνημίτονο σε γραφήματα.

3. Εξίσωση `tg x=a`

Έχει άπειρο αριθμό λύσεων για οποιεσδήποτε τιμές του 'a'.

Τύπος ρίζας: `x=arctg a + \pi n, n \in Z`

4. Εξίσωση `ctg x=a`

Έχει επίσης έναν άπειρο αριθμό λύσεων για οποιεσδήποτε τιμές του 'a'.

Τύπος ρίζας: `x=arcctg a + \pi n, n \in Z`

Τύποι για τις ρίζες των τριγωνομετρικών εξισώσεων στον πίνακα

Για ημιτονοειδή:
Για το συνημίτονο:
Για εφαπτομένη και συνεφαπτομένη:
Τύποι επίλυσης εξισώσεων που περιέχουν αντίστροφα τριγωνομετρικές συναρτήσεις:

Μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων

Η επίλυση οποιασδήποτε τριγωνομετρικής εξίσωσης αποτελείται από δύο στάδια:

• με τη βοήθεια της μετατροπής του στο απλούστερο.
• λύστε την απλούστερη εξίσωση που προκύπτει χρησιμοποιώντας τους τύπους ρίζας και τους πίνακες που γράφτηκαν παραπάνω.

Ας δούμε τις κύριες μεθόδους λύσης χρησιμοποιώντας παραδείγματα.

Αλγεβρική μέθοδος.

Αυτή η μέθοδος περιλαμβάνει την αντικατάσταση μιας μεταβλητής και την αντικατάστασή της σε μια ισότητα.

Παράδειγμα. Λύστε την εξίσωση: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`

`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,

κάντε μια αντικατάσταση: `cos(x+\frac \pi 6)=y`, μετά `2y^2-3y+1=0`,

βρίσκουμε τις ρίζες: `y_1=1, y_2=1/2`, από τις οποίες ακολουθούν δύο περιπτώσεις:

1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.

2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.

Απάντηση: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.

Παραγοντοποίηση.

Παράδειγμα. Λύστε την εξίσωση: `sin x+cos x=1`.

Λύση. Ας μετακινήσουμε όλους τους όρους της ισότητας προς τα αριστερά: `sin x+cos x-1=0`. Χρησιμοποιώντας , μετασχηματίζουμε και παραγοντοποιούμε την αριστερή πλευρά:

`sin x — 2sin^2 x/2=0`,

`2sin x/2 cos x/2-2sin^2 x/2=0`,

`2sin x/2 (cos x/2-sin x/2)=0`,

1. `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
2. `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.

Απάντηση: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.

Αναγωγή σε ομοιογενή εξίσωση

Αρχικά, πρέπει να μειώσετε αυτήν την τριγωνομετρική εξίσωση σε μία από τις δύο μορφές:

`a sin x+b cos x=0` (ομογενής εξίσωση πρώτου βαθμού) ή `a sin^2 x + b sin x cos x +c cos^2 x=0` (ομογενής εξίσωση δεύτερου βαθμού).

Στη συνέχεια, διαιρέστε και τα δύο μέρη με «cos x \ne 0» - για την πρώτη περίπτωση, και με «cos^2 x \ne 0» - για τη δεύτερη. Λαμβάνουμε εξισώσεις για «tg x»: «a tg x+b=0» και «a tg^2 x + b tg x +c =0», οι οποίες πρέπει να λυθούν χρησιμοποιώντας γνωστές μεθόδους.

Παράδειγμα. Λύστε την εξίσωση: `2 sin^2 x+sin x cos x - cos^2 x=1`.

Λύση. Ας γράψουμε τη δεξιά πλευρά ως `1=sin^2 x+cos^2 x`:

`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,

`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`

`sin^2 x+sin x cos x — 2 cos^2 x=0`.

Αυτή είναι μια ομοιογενής τριγωνομετρική εξίσωση του δεύτερου βαθμού, διαιρούμε την αριστερή και τη δεξιά πλευρά της με το «cos^2 x \ne 0», παίρνουμε:

`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`

`tg^2 x+tg x — 2=0`. Ας εισάγουμε την αντικατάσταση `tg x=t`, με αποτέλεσμα `t^2 + t - 2=0`. Οι ρίζες αυτής της εξίσωσης είναι «t_1=-2» και «t_2=1». Επειτα:

1. `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
2. `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, `n \in Z`.

Απάντηση. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.

Μετακίνηση στη μισή γωνία

Παράδειγμα. Λύστε την εξίσωση: `11 sin x - 2 cos x = 10`.

Λύση. Ας εφαρμόσουμε τους τύπους διπλής γωνίας, με αποτέλεσμα: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 συν^2 x/2`

`4 tg^2 x/2 — 11 tg x/2 +6=0`

Εφαρμόζοντας την αλγεβρική μέθοδο που περιγράφεται παραπάνω, λαμβάνουμε:

1. `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
2. `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Απάντηση. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.

Εισαγωγή βοηθητικής γωνίας

Στην τριγωνομετρική εξίσωση «a sin x + b cos x =c», όπου a,b,c είναι συντελεστές και x είναι μια μεταβλητή, διαιρέστε και τις δύο πλευρές με το «sqrt (a^2+b^2)»:

`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2 ) +b^2))».

Οι συντελεστές στην αριστερή πλευρά έχουν τις ιδιότητες του ημιτόνου και του συνημιτόνου, δηλαδή το άθροισμα των τετραγώνων τους είναι ίσο με 1 και οι μονάδες τους δεν είναι μεγαλύτερες από 1. Ας τους συμβολίσουμε ως εξής: `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, τότε:

`cos \varphi sin x + sin \varphi cos x =C`.

Ας ρίξουμε μια πιο προσεκτική ματιά στο ακόλουθο παράδειγμα:

Παράδειγμα. Λύστε την εξίσωση: `3 sin x+4 cos x=2`.

Λύση. Διαιρέστε και τις δύο πλευρές της ισότητας με το `sqrt (3^2+4^2)`, παίρνουμε:

`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))».

`3/5 αμαρτία x+4/5 cos x=2/5`.

Ας συμβολίσουμε `3/5 = cos \varphi` , `4/5=sin \varphi`. Εφόσον `sin \varphi>0`, `cos \varphi>0`, τότε λαμβάνουμε το `\varphi=arcsin 4/5` ως βοηθητική γωνία. Στη συνέχεια γράφουμε την ισότητα μας με τη μορφή:

`cos \varphi sin x+sin \varphi cos x=2/5`

Εφαρμόζοντας τον τύπο για το άθροισμα των γωνιών για το ημίτονο, γράφουμε την ισότητά μας με την ακόλουθη μορφή:

`sin (x+\varphi)=2/5`,

`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,

`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Απάντηση. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.

Κλασματικές ορθολογικές τριγωνομετρικές εξισώσεις

Πρόκειται για ισότητες με κλάσματα των οποίων οι αριθμητές και οι παρονομαστές περιέχουν τριγωνομετρικές συναρτήσεις.

Παράδειγμα. Λύστε την εξίσωση. `\frac (sin x)(1+cos x)=1-cos x`.

Λύση. Πολλαπλασιάστε και διαιρέστε τη δεξιά πλευρά της ισότητας με το «(1+cos x)». Ως αποτέλεσμα παίρνουμε:

`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`

`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`

`\frac (sin x-sin^2 x)(1+cos x)=0`

Λαμβάνοντας υπόψη ότι ο παρονομαστής δεν μπορεί να είναι ίσος με μηδέν, παίρνουμε «1+cos x \ne 0», «cos x \ne -1», «x \ne \pi+2\pi n, n \in Z».

Ας εξισώσουμε τον αριθμητή του κλάσματος με μηδέν: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Στη συνέχεια `sin x=0` ή `1-sin x=0`.

1. `sin x=0`, `x=\pi n`, `n \in Z`
2. `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.

Δεδομένου ότι ` x \ne \pi+2\pi n, n \in Z`, οι λύσεις είναι `x=2\pi n, n \in Z` και `x=\pi /2+2\pi n` , `n \σε Z`.

Απάντηση. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.

Η τριγωνομετρία, και ειδικότερα οι τριγωνομετρικές εξισώσεις, χρησιμοποιούνται σχεδόν σε όλους τους τομείς της γεωμετρίας, της φυσικής και της μηχανικής. Η φοίτηση ξεκινά στη 10η τάξη, υπάρχουν πάντα εργασίες για την Ενιαία Κρατική Εξέταση, οπότε προσπαθήστε να θυμάστε όλους τους τύπους των τριγωνομετρικών εξισώσεων - σίγουρα θα σας φανούν χρήσιμες!

Ωστόσο, δεν χρειάζεται καν να τα απομνημονεύσετε, το κύριο πράγμα είναι να κατανοήσετε την ουσία και να μπορέσετε να την αντλήσετε. Δεν είναι τόσο δύσκολο όσο φαίνεται. Δείτε μόνοι σας βλέποντας το βίντεο.

Έννοια επίλυσης τριγωνομετρικών εξισώσεων.

• Για να λύσετε μια τριγωνομετρική εξίσωση, μετατρέψτε την σε μία ή περισσότερες βασικές τριγωνομετρικές εξισώσεις. Η επίλυση μιας τριγωνομετρικής εξίσωσης καταλήγει τελικά στην επίλυση των τεσσάρων βασικών τριγωνομετρικών εξισώσεων.

Επίλυση βασικών τριγωνομετρικών εξισώσεων.

• Υπάρχουν 4 τύποι βασικών τριγωνομετρικών εξισώσεων:
• sin x = a; cos x = α
• tan x = a; ctg x = α
• Η επίλυση βασικών τριγωνομετρικών εξισώσεων περιλαμβάνει την εξέταση των διαφορετικών θέσεων "x". κύκλος μονάδας, και χρησιμοποιώντας έναν πίνακα μετατροπών (ή αριθμομηχανή).
• Παράδειγμα 1. sin x = 0,866. Χρησιμοποιώντας έναν πίνακα μετατροπών (ή αριθμομηχανή) θα λάβετε την απάντηση: x = π/3. Ο μοναδιαίος κύκλος δίνει άλλη απάντηση: 2π/3. Θυμηθείτε: όλες οι τριγωνομετρικές συναρτήσεις είναι περιοδικές, δηλαδή οι τιμές τους επαναλαμβάνονται. Για παράδειγμα, η περιοδικότητα των sin x και cos x είναι 2πn και η περιοδικότητα των tg x και ctg x είναι πn. Επομένως η απάντηση γράφεται ως εξής:
• x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
• Παράδειγμα 2. cos x = -1/2. Χρησιμοποιώντας έναν πίνακα μετατροπών (ή αριθμομηχανή) θα λάβετε την απάντηση: x = 2π/3. Ο μοναδιαίος κύκλος δίνει άλλη απάντηση: -2π/3.
• x1 = 2π/3 + 2π; x2 = -2π/3 + 2π.
• Παράδειγμα 3. tg (x - π/4) = 0.
• Απάντηση: x = π/4 + πn.
• Παράδειγμα 4. ctg 2x = 1,732.
• Απάντηση: x = π/12 + πn.

Μετασχηματισμοί που χρησιμοποιούνται στην επίλυση τριγωνομετρικών εξισώσεων.

• Για τον μετασχηματισμό τριγωνομετρικών εξισώσεων χρησιμοποιούνται αλγεβρικοί μετασχηματισμοί (παραγοντοποίηση, αναγωγή ομοιογενή μέληκ.λπ.) και τριγωνομετρικές ταυτότητες.
• Παράδειγμα 5: Χρησιμοποιώντας τριγωνομετρικές ταυτότητες, η εξίσωση sin x + sin 2x + sin 3x = 0 μετατρέπεται στην εξίσωση 4cos x*sin (3x/2)*cos (x/2) = 0. Έτσι, οι ακόλουθες βασικές τριγωνομετρικές εξισώσεις πρέπει να λυθεί: cos x = 0; sin(3x/2) = 0; cos(x/2) = 0.

• Εύρεση γωνιών χρησιμοποιώντας γνωστές τιμές συνάρτησης.

  • Πριν μάθετε πώς να λύνετε τριγωνομετρικές εξισώσεις, πρέπει να μάθετε πώς να βρίσκετε γωνίες χρησιμοποιώντας γνωστές τιμές συνάρτησης. Αυτό μπορεί να γίνει χρησιμοποιώντας έναν πίνακα μετατροπών ή μια αριθμομηχανή.
  • Παράδειγμα: cos x = 0,732. Η αριθμομηχανή θα δώσει την απάντηση x = 42,95 μοίρες. Ο μοναδιαίος κύκλος θα δώσει πρόσθετες γωνίες, το συνημίτονο του οποίου είναι επίσης 0,732.

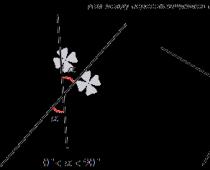
• Αφήστε το διάλυμα στην άκρη στον κύκλο της μονάδας.

  • Μπορείτε να σχεδιάσετε λύσεις σε μια τριγωνομετρική εξίσωση στον μοναδιαίο κύκλο. Οι λύσεις μιας τριγωνομετρικής εξίσωσης στον μοναδιαίο κύκλο είναι οι κορυφές ενός κανονικού πολυγώνου.
  • Παράδειγμα: Οι λύσεις x = π/3 + πn/2 στον μοναδιαίο κύκλο αντιπροσωπεύουν τις κορυφές του τετραγώνου.
  • Παράδειγμα: Οι λύσεις x = π/4 + πn/3 στον μοναδιαίο κύκλο αντιπροσωπεύουν τις κορυφές ενός κανονικού εξαγώνου.

• Μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων.

  • Εάν μια δεδομένη τριγωνομετρική εξίσωση περιέχει μόνο μία τριγωνομετρική συνάρτηση, λύστε αυτή την εξίσωση ως βασική τριγωνομετρική εξίσωση. Εάν μια δεδομένη εξίσωση περιλαμβάνει δύο ή περισσότερες τριγωνομετρικές συναρτήσεις, τότε υπάρχουν 2 μέθοδοι για την επίλυση μιας τέτοιας εξίσωσης (ανάλογα με την πιθανότητα μετασχηματισμού της).
    • Μέθοδος 1.
  • Μετατρέψτε αυτή την εξίσωση σε εξίσωση της μορφής: f(x)*g(x)*h(x) = 0, όπου f(x), g(x), h(x) είναι οι βασικές τριγωνομετρικές εξισώσεις.
  • Παράδειγμα 6. 2cos x + sin 2x = 0. (0< x < 2π)
  • Λύση. Χρησιμοποιώντας τον τύπο διπλής γωνίας sin 2x = 2*sin x*cos x, αντικαταστήστε το sin 2x.
  • 2cos x + 2*sin x*cos x = 2cos x*(sin x + 1) = 0. Λύστε τώρα τις δύο βασικές τριγωνομετρικές εξισώσεις: cos x = 0 και (sin x + 1) = 0.
  • Παράδειγμα 7. cos x + cos 2x + cos 3x = 0. (0< x < 2π)
  • Λύση: Χρησιμοποιώντας τριγωνομετρικές ταυτότητες, μετατρέψτε αυτή την εξίσωση σε εξίσωση της μορφής: cos 2x(2cos x + 1) = 0. Τώρα λύστε τις δύο βασικές τριγωνομετρικές εξισώσεις: cos 2x = 0 και (2cos x + 1) = 0.
  • Παράδειγμα 8. sin x - sin 3x = cos 2x. (0< x < 2π)
  • Λύση: Χρησιμοποιώντας τριγωνομετρικές ταυτότητες, μετατρέψτε αυτή την εξίσωση σε μια εξίσωση της μορφής: -cos 2x*(2sin x + 1) = 0. Τώρα λύστε τις δύο βασικές τριγωνομετρικές εξισώσεις: cos 2x = 0 και (2sin x + 1) = 0 .
    • Μέθοδος 2.
  • Μετατρέψτε τη δεδομένη τριγωνομετρική εξίσωση σε εξίσωση που περιέχει μόνο μία τριγωνομετρική συνάρτηση. Στη συνέχεια, αντικαταστήστε αυτήν την τριγωνομετρική συνάρτηση με κάποια άγνωστη, για παράδειγμα, t (sin x = t; cos x = t; cos 2x = t, tan x = t; tg (x/2) = t, κ.λπ.).
  • Παράδειγμα 9. 3sin^2 x - 2cos^2 x = 4sin x + 7 (0< x < 2π).
  • Λύση. Σε αυτήν την εξίσωση, αντικαταστήστε το (cos^2 x) με το (1 - sin^2 x) (σύμφωνα με την ταυτότητα). Η μετασχηματισμένη εξίσωση είναι:
  • 3sin^2 x - 2 + 2sin^2 x - 4sin x - 7 = 0. Αντικαταστήστε το sin x με t. Τώρα η εξίσωση μοιάζει με: 5t^2 - 4t - 9 = 0. Αυτή είναι μια τετραγωνική εξίσωση που έχει δύο ρίζες: t1 = -1 και t2 = 9/5. Η δεύτερη ρίζα t2 δεν ικανοποιεί το εύρος συναρτήσεων (-1< sin x < 1). Теперь решите: t = sin х = -1; х = 3π/2.
  • Παράδειγμα 10. tg x + 2 tg^2 x = ctg x + 2
  • Λύση. Αντικαταστήστε το tg x με το t. Ξαναγράψτε την αρχική εξίσωση ως εξής: (2t + 1)(t^2 - 1) = 0. Τώρα βρείτε το t και μετά βρείτε το x για t = tan x.

• Ειδικές τριγωνομετρικές εξισώσεις.

  • Υπάρχουν αρκετές ειδικές τριγωνομετρικές εξισώσεις που απαιτούν συγκεκριμένους μετασχηματισμούς. Παραδείγματα:
  • a*sin x+ b*cos x = c ; a(sin x + cos x) + b*cos x*sin x = c;
  • a*sin^2 x + b*sin x*cos x + c*cos^2 x = 0

• Περιοδικότητα τριγωνομετρικών συναρτήσεων.

  • Όπως αναφέρθηκε προηγουμένως, όλες οι τριγωνομετρικές συναρτήσεις είναι περιοδικές, που σημαίνει ότι οι τιμές τους επαναλαμβάνονται μετά από μια ορισμένη περίοδο. Παραδείγματα:
    • Η περίοδος της συνάρτησης f(x) = sin x είναι 2π.
    • Η περίοδος της συνάρτησης f(x) = tan x ισούται με π.
    • Η περίοδος της συνάρτησης f(x) = sin 2x ισούται με π.
    • Η περίοδος της συνάρτησης f(x) = cos (x/2) είναι 4π.
  • Εάν προσδιορίζεται μια περίοδος στο πρόβλημα, υπολογίστε την τιμή του "x" εντός αυτής της περιόδου.
  • Σημείωση: Η επίλυση τριγωνομετρικών εξισώσεων δεν είναι εύκολη υπόθεση και συχνά οδηγεί σε σφάλματα. Επομένως, ελέγξτε προσεκτικά τις απαντήσεις σας. Για να το κάνετε αυτό, μπορείτε να χρησιμοποιήσετε μια αριθμομηχανή γραφικών για να γράψετε τη δεδομένη εξίσωση R(x) = 0. Σε τέτοιες περιπτώσεις, οι λύσεις θα παρουσιαστούν ως δεκαδικά(δηλαδή το π αντικαθίσταται από το 3.14).