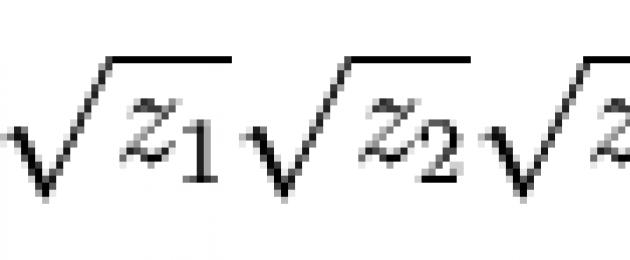Μεταβείτε στο κανάλι youtube της ιστοσελίδας μας για να μείνετε ενημερωμένοι με όλα τα νέα μαθήματα βίντεο.
Αρχικά, ας θυμηθούμε τους βασικούς τύπους των δυνάμεων και τις ιδιότητές τους.
Προϊόν ενός αριθμού έναεμφανίζεται στον εαυτό του n φορές, μπορούμε να γράψουμε αυτή την έκφραση ως a … a=a n
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n / a m = a n - m
Ισχύς ή εκθετικές εξισώσεις – πρόκειται για εξισώσεις στις οποίες οι μεταβλητές είναι σε δυνάμεις (ή εκθέτες) και η βάση είναι ένας αριθμός.
Παραδείγματα εκθετικών εξισώσεων:
Σε αυτό το παράδειγμα, ο αριθμός 6 είναι η βάση, είναι πάντα στο κάτω μέρος και η μεταβλητή Χβαθμός ή δείκτης.
Ας δώσουμε περισσότερα παραδείγματα εκθετικών εξισώσεων.
2 x *5=10
16 x - 4 x - 6=0
Τώρα ας δούμε πώς λύνονται οι εκθετικές εξισώσεις;
Ας πάρουμε μια απλή εξίσωση:
2 x = 2 3
Αυτό το παράδειγμα μπορεί να λυθεί ακόμα και στο κεφάλι σας. Μπορεί να φανεί ότι x=3. Άλλωστε έτσι ώστε το αριστερό και δεξί μέροςήταν ίσα, πρέπει να αντικαταστήσετε το x με τον αριθμό 3.
Τώρα ας δούμε πώς να επισημοποιήσετε αυτήν την απόφαση:
2 x = 2 3
x = 3
Για να λύσουμε μια τέτοια εξίσωση, αφαιρέσαμε πανομοιότυπους λόγους(δηλαδή δύο) και σημείωσε ό,τι απέμεινε, αυτά είναι πτυχία. Πήραμε την απάντηση που ψάχναμε.
Τώρα ας συνοψίσουμε την απόφασή μας.
Αλγόριθμος για την επίλυση της εκθετικής εξίσωσης:
1. Χρειάζεται έλεγχος το ίδιοαν η εξίσωση έχει βάσεις δεξιά και αριστερά. Εάν οι λόγοι δεν είναι οι ίδιοι, αναζητούμε επιλογές για να λύσουμε αυτό το παράδειγμα.
2. Αφού οι βάσεις γίνουν ίδιες, εξισώνωμοίρες και λύστε τη νέα εξίσωση που προκύπτει.
Ας δούμε τώρα μερικά παραδείγματα:
Ας ξεκινήσουμε με κάτι απλό.
Οι βάσεις στην αριστερή και δεξιά πλευρά είναι ίσες με τον αριθμό 2, που σημαίνει ότι μπορούμε να απορρίψουμε τη βάση και να εξισώσουμε τις δυνάμεις τους.
x+2=4 Λαμβάνεται η απλούστερη εξίσωση.
x=4 – 2
x=2
Απάντηση: x=2
Στο παρακάτω παράδειγμα μπορείτε να δείτε ότι οι βάσεις είναι διαφορετικές: 3 και 9.
3 3x - 9 x+8 = 0
Πρώτα, μετακινήστε το εννέα στη δεξιά πλευρά, παίρνουμε:
Τώρα πρέπει να φτιάξετε τις ίδιες βάσεις. Γνωρίζουμε ότι 9=3 2. Ας χρησιμοποιήσουμε τον τύπο ισχύος (a n) m = a nm.
3 3x = (3 2) x+8
Παίρνουμε 9 x+8 =(3 2) x+8 =3 2x+16
3 3x = 3 2x+16 Τώρα είναι σαφές ότι στην αριστερή και δεξιά πλευρά οι βάσεις είναι ίδιες και ίσες με τρεις, που σημαίνει ότι μπορούμε να τις απορρίψουμε και να εξισώσουμε τις μοίρες.
3x=2x+16 παίρνουμε την απλούστερη εξίσωση
3x - 2x=16
x=16
Απάντηση: x=16.
Ας δούμε το παρακάτω παράδειγμα:
2 2x+4 - 10 4 x = 2 4
Πρώτα από όλα, κοιτάμε τις βάσεις, τις βάσεις δύο και τέσσερις. Και χρειαζόμαστε να είναι το ίδιο. Μετασχηματίζουμε τα τέσσερα χρησιμοποιώντας τον τύπο (a n) m = a nm.
4 x = (2 2) x = 2 2x
Και χρησιμοποιούμε επίσης έναν τύπο a n a m = a n + m:
2 2x+4 = 2 2x 2 4
Προσθέστε στην εξίσωση:
2 2x 2 4 - 10 2 2x = 24
Δώσαμε ένα παράδειγμα για τους ίδιους λόγους. Μας ενοχλούν όμως άλλοι αριθμοί 10 και 24. Αν κοιτάξετε προσεκτικά, μπορείτε να δείτε ότι στην αριστερή πλευρά έχουμε 2 2 φορές επαναλαμβανόμενα, εδώ είναι η απάντηση - μπορούμε να βάλουμε 2 2 φορές εκτός παρενθέσεων:
2 2x (2 4 - 10) = 24
Ας υπολογίσουμε την έκφραση σε αγκύλες:
2 4 — 10 = 16 — 10 = 6
Διαιρούμε ολόκληρη την εξίσωση με το 6:
Ας φανταστούμε 4=2 2:
2 2x = 2 2 βάσεις είναι ίδιες, τις πετάμε και εξισώνουμε τις μοίρες.
2x = 2 είναι η απλούστερη εξίσωση. Το χωρίζουμε με το 2 και παίρνουμε
x = 1
Απάντηση: x = 1.
Ας λύσουμε την εξίσωση:
9 x – 12*3 x +27= 0
Ας μετατρέψουμε:
9 x = (3 2) x = 3 2x
Παίρνουμε την εξίσωση:
3 2x - 12 3 x +27 = 0
Οι βάσεις μας είναι ίδιες, ίσες με τρεις Σε αυτό το παράδειγμα, μπορείτε να δείτε ότι οι τρεις πρώτοι έχουν διπλάσια μοίρα (2x) από τη δεύτερη (μόλις x). Σε αυτή την περίπτωση, μπορείτε να λύσετε μέθοδος αντικατάστασης. Αντικαθιστούμε τον αριθμό με τον μικρότερο βαθμό:
Τότε 3 2x = (3 x) 2 = t 2
Αντικαθιστούμε όλες τις x δυνάμεις της εξίσωσης με t:
t 2 - 12t+27 = 0
Παίρνουμε τετραγωνική εξίσωση. Επιλύοντας μέσω της διάκρισης, παίρνουμε:
D=144-108=36
t 1 = 9
t2 = 3
Επιστρέφοντας στη μεταβλητή Χ.
Πάρτε το t 1:
t 1 = 9 = 3 x
Αυτό είναι,
3 x = 9
3 x = 3 2
x 1 = 2
Βρέθηκε μια ρίζα. Ψάχνουμε για το δεύτερο από το t 2:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Απάντηση: x 1 = 2; x 2 = 1.
Στην ιστοσελίδα μπορείτε να κάνετε όποιες ερωτήσεις μπορεί να έχετε στην ενότητα ΒΟΗΘΕΙΑ ΑΠΟΦΑΣΙΣΤΕ, σίγουρα θα σας απαντήσουμε.
Εγγραφείτε στην ομάδα
Διάλυμα Descartes-Euler
Έχοντας κάνει την αντικατάσταση, λαμβάνουμε μια εξίσωση με την ακόλουθη μορφή (λέγεται "ελλιπής"):
y 4 + Πy 2 + qy + r = 0 .Ρίζες y 1 , y 2 , y 3 , y 4 μιας τέτοιας εξίσωσης είναι ίσες με μία από τις ακόλουθες εκφράσεις:
στην οποία οι συνδυασμοί χαρακτήρων επιλέγονται με τέτοιο τρόπο ώστε να ικανοποιείται η ακόλουθη σχέση:
,
και z 1 , z 2 και z 3 είναι οι ρίζες της κυβικής εξίσωσης
Η λύση της Ferrari
Κύριο άρθρο: Μέθοδος Ferrari
Ας αναπαραστήσουμε την εξίσωση τέταρτου βαθμού με τη μορφή:
ΕΝΑΧ 4 + σιΧ 3 + ντοΧ 2 + ρεΧ + μι = 0,Η λύση του μπορεί να βρεθεί από τις παρακάτω εκφράσεις:
αν β = 0, επίλυση u 4 + α u 2 + γ = 0και, κάνοντας την αντικατάσταση 
, ας βρούμε τις ρίζες: . 
, (οποιοδήποτε σημάδι τετραγωνική ρίζαθα κάνει), (τρεις σύνθετες ρίζες, μία από τις οποίες θα κάνει) 
Δύο ± s πρέπει να έχουν το ίδιο πρόσημο, ± t - είναι ανεξάρτητα. Για να βρείτε όλες τις ρίζες, πρέπει να βρείτε x για προσημασμένους συνδυασμούς ± s ,± t = +,+ για +,− για −,+ για −,−. Οι διπλές ρίζες θα εμφανιστούν δύο φορές, οι τριπλές ρίζες τρεις φορές και οι τεταρτοταγείς ρίζες τέσσερις φορές. Η σειρά των ριζών εξαρτάται από την κυβική ρίζα Uεπιλεγμένο. δείτε επίσης
- Εύκολα λυμένοι τύποι εξισώσεων 4ου βαθμού: Διτετραγωνική εξίσωση, αμοιβαία εξίσωση τέταρτου βαθμού
Βιβλιογραφία
- Korn G., Korn T. (1974) Handbook of Mathematics.
Συνδέσεις
- Η απόφαση της Ferrari
Ίδρυμα Wikimedia. 2010.
Δείτε τι είναι η «εξίσωση τέταρτου βαθμού» σε άλλα λεξικά:
εξίσωση τέταρτου βαθμού- - [Λ.Γ.Σουμένκο. Αγγλο-ρωσικό λεξικό για την τεχνολογία της πληροφορίας. M.: State Enterprise TsNIIS, 2003.] Θέματα ΤΕΧΝΟΛΟΓΙΑ της ΠΛΗΡΟΦΟΡΙΑΣσε γενική εξίσωση EN quuartic ... Οδηγός Τεχνικού Μεταφραστή
Γράφημα πολυωνύμου 4ου βαθμού με τέσσερις ρίζες και τρία κρίσιμα σημεία. Μια εξίσωση τέταρτου βαθμού στα μαθηματικά είναι μια αλγεβρική εξίσωση της μορφής: Τέταρτου βαθμού για αλγεβρικές εξισώσειςείναι το υψηλότερο στο οποίο... ... Wikipedia
Μια εξίσωση της μορφής: anxn + an − 1xn − 1 + ... + a1x + a0 = 0 ονομάζεται αμοιβαία αν οι συντελεστές της σε συμμετρικές θέσεις είναι ίσοι, δηλαδή αν an − k = ak, για k = 0, 1, ..., n. Περιεχόμενα 1 Εξίσωση τέταρτου βαθμού ... Wikipedia
Στην οποία ο άγνωστος όρος είναι στην τέταρτη δύναμη. Πλήρες λεξικό ξένες λέξεις, που έχουν τεθεί σε χρήση στη ρωσική γλώσσα. Popov M., 1907. ΔΙΤΕΚΤΡΟΦΟΡΙΚΗ ΕΞΙΣΩΣΗ από λατ. bis, δύο φορές, και quadratum, τετράγωνο. Η εξίσωση στην οποία ο μεγαλύτερος βαθμός... ... Λεξικό ξένων λέξεων της ρωσικής γλώσσας
Μαζί με την αριθμητική υπάρχει η επιστήμη των αριθμών και, μέσω των αριθμών, των ποσοτήτων γενικότερα. Χωρίς να μελετήσουν τις ιδιότητες ορισμένων, συγκεκριμένων μεγεθών, και οι δύο αυτές επιστήμες ερευνούν τις ιδιότητες των αφηρημένων μεγεθών καθαυτές, ανεξάρτητα από... ... εγκυκλοπαιδικό λεξικόΦΑ. Brockhaus και I.A. Έφρον
Ένα σύνολο εφαρμοσμένων γνώσεων που επιτρέπει στους μηχανικούς αεροπορίας να σπουδάσουν στον τομέα της αεροδυναμικής, των προβλημάτων αντοχής, της κατασκευής κινητήρων και της δυναμικής πτήσης των αεροσκαφών (δηλαδή θεωρία) για τη δημιουργία ενός νέου αεροσκάφους ή τη βελτίωση... ... Εγκυκλοπαίδεια Collier
Η παλαιότερη μαθηματική δραστηριότητα ήταν το μέτρημα. Ήταν απαραίτητος ένας λογαριασμός για την παρακολούθηση των ζώων και τη διεξαγωγή εμπορίου. Μερικές πρωτόγονες φυλές μετρούσαν τον αριθμό των αντικειμένων ταιριάζοντάς τα με διάφορα μέρη του σώματος, κυρίως... ... Εγκυκλοπαίδεια Collier
Ιστορία της Τεχνολογίας Ανά Περίοδο και Περιοχή: Νεολιθική Επανάσταση Αρχαίες Αιγυπτιακές Τεχνολογίες Επιστήμη και Τεχνολογία αρχαία ΙνδίαΕπιστήμη και Τεχνολογία Αρχαία Κίνατεχνολογίες Αρχαία Ελλάδατεχνολογίες Αρχαία ΡώμηΤεχνολογίες του Ισλαμικού κόσμου... ... Wikipedia
Μια εξίσωση είναι μια μαθηματική σχέση που εκφράζει την ισότητα δύο αλγεβρικές εκφράσεις. Αν ισχύει η ισότητα για οποιονδήποτε αποδεκτές τιμέςάγνωστα περιλαμβάνονται σε αυτό, τότε ονομάζεται ταυτότητα. για παράδειγμα, μια αναλογία της μορφής... ... Εγκυκλοπαίδεια Collier
Το θεώρημα του Abel Ruffini δηλώνει ότι η γενική εξίσωση ισχύος στο είναι άλυτη σε ρίζες. Περιεχόμενα 1 Λεπτομέρειες... Wikipedia
Στη γενική περίπτωση, η λύση μιας εξίσωσης τέταρτου βαθμού πραγματοποιείται χρησιμοποιώντας μεθόδους για την επίλυση εξισώσεων για υψηλότερους βαθμούς, για παράδειγμα, με τη μέθοδο Ferrari ή χρησιμοποιώντας το σχήμα Horner. Αλλά μερικές εξισώσεις 4ου βαθμού έχουν μια απλούστερη λύση.
Υπάρχουν αρκετοί ειδικοί τύποι εξισώσεων τέταρτου βαθμού, τις μεθόδους επίλυσης των οποίων θα μάθετε παρακάτω:
- Διτετραγωνική εξίσωση $ax^4+bx^2+c=0$;
- Αντίστροφες εξισώσεις της μορφής $ax^4+bx^3+cx^2 +bx+ a=0$;
- Εξισώσεις της μορφής $ax^4+b=0$.
Επίλυση διτετραγωνικών εξισώσεων τέταρτου βαθμού
Οι διτετραγωνικές εξισώσεις $ax^4+bx^2+c=0$ ανάγονται σε τετραγωνικές εξισώσεις αντικαθιστώντας τη μεταβλητή $x^2$ με μια νέα, για παράδειγμα, $y$. Μετά την αντικατάσταση, λύνεται η νέα εξίσωση που προκύπτει και, στη συνέχεια, η τιμή της μεταβλητής που βρέθηκε αντικαθίσταται στην εξίσωση $x^2=y$. Το αποτέλεσμα της λύσης θα είναι οι ρίζες της εξίσωσης $x^2=y$.
Παράδειγμα 1
Λύστε την εξίσωση $x(x-1)(x-2)(x-3)=24$:
Ας επεκτείνουμε τις παρενθέσεις στο πολυώνυμο:
$(x^2-3x)(x^2-3x+2)=24$
Σε αυτή τη μορφή, γίνεται προφανές ότι μπορούμε να επιλέξουμε την έκφραση $y=x^2-3x$ ως νέα μεταβλητή.
$y\cdot (y+2)=24$
Τώρα ας λύσουμε δύο τετραγωνικές εξισώσεις $x^2-3x=-4$ και $x^2-3x=-6$.
Οι ρίζες της πρώτης εξίσωσης είναι $x_1(1,2)=4;-1$, η δεύτερη δεν έχει λύσεις.
Επίλυση αμοιβαίων εξισώσεων βαθμού 4
Αυτές οι εξισώσεις της μορφής $ax^4+bx^3+cx^2 +bx+ a=0$ επαναλαμβάνουν με τους συντελεστές τους για όρους χαμηλότερης τάξης τους συντελεστές για πολυώνυμα με υψηλότερους βαθμούς. Για να λύσετε μια τέτοια εξίσωση, πρώτα διαιρέστε την με $x^2$:
$ax^4+bx^3+cx^2 +bx+ a=0|:x^2$
$ax^2+bx+c+\frac(b)(x) + \frac(a)(x^2)=0$
$a(x^2+\frac(1)(x^2))+b(x+\frac(1)(x)) + c=0$
Στη συνέχεια αντικαταστήστε το $(x+\frac(1)(x))$ με μια νέα μεταβλητή, στη συνέχεια $(x^2+\frac(1)(x^2))=y^2-2$, μετά την αντικατάσταση παίρνουμε το παρακάτω τετράγωνο η εξίσωση:
$a(y^2-2)+by+c=0$
Μετά από αυτό, αναζητούμε τις ρίζες των εξισώσεων $x+\frac(1)(x)=y_1$ και $x+\frac(1)(x)=y_2$.
Μια παρόμοια μέθοδος χρησιμοποιείται για την επίλυση αμοιβαίων εξισώσεων της μορφής $ax^4+bx^3+cx^2 +kbx+ k^2a=0$.
Παράδειγμα 2
Λύστε την εξίσωση:
$3x^4-2x^3-9x^2-4x+12=0$
Αυτή η εξίσωση είναι μια αμοιβαία εξίσωση της μορφής $ax^4+bx^3+cx^2 +kbx+ k^2a=0$. Επομένως, διαιρούμε ολόκληρη την εξίσωση με $x^2$:
$3x^2-2x-9 \cdot \frac(2 \cdot 2)(x)+3 \cdot (\frac(2)(x))^2=0$
$3(x^2+\frac(4)(x^2))-2(x+\frac(2)(x)-9=0$
Ας αντικαταστήσουμε την έκφραση $x+\frac(2)(x)$: $3(y^2-4)-2y-9=0$
Ας υπολογίσουμε τις ρίζες αυτής της εξίσωσης, είναι ίσες με $y_1=3$ και $y_2=-\frac(7)(3)$.
Αντίστοιχα, τώρα είναι απαραίτητο να λυθούν δύο εξισώσεις $x+\frac(2)(x)=3$ και $x+\frac(2)(x)=-\frac(7)(3)$. Η λύση στην πρώτη εξίσωση είναι $x_1=1, x_2=2$, η δεύτερη εξίσωση δεν έχει ρίζες.
Επομένως, οι ρίζες της αρχικής εξίσωσης είναι $x_1=1, x_2=2$.
Εξισώσεις της μορφής $ax^4+b=0$
Οι ρίζες μιας εξίσωσης αυτού του τύπου βρίσκονται χρησιμοποιώντας συντομευμένους τύπους πολλαπλασιασμού.
Λίγο αφότου ο Cardano δημοσίευσε μια μέθοδο για την επίλυση κυβικών εξισώσεων, οι μαθητές και οι ακόλουθοί του βρήκαν τρόπους να μειώσουν τη γενική εξίσωση του τέταρτου βαθμού σε κυβική εξίσωση. Ας παρουσιάσουμε την απλούστερη μέθοδο, που ανήκει στην L. Ferrari.
Κατά την παρουσίαση της μεθόδου, θα χρειαστεί να χρησιμοποιήσετε το ακόλουθο βασικό λήμμα.
Λήμμα. Ωστε να τετραγωνικό τριώνυμοήταν το τετράγωνο ενός γραμμικού διωνύμου, είναι απαραίτητο και αρκετό η διάκρισή του να είναι ίση με μηδέν.
Απόδειξη. Ανάγκη. Αφήστε . Μετά επάρκεια. Αφήστε Τότε
Η ιδέα της μεθόδου που παρουσιάζεται είναι να παρουσιαστεί η αριστερή πλευρά της εξίσωσης ως η διαφορά δύο τετραγώνων. Τότε μπορεί να αποσυντεθεί σε δύο συντελεστές δεύτερου βαθμού και η επίλυση της εξίσωσης θα οδηγήσει στην επίλυση δύο τετραγωνικών εξισώσεων. Για να πετύχετε τον στόχο, φανταστείτε την αριστερή πλευρά ως:
Εδώ το y είναι ένα βοηθητικό άγνωστο, το οποίο πρέπει να επιλεγεί έτσι ώστε η έκφραση σε αγκύλες να αποδειχθεί ότι είναι το τετράγωνο ενός γραμμικού διωνύμου. Δυνάμει του λήμματος, για αυτό είναι απαραίτητο και αρκετό να ικανοποιηθεί η προϋπόθεση
Αυτή η συνθήκη είναι μια εξίσωση τρίτου βαθμού ως προς το y. Αφού ανοίξετε τις παρενθέσεις, μετατρέπεται στη φόρμα
Έστω μια από τις ρίζες αυτής της εξίσωσης. Τότε η συνθήκη θα ικανοποιηθεί, άρα ισχύει
για μερικά k και I. Η αρχική εξίσωση παίρνει τη μορφή
Εξισώνοντας κάθε έναν από τους παράγοντες με μηδέν, θα βρούμε τις τέσσερις ρίζες της αρχικής εξίσωσης.
Ας κάνουμε μια ακόμη παρατήρηση. Έστω οι ρίζες του πρώτου παράγοντα και ας είναι οι ρίζες του δεύτερου. Στη συνέχεια, προσθέτοντας αυτές τις ισότητες, παίρνουμε ότι
Έτσι, λάβαμε μια έκφραση για τη ρίζα της βοηθητικής κυβικής εξίσωσης ως προς τις ρίζες της αρχικής εξίσωσης του τέταρτου βαθμού.
Παράδειγμα. Λύστε την εξίσωση. Σύμφωνα με τη μέθοδο που περιγράφεται παραπάνω, μετασχηματίζουμε την αριστερή πλευρά:
Τώρα ας βάλουμε . Μετά τους σχηματισμούς παίρνουμε την εξίσωση
Είναι εύκολο να δούμε ότι μία από τις ρίζες αυτής της εξίσωσης είναι ο αριθμός. Αντικαθιστώντας το στη μετασχηματισμένη αριστερή πλευρά της αρχικής εξίσωσης, παίρνουμε:
Εξισώνοντας τους παράγοντες στο μηδέν, παίρνουμε
Όσον αφορά τις εξισώσεις υψηλότερες από τον τέταρτο βαθμό, ήταν γνωστές ορισμένες κατηγορίες εξισώσεων μιας σχετικά συγκεκριμένης μορφής, που δέχονταν αλγεβρικές λύσεις σε ρίζες, δηλαδή με τη μορφή αποτελεσμάτων αριθμητικές πράξειςκαι δράσεις εξαγωγής ριζών. Ωστόσο, οι προσπάθειες να δοθούν λύσεις σε γενικές εξισώσεις βαθμού πέντε και άνω ήταν ανεπιτυχείς μέχρι, τελικά, στις αρχές του 19ου αιώνα. Οι Ruffini και Abel δεν απέδειξαν ότι μια λύση αυτού του είδους για γενικές εξισώσεις πάνω από τον τέταρτο βαθμό είναι αδύνατη. Τελικά, το 1830, ο λαμπρός Γάλλος μαθηματικός Ε. Γκαλουά κατάφερε να βρει τα απαραίτητα και επαρκείς προϋποθέσεις(που είναι αρκετά δύσκολο να επαληθευτούν) για τη διαλυτότητα μιας συγκεκριμένης εξίσωσης σε ρίζες. Ταυτόχρονα, ο Galois δημιούργησε και χρησιμοποίησε τη θεωρία των ομάδων μετάθεσης, η οποία ήταν νέα για την εποχή του.
2x 4 + 5x 3 - 11x 2 - 20x + 12 = 0
Πρώτα πρέπει να βρείτε μια ρίζα χρησιμοποιώντας τη μέθοδο επιλογής. Συνήθως είναι διαιρέτης του ελεύθερου όρου. Στην περίπτωση αυτή, οι διαιρέτες του αριθμού 12 είναι ±1, ±2, ±3, ±4, ±6, ±12.Ας αρχίσουμε να τα αντικαθιστούμε ένα προς ένα:
1: 2 + 5 - 11 - 20 + 12 = -12 ⇒ αριθμός 1
-1: 2 - 5 - 11 + 20 + 12 = 18 ⇒ αριθμός -1 δεν είναι ρίζα πολυωνύμου
2: 2 ∙ 16 + 5 ∙ 8 - 11 ∙ 4 - 20 ∙ 2 + 12 = 0 ⇒ αριθμός 2 είναι η ρίζα του πολυωνύμου
Βρήκαμε 1 από τις ρίζες του πολυωνύμου. Η ρίζα του πολυωνύμου είναι 2, που σημαίνει ότι το αρχικό πολυώνυμο πρέπει να διαιρείται με x - 2. Για να εκτελέσουμε τη διαίρεση πολυωνύμων, χρησιμοποιούμε το σχήμα του Horner:
| 2 | 5 | -11 | -20 | 12 | |
| 2 |
Οι συντελεστές του αρχικού πολυωνύμου εμφανίζονται στην επάνω γραμμή. Η ρίζα που βρήκαμε τοποθετείται στο πρώτο κελί της δεύτερης σειράς 2. Η δεύτερη γραμμή περιέχει τους συντελεστές του πολυωνύμου που προκύπτει από τη διαίρεση. Μετρώνται ως εξής:
| Στο δεύτερο κελί της δεύτερης σειράς γράφουμε τον αριθμό 2, απλά μετακινώντας το από το αντίστοιχο κελί της πρώτης σειράς. | ||||||||||||
| 2 ∙ 2 + 5 = 9 | ||||||||||||
| 2 ∙ 9 - 11 = 7 | ||||||||||||
| 2 ∙ 7 - 20 = -6 | ||||||||||||
| 2 ∙ (-6) + 12 = 0 |
Ο τελευταίος αριθμός είναι το υπόλοιπο της διαίρεσης. Αν είναι ίσο με 0, τότε τα έχουμε υπολογίσει όλα σωστά.
2x 4 + 5x 3 - 11x 2 - 20x + 12 = (x - 2)(2x 3 + 9x 2 + 7x - 6)
Αλλά αυτό δεν είναι το τέλος. Μπορείτε να προσπαθήσετε να επεκτείνετε το πολυώνυμο με τον ίδιο τρόπο 2x 3 + 9x 2 + 7x - 6.
Και πάλι αναζητούμε μια ρίζα μεταξύ των διαιρετών του ελεύθερου όρου. Διαιρέτες αριθμών -6 είναι ±1, ±2, ±3, ±6.
1: 2 + 9 + 7 - 6 = 12 ⇒ αριθμός 1 δεν είναι ρίζα πολυωνύμου
-1: -2 + 9 - 7 - 6 = -6 ⇒ αριθμός -1 δεν είναι ρίζα πολυωνύμου
2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 - 6 = 60 ⇒ αριθμός 2 δεν είναι ρίζα πολυωνύμου
-2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) - 6 = 0 ⇒ αριθμός -2 είναι η ρίζα του πολυωνύμου
Ας γράψουμε τη ρίζα που βρέθηκε στο σχήμα Horner μας και ας αρχίσουμε να συμπληρώνουμε τα κενά κελιά:
| Στο δεύτερο κελί της τρίτης σειράς γράφουμε τον αριθμό 2, απλά μετακινώντας το από το αντίστοιχο κελί της δεύτερης σειράς. | ||||||||||||||||||
| -2 ∙ 2 + 9 = 5 | ||||||||||||||||||
| -2 ∙ 5 + 7 = -3 | ||||||||||||||||||
| -2 ∙ (-3) - 6 = 0 |
Έτσι, συνυπολογίσαμε το αρχικό πολυώνυμο:
2x 4 + 5x 3 - 11x 2 - 20x + 12 = (x - 2)(x + 2)(2x 2 + 5x - 3)
Πολυώνυμος 2x 2 + 5x - 3μπορεί επίσης να παραγοντοποιηθεί. Για να το κάνετε αυτό, μπορείτε να λύσετε την τετραγωνική εξίσωση μέσω του διαχωριστή ή μπορείτε να αναζητήσετε τη ρίζα μεταξύ των διαιρετών του αριθμού -3. Με τον ένα ή τον άλλο τρόπο, θα καταλήξουμε στο συμπέρασμα ότι η ρίζα αυτού του πολυωνύμου είναι ο αριθμός -3
| Στο δεύτερο κελί της τέταρτης σειράς γράφουμε τον αριθμό 2, απλά μετακινώντας το από το αντίστοιχο κελί της τρίτης σειράς. | ||||||||||||||||||||||||
| -3 ∙ 2 + 5 = -1 | ||||||||||||||||||||||||
| -3 ∙ (-1) - 3 = 0 |
Έτσι, αποσυνθέσαμε το αρχικό πολυώνυμο σε γραμμικούς παράγοντες.
- Σε επαφή με 0
- Google+ 0
- Εντάξει 0
- Facebook 0
