Το εμβαδόν ενός παραλληλογράμμου είναι ημίτονο. Εμβαδόν παραλληλογράμμου

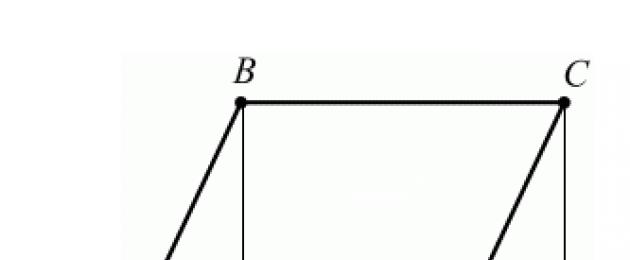
Η παραγωγή του τύπου για το εμβαδόν ενός παραλληλογράμμου καταλήγει στην κατασκευή ενός ορθογωνίου ίσου σε εμβαδόν με το δεδομένο παραλληλόγραμμο. Ας πάρουμε ως βάση τη μία πλευρά του παραλληλογράμμου και η κάθετη που σύρεται από οποιοδήποτε σημείο της απέναντι πλευράς προς την ευθεία που περιέχει τη βάση θα ονομάζεται ύψος του παραλληλογράμμου. Τότε το εμβαδόν του παραλληλογράμμου θα είναι ίσο με το γινόμενο της βάσης και του ύψους του.

Θεώρημα.Το εμβαδόν ενός παραλληλογράμμου είναι ίσο με το γινόμενο της βάσης και του ύψους του.

Απόδειξη. Θεωρήστε ένα παραλληλόγραμμο με εμβαδόν. Ας πάρουμε την πλευρά ως βάση και ας σχεδιάσουμε τα ύψη (Εικόνα 2.3.1). Αυτό απαιτείται να αποδειχθεί.

Εικόνα 2.3.1

Ας αποδείξουμε πρώτα ότι το εμβαδόν του ορθογωνίου είναι επίσης ίσο. Ένα τραπεζοειδές αποτελείται από ένα παραλληλόγραμμο και ένα τρίγωνο. Από την άλλη πλευρά, αποτελείται από ένα ορθογώνιο NVSC και ένα τρίγωνο. Αλλά τα ορθογώνια τρίγωνα είναι ίσα σε υποτείνουσα και οξεία γωνία (οι υποτείνυσές τους είναι ίσες με τις απέναντι πλευρές ενός παραλληλογράμμου και οι γωνίες 1 και 2 είναι ίσες με τις αντίστοιχες γωνίες στην τομή των παράλληλων ευθειών και ενός εγκάρσιου), άρα οι περιοχές τους είναι ίσες. Επομένως, τα εμβαδά του παραλληλογράμμου και του ορθογωνίου είναι επίσης ίσα, δηλαδή το εμβαδόν του ορθογωνίου είναι ίσο. Σύμφωνα με το θεώρημα για την περιοχή ενός ορθογωνίου, αλλά από τότε.

Το θεώρημα έχει αποδειχθεί.

Παράδειγμα 2.3.1.

Ένας κύκλος είναι εγγεγραμμένος σε ρόμβο με πλευρά και οξεία γωνία. Προσδιορίστε το εμβαδόν ενός τετράπλευρου του οποίου οι κορυφές είναι τα σημεία επαφής του κύκλου με τις πλευρές του ρόμβου.

Λύση:

Η ακτίνα ενός κύκλου εγγεγραμμένου σε ρόμβο (Εικόνα 2.3.2), αφού το Τετράγωνο είναι ορθογώνιο, αφού οι γωνίες του στηρίζονται στη διάμετρο του κύκλου. Η περιοχή του είναι όπου (πλευρά απέναντι από τη γωνία),.

Εικόνα 2.3.2

Ετσι,

Απάντηση:

Παράδειγμα 2.3.2.

Δίνεται ένας ρόμβος του οποίου οι διαγώνιοι είναι 3 cm και 4 cm Από την κορυφή μιας αμβλείας γωνίας, σχεδιάζονται τα ύψη και υπολογίζεται το εμβαδόν του τετράπλευρου.

Λύση:

Εμβαδόν ρόμβου (Εικόνα 2.3.3).

Ετσι,

Απάντηση:

Παράδειγμα 2.3.3.

Το εμβαδόν ενός τετράπλευρου είναι Βρείτε το εμβαδόν ενός παραλληλογράμμου του οποίου οι πλευρές είναι ίσες και παράλληλες με τις διαγώνιους του τετράπλευρου.

Λύση:

Αφού και (Εικόνα 2.3.4), τότε είναι παραλληλόγραμμο και, επομένως,.

Εικόνα 2.3.4

Ομοίως, παίρνουμε από το οποίο προκύπτει ότι.

Απάντηση:.

2.4 Εμβαδόν τριγώνου

Υπάρχουν διάφοροι τύποι για τον υπολογισμό του εμβαδού ενός τριγώνου. Ας δούμε αυτά που μελετώνται στο σχολείο.

Ο πρώτος τύπος προκύπτει από τον τύπο για το εμβαδόν ενός παραλληλογράμμου και προσφέρεται στους μαθητές με τη μορφή θεωρήματος.

Θεώρημα.Το εμβαδόν ενός τριγώνου είναι ίσο με το μισό γινόμενο της βάσης και του ύψους του.

Απόδειξη.Έστω το εμβαδόν του τριγώνου. Πάρτε την πλευρά στη βάση του τριγώνου και σχεδιάστε το ύψος. Ας αποδείξουμε ότι:

Εικόνα 2.4.1

Ας χτίσουμε το τρίγωνο σε παραλληλόγραμμο όπως φαίνεται στο σχήμα. Τα τρίγωνα είναι ίσα σε τρεις πλευρές (την κοινή τους πλευρά και τις απέναντι πλευρές ενός παραλληλογράμμου), άρα τα εμβαδά τους είναι ίσα. Συνεπώς, το εμβαδόν S του τριγώνου ABC είναι ίσο με το μισό του εμβαδού του παραλληλογράμμου, δηλ.

Το θεώρημα έχει αποδειχθεί.

Είναι σημαντικό να επιστήσουμε την προσοχή των μαθητών σε δύο συμπεράσματα που προκύπτουν από αυτό το θεώρημα. Και συγκεκριμένα:

τετράγωνο ορθογώνιο τρίγωνοίσο με το μισό γινόμενο των ποδιών του.

Αν τα ύψη δύο τριγώνων είναι ίσα, τότε τα εμβαδά τους σχετίζονται ως βάσεις.

Αυτές οι δύο συνέπειες παίζουν σημαντικός ρόλοςστην επίλυση διαφόρων ειδών προβλημάτων. Με βάση αυτό, αποδεικνύεται ένα άλλο θεώρημα, το οποίο έχει ευρεία εφαρμογή στην επίλυση προβλημάτων.

Θεώρημα. Αν η γωνία ενός τριγώνου είναι ίση με τη γωνία ενός άλλου τριγώνου, τότε τα εμβαδά τους σχετίζονται με το γινόμενο των πλευρών που περικλείουν ίσες γωνίες.

Απόδειξη. Έστω και είναι τα εμβαδά των τριγώνων των οποίων οι γωνίες είναι ίσες.

Εικόνα 2.4.2

Ας αποδείξουμε ότι: .

Ας προσθέσουμε ένα τρίγωνο. πάνω στο τρίγωνο έτσι ώστε η κορυφή να ευθυγραμμίζεται με την κορυφή και οι πλευρές να επικαλύπτουν τις ακτίνες αντίστοιχα.

Εικόνα 2.4.3

Τα τρίγωνα έχουν κοινό ύψος, οπότε... Τα τρίγωνα έχουν επίσης κοινό ύψος – επομένως,. Πολλαπλασιάζοντας τις ισότητες που προκύπτουν, παίρνουμε .

Το θεώρημα έχει αποδειχθεί.

Δεύτερη φόρμουλα.Το εμβαδόν ενός τριγώνου είναι ίσο με το μισό γινόμενο των δύο πλευρών του και το ημίτονο της μεταξύ τους γωνίας.Υπάρχουν διάφοροι τρόποι για να αποδείξετε αυτόν τον τύπο και θα χρησιμοποιήσω έναν από αυτούς.

Απόδειξη.Από τη γεωμετρία υπάρχει ένα πολύ γνωστό θεώρημα ότι το εμβαδόν ενός τριγώνου είναι ίσο με το μισό γινόμενο της βάσης και το ύψος που χαμηλώνει αυτή η βάση:

Στην περίπτωση οξείας τριγώνου. Σε περίπτωση αμβλείας γωνίας. Χο, και ως εκ τούτου . Έτσι, και στις δύο περιπτώσεις. Αντικατάσταση γεωμετρικός τύποςεμβαδού τριγώνου, παίρνουμε τον τριγωνομετρικό τύπο για το εμβαδόν ενός τριγώνου:

Το θεώρημα έχει αποδειχθεί.

Τρίτη φόρμουλαγια την περιοχή ενός τριγώνου - ο τύπος του Ήρωνα, που πήρε το όνομά του από τον αρχαίο Έλληνα επιστήμονα Ήρωνα της Αλεξάνδρειας, ο οποίος έζησε τον πρώτο αιώνα μ.Χ. Αυτός ο τύπος σας επιτρέπει να βρείτε το εμβαδόν ενός τριγώνου, γνωρίζοντας τις πλευρές του. Είναι βολικό γιατί σας επιτρέπει να μην κάνετε πρόσθετες κατασκευές ή να μετρήσετε γωνίες. Το συμπέρασμά του βασίζεται στον δεύτερο από τους τύπους εμβαδού τριγώνου που εξετάσαμε και στο θεώρημα συνημιτόνου: και .

Πριν προχωρήσετε στην εφαρμογή αυτού του σχεδίου, σημειώστε ότι

Με τον ίδιο ακριβώς τρόπο έχουμε:

Τώρα ας εκφράσουμε το συνημίτονο ως και:

Αφού κάθε γωνία σε ένα τρίγωνο είναι όλο και μικρότερη, τότε. Που σημαίνει, .

Τώρα μετασχηματίζουμε ξεχωριστά κάθε έναν από τους παράγοντες στη ριζική έκφραση. Εχουμε:

Αντικαθιστώντας αυτήν την έκφραση στον τύπο για εμβαδόν, παίρνουμε:

Το θέμα «Εμβαδόν τριγώνου» έχει μεγάλη σημασία στο μάθημα των μαθηματικών του σχολείου. Ένα τρίγωνο είναι το απλούστερο από τα γεωμετρικά σχήματα. Είναι ένα «δομικό στοιχείο» της σχολικής γεωμετρίας. Η συντριπτική πλειοψηφία των γεωμετρικών προβλημάτων καταλήγει στην επίλυση τριγώνων. Το πρόβλημα της εύρεσης της περιοχής ενός κανονικού και αυθαίρετου n-gon δεν αποτελεί εξαίρεση.

Παράδειγμα 2.4.1.

Ποιο είναι το εμβαδόν ενός ισοσκελούς τριγώνου αν είναι η βάση του και η πλευρά του;

Λύση:

-ισοσκελής,

Εικόνα 2.4.4

Ας χρησιμοποιήσουμε τις ιδιότητες ενός ισοσκελούς τριγώνου - διάμεσος και ύψος. Επειτα

Σύμφωνα με το Πυθαγόρειο θεώρημα:

Εύρεση του εμβαδού του τριγώνου:

Απάντηση:

Παράδειγμα 2.4.2.

Σε ένα ορθογώνιο τρίγωνο, η διχοτόμος μιας οξείας γωνίας χωρίζει το αντίθετο σκέλος σε τμήματα μήκους 4 και 5 cm.

Λύση:

Let (Εικόνα 2.4.5). Τότε (αφού ο BD είναι διχοτόμος). Από εδώ έχουμε , αυτό είναι. Που σημαίνει,

Εικόνα 2.4.5

Απάντηση:

Παράδειγμα 2.4.3.

Βρείτε το εμβαδόν ενός ισοσκελούς τριγώνου αν η βάση του είναι ίση με , και το μήκος του υψομέτρου που τραβιέται στη βάση είναι ίσο με το μήκος του τμήματος που συνδέει τα μεσαία σημεία της βάσης και της πλευράς.

Λύση:

Σύμφωνα με τη συνθήκη, – η μεσαία γραμμή (Εικόνα 2.4.6). Αφού έχουμε:

ή , από κει και πέρα,

Τι είναι ένα παραλληλόγραμμο; Παραλληλόγραμμο είναι ένα τετράπλευρο του οποίου οι απέναντι πλευρές είναι παράλληλες ανά ζεύγη.

1. Το εμβαδόν ενός παραλληλογράμμου υπολογίζεται με τον τύπο:

\[ \LARGE S = a \cdot h_(a)\]

Οπου:
α είναι η πλευρά του παραλληλογράμμου,
h a – ύψος που τραβιέται προς αυτήν την πλευρά.

2. Εάν είναι γνωστά τα μήκη δύο γειτονικών πλευρών ενός παραλληλογράμμου και η μεταξύ τους γωνία, τότε το εμβαδόν του παραλληλογράμμου υπολογίζεται με τον τύπο:

\[ \LARGE S = a \cdot b \cdot sin(\alpha) \]

3. Εάν δίνονται οι διαγώνιοι ενός παραλληλογράμμου και η γωνία μεταξύ τους είναι γνωστή, τότε το εμβαδόν του παραλληλογράμμου υπολογίζεται με τον τύπο:

\[ \LARGE S = \frac(1)(2) \cdot d_(1) \cdot d_(2) \cdot sin(\alpha) \]

Ιδιότητες παραλληλογράμμου

Σε ένα παραλληλόγραμμο, οι απέναντι πλευρές είναι ίσες: \(AB = CD\), \(BC = AD\)

Σε ένα παραλληλόγραμμο, οι απέναντι γωνίες είναι ίσες: \(\γωνία A = \γωνία C\), \(\γωνία B = \γωνία D\)

Οι διαγώνιοι ενός παραλληλογράμμου στο σημείο τομής διαιρούνται στο μισό \(AO = OC\) , \(BO = OD\)

Η διαγώνιος ενός παραλληλογράμμου το χωρίζει σε δύο ίσα τρίγωνα.

Το άθροισμα των γωνιών ενός παραλληλογράμμου δίπλα στη μία πλευρά είναι 180 o:

\(\γωνία A + \γωνία B = 180^(o)\), \(\γωνία B + \γωνία C = 180^(o)\)

\(\γωνία C + \γωνία D = 180^(o)\), \(\γωνία D + \γωνία A = 180^(o)\)

Οι διαγώνιοι και οι πλευρές ενός παραλληλογράμμου σχετίζονται με την ακόλουθη σχέση:

\(d_(1)^(2) + d_(2)^2 = 2a^(2) + 2b^(2) \)

Σε ένα παραλληλόγραμμο, η γωνία μεταξύ των υψών είναι ίση με την οξεία γωνία του: \(\γωνία K B H =\γωνία A\) .

Οι διχοτόμοι των γωνιών που γειτνιάζουν με τη μία πλευρά ενός παραλληλογράμμου είναι αμοιβαία κάθετες.

Οι διχοτόμοι δύο απέναντι γωνιών ενός παραλληλογράμμου είναι παράλληλες.

Σημάδια παραλληλογράμμου

Ένα τετράπλευρο θα είναι παραλληλόγραμμο αν:

\(AB = CD\) και \(AB || CD\)

\(AB = CD\) και \(BC = AD\)

\(AO = OC\) και \(BO = OD\)

\(\γωνία A = \γωνία C\) και \(\γωνία B = \γωνία D\)

Κατά την επίλυση προβλημάτων σχετικά με αυτό το θέμα, εκτός βασικές ιδιότητες παραλληλόγραμμοκαι τους αντίστοιχους τύπους, μπορείτε να θυμάστε και να εφαρμόσετε τα ακόλουθα:

1. Η διχοτόμος εσωτερικής γωνίας παραλληλογράμμου αποκόπτει ένα ισοσκελές τρίγωνο από αυτήν
2. Οι διχοτόμοι των εσωτερικών γωνιών που γειτνιάζουν με μία από τις πλευρές ενός παραλληλογράμμου είναι αμοιβαία κάθετες
3. Οι διχοτόμοι που προέρχονται από αντίθετες εσωτερικές γωνίες ενός παραλληλογράμμου είναι παράλληλες μεταξύ τους ή βρίσκονται στην ίδια ευθεία
4. Το άθροισμα των τετραγώνων των διαγωνίων ενός παραλληλογράμμου είναι ίσο με το άθροισμα των τετραγώνων των πλευρών του
5. Το εμβαδόν ενός παραλληλογράμμου είναι ίσο με το μισό γινόμενο των διαγωνίων και του ημιτόνου της μεταξύ τους γωνίας

Ας εξετάσουμε προβλήματα στα οποία χρησιμοποιούνται αυτές οι ιδιότητες.

Εργασία 1.

Η διχοτόμος της γωνίας Γ του παραλληλογράμμου ΑΒΓΔ τέμνει την πλευρά ΑΔ στο σημείο Μ και τη συνέχεια της πλευράς ΑΒ πέρα ​​από το σημείο Α στο σημείο Ε. Να βρείτε την περίμετρο του παραλληλογράμμου αν ΑΕ = 4, ΔΜ = 3.

Λύση.

1. Το τρίγωνο CMD είναι ισοσκελές. (Ακίνητο 1). Επομένως, CD = MD = 3 cm.

2. Το τρίγωνο ΕΑΜ είναι ισοσκελές.
Επομένως, AE = AM = 4 cm.

3. AD = AM + MD = 7 cm.

4. Περίμετρος ΑΒΓΔ = 20 cm.

Απάντηση. 20 εκ.

Εργασία 2.

Οι διαγώνιοι σχεδιάζονται σε ένα κυρτό τετράπλευρο ABCD. Είναι γνωστό ότι τα εμβαδά των τριγώνων ABD, ACD, BCD είναι ίσα. Να αποδείξετε ότι αυτό το τετράπλευρο είναι παραλληλόγραμμο.

Λύση.

1. Έστω BE το ύψος του τριγώνου ABD, CF το ύψος του τριγώνου ACD. Εφόσον, σύμφωνα με τις συνθήκες του προβλήματος, τα εμβαδά των τριγώνων είναι ίσα και έχουν κοινή βάση ΑΔ, τότε τα ύψη αυτών των τριγώνων είναι ίσα. BE = CF.

2. ΒΕ, ΚΦ είναι κάθετα στην ΑΔ. Τα σημεία Β και Γ βρίσκονται στην ίδια πλευρά σε σχέση με την ευθεία ΑΔ. BE = CF. Επομένως, ευθεία π.Χ. || ΕΝΑ Δ. (*)

3. Έστω AL το ύψος του τριγώνου ACD, BK το ύψος του τριγώνου BCD. Εφόσον, σύμφωνα με τις συνθήκες του προβλήματος, τα εμβαδά των τριγώνων είναι ίσα και έχουν κοινή βάση CD, τότε τα ύψη αυτών των τριγώνων είναι ίσα. AL = ΒΚ.

4. Το AL και το BK είναι κάθετα στο CD. Τα σημεία Β και Α βρίσκονται στην ίδια πλευρά σε σχέση με την ευθεία γραμμή CD. AL = ΒΚ. Επομένως, ευθεία ΑΒ || CD (**)

5. Από τις συνθήκες (*), (**) προκύπτει ότι το ABCD είναι παραλληλόγραμμο.

Απάντηση. Αποδεδειγμένος. Το ABCD είναι παραλληλόγραμμο.

Εργασία 3.

Στις πλευρές BC και CD του παραλληλογράμμου ABCD, σημειώνονται τα σημεία M και H, αντίστοιχα, έτσι ώστε τα τμήματα BM και HD να τέμνονται στο σημείο O.<ВМD = 95 о,