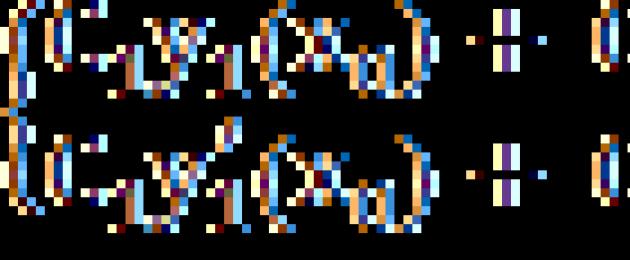Θεώρημα.Εάν και είναι γραμμικά ανεξάρτητες λύσεις της εξίσωσης (2.3), τότε ο γραμμικός συνδυασμός τους , όπου και είναι αυθαίρετες σταθερές, θα είναι μια γενική λύση αυτής της εξίσωσης.

Απόδειξη.Το γεγονός ότι υπάρχει λύση στην εξίσωση (2.3) προκύπτει από το θεώρημα για τις ιδιότητες των λύσεων στο Lodo 2ης τάξης. Πρέπει απλώς να δείξουμε ότι η λύση θα είναι γενικός, δηλ. είναι απαραίτητο να δείξουμε ότι για οποιεσδήποτε αρχικές συνθήκες, μπορεί κανείς να επιλέξει αυθαίρετες σταθερές με τέτοιο τρόπο ώστε να ικανοποιούνται αυτές οι συνθήκες. Ας γράψουμε τις αρχικές συνθήκες στη μορφή:

Οι σταθερές και από αυτό το σύστημα γραμμικών αλγεβρικών εξισώσεων προσδιορίζονται μοναδικά, αφού η ορίζουσα αυτού του συστήματος είναι η τιμή της ορίζουσας Wronski για γραμμικά ανεξάρτητες λύσεις στο Lodu στο: ,

και μια τέτοια ορίζουσα, όπως είδαμε στην προηγούμενη παράγραφο, είναι μη μηδενική. Το θεώρημα έχει αποδειχθεί.

Κατασκευή γενικής λύσης σε LODE δεύτερης τάξης με σταθερούς συντελεστές στη θήκη

13. απλές ρίζες της χαρακτηριστικής εξίσωσης (περίπτωση Δ>0) (με τεκμηρίωση).

14. πολλαπλές ρίζες της χαρακτηριστικής εξίσωσης (περίπτωση Δ=0) (με παραστατικό).

15. μιγαδικές συζυγείς ρίζες της χαρακτηριστικής εξίσωσης (περίπτωση Δ<0) (c док-вом).

Δίνεται ένας λώρος 2ης τάξης με σταθερούς συντελεστές (5.1), όπου , . Σύμφωνα με την προηγούμενη παράγραφο, η γενική λύση της 2ης τάξης lodou προσδιορίζεται εύκολα εάν είναι γνωστές δύο γραμμικά ανεξάρτητες μερικές λύσεις αυτής της εξίσωσης. Μια απλή μέθοδος για την εύρεση μερικών λύσεων σε μια εξίσωση με σταθερούς συντελεστές προτάθηκε από τον L. Euler. Αυτή η μέθοδος, που ονομάζεται μέθοδος Euler, συνίσταται στο γεγονός ότι αναζητούνται μερικές λύσεις στη μορφή.

Αντικαθιστώντας αυτή τη συνάρτηση με την εξίσωση (5.1), αφού μειώσουμε κατά , παίρνουμε μια αλγεβρική εξίσωση, η οποία ονομάζεται χαρακτηριστική: (5.2)

Η συνάρτηση θα είναι λύση στην εξίσωση (5.1) μόνο για εκείνες τις τιμές του k που είναι οι ρίζες της χαρακτηριστικής εξίσωσης (5.2). Ανάλογα με την αξία του διακριτικού, είναι δυνατές τρεις περιπτώσεις.

1. . Τότε οι ρίζες της χαρακτηριστικής εξίσωσης είναι διαφορετικές: . Οι λύσεις θα είναι γραμμικά ανεξάρτητες, γιατί και η γενική λύση (5.1) μπορεί να γραφτεί ως .

2. . Σε αυτή την περίπτωση και . Ως δεύτερη γραμμικά ανεξάρτητη λύση, μπορούμε να πάρουμε τη συνάρτηση . Ας ελέγξουμε ότι αυτή η συνάρτηση ικανοποιεί την εξίσωση (5.1). Πραγματικά, , . Αντικαθιστώντας αυτές τις εκφράσεις στην εξίσωση (5.1), λαμβάνουμε

Ή γιατί Και .

Οι συγκεκριμένες λύσεις είναι γραμμικά ανεξάρτητες, γιατί . Επομένως, η γενική λύση (5.1) έχει τη μορφή:

3. . Στην περίπτωση αυτή, οι ρίζες της χαρακτηριστικής εξίσωσης είναι μιγαδικές συζυγείς: , όπου , . Μπορεί να επαληθευτεί ότι γραμμικά ανεξάρτητες λύσεις της εξίσωσης (5.1) θα είναι οι συναρτήσεις και . Ας βεβαιωθούμε ότι η εξίσωση (5.1) ικανοποιείται, για παράδειγμα, από τη συνάρτηση y 1 . Πραγματικά, , . Αντικαθιστώντας αυτές τις εκφράσεις στην εξίσωση (5.1), λαμβάνουμε

Και οι δύο αγκύλες στην αριστερή πλευρά αυτής της ισότητας είναι πανομοιότυπα ίσες με μηδέν. Πραγματικά, ,

Έτσι, η συνάρτηση ικανοποιεί την εξίσωση (5.1). Ομοίως, δεν είναι δύσκολο να επαληθευτεί ότι υπάρχει λύση στην εξίσωση (5.1). Επειδή η , τότε η γενική λύση θα μοιάζει με: .

16. Θεώρημα για τη δομή της γενικής λύσης ΛΝΔΔΕ δεύτερης τάξης (με απόδειξη).

Θεώρημα 1.Η γενική λύση της 2ης τάξης lndu f(x) (6.1) παριστάνεται ως το άθροισμα της γενικής λύσης της αντίστοιχης ομοιογενούς εξίσωσης (6.2) και οποιασδήποτε συγκεκριμένης λύσης στο lndu (6.1).

Απόδειξη.Ας αποδείξουμε πρώτα ποια θα είναι η λύση της εξίσωσης (6.1). Για να γίνει αυτό, ας αντικαταστήσουμε την f(x) στην εξίσωση (6.1). Αυτή η ισότητα είναι ταυτότητα, γιατί και f(x). Κατά συνέπεια, υπάρχει λύση στην εξίσωση (6.1).

Ας αποδείξουμε τώρα ότι αυτή η λύση είναι γενική, δηλ. μπορείτε να επιλέξετε τις αυθαίρετες σταθερές που περιλαμβάνονται σε αυτό με τέτοιο τρόπο ώστε να πληρούνται τυχόν αρχικές συνθήκες της μορφής: , (6.3). Σύμφωνα με το θεώρημα για τη δομή της γενικής λύσης μιας γραμμικής ομογενούς διαφορικής εξίσωσης (Lod), η γενική λύση της εξίσωσης (6.2) μπορεί να παρασταθεί με τη μορφή , όπου και είναι γραμμικά ανεξάρτητες λύσεις αυτής της εξίσωσης. Έτσι: και, επομένως, οι αρχικές συνθήκες (6.3) μπορούν να γραφτούν ως: ή (6.4)

Οι αυθαίρετες σταθερές και καθορίζονται από αυτό το σύστημα γραμμικών αλγεβρικών εξισώσεων μοναδικά για οποιαδήποτε δεξιά πλευρά, επειδή η ορίζουσα αυτού του συστήματος = είναι η τιμή της ορίζουσας Wronski για γραμμικά ανεξάρτητες λύσεις της εξίσωσης (6.2) για , και μια τέτοια ορίζουσα, όπως είδαμε παραπάνω, είναι μη μηδενική. Έχοντας προσδιορίσει τις σταθερές και από το σύστημα των εξισώσεων (6.4) και αντικαθιστώντας τις στην έκφραση , λαμβάνουμε μια συγκεκριμένη λύση της εξίσωσης (6.1) που ικανοποιεί τις δεδομένες αρχικές συνθήκες. Το θεώρημα έχει αποδειχθεί.

17. Κατασκευή συγκεκριμένης λύσης LNDDE δεύτερης τάξης στην περίπτωση της δεξιάς πλευράς του εντύπου

Έστω οι συντελεστές της εξίσωσης (6.1) σταθεροί, δηλ. η εξίσωση έχει τη μορφή: f(x) (7.1) όπου .

Ας εξετάσουμε μια μέθοδο για την εύρεση μιας συγκεκριμένης λύσης στην εξίσωση (7.1) στην περίπτωση που η δεξιά πλευρά f(x) έχει ειδική μορφή. Αυτή η μέθοδος ονομάζεται μέθοδος αόριστων συντελεστών και συνίσταται στην επιλογή μιας συγκεκριμένης λύσης ανάλογα με τον τύπο της δεξιάς πλευράς f(x). Εξετάστε τις δεξιές πλευρές της παρακάτω φόρμας:

1. f(x) , όπου είναι ένα πολυώνυμο βαθμού , και ορισμένοι συντελεστές, εκτός από , μπορεί να είναι ίσοι με μηδέν. Ας υποδείξουμε τη μορφή με την οποία πρέπει να ληφθεί μια συγκεκριμένη λύση σε αυτήν την περίπτωση.

α) Αν ο αριθμός δεν είναι η ρίζα της χαρακτηριστικής εξίσωσης για την εξίσωση (5.1), τότε γράφουμε τη συγκεκριμένη λύση με τη μορφή: , πού είναι οι απροσδιόριστοι συντελεστές, που πρέπει να προσδιοριστούν με τη μέθοδο των αόριστων συντελεστών.

β) Αν είναι η ρίζα του πολλαπλασιασμού της αντίστοιχης χαρακτηριστικής εξίσωσης, τότε αναζητούμε μια συγκεκριμένη λύση με τη μορφή: , πού είναι οι απροσδιόριστοι συντελεστές.

18. f(x) , όπου και είναι πολυώνυμα βαθμού και, αντίστοιχα, και ένα από αυτά τα πολυώνυμα μπορεί να είναι ίσο με μηδέν. Ας υποδείξουμε τον τύπο της συγκεκριμένης λύσης σε αυτή τη γενική περίπτωση.

Α) Εάν ο αριθμός δεν είναι η ρίζα της χαρακτηριστικής εξίσωσης για την εξίσωση (5.1), τότε η μορφή της συγκεκριμένης λύσης θα είναι: , (7.2) όπου είναι οι απροσδιόριστοι συντελεστές και .

Β) Εάν ο αριθμός είναι η ρίζα της χαρακτηριστικής εξίσωσης για την εξίσωση (5.1) της πολλαπλότητας , τότε μια συγκεκριμένη λύση στο lndu θα έχει τη μορφή: , (7.3) δηλ. μια συγκεκριμένη λύση της μορφής (7.2) πρέπει να πολλαπλασιαστεί επί . Στην έκφραση (7.3) - πολυώνυμα με απροσδιόριστους συντελεστές και ο βαθμός τους .

19. Μέθοδος παραλλαγής για την επίλυση LDDE δεύτερης τάξης (μέθοδος Lagrange).

Η άμεση εύρεση μιας συγκεκριμένης λύσης σε μια εξίσωση, εκτός από την περίπτωση μιας εξίσωσης με σταθερούς συντελεστές και με ειδικούς ελεύθερους όρους, είναι πολύ δύσκολη. Επομένως, για να βρεθεί μια γενική λύση στην εξίσωση, χρησιμοποιείται συνήθως η μέθοδος μεταβολής των αυθαίρετων σταθερών, η οποία καθιστά πάντα δυνατή την εύρεση της γενικής λύσης της εξίσωσης σε τετράγωνα, εάν είναι γνωστό το θεμελιώδες σύστημα λύσεων στην αντίστοιχη ομοιογενή εξίσωση . Αυτή η μέθοδος είναι η εξής.

Σύμφωνα με τα παραπάνω, η γενική λύση μιας γραμμικής ομοιογενούς εξίσωσης είναι:

όπου υπάρχουν γραμμικά ανεξάρτητες λύσεις Lodu σε ένα ορισμένο διάστημα X και είναι αυθαίρετες σταθερές. Θα αναζητήσουμε μια συγκεκριμένη λύση για το lnd στη μορφή (8.1), υποθέτοντας ότι δεν είναι σταθερές, αλλά κάποιες, ακόμη άγνωστες, συναρτήσεις του : . (8.2) Ας διαφοροποιήσουμε την ισότητα (8.2): . (8.3)

Ας επιλέξουμε τις συναρτήσεις έτσι ώστε να ισχύει η ισότητα: . Τότε αντί για (8.3) θα έχουμε:

Ας διαφοροποιήσουμε ξανά αυτήν την έκφραση σε σχέση με το . Ως αποτέλεσμα παίρνουμε: . (8.5) Ας αντικαταστήσουμε τα (8.2), (8.4), (8.5) στη 2η τάξη lnd f(x):

Ή f(x). (8.6)

Εφόσον - λύσεις στο Lod, η τελευταία ισότητα (8.6) παίρνει τη μορφή: f(x).

Έτσι, η συνάρτηση (8.2) θα είναι μια λύση στο lndu εάν οι συναρτήσεις και ικανοποιούν το σύστημα εξισώσεων:

(8.7)

Εφόσον η ορίζουσα αυτού του συστήματος είναι η ορίζουσα Wronski για δύο λύσεις που αντιστοιχούν στο lod γραμμικά ανεξάρτητες στο X, δεν εξαφανίζεται σε κανένα σημείο του διαστήματος X. Επομένως, λύνοντας το σύστημα (8.7), βρίσκουμε και : και . Ενσωματώνοντας, παίρνετε , , όπου είναι η παραγωγή. γρήγορα.

Επιστρέφοντας στην ισότητα (8.2), παίρνουμε μια γενική λύση της ανομοιογενούς εξίσωσης: .

Σειρές

1. Σειρά αριθμών. Βασικές έννοιες, ιδιότητες συγκλίνουσες σειρές. Απαραίτητο σημάδι σύγκλισης (με απόδειξη).

Βασικοί ορισμοί. Ας μας δοθεί μια άπειρη αριθμητική ακολουθία . Σειρά αριθμώνονομάζεται μια εγγραφή που αποτελείται από τα μέλη αυτής της ακολουθίας. Ή .Αριθμοί που ονομάζεται μέλη της σειράς?, ονομάζεται κοινός όρος της σειράς. Ως αποτέλεσμα του υπολογισμού των τιμών αυτής της συνάρτησης στο n =1, n =2,n =3, ... θα πρέπει να ληφθούν οι όροι της σειράς.

Ας δοθεί η σειρά (18.1.1). Ας συντάξουμε από τα μέλη του πεπερασμένα αθροίσματα που καλούνται επιμέρους αθροίσματα μιας σειράς:

Ορισμός. Εάν υπάρχει ένα πεπερασμένο όριο μικρό ακολουθίες μερικών αθροισμάτων της σειράς (18.1.1) για , τότε η σειρά λέγεται ότι συγκλίνει. αριθμός μικρό ονομάζεται το άθροισμα της σειράς και γράφεται ή .

Εάν δεν υπάρχει (συμπεριλαμβανομένου του άπειρου), καλείται η σειρά αποκλίνων.

Ιδιότητες συγκλίνουσας σειράς. Απαραίτητο σημάδι σύγκλισης μιας σειράς. Κοινός όρος συγκλίνουσας σειράς τείνει στο μηδέν ως : Απόδειξη.Αν , τότε και , αλλά , επομένως .

Πρέπει να αρχίσουμε να λύνουμε οποιοδήποτε πρόβλημα για να μελετήσουμε τη σύγκλιση μιας σειράς ελέγχοντας την εκπλήρωση της συνθήκης: εάν αυτή η προϋπόθεση δεν πληρούται, τότε η σειρά προφανώς αποκλίνει. Αυτή η συνθήκη είναι απαραίτητη, αλλά όχι επαρκής για τη σύγκλιση της σειράς: ο γενικός όρος της αρμονικής σειράς είναι (18.1.2), αλλά αυτή η σειρά αποκλίνει.

Ορισμός.Η υπόλοιπη σειρά μετά n ο όρος ονομάζεται σειρά .

Εκπαιδευτικό ίδρυμα "Κράτος της Λευκορωσίας

Γεωργική Ακαδημία"

Τμήμα Ανωτάτων Μαθηματικών

Κατευθυντήριες γραμμές

να μελετήσει το θέμα «Γραμμικές διαφορικές εξισώσεις δεύτερης τάξης» από φοιτητές της σχολής λογιστικής αλληλογραφίας (NISPO)

Gorki, 2013

Γραμμικές διαφορικές εξισώσεις

δεύτερης τάξης με σταθερέςσυντελεστές

1. Γραμμικές ομοιογενείς διαφορικές εξισώσεις

Γραμμική διαφορική εξίσωση δεύτερης τάξης με σταθερούς συντελεστές ονομάζεται εξίσωση της μορφής

εκείνοι. μια εξίσωση που περιέχει την επιθυμητή συνάρτηση και τις παράγωγές της μόνο στον πρώτο βαθμό και δεν περιέχει τα γινόμενα τους. Σε αυτή την εξίσωση Και
- ορισμένοι αριθμοί και μια συνάρτηση
δίνεται σε ένα ορισμένο διάστημα
.

Αν
στο διάστημα
, τότε η εξίσωση (1) θα πάρει τη μορφή

, (2)

και καλείται γραμμικό ομοιογενές . Διαφορετικά, καλείται η εξίσωση (1). γραμμική ανομοιογενής .

Εξετάστε τη σύνθετη συνάρτηση

, (3)

Οπου
Και
- πραγματικές λειτουργίες. Αν η συνάρτηση (3) είναι σύνθετη λύση της εξίσωσης (2), τότε το πραγματικό μέρος
, και φανταστικό μέρος
λύσεις
χωριστά είναι λύσεις της ίδιας ομοιογενούς εξίσωσης. Έτσι, οποιαδήποτε σύνθετη λύση της εξίσωσης (2) δημιουργεί δύο πραγματικές λύσεις σε αυτήν την εξίσωση.

Οι λύσεις μιας ομοιογενούς γραμμικής εξίσωσης έχουν τις ακόλουθες ιδιότητες:

Αν είναι λύση της εξίσωσης (2), τότε η συνάρτηση
, Οπου ΜΕ– μια αυθαίρετη σταθερά θα είναι επίσης λύση στην εξίσωση (2).

Αν Και υπάρχουν λύσεις στην εξίσωση (2) και στη συνέχεια η συνάρτηση
θα είναι επίσης μια λύση στην εξίσωση (2).

Αν Και υπάρχουν λύσεις στην εξίσωση (2) και στη συνέχεια ο γραμμικός συνδυασμός τους
θα είναι επίσης μια λύση στην εξίσωση (2), όπου Και
– αυθαίρετες σταθερές.

Λειτουργίες
Και
λέγονται γραμμικά εξαρτώμενος στο διάστημα
, εάν υπάρχουν τέτοιοι αριθμοί Και
, όχι ίσο με μηδέν ταυτόχρονα, ότι σε αυτό το διάστημα η ισότητα

Αν η ισότητα (4) εμφανίζεται μόνο όταν
Και
, μετά τις συναρτήσεις
Και
λέγονται γραμμικά ανεξάρτητη στο διάστημα
.

Παράδειγμα 1 . Λειτουργίες
Και
εξαρτώνται γραμμικά, αφού
σε ολόκληρη την αριθμητική γραμμή. Σε αυτό το παράδειγμα
.

Παράδειγμα 2 . Λειτουργίες
Και
είναι γραμμικά ανεξάρτητες σε οποιοδήποτε διάστημα, αφού η ισότητα
είναι δυνατή μόνο στην περίπτωση που
, Και
.

1. Κατασκευή γενικής λύσης σε γραμμική ομοιογενή

εξισώσεις

Για να βρείτε μια γενική λύση στην εξίσωση (2), πρέπει να βρείτε δύο από τις γραμμικά ανεξάρτητες λύσεις της Και . Γραμμικός συνδυασμός αυτών των λύσεων
, Οπου Και
είναι αυθαίρετες σταθερές, και θα δώσει μια γενική λύση σε μια γραμμική ομοιογενή εξίσωση.

Θα αναζητήσουμε γραμμικά ανεξάρτητες λύσεις της εξίσωσης (2) στη μορφή

, (5)

Οπου – έναν ορισμένο αριθμό. Επειτα
,
. Ας αντικαταστήσουμε αυτές τις εκφράσεις στην εξίσωση (2):

Ή
.

Επειδή
, Οτι
. Η συνάρτηση λοιπόν
θα είναι λύση της εξίσωσης (2) αν θα ικανοποιήσει την εξίσωση

. (6)

Καλείται η εξίσωση (6). χαρακτηριστική εξίσωση για την εξίσωση (2). Αυτή η εξίσωση είναι μια αλγεβρική τετραγωνική εξίσωση.

Αφήνω Και υπάρχουν ρίζες αυτής της εξίσωσης. Μπορούν να είναι είτε πραγματικές και διαφορετικές, είτε σύνθετες, είτε πραγματικές και ίσες. Ας εξετάσουμε αυτές τις περιπτώσεις.

Αφήστε τις ρίζες Και οι χαρακτηριστικές εξισώσεις είναι πραγματικές και διακριτές. Τότε οι λύσεις της εξίσωσης (2) θα είναι οι συναρτήσεις
Και
. Αυτές οι λύσεις είναι γραμμικά ανεξάρτητες, αφού η ισότητα
μπορεί να πραγματοποιηθεί μόνο όταν
, Και
. Επομένως, η γενική λύση της εξίσωσης (2) έχει τη μορφή

,

Οπου Και
- αυθαίρετες σταθερές.

Παράδειγμα 3
.

Λύση . Η χαρακτηριστική εξίσωση για αυτή τη διαφορική θα είναι
. Έχοντας λύσει αυτήν την τετραγωνική εξίσωση, βρίσκουμε τις ρίζες της
Και
. Λειτουργίες
Και
είναι λύσεις της διαφορικής εξίσωσης. Η γενική λύση αυτής της εξίσωσης είναι
.

Μιγαδικός αριθμός ονομάζεται έκφραση της μορφής
, Οπου Και είναι πραγματικοί αριθμοί, και
ονομάζεται η φανταστική μονάδα. Αν
, μετά τον αριθμό
ονομάζεται καθαρά φανταστικός. Αν
, μετά τον αριθμό
ταυτίζεται με πραγματικό αριθμό .

Αριθμός ονομάζεται το πραγματικό μέρος ενός μιγαδικού αριθμού, και - φανταστικό μέρος. Εάν δύο μιγαδικοί αριθμοί διαφέρουν μεταξύ τους μόνο με το πρόσημο του φανταστικού μέρους, τότε ονομάζονται συζυγείς:
,
.

Παράδειγμα 4 . Λύστε δευτεροβάθμια εξίσωση
.

Λύση . Διακριτική εξίσωση
. Επειτα . Επίσης,
. Έτσι, αυτή η τετραγωνική εξίσωση έχει συζευγμένες μιγαδικές ρίζες.

Έστω οι ρίζες της χαρακτηριστικής εξίσωσης μιγαδικές, δηλ.
,
, Οπου
. Οι λύσεις της εξίσωσης (2) μπορούν να γραφτούν με τη μορφή
,
ή
,
. Σύμφωνα με τους τύπους του Euler

,
.

Επειτα , . Όπως είναι γνωστό, εάν μια μιγαδική συνάρτηση είναι μια λύση σε μια γραμμική ομοιογενή εξίσωση, τότε οι λύσεις αυτής της εξίσωσης είναι τόσο το πραγματικό όσο και το φανταστικό μέρος αυτής της συνάρτησης. Έτσι, οι λύσεις της εξίσωσης (2) θα είναι οι συναρτήσεις
Και
. Από την ισότητα

μπορεί να εκτελεστεί μόνο εάν
Και
, τότε αυτές οι λύσεις είναι γραμμικά ανεξάρτητες. Επομένως, η γενική λύση της εξίσωσης (2) έχει τη μορφή

Οπου Και
- αυθαίρετες σταθερές.

Παράδειγμα 5 . Να βρείτε τη γενική λύση της διαφορικής εξίσωσης
.

Λύση . Η εξίσωση
είναι χαρακτηριστικό μιας δεδομένης διαφοράς. Ας το λύσουμε και ας πάρουμε σύνθετες ρίζες
,
. Λειτουργίες
Και
είναι γραμμικά ανεξάρτητες λύσεις της διαφορικής εξίσωσης. Η γενική λύση αυτής της εξίσωσης έχει τη μορφή .

Έστω οι ρίζες της χαρακτηριστικής εξίσωσης πραγματικές και ίσες, δηλ.
. Τότε οι λύσεις της εξίσωσης (2) είναι οι συναρτήσεις
Και
. Αυτές οι λύσεις είναι γραμμικά ανεξάρτητες, αφού η έκφραση μπορεί να είναι πανομοιότυπα ίση με μηδέν μόνο όταν
Και
. Επομένως, η γενική λύση της εξίσωσης (2) έχει τη μορφή
.

Παράδειγμα 6 . Να βρείτε τη γενική λύση της διαφορικής εξίσωσης
.

Λύση . Χαρακτηριστική εξίσωση
έχει ίσες ρίζες
. Στην περίπτωση αυτή, γραμμικά ανεξάρτητες λύσεις στη διαφορική εξίσωση είναι οι συναρτήσεις
Και
. Η γενική λύση έχει τη μορφή
.

Γραμμική διαφορική εξίσωση δεύτερης τάξης ονομάζεται εξίσωση της μορφής

y"" + Π(Χ)y" + q(Χ)y = φά(Χ) ,

Οπου yείναι η συνάρτηση που πρέπει να βρεθεί, και Π(Χ) , q(Χ) Και φά(Χ) - συνεχείς συναρτήσεις σε ένα ορισμένο διάστημα ( α, β) .

Αν η δεξιά πλευρά της εξίσωσης είναι μηδέν ( φά(Χ) = 0), τότε καλείται η εξίσωση γραμμική ομοιογενής εξίσωση . Το πρακτικό μέρος αυτού του μαθήματος θα αφιερωθεί κυρίως σε τέτοιες εξισώσεις. Αν η δεξιά πλευρά της εξίσωσης δεν είναι ίση με μηδέν ( φά(Χ) ≠ 0), τότε η εξίσωση ονομάζεται .

Στα προβλήματα καλούμαστε να λύσουμε την εξίσωση για y"" :

y"" = −Π(Χ)y" − q(Χ)y + φά(Χ) .

Οι γραμμικές διαφορικές εξισώσεις δεύτερης τάξης έχουν μια μοναδική λύση Cauchy προβλήματα .

Γραμμική ομοιογενής διαφορική εξίσωση δεύτερης τάξης και η επίλυσή της

Θεωρήστε μια γραμμική ομοιογενή διαφορική εξίσωση δεύτερης τάξης:

y"" + Π(Χ)y" + q(Χ)y = 0 .

Αν y1 (Χ) Και y2 (Χ) είναι μερικές λύσεις αυτής της εξίσωσης, τότε ισχύουν οι ακόλουθες προτάσεις:

1) y1 (Χ) + y 2 (Χ) - είναι επίσης μια λύση σε αυτήν την εξίσωση.

2) Cy1 (Χ) , Οπου ντο- μια αυθαίρετη σταθερά (σταθερά), είναι επίσης μια λύση σε αυτήν την εξίσωση.

Από αυτές τις δύο προτάσεις προκύπτει ότι η συνάρτηση

ντο1 y 1 (Χ) + ντο 2 y 2 (Χ)

είναι επίσης μια λύση σε αυτήν την εξίσωση.

Τίθεται ένα δίκαιο ερώτημα: είναι αυτή η λύση γενική λύση γραμμικής ομοιογενούς διαφορικής εξίσωσης δεύτερης τάξης , δηλαδή μια τέτοια λύση στην οποία, για διαφορετικές τιμές ντο1 Και ντο2 Είναι δυνατόν να βρούμε όλες τις πιθανές λύσεις στην εξίσωση;

Η απάντηση σε αυτό το ερώτημα είναι: ίσως, αλλά υπό ορισμένες προϋποθέσεις. Αυτό προϋπόθεση για το ποιες ιδιότητες πρέπει να έχουν συγκεκριμένες λύσεις y1 (Χ) Και y2 (Χ) .

Και αυτή η συνθήκη ονομάζεται συνθήκη γραμμικής ανεξαρτησίας μερικών λύσεων.

Θεώρημα. Λειτουργία ντο1 y 1 (Χ) + ντο 2 y 2 (Χ) είναι μια γενική λύση σε μια γραμμική ομοιογενή δεύτερης τάξης διαφορική εξίσωση εάν οι συναρτήσεις y1 (Χ) Και y2 (Χ) γραμμικά ανεξάρτητη.

Ορισμός. Λειτουργίες y1 (Χ) Και y2 (Χ) ονομάζονται γραμμικά ανεξάρτητοι αν ο λόγος τους είναι σταθερός μη μηδενικός:

y1 (Χ)/y 2 (Χ) = κ ; κ = συνθ ; κ ≠ 0 .

Ωστόσο, ο καθορισμός εξ ορισμού εάν αυτές οι συναρτήσεις είναι γραμμικά ανεξάρτητες είναι συχνά πολύ επίπονος. Υπάρχει τρόπος να δημιουργηθεί γραμμική ανεξαρτησία χρησιμοποιώντας την ορίζουσα Wronski W(Χ) :

Αν η ορίζουσα Wronski δεν είναι ίση με μηδέν, τότε οι λύσεις είναι γραμμικά ανεξάρτητες . Εάν η ορίζουσα Wronski είναι μηδέν, τότε οι λύσεις εξαρτώνται γραμμικά.

Παράδειγμα 1.Να βρείτε τη γενική λύση μιας γραμμικής ομοιογενούς διαφορικής εξίσωσης.

Λύση. Ολοκληρώνουμε δύο φορές και, όπως είναι εύκολο να δούμε, για να είναι η διαφορά μεταξύ της δεύτερης παραγώγου μιας συνάρτησης και της ίδιας της συνάρτησης ίση με μηδέν, οι λύσεις πρέπει να συσχετιστούν με μια εκθετική της οποίας η παράγωγος είναι ίση με την ίδια. Δηλαδή οι επιμέρους λύσεις είναι και .

Από την ορίζουσα Wronski

δεν ισούται με μηδέν, τότε αυτές οι λύσεις είναι γραμμικά ανεξάρτητες. Επομένως, η γενική λύση αυτής της εξίσωσης μπορεί να γραφτεί ως

.

Γραμμικές ομοιογενείς διαφορικές εξισώσεις δεύτερης τάξης με σταθερούς συντελεστές: θεωρία και πράξη

Γραμμική ομοιογενής διαφορική εξίσωση δεύτερης τάξης με σταθερούς συντελεστές ονομάζεται εξίσωση της μορφής

y"" + py" + qy = 0 ,

Οπου ΠΚαι q- σταθερές τιμές.

Το γεγονός ότι πρόκειται για εξίσωση δεύτερης τάξης υποδεικνύεται από την παρουσία της δεύτερης παραγώγου της επιθυμητής συνάρτησης και η ομοιογένειά της υποδεικνύεται με μηδέν στη δεξιά πλευρά. Οι τιμές που ήδη αναφέρθηκαν παραπάνω ονομάζονται σταθεροί συντελεστές.

Προς την να λύσετε μια γραμμική ομοιογενή διαφορική εξίσωση δεύτερης τάξης με σταθερούς συντελεστές , πρέπει πρώτα να λύσετε τη λεγόμενη χαρακτηριστική εξίσωση της φόρμας

κ² + pq + q = 0 ,

η οποία, όπως φαίνεται, είναι μια συνηθισμένη τετραγωνική εξίσωση.

Ανάλογα με τη λύση της χαρακτηριστικής εξίσωσης, είναι δυνατές τρεις διαφορετικές επιλογές λύσεις γραμμικής ομοιογενούς διαφορικής εξίσωσης δεύτερης τάξης με σταθερούς συντελεστές , το οποίο θα αναλύσουμε τώρα. Για πλήρη βεβαιότητα, θα υποθέσουμε ότι όλες οι συγκεκριμένες λύσεις έχουν δοκιμαστεί από την ορίζουσα Wronski και δεν είναι ίση με το μηδέν σε όλες τις περιπτώσεις. Οι αμφίβολοι, ωστόσο, μπορούν να το ελέγξουν οι ίδιοι.

Οι ρίζες της χαρακτηριστικής εξίσωσης είναι πραγματικές και διακριτές

Με άλλα λόγια, . Σε αυτή την περίπτωση, η λύση μιας γραμμικής ομοιογενούς διαφορικής εξίσωσης δεύτερης τάξης με σταθερούς συντελεστές έχει τη μορφή

.

Παράδειγμα 2. Λύστε μια γραμμική ομοιογενή διαφορική εξίσωση

.

Παράδειγμα 3. Λύστε μια γραμμική ομοιογενή διαφορική εξίσωση

.

Λύση. Η χαρακτηριστική εξίσωση έχει τη μορφή, τις ρίζες της και είναι πραγματικές και ευδιάκριτες. Οι αντίστοιχες επιμέρους λύσεις της εξίσωσης είναι: και . Η γενική λύση αυτής της διαφορικής εξίσωσης έχει τη μορφή

.

Οι ρίζες της χαρακτηριστικής εξίσωσης είναι πραγματικές και ίσες

Αυτό είναι, . Στην περίπτωση αυτή, η λύση μιας γραμμικής ομοιογενούς διαφορικής εξίσωσης δεύτερης τάξης με σταθερούς συντελεστές έχει τη μορφή

.

Παράδειγμα 4. Λύστε μια γραμμική ομοιογενή διαφορική εξίσωση

.

Λύση. Χαρακτηριστική εξίσωση έχει ίσες ρίζες. Οι αντίστοιχες επιμέρους λύσεις της εξίσωσης είναι: και . Η γενική λύση αυτής της διαφορικής εξίσωσης έχει τη μορφή

Παράδειγμα 5. Λύστε μια γραμμική ομοιογενή διαφορική εξίσωση

.

Λύση. Η χαρακτηριστική εξίσωση έχει ίσες ρίζες. Οι αντίστοιχες επιμέρους λύσεις της εξίσωσης είναι: και . Η γενική λύση αυτής της διαφορικής εξίσωσης έχει τη μορφή

Οι ομογενείς γραμμικές διαφορικές εξισώσεις δεύτερης τάξης με σταθερούς συντελεστές έχουν τη μορφή

όπου p και q είναι πραγματικοί αριθμοί. Ας δούμε παραδείγματα για το πώς λύνονται ομοιογενείς διαφορικές εξισώσεις δεύτερης τάξης με σταθερούς συντελεστές.

Η λύση μιας γραμμικής ομογενούς διαφορικής εξίσωσης δεύτερης τάξης εξαρτάται από τις ρίζες της χαρακτηριστικής εξίσωσης. Η χαρακτηριστική εξίσωση είναι η εξίσωση k²+pk+q=0.

1) Αν οι ρίζες της χαρακτηριστικής εξίσωσης είναι διαφορετικοί πραγματικοί αριθμοί:

τότε η γενική λύση μιας γραμμικής ομογενούς διαφορικής εξίσωσης δεύτερης τάξης με σταθερούς συντελεστές έχει τη μορφή

2) Αν οι ρίζες της χαρακτηριστικής εξίσωσης είναι ίσοι πραγματικοί αριθμοί

(για παράδειγμα, με διάκριση ίση με μηδέν), τότε η γενική λύση μιας ομοιογενούς διαφορικής εξίσωσης δεύτερης τάξης είναι

3) Αν οι ρίζες της χαρακτηριστικής εξίσωσης είναι μιγαδικοί αριθμοί

(για παράδειγμα, με μια διάκριση ίση με έναν αρνητικό αριθμό), τότε η γενική λύση μιας ομοιογενούς διαφορικής εξίσωσης δεύτερης τάξης γράφεται με τη μορφή

Παραδείγματα επίλυσης γραμμικών ομοιογενών διαφορικών εξισώσεων δεύτερης τάξης με σταθερούς συντελεστές

Βρείτε γενικές λύσεις ομοιογενών διαφορικών εξισώσεων δεύτερης τάξης:

Δημιουργούμε τη χαρακτηριστική εξίσωση: k²-7k+12=0. Η διάκρισή του είναι D=b²-4ac=1>0, επομένως οι ρίζες είναι διαφορετικοί πραγματικοί αριθμοί.

Επομένως, η γενική λύση αυτής της ομοιογενούς ΔΕ 2ης τάξης είναι

Ας συνθέσουμε και λύσουμε τη χαρακτηριστική εξίσωση:

Οι ρίζες είναι πραγματικές και διακριτές. Ως εκ τούτου, έχουμε μια γενική λύση σε αυτήν την ομοιογενή διαφορική εξίσωση:

Σε αυτή την περίπτωση, η χαρακτηριστική εξίσωση

Οι ρίζες είναι διαφορετικές και έγκυρες. Επομένως, η γενική λύση της ομογενούς διαφορικής εξίσωσης 2ης τάξης είναι εδώ

Χαρακτηριστική εξίσωση

Εφόσον οι ρίζες είναι πραγματικές και ίσες, για αυτή τη διαφορική εξίσωση γράφουμε τη γενική λύση ως

Η χαρακτηριστική εξίσωση είναι εδώ

Εφόσον η διάκριση είναι αρνητικός αριθμός, οι ρίζες της χαρακτηριστικής εξίσωσης είναι μιγαδικοί αριθμοί.

Η γενική λύση αυτής της ομοιογενούς διαφορικής εξίσωσης δεύτερης τάξης έχει τη μορφή

Χαρακτηριστική εξίσωση

Από εδώ βρίσκουμε τη γενική λύση σε αυτό το διαφορικό. εξισώσεις:

Παραδείγματα για αυτοέλεγχο.

§ 9. Γραμμικές ομοιογενείς διαφορικές εξισώσεις δεύτερης τάξης με σταθερούς συντελεστές

Ορισμός LODE δεύτερης τάξης με σταθερούς συντελεστές

Χαρακτηριστική εξίσωση:

Περίπτωση 1. Διάκριση μεγαλύτερη από το μηδέν

Περίπτωση 2. Η διάκριση είναι μηδέν

Περίπτωση 3. Διάκριση μικρότερη από το μηδέν

Αλγόριθμος για την εύρεση γενικής λύσης σε LODE δεύτερης τάξης με σταθερούς συντελεστές

§ 10. Γραμμικές ανομοιογενείς διαφορικές εξισώσεις δεύτερης τάξης με σταθερούς συντελεστές

Προσδιορισμός LPDE δεύτερης τάξης με σταθερούς συντελεστές

Μέθοδος μεταβολής σταθερών

Μέθοδος επίλυσης LNDDE με ειδική δεξιά πλευρά

Θεώρημα για τη δομή της γενικής λύσης του LNDE

1. Λειτουργία r (Χ) – πολυώνυμο βαθμού Τ

2. Λειτουργία r (Χ) – γινόμενο ενός αριθμού και μιας εκθετικής συνάρτησης

3. Λειτουργία r (Χ) – άθροισμα τριγωνομετρικών συναρτήσεων

Αλγόριθμος για την εύρεση μιας γενικής λύσης σε ένα LPDE με ειδική δεξιά πλευρά

Εφαρμογή

§ 9. Γραμμικές ομοιογενείς διαφορικές εξισώσεις δεύτερης τάξης με σταθερούς συντελεστές

Η διαφορική εξίσωση δεύτερης τάξης ονομάζεται γραμμική ομογενής διαφορική εξίσωση (LODE) με σταθερούς συντελεστές, αν μοιάζει με:

Οπου ΠΚαι q

Για να βρεθεί μια γενική λύση σε ένα LODE, αρκεί να βρούμε τις δύο διαφορετικές επιμέρους λύσεις του και . Τότε η γενική λύση του LODE θα έχει τη μορφή

Οπου ΜΕ 1 και ΜΕ

Ο Leonard Euler πρότεινε να αναζητηθούν συγκεκριμένες λύσεις του LDE στη μορφή

Οπου κ– έναν ορισμένο αριθμό.

Διαφοροποίηση αυτής της συνάρτησης δύο φορές και αντικατάσταση παραστάσεων στο, y"Και y"στην εξίσωση, παίρνουμε:

Η εξίσωση που προκύπτει ονομάζεται χαρακτηριστική εξίσωση LODU. Για να το μεταγλωττίσετε, αρκεί η αντικατάσταση στην αρχική εξίσωση y", y"Και στοανάλογα με κ 2 , κκαι 1:

Έχοντας λύσει τη χαρακτηριστική εξίσωση, δηλ. βρίσκοντας τις ρίζες κ 1 και κ 2, θα βρούμε επίσης συγκεκριμένες λύσεις στο αρχικό LODE.

Η χαρακτηριστική εξίσωση είναι δευτεροβάθμια εξίσωση, οι ρίζες της βρίσκονται μέσω του διαχωριστικού

Σε αυτή την περίπτωση, είναι δυνατές οι ακόλουθες τρεις περιπτώσεις.

Περίπτωση 1. Διάκριση μεγαλύτερη από το μηδέν άρα οι ρίζες κ 1 και κ 2 έγκυρα και διακριτά:

κ 1¹ κ 2

Οπου ΜΕ 1 και ΜΕ 2 – αυθαίρετες ανεξάρτητες σταθερές.

Περίπτωση 2. Η διάκριση είναι μηδέν άρα οι ρίζες κ 1 και κ 2 πραγματικές και ίσες:

κ 1 = κ 2 = κ

Σε αυτή την περίπτωση, η γενική λύση του LOD έχει τη μορφή

Οπου ΜΕ 1 και ΜΕ 2 – αυθαίρετες ανεξάρτητες σταθερές.

Περίπτωση 3. Διάκριση μικρότερη από το μηδέν . Σε αυτήν την περίπτωση, η εξίσωση δεν έχει πραγματικές ρίζες:

Δεν υπάρχουν ρίζες.

Σε αυτή την περίπτωση, η γενική λύση του LOD έχει τη μορφή

Οπου ΜΕ 1 και ΜΕ 2 – αυθαίρετες ανεξάρτητες σταθερές,

Έτσι, η εύρεση μιας γενικής λύσης σε ένα LODE δεύτερης τάξης με σταθερούς συντελεστές καταλήγει στην εύρεση των ριζών της χαρακτηριστικής εξίσωσης και στη χρήση τύπων για τη γενική λύση της εξίσωσης (χωρίς να καταφεύγουμε στον υπολογισμό των ολοκληρωμάτων).

Αλγόριθμος για την εύρεση γενικής λύσης σε LODE δεύτερης τάξης με σταθερούς συντελεστές:

1. Μειώστε την εξίσωση στη μορφή όπου ΠΚαι q– μερικοί πραγματικοί αριθμοί.

2. Δημιουργήστε μια χαρακτηριστική εξίσωση.

3. Να βρείτε τη διάκριση της χαρακτηριστικής εξίσωσης.

4. Χρησιμοποιώντας τύπους (βλ. Πίνακα 1), ανάλογα με το πρόσημο του διακριτικού, σημειώστε τη γενική λύση.

Τραπέζι 1

Πίνακας πιθανών γενικών λύσεων