Ορισμός.Η χαρακτηριστική εξίσωση ενός γραμμικού τελεστή f είναι μια εξίσωση της μορφής , όπου λ είναι οποιοσδήποτε πραγματικός αριθμός, A είναι ο πίνακας του γραμμικού τελεστή, E είναι ο πίνακας ταυτότητας της ίδιας τάξης.
Πολυώνυμος κάλεσε χαρακτηριστικό πολυώνυμοπίνακας Α (γραμμικός τελεστής f). Σε μορφή πίνακα, η χαρακτηριστική εξίσωση έχει την ακόλουθη μορφή:
ή
.
Κατά συνέπεια, εξισώνοντας το χαρακτηριστικό πολυώνυμο με μηδέν, προκύπτει μια εξίσωση βαθμού n, όπου το λ είναι το άγνωστο, λαμβάνουμε τις τιμές των ριζών του - τους χαρακτηριστικούς αριθμούς αυτού του πίνακα. Οι χαρακτηριστικές ρίζες παίζουν σημαντικό ρόλο σε πολλούς τομείς των μαθηματικών. Ας εξετάσουμε μια από τις εφαρμογές των χαρακτηριστικών ριζών - ένα πολύ σημαντικό εργαλείο στη μελέτη γραμμικών χώρων, καθώς και στην επίλυση πολλών εφαρμοζόμενων προβλημάτων της γραμμικής άλγεβρας.
Το σύνολο όλων των ριζών της χαρακτηριστικής εξίσωσης ονομάζεται φάσμα του τελεστή φά(κάθε ρίζα θεωρείται με την πολλαπλότητα που έχει στη χαρακτηριστική εξίσωση).
Παράδειγμα.Βρείτε τις χαρακτηριστικές ρίζες του πίνακα.
Ας δημιουργήσουμε μια μήτρα
Εξισώνοντας το χαρακτηριστικό πολυώνυμο με μηδέν, παίρνουμε μια τετραγωνική εξίσωση
Τότε οι ρίζες της εξίσωσης είναι ίσες 
.
Ορισμός.Έστω f ένας γραμμικός τελεστής του χώρου και έστω κάποιο μη μηδενικό διάνυσμα για το οποίο η ισότητα
όπου είναι ένας πραγματικός αριθμός. Τότε το διάνυσμα ονομάζεται ιδιοδιάνυσμα του τελεστή και ο πίνακας του τελεστή του, ιδιοτιμή ή ιδιοτιμή του μετασχηματισμού. Σε αυτή την περίπτωση, το ιδιοδιάνυσμα λέγεται ότι αναφέρεται στην ιδιοτιμή.
Τα ιδιοδιανύσματα παίζουν σημαντικό ρόλο τόσο στα ίδια τα μαθηματικά όσο και στις εφαρμογές τους. Για παράδειγμα, συντονισμός, στον οποίο οι φυσικές συχνότητες δόνησης του συστήματος συμπίπτουν με τη συχνότητα δόνησης των εξωτερικών δυνάμεων. Στα μαθηματικά, τα ιδιοδιανύσματα είναι χρήσιμα για την επίλυση συστημάτων διαφορικών εξισώσεων.
Θεώρημα. Αν ένας γραμμικός τελεστής f έχει τον πίνακα Α στη βάση του (πρώτη βάση) και τον πίνακα Β στη βάση του (δεύτερη βάση), τότε ισχύει η ισότητα: .
Κατά συνέπεια, κατά τη μετάβαση σε μια νέα βάση, το χαρακτηριστικό πολυώνυμο του γραμμικού τελεστή δεν αλλάζει.
◌ Αν T είναι ο πίνακας μετάβασης από την πρώτη βάση στη δεύτερη, τότε . Στη συνέχεια μεταμορφώνουμε τη δεξιά πλευρά της ισότητας ●
Θεώρημα. Για να είναι ο αριθμός λ 0 από το πεδίο P ιδιοτιμή του διανύσματος του διαστήματος L n έναντι του P, είναι απαραίτητο και αρκετό ο αριθμός λ 0 να είναι η χαρακτηριστική ρίζα του τελεστή f.
Έγγρ. ΕΓΩ.Ανάγκη. Αφήνω λ 0 ιδιοτιμή χειριστή φά, μετά μέσα Lnυπάρχει ένα ιδιοδιάνυσμα τέτοιο ώστε .
Αφήνω 
είναι η γραμμή συντεταγμένων του σε κάποια βάση, λοιπόν
Από την άλλη, επειδή , όπου είναι ο πίνακας ενός γραμμικού τελεστή σε μια δεδομένη βάση, τότε
Εξισώνοντας τις δεξιές πλευρές των (1) και (2) παίρνουμε:
(3)
Οι ισότητες (3) σημαίνουν ότι ένα αριθμητικό διάνυσμα με συντεταγμένες 
είναι λύση στο παρακάτω σύστημα εξισώσεων (4).
(4)
Το διάνυσμα είναι διαφορετικό από το μηδέν (αφού είναι δικό του), επομένως το σύστημα (4) έχει μια μη μηδενική λύση, επομένως η ορίζοντή του είναι 0.
(5)
και επομένως η μεταφερόμενη ορίζουσα είναι ίση με 0.
(6)
Ετσι, λ 0 – ρίζα της χαρακτηριστικής εξίσωσης.
II.Επάρκεια. Αφήνω λ 0
– χαρακτηριστική ρίζα του χειριστή σε κάποια βάση 
. Ας το αποδείξουμε λ 0
είναι η ιδιοτιμή του τελεστή Α.
Πράγματι, αν λ 0 είναι η χαρακτηριστική ρίζα, τότε θα ικανοποιηθεί η ισότητα (6) και επομένως η ισότητα (5), και αυτό θα σημαίνει ότι το σύστημα (4) έχει μη μηδενικές λύσεις.
Ας επιλέξουμε κάποια μη μηδενική λύση του συστήματος (4): ένα αριθμητικό διάνυσμα 
. Τότε οι ισότητες (3) ικανοποιούνται.
Ας εξετάσουμε το διάνυσμα, και γι' αυτό θα ικανοποιηθεί η ισότητα (2) και, δυνάμει του τύπου, ισχύει η ισότητα (1), όπου είναι ο πίνακας του τελεστή στη βάση ΣΕ. Αυτό συνεπάγεται την ισότητα, που σημαίνει ότι το διάνυσμα είναι ένα ιδιοδιάνυσμα του τελεστή στον οποίο αντιστοιχεί η ιδιοτιμή λ 0 . Αυτό ήταν που έπρεπε να αποδειχτεί. Το θεώρημα έχει αποδειχθεί.
Σχόλιο.Για να βρούμε τις ιδιοτιμές του τελεστή, είναι απαραίτητο να συνθέσουμε και να λύσουμε την εξίσωση (5). Για να βρείτε τα ιδιοδιανύσματα του τελεστή, πρέπει να δημιουργήσετε ένα σύστημα εξισώσεων (4) και να βρείτε ένα θεμελιώδες σύνολο λύσεων σε αυτό το σύστημα.
Για τον έλεγχο της ορθότητας του υπολογισμού των ιδιοτιμών (μπορεί να συμπίπτουν ή σύνθετες), χρησιμοποιούνται δύο γεγονότα:
1) 
, όπου το τελευταίο άθροισμα του πίνακα ίχνους είναι το άθροισμα των διαγώνιων στοιχείων.
2) 
.
Παράδειγμα.Βρείτε ιδιοτιμές και ιδιοδιανύσματα 
.
Εξισώνοντας με το μηδέν παίρνουμε . .
3) . , 
.
Έστω μια ελεύθερη μεταβλητή, τότε παίρνουμε ένα διάνυσμα 
.
Ασκηση. Ελέγξτε για το διάνυσμα.
.
Η ελεύθερη λειτουργία του κυκλώματος δεν εξαρτάται από πηγές ενέργειας, καθορίζεται μόνο από τη δομή του κυκλώματος και τις παραμέτρους των στοιχείων του. Από αυτό προκύπτει ότι οι ρίζες της χαρακτηριστικής εξίσωσης p1, p2,..., pn θα είναι ίδιες για όλες τις μεταβλητές συναρτήσεις (ρεύματα και τάσεις).
Η χαρακτηριστική εξίσωση μπορεί να κατασκευαστεί χρησιμοποιώντας διάφορες μεθόδους. Η πρώτη μέθοδος είναι κλασική, όταν η χαρακτηριστική εξίσωση συντάσσεται αυστηρά σύμφωνα με τη διαφορική εξίσωση σύμφωνα με το κλασικό σχήμα. Κατά τον υπολογισμό των μεταβατικών διεργασιών σε ένα σύνθετο κύκλωμα, ένα σύστημα διαφορικών εξισώσεων «m» συντάσσεται σύμφωνα με τους νόμους του Kirchhoff για το διάγραμμα κυκλώματος μετά τη μεταγωγή. Δεδομένου ότι οι ρίζες της χαρακτηριστικής εξίσωσης είναι κοινές για όλες τις μεταβλητές, η λύση του συστήματος των διαφορικών εξισώσεων εκτελείται ως προς οποιαδήποτε μεταβλητή (προαιρετική). Ως αποτέλεσμα της λύσης, προκύπτει μια ανομοιογενής διαφορική εξίσωση με μία μεταβλητή. Να συνθέσετε μια χαρακτηριστική εξίσωση σύμφωνα με τη διαφορική εξίσωση που προκύπτει και να προσδιορίσετε τις ρίζες της.
Παράδειγμα. Σχεδιάστε μια χαρακτηριστική εξίσωση και προσδιορίστε τις ρίζες της για τις μεταβλητές στο διάγραμμα στο Σχ. 59.1. Οι παράμετροι των στοιχείων καθορίζονται σε γενική μορφή.
Σύστημα διαφορικών εξισώσεων σύμφωνα με τους νόμους του Kirchhoff:
Ας λύσουμε το σύστημα εξισώσεων για τη μεταβλητή i3, με αποτέλεσμα να λάβουμε μια μη ομοιογενή διαφορική εξίσωση:
Ο δεύτερος τρόπος για να συντάξουμε μια χαρακτηριστική εξίσωση είναι να εξισώσουμε με μηδέν την κύρια ορίζουσα του συστήματος εξισώσεων Kirchhoff για τις μεταβλητές ελεύθερης συνιστώσας.
Αφήστε το ελεύθερο συστατικό ενός αυθαίρετου ρεύματος να έχει τη μορφή iksv = Аkept, τότε:
Το σύστημα εξισώσεων για τις ελεύθερες συνιστώσες προκύπτει από το σύστημα διαφορικών εξισώσεων Kirchhoff αντικαθιστώντας τις παραγώγους των μεταβλητών με τον παράγοντα p και τα ολοκληρώματα με 1/p. Για το υπό εξέταση παράδειγμα, το σύστημα εξισώσεων για ελεύθερα συστατικά έχει τη μορφή:
Χαρακτηριστική εξίσωση και η ρίζα της:
Ο τρίτος τρόπος για να συντάξετε μια χαρακτηριστική εξίσωση (μηχανική) είναι να εξισώσετε την αντίσταση του χειριστή εισόδου του κυκλώματος στο μηδέν σε σχέση με οποιονδήποτε από τους κλάδους του.
Η αντίσταση χειριστή ενός στοιχείου προκύπτει από τη μιγαδική αντίστασή του με απλή αντικατάσταση του παράγοντα jω με p, επομένως
Για το εν λόγω παράδειγμα:
Η τρίτη μέθοδος είναι η απλούστερη και πιο οικονομική, επομένως χρησιμοποιείται συχνότερα κατά τον υπολογισμό των μεταβατικών διεργασιών σε ηλεκτρικά κυκλώματα.
Οι ρίζες της χαρακτηριστικής εξίσωσης χαρακτηρίζουν την ελεύθερη μεταβατική διαδικασία σε ένα κύκλωμα χωρίς πηγές ενέργειας. Αυτή η διαδικασία συμβαίνει με απώλειες ενέργειας και ως εκ τούτου φθείρεται με την πάροδο του χρόνου.
Από αυτό προκύπτει ότι οι ρίζες της χαρακτηριστικής εξίσωσης πρέπει να είναι αρνητικές ή να έχουν αρνητικό πραγματικό μέρος.
Στη γενική περίπτωση, η σειρά της διαφορικής εξίσωσης που περιγράφει τη μεταβατική διαδικασία στο κύκλωμα και, κατά συνέπεια, ο βαθμός της χαρακτηριστικής εξίσωσης και ο αριθμός των ριζών της είναι ίσοι με τον αριθμό των ανεξάρτητων αρχικών συνθηκών ή τον αριθμό των ανεξάρτητες συσκευές αποθήκευσης ενέργειας (πηνία L και πυκνωτές C).
Εάν το διάγραμμα κυκλώματος περιέχει παράλληλα συνδεδεμένους πυκνωτές C1, C2,... ή πηνία συνδεδεμένα σε σειρά L1, L2,..., τότε κατά τον υπολογισμό των μεταβατικών διεργασιών πρέπει να αντικατασταθούν από ένα ισοδύναμο στοιχείο SE = C1 + C2+... ή LE = L1 + L2+...
Έτσι, η γενική μορφή της λύσης για οποιαδήποτε μεταβλητή κατά τον υπολογισμό της μεταβατικής διαδικασίας μπορεί να συνταχθεί μόνο από μια ανάλυση του διαγράμματος κυκλώματος, χωρίς τη σύνταξη και επίλυση ενός συστήματος διαφορικών εξισώσεων.
- Για το παράδειγμα που συζητήθηκε παραπάνω.
- Η χαρακτηριστική εξίσωση συντάσσεται για το κύκλωμα μετά την εναλλαγή. Μπορεί να ληφθεί με τους εξής τρόπους:
- απευθείας με βάση μια διαφορική εξίσωση της μορφής (2) (βλ. διάλεξη αρ. 24), δηλ. εξαιρώντας από το σύστημα εξισώσεων που περιγράφουν την ηλεκτρομαγνητική κατάσταση του κυκλώματος με βάση τον πρώτο και τον δεύτερο νόμο του Kirchhoff, όλα τα άγνωστα μεγέθη εκτός από ένα, σε σχέση με το οποίο γράφεται η εξίσωση (2).
χρησιμοποιώντας μια έκφραση για την σύνθετη αντίσταση εισόδου ενός κυκλώματος ημιτονοειδούς ρεύματος.
με βάση την έκφραση της κύριας ορίζουσας.
Σύμφωνα με την πρώτη μέθοδο, στην προηγούμενη διάλεξη, προέκυψε μια διαφορική εξίσωση σχετικά με την τάση στον πυκνωτή για ένα κύκλωμα σειράς R-L-C, βάσει της οποίας γράφεται η χαρακτηριστική εξίσωση.
Η σύνθεση της χαρακτηριστικής εξίσωσης χρησιμοποιώντας τη μέθοδο αντίστασης εισόδου έχει ως εξής:
καταγράφεται η αντίσταση εισόδου του κυκλώματος AC.
Το jw αντικαθίσταται από τον τελεστή p.
η παράσταση που προκύπτει είναι ίση με μηδέν.
Εξίσωση
συμπίπτει με τη χαρακτηριστική.
Πρέπει να τονιστεί ότι η αντίσταση εισόδου μπορεί να γραφτεί σε σχέση με το σημείο θραύσης οποιουδήποτε κλάδου του κυκλώματος. Σε αυτή την περίπτωση, το ενεργό δίκτυο δύο τερματικών αντικαθίσταται από ένα παθητικό κατ' αναλογία με τη μέθοδο της ισοδύναμης γεννήτριας. Αυτή η μέθοδος σύνθεσης της χαρακτηριστικής εξίσωσης προϋποθέτει την απουσία μαγνητικά συζευγμένων διακλαδώσεων στο κύκλωμα. εάν υπάρχουν, είναι απαραίτητο να πραγματοποιηθεί η προκαταρκτική αποσύνδεσή τους.
Για το κύκλωμα στο Σχ. 1 σε σχέση με τα τερματικά πηγής
.
Αντικαθιστώντας το jw με p και εξισώνοντας την παράσταση που προκύπτει με μηδέν, γράφουμε
| . | (1) |
Κατά τη σύνταξη μιας χαρακτηριστικής εξίσωσης με βάση την έκφραση της κύριας ορίζουσας, ο αριθμός των αλγεβρικών εξισώσεων βάσει των οποίων γράφεται είναι ίσος με τον αριθμό των άγνωστων συνιστωσών ελεύθερου ρεύματος. Η αλγεβροποίηση του αρχικού συστήματος ολοκληρωτικών-διαφορικών εξισώσεων, που συντάχθηκε, για παράδειγμα, με βάση τους νόμους του Kirchhoff ή τη μέθοδο των ρευμάτων περιγράμματος, πραγματοποιείται αντικαθιστώντας τα σύμβολα διαφοροποίησης και ολοκλήρωσης, αντίστοιχα, με πολλαπλασιασμό και διαίρεση από τον τελεστή σελ. Η χαρακτηριστική εξίσωση προκύπτει εξισώνοντας τη γραπτή ορίζουσα με μηδέν. Δεδομένου ότι η έκφραση για την κύρια ορίζουσα δεν εξαρτάται από τις δεξιές πλευρές του συστήματος ανομοιογενών εξισώσεων, μπορεί να συνταχθεί με βάση ένα σύστημα εξισώσεων γραμμένου για τα συνολικά ρεύματα.
Για το κύκλωμα στο Σχ. 1 αλγεβροποιημένο σύστημα εξισώσεων που βασίζεται στη μέθοδο του ρεύματος βρόχου έχει τη μορφή
Εξ ου και η έκφραση για τον κύριο καθοριστικό παράγοντα αυτού του συστήματος
Εξισώνοντας το D με μηδέν, παίρνουμε ένα αποτέλεσμα παρόμοιο με το (1).
Γενική μεθοδολογία υπολογισμού μεταβατικών διεργασιών με την κλασική μέθοδο
Γενικά, η μεθοδολογία για τον υπολογισμό των μεταβατικών διεργασιών με την κλασική μέθοδο περιλαμβάνει τα ακόλουθα βήματα:
Παραδείγματα υπολογισμού μεταβατικών διεργασιών με χρήση της κλασικής μεθόδου
1. Μεταβατικές διεργασίες στο κύκλωμα R-L όταν είναι συνδεδεμένο σε πηγή τάσης
Τέτοιες διεργασίες λαμβάνουν χώρα, για παράδειγμα, κατά τη σύνδεση ηλεκτρομαγνητών, μετασχηματιστών, ηλεκτροκινητήρων κ.λπ. σε μια πηγή ισχύος.
Ας εξετάσουμε δύο περιπτώσεις:
Σύμφωνα με την εξεταζόμενη μέθοδο για το ρεύμα στο κύκλωμα στο Σχ. 2 μπορεί να γραφτεί
Χαρακτηριστική εξίσωση
εξ ου και η χρονική σταθερά 
.
Ετσι,
| . | (5) |
Αντικαθιστώντας τα (4) και (5) στη σχέση (3), γράφουμε
.
Σύμφωνα με τον πρώτο νόμο της μετατροπής. Τότε
,
Έτσι, το ρεύμα στο κύκλωμα κατά τη διάρκεια της μεταβατικής διαδικασίας περιγράφεται από την εξίσωση
,
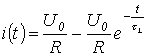και η τάση κατά μήκος του επαγωγέα δίνεται από
.
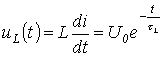Η ποιοτική εμφάνιση των καμπυλών και που αντιστοιχούν στις ληφθείσες λύσεις παρουσιάζεται στο Σχ. 3.
Με τον δεύτερο τύπο πηγής, η εξαναγκασμένη συνιστώσα υπολογίζεται χρησιμοποιώντας τη συμβολική μέθοδο:
,
Η έκφραση του ελεύθερου στοιχείου δεν εξαρτάται από τον τύπο της πηγής τάσης. Οθεν,
.
Από τότε
Έτσι, επιτέλους παίρνουμε
| . | (6) |
Η ανάλυση της προκύπτουσας έκφρασης (6) δείχνει:
Εάν είναι σημαντικό σε μέγεθος, τότε σε μισή περίοδο η ελεύθερη συνιστώσα δεν μειώνεται σημαντικά. Σε αυτή την περίπτωση, η μέγιστη τιμή του μεταβατικού ρεύματος μπορεί να υπερβεί σημαντικά το πλάτος του ρεύματος σταθερής κατάστασης. Όπως φαίνεται από το Σχ. 4, όπου
, το μέγιστο ρεύμα εμφανίζεται μετά από περίπου . Στο όριο στο .
Έτσι, για ένα γραμμικό κύκλωμα, η μέγιστη τιμή του μεταβατικού ρεύματος δεν μπορεί να υπερβαίνει το διπλάσιο του πλάτους του εξαναγκασμένου ρεύματος: .
Ομοίως για ένα γραμμικό κύκλωμα με πυκνωτή: εάν τη στιγμή της μεταγωγής η εξαναγκασμένη τάση είναι ίση με την τιμή του πλάτους της και η σταθερά χρόνου του κυκλώματος είναι αρκετά μεγάλη, τότε μετά από περίπου μισή περίοδο η τάση στον πυκνωτή φτάνει τη μέγιστη τιμή της , το οποίο δεν μπορεί να υπερβαίνει το διπλάσιο του πλάτους της εξαναγκασμένης τάσης: 
.
2. Μεταβατικές διεργασίες κατά την αποσύνδεση του επαγωγέα από την πηγή ισχύος
Όταν ανοίξει το κλειδί στο κύκλωμα στο Σχ. 5 εξαναγκασμένη συνιστώσα του ρεύματος μέσω του επαγωγέα.
Χαρακτηριστική εξίσωση
,
όπου 
Και 
.
Σύμφωνα με τον πρώτο νόμο της μετατροπής
.
Έτσι, η έκφραση για το μεταβατικό ρεύμα είναι
και τάση κατά μήκος του επαγωγέα
 .
|
(7) |
Η ανάλυση (7) δείχνει ότι όταν ανοίγουν κυκλώματα που περιέχουν επαγωγικά στοιχεία, μπορεί να προκύψουν μεγάλες υπερτάσεις, οι οποίες, χωρίς τη λήψη ειδικών μέτρων, μπορούν να βλάψουν τον εξοπλισμό. Πράγματι, όταν 
Η μονάδα τάσης στο πηνίο τη στιγμή της μεταγωγής θα είναι πολλές φορές υψηλότερη από την τάση της πηγής: . Ελλείψει αντίστασης σβέσης R, η καθορισμένη τάση εφαρμόζεται στις επαφές ανοίγματος του κλειδιού, ως αποτέλεσμα της οποίας εμφανίζεται ένα τόξο μεταξύ τους.
3. Φόρτιση και εκφόρτιση πυκνωτή
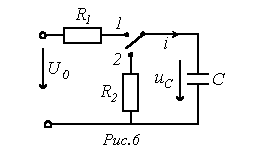
Όταν το κλειδί μετακινηθεί στη θέση 1 (βλ. Εικ. 6), ξεκινά η διαδικασία φόρτισης του πυκνωτή:
.
Εξάρτημα εξαναγκασμένης τάσης σε πυκνωτή.
Από τη χαρακτηριστική εξίσωση
προσδιορίζεται η ρίζα 
. Εξ ου και η χρονική σταθερά.
Η χαρακτηριστική εξίσωση συντάσσεται για το κύκλωμα μετά την εναλλαγή. Μπορεί να ληφθεί με τους εξής τρόπους:
Άμεσα με βάση μια διαφορική εξίσωση της μορφής (1.2), δηλ. εξαιρώντας από το σύστημα εξισώσεων που περιγράφουν την ηλεκτρομαγνητική κατάσταση του κυκλώματος με βάση τους νόμους του Kirchhoff, όλα τα άγνωστα μεγέθη, εκτός από ένα, σε σχέση με το οποίο είναι γραμμένη η εξίσωση·
Χρησιμοποιώντας την έκφραση για την σύνθετη αντίσταση εισόδου ενός κυκλώματος ημιτονοειδούς ρεύματος.
Με βάση την έκφραση της κύριας ορίζουσας.
Σύμφωνα με την πρώτη μέθοδο στο 1.4.1, προέκυψε μια διαφορική εξίσωση για την τάση uCστον πυκνωτή για σειρά r-L-C-αλυσίδες (βλ. Εικ. 1.6):
με βάση την οποία γράφεται η χαρακτηριστική εξίσωση
.
Πρέπει να σημειωθεί ότι, δεδομένου ότι το γραμμικό κύκλωμα καλύπτεται από μία μόνο μεταβατική διαδικασία, οι ρίζες της χαρακτηριστικής εξίσωσης είναι κοινές σε όλες τις ελεύθερες συνιστώσες των τάσεων και των ρευμάτων των κλάδων του κυκλώματος, οι παράμετροι των οποίων περιλαμβάνονται στη χαρακτηριστική εξίσωση. Επομένως, σύμφωνα με την πρώτη μέθοδο σύνθεσης μιας χαρακτηριστικής εξίσωσης, οποιαδήποτε ποσότητα μπορεί να επιλεγεί ως η ποσότητα σε σχέση με την οποία γράφεται.
Η σύνθεση της χαρακτηριστικής εξίσωσης χρησιμοποιώντας τη μέθοδο αντίστασης εισόδου έχει ως εξής:
1. Γράψτε την έκφραση για την αντίσταση εισόδου του κυκλώματος AC σε μιγαδική μορφή.
2. Στην έκφραση που προκύπτει jωαντικαθίσταται από τον χειριστή r;
3. Η παράσταση που προκύπτει είναι ίση με μηδέν.
Η εξίσωση συμπίπτει με τη χαρακτηριστική.
Πρέπει να τονιστεί ότι η αντίσταση εισόδου μπορεί να γραφτεί σε σχέση με το σημείο θραύσης οποιουδήποτε κλάδου του κυκλώματος. Σε αυτή την περίπτωση, οι πηγές ενέργειας αποκλείονται από το κύκλωμα και η εσωτερική τους αντίσταση παραμένει στη θέση τους.
Αυτή η μέθοδος σύνθεσης της χαρακτηριστικής εξίσωσης προϋποθέτει την απουσία μαγνητικά συζευγμένων διακλαδώσεων στο ηλεκτρικό κύκλωμα. Εάν υπάρχουν, είναι απαραίτητο να πραγματοποιηθεί μαγνητική αποσύνδεση.
Για το υπό εξέταση κύκλωμα (βλ. Εικ. 1.6) χρησιμοποιώντας τη μέθοδο αντίστασης εισόδου έχουμε:
;
;
.
Κατά τη σύνταξη μιας χαρακτηριστικής εξίσωσης με βάση την έκφραση της κύριας ορίζουσας, ο αριθμός των αλγεβρικών εξισώσεων βάσει των οποίων γράφεται είναι ίσος με τον αριθμό των άγνωστων συνιστωσών ελεύθερου ρεύματος.
Η αλγεβροποίηση του αρχικού συστήματος ολοκληρωτικών διαφορικών εξισώσεων, που συντάχθηκε, για παράδειγμα, με βάση τους νόμους του Kirchhoff ή τη μέθοδο των ρευμάτων περιγράμματος, πραγματοποιείται αντικαθιστώντας τις πράξεις διαφοροποίησης και ολοκλήρωσης, αντίστοιχα, με πολλαπλασιασμό και διαίρεση από τον τελεστή r. Η χαρακτηριστική εξίσωση προκύπτει εξισώνοντας τη γραπτή ορίζουσα με μηδέν.
Δεδομένου ότι η έκφραση για την κύρια ορίζουσα δεν εξαρτάται από τις δεξιές πλευρές του συστήματος ανομοιογενών εξισώσεων, μπορεί να συνταχθεί με βάση ένα σύστημα εξισώσεων γραμμένου για τα συνολικά ρεύματα.
Για το υπό εξέταση σχήμα (βλ. Εικ. 1.6) για ελεύθερη λειτουργία έχουμε:
.
Αντικαθιστώντας την παράγωγο και το ολοκλήρωμα στην εξίσωση, όπως αναφέρθηκε παραπάνω, λαμβάνουμε την αλγεβρική εξίσωση
ή 
.
Από πού το παίρνουμε;
ή .
Η χαρακτηριστική εξίσωση έχει τη μορφή:
Για να προσδιορίσετε τον τύπο της ελεύθερης συνιστώσας, είναι απαραίτητο να συντάξετε και να λύσετε τη χαρακτηριστική εξίσωση: z(p) = 0. Για να γράψετε τη χαρακτηριστική εξίσωση, είναι απαραίτητο να σχεδιάσετε ένα διάγραμμα στο οποίο όλες οι πηγές emf και ρεύματος θα πρέπει να είναι αντικαθίστανται από τη δική τους εσωτερική αντίσταση, και η αντίσταση αυτεπαγωγής και χωρητικότητας πρέπει να ληφθούν αντίστοιχα ίσα με Pl και , τότε είναι απαραίτητο να σπάσει οποιονδήποτε κλάδο αυτού του κυκλώματος, να γράψει την αρχική του αντίσταση σε σχέση με τα σημεία θραύσης, να την εξισώσει με το μηδέν, να λύσει και προσδιορίστε τις ρίζες του p, εάν οι ρίζες αποδειχθούν πραγματικά αρνητικές, τότε η ελεύθερη συνιστώσα της επιθυμητής συνάρτησης:
, όπου m είναι ο αριθμός των ριζών της εξίσωσης.
Ρίζες; - μόνιμα ενσωματωμένο.
Εάν οι ρίζες της εξίσωσης χαρακτήρων αποδειχθούν σύνθετες συζυγείς, τότε η ελεύθερη κατάσταση θα έχει τη μορφή:
πού είναι η συχνότητα των ελεύθερων κραδασμών;
Η αρχική φάση των ελεύθερων ταλαντώσεων.
8.Μεταβατικός χρόνος. Προσδιορισμός πρακτικά t pp. Υπολογισμός του χρόνου μεταβατικής διαδικασίας.
Ο χρόνος της μεταβατικής διαδικασίας εξαρτάται από τον συντελεστή εξασθένησης Η αντίστροφη τιμή ονομάζεται σταθερά χρόνου και αντιπροσωπεύει το χρόνο κατά τον οποίο η τιμή της ελεύθερης συνιστώσας της μεταβατικής διαδικασίας θα μειωθεί κατά e = 2,72 φορές. Η τιμή εξαρτάται από το κύκλωμα και τις παραμέτρους Έτσι για ένα κύκλωμα με σύνδεση σε σειρά r και L = και για σύνδεση σε σειρά
95% ολοκλήρωση της διαδικασίας μετάβασης 3.
Ο ευκολότερος τρόπος κατασκευής των καμπυλών των ελεύθερων συνιστωσών της μεταβατικής διαδικασίας είναι να ορίσετε τις τιμές του χρόνου t σε 0, ,2.....Εάν υπάρχουν πολλές πραγματικές ρίζες, τότε η καμπύλη που προκύπτει προκύπτει αθροίζοντας το τεταγμένες των επιμέρους όρων (Εικ. 1.)
Εικόνα 1:
9.10, Παροδική διεργασία σε κυκλώματα r, C – όταν συνδέονται σε πηγή σταθερής τάσης. Εκτελέστε την ανάλυση χρησιμοποιώντας την κλασική μέθοδο. δώστε αναλυτικές εκφράσεις για το U C (t). iC(t); γραφικά. (Κλασική μέθοδος).
Η εξίσωση της κατάστασης του κυκλώματος rC μετά την εναλλαγή είναι η εξής:
(1) ή rC (2)
Η λύση του: 
Η χωρητικότητα C μετά το κλείσιμο του κλειδιού στο t θα χρεωθεί σε μια σταθερή τιμή Free
Δεδομένου ότι οι αρχικές συνθήκες είναι μηδενικές, σύμφωνα με τον νόμο της μετατροπής 
σε t=0, ή 0=A, από όπου A=-E.
Η λύση της εξίσωσης (2) θα έχει τη μορφή:
Ρεύμα κυκλώματος i(t)=C
Εικόνα 1.
Εικόνα 2.
Τα γραφήματα των μεταβολών της τάσης και του ρεύματος i(t) φαίνονται στα σχήματα 1 και 2. Από τα σχήματα φαίνεται ότι η τάση στον πυκνωτή αυξάνεται εκθετικά από 0 σε E, ενώ η ισχύς του ρεύματος τη στιγμή της μεταγωγής φτάνει απότομα την τιμή E/r και στη συνέχεια μειώνεται στο μηδέν.
11.12.Παροδική διεργασία σε κυκλώματα r, C – όταν συνδέεται σε ημιτονοειδή πηγή τάσης. Εκτελέστε την ανάλυση χρησιμοποιώντας την κλασική μέθοδο. δώστε αναλυτικές εκφράσεις για το U C (t). iC(t); γραφικά. (Κλασική μέθοδος).
Η εξίσωση κατάστασης του κυκλώματος rC στον μεταβατικό τρόπο είναι η εξής
rC 
.
Λύση αυτής της εξίσωσης:
Δωρεάν συστατικό
όπου =rC
Δεδομένου ότι το κύκλωμα είναι γραμμικό, τότε με ημιτονοειδές φαινόμενο και σε σταθερή κατάσταση, η τάση στον πυκνωτή θα αλλάξει επίσης σύμφωνα με έναν ημιτονοειδές νόμο με τη συχνότητα του φαινομένου εισόδου. Επομένως, για να προσδιορίσουμε = θα χρησιμοποιήσουμε τη μέθοδο των μιγαδικών πλάτη :
; 
Θεωρώντας ότι j= , παίρνουμε:
Σταθερά ολοκλήρωσης Α της ελεύθερης συνιστώσας
Ας βρούμε από τις αρχικές συνθήκες στο κύκλωμα λαμβάνοντας υπόψη τον νόμο μετατροπής:
.Στο t=0 η τελευταία έκφραση έχει τη μορφή
Πού βρίσκεται το A=-
Προσθέτοντας τα εξαρτήματα και , λαμβάνουμε την τελική έκφραση για την τάση κατά μήκος του πυκνωτή στον μεταβατικό τρόπο:
= + = 
- (1)
Η ανάλυση της έκφρασης (1) δείχνει ότι η μεταβατική διαδικασία στο κύκλωμα rC υπό ημιτονοειδή επίδραση εξαρτάται από την αρχική φάση της πηγής emf τη στιγμή της μεταγωγής και από τη σταθερά χρόνου του κυκλώματος rC.
Εάν , τότε =0 και μια σταθερή κατάσταση θα εμφανιστεί στο κύκλωμα αμέσως μετά την εναλλαγή, δηλ.
Όταν η τάση = - , δηλ. Η τάση στον πυκνωτή αμέσως μετά την εναλλαγή μπορεί να φτάσει σχεδόν το διπλάσιο της τιμής του θετικού πρόσημου και στη συνέχεια να πλησιάσει σταδιακά το =.
Η διαφορά φάσης θα οδηγήσει την εξίσωση (1) στη μορφή:
Η διαφορά μεταξύ αυτής της λειτουργίας και της προηγούμενης είναι ότι η τάση στον πυκνωτή αμέσως μετά την εναλλαγή μπορεί να φτάσει σχεδόν το διπλάσιο της αρνητικής τιμής.
Για το θεωρούμενο κύκλωμα Rc με ημιτονοειδή πηγή ρεύματος σε σταθερή κατάσταση, η αρχική φάση της τάσης εισόδου δεν παίζει κανένα ρόλο, αλλά στη μεταβατική διαδικασία η επιρροή της είναι σημαντική.
13. Παροδική διεργασία σε κυκλώματα r, L, C – όταν συνδέεται σε πηγή σταθερής τάσης. Διαδικασία παρτίδας. Αναλυτικές εκφράσεις για i(t), γραφικά. (Κλασική μέθοδος).
Οι ρίζες είναι πραγματικές, αρνητικές, διαφορετικές.
I(t)=I στόμα +A1e p 1 t +A2e p 2 t
Η διαδικασία είναι περιοδική:
t=0 (i(0)=A1+A2, A1=-A2
{ 
t=0 i l (0)*r+L +Uc(0)=E A1=-A2= ()
i l (t) = ( 
)
14.Μεταβατική διεργασία σε κυκλώματα r, L, C – όταν συνδέονται σε πηγή σταθερής τάσης. Κρίσιμη διαδικασία. Αναλυτικές εκφράσεις για i(t), γραφικά. (Κλασική μέθοδος).
i l (t)=i χείλη +(B1+B2*t)*
t=0: i l (0)=β1=0
Εάν οι ρίζες αποδειχθούν πραγματικές, αρνητικές, ίσες, τότε η διαδικασία είναι κρίσιμη.
15.Μεταβατική διεργασία σε κυκλώματα r, L, C – όταν συνδέονται σε πηγή σταθερής τάσης. Ταλαντωτική διαδικασία. Αναλυτική έκφραση για i(t), γραφικά. (Κλασική μέθοδος).
P t = -δ±j*ω St ω St =
Οι ρίζες είναι αρνητικές πραγματικές, κάποιο σύνθετο συζυγές.
i l (t)=i στόμα A1e - δt *sin(ω St t+ψ)
i l (t)=i στόμα +(M*cos ω φως t+N*sin ω φως t)*
i l (t)= * 
= *
16. Μεταβατική διεργασία σε κυκλώματα r, L, C – όταν είναι συνδεδεμένη σε ημιτονοειδή πηγή τάσης. Απεριοδική διαδικασία. Αναλυτική έκφραση για i(t), γραφικά. (Κλασική μέθοδος).
R(t)=E max *sin(ωt+ψ)
2. 
Στον κλασικό αριθμό των εξισώσεων σε αυτή την περίπτωση είναι ίσος με τον αριθμό των διακλαδώσεων του κυκλώματος
Η μέθοδος βρίσκει μια λύση με τη μορφή του αθροίσματος μιας γενικής και μιας συγκεκριμένης λύσης. Ο υπολογισμός της μεταβατικής διαδικασίας περιγράφεται από ένα σύστημα συνηθισμένων διαφορικών εξισώσεων που συντάσσονται με μία από τις μεθόδους υπολογισμού για στιγμιαίες τιμές συναρτήσεων χρόνου. Η λύση για κάθε μεταβλητή αυτού του συστήματος βρίσκεται με τη μορφή του αθροίσματος των γενικών και των ειδικών λύσεων. Για τη σύνταξη μιας εξίσωσης, μπορούν να χρησιμοποιηθούν τα ακόλουθα: μια μέθοδος που βασίζεται στην εφαρμογή των νόμων του Kirchhoff, η μέθοδος των κομβικών δυναμικών, η μέθοδος των ρευμάτων βρόχου κ.λπ. Για παράδειγμα, ένα σύστημα διαφορικών εξισώσεων που συντάσσεται μετά από μετατροπή σύμφωνα με τον πρώτο και τον δεύτερο νόμο του Kirchhoff έχει τη μορφή:
Για παράδειγμα,
Ο αριθμός των εξισώσεων σε αυτή την περίπτωση είναι ίσος με τον αριθμό των διακλαδώσεων του κυκλώματος. Ας είναι απαραίτητο να βρεθεί το ρεύμα i k σε έναν κλάδο με αριθμό Κ. Εξαλείφοντας τα ρεύματα των διακλαδώσεων στη σειρά, ως αποτέλεσμα λαμβάνουμε το ρεύμα i k και τα παράγωγά του μέχρι την τάξη n:
Η σειρά της διαφορικής εξίσωσης n καθορίζεται από τον αριθμό των ανεξάρτητων ενεργών στοιχείων του κυκλώματος (m). Συνήθως n=m, αλλά ανάλογα με τη μέθοδο σύνδεσης μπορεί να είναι n Τα χωρητικά στοιχεία που συνδέονται σε σειρά μπορούν να αντικατασταθούν από ένα στοιχείο, όπως τα επαγωγικά στοιχεία με παράλληλη σύνδεση μπορούν να αντικατασταθούν από ένα ισοδύναμο. Το σχήμα 9.5 δείχνει την αντικατάσταση 2 πυκνωτών συνδεδεμένων σε σειρά με έναν ισοδύναμο. Γενικά, η σειρά της διαφορικής εξίσωσης n είναι ίση με: n=n lc -n ce -n lj, όπου n lc είναι ο αριθμός των ενεργών στοιχείων (L και C) στο κύκλωμα, n ce είναι ο αριθμός των χωρητικών κυκλώματα, n lj είναι ο αριθμός των επαγωγικών κόμβων ή τμημάτων. Με τον όρο χωρητικό εννοείται ένα κύκλωμα που αποτελείται από χωρητικά στοιχεία ή χωρητικά στοιχεία και ιδανικές πηγές emf, Εικ. 9.6.α Με τον όρο επαγωγικό εννοείται ένας κόμβος στον οποίο συγκλίνουν επαγωγικοί κλάδοι ή επαγωγικοί κλάδοι και πηγές ρεύματος (Εικ. 9.6.β). τμήματα που διασταυρώνονται μόνο επαγωγικοί κλάδοι ή επαγωγικοί κλάδοι και πηγές ρεύματος. Σημειώστε ότι το στάδιο της σύνταξης μιας διαφορικής εξίσωσης δεν είναι υποχρεωτικό και το ρεύμα ή η τάση μετάβασης μπορεί να βρεθεί χωρίς να συνταχθεί εξίσωση. Όπως αναφέρθηκε, στην κλασική μέθοδο υπολογισμού μεταβατικών διεργασιών λύνονται οι εξισώσεις Μια συγκεκριμένη λύση περιγράφει ένα καθεστώς που ονομάζεται αναγκαστικό. Η λύση μιας ομοιογενούς εξίσωσης (η δεξιά πλευρά είναι μηδέν) περιγράφει τη διαδικασία απουσία εξωτερικών πηγών EMF και ρεύματος και ονομάζεται ελεύθερη. Τα ελεύθερα και εξαναγκαστικά ρεύματα, οι τάσεις και τα φορτία λαμβάνονται υπόψη ανάλογα. Έτσι, το ρεύμα στον κλάδο με αριθμό Κ παριστάνεται ως άθροισμα.
παριστάνεται ως το άθροισμα των γενικών και των ειδικών λύσεων.
