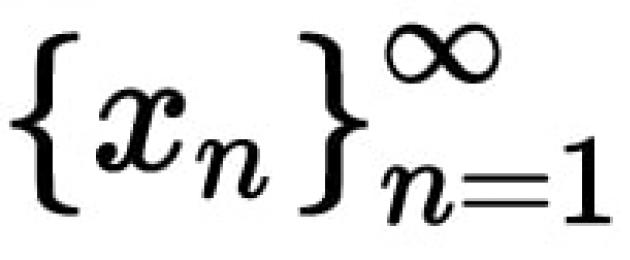Function limit- number a will be the limit of some variable value if, in the process of its change, this variable quantity approaches indefinitely a.
Or in other words, the number A is the limit of the function y = f(x) at the point x 0, if for any sequence of points from the domain of definition of the function , not equal x 0, and which converges to the point x 0 (lim x n = x0), the sequence of corresponding function values converges to the number A.
The graph of a function whose limit, given an argument that tends to infinity, is equal to L:
Meaning A is limit (limit value) of the function f(x) at the point x 0 in case for any sequence of points  , which converges to x 0, but which does not contain x 0 as one of its elements (i.e. in the punctured vicinity x 0), sequence of function values
, which converges to x 0, but which does not contain x 0 as one of its elements (i.e. in the punctured vicinity x 0), sequence of function values  converges to A.
converges to A.
Limit of a Cauchy function.
Meaning A will be limit of the function f(x) at the point x 0 if for any non-negative number taken in advance ε the corresponding non-negative number will be found δ = δ(ε) such that for each argument x, satisfying the condition 0 < | x - x0 | < δ , the inequality will be satisfied | f(x)A |< ε .
It will be very simple if you understand the essence of the limit and the basic rules for finding it. What is the limit of the function f (x) at x striving for a equals A, is written like this:

Moreover, the value to which the variable tends x, can be not only a number, but also infinity (∞), sometimes +∞ or -∞, or there may be no limit at all.
To understand how find the limits of a function, it is best to look at examples of solutions.
It is necessary to find the limits of the function f (x) = 1/x at:
x→ 2, x→ 0, x→ ∞.
Let's find a solution to the first limit. To do this, you can simply substitute x the number it tends to, i.e. 2, we get:

Let's find the second limit of the function. Here substitute pure 0 instead x it is impossible, because You cannot divide by 0. But we can take values close to zero, for example, 0.01; 0.001; 0.0001; 0.00001 and so on, and the value of the function f (x) will increase: 100; 1000; 10000; 100,000 and so on. Thus, it can be understood that when x→ 0 the value of the function that is under the limit sign will increase without limit, i.e. strive towards infinity. Which means:

Regarding the third limit. The same situation as in the previous case, it is impossible to substitute ∞ in its purest form. We need to consider the case of unlimited increase x. We substitute 1000 one by one; 10000; 100000 and so on, we have that the value of the function f (x) = 1/x will decrease: 0.001; 0.0001; 0.00001; and so on, tending to zero. That's why:

It is necessary to calculate the limit of the function 
Starting to solve the second example, we see uncertainty. From here we find the highest degree of the numerator and denominator - this is x 3, we take it out of brackets in the numerator and denominator and then reduce it by:

Answer ![]()
The first step in finding this limit, substitute the value 1 instead x, resulting in uncertainty. To solve it, let’s factorize the numerator and do this using the method of finding the roots of a quadratic equation x 2 + 2x - 3:
D = 2 2 - 4*1*(-3) = 4 +12 = 16→ √ D=√16 = 4
x 1.2 = (-2±4)/2→ x 1 = -3;x 2= 1.
So the numerator will be:
Answer ![]()
This is the determination of its specific meaning or specific area, where the function that is bounded by the limit falls.
To solve limits, follow the rules:
Having understood the essence and main rules for solving the limit, You'll get basic concept about how to solve them.
The theory of limits is one of the sections mathematical analysis. The question of solving limits is quite extensive, since there are dozens of methods for solving limits various types. There are dozens of nuances and tricks that allow you to solve this or that limit. Nevertheless, we will still try to understand the main types of limits that are most often encountered in practice.
Let's start with the very concept of a limit. But first, a brief historical background. There lived in the 19th century a Frenchman, Augustin Louis Cauchy, who laid the foundations of mathematical analysis and gave strict definitions, the definition of a limit, in particular. It must be said that this same Cauchy was, is, and will be in the nightmares of all students of physics and mathematics, since he proved a huge number of theorems of mathematical analysis, and each theorem is more disgusting than the other. In this regard, we will not consider a strict definition of the limit, but will try to do two things:
1. Understand what a limit is.
2. Learn to solve the main types of limits.
I apologize for some unscientific explanations, it is important that the material is understandable even to a teapot, which, in fact, is the task of the project.
So what is the limit?
And just an example of why to shaggy grandma....
Any limit consists of three parts:
1) The well-known limit icon.
2) Entries under the limit icon, in this case . The entry reads “X tends to one.” Most often - exactly, although instead of “X” in practice there are other variables. In practical tasks, the place of one can be absolutely any number, as well as infinity ().
3) Functions under the limit sign, in this case .
The recording itself ![]() reads like this: “the limit of a function as x tends to unity.”
reads like this: “the limit of a function as x tends to unity.”
Let's look at the next important question - what does the expression “x” mean? strives to one"? And what does “strive” even mean?
The concept of a limit is a concept, so to speak, dynamic. Let's build a sequence: first , then , , …, ![]() , ….
, ….
That is, the expression “x strives to one” should be understood as follows: “x” consistently takes on the values which approach unity infinitely close and practically coincide with it.
How to solve the above example? Based on the above, you just need to substitute one into the function under the limit sign:
So, the first rule: When given any limit, first we simply try to plug the number into the function.
We have considered the simplest limit, but these also occur in practice, and not so rarely!
Example with infinity:
Let's figure out what it is? This is the case when it increases without limit, that is: first, then, then, then, and so on ad infinitum.
What happens to the function at this time?
, , ![]() , …
, …
So: if , then the function tends to minus infinity:
![]()
Roughly speaking, according to our first rule, instead of “X” we substitute infinity into the function and get the answer.
Another example with infinity:
![]()
Again we begin to increase to infinity, and look at the behavior of the function: 
Conclusion: when the function increases without limit:![]()
And another series of examples:
Please try to mentally analyze the following for yourself and remember the simplest types of limits:
, , , , ![]() , , , ,
, , , , ![]() ,
,
If you have doubts anywhere, you can pick up a calculator and practice a little.
In the event that , try to construct the sequence , , . If , then , , .
Note: strictly speaking, this approach to constructing sequences of several numbers is incorrect, but for understanding the simplest examples it is quite suitable.
Also pay attention to the following thing. Even if given a limit with a large number at the top, even with a million: it’s all the same ![]() , since sooner or later “X” will take on such gigantic values that a million compared to them will be a real microbe.
, since sooner or later “X” will take on such gigantic values that a million compared to them will be a real microbe.
What do you need to remember and understand from the above?
1) When given any limit, first we simply try to substitute the number into the function.
2) You must understand and immediately solve the simplest limits, such as ![]() , , etc.
, , etc.
Now we will consider the group of limits when , and the function is a fraction whose numerator and denominator contain polynomials
Example:
Calculate limit ![]()
According to our rule, we will try to substitute infinity into the function. What do we get at the top? Infinity. And what happens below? Also infinity. Thus, we have what is called species uncertainty. One might think that , and the answer is ready, but in the general case this is not at all the case, and it is necessary to apply some solution technique, which we will now consider.
How to solve limits of this type?
First we look at the numerator and find the highest power: 
The leading power in the numerator is two.
Now we look at the denominator and also find it to the highest power: 
The highest degree of the denominator is two.
Then we choose the highest power of the numerator and denominator: in this example, they are the same and equal to two.
So, the solution method is as follows: in order to reveal the uncertainty, it is necessary to divide the numerator and denominator by the highest power.
![]()

Here it is, the answer, and not infinity at all.
What is fundamentally important in the design of a decision?
First, we indicate uncertainty, if any.
Secondly, it is advisable to interrupt the solution for intermediate explanations. I usually use the sign, it does not have any mathematical meaning, but means that the solution is interrupted for an intermediate explanation.
Thirdly, in the limit it is advisable to mark what is going where. When the work is drawn up by hand, it is more convenient to do it this way: 
It is better to use a simple pencil for notes.
Of course, you don’t have to do any of this, but then, perhaps, the teacher will point out shortcomings in the solution or start asking additional questions about the assignment. Do you need it?
Example 2
Find the limit ![]()
Again in the numerator and denominator we find in the highest degree: ![]()
Maximum degree in numerator: 3
Maximum degree in denominator: 4
Choose greatest value, in this case four.
According to our algorithm, to reveal uncertainty, we divide the numerator and denominator by .
The complete assignment might look like this:
![]()
Divide the numerator and denominator by

Example 3
Find the limit ![]()
Maximum degree of “X” in the numerator: 2
Maximum degree of “X” in the denominator: 1 (can be written as)
To reveal the uncertainty, it is necessary to divide the numerator and denominator by . The final solution might look like this:
![]()
Divide the numerator and denominator by

Notation does not mean division by zero (you cannot divide by zero), but division by an infinitesimal number.
Thus, by uncovering species uncertainty, we may be able to final number, zero or infinity.
Limits with uncertainty of type and method for solving them
The next group of limits is somewhat similar to the limits just considered: the numerator and denominator contain polynomials, but “x” no longer tends to infinity, but to finite number.
Example 4
Solve limit ![]()
First, let's try to substitute -1 into the fraction: ![]()
In this case, the so-called uncertainty is obtained.
General rule : if the numerator and denominator contain polynomials, and there is uncertainty of the form , then to disclose it you need to factor the numerator and denominator.
To do this, most often you need to decide quadratic equation and/or use abbreviated multiplication formulas. If these things have been forgotten, then visit the page Mathematical formulas and tables and check out methodological material Hot formulas for school mathematics course. By the way, it is best to print it out; it is required very often, and information is absorbed better from paper.
So, let's solve our limit ![]()
Factor the numerator and denominator
In order to factor the numerator, you need to solve the quadratic equation: ![]()
First we find the discriminant:
And the square root of it: .
If the discriminant is large, for example 361, we use a calculator, the extraction function square root available on the simplest calculator.
! If the root is not extracted in its entirety (a fractional number with a comma is obtained), it is very likely that the discriminant was calculated incorrectly or there was a typo in the task.
Next we find the roots: ![]()
![]()
Thus:
All. The numerator is factorized.
Denominator. The denominator is already the simplest factor, and there is no way to simplify it.
![]()
Obviously, it can be shortened to:
![]()
Now we substitute -1 into the expression that remains under the limit sign:
Naturally, in test work, during a test or exam, the solution is never written out in such detail. In the final version, the design should look something like this:
![]()
Let's factorize the numerator. ![]()
![]()
![]()
Example 5
Calculate limit ![]()
First, the “finish” version of the solution
![]()
Let's factor the numerator and denominator.
Numerator:
Denominator: ![]()
![]()
![]() ,
, ![]()

What's important in this example?
Firstly, you must have a good understanding of how the numerator is revealed, first we took 2 out of brackets, and then used the formula for the difference of squares. This is the formula you need to know and see.
For those who want to learn how to find limits, in this article we will tell you about it. We won’t delve into the theory; teachers usually give it at lectures. So the “boring theory” should be jotted down in your notebooks. If this is not the case, then you can read textbooks borrowed from the library. educational institution or on other Internet resources.
So, the concept of limit is quite important in the study of higher mathematics, especially when you come across integral calculus and understand the connection between limit and integral. In the current material we will consider simple examples, as well as ways to solve them.
Examples of solutions
| Example 1 |
| Calculate a) $ \lim_(x \to 0) \frac(1)(x) $; b)$ \lim_(x \to \infty) \frac(1)(x) $ |
| Solution |
|
a) $$ \lim \limits_(x \to 0) \frac(1)(x) = \infty $$ b)$$ \lim_(x \to \infty) \frac(1)(x) = 0 $$ People often send us these limits with a request to help solve them. We decided to highlight them as a separate example and explain that these limits just need to be remembered, as a rule. If you cannot solve your problem, then send it to us. We will provide detailed solution. You will be able to view the progress of the calculation and gain information. This will help you get your grade from your teacher in a timely manner! |
| Answer |
| $$ \text(a)) \lim \limits_(x \to 0) \frac(1)(x) = \infty \text( b))\lim \limits_(x \to \infty) \frac(1 )(x) = 0 $$ |
What to do with uncertainty of the form: $ \bigg [\frac(0)(0) \bigg ] $
| Example 3 |
| Solve $ \lim \limits_(x \to -1) \frac(x^2-1)(x+1) $ |
| Solution |
|
As always, we start by substituting the value $ x $ into the expression under the limit sign. $$ \lim \limits_(x \to -1) \frac(x^2-1)(x+1) = \frac((-1)^2-1)(-1+1)=\frac( 0)(0)$$ What's next now? What should happen in the end? Since this is uncertainty, this is not an answer yet and we continue the calculation. Since we have a polynomial in the numerators, we will factorize it using the formula familiar to everyone from school $$ a^2-b^2=(a-b)(a+b) $$. Do you remember? Great! Now go ahead and use it with the song :) We find that the numerator $ x^2-1=(x-1)(x+1) $ We continue to solve taking into account the above transformation: $$ \lim \limits_(x \to -1)\frac(x^2-1)(x+1) = \lim \limits_(x \to -1)\frac((x-1)(x+ 1))(x+1) = $$ $$ = \lim \limits_(x \to -1)(x-1)=-1-1=-2 $$ |
| Answer |
| $$ \lim \limits_(x \to -1) \frac(x^2-1)(x+1) = -2 $$ |
Let's push the limit in the last two examples to infinity and consider the uncertainty: $ \bigg [\frac(\infty)(\infty) \bigg ] $
| Example 5 |
| Calculate $ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) $ |
| Solution |
|
$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) = \frac(\infty)(\infty) $ What to do? What should I do? Don't panic, because the impossible is possible. It is necessary to take out the x in both the numerator and the denominator, and then reduce it. After this, try to calculate the limit. Let's try... $$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) =\lim \limits_(x \to \infty) \frac(x^2(1-\frac (1)(x^2)))(x(1+\frac(1)(x))) = $$ $$ = \lim \limits_(x \to \infty) \frac(x(1-\frac(1)(x^2)))((1+\frac(1)(x))) = $$ Using the definition from Example 2 and substituting infinity for x, we get: $$ = \frac(\infty(1-\frac(1)(\infty)))((1+\frac(1)(\infty))) = \frac(\infty \cdot 1)(1+ 0) = \frac(\infty)(1) = \infty $$ |
| Answer |
| $$ \lim \limits_(x \to \infty) \frac(x^2-1)(x+1) = \infty $$ |
Algorithm for calculating limits
So, let's briefly summarize the examples and create an algorithm for solving the limits:
- Substitute point x into the expression following the limit sign. If a certain number or infinity is obtained, then the limit is completely solved. Otherwise, we have uncertainty: “zero divided by zero” or “infinity divided by infinity” and proceed to the following points instructions.
- To eliminate the uncertainty of “zero divided by zero,” you need to factor the numerator and denominator. Reduce similar ones. Substitute point x into the expression under the limit sign.
- If the uncertainty is “infinity divided by infinity,” then we take out both the numerator and the denominator x to the greatest degree. We shorten the X's. We substitute the values of x from under the limit into the remaining expression.
In this article, you learned the basics of solving limits, often used in the Calculus course. Of course, these are not all types of problems offered by examiners, but only the simplest limits. We'll talk about other types of assignments in future articles, but first you need to learn this lesson in order to move forward. Let's discuss what to do if there are roots, degrees, study infinitesimals equivalent functions, remarkable limits, L'Hopital's rule.
If you can't figure out the limits yourself, don't panic. We are always happy to help!
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
Solution
2. Calculate the limit of a number sequence:
3. Calculate the limit of a number sequence:
4. Calculate the limit of a number sequence:
5. Calculate the limit of a number sequence:
6. Calculate the limit of a number sequence:
7. Calculate the limit of a number sequence:
8. Calculate the limit of a number sequence:
9. Calculate the limit of a number sequence:
10. Calculate the limit of a number sequence:
11. Calculate the limit of a number sequence:
1) From the numerator and denominator, select the factor that makes the greatest contribution and reduce by it
2) In this type of example, you need to remove the factor to the greatest extent from under the root in the denominator
3) It is necessary to expand to the greatest common factorial
4) In this example it grows much faster, so we single it out as the biggest factor
5) The quantities and tend to zero at . Based on this we calculate the limit
Majority decisions similar examples is to find the dominant factor. If it is in the numerator, then the boundary goes to infinity, in the denominator - to zero. And only when both here and there can you reduce the fraction by this factor and get the limit in the form of a constant.
Exercise:
1. Analyze the solutions of the considered examples
2. Calculate the following limits:
Section 2. Beginnings of mathematical analysis
(Independent work 48 hours)
2.1. Implicit function derivative (4 hours).
Example 1. Find the derivative of an implicit function
Solution. Since y is a function of X, then we will consider y 2 as a complex function of X. Hence, . Differentiating by X both sides of this equation, we obtain, i.e.
Example 2. Find the derivative of an implicit function
Solution. Differentiating by X
Example 3. Find the derivative of an implicit function
Solution. Differentiating by X both sides of this equation, we get
1. Find the derivative f ’(x).
2. Find stationary points of this function, i.e. points at which
3. Find the second derivative f ’’(x).
4. Investigate the sign of the second derivative at each of the stationary points. If the second derivative turns out to be negative, then the function at such a point has a maximum, and if it is positive, then it has a minimum. If the second derivative is equal to zero, then the extremum of the function must be sought using the first derivative.
5. Calculate the values of the function at the extremum points.
Example. Examine the extremum using the second derivative of the function: f(x) = x 2 – 2x - 3.
Solution: Find the derivative: f ‘(x) = 2x - 2.
Solving the equation f ’(x) = 0, we obtain a stationary point x =1. Let us now find the second derivative: f ’’(x) = 2.
Since the second derivative at) = x 2 – 2x - 3. at the stationary point is positive, f’’(1) = 2 > 0, then at x = 1 the function has a minimum: f min = f(1) = -4.
Answer: The minimum point has coordinates (1; -4).
Tasks.
1. Consider and analyze the considered solutions to examples on these topics.
2. Investigate for extremum using the second derivative of the function:
a) f(x) = 1 – x 4;
b) f(x) = x 3 - 1;
2.3. Application of the derivative to solving physical problems (11 hours).
2.4. Compiling crossnumbers on the topic “Definite Integral”
2.5 Calculation of body volume and arc length of a curve (12 hours)
The first remarkable limit is the following equality:
\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)
Since for $\alpha\to(0)$ we have $\sin\alpha\to(0)$, they say that the first remarkable limit reveals an uncertainty of the form $\frac(0)(0)$. Generally speaking, in formula (1), instead of the variable $\alpha$, any expression can be placed under the sine sign and in the denominator, as long as two conditions are met:
- The expressions under the sine sign and in the denominator simultaneously tend to zero, i.e. there is uncertainty of the form $\frac(0)(0)$.
- The expressions under the sine sign and in the denominator are the same.
Corollaries from the first remarkable limit are also often used:
\begin(equation) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(equation)
Eleven examples are solved on this page. Example No. 1 is devoted to the proof of formulas (2)-(4). Examples No. 2, No. 3, No. 4 and No. 5 contain solutions with detailed comments. Examples No. 6-10 contain solutions with virtually no comments, because detailed explanations were given in previous examples. The solution uses some trigonometric formulas that can be found.
I note that the presence trigonometric functions coupled with the uncertainty $\frac (0) (0)$ does not yet mean the mandatory application of the first remarkable limit. Sometimes simple trigonometric transformations are sufficient - for example, see.
Example No. 1
Prove that $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha )(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.
a) Since $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, then:
$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$
Since $\lim_(\alpha\to(0))\cos(0)=1$ and $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ , That:
$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$
b) Let's make the change $\alpha=\sin(y)$. Since $\sin(0)=0$, then from the condition $\alpha\to(0)$ we have $y\to(0)$. In addition, there is a neighborhood of zero in which $\arcsin\alpha=\arcsin(\sin(y))=y$, so:
$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$
The equality $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ has been proven.
c) Let's make the replacement $\alpha=\tg(y)$. Since $\tg(0)=0$, then the conditions $\alpha\to(0)$ and $y\to(0)$ are equivalent. In addition, there is a neighborhood of zero in which $\arctg\alpha=\arctg\tg(y))=y$, therefore, based on the results of point a), we will have:
$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$
The equality $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ has been proven.
Equalities a), b), c) are often used along with the first remarkable limit.
Example No. 2
Calculate the limit $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( x+7))$.
Since $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ and $\lim_( x\to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, i.e. and both the numerator and denominator of the fraction simultaneously tend to zero, then here we are dealing with an uncertainty of the form $\frac(0)(0)$, i.e. done. In addition, it is clear that the expressions under the sine sign and in the denominator coincide (i.e., and is satisfied):
So, both conditions listed at the beginning of the page are met. It follows from this that the formula is applicable, i.e. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7))=1$.
Answer: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.
Example No. 3
Find $\lim_(x\to(0))\frac(\sin(9x))(x)$.
Since $\lim_(x\to(0))\sin(9x)=0$ and $\lim_(x\to(0))x=0$, then we are dealing with an uncertainty of the form $\frac(0 )(0)$, i.e. done. However, the expressions under the sine sign and in the denominator do not coincide. Here you need to adjust the expression in the denominator to the required form. We need the expression $9x$ to be in the denominator, then it will become true. Essentially, we're missing a factor of $9$ in the denominator, which isn't that hard to enter—just multiply the expression in the denominator by $9$. Naturally, to compensate for multiplication by $9$, you will have to immediately divide by $9$:
$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$
Now the expressions in the denominator and under the sine sign coincide. Both conditions for the limit $\lim_(x\to(0))\frac(\sin(9x))(9x)$ are satisfied. Therefore, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. And this means that:
$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$
Answer: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.
Example No. 4
Find $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.
Since $\lim_(x\to(0))\sin(5x)=0$ and $\lim_(x\to(0))\tg(8x)=0$, here we are dealing with uncertainty of the form $\frac(0)(0)$. However, the form of the first remarkable limit is violated. A numerator containing $\sin(5x)$ requires a denominator of $5x$. In this situation, the easiest way is to divide the numerator by $5x$, and immediately multiply by $5x$. In addition, we will perform a similar operation with the denominator, multiplying and dividing $\tg(8x)$ by $8x$:
$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$
Reducing by $x$ and taking the constant $\frac(5)(8)$ outside the limit sign, we get:
$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$
Note that $\lim_(x\to(0))\frac(\sin(5x))(5x)$ fully satisfies the requirements for the first remarkable limit. To find $\lim_(x\to(0))\frac(\tg(8x))(8x)$ the following formula is applicable:
$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$
Answer: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.
Example No. 5
Find $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.
Since $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (remember that $\cos(0)=1$) and $\lim_(x\to(0))x^2=0$, then we are dealing with uncertainty of the form $\frac(0)(0)$. However, in order to apply the first remarkable limit, you should get rid of the cosine in the numerator, moving on to sines (in order to then apply the formula) or tangents (in order to then apply the formula). This can be done with the following transformation:
$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$
Let's go back to the limit:
$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$
The fraction $\frac(\sin^2(5x))(x^2)$ is already close to the form required for the first remarkable limit. Let's work a little with the fraction $\frac(\sin^2(5x))(x^2)$, adjusting it to the first remarkable limit (note that the expressions in the numerator and under the sine must match):
$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$
Let's return to the limit in question:
$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0 ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$
Answer: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.
Example No. 6
Find the limit $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.
Since $\lim_(x\to(0))(1-\cos(6x))=0$ and $\lim_(x\to(0))(1-\cos(2x))=0$, then we are dealing with uncertainty $\frac(0)(0)$. Let us reveal it with the help of the first remarkable limit. To do this, let's move from cosines to sines. Since $1-\cos(2\alpha)=2\sin^2(\alpha)$, then:
$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$
Passing to sines in the given limit, we will have:
$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$
Answer: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.
Example No. 7
Calculate the limit $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ subject to $\alpha\neq\ beta$.
Detailed explanations were given earlier, but here we simply note that again there is uncertainty $\frac(0)(0)$. Let's move from cosines to sines using the formula
$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$
Using this formula, we get:
$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\right| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$
Answer: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alpha^2)(2)$.
Example No. 8
Find the limit $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.
Since $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (remember that $\sin(0)=\tg(0)=0$) and $\lim_(x\to(0))x^3=0$, then here we are dealing with uncertainty of the form $\frac(0)(0)$. Let's break it down as follows:
$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$
Answer: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.
Example No. 9
Find the limit $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.
Since $\lim_(x\to(3))(1-\cos(x-3))=0$ and $\lim_(x\to(3))(x-3)\tg\frac(x -3)(2)=0$, then there is uncertainty of the form $\frac(0)(0)$. Before proceeding to its expansion, it is convenient to make a change of variable in such a way that the new variable tends to zero (note that in the formulas the variable $\alpha \to 0$). The easiest way is to introduce the variable $t=x-3$. However, for the sake of convenience of further transformations (this benefit can be seen in the course of the solution below), it is worth making the following replacement: $t=\frac(x-3)(2)$. I note that both replacements are applicable in this case, it’s just that the second replacement will allow you to work less with fractions. Since $x\to(3)$, then $t\to(0)$.
$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\right| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$
Answer: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.
Example No. 10
Find the limit $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2 )$.
Once again we are dealing with uncertainty $\frac(0)(0)$. Before proceeding to its expansion, it is convenient to make a change of variable in such a way that the new variable tends to zero (note that in the formulas the variable is $\alpha\to(0)$). The easiest way is to introduce the variable $t=\frac(\pi)(2)-x$. Since $x\to\frac(\pi)(2)$, then $t\to(0)$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\left|\frac(0)(0)\right| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0 ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$
Answer: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.
Example No. 11
Find the limits $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.
In this case we don't have to use the first wonderful limit. Please note that both the first and second limits contain only trigonometric functions and numbers. Often in examples of this kind it is possible to simplify the expression located under the limit sign. Moreover, after the aforementioned simplification and reduction of some factors, the uncertainty disappears. I gave this example for only one purpose: to show that the presence of trigonometric functions under the limit sign does not necessarily mean the use of the first remarkable limit.
Since $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (remember that $\sin\frac(\pi)(2)=1$ ) and $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (let me remind you that $\cos\frac(\pi)(2)=0$), then we have dealing with uncertainty of the form $\frac(0)(0)$. However, this does not mean that we will need to use the first wonderful limit. To reveal the uncertainty, it is enough to take into account that $\cos^2x=1-\sin^2x$:
$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$
There is a similar solution in Demidovich’s solution book (No. 475). As for the second limit, as in the previous examples in this section, we have an uncertainty of the form $\frac(0)(0)$. Why does it arise? It arises because $\tg\frac(2\pi)(3)=-\sqrt(3)$ and $2\cos\frac(2\pi)(3)=-1$. We use these values to transform the expressions in the numerator and denominator. The goal of our actions is to write down the sum in the numerator and denominator as a product. By the way, often within a similar type it is convenient to change a variable, made in such a way that the new variable tends to zero (see, for example, examples No. 9 or No. 10 on this page). However, in this example there is no point in replacing, although if desired, replacing the variable $t=x-\frac(2\pi)(3)$ is not difficult to implement.
$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2 \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$
As you can see, we didn't have to apply the first wonderful limit. Of course, you can do this if you want (see note below), but it is not necessary.
What is the solution using the first remarkable limit? show\hide
Using the first remarkable limit we get:
$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ right))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$
Answer: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.
- In contact with 0
- Google+ 0
- OK 0
- Facebook 0