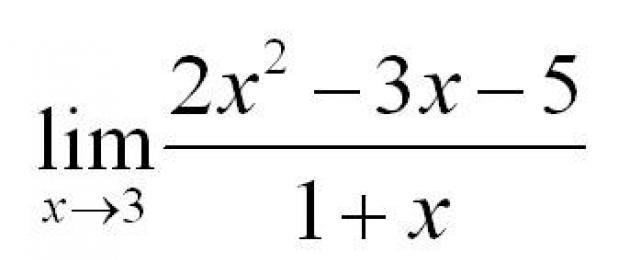The first remarkable limit is the following equality:

\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)

Since for $\alpha\to(0)$ we have $\sin\alpha\to(0)$, they say that the first remarkable limit reveals an uncertainty of the form $\frac(0)(0)$. Generally speaking, in formula (1), instead of the variable $\alpha$, any expression can be placed under the sine sign and in the denominator, as long as two conditions are met:

The expressions under the sine sign and in the denominator simultaneously tend to zero, i.e. there is uncertainty of the form $\frac(0)(0)$.
The expressions under the sine sign and in the denominator are the same.

Corollaries from the first remarkable limit are also often used:

\begin(equation) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \end(equation)

Eleven examples are solved on this page. Example No. 1 is devoted to the proof of formulas (2)-(4). Examples No. 2, No. 3, No. 4 and No. 5 contain solutions with detailed comments. Examples No. 6-10 contain solutions with virtually no comments, because detailed explanations were given in previous examples. The solution uses some trigonometric formulas that can be found.

Let me note that the presence of trigonometric functions coupled with the uncertainty $\frac (0) (0)$ does not necessarily mean the application of the first remarkable limit. Sometimes simple trigonometric transformations are sufficient - for example, see.

Example No. 1

Prove that $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha )(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.

a) Since $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, then:

$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\left|\frac(0)(0)\right| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$

Since $\lim_(\alpha\to(0))\cos(0)=1$ and $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$ , That:

$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$

b) Let's make the change $\alpha=\sin(y)$. Since $\sin(0)=0$, then from the condition $\alpha\to(0)$ we have $y\to(0)$. In addition, there is a neighborhood of zero in which $\arcsin\alpha=\arcsin(\sin(y))=y$, so:

$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$

The equality $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$ has been proven.

c) Let's make the replacement $\alpha=\tg(y)$. Since $\tg(0)=0$, then the conditions $\alpha\to(0)$ and $y\to(0)$ are equivalent. In addition, there is a neighborhood of zero in which $\arctg\alpha=\arctg\tg(y))=y$, therefore, based on the results of point a), we will have:

$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\left|\frac(0)(0)\right| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$

The equality $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$ has been proven.

Equalities a), b), c) are often used along with the first remarkable limit.

Example No. 2

Calculate the limit $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)( x+7))$.

Since $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ and $\lim_( x\to(2))\sin\left(\frac(x^2-4)(x+7)\right)=\sin(0)=0$, i.e. and both the numerator and denominator of the fraction simultaneously tend to zero, then here we are dealing with an uncertainty of the form $\frac(0)(0)$, i.e. done. In addition, it is clear that the expressions under the sine sign and in the denominator coincide (i.e., and is satisfied):

So, both conditions listed at the beginning of the page are met. It follows from this that the formula is applicable, i.e. $\lim_(x\to(2)) \frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x+ 7))=1$.

Answer: $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4)(x +7))=1$.

Example No. 3

Find $\lim_(x\to(0))\frac(\sin(9x))(x)$.

Since $\lim_(x\to(0))\sin(9x)=0$ and $\lim_(x\to(0))x=0$, then we are dealing with an uncertainty of the form $\frac(0 )(0)$, i.e. done. However, the expressions under the sine sign and in the denominator do not coincide. Here you need to adjust the expression in the denominator to the desired form. We need the expression $9x$ to be in the denominator, then it will become true. Essentially, we're missing a factor of $9$ in the denominator, which isn't that hard to enter—just multiply the expression in the denominator by $9$. Naturally, to compensate for multiplication by $9$, you will have to immediately divide by $9$:

$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$

Now the expressions in the denominator and under the sine sign coincide. Both conditions for the limit $\lim_(x\to(0))\frac(\sin(9x))(9x)$ are satisfied. Therefore, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. And this means that:

$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$

Answer: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.

Example No. 4

Find $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.

Since $\lim_(x\to(0))\sin(5x)=0$ and $\lim_(x\to(0))\tg(8x)=0$, here we are dealing with uncertainty of the form $\frac(0)(0)$. However, the form of the first remarkable limit is violated. A numerator containing $\sin(5x)$ requires a denominator of $5x$. In this situation, the easiest way is to divide the numerator by $5x$, and immediately multiply by $5x$. In addition, we will perform a similar operation with the denominator, multiplying and dividing $\tg(8x)$ by $8x$:

$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$

Reducing by $x$ and taking the constant $\frac(5)(8)$ outside the limit sign, we get:

$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$

Note that $\lim_(x\to(0))\frac(\sin(5x))(5x)$ fully satisfies the requirements for the first remarkable limit. To find $\lim_(x\to(0))\frac(\tg(8x))(8x)$ the following formula is applicable:

$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$

Answer: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.

Example No. 5

Find $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.

Since $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (remember that $\cos(0)=1$) and $\lim_(x\to(0))x^2=0$, then we are dealing with uncertainty of the form $\frac(0)(0)$. However, in order to apply the first remarkable limit, you should get rid of the cosine in the numerator, moving on to sines (in order to then apply the formula) or tangents (in order to then apply the formula). This can be done with the following transformation:

$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\left(1-\cos^2(5x)\right)=\cos(5x)\cdot\sin^2(5x).$$

Let's go back to the limit:

$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\left(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\right) $$

The fraction $\frac(\sin^2(5x))(x^2)$ is already close to the form required for the first remarkable limit. Let's work a little with the fraction $\frac(\sin^2(5x))(x^2)$, adjusting it to the first remarkable limit (note that the expressions in the numerator and under the sine must match):

$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\left(\frac(\sin(5x))(5x)\right)^2$$

Let's return to the limit in question:

$$ \lim_(x\to(0))\left(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\right) =\lim_(x\to(0 ))\left(25\cos(5x)\cdot\left(\frac(\sin(5x))(5x)\right)^2\right)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\left(\frac(\sin(5x))(5x)\right)^2 =25\cdot(1)\cdot( 1^2) =25. $$

Answer: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.

Example No. 6

Find the limit $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.

Since $\lim_(x\to(0))(1-\cos(6x))=0$ and $\lim_(x\to(0))(1-\cos(2x))=0$, then we are dealing with uncertainty $\frac(0)(0)$. Let us reveal it with the help of the first remarkable limit. To do this, let's move from cosines to sines. Since $1-\cos(2\alpha)=2\sin^2(\alpha)$, then:

$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$

Passing to sines in the given limit, we will have:

$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\left(\ frac(\sin(3x))(3x)\right)^2\cdot(9x^2))(\left(\frac(\sin(x))(x)\right)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\left(\frac(\sin(3x))(3x)\right)^2)(\displaystyle\lim_(x \to(0))\left(\frac(\sin(x))(x)\right)^2) =9\cdot\frac(1^2)(1^2) =9. $$

Answer: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.

Example No. 7

Calculate the limit $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ subject to $\alpha\neq\ beta$.

Detailed explanations were given earlier, but here we simply note that again there is uncertainty $\frac(0)(0)$. Let's move from cosines to sines using the formula

$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$

Using this formula, we get:

$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\left|\frac(0)( 0)\right| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\left(x\cdot\frac(\alpha+\beta )(2)\right)\cdot\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x^2) =-2\cdot\lim_(x\to( 0))\left(\frac(\sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x)\cdot\frac(\sin\left(x\cdot\frac (\alpha-\beta)(2)\right))(x)\right)=\\ =-2\cdot\lim_(x\to(0))\left(\frac(\sin\left(x \cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\right)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\left(x\cdot\frac(\alpha+\beta)(2)\right))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\left(x\cdot\frac(\alpha-\beta)(2)\right))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alpha^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alpha^2)(2). $$

Answer: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alpha^2)(2)$.

Example No. 8

Find the limit $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.

Since $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (remember that $\sin(0)=\tg(0)=0$) and $\lim_(x\to(0))x^3=0$, then here we are dealing with uncertainty of the form $\frac(0)(0)$. Let's break it down as follows:

$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\left|\frac(0)(0)\right| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\left(\frac(1)(\cos(x))-1\right))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\left(1-\cos(x)\right))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\left(\frac(\sin(x))(x)\cdot\left(\frac(\sin\frac(x)(2))(\frac(x)( 2))\right)^2\cdot\frac(1)(\cos(x))\right) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$

Answer: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.

Example No. 9

Find the limit $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.

Since $\lim_(x\to(3))(1-\cos(x-3))=0$ and $\lim_(x\to(3))(x-3)\tg\frac(x -3)(2)=0$, then there is uncertainty of the form $\frac(0)(0)$. Before proceeding to its expansion, it is convenient to make a change of variable in such a way that the new variable tends to zero (note that in the formulas the variable $\alpha \to 0$). The easiest way is to introduce the variable $t=x-3$. However, for the sake of convenience of further transformations (this benefit can be seen in the course of the solution below), it is worth making the following replacement: $t=\frac(x-3)(2)$. I note that both replacements are applicable in this case, it’s just that the second replacement will allow you to work less with fractions. Since $x\to(3)$, then $t\to(0)$.

$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\left|\frac (0)(0)\right| =\left|\begin(aligned)&t=\frac(x-3)(2);\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\left(\frac(\sin(t))(t)\cdot\cos(t)\right) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$

Answer: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.

Example No. 10

Find the limit $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2 )$.

Once again we are dealing with uncertainty $\frac(0)(0)$. Before proceeding to its expansion, it is convenient to make a change of variable in such a way that the new variable tends to zero (note that in the formulas the variable is $\alpha\to(0)$). The easiest way is to introduce the variable $t=\frac(\pi)(2)-x$. Since $x\to\frac(\pi)(2)$, then $t\to(0)$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\left|\frac(0)(0)\right| =\left|\begin(aligned)&t=\frac(\pi)(2)-x;\\&t\to(0)\end(aligned)\right| =\lim_(t\to(0))\frac(1-\sin\left(\frac(\pi)(2)-t\right))(t^2) =\lim_(t\to(0 ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\left(\frac(\sin\frac(t)(2))(\frac(t)(2))\right)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$

Answer: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\left(\frac(\pi)(2)-x\right)^2) =\frac(1)(2)$.

Example No. 11

Find the limits $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2\ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.

In this case we don't have to use the first wonderful limit. Please note that both the first and second limits contain only trigonometric functions and numbers. Often in examples of this kind it is possible to simplify the expression located under the limit sign. Moreover, after the aforementioned simplification and reduction of some factors, the uncertainty disappears. I gave this example for only one purpose: to show that the presence of trigonometric functions under the limit sign does not necessarily mean the use of the first remarkable limit.

Since $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (remember that $\sin\frac(\pi)(2)=1$ ) and $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (let me remind you that $\cos\frac(\pi)(2)=0$), then we have dealing with uncertainty of the form $\frac(0)(0)$. However, this does not mean that we will need to use the first wonderful limit. To reveal the uncertainty, it is enough to take into account that $\cos^2x=1-\sin^2x$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\left|\frac(0)(0)\right| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$

There is a similar solution in Demidovich’s solution book (No. 475). As for the second limit, as in the previous examples in this section, we have an uncertainty of the form $\frac(0)(0)$. Why does it arise? It arises because $\tg\frac(2\pi)(3)=-\sqrt(3)$ and $2\cos\frac(2\pi)(3)=-1$. We use these values to transform the expressions in the numerator and denominator. The goal of our actions is to write down the sum in the numerator and denominator as a product. By the way, often within a similar type it is convenient to change a variable, made in such a way that the new variable tends to zero (see, for example, examples No. 9 or No. 10 on this page). However, in this example there is no point in replacing, although if desired, replacing the variable $t=x-\frac(2\pi)(3)$ is not difficult to implement.

$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\left(\cos(x)+\frac(1)(2)\right )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\left(\ cos(x)-\cos\frac(2\pi)(3)\right))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \left(x-\frac(2\pi)(3)\right))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2 \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\left(-\frac(1)(2)\right)\cdot\left( -\frac(1)(2)\right)) =-\frac(4)(\sqrt(3)). $$

As you can see, we didn't have to apply the first wonderful limit. Of course, you can do this if you want (see note below), but it is not necessary.

What is the solution using the first remarkable limit? show\hide

Using the first remarkable limit we get:

$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\left(x-\frac(2\pi)(3)\right))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\left(\frac(\sin\left(x-\frac(2\pi)(3)\ right))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\right) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\left(-\frac(1)(2)\right)\cdot\left(-\frac(1)(2)\right)) =-\frac(4)(\sqrt( 3)). $$

Answer: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.

Limits give all mathematics students a lot of trouble. To solve a limit, sometimes you have to use a lot of tricks and choose from a variety of solution methods exactly the one that is suitable for a particular example.

In this article we will not help you understand the limits of your capabilities or comprehend the limits of control, but we will try to answer the question: how to understand limits in higher mathematics? Understanding comes with experience, so at the same time we will give several detailed examples of solving limits with explanations.

The concept of limit in mathematics

The first question is: what is this limit and the limit of what? We can talk about the limits of numerical sequences and functions. We are interested in the concept of the limit of a function, since this is what students most often encounter. But first, the most general definition of a limit:

Let's say there is some variable value. If this value in the process of change unlimitedly approaches a certain number a , That a – the limit of this value.

For a function defined in a certain interval f(x)=y such a number is called a limit A , which the function tends to when X , tending to a certain point A . Dot A belongs to the interval on which the function is defined.

It sounds cumbersome, but it is written very simply:

Lim- from English limit- limit.

There is also a geometric explanation for determining the limit, but here we will not delve into the theory, since we are more interested in the practical rather than the theoretical side of the issue. When we say that X tends to some value, this means that the variable does not take on the value of a number, but approaches it infinitely close.

Let's give a specific example. The task is to find the limit.

To solve this example, we substitute the value x=3 into a function. We get:

By the way, if you are interested, read a separate article on this topic.

In examples X can tend to any value. It can be any number or infinity. Here's an example when X tends to infinity:

Intuitively, the larger the number in the denominator, the smaller the value the function will take. So, with unlimited growth X meaning 1/x will decrease and approach zero.

As you can see, to solve the limit, you just need to substitute the value to strive for into the function X . However, this is the simplest case. Often finding the limit is not so obvious. Within the limits there are uncertainties of the type 0/0 or infinity/infinity . What to do in such cases? Resort to tricks!

Uncertainties within

Uncertainty of the form infinity/infinity

Let there be a limit:

If we try to substitute infinity into the function, we will get infinity in both the numerator and the denominator. In general, it is worth saying that there is a certain element of art in resolving such uncertainties: you need to notice how you can transform the function in such a way that the uncertainty goes away. In our case, we divide the numerator and denominator by X in the senior degree. What will happen?

From the example already discussed above, we know that terms containing x in the denominator will tend to zero. Then the solution to the limit is:

To resolve type uncertainties infinity/infinity divide the numerator and denominator by X to the highest degree.

By the way! For our readers there is now a 10% discount on

Another type of uncertainty: 0/0

As always, substituting values into the function x=-1 gives 0 in the numerator and denominator. Look a little more closely and you will notice that we have a quadratic equation in the numerator. Let's find the roots and write:

Let's reduce and get:

So, if you are faced with type uncertainty 0/0 – factor the numerator and denominator.

To make it easier for you to solve examples, we present a table with the limits of some functions:

L'Hopital's rule within

Another powerful way to eliminate both types of uncertainty. What is the essence of the method?

If there is uncertainty in the limit, take the derivative of the numerator and denominator until the uncertainty disappears.

L'Hopital's rule looks like this:

Important point : the limit in which the derivatives of the numerator and denominator stand instead of the numerator and denominator must exist.

And now - a real example:

There is typical uncertainty 0/0 . Let's take the derivatives of the numerator and denominator:

Voila, uncertainty is resolved quickly and elegantly.

We hope that you will be able to usefully apply this information in practice and find the answer to the question “how to solve limits in higher mathematics.” If you need to calculate the limit of a sequence or the limit of a function at a point, and there is absolutely no time for this work, contact a professional student service for a quick and detailed solution.

Function limit- number a will be the limit of some variable quantity if, in the process of its change, this variable quantity indefinitely approaches a.

Or in other words, the number A is the limit of the function y = f(x) at the point x 0, if for any sequence of points from the domain of definition of the function , not equal x 0, and which converges to the point x 0 (lim x n = x0), the sequence of corresponding function values converges to the number A.

The graph of a function whose limit, given an argument that tends to infinity, is equal to L:

Meaning A is limit (limit value) of the function f(x) at the point x 0 in case for any sequence of points , which converges to x 0, but which does not contain x 0 as one of its elements (i.e. in the punctured vicinity x 0), sequence of function values converges to A.

Limit of a Cauchy function.

Meaning A will be limit of the function f(x) at the point x 0 if for any non-negative number taken in advance ε the corresponding non-negative number will be found δ = δ(ε) such that for each argument x, satisfying the condition 0 < | x - x0 | < δ , the inequality will be satisfied | f(x)A |< ε .

It will be very simple if you understand the essence of the limit and the basic rules for finding it. What is the limit of the function f (x) at x striving for a equals A, is written like this:

Moreover, the value to which the variable tends x, can be not only a number, but also infinity (∞), sometimes +∞ or -∞, or there may be no limit at all.

To understand how find the limits of a function, it is best to look at examples of solutions.

It is necessary to find the limits of the function f (x) = 1/x at:

x→ 2, x→ 0, x→ ∞.

Let's find a solution to the first limit. To do this, you can simply substitute x the number it tends to, i.e. 2, we get:

Let's find the second limit of the function. Here substitute pure 0 instead x it is impossible, because You cannot divide by 0. But we can take values close to zero, for example, 0.01; 0.001; 0.0001; 0.00001 and so on, and the value of the function f (x) will increase: 100; 1000; 10000; 100,000 and so on. Thus, it can be understood that when x→ 0 the value of the function that is under the limit sign will increase without limit, i.e. strive towards infinity. Which means:

Regarding the third limit. The same situation as in the previous case, it is impossible to substitute ∞ in its purest form. We need to consider the case of unlimited increase x. We substitute 1000 one by one; 10000; 100000 and so on, we have that the value of the function f (x) = 1/x will decrease: 0.001; 0.0001; 0.00001; and so on, tending to zero. That's why:

It is necessary to calculate the limit of the function

Starting to solve the second example, we see uncertainty. From here we find the highest degree of the numerator and denominator - this is x 3, we take it out of brackets in the numerator and denominator and then reduce it by:

Answer

The first step in finding this limit, substitute the value 1 instead x, resulting in uncertainty. To solve it, let’s factorize the numerator and do this using the method of finding the roots of a quadratic equation x 2 + 2x - 3:

D = 2 2 - 4*1*(-3) = 4 +12 = 16→ √ D=√16 = 4

x 1.2 = (-2±4)/2→ x 1 = -3;x 2= 1.

So the numerator will be:

Answer

This is the definition of its specific value or a certain area where the function falls, which is limited by the limit.

To solve limits, follow the rules:

Having understood the essence and main rules for solving the limit, you will get a basic understanding of how to solve them.

Methods for solving limits. Uncertainties.
The order of growth of the function. Replacement method

Example 4

Find the limit

This is a simpler example to solve on your own. In the proposed example there is again uncertainty (of a higher order of growth than the root).

If "x" tends to "minus infinity"

The specter of “minus infinity” has been hovering in this article for a long time. Let us consider limits with polynomials in which . The principles and methods of solution will be exactly the same as in the first part of the lesson, with the exception of a number of nuances.

Let's look at 4 tricks that will be required to solve practical tasks:

1) Calculate the limit

The value of the limit depends only on the term since it has the highest order of growth. If , then infinitely large in modulus negative number to the EVEN power, in this case – in the fourth, is equal to “plus infinity”: . Constant (“two”) positive, That's why:

2) Calculate the limit

Here is the senior degree again even, That's why: . But in front of it there is a “minus” ( negative constant –1), therefore:

3) Calculate the limit

The limit value depends only on . As you remember from school, the “minus” “jumps out” from under the odd degree, so infinitely large in modulus negative number to an ODD power equals “minus infinity”, in this case: .
Constant (“four”) positive, Means:

4) Calculate the limit

The first guy in the village has again odd degree, in addition, in the bosom negative constant, which means: Thus:
.

Example 5

Find the limit

Using the above points, we come to the conclusion that there is uncertainty here. The numerator and denominator are of the same order of growth, which means that in the limit the result will be a finite number. Let's find out the answer by discarding all the fry:

The solution is trivial:

Example 6

Find the limit

This is an example for you to solve on your own. Full solution and answer at the end of the lesson.

And now, perhaps, the most subtle of cases:

Example 7

Find the limit

Considering the leading terms, we come to the conclusion that there is uncertainty here. The numerator is of a higher order of growth than the denominator, so we can immediately say that the limit is equal to infinity. But what kind of infinity, “plus” or “minus”? The technique is the same - let’s get rid of the little things in the numerator and denominator:

We decide:

Divide the numerator and denominator by

Example 15

Find the limit

This is an example for you to solve on your own. An approximate sample of the final design at the end of the lesson.

A couple more interesting examples on the topic of variable replacement:

Example 16

Find the limit

When substituting unity into the limit, uncertainty is obtained. Changing the variable already suggests itself, but first we transform the tangent using the formula. Indeed, why do we need a tangent?

Note that , therefore . If it’s not entirely clear, look at the sine values in trigonometric table. Thus, we immediately get rid of the multiplier, in addition, we get the more familiar uncertainty of 0:0. It would be nice if our limit tended to zero.

Let's replace:

If , then

Under the cosine we have “x”, which also needs to be expressed through “te”.
From the replacement we express: .

We complete the solution:

(1) We carry out the substitution

(2) Open the parentheses under the cosine.

(4) To organize first wonderful limit, artificially multiply the numerator by and the reciprocal number.

Task for independent solution:

Example 17

Find the limit

Full solution and answer at the end of the lesson.

These were simple tasks in their class, in practice everything can be worse, and, in addition reduction formulas, you have to use a variety of trigonometric formulas, as well as other tricks. In the article Complex Limits I looked at a couple of real examples =)

On the eve of the holiday, we will finally clarify the situation with another common uncertainty:

Elimination of uncertainty “one to the power of infinity”

This uncertainty is “served” second wonderful limit, and in the second part of that lesson we looked in great detail at standard examples of solutions that are found in practice in most cases. Now the picture with the exponents will be completed, in addition, the final tasks of the lesson will be devoted to “false” limits, in which it SEEMS that it is necessary to apply the 2nd wonderful limit, although this is not at all the case.

The disadvantage of the two working formulas for the 2nd remarkable limit is that the argument must tend to “plus infinity” or to zero. But what if the argument tends to a different number?

A universal formula comes to the rescue (which is actually a consequence of the second remarkable limit):

Uncertainty can be eliminated using the formula:

Somewhere I think I already explained what the square brackets mean. Nothing special, brackets are just brackets. They are usually used to highlight mathematical notation more clearly.

Let us highlight the essential points of the formula:

1) It's about only about uncertainty and nothing else.

2) The “x” argument can tend to arbitrary value(and not just to zero or), in particular, to “minus infinity” or to anyone finite number.

Using this formula you can solve all the examples in the lesson. Wonderful Limits, which belong to the 2nd remarkable limit. For example, let's calculate the limit:

In this case , and according to the formula :

True, I don’t recommend doing this; the tradition is to still use the “usual” design of the solution, if it can be applied. However using the formula it is very convenient to check"classical" examples to the 2nd remarkable limit.

Elementary functions and their graphs.

The main elementary functions are: power function, exponential function, logarithmic function, trigonometric functions and inverse trigonometric functions, as well as a polynomial and a rational function, which is the ratio of two polynomials.

Elementary functions also include those functions that are obtained from elementary ones by applying the basic four arithmetic operations and forming a complex function.

Graphs of elementary functions

	Straight line- graph of a linear function y = ax + b. The function y monotonically increases for a > 0 and decreases for a< 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)
	Parabola- graph of the quadratic trinomial function y = ax 2 + bx + c. It has a vertical axis of symmetry. If a > 0, has a minimum if a< 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax 2 + bx +c =0
	Hyperbola- graph of the function. When a > O it is located in the I and III quarters, when a< 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а >0) or y - - x(a< 0).
	Exponential function. Exhibitor(exponential function to base e) y = e x. (Another spelling y = exp(x)). Asymptote is the abscissa axis.
	Logarithmic function y = log a x(a > 0)
	y = sinx. Sine wave- periodic function with period T = 2π

Function limit.

The function y=f(x) has a number A as a limit as x tends to a, if for any number ε › 0 there is a number δ › 0 such that | y – A | ‹ ε if |x - a| ‹ δ,

or lim y = A

Continuity of function.

The function y=f(x) is continuous at the point x = a if lim f(x) = f(a), i.e.

the limit of a function at a point x = a is equal to the value of the function at a given point.

Finding the limits of functions.

Basic theorems on the limits of functions.

1. The limit of a constant value is equal to this constant value:

2. The limit of an algebraic sum is equal to the algebraic sum of the limits of these functions:

lim (f + g - h) = lim f + lim g - lim h

3. The limit of the product of several functions is equal to the product of the limits of these functions:

lim (f * g* h) = lim f * lim g * lim h

4. The limit of the quotient of two functions is equal to the quotient of the limits of these functions if the limit of the denominator is not equal to 0:

lim------- = ----------

The first remarkable limit: lim --------- = 1

Second remarkable limit: lim (1 + 1/x) x = e (e = 2, 718281..)

Examples of finding the limits of functions.

5.1. Example:

Any limit consists of three parts:

1) The well-known limit icon.

2) Entries under the limit icon. The entry reads “X tends to one.” Most often it is x, although instead of “x” there can be any other variable. In place of one there can be absolutely any number, as well as infinity 0 or .

3) Functions under the limit sign, in this case .

The recording itself reads like this: “the limit of a function as x tends to unity.”

A very important question - what does the expression “x” mean? strives to one"? The expression "x" strives to one” should be understood as follows: “x” consistently takes on the values which approach unity infinitely close and practically coincide with it.

How to solve the above example? Based on the above, you just need to substitute one into the function under the limit sign:

So the first rule : When given a limit, you first simply plug the number into the function.

5.2. Example with infinity:

Let's figure out what it is? This is the case when it increases without limit.

So: if , then the function tends to minus infinity:

According to our first rule, instead of “X” we substitute in the function infinity and we get the answer.

5.3. Another example with infinity:

Again we begin to increase to infinity, and look at the behavior of the function.
Conclusion: the function increases unlimitedly

5.4. A series of examples:

Try to mentally analyze the following examples yourself and solve the simplest types of limits:

, , , , , , , , ,

What do you need to remember and understand from the above?

When given any limit, first simply plug the number into the function. At the same time, you must understand and immediately solve the simplest limits, such as , , etc.

6. Limits with uncertainty of type and a method for solving them.

Now we will consider the group of limits when , and the function is a fraction whose numerator and denominator contain polynomials.

6.1. Example:

Calculate limit

According to our rule, we try to substitute infinity into the function. What do we get at the top? Infinity. And what happens below? Also infinity. Thus, we have what is called species uncertainty. One might think that = 1, and the answer is ready, but in the general case this is not at all the case, and you need to apply some solution technique, which we will now consider.

How to solve limits of this type?

First we look at the numerator and find the highest power:

The leading power in the numerator is two.

Now we look at the denominator and also find it to the highest power:

The highest degree of the denominator is two.

Then we choose the highest power of the numerator and denominator: in this example, they are the same and equal to two.

So, the solution method is as follows: to reveal uncertainty you need to divide the numerator and denominator by in the senior degree.

Thus, the answer is not 1.

Example

Find the limit

Again in the numerator and denominator we find in the highest degree:

Maximum degree in numerator: 3

Maximum degree in denominator: 4

Choose greatest value, in this case four.
According to our algorithm, to reveal uncertainty, we divide the numerator and denominator by .

Example

Find the limit

Maximum degree of “X” in the numerator: 2

Maximum degree of “X” in the denominator: 1 (can be written as)
To reveal the uncertainty, it is necessary to divide the numerator and denominator by . The final solution might look like this: