We begin to consider the actual process of calculating the double integral and get acquainted with its geometric meaning.

The double integral is numerically equal to the area of ​​a flat figure (region of integration). This is the simplest form of the double integral, when the function of two variables is equal to one: .

Let us first consider the problem in general terms. Now you will be surprised how simple it really is! Let's calculate the area of ​​a flat figure bounded by lines. For definiteness, we assume that on the interval . The area of ​​this figure is numerically equal to:

Let's depict the area in the drawing:

Let's choose the first way to bypass the area:

In this way:

And immediately an important technical trick: iterated integrals can be considered separately. First the inner integral, then the outer integral. This method is highly recommended for beginners in the topic teapots.

1) Calculate the internal integral, while the integration is carried out over the variable "y":

The indefinite integral here is the simplest, and then the banal Newton-Leibniz formula is used, with the only difference that the limits of integration are not numbers, but functions. First, we substituted the upper limit into the “y” (antiderivative function), then the lower limit

2) The result obtained in the first paragraph must be substituted into the external integral:

A more compact notation for the whole solution looks like this:

The resulting formula is exactly the working formula for calculating the area of ​​a flat figure using the "ordinary" definite integral! See lesson Calculating area using a definite integral, there she is at every turn!

I.e, the problem of calculating the area using a double integral little different from the problem of finding the area using a definite integral! In fact, they are one and the same!

Accordingly, no difficulties should arise! I will not consider very many examples, since you, in fact, have repeatedly encountered this problem.

Example 9

Solution: Let's depict the area in the drawing:

Let's choose the following order of traversal of the region:

Here and below, I won't go into how to traverse an area because the first paragraph was very detailed.

In this way:

As I already noted, it is better for beginners to calculate iterated integrals separately, I will adhere to the same method:

1) First, using the Newton-Leibniz formula, we deal with the internal integral:

2) The result obtained at the first step is substituted into the outer integral:

Point 2 is actually finding the area of ​​a flat figure using a definite integral.

Answer:

Here is such a stupid and naive task.

A curious example for an independent solution:

Example 10

Using the double integral, calculate the area of ​​a plane figure bounded by the lines , ,

An example of a final solution at the end of the lesson.

In Examples 9-10, it is much more profitable to use the first method of bypassing the area; curious readers, by the way, can change the order of the bypass and calculate the areas in the second way. If you do not make a mistake, then, naturally, the same area values ​​\u200b\u200bare obtained.

But in some cases, the second way to bypass the area is more effective, and in conclusion of the young nerd's course, let's look at a couple more examples on this topic:

Example 11

Using the double integral, calculate the area of ​​a plane figure bounded by lines.

Solution: we are looking forward to two parabolas with a breeze that lie on their side. No need to smile, similar things in multiple integrals are often encountered.

What is the easiest way to make a drawing?

Let's represent the parabola as two functions:
- upper branch and - lower branch.

Similarly, we represent the parabola as the upper and lower branches.

The area of ​​the figure is calculated using the double integral according to the formula:

What happens if we choose the first way to bypass the area? First, this area will have to be divided into two parts. And secondly, we will observe this sad picture: . Integrals, of course, are not of a super-complex level, but ... there is an old mathematical saying: whoever is friendly with the roots does not need a set-off.

Therefore, from the misunderstanding that is given in the condition, we express the inverse functions:

The inverse functions in this example have the advantage that they immediately set the entire parabola without any leaves, acorns, branches and roots.

According to the second method, the area traversal will be as follows:

In this way:

As they say, feel the difference.

1) We deal with the internal integral:

We substitute the result into the outer integral:

Integration over the variable "y" should not be embarrassing, if there was a letter "zyu" - it would be great to integrate over it. Although who read the second paragraph of the lesson How to calculate the volume of a body of revolution, he no longer experiences the slightest embarrassment with integration over "y".

Also pay attention to the first step: the integrand is even, and the integration segment is symmetric about zero. Therefore, the segment can be halved, and the result can be doubled. This technique is commented on in detail in the lesson. Efficient Methods for Computing the Definite Integral.

What to add…. Everything!

Answer:

To test your integration technique, you can try to calculate . The answer should be exactly the same.

Example 12

Using the double integral, calculate the area of ​​a plane figure bounded by lines

This is a do-it-yourself example. It is interesting to note that if you try to use the first way to bypass the area, then the figure will no longer be divided into two, but into three parts! And, accordingly, we get three pairs of iterated integrals. Sometimes it happens.

The master class has come to an end, and it's time to move on to the grandmaster level - How to calculate the double integral? Solution examples. I'll try not to be so manic in the second article =)

Wish you success!

Solutions and answers:

Example 2:Solution: Draw an area on the drawing:

Let's choose the following order of traversal of the region:

In this way:
Let's move on to inverse functions:


In this way:
Answer:

Example 4:Solution: Let's move on to direct functions:


Let's execute the drawing:

Let's change the order of traversal of the area:

Answer:

Area traversal order:

In this way:

1)
2)

Answer:

Definite integral. How to calculate the area of ​​a figure

We now turn to the consideration of applications of the integral calculus. In this lesson, we will analyze a typical and most common task. How to use a definite integral to calculate the area of ​​a plane figure. Finally, those who seek meaning in higher mathematics - may they find it. You never know. In real life, you will have to approximate a summer cottage with elementary functions and find its area using a certain integral.

To successfully master the material, you must:

1) Understand the indefinite integral at least at an intermediate level. Thus, dummies should first read the lesson Not.

2) Be able to apply the Newton-Leibniz formula and calculate the definite integral. You can establish warm friendly relations with certain integrals on the page Definite integral. Solution examples.

In fact, in order to find the area of ​​\u200b\u200ba figure, you do not need so much knowledge of the indefinite and definite integral. The task "calculate the area using a definite integral" always involves the construction of a drawing, so your knowledge and drawing skills will be a much more relevant issue. In this regard, it is useful to refresh the memory of the graphs of the main elementary functions, and, at a minimum, to be able to build a straight line, a parabola and a hyperbola. This can be done (many need it) with the help of methodological material and an article on geometric transformations of graphs.

Actually, everyone is familiar with the problem of finding the area using a definite integral since school, and we will go a little ahead of the school curriculum. This article might not exist at all, but the fact is that the problem occurs in 99 cases out of 100, when a student is tormented by a hated tower with enthusiasm mastering a course in higher mathematics.

The materials of this workshop are presented simply, in detail and with a minimum of theory.

Let's start with a curvilinear trapezoid.

Curvilinear trapezoid called a flat figure bounded by the axis , straight lines , and the graph of a function continuous on a segment that does not change sign on this interval. Let this figure be located not less abscissa:

Then the area of ​​a curvilinear trapezoid is numerically equal to a certain integral. Any definite integral (that exists) has a very good geometric meaning. On the lesson Definite integral. Solution examples I said that a definite integral is a number. And now it's time to state another useful fact. From the point of view of geometry, the definite integral is the AREA.

I.e, the definite integral (if it exists) geometrically corresponds to the area of ​​some figure. For example, consider the definite integral . The integrand defines a curve on the plane that is located above the axis (those who wish can complete the drawing), and the definite integral itself is numerically equal to the area of ​​the corresponding curvilinear trapezoid.

Example 1

This is a typical task statement. The first and most important moment of the decision is the construction of a drawing. Moreover, the drawing must be built RIGHT.

When building a blueprint, I recommend the following order: at first it is better to construct all lines (if any) and only Then- parabolas, hyperbolas, graphs of other functions. Function graphs are more profitable to build point by point, with the technique of pointwise construction can be found in the reference material Graphs and properties of elementary functions. There you can also find material that is very useful in relation to our lesson - how to quickly build a parabola.

In this problem, the solution might look like this.
Let's make a drawing (note that the equation defines the axis):

I will not hatch a curvilinear trapezoid, it is obvious what area we are talking about here. The solution continues like this:

On the segment, the graph of the function is located over axis, that's why:

Answer:

Who has difficulty calculating the definite integral and applying the Newton-Leibniz formula , refer to the lecture Definite integral. Solution examples.

After the task is completed, it is always useful to look at the drawing and figure out if the answer is real. In this case, “by eye” we count the number of cells in the drawing - well, about 9 will be typed, it seems to be true. It is quite clear that if we had, say, the answer: 20 square units, then, obviously, a mistake was made somewhere - 20 cells obviously do not fit into the figure in question, at most a dozen. If the answer turned out to be negative, then the task was also solved incorrectly.

Example 2

Calculate the area of ​​the figure bounded by the lines , , and the axis

This is a do-it-yourself example. Full solution and answer at the end of the lesson.

What to do if the curvilinear trapezoid is located under axle?

Example 3

Calculate the area of ​​the figure bounded by lines and coordinate axes.

Solution: Let's make a drawing:

If the curvilinear trapezoid is located under axle(or at least not higher given axis), then its area can be found by the formula:
In this case:

Attention! Don't confuse the two types of tasks:

1) If you are asked to solve just a definite integral without any geometric meaning, then it can be negative.

2) If you are asked to find the area of ​​a figure using a definite integral, then the area is always positive! That is why the minus appears in the formula just considered.

In practice, most often the figure is located in both the upper and lower half-planes, and therefore, from the simplest school problems, we move on to more meaningful examples.

Example 4

Find the area of ​​a flat figure bounded by lines , .

Solution: First you need to complete the drawing. Generally speaking, when constructing a drawing in area problems, we are most interested in the intersection points of lines. Let's find the points of intersection of the parabola and the line. This can be done in two ways. The first way is analytical. We solve the equation:

Hence, the lower limit of integration , the upper limit of integration .
It is best not to use this method if possible..

It is much more profitable and faster to build the lines point by point, while the limits of integration are found out as if “by themselves”. The point-by-point construction technique for various charts is discussed in detail in the help Graphs and properties of elementary functions. Nevertheless, the analytical method of finding the limits still sometimes has to be used if, for example, the graph is large enough, or the threaded construction did not reveal the limits of integration (they can be fractional or irrational). And we will also consider such an example.

We return to our task: it is more rational to first construct a straight line and only then a parabola. Let's make a drawing:

I repeat that with pointwise construction, the limits of integration are most often found out “automatically”.

And now the working formula: If there is some continuous function on the interval greater than or equal some continuous function, then the area of ​​the figure bounded by the graphs of these functions and straight lines, can be found by the formula:

Here it is no longer necessary to think about where the figure is located - above the axis or below the axis, and, roughly speaking, it matters which chart is ABOVE(relative to another graph), and which one is BELOW.

In the example under consideration, it is obvious that on the segment the parabola is located above the straight line, and therefore it is necessary to subtract from

The completion of the solution might look like this:

The desired figure is limited by a parabola from above and a straight line from below.
On the segment , according to the corresponding formula:

Answer:

In fact, the school formula for the area of ​​a curvilinear trapezoid in the lower half-plane (see simple example No. 3) is a special case of the formula . Since the axis is given by the equation , and the graph of the function is located not higher axes, then

And now a couple of examples for an independent decision

Example 5

Example 6

Find the area of ​​the figure enclosed by the lines , .

In the course of solving problems for calculating the area using a certain integral, a funny incident sometimes happens. The drawing was made correctly, the calculations were correct, but due to inattention ... found the area of ​​the wrong figure, that's how your obedient servant screwed up several times. Here is a real life case:

Example 7

Calculate the area of ​​the figure bounded by the lines , , , .

Solution: Let's make a drawing first:

…Eh, the drawing came out crap, but everything seems to be legible.

The figure whose area we need to find is shaded in blue.(carefully look at the condition - how the figure is limited!). But in practice, due to inattention, a “glitch” often occurs, that you need to find the area of ​​\u200b\u200bthe figure that is shaded in green!

This example is also useful in that in it the area of ​​\u200b\u200bthe figure is calculated using two definite integrals. Really:

1) On the segment above the axis there is a straight line graph;

2) On the segment above the axis is a hyperbola graph.

It is quite obvious that the areas can (and should) be added, therefore:

Answer:

Let's move on to one more meaningful task.

Example 8

Calculate the area of ​​a figure bounded by lines,
Let's present the equations in a "school" form, and perform a point-by-point drawing:

It can be seen from the drawing that our upper limit is “good”: .
But what is the lower limit? It is clear that this is not an integer, but what? May be ? But where is the guarantee that the drawing is made with perfect accuracy, it may well turn out that. Or root. What if we didn't get the graph right at all?

In such cases, one has to spend additional time and refine the limits of integration analytically.

Let's find the points of intersection of the line and the parabola.
To do this, we solve the equation:


,

Really, .

The further solution is trivial, the main thing is not to get confused in substitutions and signs, the calculations here are not the easiest.

On the segment , according to the corresponding formula:

Answer:

Well, in conclusion of the lesson, we will consider two tasks more difficult.

Example 9

Calculate the area of ​​the figure bounded by lines , ,

Solution: Draw this figure in the drawing.

Damn, I forgot to sign the schedule, and redoing the picture, sorry, not hotz. Not a drawing, in short, today is the day =)

For point-by-point construction, it is necessary to know the appearance of the sinusoid (and in general it is useful to know graphs of all elementary functions), as well as some sine values, they can be found in trigonometric table. In some cases (as in this case), it is allowed to construct a schematic drawing, on which graphs and integration limits must be displayed in principle correctly.

There are no problems with the integration limits here, they follow directly from the condition: - "x" changes from zero to "pi". We make a further decision:

On the segment, the graph of the function is located above the axis, therefore:

In this lesson we will learn how to calculate areas of flat figures, which are called curvilinear trapezoids .

Examples of such figures are in the figure below.

On the one hand, finding the area of ​​a flat figure using a definite integral is extremely simple. We are talking about the area of ​​\u200b\u200bthe figure, which is limited from above by a certain curve, from below - by the abscissa axis ( Ox), and on the left and right are some straight lines. The simplicity is that the definite integral of the function to which the curve is given, and there is the area of ​​such a figure(curvilinear trapezoid).

To calculate the area of ​​a figure, we need:

1. Definite integral of the function defining the curve , which limits the curvilinear trapezoid from above. And here comes the first significant nuance: a curvilinear trapezoid can be limited by a curve not only from above, but also from below . How to act in this case? Simple but important to remember: the integral in this case is taken with a minus sign .
2. Limits of integration a And b, which we find from the equations of lines that bound the figure on the left and right: x = a , x = b, where a And b- numbers.

Separately, some more nuances.

The curve that limits the curvilinear trapezoid from above (or below) must be graph of a continuous and non-negative function y = f(x) .

X values ​​must belong to the segment [a, b] . That is, such, for example, lines as a section of a mushroom are not taken into account, in which the leg fits perfectly into this segment, and the hat is much wider.

Side segments can degenerate into points . If you saw such a figure in the drawing, this should not confuse you, since this point always has its own value on the x-axis. So everything is in order with the limits of integration.

Now you can move on to formulas and calculations. So the area s curvilinear trapezoid can be calculated by the formula

If f(x) ≤ 0 (the graph of the function is located below the axis Ox), then area of ​​a curved trapezoid can be calculated by the formula

There are also cases when both the upper and lower boundaries of the figure are functions, respectively y = f(x) And y = φ (x) , then the area of ​​such a figure is calculated by the formula

. (3)

We solve problems together

Let's start with cases where the area of ​​a figure can be calculated using formula (1).

Example 1Ox) and direct x = 1 , x = 3 .

Solution. Because y = 1/x> 0 on the segment , then the area of ​​the curvilinear trapezoid is found by the formula (1):

.

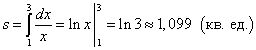Example 2 Find the area of ​​the figure bounded by the graph of the function , straight line x= 1 and the x-axis ( Ox ).

Solution. The result of applying formula (1):

If then s= 1/2; if then s= 1/3 , etc.

Example 3 Find the area of ​​\u200b\u200bthe figure bounded by the graph of the function, the x-axis ( Ox) and direct x = 4 .

Solution. The figure corresponding to the condition of the problem is a curvilinear trapezoid, in which the left segment has degenerated into a point. The integration limits are 0 and 4. Since, according to formula (1), we find the area of ​​the curvilinear trapezoid:

.

Example 4 Find the area of ​​the figure bounded by the lines , , and located in the 1st quarter.

Solution. To use formula (1), we represent the area of ​​the figure given by the conditions of the example as the sum of the areas of a triangle OAB and curvilinear trapezoid ABC. When calculating the area of ​​a triangle OAB the limits of integration are the abscissas of the points O And A, and for the figure ABC- abscissas of points A And C (A is the point of intersection of the line OA and parabolas, and C- point of intersection of the parabola with the axis Ox). Solving jointly (as a system) the equations of a straight line and a parabola, we obtain (the abscissa of the point A) and (the abscissa of another point of intersection of the line and the parabola, which is not needed for the solution). Similarly, we obtain , (abscissas of points C And D). Now we have everything to find the area of ​​the figure. We find:

Example 5 Find the area of ​​a curvilinear trapezoid ACDB, if the equation of the curve CD and abscissa A And B respectively 1 and 2.

Solution. We express this equation of the curve through Y: The area of ​​the curvilinear trapezoid is found by the formula (1):

.

Let's move on to cases where the area of ​​a figure can be calculated using formula (2).

Example 6 Find the area of ​​the figure bounded by the parabola and the x-axis ( Ox ).

Solution. This figure is located below the x-axis. Therefore, to calculate its area, we use formula (2). The limits of integration are the abscissas and points of intersection of the parabola with the axis Ox. Consequently,

Example 7 Find the area between the x-axis ( Ox) and two neighboring sine waves.

Solution. The area of ​​this figure can be found by the formula (2):

.

Let's find each term separately:

.

.

Finally we find the area:

.

Example 8 Find the area of ​​the figure enclosed between the parabola and the curve.

Solution. Let's express the equations of the lines in terms of Y:

The area according to the formula (2) will be obtained as

,

where a And b- abscissas of points A And B. We find them by solving the equations together:

Finally we find the area:

And, finally, there are cases when the area of ​​a figure can be calculated using formula (3).

Example 9 Find the area of ​​the figure enclosed between the parabolas And .

We figured out how to find the area of ​​a curvilinear trapezoid G. Here are the resulting formulas:
for a continuous and non-negative function y=f(x) on the segment ,
for a continuous and non-positive function y=f(x) on the segment .

However, when solving problems of finding the area, one often has to deal with more complex figures.

In this article, we will talk about calculating the area of ​​figures whose boundaries are explicitly specified by functions, that is, as y=f(x) or x=g(y) , and analyze in detail the solution of typical examples.

Page navigation.

Formula for calculating the area of ​​a figure bounded by lines y=f(x) or x=g(y) .

Theorem.

Let the functions and be defined and continuous on the segment , and for any value x from . Then area of ​​figure G, bounded by lines x=a , x=b , and is calculated by the formula .

A similar formula is valid for the area of ​​\u200b\u200bthe figure bounded by the lines y \u003d c, y \u003d d, and: .

Proof.

Let us show the validity of the formula for three cases:

In the first case, when both functions are non-negative, due to the additivity property of the area, the sum of the area of ​​the original figure G and the curvilinear trapezoid is equal to the area of ​​the figure. Consequently,

That's why, . The last transition is possible due to the third property of the definite integral.

Similarly, in the second case, the equality is true. Here is a graphic illustration:

In the third case, when both functions are nonpositive, we have . Let's illustrate this:

Now we can move on to the general case when the functions and cross the Ox axis.

Let's denote the intersection points. These points divide the segment into n parts , where . The figure G can be represented by the union of the figures . It is obvious that on its interval falls under one of the three cases considered earlier, therefore their areas are found as

Consequently,

The last transition is valid due to the fifth property of the definite integral.

Graphic illustration of the general case.

Thus the formula proven.

It's time to move on to solving examples for finding the area of ​​figures bounded by the lines y=f(x) and x=g(y) .

Examples of calculating the area of ​​a figure bounded by lines y=f(x) or x=g(y) .

We will begin the solution of each problem by constructing a figure on a plane. This will allow us to represent a complex figure as a union of simpler figures. In case of difficulties with the construction, refer to the articles:; And .

Example.

Calculate the area of ​​a figure bounded by a parabola and straight lines , x=1 , x=4 .

Solution.

Let's build these lines on the plane.

Everywhere on the segment, the graph of a parabola above straight. Therefore, we apply the previously obtained formula for the area and calculate the definite integral using the Newton-Leibniz formula:

Let's complicate the example a bit.

Example.

Calculate the area of ​​the figure bounded by lines.

Solution.

How is this different from previous examples? Previously, we always had two straight lines parallel to the x-axis, and now only one x=7 . The question immediately arises: where to take the second limit of integration? Let's take a look at the drawing for this.

It became clear that the lower limit of integration when finding the area of ​​\u200b\u200bthe figure is the abscissa of the point of intersection of the graph of the straight line y \u003d x and the semi-parabola. We find this abscissa from the equality:

Therefore, the abscissa of the intersection point is x=2 .

Note.

In our example and in the drawing, it can be seen that the lines and y=x intersect at the point (2;2) and the previous calculations seem redundant. But in other cases, things may not be so obvious. Therefore, we recommend that you always analytically calculate the abscissas and ordinates of the points of intersection of lines.

Obviously, the graph of the function y=x is located above the graph of the function on the interval . We apply the formula to calculate the area:

Let's complicate the task even more.

Example.

Calculate the area of ​​the figure bounded by the graphs of functions and .

Solution.

Let's build a graph of inverse proportionality and a parabola .

Before applying the formula for finding the area of ​​a figure, we need to decide on the limits of integration. To do this, we find the abscissas of the intersection points of the lines by equating the expressions and .

For values ​​of x other than zero, the equality equivalent to third degree equation with integer coefficients. You can refer to the section to recall the algorithm for solving it.

It is easy to check that x=1 is the root of this equation: .

Dividing the expression to the binomial x-1 , we have:

Thus, the remaining roots are found from the equation :

Now from the drawing it became clear that the figure G is enclosed above the blue and below the red line in the interval . Thus, the required area will be equal to

Let's look at another typical example.

Example.

Calculate the area of ​​a figure bounded by curves and the abscissa axis.

Solution.

Let's make a drawing.

This is an ordinary power function with an exponent of one third, the plot of the function can be obtained from the graph by displaying it symmetrically about the x-axis and lifting it up by one.

Find the intersection points of all lines.

The x-axis has the equation y=0 .

The graphs of the functions and y=0 intersect at the point (0;0) since x=0 is the only real root of the equation.

Function Graphs and y=0 intersect at (2;0) , since x=2 is the only root of the equation .

Function graphs and intersect at the point (1;1) since x=1 is the only root of the equation . This statement is not entirely obvious, but is a strictly increasing function, and - strictly decreasing, therefore, the equation has at most one root.

The only remark: in this case, to find the area, you will have to use a formula of the form . That is, the bounding lines must be represented as functions of the argument y , but with a black line .

Let's define the points of intersection of the lines.

Let's start with graphs of functions and :

Let's find the point of intersection of graphs of functions and :

It remains to find the point of intersection of the lines and :

As you can see, the values ​​match.

Summarize.

We have analyzed all the most common cases of finding the area of ​​a figure bounded by explicitly given lines. To do this, you need to be able to build lines on a plane, find the points of intersection of lines and apply the formula to find the area, which implies the ability to calculate certain integrals.

Example1 . Calculate the area of ​​the figure bounded by lines: x + 2y - 4 = 0, y = 0, x = -3, and x = 2

Let's build a figure (see Fig.) We build a straight line x + 2y - 4 \u003d 0 along two points A (4; 0) and B (0; 2). Expressing y in terms of x, we get y \u003d -0.5x + 2. According to formula (1), where f (x) \u003d -0.5x + 2, a \u003d -3, b \u003d 2, we find

S \u003d \u003d [-0.25 \u003d 11.25 sq. units

Example 2 Calculate the area of ​​​​the figure bounded by lines: x - 2y + 4 \u003d 0, x + y - 5 \u003d 0 and y \u003d 0.

Solution. Let's build a figure.

Let's build a straight line x - 2y + 4 = 0: y = 0, x = - 4, A (-4; 0); x = 0, y = 2, B(0; 2).

Let's construct a straight line x + y - 5 = 0: y = 0, x = 5, С(5; 0), x = 0, y = 5, D(0; 5).

Find the point of intersection of the lines by solving the system of equations:

x = 2, y = 3; M(2; 3).

To calculate the required area, we divide the AMC triangle into two triangles AMN and NMC, since when x changes from A to N, the area is limited by a straight line, and when x changes from N to C, it is a straight line

For triangle AMN we have: ; y \u003d 0.5x + 2, i.e. f (x) \u003d 0.5x + 2, a \u003d - 4, b \u003d 2.

For the NMC triangle we have: y = - x + 5, i.e. f(x) = - x + 5, a = 2, b = 5.

Calculating the area of ​​each of the triangles and adding the results, we find:

sq. units

sq. units

9 + 4, 5 = 13.5 sq. units Check: = 0.5AC = 0.5 sq. units

Example 3 Calculate the area of ​​a figure bounded by lines: y = x 2 , y = 0, x = 2, x = 3.

In this case, it is required to calculate the area of ​​a curvilinear trapezoid bounded by a parabola y = x 2 , straight lines x \u003d 2 and x \u003d 3 and the Ox axis (see Fig.) According to formula (1), we find the area of ​​\u200b\u200ba curvilinear trapezoid

= = 6kv. units

Example 4 Calculate the area of ​​​​a figure bounded by lines: y \u003d - x 2 + 4 and y = 0

Let's build a figure. The desired area is enclosed between the parabola y \u003d - x 2 + 4 and axis Oh.

Find the points of intersection of the parabola with the x-axis. Assuming y \u003d 0, we find x \u003d Since this figure is symmetrical about the Oy axis, we calculate the area of ​​\u200b\u200bthe figure located to the right of the Oy axis, and double the result: \u003d + 4x] square. units 2 = 2 sq. units

Example 5 Calculate the area of ​​a figure bounded by lines: y 2 = x, yx = 1, x = 4

Here it is required to calculate the area of ​​the curvilinear trapezoid bounded by the upper branch of the parabola y 2 \u003d x, the Ox axis and straight lines x \u003d 1x \u003d 4 (see Fig.)

According to formula (1), where f(x) = a = 1 and b = 4, we have = (= sq. units

Example 6 . Calculate the area of ​​the figure bounded by lines: y = sinx, y = 0, x = 0, x= .

The desired area is limited by a half-wave sinusoid and the Ox axis (see Fig.).

We have - cosx \u003d - cos \u003d 1 + 1 \u003d 2 square meters. units

Example 7 Calculate the area of ​​the figure bounded by lines: y \u003d - 6x, y \u003d 0 and x \u003d 4.

The figure is located under the Ox axis (see Fig.).

Therefore, its area is found by the formula (3)

= =

Example 8 Calculate the area of ​​\u200b\u200bthe figure bounded by the lines: y \u003d and x \u003d 2. We will build the curve y \u003d by points (see figure). Thus, the area of ​​\u200b\u200bthe figure is found by the formula (4)

Example 9 .

X 2 + y 2 = r 2 .

Here you need to calculate the area bounded by the circle x 2 + y 2 = r 2 , i.e. the area of ​​a circle of radius r centered at the origin. Let's find the fourth part of this area, taking the limits of integration from 0

dor; we have: 1 = = [

Consequently, 1 =

Example 10 Calculate the area of ​​\u200b\u200bthe figure bounded by lines: y \u003d x 2 and y = 2x

This figure is limited by the parabola y \u003d x 2 and straight line y \u003d 2x (see Fig.) To determine the intersection points of the given lines, we solve the system of equations: x 2 – 2x = 0 x = 0 and x = 2

Using formula (5) to find the area, we obtain

= }