Newton's first law tells us that in inertial frames of reference, bodies can change speed only if they are influenced by other bodies. With the help of force ($\overline(F)$) they express the mutual action of bodies on each other. A force can change the magnitude and direction of a body's velocity. $\overline(F)$ is a vector quantity, that is, it has a modulus (magnitude) and direction.
Definition and formula of the resultant of all forces
In classical dynamics, the main law by which the direction and magnitude of the resultant force is found is Newton’s second law:
\[\overline(F)=m\overline(a)\ \left(1\right),\]
where $m$ is the mass of the body on which the force $\overline(F)$ acts; $\overline(a)$ is the acceleration that the force $\overline(F)$ imparts to the body in question. The meaning of Newton's second law is that the forces that act on a body determine the change in the speed of the body, and not just its speed. You should know that Newton's second law is true for inertial frames of reference.
Not one, but a certain combination of forces can act on a body. The total action of these forces is characterized using the concept of resultant force. Let several forces act on a body at the same moment in time. The acceleration of the body in this case is equal to the sum of the acceleration vectors that would arise in the presence of each force separately. The forces that act on the body should be summed up in accordance with the rule of vector addition. The resultant force ($\overline(F)$) is the vector sum of all forces that act on the body at the considered moment in time:
\[\overline(F)=(\overline(F))_1+(\overline(F))_2+\dots +(\overline(F))_N=\sum\limits^N_(i=1)((\ overline(F))_i)\ \left(2\right).\]
Formula (2) is the formula for the resultant of all forces applied to the body. The resultant force is an artificial quantity that is introduced for the convenience of calculations. The resultant force is directed as the acceleration vector of the body.
The basic law of the dynamics of translational motion in the presence of several forces
If several forces act on a body, then Newton's second law is written as:
\[\sum\limits^N_(i=1)((\overline(F))_i)=m\overline(a)\left(3\right).\]
$\overline(F)=0$, if the forces applied to the body cancel each other out. Then in the inertial reference frame the speed of the body is constant.
When depicting the forces acting on a body in the figure, in the case of uniformly accelerated motion, the resultant force is depicted as longer than the sum of the forces that are directed opposite to it. If the body moves at a constant speed or is at rest, the lengths of the force vectors (the resultant and the sum of the remaining forces) are the same and they are directed in opposite directions.
When the resultant of the forces is found, all the forces taken into account in the problem are shown in the figure. These forces are summed up in accordance with the rules of vector addition.
Examples of problems on resultant forces
Example 1
Exercise. A material point is acted upon by two forces directed at an angle $\alpha =60()^\circ $ to each other. What is the resultant of these forces if $F_1=20\ $N; $F_2=10\ $H?
Solution. Let's make a drawing.
Forces in Fig. We add 1 according to the parallelogram rule. The length of the resultant force $\overline(F)$ can be found using the cosine theorem:
Let's calculate the module of the resultant force:
Answer.$F=26.5$ N
Example 2
Exercise. Forces act on a material point (Fig. 2). What is the resultant of these forces?

Solution. The resultant of the forces applied to the point (Fig. 2) is equal to:
\[\overline(F)=(\overline(F))_1+(\overline(F))_2+(\overline(F))_3+(\overline(F))_4\left(2.1\right).\]

Let us find the resultant of the forces $(\overline(F))_1$ and $(\overline(F))_2$. These forces are directed along the same straight line, but in opposite directions, therefore:
Since $F_1>F_2$, then the force $(\overline(F))_(12)$ is directed in the same direction as the force $(\overline(F))_1$.
Let us find the resultant of the forces $(\overline(F))_3$ and $(\overline(F))_4$. These forces are directed along one vertical straight line (Fig. 1), which means:
The direction of the force $(\overline(F))_(34)$ coincides with the direction of the vector $(\overline(F))_3$, since $(\overline(F))_3>(\overline(F))_4 $.
We find the resultant that acts on the material point as:
\[\overline(F)=(\overline(F))_(12)+(\overline(F))_(34)\left(2.2\right).\]
The forces $(\overline(F))_(12)$ and $(\overline(F))_(34)$ are mutually perpendicular. Let's find the length of the vector $\overline(F)$ using the Pythagorean theorem:
DEFINITION
Force is a vector quantity that is a measure of the action of other bodies or fields on a given body, as a result of which a change in the state of this body occurs. In this case, a change in state means a change or deformation.
The concept of force refers to two bodies. You can always indicate the body on which the force acts and the body from which it acts.
Strength is characterized by:
- module;
- direction;
- application point.
The magnitude and direction of the force are independent of the choice.
The unit of force in the C system is 1 Newton.
In nature, there are no material bodies that are outside the influence of other bodies, and, therefore, all bodies are under the influence of external or internal forces.
Several forces can act on a body at the same time. In this case, the principle of independence of action is valid: the action of each force does not depend on the presence or absence of other forces; the combined action of several forces is equal to the sum of the independent actions of the individual forces.
Resultant force
To describe the motion of a body in this case, the concept of resultant force is used.
DEFINITION
Resultant force is a force whose action replaces the action of all forces applied to the body. Or, in other words, the resultant of all forces applied to the body is equal to the vector sum of these forces (Fig. 1).
Fig.1. Determination of resultant forces
Since the movement of a body is always considered in some coordinate system, it is convenient to consider not the force itself, but its projections onto the coordinate axes (Fig. 2, a). Depending on the direction of the force, its projections can be either positive (Fig. 2, b) or negative (Fig. 2, c).

Fig.2. Projections of force onto coordinate axes: a) on a plane; b) on a straight line (the projection is positive);
c) on a straight line (projection is negative)

Fig.3. Examples illustrating the vector addition of forces
We often see examples illustrating the vector addition of forces: a lamp hangs on two cables (Fig. 3, a) - in this case, equilibrium is achieved due to the fact that the resultant of the tension forces is compensated by the weight of the lamp; the block slides along an inclined plane (Fig. 3, b) - the movement occurs due to the resultant forces of friction, gravity and support reaction. Famous lines from the fable by I.A. Krylova “and the cart is still there!” - also an illustration of the equality of the resultant of three forces to zero (Fig. 3, c).
Examples of problem solving
EXAMPLE 1
| Exercise | Two forces act on the body and . Determine the modulus and direction of the resultant of these forces if: a) the forces are directed in one direction; b) forces are directed in opposite directions; c) the forces are directed perpendicular to each other. |
| Solution | a) forces are directed in one direction;
Resultant force:
b) forces are directed in opposite directions;
Resultant force:
Let's project this equality onto the coordinate axis: c) forces are directed perpendicular to each other;
Resultant force:
|
When they talk about the resultant, they mean a force that is equal to the action of two or more forces simultaneously applied to a body.
When several forces act on a body, their combined effect can be different; it depends both on the direction of the different forces and on their numerical values. In any case, you can always find one force that results in them.
For example, a brick was placed on a trampoline. There are two forces acting on the brick - gravity and the elastic force of the trampoline. At the moment when the brick was just laid, the force of gravity was greater than the force of elasticity, and the brick moved downwards. As soon as the forces were equal, the brick stopped.
If the brick were not placed on the trampoline, but thrown with all its strength from above, then it would move down not only under the influence of gravity, but also the throwing force transferred to it. Under the influence of these two forces, the trampoline would bend more, since the elastic force that would balance these forces should be greater.
When the balance of forces is achieved and the movement stops, the balance will be disrupted again, since the throwing force will no longer act on the brick, but only the forces of gravity and elasticity. But the elastic force was achieved not only due to the weight of the brick, but due to the force of the throw. Therefore, the elastic force will be greater than the force of gravity, and the brick will jump, that is, it will begin to move upward.
In the simplest cases, the resultant of forces directed either in one direction or in the opposite direction is considered.
If two forces acting on a body are directed in the same direction, then their resultant will be equal to their sum: F 1 + F 2. For example, if a body is pushed in one direction by two forces of 10 N and 20 N, then the resultant force of these two will be equal to 30 N.
If two forces acting on a body are directed in opposite directions, then their resultant is equal to the magnitude of the difference between the forces and is directed towards the larger one: |F 1 – F 2 |. For example, if one force of 10 N pushes a body to the left, and another force of 15 N pushes it to the right, then the body will move to the right under the influence of a force of 5 N (|10 – 15| = 5).
When the forces are directed oppositely, but are equal in numerical value, then their resultant will be equal to zero. This means that the resultant force has no effect on the body. If the body was at rest, it will remain there. If the body moved straight and evenly, it will continue to move. Thus, although two new forces acted on the body, they “mutually annihilated.”
Let's say three forces act on a body, two of which are directed in one direction, and the third in the other. In this case, you first need to find the resultant of two forces directed in one direction by adding them. Then compare it with the third force to determine in which direction the resultant of the three forces will be directed. And find the modulus of the difference between the sum of the first two and the third: |F 1 + F 2 – F 3 |.
Often, not one, but several forces act on the body at the same time. Let's consider the case when the body is affected by two forces ( and ). For example, a body resting on a horizontal surface is affected by the force of gravity () and the reaction of the surface support () (Fig. 1).

These two forces can be replaced by one, which is called the resultant force (). Find it as a vector sum of forces and:
Determination of the resultant of two forces
DEFINITION
Resultant of two forces called a force that produces an effect on a body similar to the action of two separate forces.
Note that the action of each force does not depend on whether there are other forces or not.
Newton's second law for the resultant of two forces
If two forces act on a body, then we write Newton’s second law as:
The direction of the resultant always coincides in direction with the direction of acceleration of the body.
This means that if a body is affected by two forces () at the same moment in time, then the acceleration () of this body will be directly proportional to the vector sum of these forces (or proportional to the resultant forces):
![]()
M is the mass of the body in question. The essence of Newton's second law is that the forces acting on a body determine how the body's speed changes, and not just the magnitude of the body's speed. Note that Newton's second law is satisfied exclusively in inertial frames of reference.
The resultant of two forces can be equal to zero if the forces acting on the body are directed in different directions and are equal in magnitude.
Finding the magnitude of the resultant of two forces
To find the resultant, you should depict in the drawing all the forces that must be taken into account in the problem acting on the body. Forces should be added according to the rules of vector addition.
Let us assume that the body is acted upon by two forces that are directed along the same straight line (Fig. 1). It can be seen from the figure that they are directed in different directions.
The resultant forces () applied to the body will be equal to:
To find the modulus of the resultant forces, we select an axis, denote it X, and direct it along the direction of action of the forces. Then, projecting expression (4) onto the X axis, we obtain that the magnitude (modulus) of the resultant (F) is equal to:
where are the modules of the corresponding forces.
Let's imagine that two forces and are acting on the body, directed at a certain angle to each other (Fig. 2). We find the resultant of these forces using the parallelogram rule. The magnitude of the resultant will be equal to the length of the diagonal of this parallelogram.

Examples of problem solving
EXAMPLE 1
| Exercise | A body with a mass of 2 kg is moved vertically upward by a thread, while its acceleration is equal to 1. What is the magnitude and direction of the resultant force? What forces are applied to the body? |
| Solution | The force of gravity () and the reaction force of the thread () are applied to the body (Fig. 3). The resultant of the above forces can be found using Newton's second law: In projection onto the X axis, equation (1.1) takes the form: Let's calculate the magnitude of the resultant force: |
| Answer | N, the resultant force is directed in the same way as the acceleration of the body, that is, vertically upward. There are two forces acting on the body and . |
Force acts as a quantitative measure of the interaction of bodies. This is an important physical quantity, since in an inertial frame of reference any change in the speed of a body can only occur when interacting with other bodies. In other words, when a force acts on a body.
The interactions of bodies can be of different natures, for example, there are electrical, magnetic, gravitational and other interactions. But when studying the mechanical motion of a body, the nature of the forces causing acceleration in the body does not matter. Mechanics does not deal with the problem of the origin of interaction. For any interaction, force becomes a numerical measure. Forces of different natures are measured in the same units (in the International System of Units in newtons), and the same standards are used. In view of this universality, mechanics deals with the study and description of the movement of bodies that are influenced by forces of any nature.
The result of the action of a force on a body is the acceleration of the body (a change in the speed of its movement) and/or its deformation.
Addition of forces
Force is a vector quantity. In addition to the module, it has a direction and point of application. Regardless of their nature, all forces add up as vectors.
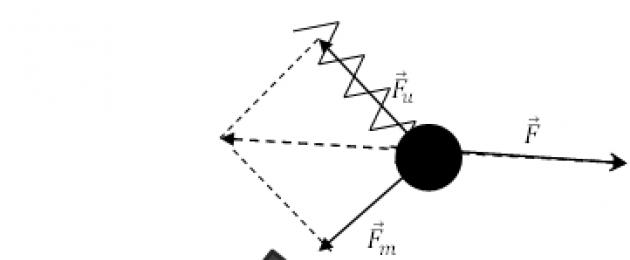
Let a metal ball be held by an elastic spring and be attracted by a magnet (Fig. 1). Then two forces act on it: the elastic force from the spring ($(\overline(F))_u$) and the magnetic force ($(\overline(F))_m$) from the magnet. We assume that their values are known. Under the combined action of these forces, the ball will be at rest if it is acted upon by a third force ($\overline(F)$), which satisfies the equality:
\[\overline(F)=-\left((\overline(F))_u+(\overline(F))_m\right)\left(1\right).\]
This experience makes it possible to conclude that several forces acting on one body can be replaced by one resultant, and the nature of the forces is not important. The resultant is obtained as a result of the vector summation of the forces acting on the body.
Definition and formula of resultant force
And so, the vector sum of all forces acting on a body at the same moment in time is called the resultant force ($\overline(F)$):
\[\overline(F)=(\overline(F))_1+(\overline(F))_2+\dots +(\overline(F))_N=\sum\limits^N_(i=1)((\ overline(F))_i)\ \left(2\right).\]
Sometimes the resultant force is denoted $\overline(R)$ for emphasis, but this is not necessary.
The summation of forces can be done graphically. In this case, the rules of polygon, parallelogram and triangle are used. If, with this addition of forces, the polygon turns out to be closed, then the resultant is equal to zero. When the resultant is equal to zero, the system is called balanced.
Writing Newton's second law using resultant force
Newton's second law is the fundamental law in classical dynamics. It connects the forces that affect the body and its acceleration and allows you to solve the main problem of dynamics. If a body is under the influence of several forces, then I write Newton’s second law as follows:
\[\overline(R)=\sum\limits^N_(i=1)((\overline(F))_i)=m\overline(a)\left(3\right).\]
Formula (3) means that the resultant of all forces applied to the body can be equal to zero if mutual compensation of forces occurs. Then the body moves at a constant speed or is at rest in an inertial frame of reference. We can say the opposite: if a body moves uniformly and rectilinearly in an inertial frame of reference, then no forces act on it or their resultant is zero.
When solving problems and indicating on diagrams the forces acting on a body when the body moves with constant acceleration, the resultant force is directed along the acceleration and is depicted as longer than the oppositely directed force (sum of forces). With uniform motion (or if the body is at rest), the length of force vectors having opposite directions is the same (the resultant is zero).
By examining the conditions of the problem, it is necessary to determine which forces act on the body and will be taken into account in the resultant, which forces do not have a significant effect on the movement of the body and can be discarded. Significant forces are depicted in the figure. The forces are added according to the rules of vector addition.
Examples of problems with solutions
Example 1
Exercise. At what angle should the forces in Fig. be located? 2, so that their resultant is equal in magnitude to each of its constituent forces?

Solution. To solve the problem, we use the cosine theorem:
Since according to the conditions of the problem:
then we transform expression (1.1) to the form: $\ $
The solution to the resulting trigonometric equation is the angles:
\[\alpha =\frac(2\pi )(3)+\pi n\ ;;\ \alpha =\frac(4\pi )(3)+\pi n\ \left(where\ n is an integer\ number\right).\ \]
Based on the figure (Fig. 2), the answer is $\alpha =\frac(2\pi )(3)$.
Answer.$\alpha =\frac(2\pi )(3)$
Example 2
Exercise. What is the resultant force if the forces presented in Fig. 3 act on the body?

Solution. We find the resultant force by vector summation using the polygon rule. Sequentially, each subsequent force vector is set aside from the end of the previous one. As a result, the vector of the resultant of all forces will have its beginning at the point from which the first vector comes out (we have the vector $(\overline(F))_1$), its end will arrive at the point where the last vector ends ($(\overline(F) ))_4$). As a result, we obtain Fig. 4.

As a result of the construction, a closed polygon is obtained, which means that the resultant of the forces applied to the body is equal to zero.
Answer.$\overline(R)=0$
- In contact with 0
- Google+ 0
- OK 0
- Facebook 0