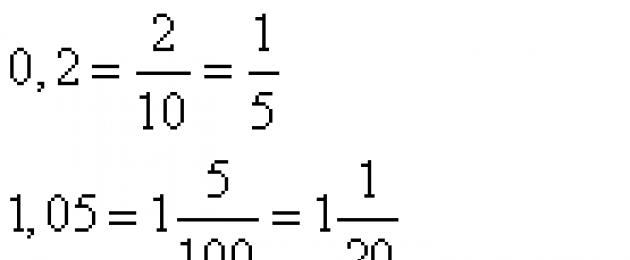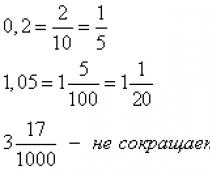In dry mathematical language, a fraction is a number that is represented as a part of one. Fractions are widely used in human life: we use fractions to indicate proportions in culinary recipes, give decimal scores in competitions, or use them to calculate discounts in stores.
Representation of fractions
There are at least two forms of writing one fractional number: in decimal form or in the form of an ordinary fraction. In decimal form, the numbers look like 0.5; 0.25 or 1.375. We can represent any of these values as an ordinary fraction:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
And if we easily convert 0.5 and 0.25 from an ordinary fraction to a decimal and back, then in the case of the number 1.375 everything is not obvious. How to quickly convert any decimal number to a fraction? There are three simple ways.
Getting rid of the comma
The simplest algorithm involves multiplying a number by 10 until the comma disappears from the numerator. This transformation is carried out in three steps:
Step 1: To begin with, we write the decimal number as a fraction “number/1”, that is, we get 0.5/1; 0.25/1 and 1.375/1.
Step 2: After this, multiply the numerator and denominator of the new fractions until the comma disappears from the numerators:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Step 3: We reduce the resulting fractions to a digestible form:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.
The number 1.375 had to be multiplied by 10 three times, which is no longer very convenient, but what do we have to do if we need to convert the number 0.000625? In this situation, we use the following method of converting fractions.
Getting rid of commas even easier
The first method describes in detail the algorithm for “removing” a comma from a decimal, but we can simplify this process. Again, we follow three steps.
Step 1: We count how many digits are after the decimal point. For example, the number 1.375 has three such digits, and 0.000625 has six. We will denote this quantity by the letter n.
Step 2: Now we just need to represent the fraction in the form C/10 n, where C are the significant digits of the fraction (without zeros, if any), and n is the number of digits after the decimal point. For example:
- for the number 1.375 C = 1375, n = 3, the final fraction according to the formula 1375/10 3 = 1375/1000;
- for the number 0.000625 C = 625, n = 6, the final fraction according to the formula 625/10 6 = 625/1000000.
Essentially, 10n is a 1 with n zeros, so you don't have to bother raising the ten to the power - just 1 with n zeros. After this, it is advisable to reduce a fraction so rich in zeros.
Step 3: We reduce the zeros and get the final result:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
The fraction 11/8 is an improper fraction because its numerator is greater than its denominator, which means we can isolate the whole part. In this situation, we subtract the whole part of 8/8 from 11/8 and get the remainder 3/8, therefore the fraction looks like 1 and 3/8.
Conversion by ear
For those who can read decimals correctly, the easiest way to convert them is by hearing. If you read 0.025 not as “zero, zero, twenty-five” but as “25 thousandths,” then you will have no problem converting decimals to fractions.
0,025 = 25/1000 = 1/40
Thus, reading a decimal number correctly allows you to immediately write it down as a fraction and reduce it if necessary.
Examples of using fractions in everyday life
At first glance, ordinary fractions are practically not used in everyday life or at work, and it is difficult to imagine a situation when you need to convert a decimal fraction into a regular fraction outside of school tasks. Let's look at a couple of examples.
Job
So, you work in a candy store and sell halva by weight. To make the product easier to sell, you divide the halva into kilogram briquettes, but few buyers are willing to purchase a whole kilogram. Therefore, you have to divide the treat into pieces each time. And if the next buyer asks you for 0.4 kg of halva, you will sell him the required portion without any problems.
0,4 = 4/10 = 2/5
Life
For example, you need to make a 12% solution to paint the model in the shade you want. To do this, you need to mix paint and solvent, but how to do it correctly? 12% is a decimal fraction of 0.12. Convert the number to a common fraction and get:
0,12 = 12/100 = 3/25
Knowing the fractions will help you mix the ingredients correctly and get the color you want.
Conclusion
Fractions are commonly used in everyday life, so if you frequently need to convert decimals to fractions, you'll want to use an online calculator that can instantly get your result as a reduced fraction.
Decimal numbers such as 0.2; 1.05; 3.017, etc. as they are heard, so they are written. Zero point two, we get a fraction. One point five hundredths, we get a fraction. Three point seventeen thousandths, we get the fraction. The numbers before the decimal point are the whole part of the fraction. The number after the decimal point is the numerator of the future fraction. If there is a single-digit number after the decimal point, the denominator will be 10, if there is a two-digit number - 100, a three-digit number - 1000, etc. Some resulting fractions can be reduced. In our examples 
Converting a fraction to a decimal
This is the reverse of the previous transformation. What is the characteristic of a decimal fraction? Its denominator is always 10, or 100, or 1000, or 10000, and so on. If your common fraction has a denominator like this, there's no problem. For example, or
If the fraction is, for example . In this case, it is necessary to use the basic property of a fraction and convert the denominator to 10 or 100, or 1000... In our example, if we multiply the numerator and denominator by 4, we get a fraction that can be written as a decimal number 0.12.
Some fractions are easier to divide than to convert the denominator. For example,
Some fractions cannot be converted to decimals!
For example,
Converting a mixed fraction to an improper fraction
A mixed fraction, for example, can be easily converted to an improper fraction. To do this, you need to multiply the whole part by the denominator (bottom) and add it with the numerator (top), leaving the denominator (bottom) unchanged. That is

When converting a mixed fraction to an improper fraction, you can remember that you can use fraction addition
Converting an improper fraction to a mixed fraction (highlighting the whole part)
An improper fraction can be converted to a mixed fraction by highlighting the whole part. Let's look at an example. We determine how many integer times “3” fits into “23”. Or divide 23 by 3 on a calculator, the whole number to the decimal point is the desired one. This is "7". Next, we determine the numerator of the future fraction: we multiply the resulting “7” by the denominator “3” and subtract the result from the numerator “23”. ![]() It’s as if we find the extra that remains from the numerator “23” if we remove the maximum amount of “3”. We leave the denominator unchanged. Everything is done, write down the result
It’s as if we find the extra that remains from the numerator “23” if we remove the maximum amount of “3”. We leave the denominator unchanged. Everything is done, write down the result
Enter fraction:
Let's consider the problem of converting a decimal fraction into an ordinary fraction with the required accuracy. For example,
0,3333333 = 1/3
It is assumed that the decimal fraction entered does not have an integer part.
To solve the problem, we will use two variables, representing the numerator and denominator of the fraction.
Finding a solution will consist of two stages:
- Search for an approximate solution
- Refining the solution until the required accuracy is obtained
At the first stage, we take the initial values of the numerator and denominator equal to 1. At each step, we increase the value of the denominator by 1 and find the fraction
Numerator/Denominator
At the first iteration, the denominator is 1, and 1/1=1, and this value is greater than the entered decimal fraction. We increase the denominator by 1 until we get
Numerator/Denominator - EnteredFraction< 0
Thus, we have found the first approximation. We know that the entered fraction corresponds to an ordinary fraction between
Numerator / (Denominator - 1) And Numerator/Denominator
At the second stage, we multiply the numerator and denominator of the obtained first approximation by a factor that will take sequential values 2, 3, 4, etc.
Again, increasing the denominator by 1, we obtain the following approximation, and if it suits us in terms of accuracy, then we will assume that the required ordinary fraction has been found.
Implementation in C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include
using namespace std;
void func( do uble num, do uble eps, int &ch, int &zn)
{
int a = 1; int b = 1;
int mn = 2; // multiplier for initial approximation
int iter = 0;
ch = a; zn = b;
// Search for initial approximation
do uble c = 1;
do (
b++;
c = ( do uble)a/b;
) while ((num - c)< 0);
if ((num - c)< eps)
{
ch = a; zn = b;
return ;
}
b—;
c = ( do uble)a/b;
if ((num - c) > -eps)
{
ch = a; zn = b;
return ;
}
// Clarification
while (iter< 20000)
{
int cc = a*mn, zz = b*mn;
iter++;
do (
zz++;
c = ( do uble)cc/zz;
) while ((num - c)< 0);
if ((num - c)< eps)
{
ch = cc; zn = zz;
return ;
}
zz—;
c = ( do uble)cc/zz;
if ((num - c) > -eps)
{
ch = cc; zn = zz;
return ;
}
mn++;
}
}
int main()
{
do uble inp;
int ch, zn;
do uble eps = 0.0000001;
cout<<
"num="
;
cin >> inp;
func(inp, eps, ch, zn);
cout<<
ch <<
" / "
<<
zn <<
endl;
cin.get(); cin.get();
return 1;
}
Execution result


If we need to divide 497 by 4, then when dividing we will see that 497 is not evenly divisible by 4, i.e. the remainder of the division remains. In such cases it is said that it is completed division with remainder, and the solution is written as follows:
497: 4 = 124 (1 remainder).
The division components on the left side of the equality are called the same as in division without a remainder: 497 - dividend, 4 - divider. The result of division when divided with a remainder is called incomplete private. In our case, this is the number 124. And finally, the last component, which is not in ordinary division, is remainder. In cases where there is no remainder, one number is said to be divided by another without a trace, or completely. It is believed that with such a division the remainder is zero. In our case, the remainder is 1.
The remainder is always less than the divisor.
Division can be checked by multiplication. If, for example, there is an equality 64: 32 = 2, then the check can be done like this: 64 = 32 * 2.
Often in cases where division with a remainder is performed, it is convenient to use the equality
a = b * n + r,
where a is the dividend, b is the divisor, n is the incomplete quotient, r is the remainder.
The quotient of natural numbers can be written as a fraction.
The numerator of a fraction is the dividend, and the denominator is the divisor.
Since the numerator of a fraction is the dividend, and the denominator is the divisor, believe that the line of a fraction means the action of division. Sometimes it is convenient to write division as a fraction without using the ":" sign.
The quotient of the division of natural numbers m and n can be written as a fraction \(\frac(m)(n) \), where the numerator m is the dividend, and the denominator n is the divisor:
\(m:n = \frac(m)(n) \)
The following rules are true:
To get the fraction \(\frac(m)(n)\), you need to divide the unit into n equal parts (shares) and take m such parts.
To get the fraction \(\frac(m)(n)\), you need to divide the number m by the number n.
To find a part of a whole, you need to divide the number corresponding to the whole by the denominator and multiply the result by the numerator of the fraction that expresses this part.
To find a whole from its part, you need to divide the number corresponding to this part by the numerator and multiply the result by the denominator of the fraction that expresses this part.
If both the numerator and denominator of a fraction are multiplied by the same number (except zero), the value of the fraction will not change:
\(\large \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)
If both the numerator and denominator of a fraction are divided by the same number (except zero), the value of the fraction will not change:
\(\large \frac(a)(b) = \frac(a: m)(b: m) \)
This property is called main property of a fraction.
The last two transformations are called reducing a fraction.
If fractions need to be represented as fractions with the same denominator, then this action is called reducing fractions to a common denominator.
Proper and improper fractions. Mixed numbers
You already know that a fraction can be obtained by dividing a whole into equal parts and taking several such parts. For example, the fraction \(\frac(3)(4)\) means three-quarters of one. In many of the problems in the previous paragraph, fractions were used to represent parts of a whole. Common sense dictates that the part should always be less than the whole, but what about fractions such as \(\frac(5)(5)\) or \(\frac(8)(5)\)? It is clear that this is no longer part of the unit. This is probably why fractions whose numerator is greater than or equal to the denominator are called improper fractions. The remaining fractions, i.e. fractions whose numerator is less than the denominator, are called correct fractions.
As you know, any common fraction, both proper and improper, can be thought of as the result of dividing the numerator by the denominator. Therefore, in mathematics, unlike ordinary language, the term “improper fraction” does not mean that we did something wrong, but only that the numerator of this fraction is greater than or equal to the denominator.
If a number consists of an integer part and a fraction, then fractions are called mixed.
For example:
\(5:3 = 1\frac(2)(3) \) : 1 is the integer part, and \(\frac(2)(3) \) is the fractional part.
If the numerator of the fraction \(\frac(a)(b) \) is divisible by a natural number n, then in order to divide this fraction by n, its numerator must be divided by this number:
\(\large \frac(a)(b) : n = \frac(a:n)(b) \)
If the numerator of the fraction \(\frac(a)(b) \) is not divisible by a natural number n, then to divide this fraction by n, you need to multiply its denominator by this number:
\(\large \frac(a)(b) : n = \frac(a)(bn) \)
Note that the second rule is also true when the numerator is divisible by n. Therefore, we can use it when it is difficult to determine at first glance whether the numerator of a fraction is divisible by n or not.
Actions with fractions. Adding fractions.
You can perform arithmetic operations with fractional numbers, just like with natural numbers. Let's look at adding fractions first. It's easy to add fractions with like denominators. Let us find, for example, the sum of \(\frac(2)(7)\) and \(\frac(3)(7)\). It is easy to understand that \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \)
To add fractions with the same denominators, you need to add their numerators and leave the denominator the same.
Using letters, the rule for adding fractions with like denominators can be written as follows:
\(\large \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)
If you need to add fractions with different denominators, they must first be reduced to a common denominator. For example:
\(\large \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3 ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)
For fractions, as for natural numbers, the commutative and associative properties of addition are valid.
Adding mixed fractions
Notations such as \(2\frac(2)(3)\) are called mixed fractions. In this case, the number 2 is called whole part mixed fraction, and the number \(\frac(2)(3)\) is its fractional part. The entry \(2\frac(2)(3)\) is read as follows: “two and two thirds.”
When dividing the number 8 by the number 3, you can get two answers: \(\frac(8)(3)\) and \(2\frac(2)(3)\). They express the same fractional number, i.e. \(\frac(8)(3) = 2 \frac(2)(3)\)
Thus, the improper fraction \(\frac(8)(3)\) is represented as a mixed fraction \(2\frac(2)(3)\). In such cases they say that from an improper fraction highlighted the whole part.
Subtracting fractions (fractional numbers)
Subtraction of fractional numbers, like natural numbers, is determined on the basis of the action of addition: subtracting another from one number means finding a number that, when added to the second, gives the first. For example:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) since \(\frac(7)(9)+\frac(1)(9 ) = \frac(8)(9)\)
The rule for subtracting fractions with like denominators is similar to the rule for adding such fractions:
To find the difference between fractions with the same denominators, you need to subtract the numerator of the second from the numerator of the first fraction, and leave the denominator the same.
Using letters, this rule is written like this:
\(\large \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)
Multiplying fractions
To multiply a fraction by a fraction, you need to multiply their numerators and denominators and write the first product as the numerator, and the second as the denominator.
Using letters, the rule for multiplying fractions can be written as follows:
\(\large \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)
Using the formulated rule, you can multiply a fraction by a natural number, by a mixed fraction, and also multiply mixed fractions. To do this, you need to write a natural number as a fraction with a denominator of 1, and a mixed fraction as an improper fraction.
The result of multiplication should be simplified (if possible) by reducing the fraction and isolating the whole part of the improper fraction.
For fractions, as for natural numbers, the commutative and combinative properties of multiplication, as well as the distributive property of multiplication relative to addition, are valid.
Division of fractions
Let's take the fraction \(\frac(2)(3)\) and “flip” it, swapping the numerator and denominator. We get the fraction \(\frac(3)(2)\). This fraction is called reverse fractions \(\frac(2)(3)\).
If we now “reverse” the fraction \(\frac(3)(2)\), we will get the original fraction \(\frac(2)(3)\). Therefore, fractions such as \(\frac(2)(3)\) and \(\frac(3)(2)\) are called mutually inverse.
For example, the fractions \(\frac(6)(5) \) and \(\frac(5)(6) \), \(\frac(7)(18) \) and \(\frac (18)(7)\).
Using letters, reciprocal fractions can be written as follows: \(\frac(a)(b) \) and \(\frac(b)(a) \)
It is clear that the product of reciprocal fractions is equal to 1. For example: \(\frac(2)(3) \cdot \frac(3)(2) =1 \)
Using reciprocal fractions, you can reduce division of fractions to multiplication.
The rule for dividing a fraction by a fraction is:
To divide one fraction by another, you need to multiply the dividend by the reciprocal of the divisor.
Using letters, the rule for dividing fractions can be written as follows:
\(\large \frac(a)(b) : \frac(c)(d) = \frac(a)(b) \cdot \frac(d)(c) \)
If the dividend or divisor is a natural number or a mixed fraction, then in order to use the rule for dividing fractions, it must first be represented as an improper fraction.
In this article we will look at how converting fractions to decimals, and also consider the reverse process - converting decimal fractions into ordinary fractions. Here we will outline the rules for converting fractions and provide detailed solutions to typical examples.
Page navigation.
Converting fractions to decimals
Let us denote the sequence in which we will deal with converting fractions to decimals.
First, we'll look at how to represent fractions with denominators 10, 100, 1,000, ... as decimals. This is explained by the fact that decimal fractions are essentially a compact form of writing ordinary fractions with denominators 10, 100, ....
After that, we will go further and show how to write any ordinary fraction (not just those with denominators 10, 100, ...) as a decimal fraction. When ordinary fractions are treated in this way, both finite decimal fractions and infinite periodic decimal fractions are obtained.
Now let's talk about everything in order.
Converting common fractions with denominators 10, 100, ... to decimals
Some proper fractions require "preliminary preparation" before being converted to decimals. This applies to ordinary fractions, the number of digits in the numerator of which is less than the number of zeros in the denominator. For example, the common fraction 2/100 must first be prepared for conversion to a decimal fraction, but the fraction 9/10 does not need any preparation.
“Preliminary preparation” of proper ordinary fractions for conversion to decimal fractions consists of adding so many zeros to the left in the numerator that the total number of digits there becomes equal to the number of zeros in the denominator. For example, a fraction after adding zeros will look like .
Once you have a proper fraction prepared, you can begin converting it to a decimal.
Let's give rule for converting a proper common fraction with a denominator of 10, or 100, or 1,000, ... into a decimal fraction. It consists of three steps:
- write 0;
- after it we put a decimal point;
- We write down the number from the numerator (along with added zeros, if we added them).
Let's consider the application of this rule when solving examples.
Example.
Convert the proper fraction 37/100 to a decimal.
Solution.
The denominator contains the number 100, which has two zeros. The numerator contains the number 37, its notation has two digits, therefore, this fraction does not need to be prepared for conversion to a decimal fraction.
Now we write 0, put a decimal point, and write the number 37 from the numerator, and we get the decimal fraction 0.37.
Answer:
0,37 .
To strengthen the skills of converting proper ordinary fractions with numerators 10, 100, ... into decimal fractions, we will analyze the solution to another example.
Example.
Write the proper fraction 107/10,000,000 as a decimal.
Solution.
The number of digits in the numerator is 3, and the number of zeros in the denominator is 7, so this common fraction needs to be prepared for conversion to a decimal. We need to add 7-3=4 zeros to the left in the numerator so that the total number of digits there becomes equal to the number of zeros in the denominator. We get.
All that remains is to create the required decimal fraction. To do this, firstly, we write 0, secondly, we put a comma, thirdly, we write the number from the numerator together with zeros 0000107, as a result we have a decimal fraction 0.0000107.
Answer:
0,0000107 .
Improper fractions do not require any preparation when converting to decimals. The following should be adhered to rules for converting improper fractions with denominators 10, 100, ... into decimals:
- write down the number from the numerator;
- We use a decimal point to separate as many digits on the right as there are zeros in the denominator of the original fraction.
Let's look at the application of this rule when solving an example.
Example.
Convert the improper fraction 56,888,038,009/100,000 to a decimal.
Solution.
Firstly, we write down the number from the numerator 56888038009, and secondly, we separate the 5 digits on the right with a decimal point, since the denominator of the original fraction has 5 zeros. As a result, we have the decimal fraction 568880.38009.
Answer:
568 880,38009 .
To convert a mixed number into a decimal fraction, the denominator of the fractional part of which is the number 10, or 100, or 1,000, ..., you can convert the mixed number into an improper ordinary fraction, and then convert the resulting fraction into a decimal fraction. But you can also use the following the rule for converting mixed numbers with a fractional denominator of 10, or 100, or 1,000, ... into decimal fractions:
- if necessary, we perform “preliminary preparation” of the fractional part of the original mixed number by adding the required number of zeros to the left in the numerator;
- write down the integer part of the original mixed number;
- put a decimal point;
- We write down the number from the numerator along with the added zeros.
Let's look at an example in which we complete all the necessary steps to represent a mixed number as a decimal fraction.
Example.
Convert the mixed number to a decimal.
Solution.
The denominator of the fractional part has 4 zeros, but the numerator contains the number 17, consisting of 2 digits, therefore, we need to add two zeros to the left in the numerator so that the number of digits there becomes equal to the number of zeros in the denominator. Having done this, the numerator will be 0017.
Now we write down the whole part of the original number, that is, the number 23, put a decimal point, after which we write the number from the numerator along with the added zeros, that is, 0017, and we get the desired decimal fraction 23.0017.
Let's write down the whole solution briefly: ![]() .
.
Of course, it was possible to first represent the mixed number as an improper fraction and then convert it to a decimal. With this approach, the solution looks like this: .
Answer:
23,0017 .
Converting fractions to finite and infinite periodic decimals
Not only ordinary fractions with denominators 10, 100, ... can be converted into decimal fractions, but ordinary fractions with other denominators. Now we will figure out how this is done.
In some cases, the original ordinary fraction is easily reduced to one of the denominators 10, or 100, or 1,000, ... (see bringing an ordinary fraction to a new denominator), after which it is not difficult to represent the resulting fraction as a decimal fraction. For example, it is obvious that the fraction 2/5 can be reduced to a fraction with a denominator 10, for this you need to multiply the numerator and denominator by 2, which will give the fraction 4/10, which, according to the rules discussed in the previous paragraph, is easily converted to the decimal fraction 0, 4.
In other cases, you have to use another method of converting an ordinary fraction into a decimal, which we now proceed to consider.
To convert an ordinary fraction to a decimal fraction, the numerator of the fraction is divided by the denominator, the numerator is first replaced by an equal decimal fraction with any number of zeros after the decimal point (we talked about this in the section equal and unequal decimal fractions). In this case, division is performed in the same way as division by a column of natural numbers, and in the quotient a decimal point is placed when the division of the whole part of the dividend ends. All this will become clear from the solutions to the examples given below.
Example.
Convert the fraction 621/4 to a decimal.
Solution.
Let's represent the number in the numerator 621 as a decimal fraction, adding a decimal point and several zeros after it. First, let's add 2 digits 0, later, if necessary, we can always add more zeros. So, we have 621.00.
Now let's divide the number 621,000 by 4 with a column. The first three steps are no different from dividing natural numbers by a column, after which we arrive at the following picture: 
This is how we get to the decimal point in the dividend, and the remainder is different from zero. In this case, we put a decimal point in the quotient and continue dividing in a column, not paying attention to the commas: 
This completes the division, and as a result we get the decimal fraction 155.25, which corresponds to the original ordinary fraction.
Answer:
155,25 .
To consolidate the material, consider the solution to another example.
Example.
Convert the fraction 21/800 to a decimal.
Solution.
To convert this common fraction to a decimal, we divide with a column of the decimal fraction 21,000... by 800. After the first step, we will have to put a decimal point in the quotient, and then continue the division: 
Finally, we got the remainder 0, this completes the conversion of the common fraction 21/400 to a decimal fraction, and we arrived at the decimal fraction 0.02625.
Answer:
0,02625 .
It may happen that when dividing the numerator by the denominator of an ordinary fraction, we still do not get a remainder of 0. In these cases, division can be continued indefinitely. However, starting from a certain step, the remainders begin to repeat periodically, and the numbers in the quotient also repeat. This means that the original fraction is converted to an infinitely periodic decimal fraction. Let's show this with an example.
Example.
Write the fraction 19/44 as a decimal.
Solution.
To convert an ordinary fraction to a decimal, perform division by column: 
It is already clear that during division the residues 8 and 36 began to be repeated, while in the quotient the numbers 1 and 8 are repeated. Thus, the original common fraction 19/44 is converted into a periodic decimal fraction 0.43181818...=0.43(18).
Answer:
0,43(18) .
To conclude this point, we will figure out which ordinary fractions can be converted into finite decimal fractions, and which ones can only be converted into periodic ones.
Let us have an irreducible ordinary fraction in front of us (if the fraction is reducible, then we first reduce the fraction), and we need to find out which decimal fraction it can be converted into - finite or periodic.
It is clear that if an ordinary fraction can be reduced to one of the denominators 10, 100, 1,000, ..., then the resulting fraction can be easily converted into a final decimal fraction according to the rules discussed in the previous paragraph. But to the denominators 10, 100, 1,000, etc. Not all ordinary fractions are given. Only fractions whose denominators are at least one of the numbers 10, 100, ... can be reduced to such denominators. And what numbers can be divisors of 10, 100, ...? The numbers 10, 100, ... will allow us to answer this question, and they are as follows: 10 = 2 5, 100 = 2 2 5 5, 1,000 = 2 2 2 5 5 5, .... It follows that the divisors are 10, 100, 1,000, etc. There can only be numbers whose decompositions into prime factors contain only the numbers 2 and (or) 5.
Now we can make a general conclusion about converting ordinary fractions to decimals:
- if in the decomposition of the denominator into prime factors there are only numbers 2 and (or) 5, then this fraction can be converted into a final decimal fraction;
- if, in addition to twos and fives, there are other prime numbers in the expansion of the denominator, then this fraction is converted to an infinite decimal periodic fraction.
Example.
Without converting ordinary fractions to decimals, tell me which of the fractions 47/20, 7/12, 21/56, 31/17 can be converted into a final decimal fraction, and which ones can only be converted into a periodic fraction.
Solution.
The denominator of the fraction 47/20 is factorized into prime factors as 20=2·2·5. This expansion contains only twos and fives, so this fraction can be reduced to one of the denominators 10, 100, 1,000, ... (in this example, to the denominator 100), therefore, can be converted to a final decimal fraction.
The decomposition of the denominator of the fraction 7/12 into prime factors has the form 12=2·2·3. Since it contains a prime factor of 3, different from 2 and 5, this fraction cannot be represented as a finite decimal, but can be converted into a periodic decimal.
Fraction 21/56 – contractile, after contraction it takes the form 3/8. Factoring the denominator into prime factors contains three factors equal to 2, therefore, the common fraction 3/8, and therefore the equal fraction 21/56, can be converted into a final decimal fraction.
Finally, the expansion of the denominator of the fraction 31/17 is 17 itself, therefore this fraction cannot be converted into a finite decimal fraction, but can be converted into an infinite periodic fraction.
Answer:
47/20 and 21/56 can be converted to a finite decimal fraction, but 7/12 and 31/17 can only be converted to a periodic fraction.
Ordinary fractions do not convert to infinite non-periodic decimals
The information in the previous paragraph gives rise to the question: “Can dividing the numerator of a fraction by the denominator result in an infinite non-periodic fraction?”
Answer: no. When converting a common fraction, the result can be either a finite decimal fraction or an infinite periodic decimal fraction. Let us explain why this is so.
From the theorem on divisibility with a remainder, it is clear that the remainder is always less than the divisor, that is, if we divide some integer by an integer q, then the remainder can only be one of the numbers 0, 1, 2, ..., q−1. It follows that after the column has completed dividing the integer part of the numerator of a common fraction by the denominator q, in no more than q steps one of the following two situations will arise:
- or we will get a remainder of 0, this will end the division, and we will get the final decimal fraction;
- or we will get a remainder that has already appeared before, after which the remainders will begin to repeat as in the previous example (since when dividing equal numbers by q, equal remainders are obtained, which follows from the already mentioned divisibility theorem), this will result in an infinite periodic decimal fraction.
There cannot be any other options, therefore, when converting an ordinary fraction to a decimal fraction, an infinite non-periodic decimal fraction cannot be obtained.
From the reasoning given in this paragraph it also follows that the length of the period of a decimal fraction is always less than the value of the denominator of the corresponding ordinary fraction.
Converting decimals to fractions
Now let's figure out how to convert a decimal fraction into an ordinary fraction. Let's start by converting final decimal fractions to ordinary fractions. After this, we will consider a method for inverting infinite periodic decimal fractions. In conclusion, let's say about the impossibility of converting infinite non-periodic decimal fractions into ordinary fractions.
Converting trailing decimals to fractions
Obtaining a fraction that is written as a final decimal is quite simple. The rule for converting a final decimal fraction to a common fraction consists of three steps:
- firstly, write the given decimal fraction into the numerator, having previously discarded the decimal point and all zeros on the left, if any;
- secondly, write one into the denominator and add as many zeros to it as there are digits after the decimal point in the original decimal fraction;
- thirdly, if necessary, reduce the resulting fraction.
Let's look at the solutions to the examples.
Example.
Convert the decimal 3.025 to a fraction.
Solution.
If we remove the decimal point from the original decimal fraction, we get the number 3,025. There are no zeros on the left that we would discard. So, we write 3,025 in the numerator of the desired fraction.
We write the number 1 into the denominator and add 3 zeros to the right of it, since in the original decimal fraction there are 3 digits after the decimal point.
So we got the common fraction 3,025/1,000. This fraction can be reduced by 25, we get  .
.
Answer:
 .
.
Example.
Convert the decimal fraction 0.0017 to a fraction.
Solution.
Without a decimal point, the original decimal fraction looks like 00017, discarding the zeros on the left we get the number 17, which is the numerator of the desired ordinary fraction.
We write one with four zeros in the denominator, since the original decimal fraction has 4 digits after the decimal point.
As a result, we have an ordinary fraction 17/10,000. This fraction is irreducible, and the conversion of a decimal fraction to an ordinary fraction is complete.
Answer:
 .
.
When the integer part of the original final decimal fraction is non-zero, it can be immediately converted to a mixed number, bypassing the common fraction. Let's give rule for converting a final decimal fraction to a mixed number:
- the number before the decimal point must be written as an integer part of the desired mixed number;
- in the numerator of the fractional part you need to write the number obtained from the fractional part of the original decimal fraction after discarding all the zeros on the left;
- in the denominator of the fractional part you need to write down the number 1, to which add as many zeros to the right as there are digits after the decimal point in the original decimal fraction;
- if necessary, reduce the fractional part of the resulting mixed number.
Let's look at an example of converting a decimal fraction to a mixed number.
Example.
Express the decimal fraction 152.06005 as a mixed number
- VKontakte 0
- Google+ 0
- OK 0
- Facebook 0