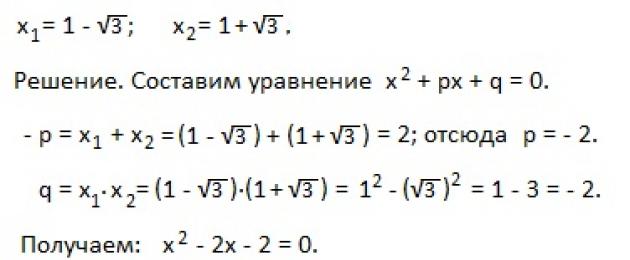I. Vieta's theorem for the given quadratic equation.
Sum of roots of the reduced quadratic equation x 2 +px+q=0 is equal to the second coefficient taken with the opposite sign, and the product of the roots is equal to the free term:
x 1 + x 2 = -p; x 1 ∙x 2 =q.
Find the roots of the given quadratic equation using Vieta's theorem.
Example 1) x 2 -x-30=0. This is the reduced quadratic equation ( x 2 +px+q=0), second coefficient p=-1, and the free member q=-30. First, let's make sure that this equation has roots, and that the roots (if any) will be expressed in integers. To do this, it is enough that the discriminant be a perfect square of an integer.
Finding the discriminant D=b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121= 11 2 .
Now, according to Vieta’s theorem, the sum of the roots must be equal to the second coefficient taken with the opposite sign, i.e. ( -p), and the product is equal to the free term, i.e. ( q). Then:
x 1 +x 2 =1; x 1 ∙x 2 =-30. We need to choose two numbers such that their product is equal to -30 , and the amount is unit. These are numbers -5 And 6 . Answer: -5; 6.
Example 2) x 2 +6x+8=0. We have the reduced quadratic equation with the second coefficient p=6 and free member q=8. Let's make sure that there are integer roots. Let's find the discriminant D 1 D 1=3 2 -1∙8=9-8=1=1 2 . The discriminant D 1 is the perfect square of the number 1 , which means that the roots of this equation are integers. Let us select the roots using Vieta’s theorem: the sum of the roots is equal to –р=-6, and the product of the roots is equal to q=8. These are numbers -4 And -2 .
In fact: -4-2=-6=-р; -4∙(-2)=8=q. Answer: -4; -2.
Example 3) x 2 +2x-4=0. In this reduced quadratic equation, the second coefficient p=2, and the free member q=-4. Let's find the discriminant D 1, since the second coefficient is even number. D 1=1 2 -1∙(-4)=1+4=5. The discriminant is not a perfect square of the number, so we do conclusion: The roots of this equation are not integers and cannot be found using Vieta’s theorem. This means that we solve this equation, as usual, using the formulas (in this case, using the formulas). We get:
Example 4). Write a quadratic equation using its roots if x 1 =-7, x 2 =4.
Solution. The required equation will be written in the form: x 2 +px+q=0, and, based on Vieta’s theorem –p=x 1 +x 2=-7+4=-3 → p=3; q=x 1 ∙x 2=-7∙4=-28 . Then the equation will take the form: x 2 +3x-28=0.
Example 5). Write a quadratic equation using its roots if:

II. Vieta's theorem for a complete quadratic equation ax 2 +bx+c=0.
The sum of the roots is minus b, divided by A, the product of the roots is equal to With, divided by
Between the roots and coefficients of a quadratic equation, in addition to the root formulas, there are other useful relationships that are given Vieta's theorem. In this article we will give a formulation and proof of Vieta's theorem for a quadratic equation. Next we consider the theorem converse to Vieta’s theorem. After this, we will analyze the solutions to the most typical examples. Finally, we write down the Vieta formulas that define the relationship between the real roots algebraic equation degree n and its coefficients.
Page navigation.
Vieta's theorem, formulation, proof
From the formulas of the roots of the quadratic equation a·x 2 +b·x+c=0 of the form, where D=b 2 −4·a·c, the following relations follow: x 1 +x 2 =−b/a, x 1 ·x 2 = c/a . These results are confirmed Vieta's theorem:
Theorem.
If x 1 and x 2 are the roots of the quadratic equation a x 2 +b x+c=0, then the sum of the roots is equal to the ratio of the coefficients b and a, taken with the opposite sign, and the product of the roots is equal to the ratio of the coefficients c and a, that is, .
Proof.
We will carry out the proof of Vieta's theorem according to the following scheme: we compose the sum and product of the roots of the quadratic equation using known root formulas, then we transform the resulting expressions and make sure that they are equal to −b/a and c/a, respectively.
Let's start with the sum of the roots and make it up. Now we bring the fractions to a common denominator, we have . In the numerator of the resulting fraction, after which:. Finally, after on 2, we get . This proves the first relation of Vieta's theorem for the sum of the roots of a quadratic equation. Let's move on to the second.
We compose the product of the roots of the quadratic equation: . According to the rule for multiplying fractions, last piece can be written as . Now we multiply a bracket by a bracket in the numerator, but it’s faster to collapse this product by square difference formula, So . Then, remembering, we perform the next transition. And since the discriminant of the quadratic equation corresponds to the formula D=b 2 −4·a·c, then instead of D in the last fraction we can substitute b 2 −4·a·c, we get. After opening the parentheses and bringing similar terms, we arrive at the fraction , and its reduction by 4·a gives . This proves the second relation of Vieta's theorem for the product of roots.
If we omit the explanations, the proof of Vieta’s theorem will take a laconic form:
,
.
It remains only to note that if the discriminant is equal to zero, the quadratic equation has one root. However, if we assume that the equation in this case has two identical roots, then the equalities from Vieta’s theorem also hold. Indeed, when D=0 the root of the quadratic equation is equal to , then and , and since D=0, that is, b 2 −4·a·c=0, whence b 2 =4·a·c, then .
In practice, Vieta’s theorem is most often used in relation to the reduced quadratic equation (with the leading coefficient a equal to 1) of the form x 2 +p·x+q=0. Sometimes it is formulated for quadratic equations of just this type, which does not limit the generality, since any quadratic equation can be replaced by an equivalent equation by dividing both sides by a non-zero number a. Let us give the corresponding formulation of Vieta’s theorem:
Theorem.
The sum of the roots of the reduced quadratic equation x 2 +p x+q=0 is equal to the coefficient of x taken with the opposite sign, and the product of the roots is equal to the free term, that is, x 1 +x 2 =−p, x 1 x 2 = q.
Theorem converse to Vieta's theorem
The second formulation of Vieta’s theorem, given in the previous paragraph, indicates that if x 1 and x 2 are the roots of the reduced quadratic equation x 2 +p x+q=0, then the relations x 1 +x 2 =−p, x 1 x 2 =q. On the other hand, from the written relations x 1 +x 2 =−p, x 1 x 2 =q it follows that x 1 and x 2 are the roots of the quadratic equation x 2 +p x+q=0. In other words, the converse of Vieta’s theorem is true. Let's formulate it in the form of a theorem and prove it.
Theorem.
If the numbers x 1 and x 2 are such that x 1 +x 2 =−p and x 1 · x 2 =q, then x 1 and x 2 are the roots of the reduced quadratic equation x 2 +p · x+q=0.
Proof.
After replacing the coefficients p and q in the equation x 2 +p·x+q=0 with their expressions through x 1 and x 2, it is transformed into an equivalent equation.
Let us substitute the number x 1 instead of x into the resulting equation, and we have the equality x 1 2 −(x 1 +x 2) x 1 +x 1 x 2 =0, which for any x 1 and x 2 represents the correct numerical equality 0=0, since x 1 2 −(x 1 +x 2) x 1 +x 1 x 2 = x 1 2 −x 1 2 −x 2 ·x 1 +x 1 ·x 2 =0. Therefore, x 1 is the root of the equation x 2 −(x 1 +x 2) x+x 1 x 2 =0, which means x 1 is the root of the equivalent equation x 2 +p·x+q=0.
If in the equation x 2 −(x 1 +x 2) x+x 1 x 2 =0 substitute the number x 2 instead of x, we get the equality x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 =0. This is a true equality, since x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 = x 2 2 −x 1 ·x 2 −x 2 2 +x 1 ·x 2 =0. Therefore, x 2 is also a root of the equation x 2 −(x 1 +x 2) x+x 1 x 2 =0, and therefore the equations x 2 +p·x+q=0.
This completes the proof of the theorem, converse of the theorem Vieta.
Examples of using Vieta's theorem
It's time to talk about the practical application of Vieta's theorem and its converse theorem. In this section we will analyze solutions to several of the most typical examples.
Let's start by applying the theorem converse to Vieta's theorem. It is convenient to use to check whether given two numbers are roots of a given quadratic equation. In this case, their sum and difference are calculated, after which the validity of the relations is checked. If both of these relations are satisfied, then by virtue of the theorem converse to Vieta’s theorem, it is concluded that these numbers are the roots of the equation. If at least one of the relations is not satisfied, then these numbers are not the roots of the quadratic equation. This approach can be used when solving quadratic equations to check the roots found.
Example.
Which of the pairs of numbers 1) x 1 =−5, x 2 =3, or 2) or 3) is a pair of roots of the quadratic equation 4 x 2 −16 x+9=0?
Solution.
The coefficients of the given quadratic equation 4 x 2 −16 x+9=0 are a=4, b=−16, c=9. According to Vieta's theorem, the sum of the roots of a quadratic equation should be equal to −b/a, that is, 16/4=4, and the product of the roots should be equal to c/a, that is, 9/4.
Now let's calculate the sum and product of the numbers in each of the three given pairs, and compare them with the values we just obtained.
In the first case we have x 1 +x 2 =−5+3=−2. The resulting value is different from 4, so no further check can be carried out, but using the theorem inverse to Vieta’s theorem, one can immediately conclude that the first pair of numbers is not a pair of roots of the given quadratic equation.
Let's move on to the second case. Here, that is, the first condition is met. We check the second condition: the resulting value is different from 9/4. Consequently, the second pair of numbers is not a pair of roots of the quadratic equation.
There is one last case left. Here and . Both conditions are met, so these numbers x 1 and x 2 are the roots of the given quadratic equation.
Answer:
The converse of Vieta's theorem can be used in practice to find the roots of a quadratic equation. Usually, integer roots of the given quadratic equations with integer coefficients are selected, since in other cases this is quite difficult to do. In this case, they use the fact that if the sum of two numbers is equal to the second coefficient of a quadratic equation, taken with a minus sign, and the product of these numbers is equal to the free term, then these numbers are the roots of this quadratic equation. Let's understand this with an example.
Let's take the quadratic equation x 2 −5 x+6=0. For the numbers x 1 and x 2 to be the roots of this equation, two equalities must be satisfied: x 1 + x 2 =5 and x 1 ·x 2 =6. All that remains is to select such numbers. In this case, this is quite simple to do: such numbers are 2 and 3, since 2+3=5 and 2·3=6. Thus, 2 and 3 are the roots of this quadratic equation.
The theorem inverse to Vieta's theorem is especially convenient to use to find the second root of a reduced quadratic equation when one of the roots is already known or obvious. In this case, the second root can be found from any of the relations.
For example, let's take the quadratic equation 512 x 2 −509 x −3=0. Here it is easy to see that unity is the root of the equation, since the sum of the coefficients of this quadratic equation is equal to zero. So x 1 =1. The second root x 2 can be found, for example, from the relation x 1 ·x 2 =c/a. We have 1 x 2 =−3/512, from which x 2 =−3/512. This is how we determined both roots of the quadratic equation: 1 and −3/512.
It is clear that the selection of roots is advisable only in the simplest cases. In other cases, to find roots, you can use formulas for the roots of a quadratic equation through a discriminant.
Another practical use The theorem, converse to Vieta's theorem, consists in composing quadratic equations given the roots x 1 and x 2. To do this, it is enough to calculate the sum of the roots, which gives the coefficient of x with the opposite sign of the given quadratic equation, and the product of the roots, which gives the free term.
Example.
Write a quadratic equation whose roots are −11 and 23.
Solution.
Let's denote x 1 =−11 and x 2 =23. We calculate the sum and product of these numbers: x 1 +x 2 =12 and x 1 ·x 2 =−253. Therefore, the indicated numbers are the roots of the reduced quadratic equation with a second coefficient of −12 and a free term of −253. That is, x 2 −12·x−253=0 is the required equation.
Answer:
x 2 −12·x−253=0 .
Vieta's theorem is very often used when solving problems related to the signs of the roots of quadratic equations. How is Vieta’s theorem related to the signs of the roots of the reduced quadratic equation x 2 +p·x+q=0? Here are two relevant statements:
- If the free term q is a positive number and if the quadratic equation has real roots, then either they are both positive or both negative.
- If the free term q is a negative number and if the quadratic equation has real roots, then their signs are different, in other words, one root is positive and the other is negative.
These statements follow from the formula x 1 · x 2 =q, as well as the rules of positive multiplication, negative numbers and numbers with different signs. Let's look at examples of their application.
Example.
R it is positive. Using the discriminant formula we find D=(r+2) 2 −4 1 (r−1)= r 2 +4 r+4−4 r+4=r 2 +8, the value of the expression r 2 +8 is positive for any real r, thus D>0 for any real r. Consequently, the original quadratic equation has two roots for any real values of the parameter r.
Now let's find out when the roots have different signs. If the signs of the roots are different, then their product is negative, and according to Vieta’s theorem, the product of the roots of the reduced quadratic equation is equal to the free term. Therefore, we are interested in those values of r for which the free term r−1 is negative. Thus, to find the values of r we are interested in, we need solve linear inequality r−1<0 , откуда находим r<1 .
Answer:
at r<1 .
Vieta formulas
Above we talked about Vieta’s theorem for a quadratic equation and analyzed the relationships it asserts. But there are formulas that connect the real roots and coefficients of not only quadratic equations, but also cubic equations, equations of the fourth degree, and in general, algebraic equations degree n. They are called Vieta's formulas.
Let us write the Vieta formula for an algebraic equation of degree n of the form, and we will assume that it has n real roots x 1, x 2, ..., x n (among them there may be coinciding ones): 
Vieta's formulas can be obtained theorem on the decomposition of a polynomial into linear factors, as well as the definition of equal polynomials through the equality of all their corresponding coefficients. So the polynomial and its expansion into linear factors of the form are equal. Opening the brackets in the last product and equating the corresponding coefficients, we obtain Vieta’s formulas.
In particular, for n=2 we have the already familiar Vieta formulas for a quadratic equation.
For a cubic equation, Vieta's formulas have the form 
It remains only to note that on the left side of Vieta’s formulas there are the so-called elementary symmetric polynomials.
Bibliography.
- Algebra: textbook for 8th grade. general education institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edited by S. A. Telyakovsky. - 16th ed. - M.: Education, 2008. - 271 p. : ill. - ISBN 978-5-09-019243-9.
- Mordkovich A. G. Algebra. 8th grade. In 2 hours. Part 1. Textbook for students of general education institutions / A. G. Mordkovich. - 11th ed., erased. - M.: Mnemosyne, 2009. - 215 p.: ill. ISBN 978-5-346-01155-2.
- Algebra and the beginning of mathematical analysis. 10th grade: textbook. for general education institutions: basic and profile. levels / [Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; edited by A. B. Zhizhchenko. - 3rd ed. - M.: Education, 2010.- 368 p. : ill. - ISBN 978-5-09-022771-1.
Vieta's theorem is often used to check roots that have already been found. If you have found the roots, you can use the formulas \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) to calculate the values of \(p\) and \(q\ ). And if they turn out to be the same as in the original equation, then the roots are found correctly.
For example, let us, using , solve the equation \(x^2+x-56=0\) and get the roots: \(x_1=7\), \(x_2=-8\). Let's check if we made a mistake in the solution process. In our case, \(p=1\), and \(q=-56\). By Vieta's theorem we have:
\(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)7+(-8)=-1 \\7\cdot(-8)=-56\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)-1=-1\\-56=-56\end(cases)\ )
Both statements converged, which means we solved the equation correctly.
This check can be done orally. It will take 5 seconds and will save you from stupid mistakes.
Vieta's converse theorem
If \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\), then \(x_1\) and \(x_2\) are the roots of the quadratic equation \(x^ 2+px+q=0\).
Or in a simple way: if you have an equation of the form \(x^2+px+q=0\), then solving the system \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\ end(cases)\) you will find its roots.
Thanks to this theorem, you can quickly find the roots of a quadratic equation, especially if these roots are . This skill is important because it saves a lot of time.
Example . Solve the equation \(x^2-5x+6=0\).
Solution
: Using Vieta’s inverse theorem, we find that the roots satisfy the conditions: \(\begin(cases)x_1+x_2=5 \\x_1 \cdot x_2=6\end(cases)\).
Look at the second equation of the system \(x_1 \cdot x_2=6\). What two can the number \(6\) be decomposed into? On \(2\) and \(3\), \(6\) and \(1\) or \(-2\) and \(-3\), and \(-6\) and \(- 1\). The first equation of the system will tell you which pair to choose: \(x_1+x_2=5\). \(2\) and \(3\) are similar, since \(2+3=5\).
Answer
: \(x_1=2\), \(x_2=3\).
Examples
. Using the converse of Vieta's theorem, find the roots of the quadratic equation:
a) \(x^2-15x+14=0\); b) \(x^2+3x-4=0\); c) \(x^2+9x+20=0\); d) \(x^2-88x+780=0\).
Solution
:
a) \(x^2-15x+14=0\) – what factors does \(14\) decompose into? \(2\) and \(7\), \(-2\) and \(-7\), \(-1\) and \(-14\), \(1\) and \(14\ ). What pairs of numbers add up to \(15\)? Answer: \(1\) and \(14\).
b) \(x^2+3x-4=0\) – what factors does \(-4\) decompose into? \(-2\) and \(2\), \(4\) and \(-1\), \(1\) and \(-4\). What pairs of numbers add up to \(-3\)? Answer: \(1\) and \(-4\).
c) \(x^2+9x+20=0\) – what factors does \(20\) decompose into? \(4\) and \(5\), \(-4\) and \(-5\), \(2\) and \(10\), \(-2\) and \(-10\ ), \(-20\) and \(-1\), \(20\) and \(1\). What pairs of numbers add up to \(-9\)? Answer: \(-4\) and \(-5\).
d) \(x^2-88x+780=0\) – what factors does \(780\) decompose into? \(390\) and \(2\). Will they add up to \(88\)? No. What other multipliers does \(780\) have? \(78\) and \(10\). Will they add up to \(88\)? Yes. Answer: \(78\) and \(10\).
It is not necessary to expand the last term into all possible factors (as in the last example). You can immediately check whether their sum gives \(-p\).
Important! Vieta's theorem and the converse theorem only work with , that is, one for which the coefficient of \(x^2\) is equal to one. If we were initially given a non-reduced equation, then we can make it reduced by simply dividing by the coefficient in front of \(x^2\).
For example, let the equation \(2x^2-4x-6=0\) be given and we want to use one of Vieta’s theorems. But we can’t, since the coefficient of \(x^2\) is equal to \(2\). Let's get rid of it by dividing the entire equation by \(2\).
\(2x^2-4x-6=0\) \(|:2\)
\(x^2-2x-3=0\)
Ready. Now you can use both theorems.
Answers to frequently asked questions
Question:
Using Vieta's theorem, you can solve any ?
Answer:
Unfortunately no. If the equation does not contain integers or the equation has no roots at all, then Vieta’s theorem will not help. In this case you need to use discriminant
. Fortunately, 80% of the equations in school mathematics have integer solutions.
Before moving on to Vieta's theorem, we introduce a definition. Quadratic equation of the form x² + px + q= 0 is called reduced. In this equation, the leading coefficient is equal to one. For example, the equation x² - 3 x- 4 = 0 is reduced. Any quadratic equation of the form ax² + b x + c= 0 can be reduced by dividing both sides of the equation by A≠ 0. For example, equation 4 x² + 4 x— 3 = 0 by dividing by 4 is reduced to the form: x² + x— 3/4 = 0. Let us derive the formula for the roots of the reduced quadratic equation; for this we use the formula for the roots of a general quadratic equation: ax² + bx + c = 0
Reduced equation x² + px + q= 0 coincides with a general equation in which A = 1, b = p, c = q. Therefore, for the given quadratic equation the formula takes the form: 

the last expression is called the formula for the roots of the reduced quadratic equation; it is especially convenient to use this formula when R- even number. For example, let's solve the equation x² — 14 x — 15 = 0
![]()
In response, we write the equation has two roots.
![]()
For the reduced quadratic equation with positive, the following theorem holds.
Vieta's theorem
If x 1 and x 2 - roots of the equation x² + px + q= 0, then the formulas are valid:
x 1 + x 2 = — R
x 1 * x 2 = q, that is, the sum of the roots of the reduced quadratic equation is equal to the second coefficient taken with the opposite sign, and the product of the roots is equal to the free term.
Based on the formula for the roots of the above quadratic equation, we have:

Adding these equalities, we get: x 1 + x 2 = —R.
Multiplying these equalities, using the difference of squares formula we get:

Note that Vieta’s theorem is also valid when the discriminant is equal to zero, if we assume that in this case the quadratic equation has two identical roots: x 1 = x 2 = — R/2.
Without solving equations x² — 13 x+ 30 = 0 find the sum and product of its roots x 1 and x 2. this equation D= 169 – 120 = 49 > 0, so Vieta’s theorem can be applied: x 1 + x 2 = 13, x 1 * x 2 = 30. Let's look at a few more examples. One of the roots of the equation x² — px- 12 = 0 is equal x 1 = 4. Find coefficient R and the second root x 2 of this equation. By Vieta's theorem x 1 * x 2 =— 12, x 1 + x 2 = — R. Because x 1 = 4, then 4 x 2 = - 12, from where x 2 = — 3, R = — (x 1 + x 2) = - (4 - 3) = - 1. In answer we write down the second root x 2 = - 3, coefficient p = — 1.
Without solving equations x² + 2 x- 4 = 0 let’s find the sum of the squares of its roots. Let x 1 and x 2 - roots of the equation. By Vieta's theorem x 1 + x 2 = — 2, x 1 * x 2 = — 4. Because x 1²+ x 2² = ( x 1 + x 2)² - 2 x 1 x 2 then x 1²+ x 2² =(- 2)² -2 (- 4) = 12.
Let's find the sum and product of the roots of equation 3 x² + 4 x- 5 = 0. This equation has two different roots, since the discriminant D= 16 + 4*3*5 > 0. To solve the equation, we use Vieta’s theorem. This theorem has been proven for the given quadratic equation. So let's divide this equation by 3.

Therefore, the sum of the roots is equal to -4/3, and their product is equal to -5/3.
In general, the roots of the equation ax² + b x + c= 0 are related by the following equalities: x 1 + x 2 = — b/a, x 1 * x 2 = c/a, To obtain these formulas, it is enough to divide both sides of this quadratic equation by A ≠ 0 and apply Vieta’s theorem to the resulting reduced quadratic equation. Let's consider an example: you need to create a reduced quadratic equation whose roots x 1 = 3, x 2 = 4. Because x 1 = 3, x 2 = 4 - roots of quadratic equation x² + px + q= 0, then by Vieta’s theorem R = — (x 1 + x 2) = — 7, q = x 1 x 2 = 12. We write the answer as x² — 7 x+ 12 = 0. When solving some problems, the following theorem is used.
Theorem converse to Vieta's theorem
If the numbers R, q, x 1 , x 2 are such that x 1 + x 2 = — p, x 1 * x 2 = q, That x 1 And x 2- roots of the equation x² + px + q= 0. Substitute into the left side x² + px + q instead of R expression - ( x 1 + x 2), and instead q- work x 1 * x 2 . We get: x² + px + q = x² — ( x 1 + x 2) x + x 1 x 2 = x² - x 1 x - x 2 x + x 1 x 2 = (x - x 1) (x - x 2). Thus, if the numbers R, q, x 1 and x 2 are connected by these relations, then for all X equality holds x² + px + q = (x - x 1) (x - x 2), from which it follows that x 1 and x 2 - roots of the equation x² + px + q= 0. Using the theorem inverse to Vieta’s theorem, you can sometimes find the roots of a quadratic equation by selection. Let's look at an example, x² — 5 x+ 6 = 0. Here R = — 5, q= 6. Let's choose two numbers x 1 and x 2 so that x 1 + x 2 = 5, x 1 * x 2 = 6. Noticing that 6 = 2 * 3, and 2 + 3 = 5, by the theorem inverse to Vieta’s theorem, we obtain that x 1 = 2, x 2 = 3 - roots of the equation x² — 5 x + 6 = 0.
When studying methods for solving second-order equations in a school algebra course, the properties of the resulting roots are considered. They are currently known as Vieta's theorem. Examples of its use are given in this article.
Quadratic equation
The second order equation is the equality shown in the photo below.
Here the symbols a, b, c are some numbers called the coefficients of the equation under consideration. To solve an equality, you need to find values of x that make it true.
Note that since the maximum power to which x can be raised is two, then the number of roots in the general case is also two.
There are several ways to solve this type of equalities. In this article we will consider one of them, which involves the use of the so-called Vieta theorem.
Formulation of Vieta's theorem

At the end of the 16th century, the famous mathematician Francois Viète (French) noticed, while analyzing the properties of the roots of various quadratic equations, that certain combinations of them satisfy specific relationships. In particular, these combinations are their product and sum.
Vieta's theorem establishes the following: the roots of a quadratic equation, when summed, give the ratio of the linear to quadratic coefficients taken with the opposite sign, and when they are multiplied, they lead to the ratio of the free term to the quadratic coefficient.
If the general form of the equation is written as shown in the photo in the previous section of the article, then mathematically this theorem can be written in the form of two equalities:
- r 2 + r 1 = -b / a;
- r 1 x r 2 = c / a.
Where r 1, r 2 is the value of the roots of the equation in question.
The above two equalities can be used to solve a number of different mathematical problems. The use of Vieta's theorem in examples with solutions is given in the following sections of the article.
- In contact with 0
- Google+ 0
- OK 0
- Facebook 0