To understand how to solve trapezoid problems, it is useful to remember three basic solutions.
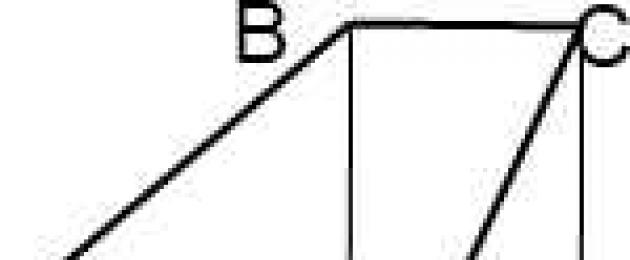
I. Draw two heights.
Ia. The quadrilateral BCKF is a rectangle (since all its angles are right). Therefore FK=BC.
AD=AF+FK+KD, hence AD=AF+BC+KD.
Triangles ABF and DCK are right triangles.
(Another option should be taken into account:
Ib.
In this case AD=AF+FD=AF+FK-DK=AF+BC-DK.)
Ic. If the trapezoid is isosceles, the solution to the problem is simplified:
In this case, right triangles ABF and DCK are equal, for example, along the leg and hypotenuse (AB=CD by condition, BF=CK as the altitude of the trapezoid). From the equality of triangles it follows that the corresponding sides are equal:
AF=KD=(AD-FK):2=(AD-BC):2.
II. Draw a straight line parallel to the side.
IIa. BM∥ CD. Since BC∥ AD (like the bases of a trapezoid), then BCDM is a parallelogram. Therefore, MD=BC, BM=CD, AM=AD-BC.
IIb. In particular, for an isosceles trapezoid
BM∥ CD. Since CD=AB, then BM=AB. That is, we get an isosceles triangle ABM and a parallelogram BCDM.
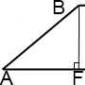
III. Continue the sides and get a triangle.
Lines AB and CD intersect at point P.
Triangles APD and BPC are similar in two angles (angle P is common, ∠ PAD= ∠ PBC as corresponding with BC∥ AD and secant AP).
Therefore, their sides are proportional:
These three approaches to solving trapezoid problems are the main ones. Besides these, there are many other ways. Some are reviewed on this site. For example, how to solve problems with a trapezoid whose diagonals are perpendicular.
In this article, another selection of problems with trapezoid has been made for you. The conditions are somehow related to its midline. Task types are taken from an open bank of typical tasks. If you wish, you can refresh your theoretical knowledge. The blog has already discussed tasks whose conditions are related to, as well as. Briefly about the middle line:
The midline of the trapezoid connects the midpoints of the lateral sides. It is parallel to the bases and equal to their half-sum.
Before solving problems, let's look at a theoretical example.
Given a trapezoid ABCD. The diagonal AC intersecting with the middle line forms the point K, the diagonal BD the point L. Prove that the segment KL is equal to half the difference of the bases.
Let's first note the fact that the midline of a trapezoid bisects any segment whose ends lie on its bases. This conclusion suggests itself. Imagine a segment connecting two points of the bases; it will split this trapezoid into two others. It turns out that a segment parallel to the bases of the trapezoid and passing through the middle of the side will pass through the middle of the other side.
This is also based on Thales' theorem:
If several equal segments are laid out in succession on one of two lines and parallel lines are drawn through their ends that intersect the second line, then they will cut off equal segments on the second line.
That is, in this case, K is the middle of AC and L is the middle of BD. Therefore EK is the midline of triangle ABC, LF is the midline of triangle DCB. According to the property of the midline of a triangle:
We can now express the segment KL in terms of bases:
Proven!
This example is given for a reason. In tasks for independent solution there is just such a task. Only it doesn’t say that the segment connecting the midpoints of the diagonals lies on the midline. Let's consider the tasks:
27819. Find the midline of the trapezoid if its bases are 30 and 16.
We calculate using the formula:
27820. The midline of the trapezoid is 28 and the smaller base is 18. Find the larger base of the trapezoid.
Let's express the larger base:
Thus:
27836. A perpendicular dropped from the vertex of an obtuse angle to the larger base of an isosceles trapezoid divides it into parts having lengths 10 and 4. Find the midline of this trapezoid.
In order to find the middle line you need to know the bases. The base AB is easy to find: 10+4=14. Let's find DC.
Let's construct the second perpendicular DF:
The segments AF, FE and EB will be equal to 4, 6 and 4 respectively. Why?
In an isosceles trapezoid, perpendiculars lowered to the larger base divide it into three segments. Two of them, which are the legs of the cut-off right triangles, are equal to each other. The third segment is equal to the smaller base, since when constructing the indicated heights, a rectangle is formed, and in a rectangle the opposite sides are equal. In this task:
Thus DC=6. We calculate:
27839. The bases of the trapezoid are in the ratio 2:3, and the midline is 5. Find the smaller base.
Let's introduce the proportionality coefficient x. Then AB=3x, DC=2x. We can write:
Therefore, the smaller base is 2∙2=4.
27840. The perimeter of an isosceles trapezoid is 80, its midline is equal to the lateral side. Find the side of the trapezoid.
Based on the condition, we can write:
If we denote the middle line through the value x, we get:
The second equation can already be written as:
27841. The midline of the trapezoid is 7, and one of its bases is 4 greater than the other. Find the larger base of the trapezoid.
Let us denote the smaller base (DC) as x, then the larger one (AB) will be equal to x+4. We can write it down
We found that the smaller base is early five, which means the larger one is equal to 9.
27842. The midline of the trapezoid is 12. One of the diagonals divides it into two segments, the difference of which is 2. Find the larger base of the trapezoid.
We can easily find the larger base of the trapezoid if we calculate the segment EO. It is the midline in triangle ADB, and AB=2∙EO.
What do we have? It is said that the middle line is equal to 12 and the difference between the segments EO and ОF is equal to 2. We can write two equations and solve the system:
It is clear that in this case you can select a pair of numbers without calculations, these are 5 and 7. But, nevertheless, let’s solve the system:
So EO=12–5=7. Thus, the larger base is equal to AB=2∙EO=14.
27844. In an isosceles trapezoid, the diagonals are perpendicular. The height of the trapezoid is 12. Find its midline.
Let us immediately note that the height drawn through the intersection point of the diagonals in an isosceles trapezoid lies on the axis of symmetry and divides the trapezoid into two equal rectangular trapezoids, that is, the bases of this height are divided in half.
It would seem that to calculate the middle line we must find reasons. Here a small dead end arises... How, knowing the height, in this case, calculate the bases? No way! There are many such trapezoids with a fixed height and diagonals intersecting at an angle of 90 degrees. What should I do?
Look at the formula for the midline of a trapezoid. After all, we do not need to know the reasons themselves; it is enough to know their sum (or half-sum). We can do this.
Since the diagonals intersect at right angles, isosceles right triangles are formed with height EF:
From the above it follows that FO=DF=FC, and OE=AE=EB. Now let’s write down what the height is equal to, expressed through the segments DF and AE:
So the middle line is 12.
*In general, this is a problem, as you understand, for mental calculation. But I am sure that the detailed explanation provided is necessary. And so... If you look at the figure (provided that the angle between the diagonals is observed during construction), the equality FO=DF=FC, and OE=AE=EB immediately catches your eye.
The prototypes also include types of tasks with trapezoids. It is built on a sheet of paper in a square and you need to find the middle line; the side of the cell is usually equal to 1, but it can be a different value.
27848. Find the midline of the trapezoid ABCD, if the sides of square cells are equal to 1.
It’s simple, we calculate the bases by cells and use the formula: (2+4)/2=3
If the bases are built at an angle to the cell grid, then there are two ways. For example!
It will be useful for all graduates who are preparing to take the Unified State Exam in mathematics to refresh their memory on the topic “Free trapezoid”. As many years of practice have shown, planimetric problems from this section cause certain difficulties for many high school students. At the same time, solving the Unified State Examination problems on the topic “Free trapezoid” is required when passing both the basic and profile levels of the certification test. Therefore, all graduates should be able to cope with such exercises.
How to prepare for the exam?
Most planimetric problems are solved by classical constructions. If in a Unified State Examination problem you need to find, for example, the area of the trapezoid shown in the figure, it is worth marking all the known parameters on the drawing. After that, remember the main theorems related to them. By applying them you will be able to find the correct answer.
To make your preparation for the exam truly effective, refer to the Shkolkovo educational portal. Here you will find all the basic material on the topics “Free trapeze or which will help you successfully pass the Unified State Exam. The main properties of the figure, formulas and theorems are collected in the “Theoretical Information” section.
Graduates will also be able to improve their problem-solving skills on our mathematical portal. The “Catalogue” section presents a large selection of relevant exercises of varying difficulty levels. Our specialists regularly update and supplement the list of tasks.
Students from Moscow and other cities can consistently perform the exercises online. If necessary, any task can be saved in the “Favorites” section and later returned to it to discuss with the teacher.
The practice of last year's Unified State Exam and State Examination shows that geometry problems cause difficulties for many schoolchildren. You can easily cope with them if you memorize all the necessary formulas and practice solving problems.
In this article you will see formulas for finding the area of a trapezoid, as well as examples of problems with solutions. You may come across the same ones in KIMs during certification exams or at Olympiads. Therefore, treat them carefully.
What you need to know about the trapezoid?
To begin with, let us remember that trapezoid is called a quadrilateral in which two opposite sides, also called bases, are parallel, and the other two are not.
In a trapezoid, the height (perpendicular to the base) can also be lowered. The middle line is drawn - this is a straight line that is parallel to the bases and equal to half of their sum. As well as diagonals that can intersect, forming acute and obtuse angles. Or, in some cases, at a right angle. In addition, if the trapezoid is isosceles, a circle can be inscribed in it. And describe a circle around it.
Trapezoid area formulas
First, let's look at the standard formulas for finding the area of a trapezoid. We will consider ways to calculate the area of isosceles and curvilinear trapezoids below.
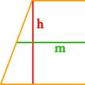
So, imagine that you have a trapezoid with bases a and b, in which height h is lowered to the larger base. Calculating the area of a figure in this case is as easy as shelling pears. You just need to divide the sum of the lengths of the bases by two and multiply the result by the height: S = 1/2(a + b)*h.
Let's take another case: suppose in a trapezoid, in addition to the height, there is a middle line m. We know the formula for finding the length of the middle line: m = 1/2(a + b). Therefore, we can rightfully simplify the formula for the area of a trapezoid to the following form: S = m* h. In other words, to find the area of a trapezoid, you need to multiply the center line by the height.
Let's consider another option: the trapezoid contains diagonals d 1 and d 2, which do not intersect at right angles α. To calculate the area of such a trapezoid, you need to divide the product of the diagonals by two and multiply the result by the sin of the angle between them: S= 1/2d 1 d 2 *sinα.
Now consider the formula for finding the area of a trapezoid if nothing is known about it except the lengths of all its sides: a, b, c and d. This is a cumbersome and complex formula, but it will be useful for you to remember it just in case: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2.
By the way, the above examples are also true for the case when you need the formula for the area of a rectangular trapezoid. This is a trapezoid, the side of which adjoins the bases at a right angle.
Isosceles trapezoid
A trapezoid whose sides are equal is called isosceles. We will consider several options for the formula for the area of an isosceles trapezoid.
First option: for the case when a circle with radius r is inscribed inside an isosceles trapezoid, and the side and larger base form an acute angle α. A circle can be inscribed in a trapezoid provided that the sum of the lengths of its bases is equal to the sum of the lengths of the sides.
The area of an isosceles trapezoid is calculated as follows: multiply the square of the radius of the inscribed circle by four and divide it all by sinα: S = 4r 2 /sinα. Another area formula is a special case for the option when the angle between the large base and the side is 30 0: S = 8r2.
Second option: this time we take an isosceles trapezoid, in which in addition the diagonals d 1 and d 2 are drawn, as well as the height h. If the diagonals of a trapezoid are mutually perpendicular, the height is half the sum of the bases: h = 1/2(a + b). Knowing this, it is easy to transform the formula for the area of a trapezoid already familiar to you into this form: S = h 2.
Formula for the area of a curved trapezoid
Let's start by figuring out what a curved trapezoid is. Imagine a coordinate axis and a graph of a continuous and non-negative function f that does not change sign within a given segment on the x-axis. A curvilinear trapezoid is formed by the graph of the function y = f(x) - at the top, the x axis is at the bottom (segment), and on the sides - straight lines drawn between points a and b and the graph of the function.
It is impossible to calculate the area of such a non-standard figure using the above methods. Here you need to apply mathematical analysis and use the integral. Namely: the Newton-Leibniz formula - S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a). In this formula, F is the antiderivative of our function on the selected segment. And the area of a curvilinear trapezoid corresponds to the increment of the antiderivative on a given segment.
Sample problems
To make all these formulas easier to understand in your head, here are some examples of problems for finding the area of a trapezoid. It will be best if you first try to solve the problems yourself, and only then compare the answer you receive with the ready-made solution.
Task #1: Given a trapezoid. Its larger base is 11 cm, the smaller one is 4 cm. The trapezoid has diagonals, one 12 cm long, the second 9 cm.
Solution: Construct a trapezoid AMRS. Draw a straight line РХ through vertex P so that it is parallel to the diagonal MC and intersects the straight line AC at point X. You will get a triangle APХ.
We will consider two figures obtained as a result of these manipulations: triangle APX and parallelogram CMRX.
Thanks to the parallelogram, we learn that PX = MC = 12 cm and CX = MR = 4 cm. From where we can calculate the side AX of the triangle ARX: AX = AC + CX = 11 + 4 = 15 cm.
We can also prove that the triangle APX is right-angled (to do this, apply the Pythagorean theorem - AX 2 = AP 2 + PX 2). And calculate its area: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 cm 2.
Next you will need to prove that triangles AMP and PCX are equal in area. The basis will be the equality of the parties MR and CX (already proven above). And also the heights that you lower on these sides - they are equal to the height of the AMRS trapezoid.
All this will allow you to say that S AMPC = S APX = 54 cm 2.
Task #2: The trapezoid KRMS is given. On its lateral sides there are points O and E, while OE and KS are parallel. It is also known that the areas of trapezoids ORME and OKSE are in the ratio 1:5. RM = a and KS = b. You need to find OE.
Solution: Draw a line parallel to RK through point M, and designate the point of its intersection with OE as T. A is the point of intersection of a line drawn through point E parallel to RK with the base KS.
Let's introduce one more notation - OE = x. And also the height h 1 for the triangle TME and the height h 2 for the triangle AEC (you can independently prove the similarity of these triangles).
We will assume that b > a. The areas of the trapezoids ORME and OKSE are in the ratio 1:5, which gives us the right to create the following equation: (x + a) * h 1 = 1/5(b + x) * h 2. Let's transform and get: h 1 / h 2 = 1/5 * ((b + x)/(x + a)).
Since the triangles TME and AEC are similar, we have h 1 / h 2 = (x – a)/(b – x). Let’s combine both entries and get: (x – a)/(b – x) = 1/5 * ((b + x)/(x + a)) ↔ 5(x – a)(x + a) = (b + x)(b – x) ↔ 5(x 2 – a 2) = (b 2 – x 2) ↔ 6x 2 = b 2 + 5a 2 ↔ x = √(5a 2 + b 2)/6.
Thus, OE = x = √(5a 2 + b 2)/6.
Conclusion
Geometry is not the easiest of sciences, but you can certainly cope with the exam questions. It is enough to show a little perseverance in preparation. And, of course, remember all the necessary formulas.
We tried to collect all the formulas for calculating the area of a trapezoid in one place so that you can use them when you prepare for exams and revise the material.
Be sure to tell your classmates and friends on social networks about this article. Let there be more good grades for the Unified State Examination and State Examinations!
website, when copying material in full or in part, a link to the source is required.
- In contact with 0
- Google+ 0
- OK 0
- Facebook 0
