Tasks on statistics
1. During the quarter, Sergey received the following marks in mathematics: one "deuce", three "triples", five "fours" and one "five". Find the sum of the arithmetic mean and the mode of its estimates.
Answer. 8,6.
2. Recorded average daily temperature (in degrees) in Moscow for five days in the month of October: 6; 7; 7; nine; 11. How different is the arithmetic mean of this set of numbers from its median?
Answer. 1.
3. The height (in centimeters) of five students is recorded: 156, 166, 134, 132, 132. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 10.
4. The table shows the results of four shooters, shown by them in training.
|
Shooter's name |
Number of shots |
Number of hits |
|
Veronica | ||
Answer. 2.
5. Five friends found deviations (in minutes) of their wristwatches from the exact time: -2, 0, 3, -5, -1. Find the sum of the arithmetic mean of this set of numbers and its median.
Answer. - 2.
6. The cost (in rubles) of glazed curds "Vkusnyashka" in the shops of the microdistrict is recorded: 3, 5, 6, 7, 9, 4, 8. How much does the arithmetic mean of this set differ from its median?
Answer. 0.
7. In the series of numbers 3, 7, 15, ___, 23, one number is missing. Find this number if you know that the arithmetic mean of this series of numbers is 13.
Answer. 17.
8. The consumption of electricity (in kW) by a certain family during the first five months of the year is recorded: 138, 140, 135, 132, 125. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 2.
9. The table shows data on the sale of potatoes in a certain vegetable stall during the week.
|
Day of the week |
Monday |
Tuesday |
Wednesday |
Thursday |
Friday |
Saturday |
Sunday |
|
Quantity of potatoes sold, kg |
How many kilograms of potatoes were sold on average daily this week?
Answer. 125.
10. The arithmetic mean of a series of ten numbers is 16. The number 27 was assigned to this series. What is the arithmetic mean of the new series of numbers?
Answer. 17.
11. The arithmetic mean of a series of ten numbers is 16. The number 7 has been crossed out from this series. What is the arithmetic mean of the new series of numbers?
Answer. 17.
12. Each of the nine participants in the shooting competition fired ten shots. The number of hits on the target of each of these participants is recorded: 12, 10, 5, 4, 6, 8, 9, 5, 4. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 1.
13. Five employees of the department purchased shares of the same value of some joint-stock company. The number of these shares purchased by each of the employees is recorded: 5, 10, 12, 7, 3. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 0,4.
14. The university keeps a daily record of received letters. Based on this account, the following data series was obtained (the number of letters received daily during this week): 39, 43, 40, 56, 38, 21.1. How much does the mean of this set of numbers differ from its median?
Answer. 5.
15. During the quarter, Alexey received the following grades in physics: two "deuces", two "triples", four "fours" and two "fives". Find the sum of the arithmetic mean and the median of its scores.
Answer. 8.
16. The average daily temperature (in degrees) in Moscow was recorded for five days in the month of September: 15, 10, 18, 11, 11. How much does the arithmetic mean of this set of numbers differ from its mode?
Answer. 2.
17. The height (in centimeters) of five students is recorded: 164, 162, 156, 132, 136. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 6.
18. The table shows the results of four shooters, shown by them in training.
|
Shooter's name |
Number of shots |
Number of hits |
|
Veronica | ||
The coach decided to send the shooter with the higher relative hit rate to the competition. Which shooter will the coach choose?
1) Veronica 2) Evgenia 3) Oleg 4) Irina
Answer. 2.
19. Five friends found deviations (in minutes) of their wristwatch readings from the exact time: -1, 0, -4, -1, 1. Find the sum of the arithmetic mean of this set of numbers and its mode.
Answer. - 2.
20. The cost (in rubles) of glazed cheese curds "Baby" in the shops of the microdistrict is recorded: 4, 4, 6, 7, 11, 9, 8. Find the sum of the arithmetic mean of this set and its mode.
Answer. 11.
21. In the series of numbers 3, 7, 15, ___, 21, one number is missing. Find this number if you know that the arithmetic mean of this series of numbers is 12.
Answer. 14.
22. The consumption of electricity (in kW) by a certain family during the first five months of the year is recorded: 146, 140, 138, 136, 130. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 0.
23. The consumption of electricity (in kW) by a certain family during the first five months of the year is recorded: 152, 150, 148, 140, 130. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 4.
24. The table shows data on the sale of potatoes in a certain vegetable stall during the week.
|
Day of the week |
Monday |
Tuesday |
Thursday |
Friday |
Saturday |
Sunday |
|
|
Quantity of potatoes sold, kg |
How different is the arithmetic mean of the number of potatoes (in kg) sold daily in this stall from its median?
Answer. 5.
25. The arithmetic mean of a series of ten numbers is 18. The number 29 was assigned to this series. What is the arithmetic mean of the new series of numbers?
Answer. 19.
26. The arithmetic mean of a series of ten numbers is 18. The number 36 has been crossed out from this series. What is the arithmetic mean of the new series of numbers?
Answer. 16.
27. Each of the nine participants in the shooting competition fired ten shots. The number of hits on the target of each of these participants is recorded: 9, 8, 6, 5, 6, 9, 6, 5, 9. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 1.
28. Five employees of the department purchased shares of the same value of some joint-stock company. The number of these shares purchased by each of the employees is recorded: 5, 7, 10, 11, 7. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 1.
29. The university keeps a daily record of received letters. Based on this account, the following series of data was obtained (the number of letters received daily during this week): 39, 42, 45, 50, 38, 0.17. How much does the mean of this set of numbers differ from its median?
Answer. 6.
30. The average daily temperature (in degrees) in Moscow was recorded for five days in the month of June: 25, 27, 29, 24, 25, How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 1.
31. The height (in centimeters) of five students is recorded: 164, 161, 152, 150, 148. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 3.
32. The table shows the results of four shooters, shown by them in training.
|
Shooter's name |
Number of shots |
Number of hits |
|
Anastasia | ||
The coach decided to send the shooter with the higher relative hit rate to the competition.
Which shooter will the coach choose?
1) Anastasia 2) Evgeny 3) Sergey 4) Irina
Answer. 3.
33. The cost (in rubles) of sour cream in the shops of the microdistrict is recorded: 24, 25, 27, 27, 27, 24, 28. How much does the arithmetic mean of this set differ from its median?
Answer. 1.
34. In the series of numbers 3, 7, 17, ___, 23, one number is missing. Find this number if you know that the arithmetic mean of this series of numbers is 14.
Answer. 20.
35. The consumption of electricity (in kWh) by a certain family during the first five months of the year is recorded: 141, 130, 130, 124, 120. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 1.
36. The table shows data on the sale of carrots in a certain vegetable stall during the week.
|
Day of the week |
Monday |
Tuesday |
Thursday |
Friday |
Saturday |
Sunday |
|
|
Number of carrots sold, kg |
How many kilograms of carrots were sold on average daily this week?
Answer. 54.
37. A dice is rolled 100 times. The results are presented in the table.
|
Number of points dropped | ||||||
|
Number of occurrences of the event |
What is the relative frequency of getting at least five points?
Answer. 0,35.
38. The arithmetic mean of a series of ten numbers is 12. The number 34 was assigned to this series. What is the arithmetic mean of the new series of numbers?
Answer. 14.
39. The basketball player, having completed 50 throws in training, hit the ring 36 times. What is the relative hitting frequency of this basketball player?
Answer. Chernov in a white suit, Belov in a gray one, Serov in a black one.
40. The arithmetic mean of a series of ten numbers is 14. The number 32 has been crossed out from this series. What is the arithmetic mean of the new series of numbers?
Answer. 12.
41. Each of the seven students in the 9th grade on a given day noted the time (in minutes) spent on doing their homework in algebra. The result is the following series of numbers: 24, 45, 40, 50, 30, 35, 42. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 2.
42. Five employees of a certain joint-stock company purchased shares of the same value of this company. The number of these shares purchased by each of the employees is recorded: 7, 12, 15, 8, 3. How much does the arithmetic mean of this set of numbers differ from its median?
Answer. 1.
43. Each of the seven participants in the shooting competition fired ten shots. The number of hits on the target of each of these participants is recorded: 9, 6, 5, 8, 9, 6, 6. How much does the arithmetic mean of the second set of numbers differ from its mode?
Answer. 1.
44. The table shows data on the sale of digital cameras in one of the campaign offices during the week.
|
Day of the week |
Monday |
Tuesday |
Thursday |
Friday |
Saturday |
Sunday |
|
|
Number of sold digital cameras, pcs. |
What is the average number of digital cameras sold daily in this office?
Answer. 19.
45. The table shows data on the sale of mobile phones in one of the offices of the campaign during the week.
|
Day of the week |
Monday |
Tuesday |
Wednesday |
Thursday |
Friday |
Saturday |
Sunday |
|
Number of phones sold, pcs. |
What is the average number of mobile phones sold daily in this office?
Answer. 37.
46. The table shows the results of four shooters, shown by them in training.
|
Shooter's name |
Number of shots |
Number of hits |
|
Veronica | ||
The coach decided to send the shooter with the higher relative hit rate to the competition. Which shooter will the coach choose?
1) Veronica 2) Evgenia 3) Oleg 4) Irina
Answer. 2.
47. Five friends found deviations (in minutes) of their wristwatch readings from the exact time: -1, 0 -3, -2, 1. Find the sum of the arithmetic mean of this set of numbers and its median.
Answer. -2.
48. In a lesson on probability theory, six guys tossed coins. They wrote down in the table how many times they got heads and tails.
1. How many times did Vova get heads?
2. What did Dasha get more often: heads or tails, and how many times?
3. Which of the guys has the most tails?
4. How many times did it come up heads?
5. How many times did Olya toss a coin?
6. Which of the students threw a coin the most times and how many?
7. How many times did the students toss a coin in total?
Answer. 1) 11; 2) Tails, 8; 3) At Asya; 4) 48; 5) 13; 6) Asya, 22;
49. In a lesson on probability theory, Tanya, Vanya, Mitya and Vika were tossing dice. They wrote down in the table how many times each number fell out.
|
Tanya | ||||||
|
Vania | ||||||
|
Mitya | ||||||
|
Vika |
1. How many times has Vika rolled a three?
2. What value did Vanya most often drop out and how many times?
3. Which one has the most fours?
4. How many times did a five come up in total?
5. How many times did Tanya roll the dice?
6. How many times did the students roll the dice in total?
Answer. fourteen; 2) Two, 11; 3) Vicki; 4) 28; 5) 56;
50. The school has two sixth grades. On the control work in 6 "A" class, 5 deuces were received, and in 6 "B" - 4 deuces. At the same time, 20 students study at 6 "A", and 25 at 6 "B".
a) What percentage of students in 6 "A" received a deuce?
b) What percentage of students in 6 "B" received a deuce?
c) Find the arithmetic mean of the results of tasks a) and b).
d) Find what percentage of all sixth graders received
deuce.
e) Explain why the results in tasks c) and d) do not match.
Answer. a) 25%; b) 16%; c) 20.5%; d) 20%; e) because there are different numbers of students in the classes.
"BASIC CONCEPTS OF MATHEMATICAL STATISTICS"
1. Below are the clothing sizes of 50 students in grade 9:
50 40 44 44 46 46 44 48 46 44
38 44 48 50 40 42 50 46 54 44
42 42 52 44 46 38 46 42 44 48
46 48 44 40 52 44 48 50 46 46
48 40 46 42 44 50 46 44 46 48.
Based on these data, compile tables of distribution by frequency and relative frequency of the values of the random variable X - the sizes of clothes for students in grade 9.
2. The sample consists of all the letters included in the couplet: “... This tree is a pine,
And the fate of the pine is clear ... ".
a) Write down the data series (variant values) of the sample;
b) find the sample size;
c) determine the multiplicity and frequency options "O";
d) What is the highest percentage frequency of the sampling option?
3. When studying the workload, students were asked 32 eighth-graders to note the time (with an accuracy of 0.1 hour) that they spent on a certain day doing homework. We received the following data:
2,7; 2,5; 3,1; 3,2; 3,4; 1,6; 1,8; 4,2;
2,6; 3,4; 3,2; 2,9; 1,9; 1,5; 3,7; 3,6;
3,1; 2,9; 2,8; 1,5; 3,1; 3,4; 2,2; 2,8;
4,1; 2,4; 4,3; 1,9; 3,6; 1,8; 2,8; 3.9.
Present the data obtained as an interval series with intervals of length 0.5.
4. The table shows the distribution of district recruits by height.
| Height, cm | Frequency |
| 155-160 | |
| 160-165 | |
| 165-170 | |
| 170-175 | |
| 175-180 | |
| 180-185 | |
| 185-190 | |
| 190-195 |
According to this table, draw up a new table with an interval of 10 cm. Find the average height of recruits.
5. The average daily processing of sugar (in thousand centners) by the sugar industry plants of a certain region is shown below:
12,0; 13,6; 14,7; 18,9; 17,3; 16,1;
20,1; 16,9; 19,1; 18,4; 17,8; 15,6;
20,8; 19,7; 18,9; 19,0; 16,1; 15,8.
Present this data as an interval series with intervals of three units. Find how much sugar the plant in the region processed on average per day: a) replacing each interval with its middle; b) using a given row. In which case will the average output be more accurate?
6. In the farm, three plots are allocated for wheat, the area of which is 12 hectares, 8 hectares and 6 hectares. The average yield in the first plot is 18 centners per hectare, in the second - 19 centners per hectare, in the third - 23 centners per hectare. What is the average wheat yield on this farm?
7. At the figure skating competition, the judges gave the athlete the following marks: 5.2; 5.4; 5.5; 5.4; 5.1; 5.1; 5.4; 5.5 5.3.
8. Each of the 24 participants in the shooting competition fired 10 shots. Noting each time the number of hits on the target, we received the following series of data:
6, 5, 5, 6, 8, 3, 7, 6, 8, 5, 4, 9,
7, 7, 9, 8, 6, 6, 5, 6, 4, 3, 6, 5.
For the resulting data series, find the arithmetic mean, median, range, and mode. What characterizes each of these indicators?
9. Below is the average daily processing of sugar (in thousand centners) by the sugar industry plants of a certain region.
12,2; 13,2; 13,7; 18,0; 18,6; 12,2; 18,5; 12,4; 14,2; 17,8.
For the resulting data series, find the arithmetic mean, median, range, and mode. What characterizes each of these indicators?
10. Find the range, mode and median of the sample:
a) 1, 3, -2, 4, -2, 0, 2, 3, 1, -2, 4;
b) 0.2; 0.4; 0.1; 0.5; 0.1; 0.2; 0.3; 0.5; 0.4; 0.6.
11. The table shows data on the length of service (in years) of the laboratory staff. Find the mean, mode, median of the population under consideration.
12. Find the variance of the set of values of the random variable X given by the frequency distribution.
15. Determine which sample -1, 0, 2, 3, 5, 3 or -5, -3, 0, -3, -1 has less data scatter around its mean.
16. When checking 70 works in the Russian language, the number of spelling errors made by students was noted. The resulting data series was presented in the form of a frequency table.
What is the largest difference in the number of errors made? What is the typical number of errors for this group of students? Indicate what statistical characteristics were used in answering the questions.
The date of the __________
Lesson topic: Arithmetic mean, range and mode.
Lesson Objectives: to repeat the concepts of such statistical characteristics as the arithmetic mean, range and mode, to form the ability to find the average statistical characteristics of various series; develop logical thinking, memory and attention; to bring up diligence, discipline, perseverance, accuracy in children; to develop in children an interest in mathematics.
During the classes
Class organization
Repetition ( Equation and its roots)
Define an equation with one variable.
What is the root of an equation?
What does it mean to solve an equation?
Solve the equation:
6x + 5 \u003d 23 -3x 2 (x - 5) + 3x \u003d 11 -2x 3x - (x - 5) \u003d 14 -2x
Knowledge update repeat the concepts of such statistical characteristics as the arithmetic mean, range, mode and median.
Statistics - is a science that collects, processes, analyzes quantitative data on a variety of mass phenomena occurring in nature and society.
Average is the sum of all numbers divided by their number. (The arithmetic mean is called the average value of the number series.)
Range of numbers is the difference between the largest and smallest of these numbers.
Number series fashion - This is the number that occurs in this series more often than others.
median an ordered series of numbers with an odd number of members is called the number written in the middle, and with an even number of members is called the arithmetic mean of two numbers written in the middle.
The word statistics is translated from the Latin language status - state, state of affairs.
Statistical characteristics: arithmetic mean, range, mode, median.
Assimilation of new material
Task number 1: 12 seventh graders were asked to mark the time (in minutes) spent doing their algebra homework. We got the following data: 23,18,25,20,25,25,32,37,34,26,34,25. How many minutes did students spend on average doing homework?
Decision: 1) find the arithmetic mean:
2) find the range of the series: 37-18=19 (min)
3) fashion 25.
Task number 2: In the city of Schastlivy, it was measured daily at 18 00 air temperature (in degrees Celsius for 10 days), as a result of which the table was filled:
T Wed = 0 WITH,
Range = 25-13=12 0 WITH,
Task number 3: Find the range of numbers 2, 5, 8, 12, 33.
Decision: The largest number here is 33, the smallest is 2. So, the range is: 33 - 2 = 31.
Task number 4: Find the mode of the distribution series:
a) 23 25 27 23 26 29 23 28 33 23 (mode 23);
b) 14 18 22 26 30 28 26 24 22 20 (modes: 22 and 26);
c) 14 18 22 26 30 32 34 36 38 40 (no fashion).
Task number 5 : Find the arithmetic mean, range and mode of a series of numbers 1, 7, 3, 8, 7, 12, 22, 7, 11,22,8.
Decision: 1) Most often in this series of numbers the number 7 occurs (3 times). It is the mode of the given series of numbers.
Exercise Solution
BUT) Find the arithmetic mean, median, range and mode of a series of numbers:
1) 32, 26, 18, 26, 15, 21, 26;
2) 21, 18, 5, 25, 3, 18, 5, 17, 9;
3) 67,1 68,2 67,1 70,4 68,2;
4) 0,6 0,8 0,5 0,9 1,1.
B) The arithmetic mean of a series of ten numbers is 15. The number 37 was assigned to this series. What is the arithmetic mean of the new series of numbers.
AT) In the series of numbers 2, 7, 10, __, 18, 19, 27, one number turned out to be erased. Restore it knowing that the arithmetic mean of this series of numbers is 14.
G) Each of the 24 participants in the shooting competition fired ten shots. Noting each time the number of hits on the target, we received the following series of data: 6, 5, 5, 6, 8, 3, 7, 6, 8, 5, 4, 9, 7, 7, 9, 8, 6, 6, 5 , 6, 4, 3, 6, 5. Find scope and fashion for this series. What characterizes each of these indicators.
Summarizing
What is the arithmetic mean? Fashion? Median? Swipe?
Homework:
№164 (repetition task), pp36-39 read
№167(a,b), #177, 179
Sections: Mathematics
Statistics(from the Latin status, state of affairs) is a science that deals with obtaining, processing and analyzing quantitative data on a variety of mass phenomena occurring in nature and in society. Statistics studies the number of individual groups of the population, the production and consumption of various types of products, natural resources. The results of statistical studies are widely used for practical and scientific conclusions. Annex 2.
Arithmetic mean, range and mode.
- The arithmetic mean of a series of numbers is called the quotient of dividing the sum of these numbers by the number of terms.
When studying the teaching load of students, a group of 12 seventh-graders was singled out. They were asked to mark the time (in minutes) spent on a given day doing their algebra homework. We received the following data:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.
With this data series, we can determine how many minutes students spent on average doing their algebra homework.
To do this, these numbers must be added and the sum divided by 12.
= = 27
The resulting number 27 is called arithmetic mean considered series of numbers.
No. 1. Find the arithmetic mean of numbers:
A) 24, 22, 27, 20.16, 31
B) 11, 9, 7, 6, 2, 0.1
C) 30, 5, 23, 5, 28, 30
D) 144, 146, 114, 138.
No. 2. The table shows data on the sale during the week of potatoes brought to the vegetable tent:
How many potatoes were sold daily this week on average?
No. 3. In the certificate of secondary education, four friends - school graduates - had the following marks:
Ilyin: 4, 4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 4, 5, 4, 4
Romanov: 3, 3, 4, 4, 4, 4, 4, 3, 4, 4, 4, 5, 3, 4, 4
Semenov: 3, 4, 3, 3, 3, 3, 4, 3, 3, 3, 3, 4, 4, 5, 4
Popov: 5, 5, 5, 5, 5, 4, 4, 5, 5, 5, 5, 5, 4, 4, 4.
With what average score did each of these graduates graduate from high school?
- Sweep row of numbers
The range of a series is found when they want to determine how large the spread of data in a series is.
No. 1. Each of the 24 participants in the shooting competition fired ten shots. Noting each time, the number of hits on the target received the following series of data:
6, 5, 5, 6, 8, 3, 7, 6, 8, 5, 4, 9, 7, 7, 9, 8, 6, 6, 5, 6, 4, 3, 6, 5.
Find the range for this series.
No. 2. At the figure skating competition, the judges gave the athlete the following marks:
5,2; 5,4; 5,5; 5,4; 5,1; 5,1; 5,4; 5,5; 5,3.
For the resulting series of numbers, find the range and arithmetic mean. What is the meaning of each of these indicators?
No. 3. Find the range of a series of numbers.
A) 32, 26, 18, 26, 15, 21, 26;
B) 21, 18.5, 25.3, 18.5, 17.9;
C) 67.1, 68.2, 67.1, 70.4, 68.2;
D) 0.6, 0.8, 0.5, 0.9, 1.1.
- Fashion series of numbers
A series of numbers may have more than one mode or none at all.
47, 46, 50, 52, 47, 52, 49, 45, 43, 53 - (has)
69, 68, 66, 70, 67, 71, 74, 63, 73, 72 - (does not have)
Example. Let, after taking into account the parts manufactured during the shift by the workers of one team, we received the following series of data:
36, 35, 35,36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38 ,38, 39 ,39, 36.
Find for him the mode of a series of numbers. To do this, it is convenient to preliminarily compile an ordered series of numbers from the obtained data, i.e. such a series in which each subsequent number is less (or more) than the previous one.
Got:
35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 38, 38, 38, 39, 39, 39 ,39.
Answer. Number 36 is the mode of this series of numbers.
No. 1. Find the fashion of a series of numbers.
45, 48, 85, 31, 23, 45, 67, 45, 19, 48, 45, 85, 19, 27,45, 62, 45, 23, 67, 45, 89, 19, 87, 45, 56, 45, 43, 23, 12, 45, 78, 28, 19, 45, 65, 45, 81, 83, 45.
No. 2. The table contains the results of daily measurements at the weather station at noon of air temperature (in degrees Celsius) during the first decade of March:
Find the mode of a series of numbers and draw a conclusion on what dates in March the air temperature was the same. Find the average air temperature. Make a table of deviations from the average air temperature at noon on each day of the decade.
No. 3. The table shows the number of parts manufactured per shift by workers of one team:
For the series of numbers presented in the table, find the mode. What is the meaning of this indicator?
Median as a statistical characteristic.
- The median of an ordered series of numbers with an odd number of members is the number written in the middle, and the median of an ordered series of numbers with an even number of members is the arithmetic mean of the two numbers written in the middle.
Median of an arbitrary series of numbers is called the median of the corresponding ordered series.
The table shows the electricity consumption in January by residents of nine apartments:
Let's make an ordered series from the data given in the table:
64, 72, 72, 75, 78, 82, 85, 91, 93.
There are nine numbers in the resulting ordered series. It is easy to see that in the middle of the row is the number 78 : four numbers are written to the left of it and four numbers to the right. They say that the number 78 is the middle number, or, in other words, median, the ordered series of numbers under consideration (from the Latin word mediana which means "medium"). This number is considered the median of the original data series.
Suppose that when collecting data on electricity consumption, a tenth was added to the indicated nine apartments. We got this table:
As in the first case, we present the received data as an ordered series of numbers:
64, 72, 72, 75, 78, 82, 85, 88, 91, 93.
This number series has an even number of members and there are two numbers located in the middle of the series: 78 and 82. Let's find the arithmetic mean of these numbers: =80. The number 80, not being a member of the series, divides this series into two groups of equal size: to the left of it there are five members of the series and to the right there are also five members of the series:
64, 72, 72, 75, , 85, 88, 91, 93.
It is said that in this case the median of the ordered series under consideration, as well as the original data series recorded in the table, is the number 80 .
No. 1. Find the median of a series of numbers:
A) 30, 32, 37, 40, 41, 42, 45, 49, 52;
B) 102, 104, 205, 207, 327,408,417;
C) 16, 18, 20, 22, 24, 26;
D) 1.2 1.4 2.2, 2.6, 3.2 3.8 4.4 5, 6.
No. 2. The table shows the number of visitors to the exhibition on different days of the week:
Find the median of a series of numbers. Build a histogram and see on which day there were more visitors.
No. 3. Below is the average daily processing of sugar (in thousand centners) by the sugar industry plants in some regions:
12,2, 13,2, 13,7, 18,0 18,6 12,2 18,5 12,4 14,2 17,8.
Find the median for the given data series. What characterizes this indicator?
Assignments for independent work.
1. Three candidates will run for mayor of the city: Alekseeva, Ivanov, Karpov (let's denote them by letters A, I, K). By conducting a survey of 50 voters, we found out which of the candidates they are going to vote for. We got the following data: I, A, I, I, K, K, I, I, I, A, K, A, A, A, K, K, I, K, A, A, I, K, I, I, K, I, K, A, I, I, I, A, I, I, K, I, A, I, K, K, I, K, A, I, I, I, A, A, K, I. Present this data in the form of a table of frequencies.
2. The table shows the student's expenses for 4 days:
Someone processed this data and wrote down the following:
a) 18 + 25 + 24 + 25 = 92; 92:4 = 23. (……………………….………..) = 23(p.)
b) 18, 24, 25, 25; (24 + 25): 2 = 24.5. (………………………….) = 24.5 (p.)
c) 18, 25, 24, 25; (…………………….) = 25 (p.)
d) 25 - 18 \u003d 7. (……………………………) \u003d 7 (p.)
Names of statistical characteristics are given in parentheses. Determine which of the statistics is in each task.
3. During the year, Lena received the following marks for the control tests in algebra: one "deuce", three "triples", four "fours" and three "fives". Find the mean, mode, and median of this data.
4. The president of the company receives 100,000 rubles. per year, four of his deputies receive 20,000 rubles each. per year, and 20 employees of the company receive 10,000 rubles. in year. Find all averages (arithmetic mean, mode, median) of salaries in the company.
Visual presentation of statistical information.
1. One of the well-known ways to represent a series of data is to construct bar charts.
Column charts are used when they want to illustrate the dynamics of data changes over time or the distribution of data obtained as a result of statistical studies.
A bar chart is made up of rectangles of equal width, with arbitrarily chosen bases, spaced at the same distance from each other. The height of each rectangle is equal (with the selected scale) to the value under study (frequency).
2. For a visual representation of the relationship between the parts of the population under study, it is convenient to use pie charts.
If the result of a statistical study is presented in the form of a table of relative frequencies, then to construct a pie chart, the circle is divided into sectors, the central angles of which are proportional to the relative frequencies determined for each group.
The pie chart retains its visibility and expressiveness only with a small number of parts of the population.
3. The dynamics of changes in statistical data over time is often illustrated using landfill. To construct a polygon, points are marked in the coordinate plane, the abscissas of which are points in time, and the ordinates are the corresponding statistical data. By connecting these points in series with segments, a polyline is obtained, which is called a polygon.
If the data is presented in the form of a table of frequencies or relative frequencies, then to build a polygon, points are marked in the coordinate plane, the abscissas of which are statistical data, and the ordinates are their frequencies or relative frequencies. By connecting these points in series with segments, a data distribution polygon is obtained.
4. Interval data series are depicted using histograms. The histogram is a stepped figure made up of closed rectangles. The base of each rectangle is equal to the length of the interval, and the height is equal to the frequency or relative frequency. In a histogram, unlike a bar chart, the bases of the rectangles are not chosen arbitrarily, but are strictly determined by the length of the interval.
Tasks for independent decision.
No. 1. Build a bar chart showing the distribution of shop workers by wage categories, which is presented in the following table:
No. 2. In a farm, the areas allocated for grain crops are distributed as follows: wheat - 63%; oats - 16%; millet - 12%; buckwheat - 9%. Construct a pie chart illustrating the distribution of area devoted to cereals.
No. 3. The table shows the grain yield in 43 farms of the region.
Construct a polygon for the distribution of farms by grain yield.
No. 4. When studying the distribution of families living in the house, by the number of family members, a table was compiled in which, for each family with the same number of members, the relative frequency is indicated:
Using the table, construct a polygon of relative frequencies.
No. 5. Based on the survey, the following table was compiled of the distribution of students by the time they spent watching television on a certain school day:
| Time, h | Frequency |
| 0–1 | 12 |
| 1–2 | 24 |
| 2–3 | 8 |
| 3–4 | 5 |
Using the table, build the corresponding histogram.
No. 6. In the health camp, the following data were obtained on the weight of 28 boys (with an accuracy of 0.1 kg):
21,8; 29,3, 30,2, 20,0, 23,8, 24,5, 24,0, 20,8, 22,0, 20,8, 22,0, 25,0, 25,5, 28,2, 22,5, 21,0, 24,5, 24,8, 24,6, 24,3, 26,0, 26,8, 23,2, 27,0, 29,5, 23,0 22,8, 31,2.
Fill in the tables using this data:
| Weight, kg | Frequency | Weight, kg | Frequency | |
| 20–22 | 20–23 | |||
| 22–24 | 23–26 | |||
| 24–26 | 26–29 | |||
| 26–28 | 29–32 | |||
| 28–30 | ||||
| 30–32 |
According to these tables, build two histograms on different figures on the same scale. What do these histograms have in common and how do they differ?
No. 7. According to quarterly grades in geometry, students of one class were distributed as follows: “5” - 4 students; “4” - 10 students; “3” - 18 students; "2" - 2 students. Construct a bar chart that characterizes the distribution of students by quarter geometry grades.
References:
- Tkacheva M.V."Elements of statistics and probability": textbook. allowance for 7–9 cells. general education institutions / M.V. Tkacheva, N.E. Fedorov. - M .: Education, 2005.
- Makarychev Yu.N. Algebra: elements of statistics and probability theory: textbook. allowance for 7–9 cells. general education Institutions / Yu.N. Makarychev, N.G. Mindyuk; ed. S.A. Telyakovsky - M. : Education, 2004.
- Sheveleva N.V. Mathematics (algebra, elements of statistics and probability theory). Grade 9 / N.V. Sheveleva, T.A. Koreshkova, V.V. Miroshin. - M. : National education, 2011.
The following systems can be used for tennis competitions:
The Olympic system, in addition to the classic version, has several modifications:
Under the Olympic system, a participant or team (hereinafter in the text the words "player" or "participant" will also mean "team") is eliminated from the competition after the first defeat, and with improved Olympic systems - after several defeats.
The round robin system involves the participation of players in the competition until each participant meets with all the others. The winner is the participant with the most points.
The mixed system is based on the principle of combining the circular system and the Olympic system. As a rule, at the preliminary (initial) stage of the competition, a circular system is used, and at the final stage, the Olympic system. At the preliminary stage of the draw, the participants are divided into subgroups according to the qualification or territorial (as a rule, in team competitions). The strongest in the subgroups go to the final stage, where the Olympic system is applied.
Let's take a closer look at each of the systems.
(sometimes called the "elimination system") is used only to determine the winner. After the first defeat, the participant is eliminated from the competition. As a result, the winner is the participant who has not lost a single match.
Used in all tournaments ITF, ATP, WTA(except for the final tournament of the strongest) and at the Olympic Games.
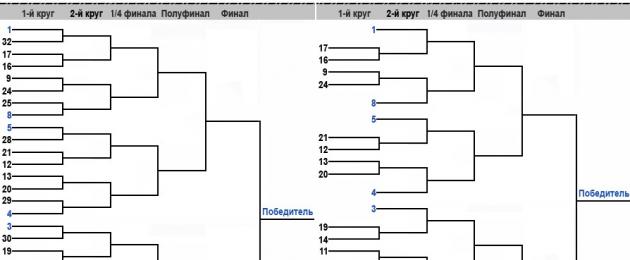
The principle of appointing matches between the participants of the competition and recording their results is carried out according to a special table, which is commonly called the "tournament grid". It has an unchanged scheme and is formed for the number of participants 8; sixteen; 32; 64; 128. Tournament draws may also be used for 24 or 48 participants, which are incomplete draws for 32 and 64 participants, respectively. As an example, tournament brackets for 32 and 24 participants, respectively, are given. The maximum number of players, limited by the above series of numbers, is called size tournament grid.

In the leftmost row, the names of the participants are located on the corresponding lines according to one of three options:
- seeding (placement) based on the rating (in this case, the first matches between the participants are formed according to the principle "strong against weak");
- lots (randomly);
- combinations of the first two options: first, a certain number of participants with the best rating are sown, and then a blind lot is drawn for the rest of the participants.
Table 1 shows the allowed number of seeded players depending on the size of the tournament bracket.
Table 1
The principle of drawing up the tournament grid is described in the section "Compilation of tournament grids".
The competition is held in several circles or rounds (in international terminology "rounds" - Round). Each circle in the tournament grid corresponds to one vertical row. Each such row consists of horizontal lines in which the names of the participants or the names of the teams are indicated. In each circle, participants meet among themselves, whose names are located in the same row on adjacent (adjacent) lines connected to the right by a vertical line, that is, the participants are divided into pairs in which they meet each other.
Match Winners 1st circles fall into 2nd circle (in the tournament bracket - to the next vertical row), winners in matches 2nd circle - in 3rd etc.
A round in which 8 participants meet is called a quarter-final ( Quarterfinal), 4 participants – semi-finals ( semi-final, Semis), 2 participants – final ( Final). The winner of the final match becomes the winner ( Winner) competitions.
The dependence of the number of circles on the number of participants is shown in Table 2.
table 2
The number of game days required for the competition (assuming that each participant plays one match per day) is equal to the number of laps.
Total number of matches ( M O ) is determined by the formula M O \u003d N - 1 , where N - the number of participants.
Sometimes in competitions held according to the Olympic system, 3rd place is played between participants who have lost semi-final matches (for example, the Olympic Games).
The disadvantage of the Olympic system is that the promotion in the tournament grid is quite random. A obviously strong player can lose to a weak one ("well, it was not his day") and end his performances on this. At the same time, its winner, as a rule, loses in the next round. In addition, most participants are eliminated after a relatively small number of matches played.
Designed to play all the places where after each defeat the athlete is not eliminated from the competition, but only from the fight for a certain place. As a result, the winner is the participant who has not lost a single match, and the last place is occupied by the player who has not won a single victory. All other places are distributed among the rest of the participants, depending on the sequence of their victories and defeats.
The tournament is divided into several tournament brackets - main (winners bracket) and additional (losers brackets), which are called "repechage brackets". All participants start the tournament in the main draw. The principle of compiling the main grid is the same as in the Olympic system. The names of the participants fall into the additional brackets from the main one after the first defeat of the player, depending on which round he lost. In each round, starting from the second, there are participants who have the same sequence of victories and defeats in the previous rounds of the competition.
As an example, the main and additional grids for 16 participants are given.

Explanation. In the grid, each pair in the 1st round and in subsequent rounds is assigned its own number (numbering is conditional and is not used in the grids used in the competition). The player who loses the match in a pair is assigned a number corresponding to this pair with a “-” sign and is indicated in red. Of the losing participants, a repechage net is formed corresponding to a certain place being played.
By analogy with the grid for 16 participants, it is easy to form tournament grids for 24, 32, 64 participants.
The number of matches and rounds depending on the number of participants is given in Table 3.
Table 3
| Number of participants | Total matches | Number of matches in each round | |||||
|---|---|---|---|---|---|---|---|
| 1m | 2nd | 3m | 4th | 5th | 6th | ||
Allows participants who lose in the first rounds to continue participating until the next defeat. Additional brackets are drawn up as for the regular improved Olympic system, however, not all places are played in them. For example, for a grid of 16 participants, 1, 2, 3, 4, 5, 6, 9 and 10 places are determined, and for 64 participants - 1, 2, 3, 4, 5, 6, 9, 10, 17, 18, 33, 34. As an example, a tournament grid for 16 participants is given.

The principle of advancing participants in the main and additional grids is the same as explained in the previous version (advanced Olympic system).
According to this system, competitions with an entrance (starting) fee are often played.
A participant who loses one match during the entire competition will play only one match less than the winner of the competition.
Table 4 shows the total number of matches based on the number of participants.
Table 4
(sometimes called " backing track") involves the participation of the player up to 2 defeats. It is more objective than the Olympic system and all its varieties, but longer. The main distinguishing feature is that the player once lost does not lose the right to win the tournament.
The competition is held in two grids - upper (main) and lower (additional). As an example of a tournament bracket for 16 participants. In the main draw, matches take place according to the Olympic system.

In each pair of opponents, the winning participant advances to the next round. Participants who lose in the 1st round of the upper bracket move to the lower bracket in the 2nd round. In the future, the countdown of circles is carried out on the upper grid. The participant who loses in the 2nd round of the upper bracket falls into the lower bracket in the 3rd round, and so on.
The participant who loses in the lower bracket is eliminated from the competition.
In the last round (superfinal), the participant who passed through the main draw without defeat and the participant who reached the superfinal in the lower bracket meet. Third place goes to the loser of the final in the lower bracket.
- if the winner of the upper bracket wins, the competition ends, and if the winner of the lower bracket wins, then the participants play one more match (with a full super final);
- only one meeting is held (with a simple superfinal).
The advantage of this system is that it works the same for any number of participants and is the most objective in determining the winner and prize-winners. The disadvantage is the determination of only the first three places and in a large number of matches, as well as the difference in the number of matches that participants play to reach the final in the upper and lower brackets. For example, for a tournament with 8 participants, the finalist of the lower bracket must play 6 games more, with 16 participants - by 12, with 32 participants - by 24. However, those who have not lost to anyone play in the upper bracket, and we can assume that the higher the level of rivals compensates for the difference in the number of matches.
Table 5 shows the number of matches by brackets (upper/lower) when using the first version of the system.
Table 5
| Number of participants | Number of matches | 1 circle | 2 circle | 3 circle | 4 circle | 5 circle | 6 circle | 7 circle | 8 circle | 9 circle |
|---|---|---|---|---|---|---|---|---|---|---|
This system was used during the final WTA tournaments in 1978-1982.
To reduce the number of matches, a grid can be used in which once losers continue to fight not for first place, but for third. The mesh is shown below.

IMPROVED OLYMPIC SYSTEM WITH CONFUSION PRIZE involves holding a repechage competition with those participants who lost in the first round. The winner of the consolation tournament is awarded a commemorative prize or award. Both tournament grids: main and repechage are compiled as for the usual Olympic system (with elimination), i.e., for example, for 22 participants who took part in the competition, 1st, 2nd and 13th places are played.
The advantage of such a system is that a strong participant who is not in the mood for a match or who for some other reason loses to a obviously weaker opponent (which often happens) has the opportunity to continue playing in the tournament and compete for a consolation prize, which can be quite worthy. According to such a system, for example, World Championships among veterans are held.
ROUND SYSTEM provides for the drawing of all places during matches between all participants in the competition.
The places occupied by the participants are determined by the number of points scored. For a won match (personal or team) one point is awarded, for a lost one - zero. In case of non-appearance of the participant for the match or refusal from it, a defeat is counted to him (without specifying the score). If the participant has played less than half of the matches provided for in the competition table, all his results will be canceled (only to determine the place in the table, but not to be taken into account in the classification).
In tennis, as a rule, the result of the match is entered into the standings only in the field of the winner. If the results of any participant are viewed in the row of the table and the corresponding field contains only " 0 ”, then it is not difficult to find the field of his opponent for this match (diagonally, taking into account the number of the arrangement) and clarify the score. In the example, the account is indicated in all fields.
The winner is the participant with the most points.
If two participants have equal points (in a personal or team competition), the winner of the match between them gets the advantage. In case of equality of points among three or more participants in an individual competition, the advantage is received by the participant according to the following consistently applied principles :
1. In matches between them:
b) by the best difference between won and lost sets;
c) by the best difference between won and lost games.
2. In all matches:
b) by the best difference between won and lost games;
c) by lot.
In the example, the first three participants scored the same number of points - 5 each. The number of points scored between them also turned out to be the same - 1 each. When calculating won and lost sets, the indicators are as follows: 1st participant - 4 (winning) /3 (lost); 2nd participant - 4/3 ; 3rd participant - 5/2 . Best set difference 3rd participant, he is the winner. At 1st and 2nd participant, the difference is the same. The distribution of places among the winners, in this case, is determined based on their personal meeting.
In case of equality of points among three or more participants in a team competition, the team gains an advantage in the following successively applied indicators:
1. In team matches between them:
a) by the number of points scored;
b) by the best difference between won and lost singles and doubles matches;
c) by the best difference between won and lost sets;
d) by the best difference between won and lost games
2. In all team matches:
a) by the best difference between won and lost sets;
b) by the best difference between won and lost games.
If a participant refuses after the first round, there are three options for taking into account (or not taking into account) the results of matches played by him:
- cancellation of results;
- awarding technical victories in the remaining matches;
- if the eliminated participant has played half or more of his matches, then in the remaining matches his opponents are awarded a technical victory, otherwise the results of his games are canceled.
In the first case, the participants find themselves in unequal conditions: those who won the eliminated player lose points, while those who lose to him lose nothing. In the second, those who did not have time to meet him will get an advantage. Therefore, it is recommended to use the third option.
How a decision will be made in the event of a participant's elimination should be specified in the Regulations of the tournament.
The order of matches of opponents with each other in a round-robin system is not of great importance, but it is recommended to schedule according to the principle below (Tal.6).
Table 6
| For 8 participants | ||||||
|---|---|---|---|---|---|---|
|
5↔6 |
||||||
It is based on the principle of rotating all numbers counterclockwise around the first number. In each subsequent round, the numbers are shifted by one order. With an even number of players, there will be an odd number of circles, i.e. one less than the total number of participants. If the number of participants is odd, then the laps are counted from an even number, i.e. one more. In this case, the last number in the table remains unoccupied and the player who gets the match in the next round with this number is free.
The number of game days required to hold a round robin competition (provided that each participant plays no more than one match per day) is one less than the number of participants, if it is even, and is equal to the number of participants, if it is odd.
Total number of matches ( M K ) is determined by the formula: M K \u003d N (N - 1) / 2 , where N - the number of participants in the competition.
The number of laps (if there is a technical possibility of holding a sufficient number of matches at the same time) is equal to N–1 for an even number of participants and N for an odd one (in the latter case, each participant misses one round in which he has no opponent).
The advantages of this system are that the maximum possible objectivity of the tournament is achieved: everyone will play with everyone, the final result is determined by the balance of power of all pairs of opponents.
The disadvantage is a large number of matches (the maximum among all systems) and, accordingly, a significant number of days for the tournament. The number of meetings increases quadratically with the number of participants. The practical limit for a round robin in tennis is 8 players. As a result, large round robin tournaments are rare. In addition, towards the end of the tournament there are matches that partially or completely do not affect the positions of certain participants. And that can lead to match-fixing.
A two-stage circular system is possible. At the preliminary stage, the participants are divided into several subgroups: 3, 4, 5, etc., as a rule, 3-4 participants in a subgroup, and then at the main (final) stage, the winners of the subgroups form a group in which they also play in a round robin system to identify the winner and prize-winners. If there are two subgroups, two participants with the best results from each subgroup go to the main stage. In the example, there are 4 subgroups with 4 participants each, but in one or three subgroups there may be 3 participants.
According to this system, it is possible to draw further places at the main stage. To do this, tables are compiled that combine separately the 2nd, 3rd, 4th and subsequent places.
MIXED SYSTEMS are various combinations of the circular, Olympic and advanced Olympic systems, each of which can be used at different stages of the competition. The most widespread is the mixed system, which provides for the first (preliminary) stage of the competition to hold matches in a round robin system in subgroups, and in the final (final) - according to the Olympic (playoff) or improved Olympic system. The number of groups and the number of participants from each group participating in the final part of the competition must be indicated in the Regulations of the tournament. The example shows a mixed system, consisting at the preliminary stage of 4 groups of three to four participants in each, meeting in a round robin system, with the subsequent formation of the Olympic bracket from the two best participants from each group.
Groups, based on the seeding and lot of participants, are formed according to the so-called "Snake" scheme. Table 7 shows an example for 4 groups.
Table 7
| Group I | Group II | Group III | Group IV |
|---|---|---|---|
|
etc. |
The number of rows corresponds to the number of groups being formed, the number of rows corresponds to the number of participants in each group.
If there are only two groups, then at the final stage the following can be carried out:
- Docking matches between participants who took the same places in groups. The winners in subgroups at the first stage of the competition meet among themselves for 1-2 places, those who took 2 places in groups - for 3-4 places, etc.
- Semi-finals in which the winner from one group meets the player who took 2nd place from another group. The winners of the semi-finals meet in the final, and the match for 3rd place is played between the losing semi-finalists.
The group stage has its obvious pluses and minuses. On the one hand, it guarantees the participation of players in several matches (for example, with 4 participants - three matches). In addition, all participants have a chance to advance from the group to the final stage, even if they lose. On the other hand, the complexity of perception and the need to count sets, and sometimes games, to determine the winner of the group. Often, the players themselves do not always understand the essence of determining places in the group. For example, at the 2012 ATP Finals, Andy Murray, after winning the first set against Jo-Wilfried Tsonga in the last match (he had one win and one loss), asked the referee whether he was going to the semi-finals. And in the other group "B" group, David Ferrer was left out of the playoffs, despite two victories, as did Roger Federer and Juan Martin del Potro, who respectively took 1st and 2nd places.
- In contact with 0
- Google Plus 0
- OK 0
- Facebook 0