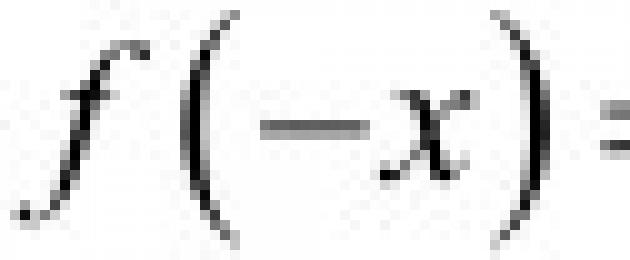Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.
How we use your personal information:
- The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.
1) Function domain and function range.
The domain of a function is the set of all valid valid argument values x(variable x), for which the function y = f(x) determined. The range of a function is the set of all real values y, which the function accepts.
In elementary mathematics, functions are studied only on the set of real numbers.
2) Function zeros.
Function zero is the value of the argument at which the value of the function is equal to zero.
3) Intervals of constant sign of a function.
Intervals of constant sign of a function are sets of argument values on which the function values are only positive or only negative.
4) Monotonicity of the function.
An increasing function (in a certain interval) is a function in which a larger value of the argument from this interval corresponds to a larger value of the function.
A decreasing function (in a certain interval) is a function in which a larger value of the argument from this interval corresponds to a smaller value of the function.
5) Even (odd) function.
An even function is a function whose domain of definition is symmetrical with respect to the origin and for any X from the domain of definition the equality f(-x) = f(x). The graph of an even function is symmetrical about the ordinate.
An odd function is a function whose domain of definition is symmetrical with respect to the origin and for any X from the domain of definition the equality is true f(-x) = - f(x). The graph of an odd function is symmetrical about the origin.
6) Limited and unlimited functions.
A function is called bounded if there is a positive number M such that |f(x)| ≤ M for all values of x. If such a number does not exist, then the function is unlimited.
7) Periodicity of the function.
A function f(x) is periodic if there is a non-zero number T such that for any x from the domain of definition of the function the following holds: f(x+T) = f(x). This smallest number is called the period of the function. All trigonometric functions are periodic. (Trigonometric formulas).
19. Basic elementary functions, their properties and graphs. Application of functions in economics.
Basic elementary functions. Their properties and graphs
1. Linear function.
Linear function is called a function of the form , where x is a variable, a and b are real numbers.
Number A called the slope of the line, it is equal to the tangent of the angle of inclination of this line to the positive direction of the x-axis. The graph of a linear function is a straight line. It is defined by two points.
Properties of a Linear Function
1. Domain of definition - the set of all real numbers: D(y)=R
2. The set of values is the set of all real numbers: E(y)=R
3. The function takes a zero value when or.
4. The function increases (decreases) over the entire domain of definition.
5. A linear function is continuous over the entire domain of definition, differentiable and .
2. Quadratic function.
A function of the form, where x is a variable, coefficients a, b, c are real numbers, is called quadratic
Definition: A numerical function is a correspondence that associates each number x from some given set with a single number y.
Designation:
where x is the independent variable (argument), y is the dependent variable (function). The set of values of x is called the domain of the function (denoted D(f)). The set of values of y is called the range of values of the function (denoted E(f)). The graph of a function is the set of points in the plane with coordinates (x, f(x))
Methods for specifying a function.
- analytical method (using a mathematical formula);
- tabular method (using a table);
- descriptive method (using verbal description);
- graphical method (using a graph).
Basic properties of the function.
1. Even and odd
A function is called even if
– the domain of definition of the function is symmetrical about zero
f(-x) = f(x)
The graph of an even function is symmetrical about the axis 0y
A function is called odd if
– the domain of definition of the function is symmetrical about zero
– for any x from the domain of definition f(-x) = –f(x)
The graph of an odd function is symmetrical about the origin.
2. Frequency
A function f(x) is called periodic with period if for any x from the domain of definition f(x) = f(x+T) = f(x-T) .
The graph of a periodic function consists of unlimitedly repeating identical fragments.
3. Monotony (increasing, decreasing)
The function f(x) is increasing on the set P if for any x 1 and x 2 from this set such that x 1
The function f(x) decreases on the set P if for any x 1 and x 2 from this set, such that x 1 f(x 2) .
4. Extremes
A point X max is called a maximum point of the function f(x) if for all x from some neighborhood of X max the inequality f(x) f(X max) is satisfied.
The value Y max =f(X max) is called the maximum of this function.
X max – maximum point
At max - maximum
A point X min is called a minimum point of the function f(x) if for all x from some neighborhood of X min, the inequality f(x) f(X min) is satisfied.
The value Y min =f(X min) is called the minimum of this function.
X min – minimum point
Y min – minimum
X min , X max – extremum points
Y min , Y max – extrema.
5. Zeros of the function
The zero of a function y = f(x) is the value of the argument x at which the function becomes zero: f(x) = 0.
X 1, X 2, X 3 – zeros of the function y = f(x).
Tasks and tests on the topic "Basic properties of a function"
- Function Properties - Numerical functions 9th grade
Lessons: 2 Assignments: 11 Tests: 1
- Properties of logarithms - Exponential and logarithmic functions grade 11
Lessons: 2 Assignments: 14 Tests: 1
- Square root function, its properties and graph - Square root function. Properties of square root grade 8
Lessons: 1 Assignments: 9 Tests: 1
- Functions - Important topics for reviewing the Unified State Examination in mathematics
Tasks: 24
- Power functions, their properties and graphs - Degrees and roots. Power functions grade 11
Lessons: 4 Assignments: 14 Tests: 1
Having studied this topic, you should be able to find the domain of definition of various functions, determine the monotonicity intervals of a function using graphs, and examine functions for evenness and oddness. Let's consider solving similar problems using the following examples.
Examples.
1. Find the domain of definition of the function.
Solution: the domain of definition of the function is found from the condition
therefore, the function f(x) is even.
Answer: even
D(f) = [-1; 1] – symmetrical about zero.
| 2) |
hence the function is neither even nor odd.
Answer: neither even nor uneven.
A function graph is a visual representation of the behavior of a function on a coordinate plane. Graphs help you understand various aspects of a function that cannot be determined from the function itself. You can build graphs of many functions, and each of them will be given a specific formula. The graph of any function is built using a specific algorithm (in case you have forgotten the exact process of graphing a specific function).
Steps
Graphing a Linear Function
- If the slope is negative, the function is decreasing.
-
From the point where the straight line intersects the Y axis, plot a second point using vertical and horizontal distances. A linear function can be graphed using two points. In our example, the intersection point with the Y axis has coordinates (0.5); From this point, move 2 spaces up and then 1 space to the right. Mark a point; it will have coordinates (1,7). Now you can draw a straight line.
Using a ruler, draw a straight line through two points. To avoid mistakes, find the third point, but in most cases the graph can be plotted using two points. Thus, you have plotted a linear function.
Determine whether the function is linear. The linear function is given by a formula of the form F (x) = k x + b (\displaystyle F(x)=kx+b) or y = k x + b (\displaystyle y=kx+b)(for example, ), and its graph is a straight line. Thus, the formula includes one variable and one constant (constant) without any exponents, root signs, or the like. If a function of a similar type is given, it is quite simple to plot a graph of such a function. Here are other examples of linear functions:
Use a constant to mark a point on the Y axis. The constant (b) is the “y” coordinate of the point where the graph intersects the Y axis. That is, it is a point whose “x” coordinate is equal to 0. Thus, if x = 0 is substituted into the formula, then y = b (constant). In our example y = 2 x + 5 (\displaystyle y=2x+5) the constant is equal to 5, that is, the point of intersection with the Y axis has coordinates (0.5). Plot this point on the coordinate plane.
Find the slope of the line. It is equal to the multiplier of the variable. In our example y = 2 x + 5 (\displaystyle y=2x+5) with the variable “x” there is a factor of 2; thus, the slope coefficient is equal to 2. The slope coefficient determines the angle of inclination of the straight line to the X axis, that is, the greater the slope coefficient, the faster the function increases or decreases.
Write the slope as a fraction. The angular coefficient is equal to the tangent of the angle of inclination, that is, the ratio of the vertical distance (between two points on a straight line) to the horizontal distance (between the same points). In our example, the slope is 2, so we can state that the vertical distance is 2 and the horizontal distance is 1. Write this as a fraction: 2 1 (\displaystyle (\frac (2)(1))).
Plotting points on the coordinate plane
- -1: -1 + 2 = 1
- 0: 0 +2 = 2
- 1: 1 + 2 = 3
-
Plot the points on the coordinate plane. For each pair of coordinates, do the following: find the corresponding value on the X axis and draw a vertical line (dotted); find the corresponding value on the Y axis and draw a horizontal line (dashed line). Mark the intersection point of the two dotted lines; thus, you have plotted a point on the graph.
Erase the dotted lines. Do this after plotting all the points on the graph on the coordinate plane. Note: the graph of the function f(x) = x is a straight line passing through the coordinate center [point with coordinates (0,0)]; the graph f(x) = x + 2 is a line parallel to the line f(x) = x, but shifted upward by two units and therefore passing through the point with coordinates (0,2) (because the constant is 2).
Define a function. The function is denoted as f(x). All possible values of the variable "y" are called the domain of the function, and all possible values of the variable "x" are called the domain of the function. For example, consider the function y = x+2, namely f(x) = x+2.
Draw two intersecting perpendicular lines. The horizontal line is the X axis. The vertical line is the Y axis.
Label the coordinate axes. Divide each axis into equal segments and number them. The intersection point of the axes is 0. For the X axis: positive numbers are plotted to the right (from 0), and negative numbers to the left. For the Y axis: positive numbers are plotted on top (from 0), and negative numbers on the bottom.
Find the values of "y" from the values of "x". In our example, f(x) = x+2. Substitute specific x values into this formula to calculate the corresponding y values. If given a complex function, simplify it by isolating the “y” on one side of the equation.
Graphing a Complex Function
-
Find the coordinates of several points and plot them on the coordinate plane. Simply select several x values and plug them into the function to find the corresponding y values. Then plot the points on the coordinate plane. The more complex the function, the more points you need to find and plot. In most cases, substitute x = -1; x = 0; x = 1, but if the function is complex, find three points on each side of the origin.
- In case of function y = 5 x 2 + 6 (\displaystyle y=5x^(2)+6) plug in the following x values: -1, 0, 1, -2, 2, -10, 10. You will get a sufficient number of points.
- Choose your x values wisely. In our example, it is easy to understand that the negative sign does not matter: the value of “y” at x = 10 and at x = -10 will be the same.
-
- If you don't know what to do, start by plugging different x values into the function to find the y values (and therefore the coordinates of the points). Theoretically, a graph of a function can be constructed using only this method (if, of course, one substitutes an infinite variety of “x” values).
Find the zeros of the function. The zeros of a function are the values of the x variable where y = 0, that is, these are the points where the graph intersects the X-axis. Keep in mind that not all functions have zeros, but they are the first step in the process of graphing any function. To find the zeros of a function, equate it to zero. For example:
Find and mark the horizontal asymptotes. An asymptote is a line that the graph of a function approaches but never intersects (that is, in this region the function is not defined, for example, when dividing by 0). Mark the asymptote with a dotted line. If the variable "x" is in the denominator of a fraction (for example, y = 1 4 − x 2 (\displaystyle y=(\frac (1)(4-x^(2))))), set the denominator to zero and find “x”. In the obtained values of the variable “x” the function is not defined (in our example, draw dotted lines through x = 2 and x = -2), because you cannot divide by 0. But asymptotes exist not only in cases where the function contains a fractional expression. Therefore, it is recommended to use common sense:
The length of the segment on the coordinate axis is determined by the formula:
The length of a segment on the coordinate plane is found using the formula:
To find the length of a segment in a three-dimensional coordinate system, use the following formula:
The coordinates of the middle of the segment (for the coordinate axis only the first formula is used, for the coordinate plane - the first two formulas, for a three-dimensional coordinate system - all three formulas) are calculated using the formulas:
Function– this is a correspondence of the form y= f(x) between variable quantities, due to which each considered value of some variable quantity x(argument or independent variable) corresponds to a certain value of another variable, y(dependent variable, sometimes this value is simply called the value of the function). Note that the function assumes that one argument value X only one value of the dependent variable can correspond at. However, the same value at can be obtained with different X.
Function Domain– these are all the values of the independent variable (function argument, usually this X), for which the function is defined, i.e. its meaning exists. The area of definition is indicated D(y). By and large, you are already familiar with this concept. The domain of definition of a function is otherwise called the domain of permissible values, or VA, which you have long been able to find.
Function Range are all possible values of the dependent variable of a given function. Designated E(at).
Function increases on the interval in which a larger value of the argument corresponds to a larger value of the function. The function is decreasing on the interval in which a larger value of the argument corresponds to a smaller value of the function.
Intervals of constant sign of a function- these are the intervals of the independent variable over which the dependent variable retains its positive or negative sign.
Function zeros– these are the values of the argument at which the value of the function is equal to zero. At these points, the function graph intersects the abscissa axis (OX axis). Very often, the need to find the zeros of a function means the need to simply solve the equation. Also, often the need to find intervals of constancy of sign means the need to simply solve the inequality.
Function y = f(x) are called even X
![]()
This means that for any opposite values of the argument, the values of the even function are equal. The graph of an even function is always symmetrical with respect to the ordinate axis of the op-amp.
Function y = f(x) are called odd, if it is defined on a symmetric set and for any X from the domain of definition the equality holds:
![]()
This means that for any opposite values of the argument, the values of the odd function are also opposite. The graph of an odd function is always symmetrical about the origin.
The sum of the roots of even and odd functions (the points of intersection of the x-axis OX) is always equal to zero, because for every positive root X has a negative root - X.
It is important to note: some function does not have to be even or odd. There are many functions that are neither even nor odd. Such functions are called general functions, and for them none of the equalities or properties given above is satisfied.
Linear function is a function that can be given by the formula:
The graph of a linear function is a straight line and in the general case looks like this (an example is given for the case when k> 0, in this case the function is increasing; for the occasion k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону - слева направо):

Graph of a quadratic function (Parabola)
The graph of a parabola is given by a quadratic function:
A quadratic function, like any other function, intersects the OX axis at the points that are its roots: ( x 1 ; 0) and ( x 2 ; 0). If there are no roots, then the quadratic function does not intersect the OX axis; if there is only one root, then at this point ( x 0 ; 0) the quadratic function only touches the OX axis, but does not intersect it. The quadratic function always intersects the OY axis at the point with coordinates: (0; c). The graph of a quadratic function (parabola) may look like this (the figure shows examples that do not exhaust all possible types of parabolas):

In this case:
- if the coefficient a> 0, in function y = ax 2 + bx + c, then the branches of the parabola are directed upward;
- if a < 0, то ветви параболы направлены вниз.
The coordinates of the vertex of a parabola can be calculated using the following formulas. X tops (p- in the pictures above) parabolas (or the point at which the quadratic trinomial reaches its largest or smallest value):
Igrek tops (q- in the figures above) parabolas or the maximum if the branches of the parabola are directed downwards ( a < 0), либо минимальное, если ветви параболы направлены вверх (a> 0), the value of the quadratic trinomial:
Graphs of other functions
Power function
Here are some examples of graphs of power functions:

Inversely proportional is a function given by the formula:
Depending on the sign of the number k An inversely proportional dependence graph can have two fundamental options:

Asymptote is a line that the graph of a function approaches infinitely close to but does not intersect. The asymptotes for the inverse proportionality graphs shown in the figure above are the coordinate axes to which the graph of the function approaches infinitely close, but does not intersect them.
Exponential function with base A is a function given by the formula:
a The graph of an exponential function can have two fundamental options (we also give examples, see below):

Logarithmic function is a function given by the formula:
Depending on whether the number is greater or less than one a The graph of a logarithmic function can have two fundamental options:

Graph of a function y = |x| looks like this:

Graphs of periodic (trigonometric) functions
Function at = f(x) is called periodic, if there is such a non-zero number T, What f(x + T) = f(x), for any X from the domain of the function f(x). If the function f(x) is periodic with period T, then the function:
Where: A, k, b are constant numbers, and k not equal to zero, also periodic with period T 1, which is determined by the formula:
Most examples of periodic functions are trigonometric functions. We present graphs of the main trigonometric functions. The following figure shows part of the graph of the function y= sin x(the entire graph continues indefinitely left and right), graph of the function y= sin x called sinusoid:

Graph of a function y=cos x called cosine. This graph is shown in the following figure. Since the sine graph continues indefinitely along the OX axis to the left and right:

Graph of a function y= tg x called tangentoid. This graph is shown in the following figure. Like the graphs of other periodic functions, this graph repeats indefinitely along the OX axis to the left and right.

And finally, the graph of the function y=ctg x called cotangentoid. This graph is shown in the following figure. Like the graphs of other periodic and trigonometric functions, this graph repeats indefinitely along the OX axis to the left and right.

Successful, diligent and responsible implementation of these three points will allow you to show an excellent result at the CT, the maximum of what you are capable of.
Found a mistake?
If you think you have found an error in the training materials, please write about it by email. You can also report an error on the social network (). In the letter, indicate the subject (physics or mathematics), the name or number of the topic or test, the number of the problem, or the place in the text (page) where, in your opinion, there is an error. Also describe what the suspected error is. Your letter will not go unnoticed, the error will either be corrected, or you will be explained why it is not an error.
- VKontakte 0
- Google+ 0
- OK 0
- Facebook 0