El razonamiento basado únicamente en hechos precisos e inferencias precisas a partir de esos hechos se denomina razonamiento estricto. En los casos en los que se deben utilizar hechos inciertos para tomar decisiones, el razonamiento riguroso resulta inadecuado. Por lo tanto, una de las mayores fortalezas de cualquier sistema experto es su capacidad para formar razonamientos en condiciones de incertidumbre con tanto éxito como lo hacen los expertos humanos. Este razonamiento no es riguroso. Podemos hablar con seguridad de presencia. lógica difusa.
Incertidumbre, y como consecuencia, la lógica difusa puede considerarse como una falta de información adecuada para la toma de decisiones. La incertidumbre se convierte en un problema porque puede dificultar la creación de la mejor solución e incluso provocar que se encuentre una solución deficiente. Cabe señalar que una solución de alta calidad encontrada en tiempo real a menudo se considera más aceptable que una solución mejor cuyo cálculo requiere mucho tiempo. Por ejemplo, retrasar el tratamiento para permitir pruebas adicionales puede provocar que el paciente muera antes de recibir el tratamiento.
El motivo de la incertidumbre es la presencia de diversos errores en la información. Clasificación simplificada Estos errores se pueden presentar en su división en los siguientes tipos:
- ambigüedad de la información, cuya aparición se debe al hecho de que cierta información puede interpretarse de diferentes maneras;
- información incompleta por falta de determinados datos;
- insuficiencia de información debido al uso de datos que no se corresponden con la situación real ( posibles razones son errores subjetivos: mentiras, desinformación, mal funcionamiento del equipo);
- errores de medición que surgen debido al incumplimiento de los requisitos de exactitud y exactitud de los criterios para la presentación cuantitativa de datos;
- errores aleatorios, cuya manifestación son fluctuaciones aleatorias en los datos en relación con su valor promedio (la razón puede ser: falta de confiabilidad del equipo, movimiento browniano, efectos térmicos, etc.).
Hoy en día, se ha desarrollado un número significativo de teorías de la incertidumbre que intentan eliminar algunos o incluso todos los errores y proporcionar inferencias lógicas confiables en condiciones de incertidumbre. Las teorías más utilizadas en la práctica son las basadas en la definición clásica de probabilidad y en la probabilidad posterior.
Una de las herramientas de resolución de problemas más antiguas e importantes. inteligencia artificial es probabilidad. Probabilidad es una forma cuantitativa de dar cuenta de la incertidumbre. La probabilidad clásica se origina a partir de una teoría propuesta por primera vez por Pascal y Fermat en 1654. Desde entonces, se ha trabajado mucho en el campo de la probabilidad y la implementación de numerosas aplicaciones de la probabilidad en ciencia, tecnología, negocios, economía y otros campos.
probabilidad clásica
probabilidad clásica También se llama probabilidad a priori, ya que su definición se aplica a sistemas ideales. El término “a priori” significa una probabilidad que se determina “a eventos”, sin tener en cuenta muchos factores que ocurren en mundo real. El concepto de probabilidad a priori se extiende a eventos que ocurren en sistemas ideales que son propensos al desgaste o a la influencia de otros sistemas. En un sistema ideal, la ocurrencia de cualquiera de los eventos ocurre de la misma manera, haciendo mucho más fácil su análisis.
La fórmula fundamental de la probabilidad clásica (P) se define de la siguiente manera:
En esta fórmula W.- el número de eventos esperados, y norte- el número total de eventos con iguales probabilidades que son posibles resultados de un experimento o prueba. Por ejemplo, la probabilidad de obtener cualquier arista hexagonal. dado es 1/6, y sacar cualquier carta de una baraja que contenga 52 cartas diferentes es 1/52.
Axiomas de la teoría de la probabilidad.
Se puede crear una teoría formal de la probabilidad sobre la base de tres axiomas:

Los axiomas anteriores permitieron sentar las bases de la teoría de la probabilidad, pero no consideran la probabilidad de que ocurran eventos en sistemas reales no ideales. A diferencia del enfoque a priori, en sistemas reales, para determinar la probabilidad de algún evento EDUCACIÓN FÍSICA), el método utilizado para determinar probabilidad experimental como límite de distribución de frecuencia:

Probabilidad posterior
En esta fórmula f(E) denota la frecuencia de ocurrencia de algún evento entre norte-número de observaciones de resultados globales. Este tipo de probabilidad también se llama probabilidad posterior, es decir. probabilidad determinada “después de los acontecimientos”. La base para determinar la probabilidad posterior es la medición de la frecuencia con la que ocurre un evento durante un gran número de ensayos. Por ejemplo, determinar el tipo social de un cliente bancario solvente basándose en la experiencia empírica.
Los acontecimientos que no son mutuamente excluyentes pueden influirse entre sí. Estos eventos se clasifican como complejos. La probabilidad de eventos complejos se puede calcular analizando sus correspondientes espacios muestrales. Estos espacios muestrales se pueden representar mediante diagramas de Venn, como se muestra en la figura. 1

Fig. 1 Espacio muestral para dos eventos no mutuamente excluyentes
La probabilidad de que ocurra el evento A, que se determina teniendo en cuenta el hecho de que ocurrió el evento B, se llama probabilidad condicional y se denota P(A|B). La probabilidad condicional se define de la siguiente manera:

probabilidad previa
En esta fórmula, la probabilidad P(B) no debe ser igual a cero y representa una probabilidad a priori que se determina antes de que se conozca otra información adicional. probabilidad previa, que se utiliza en relación con el uso de probabilidad condicional, a veces se denomina probabilidad absoluta.
Existe un problema que es esencialmente lo opuesto al problema de calcular la probabilidad condicional. Consiste en determinar la probabilidad inversa, que muestra la probabilidad de un evento anterior teniendo en cuenta aquellos eventos ocurridos en el futuro. En la práctica, este tipo de probabilidad ocurre con bastante frecuencia, por ejemplo, durante diagnósticos médicos o diagnósticos de equipos, en los que se identifican ciertos síntomas y la tarea es encontrar una posible causa.
Para resolver este problema, utilice Teorema de Bayes, lleva el nombre del matemático británico del siglo XVIII Thomas Bayes. La teoría bayesiana se utiliza ahora ampliamente para analizar árboles de decisión en economía y ciencias sociales. El método de búsqueda de soluciones bayesianas también se utiliza en el sistema experto PROSPECTOR al identificar sitios prometedores para la exploración mineral. El sistema PROSPECTOR ganó gran popularidad como el primer sistema experto con el que se descubrió un valioso yacimiento de molibdeno valorado en 100 millones de dólares.
Un evento aleatorio se evalúa mediante un número que determina la intensidad de la manifestación de este evento. este numero se llama probabilidad eventos PAG()
. Probabilidad de un evento elemental –  . La probabilidad de un evento es una medida numérica del grado de objetividad, la posibilidad de este evento. Cuanto mayor sea la probabilidad, más posible será el evento.
. La probabilidad de un evento es una medida numérica del grado de objetividad, la posibilidad de este evento. Cuanto mayor sea la probabilidad, más posible será el evento.
Cualquier evento que coincida con todo el espacio de resultados. S, llamado evento confiable, es decir. tal evento que como resultado del experimento necesariamente debe ocurrir (por ejemplo, la pérdida de cualquier número de puntos del 1 al 6 en un dado). Si el evento no pertenece al conjunto S, entonces se considera imposible(por ejemplo, lanzar un número mayor que 6 en un dado). La probabilidad de un evento imposible es 0, la probabilidad de un evento determinado es 1. Todos los demás eventos tienen una probabilidad de 0 a 1.
Eventos mi Y  son llamados opuesto, Si mi llega cuando no llega
son llamados opuesto, Si mi llega cuando no llega  . Por ejemplo, evento mi– “obtener un número par de puntos”, entonces el evento
. Por ejemplo, evento mi– “obtener un número par de puntos”, entonces el evento  - “sacar un número impar de puntos”. Dos eventos mi 1
Y mi 2
son llamados incompatible, si no hay un resultado común a ambos eventos.
- “sacar un número impar de puntos”. Dos eventos mi 1
Y mi 2
son llamados incompatible, si no hay un resultado común a ambos eventos.
Para determinar las probabilidades de eventos aleatorios se utilizan métodos directos o indirectos. Al calcular directamente la probabilidad, se distinguen esquemas de cálculo a priori y a posteriori, cuando realizar observaciones (experimentos) o contar a priori el número de experimentos metro, en el que se manifestó el evento, y el número total de experimentos realizados norte. Los métodos indirectos se basan en la teoría axiomática. Dado que los eventos se definen como conjuntos, todas las operaciones de teoría de conjuntos se pueden realizar sobre ellos. La teoría de conjuntos y el análisis funcional fueron propuestos por el académico A.N. Kolmogorov y formó la base de la teoría axiomática de la probabilidad. Presentemos los axiomas de probabilidad.
AxiomaI. Campo de eventoF(S) es un álgebra de conjuntos.
Este axioma apunta a la analogía entre la teoría de conjuntos y la teoría de la probabilidad.
AxiomaII.
a cada conjunto deF(S) está asociado con un número real P(
deF(S) está asociado con un número real P( ), llamada probabilidad del evento
), llamada probabilidad del evento :
:
dado que S 1 S 2 = (para eventos incompatibles S 1 Y S 2 ), o para un conjunto de eventos incompatibles
Dónde norte– el número de eventos elementales (resultados posibles).
Probabilidad evento al azar
|
|
Dónde  – probabilidades de eventos elementales
– probabilidades de eventos elementales  incluido en el subconjunto
incluido en el subconjunto  .
.
Ejemplo 1.1. Determinar la probabilidad de obtener cada número al lanzar un dado, obteniendo un número par, número 4 .
Solución. La probabilidad de que cada número caiga fuera del conjunto.
S = (1, 2, 3, 4, 5, 6)
 1/6.
1/6.
La probabilidad de obtener un número par, es decir  ={2,
4, 6},
basado en (1.6) será PAG(
={2,
4, 6},
basado en (1.6) será PAG(  )
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2
.
)
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2
.
Probabilidad de obtener un número 4
, es decir.  =
{4, 5, 6 }
,
=
{4, 5, 6 }
,
PAG(  )
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2.
)
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2.
Tareas para el trabajo independiente.
1. Hay 20 bolas blancas, 30 negras y 50 rojas en una canasta. Determine la probabilidad de que la primera bola extraída de la canasta sea blanca; negro; rojo.
2. Hay 12 niños y 10 niñas en el grupo de estudiantes. ¿Cuál es la probabilidad de que falten en el seminario de teoría de la probabilidad: 1) un joven; 2) niña; 3) ¿dos jóvenes?
3. Durante el año se distinguieron 51 días por el hecho de que en estos días llovió (o nevó). ¿Cuál es la probabilidad de que corra el riesgo de quedar atrapado en la lluvia (o nieve): 1) yendo a trabajar; 2) ¿vas a hacer una caminata durante 5 días?
4. Redacte un problema sobre el tema de esta tarea y resuélvalo.
1.1.3. Definición de probabilidad posterior (probabilidad estadística o frecuencia
evento al azar)
Al determinar la probabilidad a priori, se asumió que  igualmente probable. Esto no siempre es cierto; más a menudo sucede que
igualmente probable. Esto no siempre es cierto; más a menudo sucede que  en
en  . Suposición
. Suposición  conduce a un error en la determinación a priori PAG(
conduce a un error en la determinación a priori PAG(  )
según el esquema establecido. Para determinar
)
según el esquema establecido. Para determinar  , y en el caso general PAG(
, y en el caso general PAG(  )
realizar pruebas específicas. Durante tales pruebas (por ejemplo, los resultados de las pruebas en los Ejemplos 1.2, 1.3) en diferentes condiciones de diversas condiciones, influencias, factores causantes, es decir. en diferentes casos, varios resultados(varias manifestaciones de la información del objeto en estudio). Cada resultado de la prueba corresponde a un elemento.
)
realizar pruebas específicas. Durante tales pruebas (por ejemplo, los resultados de las pruebas en los Ejemplos 1.2, 1.3) en diferentes condiciones de diversas condiciones, influencias, factores causantes, es decir. en diferentes casos, varios resultados(varias manifestaciones de la información del objeto en estudio). Cada resultado de la prueba corresponde a un elemento.  o un subconjunto
o un subconjunto
 conjuntos S.Si definimos metro como el número de eventos favorables A resultados resultantes de norte pruebas, entonces la probabilidad posterior (probabilidad estadística o frecuencia de un evento aleatorio A)
conjuntos S.Si definimos metro como el número de eventos favorables A resultados resultantes de norte pruebas, entonces la probabilidad posterior (probabilidad estadística o frecuencia de un evento aleatorio A)
Basado en la ley números grandes Para
 A
A
|
|
aquellos. a medida que aumenta el número de ensayos, la frecuencia de un evento aleatorio (probabilidad posterior o estadística) tiende a la probabilidad de este evento.
Ejemplo 1.2. Determinada por el esquema de casos, la probabilidad de que salga cara al lanzar una moneda es 0,5. Debes lanzar una moneda 10, 20, 30... veces y determinar la frecuencia del evento aleatorio de cara después de cada serie de pruebas.
Solución. C. Poisson lanzó una moneda 24.000 veces y salió cara 11.998 veces. Entonces, según la fórmula (1.7), la probabilidad de que aterricen caras.
 .
.
Tareas para el trabajo independiente.
Basado en gran material estadístico ( norte ) Se obtuvieron los valores de las probabilidades de aparición de letras individuales del alfabeto ruso y el espacio () en los textos, que se dan en la Tabla 1.1.
Tabla 1.1. Probabilidad de que aparezcan letras del alfabeto en el texto.
|
| ||||||||
|
| ||||||||
|
| ||||||||
|
|
Tome una página de cualquier texto y determine la frecuencia de aparición de diferentes letras en esa página. Aumente la extensión de las pruebas a dos páginas. Compara los resultados obtenidos con los datos de la tabla. Obtener una conclusión.
Al disparar a objetivos, se obtuvo el siguiente resultado (ver Tabla 1.2).
Tabla 1.2. Resultados de tiro al blanco
¿Cuál es la probabilidad de que el objetivo sea alcanzado con el primer disparo si fuera más pequeño que “diez”, “nueve”, etc.?
3. Planificar y realizar pruebas similares para otros eventos. Presentar sus resultados.
I. Probabilidades condicionales. Probabilidad previa y posterior. 3
II.Eventos independientes. 5
III.Prueba de hipótesis estadísticas. Significancia estadística. 7
IV.Uso de la prueba chi-cuadrado 19
1. Determinar la confiabilidad de la diferencia entre un conjunto de frecuencias y un conjunto de probabilidades. 19
2. Determinación de la fiabilidad de la diferencia entre varios conjuntos de frecuencias. 26
TAREA INDEPENDIENTE 33
Lección No. 2
Probabilidades condicionales. Probabilidad previa y posterior.
Una variable aleatoria está especificada por tres objetos: un conjunto de eventos elementales, un conjunto de eventos y una probabilidad de eventos. Los valores que puede tomar una variable aleatoria se llaman acontecimientos elementales. Los conjuntos de eventos elementales se llaman eventos. Para numéricos y otros no muy complejos variables aleatorias cualquier conjunto específicamente dado de eventos elementales es un evento.
Pongamos un ejemplo: tirar un dado.
Hay 6 eventos elementales en total: “punto”, “2 puntos”, “3 puntos”... “6 puntos”. Evento – cualquier conjunto de eventos elementales, por ejemplo “par” - la suma de los eventos elementales “2 puntos”, “4 puntos” y “6 puntos”.
La probabilidad de cualquier evento elemental P(A) es 1/6:
la probabilidad de un evento es el número de eventos elementales incluidos en él, dividido por 6.
Muy a menudo, además de la probabilidad conocida de un evento, existe información adicional que cambia esta probabilidad. Por ejemplo, la mortalidad de los pacientes. de los ingresados en el hospital con úlcera gástrica sangrante aguda es aproximadamente el 10%. Sin embargo, si el paciente tiene más de 80 años, esta tasa de mortalidad es del 30%.
Para describir tales situaciones, el llamado probabilidades condicionales. Se denotan como P(A/B) y se leen "la probabilidad del evento A dado el evento B". Para calcular la probabilidad condicional, se utiliza la fórmula:
Volvamos al ejemplo anterior:
Supongamos que entre los pacientes ingresados en el hospital con úlcera gástrica sangrante aguda, el 20% son pacientes mayores de 80 años. Además, entre todos los pacientes, la proporción de pacientes fallecidos mayores de 80 años es del 6% (recordemos que la proporción de todas las muertes es del 10%). En este caso
Al definir probabilidades condicionales, los términos se utilizan a menudo a priori(literalmente – antes de la experiencia) y posteriormente(literalmente - después de la experiencia) probabilidad.
Al utilizar probabilidades condicionales, puede utilizar una probabilidad para calcular otras, por ejemplo, intercambiar un evento y una condición.
Consideremos esta técnica usando el ejemplo del análisis de la relación entre el riesgo de fiebre reumática (fiebre reumática) y uno de los antígenos que es un factor de riesgo.
La incidencia del reumatismo es aproximadamente del 1%. Denotemos la presencia de reumatismo como R +, mientras que P(R +) = 0,01.
La presencia de antígeno se designará como A+. Se encuentra en el 95% de los pacientes con reumatismo y en el 6% de las personas que no padecen reumatismo. En nuestra notación, estas son: probabilidades condicionales P(A + /R +) = 0,95 y P(A + /R -) = 0,06.
A partir de estas tres probabilidades determinaremos sucesivamente otras probabilidades.
En primer lugar, si la incidencia de reumatismo es P(R +) = 0,01, entonces la probabilidad de no enfermarse es P(R -) = 1-P(R +) = 0,99.
De la fórmula de probabilidad condicional encontramos que
P(A + y R +) = P(A + /R +) * P(R +) = 0,95*0,01 = 0,0095, o el 0,95% de la población padece reumatismo y tiene el antígeno.
Asimismo
P(A + yR -) = P(A + /R -) * P(R -) = 0,06*0,99 = 0,0594, o el 5,94% de la población es portadora del antígeno, pero no padece reumatismo.
Dado que todos los que tienen el antígeno padecen reumatismo o no padecen reumatismo (pero no ambos al mismo tiempo), la suma de las dos últimas probabilidades da la frecuencia de portación del antígeno en el conjunto de la población:
P(A +)= P(A + yR +) + P(A + yR -) = 0,0095 + 0,0594 = 0,0689
En consecuencia, la proporción de personas que no tienen el antígeno es igual a
P(A -)=1- P(A +) = 0,9311
Dado que la incidencia de reumatismo es del 1% y la proporción de personas que tienen el antígeno y padecen reumatismo es del 0,95%, entonces la proporción de personas que tienen reumatismo y no tienen el antígeno es igual a:
P(A - yR +) = P(R +) - P(A + yR +) = 0,01 – 0,0095 = 0,0005
Ahora avanzaremos en la dirección opuesta, pasando de las probabilidades de eventos y sus combinaciones a probabilidades condicionales. Según la fórmula de probabilidad condicional original P(A + /R +) = P(R + y A +)/ P(A +) = 0,0095/0,06890,1379, o aproximadamente el 13,8% de los individuos portadores del antígeno, contraerán reumatismo . Dado que la incidencia de la población en su conjunto es solo del 1%, el hecho de identificar un antígeno aumenta 14 veces la probabilidad de desarrollar reumatismo.
De manera similar, P(R + /A -) = P(R + yA -)/ P(A -) = 0,0005/0,93110,000054, es decir, el hecho de que no se detecte ningún antígeno durante la prueba reduce la probabilidad de desarrollar reumatismo. 19 veces.
Formateemos esta tarea en una hoja de cálculo de Excel:
|
Presencia de reumatismo R+ | ||
|
Presencia de antígeno en pacientes con A+ | ||
|
Presencia de antígeno en pacientes A+ no enfermos | ||
|
Probabilidad de no enfermarse |
P(R-)=1-P(R+) | |
|
Al mismo tiempo padecen reumatismo y tienen el antígeno |
P(A+ y R+)= P(A+ /R+) * P(R+) | |
|
Portan el antígeno, pero no enferman de reumatismo. |
P(A + y R -)= P(A + /R -) * P(R -) | |
|
Frecuencia de transporte de antígenos en la población general. |
P(A +)= P(A + y R +) + P(A + y R -) | |
|
Proporción de personas sin antígeno |
P(A-)=1-P(A+) | |
|
Proporción de personas con reumatismo que no tienen antígeno |
P(A - y R +) = P(R +) - P(A + y R +) | |
|
Las personas portadoras del antígeno desarrollarán reumatismo. |
P(A + /R +)= P(R + y A +)/ P(A +) | |
|
Las personas que no portan el antígeno no desarrollarán reumatismo. |
P(R + /A -)=P(R + y A -)/ P(A -) |
Puedes ver el proceso de creación de una tabla image2\p2-1.gif
Pregunta No. 38. Grupo completo de eventos. Fórmula de probabilidad total. Fórmulas de Bayes.
Dos eventos. Independencia en conjunto. Formulación del teorema de la multiplicación en este caso.
Pregunta No. 37. Probabilidad condicional. Teorema de la multiplicación. Definición de independencia
La probabilidad condicional es la probabilidad de que ocurra un evento dado que ya ha ocurrido otro evento.
P(A│B)= p(AB)/p(B)
La probabilidad condicional refleja la influencia de un evento sobre la probabilidad de otro.
Teorema de la multiplicación.
La probabilidad de ocurrencia de eventos está determinada por la fórmula P(A 1,A 2,….A n)= P(A 1)P(A 2/ A 1)…P(A n / A 1 A 2… Un -1)
Para el producto de dos eventos se sigue que
P(AB)=P(A/B)P(B)=P(B/A)P(A)
Si un evento no depende del otro, si la ocurrencia de uno de ellos no afecta la probabilidad de ocurrencia del otro, entonces este último tampoco depende del primero. Esto da todas las razones para llamar a tales eventos independientes. Matemáticamente, independencia significa que la probabilidad condicional de un evento es igual a su probabilidad (probabilidad incondicional).
1. Dicen que el evento A no depende del evento B si
P(A│B)=P(A)
Si el evento A no depende del evento B, entonces el evento B no depende del evento A.
2. Si los eventos A y B son independientes, entonces P(AB) = P(A)P(B); esta igualdad se utiliza para determinar eventos independientes.
Es necesario distinguir entre independencia de eventos por pares e independencia en conjunto.
Los eventos A1, A2,….An se llaman colectivamente independientes si son independientes por pares y cada uno de ellos no depende del producto de ningún conjunto de otros eventos.
Si los eventos A1, A2,….An son independientes en su totalidad entonces
P(A 1,A 2,….A n)=P(A 1)P(A 2)…P(A n).
En cada grupo, algún evento definitivamente ocurrirá como resultado de la prueba, y la ocurrencia de uno de ellos excluye la ocurrencia de todos los demás. Estos eventos se denominan grupo de eventos completo.
Definición: Si un grupo de eventos es tal que al menos uno de ellos debe ocurrir como resultado de la prueba, y dos de ellos son incompatibles, entonces este grupo de eventos se llama grupo completo.
Cada evento de un grupo completo se llama evento elemental. Todo evento elemental es igualmente posible, porque no hay razón para creer que alguno de ellos sea más posible que cualquier otro evento del grupo completo.
Dos acontecimientos opuestos constituyen un grupo completo.
La frecuencia relativa del evento A es la relación entre el número de experimentos como resultado de los cuales ocurrió el evento A. numero total experimentos.
La diferencia entre frecuencia relativa y probabilidad es que la probabilidad se calcula sin experimentación directa y la frecuencia relativa se calcula después de la experimentación.
Fórmula de probabilidad total
(donde A es algún evento, H1, H2 ... Hi son incompatibles por pares, formando un grupo completo, y A puede ocurrir junto con H1, H2 Hi)
P(A)=P(A|H 1) P(H 1)+P(A|H 2)P(H 2)+P(A|H 3)P(H 3)+…+P(A| Hn)P(Hn)
fórmula de bayes
Comentario. Los eventos Hi se denominan hipótesis de probabilidad, p(Hi) son probabilidades a priori de la hipótesis Hi y las probabilidades P(Hi/A) son probabilidades a posteriori de la hipótesis Hi.
Conozcamos el resultado del experimento, es decir, que ocurrió el evento A. Este hecho puede cambiar las probabilidades a priori (es decir, conocidas antes del experimento) de las hipótesis. Para reestimar las probabilidades de hipótesis con un resultado experimental conocido se utiliza la fórmula de Bayes:
Ejemplo. Después de dos disparos de dos tiradores, cuyas probabilidades de acertar eran iguales a 0,6 y 0,7, apareció un agujero en el objetivo. Calcula la probabilidad de que el primer tirador acertara.
Solución. Sea el evento A un golpe con dos tiros,
e hipótesis: H1 – el primer acierto y el segundo fallido,
H2 – el primero falló y el segundo acertó,
H3 - ambos impactaron,
H4 – ambos fallaron.
Probabilidades de hipótesis:
ð(Н1) = 0,6·0,3 = 0,18,
p(H2) = 0,4·0,7 = 0,28,
p(H3) = 0,6·0,7 = 0,42,
p(H4) = 0,4 0,3 = 0,12.
Entonces p(A/H1) = p(A/H2) = 1,
p(A/H3) = p(A/H4) = 0.
Por tanto, la probabilidad total p(A) = 0,18 1 + 0,28 1 + 0,42 0 + 0,12 0 = 0,46.
La fórmula de probabilidad total permite calcular la probabilidad de un evento de interés a través de las probabilidades condicionales de este evento bajo el supuesto de ciertas hipótesis, así como las probabilidades de estas hipótesis.
Definición 3.1. Sea el evento A sólo puede ocurrir junto con uno de los eventos H1, H2,..., Hn, formando un grupo completo de eventos incompatibles. Entonces los eventos Н1, Н2,…, Нп se denominan hipótesis.
Teorema 3.1. La probabilidad de que el evento A ocurra junto con las hipótesis H1, H2,..., Hn es igual a:
donde p(Hi) es la probabilidad de la i-ésima hipótesis, y p(A/Hi) es la probabilidad del evento A, sujeto a la implementación de esta hipótesis. La fórmula (P(A)= ) se llama fórmula de probabilidad total
Pregunta No. 39. Esquema Bernoulli. Probabilidad de m éxitos en una serie de n ensayos
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0

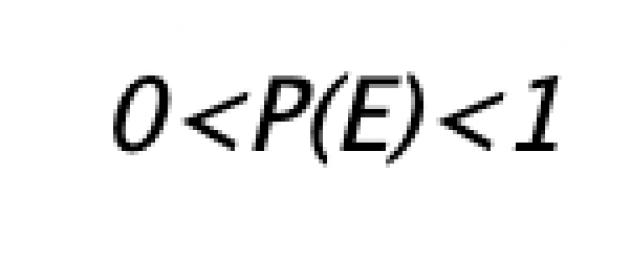
 ,
, ,
norte
,
,
norte
,









