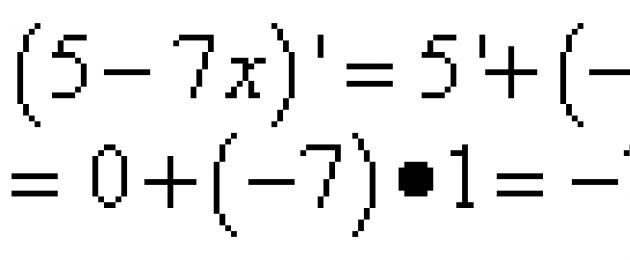La derivada de la función y es la raíz de x. Encuentra la derivada: algoritmo y ejemplos de soluciones.

La operación de encontrar una derivada se llama diferenciación.

Como resultado de resolver problemas de encontrar derivadas de las funciones más simples (y no muy simples) definiendo la derivada como el límite de la relación del incremento al incremento del argumento, apareció una tabla de derivadas y reglas de diferenciación definidas con precisión. . Isaac Newton (1643-1727) y Gottfried Wilhelm Leibniz (1646-1716) fueron los primeros en trabajar en el campo de la búsqueda de derivadas.

Por lo tanto, en nuestro tiempo, para encontrar la derivada de cualquier función, no es necesario calcular el límite mencionado anteriormente de la relación entre el incremento de la función y el incremento del argumento, sino que solo es necesario usar la tabla de derivadas y las reglas de diferenciación. El siguiente algoritmo es adecuado para encontrar la derivada.

Para encontrar la derivada, necesitas una expresión debajo del signo de trazo desglosar funciones simples y determinar qué acciones (producto, suma, cociente) estas funciones están relacionadas. Además, encontramos las derivadas de funciones elementales en la tabla de derivadas y las fórmulas para las derivadas del producto, la suma y el cociente, en las reglas de diferenciación. La tabla de derivadas y las reglas de derivación se dan después de los dos primeros ejemplos.

Ejemplo 1 Encontrar la derivada de una función

Solución. A partir de las reglas de derivación encontramos que la derivada de la suma de funciones es la suma de las derivadas de funciones, es decir

De la tabla de derivadas, encontramos que la derivada de "X" es igual a uno, y la derivada del seno es coseno. Sustituimos estos valores en la suma de derivadas y encontramos la derivada requerida por la condición del problema:

Ejemplo 2 Encontrar la derivada de una función

Solución. Deriva como derivada de la suma, en la que el segundo término con un factor constante, se puede sacar del signo de la derivada:

Si todavía hay preguntas sobre de dónde viene algo, por regla general, se aclaran después de leer la tabla de derivadas y las reglas de diferenciación más simples. Vamos a ellos ahora mismo.

Tabla de derivadas de funciones simples

1. Derivada de una constante (número). Cualquier número (1, 2, 5, 200...) que esté en la expresión de la función. Siempre cero. Es muy importante recordar esto, ya que se requiere muy a menudo
2. Derivada de la variable independiente. Más a menudo "x". Siempre igual a uno. Esto también es importante recordar
3. Derivada de grado. Al resolver problemas, debe convertir las raíces no cuadradas en una potencia.
4. Derivada de una variable a la potencia de -1
5. Derivada de la raíz cuadrada
6. Derivada del seno
7. Derivada del coseno
8. Derivada tangente
9. Derivada de cotangente
10. Derivada del arcoseno
11. Derivada del arco coseno
12. Derivada del arco tangente
13. Derivada de la tangente inversa
14. Derivada del logaritmo natural
15. Derivada de una función logarítmica
16. Derivada del exponente
17. Derivada de función exponencial

Reglas de diferenciación

1. Derivada de la suma o diferencia
2. Derivado de un producto
2a. Derivada de una expresión multiplicada por un factor constante
3. Derivada del cociente
4. Derivada de una función compleja

Regla 1si funciones

son diferenciables en algún punto, entonces en el mismo punto las funciones

y

esos. la derivada de la suma algebraica de funciones es igual a la suma algebraica de las derivadas de estas funciones.

Consecuencia. Si dos funciones derivables difieren en una constante, entonces sus derivadas son, es decir.

Regla 2si funciones

son diferenciables en algún punto, entonces su producto también es diferenciable en el mismo punto

y

esos. la derivada del producto de dos funciones es igual a la suma de los productos de cada una de estas funciones y la derivada de la otra.

Consecuencia 1. El factor constante se puede sacar del signo de la derivada:

consecuencia 2. La derivada del producto de varias funciones diferenciables es igual a la suma de los productos de la derivada de cada uno de los factores y todos los demás.

Por ejemplo, para tres multiplicadores:

regla 3si funciones

diferenciable en algún punto Y , entonces en este punto su cociente también es derivable.u/v, y

esos. la derivada de un cociente de dos funciones es igual a una fraccion cuyo numerador es la diferencia entre los productos del denominador y la derivada del numerador y el numerador y la derivada del denominador, y el denominador es el cuadrado del numerador anterior .

Dónde buscar en otras páginas

Al encontrar la derivada del producto y el cociente en problemas reales, siempre es necesario aplicar varias reglas de diferenciación a la vez, por lo que hay más ejemplos de estas derivadas en el artículo."La derivada de un producto y un cociente".

Comentario.¡No debe confundir una constante (es decir, un número) como un término en la suma y como un factor constante! En el caso de un término, su derivada es igual a cero, y en el caso de un factor constante, se saca del signo de las derivadas. Este es un error típico que ocurre en la etapa inicial de estudiar derivadas, pero a medida que el estudiante promedio resuelve varios ejemplos de uno y dos componentes, este error ya no se comete.

Y si al derivar un producto o un cociente tienes un término tu"v, en el cual tu- un número, por ejemplo, 2 o 5, es decir, una constante, entonces la derivada de este número será igual a cero y, por lo tanto, todo el término será igual a cero (tal caso se analiza en el ejemplo 10) .

Otro error común es la solución mecánica de la derivada de una función compleja como derivada de una función simple. Es por eso derivada de una función compleja dedicado a un artículo aparte. Pero primero aprenderemos a encontrar derivadas de funciones simples.

En el camino, no puedes prescindir de las transformaciones de expresiones. Para hacer esto, es posible que deba abrir en nuevos manuales de Windows Acciones con potencias y raíces. Y Acciones con fracciones .

Si está buscando soluciones para derivadas con potencias y raíces, es decir, cuando la función se ve como , luego siga la lección " Derivado de la suma de fracciones con potencias y raíces".

Si tienes una tarea como , entonces estás en la lección "Derivadas de funciones trigonométricas simples".

Ejemplos paso a paso: cómo encontrar la derivada

Ejemplo 3 Encontrar la derivada de una función

Solución. Determinamos las partes de la expresión de la función: la expresión completa representa el producto, y sus factores son sumas, en la segunda de las cuales uno de los términos contiene un factor constante. Aplicamos la regla de diferenciación del producto: la derivada del producto de dos funciones es igual a la suma de los productos de cada una de estas funciones y la derivada de la otra:

A continuación, aplicamos la regla de derivación de la suma: la derivada de la suma algebraica de funciones es igual a la suma algebraica de las derivadas de estas funciones. En nuestro caso, en cada suma, el segundo término con signo menos. En cada suma vemos tanto una variable independiente, cuya derivada es igual a uno, como una constante (número), cuya derivada es igual a cero. Entonces, "x" se convierte en uno, y menos 5, en cero. En la segunda expresión, "x" se multiplica por 2, entonces multiplicamos dos por la misma unidad que la derivada de "x". Obtenemos los siguientes valores de derivadas:

Sustituimos las derivadas encontradas en la suma de productos y obtenemos la derivada de toda la función requerida por la condición del problema:

Y puedes verificar la solución del problema en la derivada en .

Ejemplo 4 Encontrar la derivada de una función

Solución. Estamos obligados a encontrar la derivada del cociente. Aplicamos la fórmula para diferenciar un cociente: la derivada de un cociente de dos funciones es igual a una fracción cuyo numerador es la diferencia entre los productos del denominador y la derivada del numerador y el numerador y la derivada del denominador, y el denominador es el cuadrado del numerador anterior. Obtenemos:

Ya hemos encontrado la derivada de los factores en el numerador en el Ejemplo 2. Tampoco olvidemos que el producto, que es el segundo factor en el numerador, se toma con un signo menos en el ejemplo actual:

Si está buscando soluciones a problemas en los que necesita encontrar la derivada de una función, donde hay una pila continua de raíces y grados, como, por ejemplo, entonces bienvenido a clase "La derivada de la suma de fracciones con potencias y raíces" .

Si necesitas aprender más sobre las derivadas de senos, cosenos, tangentes y otras funciones trigonométricas, es decir, cuando la función se ve como , entonces tienes una lección "Derivadas de funciones trigonométricas simples" .

Ejemplo 5 Encontrar la derivada de una función

Solución. En esta función vemos un producto, uno de cuyos factores es la raíz cuadrada de la variable independiente, con cuya derivada nos familiarizamos en la tabla de derivadas. De acuerdo con la regla de diferenciación del producto y el valor tabular de la derivada de la raíz cuadrada, obtenemos:

Puedes comprobar la solución del problema de derivadas en calculadora de derivadas en línea .

Ejemplo 6 Encontrar la derivada de una función

Solución. En esta función vemos el cociente, cuyo dividendo es la raíz cuadrada de la variable independiente. Según la regla de derivación del cociente, que repetimos y aplicamos en el ejemplo 4, y el valor tabular de la derivada de la raíz cuadrada, obtenemos:

Para deshacerse de la fracción en el numerador, multiplique el numerador y el denominador por .

1. El caso general de la fórmula para la derivada de una raíz de grado arbitrario- una fracción, cuyo numerador es uno, y el denominador es un número igual al grado de la raíz para la cual se calculó la derivada, multiplicado por la raíz del mismo grado, cuya expresión raíz es una variable en el grado de la raíz para la que se calculó la derivada, reducido en uno
2. Derivada de la raíz cuadrada- es un caso especial de la fórmula anterior. Derivada de la raíz cuadrada de x es una fracción cuyo numerador es uno y el denominador es dos veces la raíz cuadrada de x
3. Derivado de raíz cúbica, también un caso especial de la fórmula general. La derivada de la raíz cúbica es la unidad dividida por las tres raíces cúbicas x al cuadrado.

A continuación hay transformaciones que explican por qué las fórmulas para encontrar la derivada de las raíces cuadradas y cúbicas son exactamente como se muestran en la figura.

Por supuesto, estas fórmulas no se pueden memorizar en absoluto, si tenemos en cuenta que sacar la raíz de un grado derivado es lo mismo que elevar una fracción a la potencia, cuyo denominador es igual al mismo grado. Luego encontrar la derivada de la raíz se reduce a aplicar la fórmula para encontrar la derivada del grado de la fracción correspondiente.

Derivada de una variable bajo la raíz cuadrada

(√x)" = 1 / (2√x) o 1/2 x -1/2

Explicación:
(√x)" = (x 1/2)"

La raíz cuadrada es exactamente la misma operación que elevar a la potencia de 1/2,esto significa que para encontrar la derivada de la raíz, puedes aplicar la fórmula de la regla para encontrar la derivada de una variable en un grado arbitrario:

(x 1/2)" \u003d 1/2 x -1/2 \u003d 1 / (2√x)

Derivada de la raíz cúbica (derivada de la raíz de tercer grado)

La derivada de la raíz cúbica es exactamente igual a la raíz cuadrada.

Imagina la raíz cúbica como una potencia de 1/3 y encuentra la derivada de acuerdo con las reglas generales de diferenciación. Se puede ver una breve fórmula en la imagen de arriba, y a continuación hay una explicación de por qué esto es así.

La potencia -2/3 se obtiene restando uno a 1/3

Las funciones complejas no siempre se ajustan a la definición de una función compleja. Si hay una función de la forma y \u003d sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, entonces no puede considerarse compleja, a diferencia de y \u003d sin 2 x.

En este artículo se mostrará el concepto de función compleja y su identificación. Trabajemos con fórmulas para encontrar la derivada con ejemplos de soluciones en la conclusión. El uso de la tabla de derivadas y las reglas de diferenciación reducen significativamente el tiempo para encontrar la derivada.

Definiciones basicas

Definición 1

Una función compleja es una función cuyo argumento también es una función.

Se denota de esta manera: f (g (x)) . Tenemos que la función g (x) se considera un argumento f (g (x)) .

Definición 2

Si existe una función f y es una función cotangente, entonces g(x) = ln x es la función logaritmo natural. Obtenemos que la función compleja f (g (x)) se escribirá como arctg (lnx). O una función f, que es una función elevada a la cuarta potencia, donde g (x) \u003d x 2 + 2 x - 3 se considera una función racional completa, obtenemos que f (g (x)) \u003d (x 2 + 2 x - 3) 4 .

Obviamente, g(x) puede ser complicado. Del ejemplo y \u003d sin 2 x + 1 x 3 - 5, se puede ver que el valor de g tiene una raíz cúbica con una fracción. Esta expresión se puede denotar como y = f (f 1 (f 2 (x))) . De donde tenemos que f es una función seno, y f 1 es una función ubicada debajo de la raíz cuadrada, f 2 (x) \u003d 2 x + 1 x 3 - 5 es una función racional fraccionaria.

Definición 3

El grado de anidamiento se define por cualquier número natural y se escribe como y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .

Definición 4

El concepto de composición de funciones se refiere al número de funciones anidadas según el enunciado del problema. Para la solución, la fórmula para encontrar la derivada de una función compleja de la forma

(f(g(x)))"=f"(g(x)) g"(x)

Ejemplos

Ejemplo 1

Encuentra la derivada de una función compleja de la forma y = (2 x + 1) 2 .

Solución

Por convención, f es una función que eleva al cuadrado y g(x) = 2 x + 1 se considera una función lineal.

Aplicamos la fórmula de la derivada para una función compleja y escribimos:

f "(g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g "(x) = (2x + 1)" = (2x)" + 1" = 2 x" + 0 = 2 1 x 1 - 1 = 2 ⇒ (f(g(x))) "=f" ( g(x)) g"(x) = 2 (2x + 1) 2 = 8x + 4

Es necesario encontrar una derivada con una forma inicial simplificada de la función. Obtenemos:

y = (2x + 1) 2 = 4x2 + 4x + 1

Por lo tanto tenemos que

y"=(4x2+4x+1)"=(4x2)"+(4x)"+1"=4(x2)"+4(x)"+0==4 2 x 2 - 1 + 4 1 x 1 - 1 = 8x + 4

Los resultados coincidieron.

Al resolver problemas de este tipo, es importante comprender dónde se ubicará la función de la forma f y g (x).

Ejemplo 2

Debes encontrar las derivadas de funciones complejas de la forma y \u003d sin 2 x e y \u003d sin x 2.

Solución

La primera entrada de la función dice que f es la función cuadrática y g(x) es la función seno. Entonces obtenemos eso

y "= (sen 2 x)" = 2 sen 2 - 1 x (sen x)" = 2 sen x cos x

La segunda entrada muestra que f es una función seno y g (x) = x 2 denota la función potencia. De ello se deduce que el producto de una función compleja se puede escribir como

y " \u003d (sin x 2) " \u003d cos (x 2) (x 2) " \u003d cos (x 2) 2 x 2 - 1 \u003d 2 x cos (x 2)

La fórmula para la derivada y \u003d f (f 1 (f 2 (f 3 (. . . (fn (x))))))) se escribirá como y "= f" (f 1 (f 2 (f 3 (. . . (fn (x)))))) f 1 "(f 2 (f 3 (. . . (fn (x))))) f 2 " (f 3 (. . . (fn (x) )) )) . . . f n "(x)

Ejemplo 3

Encuentra la derivada de la función y = sen (ln 3 a r c t g (2 x)) .

Solución

Este ejemplo muestra la complejidad de escribir y determinar la ubicación de las funciones. Entonces y \u003d f (f 1 (f 2 (f 3 (f 4 (x)))))) denotar, donde f , f 1 , f 2 , f 3 , f 4 (x) es la función seno, la función de elevar a 3 grados, una función con logaritmo y base e, una función del arco tangente y una lineal.

De la fórmula para la definición de una función compleja, tenemos que

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x)

Conseguir qué encontrar

1. f "(f 1 (f 2 (f 3 (f 4 (x)))))) como la derivada del seno en la tabla de derivadas, entonces f "(f 1 (f 2 (f 3 (f 4 (x) ))))) ) = cos (ln 3 arctg (2 x)) .
2. f 1 "(f 2 (f 3 (f 4 (x)))) como derivada de una función de potencia, entonces f 1 "(f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 arctg (2 x) = 3 ln 2 arctg (2 x) .
3. f 2 "(f 3 (f 4 (x))) como una derivada logarítmica, entonces f 2 "(f 3 (f 4 (x))) = 1 a r c t g (2 x) .
4. f 3 "(f 4 (x)) como derivada del arco tangente, entonces f 3 "(f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. Al encontrar la derivada f 4 (x) \u003d 2 x, saque 2 del signo de la derivada usando la fórmula para la derivada de la función de potencia con un exponente que es 1, luego f 4 "(x) \u003d ( 2 x)" \u003d 2 x "\u003d 2 · 1 · x 1 - 1 = 2 .

Combinamos los resultados intermedios y obtenemos que

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 arctan (2 x)) 3 ln 2 arctan (2 x) 1 arctan (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arctan (2 x)) ln 2 arctan (2 x) arctan (2 x) (1 + 4 x 2)

El análisis de tales funciones se asemeja a muñecos de anidación. Las reglas de diferenciación no siempre se pueden aplicar explícitamente utilizando una tabla de derivadas. A menudo es necesario aplicar la fórmula para encontrar derivadas de funciones complejas.

Existen algunas diferencias entre una vista compleja y una función compleja. Con una capacidad clara para distinguir esto, encontrar derivados será especialmente fácil.

Ejemplo 4

Es necesario considerar traer tal ejemplo. Si existe una función de la forma y = tg 2 x + 3 tgx + 1 , entonces puede considerarse como una función compleja de la forma g (x) = tgx , f (g) = g 2 + 3 g + 1 . Obviamente, es necesario aplicar la fórmula para la derivada compleja:

f "(g (x)) \u003d (g 2 (x) + 3 g (x) + 1) " \u003d (g 2 (x)) " + (3 g (x)) " + 1 " == 2 g 2 - 1 (x) + 3 g "(x) + 0 \u003d 2 g (x) + 3 1 g 1 - 1 (x) \u003d \u003d 2 g (x) + 3 \u003d 2 tgx + 3; g " (x) = (tgx) " = 1 porque 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tanx + 3 cos 2 x

Una función de la forma y = t g x 2 + 3 t g x + 1 no se considera compleja, ya que tiene la suma de t g x 2 , 3 t g x y 1 . Sin embargo, t g x 2 se considera una función compleja, luego obtenemos una función de potencia de la forma g (x) \u003d x 2 y f, que es una función de la tangente. Para hacer esto, necesita diferenciar por la cantidad. eso lo conseguimos

y " = (tgx 2 + 3 tgx + 1) " = (tgx 2) " + (3 tgx) " + 1 " == (tgx 2) " + 3 (tgx) " + 0 = (tgx 2) " + 3 porque 2 x

Pasemos a encontrar la derivada de una función compleja (t g x 2) ":

f "(g (x)) \u003d (tg (g (x))) " \u003d 1 cos 2 g (x) \u003d 1 cos 2 (x 2) g " (x) \u003d (x 2) " \u003d 2 x 2 - 1 \u003d 2 x ⇒ (tgx 2) " \u003d f " (g (x)) g " (x) \u003d 2 x cos 2 (x 2)

Obtenemos que y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Las funciones complejas se pueden incluir en funciones complejas, y las funciones complejas en sí mismas pueden ser funciones compuestas de la forma compleja.

Ejemplo 5

Por ejemplo, considere una función compleja de la forma y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Esta función se puede representar como y = f (g (x)), donde el valor de f es una función del logaritmo en base 3, y g (x) se considera la suma de dos funciones de la forma h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 y k (x) = ln 2 x (x 2 + 1) . Obviamente, y = f (h (x) + k (x)) .

Considere la función h(x) . Esta es la razón de l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 a m (x) = e x 2 + 3 3

Tenemos que l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) es la suma de dos funciones n (x) = x 2 + 7 y p ( x) \u003d 3 cos 3 (2 x + 1) , donde p (x) \u003d 3 p 1 (p 2 (p 3 (x))) es una función compleja con un coeficiente numérico de 3, y p 1 es una función cúbica, p 2 función coseno, p 3 (x) = 2 x + 1 - función lineal.

Encontramos que m (x) = ex 2 + 3 3 = q (x) + r (x) es la suma de dos funciones q (x) = ex 2 y r (x) = 3 3 , donde q (x) = q 1 (q 2 (x)) es una función compleja, q 1 es una función con exponente, q 2 (x) = x 2 es una función potencia.

Esto muestra que h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)

Al pasar a una expresión de la forma k (x) \u003d ln 2 x (x 2 + 1) \u003d s (x) t (x), está claro que la función se representa como un complejo s (x) \ u003d ln 2 x \u003d s 1 ( s 2 (x)) con un entero racional t (x) = x 2 + 1, donde s 1 es una función cuadrática, y s 2 (x) = ln x es logarítmica con base mi.

De ello se deduce que la expresión tomará la forma k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x) .

Entonces obtenemos eso

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

De acuerdo con las estructuras de la función, quedó claro cómo y qué fórmulas se deben aplicar para simplificar la expresión cuando se deriva. Para familiarizarse con tales problemas y comprender su solución, es necesario referirse al punto de diferenciar una función, es decir, encontrar su derivada.

Si nota un error en el texto, resáltelo y presione Ctrl+Enter

Derivación de la fórmula para la derivada de una función potencia (xa la potencia de a). Se consideran las derivadas de las raíces de x. La fórmula para la derivada de una función de potencia de orden superior. Ejemplos de cálculo de derivadas.

Contenido

Ver también: Función de potencia y raíces, fórmulas y gráfico.
Gráficas de función de potencia

Fórmulas básicas

La derivada de x elevado a a es a por x elevado a a menos uno:
(1) .

La derivada de la n-ésima raíz de x a la m-ésima potencia es:
(2) .

Derivación de la fórmula para la derivada de una función potencia

Caso x > 0

Considere una función de potencia de la variable x con exponente a :
(3) .
Aquí a es un número real arbitrario. Consideremos primero el caso.

Para encontrar la derivada de la función (3), usamos las propiedades de la función potencia y la transformamos a la siguiente forma:
.

Ahora encontramos la derivada aplicando:
;
.
Aquí .

La fórmula (1) está probada.

Derivación de la fórmula para la derivada de la raíz del grado n de x al grado m

Ahora considere una función que es la raíz de la siguiente forma:
(4) .

Para encontrar la derivada, convertimos la raíz en una función de potencia:
.
Comparando con la fórmula (3), vemos que
.
Luego
.

Por la fórmula (1) encontramos la derivada:
(1) ;
;
(2) .

En la práctica, no es necesario memorizar la fórmula (2). Es mucho más conveniente convertir primero las raíces en funciones de potencia y luego encontrar sus derivadas usando la fórmula (1) (ver ejemplos al final de la página).

Caso x = 0

Si , entonces la función exponencial también está definida para el valor de la variable x = 0 . Encontremos la derivada de la función (3) para x = 0 . Para hacer esto, usamos la definición de un derivado:
.

Sustituye x = 0 :
.
En este caso, por derivada nos referimos al límite de la derecha para el cual .

Entonces encontramos:
.
De esto se puede ver que en , .
En , .
En , .
Este resultado también se obtiene por la fórmula (1):
(1) .
Por lo tanto, la fórmula (1) también es válida para x = 0 .

caso x< 0

Considere la función (3) nuevamente:
(3) .
Para algunos valores de la constante a, también se define para valores negativos de la variable x. Es decir, sea a un número racional. Entonces se puede representar como una fracción irreducible:
,
donde m y n son números enteros sin divisor común.

Si n es impar, entonces la función exponencial también se define para valores negativos de la variable x. Por ejemplo, para n = 3 y m = 1 tenemos la raíz cúbica de x:
.
También se define para valores negativos de x.

Encontremos la derivada de la función potencia (3) para y para valores racionales de la constante a, para los cuales está definida. Para ello, representamos x de la siguiente forma:
.
Luego ,
.
Encontramos la derivada sacando la constante del signo de la derivada y aplicando la regla de diferenciación de una función compleja:

.
Aquí . Pero
.
Desde entonces
.
Luego
.
Es decir, la fórmula (1) también es válida para:
(1) .

Derivados de órdenes superiores

Ahora encontramos las derivadas de orden superior de la función potencia
(3) .
Ya hemos encontrado la derivada de primer orden:
.

Sacando la constante a del signo de la derivada, encontramos la derivada de segundo orden:
.
Del mismo modo, encontramos derivadas de tercer y cuarto orden:
;

.

A partir de aquí es claro que derivada de un enésimo orden arbitrario tiene la siguiente forma:
.

Darse cuenta de si a es un numero natural, , entonces la n-ésima derivada es constante:
.
Entonces todas las derivadas posteriores son iguales a cero:
,
en .

Ejemplos de derivados

Ejemplo

Encuentra la derivada de la función:
.

Convirtamos las raíces en potencias:
;
.
Entonces la función original toma la forma:
.

Encontramos derivadas de grados:
;
.
La derivada de una constante es cero:
.

Instrucción

Antes de encontrar la derivada de la raíz, presta atención a las otras funciones que están presentes en el ejemplo que se está resolviendo. Si el problema tiene muchas expresiones radicales, entonces usa la siguiente regla para encontrar la derivada de la raíz cuadrada:

(√x)" = 1 / 2√x.

Y para encontrar la derivada de la raíz cúbica, aplica la fórmula:

(³√x)" \u003d 1 / 3 (³√x)²,

donde ³√x denota la raíz cúbica de x.

Si, destinado a la diferenciación, hay una variable en fraccionario, entonces convierta la raíz en una función de potencia con el exponente apropiado. Para una raíz cuadrada será una potencia de ½ y para una raíz cúbica será ⅓:

√x \u003d x ^ ½,
³√x = x ^ ⅓,

donde ^ representa exponenciación.

Para encontrar la derivada de una función de potencia en general y x^1, x^⅓ en particular, usa la siguiente regla:

(x ^ n)" = n * x ^ (n-1).

Para la derivada de la raíz, esta relación implica:

(x^½)" = ½ x ^ (-½) y
(x^⅓)" = ⅓ x ^ (-⅔).

Habiendo diferenciado todo, observe de cerca el resto del ejemplo. Si obtuviste una expresión muy engorrosa en tu respuesta, seguro que se puede simplificar. La mayoría de los ejemplos escolares están diseñados de tal manera que el resultado es un número pequeño o una expresión compacta.

En muchos problemas de derivadas, las raíces (cuadradas y cúbicas) ocurren junto con otras funciones. Para encontrar la derivada de la raíz en este caso, aplica las siguientes reglas:
la derivada de una constante (un número constante, C) es igual a cero: C" = 0;
el factor constante se saca del signo de la derivada: (k*f)" = k * (f)" (f es una función arbitraria) ;
la derivada de la suma de varias funciones es igual a la suma de las derivadas: (f + g)" = (f)" + (g)";
la derivada del producto de dos funciones es... no, no el producto de las derivadas, sino la siguiente expresión: (fg)" = (f)"g + f (g)";
la derivada del cociente tampoco es igual al cociente de las derivadas, sino que se encuentra de acuerdo con la siguiente regla: (f / g)" = ((f)"g - f(g)") / g².

Nota

En esta página, puede calcular la derivada de una función en línea con una solución detallada al problema. La solución de las derivadas de una función se realiza utilizando las reglas de diferenciación que estudian los estudiantes en el curso de análisis matemático del instituto. Para encontrar la derivada de una función, debe ingresar una función para la diferenciación en el campo "Función" de acuerdo con las reglas de entrada de datos.

Aviso util

La derivada de una función es el límite de la razón del incremento de la función al incremento del argumento cuando el incremento del argumento tiende a cero: El significado matemático de esta definición no es muy fácil de entender, ya que en la escuela curso de álgebra el concepto de límite de una función o no se estudia en absoluto, o se estudia muy superficialmente. Pero para aprender a encontrar derivadas de varias funciones, esto no es necesario.

Fuentes:

• raíz derivada de x