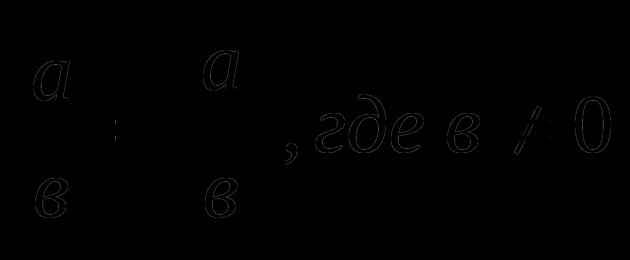Instrucciones
Si un módulo se representa como una función continua, entonces el valor de su argumento puede ser positivo o negativo: |x| = x, x ≥ 0; |x| = - x, x
El módulo es cero y el módulo de cualquier número positivo es. Si el argumento es negativo, después de abrir los corchetes su signo cambia de menos a más. De esto se desprende que los módulos de los opuestos son iguales: |-x| = |x| =x.
El módulo de un número complejo se encuentra mediante la fórmula: |a| = √b ² + c ², y |a + b| ≤ |a| + |b|. Si el argumento contiene un número positivo como multiplicador, entonces se puede quitar del signo entre corchetes, por ejemplo: |4*b| = 4*|b|.
Si el argumento se presenta como un número complejo, entonces, para facilitar los cálculos, se permite el orden de los términos de la expresión entre corchetes rectangulares: |2-3| = |3-2| = 3-2 = 1 porque (2-3) es menor que cero.
El argumento elevado a una potencia está simultáneamente bajo el signo de una raíz del mismo orden; se resuelve usando: √a² = |a| = ±a.
Si tiene una tarea en la que no se especifica la condición para expandir los soportes del módulo, entonces no es necesario deshacerse de ellos; este será el resultado final. Y si necesitas abrirlos, entonces deberás indicar el signo ±. Por ejemplo, necesitas encontrar el valor de la expresión √(2 * (4-b))². Su solución se ve así: √(2 * (4-b))² = |2 * (4-b)| = 2 * |4-b|. Como se desconoce el signo de la expresión 4-b, se debe dejar entre paréntesis. Si agrega una condición adicional, por ejemplo, |4-b| >
El módulo de cero es igual a cero y el módulo de cualquier número positivo es igual a sí mismo. Si el argumento es negativo, después de abrir los corchetes su signo cambia de menos a más. De esto se desprende que los módulos de números opuestos son iguales: |-x| = |x| =x.
El módulo de un número complejo se encuentra mediante la fórmula: |a| = √b ² + c ², y |a + b| ≤ |a| + |b|. Si el argumento contiene un número entero positivo como factor, entonces se puede quitar del signo entre corchetes, por ejemplo: |4*b| = 4*|b|.
El módulo no puede ser negativo, por lo que cualquier número negativo se convierte en positivo: |-x| =x, |-2| = 2, |-1/7| = 1/7, |-2,5| = 2,5.
Si el argumento se presenta en forma de un número complejo, entonces, para facilitar los cálculos, se permite cambiar el orden de los términos de la expresión encerrados entre corchetes rectangulares: |2-3| = |3-2| = 3-2 = 1 porque (2-3) es menor que cero.
Si tiene una tarea en la que no se especifica la condición para expandir los soportes del módulo, entonces no es necesario deshacerse de ellos; este será el resultado final. Y si necesitas abrirlos, entonces deberás indicar el signo ±. Por ejemplo, necesitas encontrar el valor de la expresión √(2 * (4-b))². Su solución se ve así: √(2 * (4-b))² = |2 * (4-b)| = 2 * |4-b|. Como se desconoce el signo de la expresión 4-b, se debe dejar entre paréntesis. Si agrega una condición adicional, por ejemplo, |4-b| > 0, entonces el resultado será 2 * |4-b| = 2 *(4-b). El elemento desconocido también se puede establecer en un número específico, que debe tenerse en cuenta porque influirá en el signo de la expresión.
Escuela secundaria MBOU nº 17, Ivanovo
« Ecuaciones con módulo"
Desarrollo metodológico
compilado
profesor de matemáticas
Lebedeva N.V.20010
Nota explicativa
Capítulo 1 Introducción
Sección 2. Propiedades básicas Sección 3. Interpretación geométrica del concepto de módulo de un número Sección 4. Gráfica de la función y = |x| Sección 5. ConvencionesCapítulo 2. Resolver ecuaciones que contienen un módulo.
Sección 1. Ecuaciones de la forma |F(x)| = m (más simple) Sección 2. Ecuaciones de la forma F(|x|) = m Sección 3. Ecuaciones de la forma |F(x)| = G(x) Sección 4. Ecuaciones de la forma |F(x)| = ± F(x) (más bella) Sección 5. Ecuaciones de la forma |F(x)| = |G(x)| Sección 6. Ejemplos de resolución de ecuaciones no estándar. Sección 7. Ecuaciones de la forma |F(x)| + |G(x)| = 0 Sección 8. Ecuaciones de la forma |a 1 x ± b 1 | ± |a 2 x ± en 2 | ± …|a n x ± en n | = metro Sección 9. Ecuaciones que contienen varios módulos.Capítulo 3. Ejemplos de resolución de varias ecuaciones con módulo.
Sección 1. Ecuaciones trigonométricas Sección 2. Ecuaciones exponenciales Sección 3. Ecuaciones logarítmicas Sección 4. Ecuaciones irracionales Sección 5. Tareas avanzadas respuestas a ejercicios BibliografíaNota explicativa.
El concepto de valor absoluto (módulo) de un número real es una de sus características esenciales. Este concepto está muy extendido en diversas ramas de las ciencias físicas, matemáticas y técnicas. En la práctica de enseñar cursos de matemáticas en las escuelas secundarias de acuerdo con el Programa del Ministerio de Defensa de la Federación de Rusia, el concepto de "valor absoluto de un número" se encuentra repetidamente: en el sexto grado, la definición de módulo y se introduce su significado geométrico; en octavo grado, se forma el concepto de error absoluto, se considera la solución de las ecuaciones y desigualdades más simples que contienen un módulo y se estudian las propiedades de la raíz cuadrada aritmética; en 11º grado el concepto se encuentra en la sección “Raíz norte-ésimo grado." La experiencia docente demuestra que los estudiantes suelen encontrar dificultades para resolver tareas que requieren conocimiento de este material, y muchas veces se las saltan sin empezar a completarlas. Los textos de los exámenes de los cursos de 9º y 11º grado también incluyen tareas similares. Además, los requisitos que las universidades imponen a los graduados escolares son diferentes, es decir, en un nivel más alto que los requisitos del plan de estudios escolar. Para la vida en la sociedad moderna, es muy importante la formación de un estilo de pensamiento matemático, manifestado en ciertas habilidades mentales. En el proceso de resolución de problemas con módulos se requiere la capacidad de utilizar técnicas como generalización y especificación, análisis, clasificación y sistematización, y analogía. Resolver tales tareas le permite poner a prueba su conocimiento de las secciones principales del curso escolar, el nivel de pensamiento lógico y las habilidades de investigación iniciales. Este trabajo está dedicado a una de las secciones: la resolución de ecuaciones que contienen el módulo. Consta de tres capítulos. El primer capítulo introduce los conceptos básicos y las consideraciones teóricas más importantes. El segundo capítulo propone nueve tipos principales de ecuaciones que contienen un módulo, analiza métodos para resolverlas y examina ejemplos de diferentes niveles de complejidad. El tercer capítulo ofrece ecuaciones más complejas y no estándar (trigonométricas, exponenciales, logarítmicas e irracionales). Para cada tipo de ecuación hay ejercicios para resolver de forma independiente (se adjuntan respuestas e instrucciones). El objetivo principal de este trabajo es brindar asistencia metodológica a los docentes en la preparación de las lecciones y en la organización de cursos optativos. El material también se puede utilizar como material didáctico para estudiantes de secundaria. Las tareas propuestas en el trabajo son interesantes y no siempre fáciles de resolver, lo que permite concienciar la motivación educativa de los estudiantes, poner a prueba sus habilidades y aumentar el nivel de preparación de los graduados escolares para ingresar a las universidades. Una selección diferenciada de los ejercicios propuestos implica una transición del nivel reproductivo de dominio del material al creativo, así como la oportunidad de enseñar cómo aplicar sus conocimientos a la hora de resolver problemas atípicos.Capítulo 1 Introducción.
Sección 1. Determinación del valor absoluto .
Definición : El valor absoluto (módulo) de un número real. A un número no negativo se llama: A o -A. Designación: │ A │ La entrada dice lo siguiente: “módulo del número a” o “valor absoluto del número a”│ a, si a > 0
│a│ = │ 0, si a = 0 (1)
│ - y, si unEjemplos: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
- Expandir módulo de expresión:
Sección 2. Propiedades básicas.
Consideremos las propiedades básicas del valor absoluto. Propiedad #1: Los números opuestos tienen módulos iguales, es decir │а│=│- а│ Demostremos que la igualdad es verdadera. Anotemos la definición del número. - A : │- un│= (2) Comparemos los conjuntos (1) y (2). Evidentemente, las definiciones de los valores absolutos de los números. A Y - A emparejar. Por eso, │а│=│- а│Al considerar las siguientes propiedades, nos limitaremos a su formulación, ya que su prueba se da en Propiedad #2: El valor absoluto de la suma de un número finito de números reales no excede la suma de los valores absolutos de los términos: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Propiedad #3: El valor absoluto de la diferencia entre dos números reales no excede la suma de sus valores absolutos: │а - в│ ≤│а│+│в│ Propiedad #4: El valor absoluto del producto de un número finito de números reales es igual al producto de los valores absolutos de los factores: │а·в│=│а│·│в│ Propiedad #5: El valor absoluto del cociente de números reales es igual al cociente de sus valores absolutos:

Sección 3. Interpretación geométrica del concepto de módulo de un número.
Cada número real se puede asociar a un punto de la recta numérica, que será una imagen geométrica de este número real. Cada punto de la recta numérica corresponde a su distancia del origen, es decir la longitud del segmento desde el origen hasta un punto dado. Esta distancia siempre se considera un valor no negativo. Por tanto, la longitud del segmento correspondiente será la interpretación geométrica del valor absoluto de un número real dado.
La ilustración geométrica presentada confirma claramente la propiedad número 1, es decir los módulos de los números opuestos son iguales. De aquí se entiende fácilmente la validez de la igualdad: │х – а│= │а – x│. La solución a la ecuación │х│= m, donde m ≥ 0, es decir, x 1,2 = ± m, también se vuelve más obvia. Ejemplos: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
 x 1,2 = 2; 4
x 1,2 = 2; 4 Sección 4. Gráfica de la función y = │х│
El dominio de esta función son todos los números reales.Sección 5. Convenios.
En el futuro, al considerar ejemplos de resolución de ecuaciones, se utilizarán las siguientes convenciones: ( - signo del sistema [ - signo de la totalidad Al resolver un sistema de ecuaciones (desigualdades), se encuentra la intersección de las soluciones de las ecuaciones (desigualdades) incluidas en el sistema. Al resolver un conjunto de ecuaciones (desigualdades), se encuentra la unión de soluciones incluidas en el conjunto de ecuaciones (desigualdades).Capítulo 2. Resolución de ecuaciones que contienen un módulo.
En este capítulo veremos métodos algebraicos para resolver ecuaciones que contienen uno o más módulos.Sección 1. Ecuaciones de la forma │F (x)│= m
Una ecuación de este tipo se llama la más simple. Tiene solución si y sólo si m ≥ 0. Por definición del módulo, la ecuación original es equivalente a un conjunto de dos ecuaciones: │ F(x)│=metro
 Ejemplos:
Ejemplos:
№1. Resuelve la ecuación: │7х - 2│= 9


 Respuesta:x 1
= - 1; X 2
= 1
4
/
7
№2
Respuesta:x 1
= - 1; X 2
= 1
4
/
7
№2
│x 2 + 3x + 1│= 1

 x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x2 = -3 Respuesta: la suma de las raíces es - 2.№3
x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x2 = -3 Respuesta: la suma de las raíces es - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 denotemos x 2 = m, m ≥ 0 x = 0 ; ±√5 metro 2 – 5 metro + 4 = 0 metro = 1; 4 – ambos valores satisfacen la condición m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Respuesta: número de raíces de la ecuación 7. Ejercicios:
№1. Resuelve la ecuación e indica la suma de las raíces: │х - 5│= 3 №2 . Resuelve la ecuación e indica la raíz más pequeña: │x 2 + x│= 0 №3 . Resuelve la ecuación e indica la raíz mayor: │x 2 – 5x + 4│= 4 №4 .Resuelve la ecuación e indica la raíz entera: │2x 2 – 7x + 6│= 1 №5 .Resolver la ecuación e indicar el número de raíces: │x 4 – 13x 2 + 50│= 14
Sección 2. Ecuaciones de la forma F(│х│) = m
El argumento de la función en el lado izquierdo está debajo del signo del módulo y el lado derecho es independiente de la variable. Consideremos dos formas de resolver ecuaciones de este tipo. 1 vía: Por definición de valor absoluto, la ecuación original equivale a la combinación de dos sistemas. En cada uno de los cuales se impone una condición a una expresión submodular. F(│х│) =metro Dado que la función F(│x│) es par en todo el dominio de definición, las raíces de las ecuaciones F(x) = my F(- x) = m son pares de números opuestos. Por lo tanto, basta con resolver uno de los sistemas (al considerar ejemplos de esta manera, se dará la solución a un sistema). Método 2: Aplicación del método de introducción de una nueva variable. En este caso, se introduce la designación │x│= a, donde a ≥ 0. Este método tiene un diseño menos voluminoso.
Dado que la función F(│x│) es par en todo el dominio de definición, las raíces de las ecuaciones F(x) = my F(- x) = m son pares de números opuestos. Por lo tanto, basta con resolver uno de los sistemas (al considerar ejemplos de esta manera, se dará la solución a un sistema). Método 2: Aplicación del método de introducción de una nueva variable. En este caso, se introduce la designación │x│= a, donde a ≥ 0. Este método tiene un diseño menos voluminoso. Ejemplos: №1 . Resuelve la ecuación: 3x 2 – 4│x│= - 1 Usemos la introducción de una nueva variable. Denotemos │x│= a, donde a ≥ 0. Obtenemos la ecuación 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Regresamos a la variable original: │ x│=1 y │х│= 1/3. Cada ecuación tiene dos raíces. Respuesta:x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Resuelve la ecuación: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
 Encontremos la solución al primer sistema de la población: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Tenga en cuenta que x 2 no satisface la condición x ≥ 0. Solución el segundo sistema será el número opuesto al valor x 1. Respuesta:x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Resolver la ecuación: x 4 – │х│= 0 Denotemos │х│= a, donde a ≥ 0. Obtenemos la ecuación a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Regresar a la variable original: │х│=0 y │х│= 1 x = 0; ± 1 Respuesta:x 1
= 0; X 2
= 1; X 3
= - 1.
Encontremos la solución al primer sistema de la población: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Tenga en cuenta que x 2 no satisface la condición x ≥ 0. Solución el segundo sistema será el número opuesto al valor x 1. Respuesta:x 1
=
-5+√57
/
8
; X 2
=
5-√57
/
8
.№3
.
Resolver la ecuación: x 4 – │х│= 0 Denotemos │х│= a, donde a ≥ 0. Obtenemos la ecuación a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Regresar a la variable original: │х│=0 y │х│= 1 x = 0; ± 1 Respuesta:x 1
= 0; X 2
= 1; X 3
= - 1.
Ejercicios: №6. Resuelve la ecuación: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Resuelve la ecuación, indica el número de raíces en tu respuesta: 3x 2 - 7│x│ + 2 = 0 №8 . Resuelve la ecuación, indica soluciones enteras en tu respuesta: x 4 + │x│ - 2 = 0
Sección 3. Ecuaciones de la forma │F(x)│ = G(x)
El lado derecho de una ecuación de este tipo depende de una variable y, por lo tanto, tiene solución si y sólo si el lado derecho es una función G(x) ≥ 0. La ecuación original se puede resolver de dos maneras : 1 vía: Estándar, basado en la divulgación de un módulo en función de su definición y consiste en una transición equivalente a una combinación de dos sistemas. │ F(x)│ =GRAMO(X)
 Este método puede usarse racionalmente en el caso de una expresión compleja para la función G(x) y una menos compleja para la función F(x), ya que se supone que las desigualdades con la función F(x) serán resueltas. Método 2: Consiste en la transición a un sistema equivalente en el que se impone una condición en el lado derecho. │ F(X)│=
GRAMO(X)
Este método puede usarse racionalmente en el caso de una expresión compleja para la función G(x) y una menos compleja para la función F(x), ya que se supone que las desigualdades con la función F(x) serán resueltas. Método 2: Consiste en la transición a un sistema equivalente en el que se impone una condición en el lado derecho. │ F(X)│=
GRAMO(X)

 Este método es más conveniente de usar si la expresión para la función G(x) es menos compleja que para la función F(x), ya que se supone la solución a la desigualdad G(x) ≥ 0. Además, en el caso de varios módulos, se recomienda utilizar la segunda opción. Ejemplos:
№1.
Resuelve la ecuación: │x + 2│= 6 -2x
Este método es más conveniente de usar si la expresión para la función G(x) es menos compleja que para la función F(x), ya que se supone la solución a la desigualdad G(x) ≥ 0. Además, en el caso de varios módulos, se recomienda utilizar la segunda opción. Ejemplos:
№1.
Resuelve la ecuación: │x + 2│= 6 -2x  (1 vía) Respuesta: x = 1 1
/
3
№2.
(1 vía) Respuesta: x = 1 1
/
3
№2.
│х 2 – 2х - 1│= 2·(x + 1)
 (2 vías) Respuesta: El producto de las raíces es 3.
(2 vías) Respuesta: El producto de las raíces es 3.№3. Resuelve la ecuación e indica la suma de las raíces en tu respuesta:
│x - 6│= x 2 - 5x + 9

Respuesta: la suma de las raíces es 4.
Ejercicios: №9. │x + 4│= - 3x №10. Resuelve la ecuación, indica el número de soluciones en tu respuesta:│x 2 + x - 1│= 2x – 1 №11 . Resuelve la ecuación, indica el producto de las raíces en tu respuesta:│x + 3│= x 2 + x – 6
Sección 4. Ecuaciones de la forma │F(x)│= F(x) y │F(x)│= - F(x)
A las ecuaciones de este tipo a veces se las llama “las más hermosas”. Dado que el lado derecho de las ecuaciones depende de la variable, existen soluciones si y sólo si el lado derecho no es negativo. Por tanto, las ecuaciones originales son equivalentes a las desigualdades:│F(x)│= F(x) F(x) ≥ 0 y │F(x)│= - F(x) F(x) Ejemplos: №1 . Resuelve la ecuación, indica la raíz entera más pequeña en tu respuesta: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0.6 Respuesta: x = 1№2. Resuelve la ecuación, indica la longitud del intervalo en tu respuesta: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Respuesta: la longitud del espacio es 6.№3 . Resuelve la ecuación e indica el número de soluciones enteras en tu respuesta: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Respuesta: 4 soluciones completas.№4 . Resuelve la ecuación e indica la raíz más grande en tu respuesta:
│4 – x -
 │= 4 – x –
│= 4 – x –  x 2 – 5x + 5 = 0 D = 5 x 1,2 =
x 2 – 5x + 5 = 0 D = 5 x 1,2 =  ≈ 1,4
≈ 1,4Respuesta: x = 3.
Ejercicios:
№12.
Resuelve la ecuación, indica la raíz completa en tu respuesta: │x 2 + 6x + 8│= x 2 + 6x + 8 №13.
Resuelve la ecuación, indica el número de soluciones enteras en tu respuesta: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14.
Resuelve la ecuación; en tu respuesta, indica un número entero que no sea la raíz de la ecuación: 
Sección 5. Ecuaciones de la forma │F(x)│= │G(x)│
Dado que ambos lados de la ecuación no son negativos, la solución implica considerar dos casos: las expresiones submodulares son iguales o de signo opuesto. Por tanto, la ecuación original es equivalente a la combinación de dos ecuaciones: │ F(X)│= │ GRAMO(X)│ Ejemplos:
№1.
Resuelve la ecuación, indica la raíz completa en tu respuesta: │x + 3│=│2x - 1│
Ejemplos:
№1.
Resuelve la ecuación, indica la raíz completa en tu respuesta: │x + 3│=│2x - 1│  Respuesta: raíz entera x = 4.№2.
Resuelve la ecuación: │
x – x 2 - 1│=│2x – 3 – x 2 │
Respuesta: raíz entera x = 4.№2.
Resuelve la ecuación: │
x – x 2 - 1│=│2x – 3 – x 2 │  Respuesta: x = 2.№3
.
Resuelve la ecuación e indica el producto de las raíces en tu respuesta:
Respuesta: x = 2.№3
.
Resuelve la ecuación e indica el producto de las raíces en tu respuesta: 


 Ecuaciones raíz 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Respuesta: el producto de las raíces es – 0,25. Ejercicios:
№15
. Resuelve la ecuación e indica la solución completa en tu respuesta: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Resuelve la ecuación, indica la raíz más pequeña en tu respuesta:│5x - 3│=│7 - x│ №17
. Resuelve la ecuación e indica la suma de las raíces en tu respuesta:
Ecuaciones raíz 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Respuesta: el producto de las raíces es – 0,25. Ejercicios:
№15
. Resuelve la ecuación e indica la solución completa en tu respuesta: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16.
Resuelve la ecuación, indica la raíz más pequeña en tu respuesta:│5x - 3│=│7 - x│ №17
. Resuelve la ecuación e indica la suma de las raíces en tu respuesta: 
Sección 6. Ejemplos de resolución de ecuaciones no estándar.
En esta sección veremos ejemplos de ecuaciones no estándar, cuya resolución revela el valor absoluto de la expresión por definición. Ejemplos:№1.
Resuelve la ecuación, indica la suma de las raíces en tu respuesta: x · │x│- 5x – 6 = 0  Respuesta: la suma de las raíces es 1 №2.
.
Resuelve la ecuación, indica la raíz más pequeña en tu respuesta: x 2 - 4x ·
Respuesta: la suma de las raíces es 1 №2.
.
Resuelve la ecuación, indica la raíz más pequeña en tu respuesta: x 2 - 4x ·  - 5 = 0
- 5 = 0  Respuesta: raíz más pequeña x = - 5. №3.
Resuelve la ecuación:
Respuesta: raíz más pequeña x = - 5. №3.
Resuelve la ecuación:  Respuesta: x = -1. Ejercicios:
№18.
Resuelve la ecuación e indica la suma de las raíces: x · │3x + 5│= 3x 2 + 4x + 3
Respuesta: x = -1. Ejercicios:
№18.
Resuelve la ecuación e indica la suma de las raíces: x · │3x + 5│= 3x 2 + 4x + 3
№19.
Resuelve la ecuación: x 2 – 3x = 
№20.
Resuelve la ecuación: 
Sección 7. Ecuaciones de la forma │F(x)│+│G(x)│=0
Es fácil notar que en el lado izquierdo de una ecuación de este tipo está la suma de cantidades no negativas. Por lo tanto, la ecuación original tiene solución si y sólo si ambos términos son iguales a cero al mismo tiempo. La ecuación es equivalente al sistema de ecuaciones: │ F(X)│+│ GRAMO(X)│=0 Ejemplos:
№1
. Resuelve la ecuación:
Ejemplos:
№1
. Resuelve la ecuación:  Respuesta: x = 2. №2.
Resuelve la ecuación: Respuesta: x = 1. Ejercicios:
№21.
Resuelve la ecuación: №22
. Resuelve la ecuación e indica la suma de las raíces en tu respuesta: №23
. Resuelve la ecuación e indica el número de soluciones en tu respuesta:
Respuesta: x = 2. №2.
Resuelve la ecuación: Respuesta: x = 1. Ejercicios:
№21.
Resuelve la ecuación: №22
. Resuelve la ecuación e indica la suma de las raíces en tu respuesta: №23
. Resuelve la ecuación e indica el número de soluciones en tu respuesta: Sección 8. Ecuaciones de la forma │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m
Para resolver ecuaciones de este tipo se utiliza el método del intervalo. Si lo resolvemos mediante expansión secuencial de módulos, obtenemos norte conjuntos de sistemas, lo cual es muy engorroso e inconveniente. Consideremos el algoritmo del método de intervalo: 1). Encuentra valores variables X, para lo cual cada módulo es igual a cero (ceros de expresiones submodulares): 2). Marque los valores encontrados en una recta numérica, que se divide en intervalos (el número de intervalos es respectivamente igual a norte+1
) 3). Determine con qué signo se revela cada módulo en cada uno de los intervalos obtenidos (al hacer una solución, puede usar una recta numérica, marcando los signos en ella) 4). La ecuación original es equivalente a la suma norte+1
sistemas, en cada uno de los cuales se indica la pertenencia de la variable X uno de los intervalos. Ejemplos:
№1
. Resuelve la ecuación e indica la raíz más grande en tu respuesta:
2). Marque los valores encontrados en una recta numérica, que se divide en intervalos (el número de intervalos es respectivamente igual a norte+1
) 3). Determine con qué signo se revela cada módulo en cada uno de los intervalos obtenidos (al hacer una solución, puede usar una recta numérica, marcando los signos en ella) 4). La ecuación original es equivalente a la suma norte+1
sistemas, en cada uno de los cuales se indica la pertenencia de la variable X uno de los intervalos. Ejemplos:
№1
. Resuelve la ecuación e indica la raíz más grande en tu respuesta:  1). Encontremos los ceros de las expresiones submodulares: x = 2; x = -3 2). Marquemos los valores encontrados en la recta numérica y determinemos con qué signo se revela cada módulo en los intervalos resultantes:
1). Encontremos los ceros de las expresiones submodulares: x = 2; x = -3 2). Marquemos los valores encontrados en la recta numérica y determinemos con qué signo se revela cada módulo en los intervalos resultantes: x – 2 x – 2 x – 2 - - + - 3 2x 2x + 6 2x + 6 2x + 6 - + + 3)
 - no hay soluciones La ecuación tiene dos raíces. Respuesta: la raíz más grande x = 2. №2.
Resuelve la ecuación y proporciona la raíz completa en tu respuesta:
- no hay soluciones La ecuación tiene dos raíces. Respuesta: la raíz más grande x = 2. №2.
Resuelve la ecuación y proporciona la raíz completa en tu respuesta:  1). Encontremos los ceros de las expresiones submodulares: x = 1,5; x = - 1 2). Marquemos los valores encontrados en la recta numérica y determinemos con qué signo se revela cada módulo en los intervalos resultantes: x + 1 x + 1 x + 1 - + +
1). Encontremos los ceros de las expresiones submodulares: x = 1,5; x = - 1 2). Marquemos los valores encontrados en la recta numérica y determinemos con qué signo se revela cada módulo en los intervalos resultantes: x + 1 x + 1 x + 1 - + + -1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
 El último sistema no tiene soluciones, por lo tanto la ecuación tiene dos raíces. Al resolver la ecuación, debes prestar atención al signo "-" delante del segundo módulo. Respuesta: raíz entera x = 7. №3.
Resuelve la ecuación, indica la suma de las raíces en tu respuesta: 1). Encontremos los ceros de las expresiones submodulares: x = 5; x = 1; x = - 2 2). Marquemos los valores encontrados en la recta numérica y determinemos con qué signo se revela cada módulo en los intervalos resultantes: x – 5 x – 5 x – 5 x – 5 - - - +
El último sistema no tiene soluciones, por lo tanto la ecuación tiene dos raíces. Al resolver la ecuación, debes prestar atención al signo "-" delante del segundo módulo. Respuesta: raíz entera x = 7. №3.
Resuelve la ecuación, indica la suma de las raíces en tu respuesta: 1). Encontremos los ceros de las expresiones submodulares: x = 5; x = 1; x = - 2 2). Marquemos los valores encontrados en la recta numérica y determinemos con qué signo se revela cada módulo en los intervalos resultantes: x – 5 x – 5 x – 5 x – 5 - - - + -2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
 La ecuación tiene dos raíces x = 0 y 2. Respuesta: la suma de las raíces es 2. №4
.
Resuelve la ecuación: 1). Encontremos los ceros de las expresiones submodulares: x = 1; x = 2; x = 3.2). Determinemos con qué signo se revela cada módulo en los intervalos resultantes. 3).
La ecuación tiene dos raíces x = 0 y 2. Respuesta: la suma de las raíces es 2. №4
.
Resuelve la ecuación: 1). Encontremos los ceros de las expresiones submodulares: x = 1; x = 2; x = 3.2). Determinemos con qué signo se revela cada módulo en los intervalos resultantes. 3).  Combinemos las soluciones de los tres primeros sistemas. Respuesta: ; x = 5.
Combinemos las soluciones de los tres primeros sistemas. Respuesta: ; x = 5.Ejercicios: №24. Resuelve la ecuación:
 №25.
Resuelve la ecuación e indica la suma de las raíces en tu respuesta: №26.
Resuelve la ecuación e indica la raíz más pequeña en tu respuesta: №27.
Resuelve la ecuación e indica la raíz mayor en tu respuesta:
№25.
Resuelve la ecuación e indica la suma de las raíces en tu respuesta: №26.
Resuelve la ecuación e indica la raíz más pequeña en tu respuesta: №27.
Resuelve la ecuación e indica la raíz mayor en tu respuesta: Sección 9. Ecuaciones que contienen varios módulos.
Las ecuaciones que contienen varios módulos asumen la presencia de valores absolutos en expresiones submodulares. El principio básico para resolver ecuaciones de este tipo es la divulgación secuencial de módulos, comenzando por el "externo". Durante la solución se utilizan las técnicas comentadas en los apartados N° 1, N° 3.Ejemplos:
№1.
Resuelve la ecuación:  Respuesta: x = 1; - once. №2.
Resuelve la ecuación:
Respuesta: x = 1; - once. №2.
Resuelve la ecuación:
Respuesta: x = 0; 4; - 4. №3.
Resuelve la ecuación e indica el producto de las raíces en tu respuesta:  Respuesta: el producto de las raíces es – 8. №4.
Resuelve la ecuación:
Respuesta: el producto de las raíces es – 8. №4.
Resuelve la ecuación:  Denotamos las ecuaciones de la población. (1)
Y (2)
y considere la solución para cada uno de ellos por separado para facilitar el diseño. Dado que ambas ecuaciones contienen más de un módulo, es más conveniente realizar una transición equivalente a conjuntos de sistemas. (1)
Denotamos las ecuaciones de la población. (1)
Y (2)
y considere la solución para cada uno de ellos por separado para facilitar el diseño. Dado que ambas ecuaciones contienen más de un módulo, es más conveniente realizar una transición equivalente a conjuntos de sistemas. (1)

 (2)
(2)


 Respuesta:
Respuesta:
Ejercicios:
№36.
Resuelve la ecuación, indica la suma de las raíces en tu respuesta: 5 │3x-5│ = 25 x №37.
Resuelve la ecuación, si hay más de una raíz, indica la suma de las raíces en tu respuesta: │x + 2│ x – 3x – 10 = 1 №38.
Resuelve la ecuación: 3 │2х -4│ = 9 │х│ №39.
Resuelve la ecuación e indica el número de raíces en tu respuesta: 2 │ sen x│ = √2 №40
. Resuelve la ecuación e indica el número de raíces en tu respuesta:
Sección 3. Ecuaciones logarítmicas.
Antes de resolver las siguientes ecuaciones es necesario repasar las propiedades de los logaritmos y la función logarítmica. Ejemplos: №1. Resuelve la ecuación, indica el producto de las raíces en tu respuesta: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1Caso 1: si x ≥ - 1, entonces log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – satisface la condición x ≥ - 1 2 caso: si x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – satisface la condición x - 1
Respuesta: el producto de las raíces es – 15.
№2.
Resuelve la ecuación, indica la suma de las raíces en tu respuesta: lg  O.D.Z.
O.D.Z. 



Respuesta: la suma de las raíces es 0,5.
№3.
Resuelve la ecuación: log 5  O.D.Z.
O.D.Z. 
 Respuesta: x = 9. №4.
Resuelve la ecuación: │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Usemos la fórmula para pasar a otra base. │2 - iniciar sesión 5 x│+ 3 = │1 + iniciar sesión 5 x│
Respuesta: x = 9. №4.
Resuelve la ecuación: │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Usemos la fórmula para pasar a otra base. │2 - iniciar sesión 5 x│+ 3 = │1 + iniciar sesión 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Encontremos los ceros de las expresiones submodulares: x = 25; x = Estos números dividen el rango de valores aceptables en tres intervalos, por lo que la ecuación equivale a un conjunto de tres sistemas.  Respuesta:
Respuesta:
Otro dato importante: El módulo nunca es negativo.. Cualquiera que sea el número que tomemos, ya sea positivo o negativo, su módulo siempre resulta positivo (o, en casos extremos, cero). Es por eso que al módulo a menudo se le llama valor absoluto de un número.
Además, si combinamos la definición del módulo para un número positivo y negativo, obtenemos una definición global del módulo para todos los números. A saber: el módulo de un número es igual al número mismo si el número es positivo (o cero), o igual al número opuesto si el número es negativo. Puedes escribir esto como una fórmula:
También existe un módulo cero, pero siempre es igual a cero. Además, el cero es el único número que no tiene opuesto.
Así, si consideramos la función $y=\left| x \right|$ e intenta dibujar su gráfica, obtendrás algo como esto:
Gráfico de módulo y ejemplo de resolución de la ecuación.
De esta imagen queda inmediatamente claro que $\left| -m \derecha|=\izquierda| m \right|$, y la gráfica del módulo nunca cae por debajo del eje x. Pero eso no es todo: la línea roja marca la recta $y=a$, que, para $a$ positivo, nos da dos raíces a la vez: $((x)_(1))$ y $((x) _(2)) $, pero hablaremos de eso más tarde. :)
Además de la definición puramente algebraica, existe una geométrica. Digamos que hay dos puntos en la recta numérica: $((x)_(1))$ y $((x)_(2))$. En este caso, la expresión $\left| ((x)_(1))-((x)_(2)) \right|$ es simplemente la distancia entre los puntos especificados. O, si lo prefieres, la longitud del segmento que conecta estos puntos:
 El módulo es la distancia entre puntos en una recta numérica.
El módulo es la distancia entre puntos en una recta numérica. Esta definición también implica que el módulo siempre es no negativo. Pero basta de definiciones y teorías: pasemos a las ecuaciones reales. :)
Fórmula básica
Bien, hemos resuelto la definición. Pero eso no lo hizo más fácil. ¿Cómo resolver ecuaciones que contienen este mismo módulo?
Calma, solo calma. Empecemos por las cosas más sencillas. Considere algo como esto:
\[\izquierda| x\derecha|=3\]
Entonces, el módulo de $x$ es 3. ¿A qué podría ser igual $x$? Bueno, a juzgar por la definición, estamos bastante contentos con $x=3$. En realidad:
\[\izquierda| 3\derecha|=3\]
¿Hay otros números? Cap parece estar insinuando que sí. Por ejemplo, $x=-3$ también es $\left| -3 \right|=3$, es decir se cumple la igualdad requerida.
Entonces, ¿tal vez si buscamos y pensamos, encontraremos más números? Pero seamos realistas: no hay más números. Ecuación $\izquierda| x \right|=3$ tiene solo dos raíces: $x=3$ y $x=-3$.
Ahora compliquemos un poco la tarea. Deje que la función $f\left(x \right)$ cuelgue debajo del signo del módulo en lugar de la variable $x$, y coloque un número arbitrario $a$ en lugar del triple de la derecha. Obtenemos la ecuación:
\[\izquierda| f\izquierda(x \derecha) \derecha|=a\]
Entonces, ¿cómo podemos solucionar esto? Déjame recordarte: $f\left(x \right)$ es una función arbitraria, $a$ es cualquier número. Aquellos. ¡Nada en absoluto! Por ejemplo:
\[\izquierda| 2x+1 \derecha|=5\]
\[\izquierda| 10x-5 \derecha|=-65\]
Prestemos atención a la segunda ecuación. Se puede decir inmediatamente de él: no tiene raíces. ¿Por qué? Todo es correcto: porque requiere que el módulo sea igual a un número negativo, lo que nunca ocurre, pues ya sabemos que el módulo es siempre un número positivo o, en casos extremos, cero.
Pero con la primera ecuación todo es más divertido. Hay dos opciones: o hay una expresión positiva bajo el signo del módulo y luego $\left| 2x+1 \right|=2x+1$, o esta expresión sigue siendo negativa, y luego $\left| 2x+1 \right|=-\left(2x+1 \right)=-2x-1$. En el primer caso, nuestra ecuación se reescribirá de la siguiente manera:
\[\izquierda| 2x+1 \right|=5\Flecha derecha 2x+1=5\]
Y de repente resulta que la expresión submodular $2x+1$ es realmente positiva: es igual al número 5. Es decir Podemos resolver esta ecuación con seguridad: la raíz resultante será una parte de la respuesta:
Aquellos que sean particularmente desconfiados pueden intentar sustituir la raíz encontrada en la ecuación original y asegurarse de que realmente haya un número positivo debajo del módulo.
Ahora veamos el caso de una expresión submodular negativa:
\[\left\( \begin(align)& \left| 2x+1 \right|=5 \\& 2x+1 \lt 0 \\\end(align) \right.\Rightarrow -2x-1=5 \Flecha derecha 2x+1=-5\]
¡Ups! Nuevamente, todo está claro: asumimos que $2x+1 \lt 0$, y como resultado obtuvimos que $2x+1=-5$; de hecho, esta expresión es menor que cero. Resolvemos la ecuación resultante, sabiendo con certeza que la raíz encontrada nos conviene:
En total, nuevamente recibimos dos respuestas: $x=2$ y $x=3$. Sí, la cantidad de cálculos resultó ser un poco mayor que en la ecuación muy simple $\left| x \right|=3$, pero nada ha cambiado fundamentalmente. Entonces, ¿tal vez exista algún tipo de algoritmo universal?
Sí, existe tal algoritmo. Y ahora lo analizaremos.
Deshacerse del signo del módulo
Tengamos la ecuación $\left| f\left(x \right) \right|=a$, y $a\ge 0$ (de lo contrario, como ya sabemos, no hay raíces). Luego puedes deshacerte del signo del módulo usando la siguiente regla:
\[\izquierda| f\left(x \right) \right|=a\Rightarrow f\left(x \right)=\pm a\]
Por lo tanto, nuestra ecuación con módulo se divide en dos, pero sin módulo. ¡Eso es toda la tecnología! Intentemos resolver un par de ecuaciones. Empecemos con esto
\[\izquierda| 5x+4 \right|=10\Rightarrow 5x+4=\pm 10\]
Consideremos por separado cuando hay un diez más a la derecha y por separado cuando hay un menos. Tenemos:
\[\begin(align)& 5x+4=10\Rightarrow 5x=6\Rightarrow x=\frac(6)(5)=1,2; \\& 5x+4=-10\Flecha derecha 5x=-14\Flecha derecha x=-\frac(14)(5)=-2.8. \\\end(alinear)\]
¡Eso es todo! Tenemos dos raíces: $x=1.2$ y $x=-2.8$. La solución completa tomó literalmente dos líneas.
Ok, no hay duda, veamos algo un poco más serio:
\[\izquierda| 7-5x\derecha|=13\]
Nuevamente abrimos el módulo con más y menos:
\[\begin(align)& 7-5x=13\Rightarrow -5x=6\Rightarrow x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Flecha derecha -5x=-20\Flecha derecha x=4. \\\end(alinear)\]
Un par de líneas más y ¡la respuesta está lista! Como dije, los módulos no tienen nada de complicado. Sólo necesitas recordar algunas reglas. Por tanto, seguimos adelante y comenzamos con tareas verdaderamente más complejas.
El caso de una variable del lado derecho
Ahora considere esta ecuación:
\[\izquierda| 3x-2 \derecha|=2x\]
Esta ecuación es fundamentalmente diferente de todas las anteriores. ¿Cómo? Y el hecho de que a la derecha del signo igual está la expresión $2x$, y no podemos saber de antemano si es positiva o negativa.
¿Qué hacer en este caso? Primero, debemos entender de una vez por todas que Si el lado derecho de la ecuación resulta ser negativo, entonces la ecuación no tendrá raíces.- ya sabemos que el módulo no puede ser igual a un número negativo.
Y en segundo lugar, si la parte derecha sigue siendo positiva (o igual a cero), entonces puedes actuar exactamente de la misma manera que antes: simplemente abre el módulo por separado con un signo más y por separado con un signo menos.
Por lo tanto, formulamos una regla para funciones arbitrarias $f\left(x \right)$ y $g\left(x \right)$ :
\[\izquierda| f\left(x \right) \right|=g\left(x \right)\Rightarrow \left\( \begin(align)& f\left(x \right)=\pm g\left(x \right) ), \\& g\left(x \right)\ge 0. \\\end(align) \right.\]
En relación a nuestra ecuación obtenemos:
\[\izquierda| 3x-2 \right|=2x\Rightarrow \left\( \begin(align)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end(align) \right.\]
Bueno, de alguna manera podremos hacer frente al requisito $2x\ge 0$. Al final, podemos sustituir estúpidamente las raíces que obtenemos de la primera ecuación y comprobar si la desigualdad se cumple o no.
Entonces resolvamos la ecuación en sí:
\[\begin(align)& 3x-2=2\Rightarrow 3x=4\Rightarrow x=\frac(4)(3); \\& 3x-2=-2\Flecha derecha 3x=0\Flecha derecha x=0. \\\end(alinear)\]
Bueno, ¿cuál de estas dos raíces satisface el requisito $2x\ge 0$? ¡Si ambos! Por lo tanto, la respuesta serán dos números: $x=(4)/(3)\;$ y $x=0$. Esa es la solución. :)
Sospecho que algunos de los estudiantes ya están empezando a aburrirse. Bueno, veamos una ecuación aún más compleja:
\[\izquierda| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\]
Aunque parezca malo, en realidad sigue siendo la misma ecuación de la forma “módulo es igual a función”:
\[\izquierda| f\left(x \right) \right|=g\left(x \right)\]
Y se soluciona exactamente de la misma forma:
\[\izquierda| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\Rightarrow \left\( \begin(align)& ( (x)^(3))-3((x)^(2))+x=\pm \left(x-((x)^(3)) \right), \\& x-((x )^(3))\ge 0. \\\end(align) \right.\]
Nos ocuparemos de la desigualdad más adelante; de alguna manera es demasiado mala (de hecho, es simple, pero no la resolveremos). Por ahora, es mejor ocuparnos de las ecuaciones resultantes. Consideremos el primer caso: es cuando el módulo se expande con un signo más:
\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]
Bueno, es obvio que necesitas recolectar todo lo de la izquierda, traer otros similares y ver qué pasa. Y esto es lo que pasa:
\[\begin(align)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\end(alinear)\]
Sacamos el factor común $((x)^(2))$ de paréntesis y obtenemos una ecuación muy simple:
\[((x)^(2))\left(2x-3 \right)=0\Rightarrow \left[ \begin(align)& ((x)^(2))=0 \\& 2x-3 =0 \\\end(align) \right.\]
\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1.5.\]
Aquí aprovechamos una propiedad importante del producto, por la cual factorizamos el polinomio original: el producto es igual a cero cuando al menos uno de los factores es igual a cero.
Ahora tratemos exactamente de la misma manera la segunda ecuación, que se obtiene expandiendo el módulo con un signo menos:
\[\begin(align)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\izquierda(-3x+2 \derecha)=0. \\\end(alinear)\]
De nuevo lo mismo: el producto es igual a cero cuando al menos uno de los factores es igual a cero. Tenemos:
\[\left[ \begin(align)& x=0 \\& -3x+2=0 \\\end(align) \right.\]
Bueno, tenemos tres raíces: $x=0$, $x=1.5$ y $x=(2)/(3)\;$. Bueno, ¿cuál de este conjunto entrará en la respuesta final? Para ello recordemos que tenemos una restricción adicional en forma de desigualdad:
¿Cómo tener en cuenta este requisito? Simplemente sustituyamos las raíces encontradas y comprobemos si la desigualdad se cumple para estos $x$ o no. Tenemos:
\[\begin(align)& x=0\Rightarrow x-((x)^(3))=0-0=0\ge 0; \\& x=1.5\Rightarrow x-((x)^(3))=1.5-((1.5)^(3)) \lt 0; \\& x=\frac(2)(3)\Rightarrow x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\end(alinear)\]
Por tanto, la raíz $x=1.5$ no nos conviene. Y en respuesta solo habrá dos raíces:
\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]
Como puede ver, incluso en este caso no hubo nada complicado: las ecuaciones con módulos siempre se resuelven mediante un algoritmo. Sólo necesitas tener un buen conocimiento de los polinomios y las desigualdades. Por lo tanto, pasamos a tareas más complejas: ya no habrá uno, sino dos módulos.
Ecuaciones con dos módulos
Hasta ahora, hemos estudiado sólo las ecuaciones más simples: había un módulo y algo más. Enviamos este “algo más” a otra parte de la desigualdad, lejos del módulo, para que al final todo se redujera a una ecuación de la forma $\left| f\left(x \right) \right|=g\left(x \right)$ o incluso más simple $\left| f\left(x \right) \right|=a$.
Pero el jardín de infancia terminó: es hora de pensar en algo más serio. Comencemos con ecuaciones como esta:
\[\izquierda| f\left(x \right) \right|=\left| g\izquierda(x \derecha) \derecha|\]
Esta es una ecuación de la forma “módulo es igual a módulo”. Un punto de fundamental importancia es la ausencia de otros términos y factores: sólo un módulo a la izquierda, otro módulo a la derecha y nada más.
Alguien pensará ahora que este tipo de ecuaciones son más difíciles de resolver que las que hemos estudiado hasta ahora. Pero no: estas ecuaciones son aún más fáciles de resolver. Aquí está la fórmula:
\[\izquierda| f\left(x \right) \right|=\left| g\left(x \right) \right|\Rightarrow f\left(x \right)=\pm g\left(x \right)\]
¡Todo! Simplemente equiparamos expresiones submodulares poniendo un signo más o menos delante de una de ellas. Y luego resolvemos las dos ecuaciones resultantes, ¡y las raíces están listas! Sin restricciones adicionales, sin desigualdades, etc. Todo es muy sencillo.
Intentemos resolver este problema:
\[\izquierda| 2x+3 \derecha|=\izquierda| 2x-7 \derecha|\]
¡Watson elemental! Ampliando los módulos:
\[\izquierda| 2x+3 \derecha|=\izquierda| 2x-7 \right|\Rightarrow 2x+3=\pm \left(2x-7 \right)\]
Consideremos cada caso por separado:
\[\begin(align)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\left(2x-7 \right)\Rightarrow 2x+3=-2x+7. \\\end(alinear)\]
La primera ecuación no tiene raíces. Porque ¿cuándo es $3=-7$? ¿A qué valores de $x$? “¿Qué diablos es $x$? ¿Estas drogado? No hay ningún $x$ allí en absoluto”, dices. Y tendrás razón. Hemos obtenido una igualdad que no depende de la variable $x$, y al mismo tiempo la igualdad en sí es incorrecta. Por eso no hay raíces. :)
Con la segunda ecuación todo es un poco más interesante, pero también muy, muy sencillo:
Como puedes ver, todo se resolvió literalmente en un par de líneas; no esperábamos nada más de una ecuación lineal. :)
Como resultado, la respuesta final es: $x=1$.
¿Así que cómo? ¿Difícil? Por supuesto que no. Probemos algo más:
\[\izquierda| x-1 \derecha|=\izquierda| ((x)^(2))-3x+2 \derecha|\]
Nuevamente tenemos una ecuación de la forma $\left| f\left(x \right) \right|=\left| g\left(x \right) \right|$. Por lo tanto, lo reescribimos inmediatamente, revelando el signo del módulo:
\[((x)^(2))-3x+2=\pm \left(x-1 \right)\]
Quizás ahora alguien pregunte: “Oye, ¿qué tontería? ¿Por qué aparece “más-menos” en la expresión de la derecha y no en la izquierda? Cálmate, ahora te lo explicaré todo. De hecho, en el buen sentido deberíamos haber reescrito nuestra ecuación de la siguiente manera:
Luego debes abrir los corchetes, mover todos los términos a un lado del signo igual (ya que la ecuación, obviamente, será cuadrada en ambos casos) y luego encontrar las raíces. Pero hay que admitirlo: cuando "más-menos" aparece antes de tres términos (especialmente cuando uno de estos términos es una expresión cuadrática), de alguna manera parece más complicado que la situación cuando "más-menos" aparece antes de sólo dos términos.
Pero nada nos impide reescribir la ecuación original de la siguiente manera:
\[\izquierda| x-1 \derecha|=\izquierda| ((x)^(2))-3x+2 \right|\Rightarrow \left| ((x)^(2))-3x+2 \right|=\left| x-1 \derecha|\]
¿Qué pasó? Nada especial: simplemente intercambiaron los lados izquierdo y derecho. Una cosita que al final nos hará la vida un poco más fácil. :)
En general, resolvemos esta ecuación considerando opciones con más y menos:
\[\begin(align)& ((x)^(2))-3x+2=x-1\Rightarrow ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\left(x-1 \right)\Rightarrow ((x)^(2))-2x+1=0. \\\end(alinear)\]
La primera ecuación tiene raíces $x=3$ y $x=1$. El segundo es generalmente un cuadrado exacto:
\[((x)^(2))-2x+1=((\left(x-1 \right))^(2))\]
Por lo tanto, tiene una sola raíz: $x=1$. Pero esta raíz ya la hemos obtenido anteriormente. Por lo tanto, sólo dos números entrarán en la respuesta final:
\[((x)_(1))=3;\quad ((x)_(2))=1.\]
¡Misión cumplida! Puedes coger un pastel del estante y comértelo. Hay 2, el tuyo es el del medio. :)
Nota IMPORTANTE. La presencia de raíces idénticas para diferentes variantes de expansión del módulo significa que los polinomios originales están factorizados, y entre estos factores seguramente habrá uno común. En realidad:
\[\begin(align)& \left| x-1 \derecha|=\izquierda| ((x)^(2))-3x+2 \derecha|; \\& \izquierda| x-1 \derecha|=\izquierda| \left(x-1 \right)\left(x-2 \right) \right|. \\\end(alinear)\]
Una de las propiedades del módulo: $\left| a\cdot b \right|=\left| a \right|\cdot \left| b \right|$ (es decir, el módulo del producto es igual al producto de los módulos), por lo que la ecuación original se puede reescribir de la siguiente manera:
\[\izquierda| x-1 \derecha|=\izquierda| x-1 \right|\cdot \izquierda| x-2 \derecha|\]
Como puedes ver, realmente tenemos un factor común. Ahora, si recoges todos los módulos en un lado, puedes sacar este factor del soporte:
\[\begin(align)& \left| x-1 \derecha|=\izquierda| x-1 \right|\cdot \izquierda| x-2 \derecha|; \\& \izquierda| x-1 \derecha|-\izquierda| x-1 \right|\cdot \izquierda| x-2 \derecha|=0; \\& \izquierda| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0. \\\end(alinear)\]
Bueno, ahora recuerda que el producto es igual a cero cuando al menos uno de los factores es igual a cero:
\[\left[ \begin(align)& \left| x-1 \right|=0, \\& \left| x-2\derecha|=1. \\\end(align) \right.\]
Así, la ecuación original con dos módulos se ha reducido a las dos ecuaciones más simples de las que hablamos al principio de la lección. Estas ecuaciones se pueden resolver literalmente en un par de líneas. :)
Esta observación puede parecer innecesariamente compleja e inaplicable en la práctica. Sin embargo, en realidad, es posible que se encuentre con problemas mucho más complejos que los que analizamos hoy. En ellos se pueden combinar módulos con polinomios, raíces aritméticas, logaritmos, etc. Y en tales situaciones, la capacidad de reducir el grado general de la ecuación quitando algo de los corchetes puede ser muy, muy útil. :)
Ahora me gustaría ver otra ecuación, que a primera vista puede parecer una locura. Muchos estudiantes se quedan estancados, incluso aquellos que creen que comprenden bien los módulos.
Sin embargo, esta ecuación es incluso más fácil de resolver que la que vimos anteriormente. Y si entiendes por qué, obtendrás otro truco para resolver rápidamente ecuaciones con módulos.
Entonces la ecuación es:
\[\izquierda| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\]
No, esto no es un error tipográfico: es un plus entre los módulos. Y necesitamos encontrar en qué $x$ la suma de dos módulos es igual a cero. :)
¿Cuál es el problema de todos modos? Pero el problema es que cada módulo es un número positivo o, en casos extremos, cero. ¿Qué pasa si sumas dos números positivos? Obviamente un número positivo nuevamente:
\[\begin(align)& 5+7=12 \gt 0; \\& 0.004+0.0001=0.0041 \gt 0; \\& 5+0=5 \gt 0. \\\end(align)\]
La última línea puede darte una idea: la única vez que la suma de los módulos es cero es si cada módulo es cero:
\[\izquierda| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\Rightarrow \left\( \begin(align)& \left| x-((x)^(3)) \right|=0, \\& \left| ((x)^(2))+x-2 \right|=0. \\\end(align) \right.\]
¿Y cuándo el módulo es igual a cero? Sólo en un caso, cuando la expresión submodular es igual a cero:
\[((x)^(2))+x-2=0\Rightarrow \left(x+2 \right)\left(x-1 \right)=0\Rightarrow \left[ \begin(align)& x=-2 \\& x=1 \\\end(align) \right.\]
Así, tenemos tres puntos en los que el primer módulo se pone a cero: 0, 1 y −1; así como dos puntos en los que el segundo módulo se pone a cero: −2 y 1. Sin embargo, necesitamos que ambos módulos se pongan a cero al mismo tiempo, por lo que entre los números encontrados debemos elegir aquellos que están incluidos en ambos conjuntos. Obviamente, sólo existe uno de esos números: $x=1$; esta será la respuesta final.
método de escisión
Bueno, ya cubrimos muchos problemas y aprendimos muchas técnicas. ¿Crees que eso es todo? ¡Pero no! Ahora veremos la técnica final y, al mismo tiempo, la más importante. Hablaremos de dividir ecuaciones con módulo. ¿De qué hablaremos siquiera? Retrocedamos un poco y veamos una ecuación simple. Por ejemplo este:
\[\izquierda| 3x-5 \derecha|=5-3x\]
En principio, ya sabemos cómo resolver dicha ecuación, porque es una construcción estándar de la forma $\left| f\left(x \right) \right|=g\left(x \right)$. Pero intentemos ver esta ecuación desde un ángulo ligeramente diferente. Más precisamente, considere la expresión bajo el signo del módulo. Permítanme recordarles que el módulo de cualquier número puede ser igual al número mismo o puede ser opuesto a este número:
\[\izquierda| a \right|=\left\( \begin(align)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\end(align) \right.\]
En realidad, esta ambigüedad es todo el problema: dado que el número bajo el módulo cambia (depende de la variable), no tenemos claro si es positivo o negativo.
Pero ¿qué pasa si inicialmente requieres que este número sea positivo? Por ejemplo, requerimos que $3x-5 \gt 0$; en este caso, tenemos la garantía de obtener un número positivo bajo el signo del módulo, y podemos deshacernos por completo de este mismo módulo:
Así, nuestra ecuación se volverá lineal, lo que se puede resolver fácilmente:
Es cierto que todos estos pensamientos tienen sentido solo bajo la condición $3x-5 \gt 0$; nosotros mismos introdujimos este requisito para revelar el módulo sin ambigüedades. Por lo tanto, sustituyamos el $x=\frac(5)(3)$ encontrado en esta condición y verifiquemos:
Resulta que para el valor especificado de $x$ nuestro requisito no se cumple, porque la expresión resultó ser igual a cero y necesitamos que sea estrictamente mayor que cero. Triste. :(
¡Pero esta bien! Después de todo, existe otra opción $3x-5 \lt 0$. Además, también existe el caso $3x-5=0$; esto también debe tenerse en cuenta, de lo contrario la solución estará incompleta. Entonces, considere el caso $3x-5 \lt 0$:
Evidentemente el módulo se abrirá con un signo menos. Pero entonces surge una situación extraña: tanto a la izquierda como a la derecha de la ecuación original sobresaldrá la misma expresión:
Me pregunto en qué $x$ la expresión $5-3x$ será igual a la expresión $5-3x$. Incluso el Capitán Obviedad se atragantaría con la saliva con tales ecuaciones, pero lo sabemos: esta ecuación es una identidad, es decir. ¡Es cierto para cualquier valor de la variable!
Esto significa que cualquier $x$ nos conviene. Sin embargo, tenemos una limitación:
En otras palabras, la respuesta no será un solo número, sino un intervalo completo:
Finalmente, queda un caso más por considerar: $3x-5=0$. Aquí todo es simple: debajo del módulo habrá cero, y el módulo cero también es igual a cero (esto se desprende directamente de la definición):
Pero entonces la ecuación original $\left| 3x-5 \right|=5-3x$ se reescribirá de la siguiente manera:
Ya obtuvimos esta raíz arriba cuando consideramos el caso de $3x-5 \gt 0$. Además, esta raíz es una solución a la ecuación $3x-5=0$; esta es la limitación que nosotros mismos introdujimos para restablecer el módulo. :)
Así, además del intervalo, también estaremos satisfechos con el número que se encuentra al final de este intervalo:
 Combinando raíces en ecuaciones de módulo
Combinando raíces en ecuaciones de módulo Respuesta final total: $x\in \left(-\infty ;\frac(5)(3) \right]$ No es muy común ver semejante basura en la respuesta a una ecuación bastante simple (esencialmente lineal) con módulo , Bueno, acostúmbrate: la dificultad del módulo es que las respuestas en este tipo de ecuaciones pueden resultar completamente impredecibles.
Algo más es mucho más importante: ¡acabamos de analizar un algoritmo universal para resolver una ecuación con módulo! Y este algoritmo consta de los siguientes pasos:
- Iguala cada módulo de la ecuación a cero. Obtenemos varias ecuaciones;
- Resuelve todas estas ecuaciones y marca las raíces en la recta numérica. Como resultado, la línea recta se dividirá en varios intervalos, en cada uno de los cuales todos los módulos se revelan de forma única;
- Resuelve la ecuación original para cada intervalo y combina tus respuestas.
¡Eso es todo! Sólo queda una pregunta: ¿qué hacer con las raíces obtenidas en el paso 1? Digamos que tenemos dos raíces: $x=1$ y $x=5$. Dividirán la recta numérica en 3 partes:
 Dividir la recta numérica en intervalos usando puntos
Dividir la recta numérica en intervalos usando puntos ¿Cuáles son entonces los intervalos? Está claro que hay tres de ellos:
- El más a la izquierda: $x \lt 1$ — la unidad en sí no está incluida en el intervalo;
- Central: $1\le x \lt 5$ - aquí se incluye uno en el intervalo, pero cinco no;
- Extremo derecho: $x\ge 5$ - ¡cinco solo se incluyen aquí!
Creo que ya entiendes el patrón. Cada intervalo incluye el extremo izquierdo y no incluye el derecho.
A primera vista, una entrada así puede parecer inconveniente, ilógica y, en general, una especie de locura. Pero créame: después de un poco de práctica, descubrirá que este enfoque es el más confiable y no interfiere con la apertura inequívoca de los módulos. Es mejor utilizar este esquema que pensar cada vez: dar el extremo izquierdo/derecho al intervalo actual o "tirarlo" al siguiente.
Esto concluye la lección. Descarga problemas para resolverlos tú mismo, practica, compara con las respuestas y nos vemos en la próxima lección, que estará dedicada a las desigualdades con módulos. :)
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0