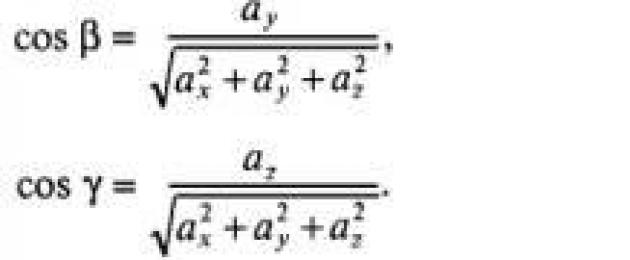Sea el vector ( X , en , z ).
Denotemos los ángulos de inclinación de este vector a los ejes. Oh, oh Y Onz letras en consecuencia ,Y. tres numeros porque, porque Y porque generalmente llamado cosenos directores del vector. Creyendo = (1; 0; 0 ) obtenemos de (9)
Asimismo
De las fórmulas (11) - (13) se deduce:
1) porque 2 +porque 2 +porque 2 = 1 ,
aquellos. la suma de los cuadrados de los cosenos directores de cualquier vector distinto de cero es igual a uno;
aquellos.los cosenos directores de este vector son proporcionales a sus proyecciones correspondientes.
Nota. De las fórmulas (11)-(13) queda claro que las proyecciones de cualquier vector unitario sobre los ejes de coordenadas coinciden respectivamente con sus cosenos directores y, por tanto,
Ejemplo. Encuentra los cosenos directores de un vector. (1; 2; 2). Según las fórmulas (11)-(13) tenemos
4. Producto vectorial de dos vectores y sus principales propiedades.
Definición. El producto cruzado de dos vectores.Y Se llama un nuevo vector, cuyo módulo es igual al área del paralelogramo construido sobre vectores y reducido a un origen común, y que es perpendicular a los vectores que se multiplican (es decir, perpendicular al plano del paralelogramo construido sobre ellos) y dirigido en una dirección tal que la rotación más corta alrededor del vector resultante parece ocurrir en sentido antihorario cuando se ve desde el extremo del vector (Fig. 40).
Si los vectores son colineales, entonces su producto vectorial se considera igual al vector cero. De esta definición se deduce que
|| = || || pecado
¿Dónde está el ángulo entre los vectores? 0 ). El producto vectorial de los vectores y se denota con el símbolo.
x o o [,].
Descubramos el significado físico del producto vectorial. Si un vector representa aplicado en algún punto EM limo, y el vector viene de un cierto punto ACERCA DE exactamente METRO, entonces el vector = representa el momento de fuerza respecto de un punto ACERCA DE.
Propiedades de un producto cruzado
1 . Al reordenar los factores, el producto vectorial cambia de signo, es decir
x = -(x).
()x=x()=(x), donde es un escalar.
3. El producto vectorial obedece a la ley de distribución, es decir
4. Si el producto vectorial de dos vectores es igual al vector cero, entonces al menos uno de los vectores multiplicados es igual al vector cero (caso trivial), o el seno del ángulo entre ellos es igual a cero, es decir los vectores son colineales.
Atrás, Si dos vectores distintos de cero son colineales, entonces su producto vectorial es igual al vector cero.
De este modo , Para que dos vectores distintos de cero sean colineales, es necesario y suficiente que su producto vectorial sea igual al vector cero.
De aquí, en particular, se deduce que el producto vectorial de un vector consigo mismo es igual al vector cero:
x =0
(X también llamado vector cuadrado .
5. Producto mixto de tres vectores y sus principales propiedades.
Sean dados tres vectores, y. Imaginemos que un vector se multiplica vectorialmente por un vector y el vector resultante se multiplica escalarmente por un vector, determinando así el número (x). se llama o trabajo mixto tres vectores, y.
Para abreviar, denotaremos el producto mixto (x) o ().
Descubramos el significado geométrico del producto mixto. Sean los vectores considerados no coplanares. Construyamos un paralelepípedo sobre vectores y aristas.
El producto vectorial x es un vector (=) numéricamente igual al área del paralelogramo OADB (la base del paralelepípedo construido), construido sobre una vectora dirigida perpendicular al plano del paralelogramo (Fig. 41).
El producto escalar (x) = es el producto del módulo del vector y la proyección del vector (ver párrafo 1, (2)).
La altura del paralelepípedo construido es el valor absoluto de esta proyección.
Por tanto, el producto | |en valor absoluto es igual al producto del área de la base del paralelepípedo por su altura, es decir el volumen de un paralelepípedo construido sobre vectores, y.
Es importante señalar que el producto escalar da el volumen del paralelepípedo, a veces con signo positivo y otras con signo negativo. Se obtiene signo positivo si el ángulo entre los vectores es agudo; negativo - si es estúpido. Con un ángulo agudo entre y el vector se encuentra en el mismo lado del plano. OADB , que es un vector y, por tanto, desde el final del vector, la rotación desde él será visible de la misma forma que desde el final del vector, es decir en sentido positivo (en el sentido contrario a las agujas del reloj).
En un ángulo obtuso entre el vector se encuentra al otro lado del plano. OADB que el vector, y por lo tanto, desde el final del vector, la rotación se verá en la dirección negativa (en el sentido de las agujas del reloj). En otras palabras, el producto es positivo si los vectores y forman un sistema del mismo nombre con el Oxyz principal (ubicados mutuamente de la misma manera que los ejes Ox, Oy, Oz), y es negativo si los vectores forman un sistema. del mismo nombre que el principal.
De este modo, el producto mixto es un número,cuyo valor absoluto expresa el volumen del paralelepípedo,construido sobre vectores,como en las costillas.
El signo del producto es positivo si los vectores forman un sistema del mismo nombre que el principal, y negativo en caso contrario.
De ello se deduce que el valor absoluto del producto =(x) seguirá siendo el mismo, sin importar en qué orden tomemos los factores. En cuanto al signo, será positivo en algunos casos, negativo en otros; Depende de si nuestros tres vectores, tomados en un orden determinado, forman o no un sistema del mismo nombre que el principal. Tenga en cuenta que nuestros ejes de coordenadas están ubicados de manera que se suceden en sentido antihorario cuando se mira hacia el interior (Fig. 42). La secuencia no se viola si iniciamos el recorrido desde el segundo o tercer eje, siempre que se haga en la misma dirección, es decir en sentido anti-horario. En este caso, los factores se reordenan de forma circular (cíclicamente). Así obtenemos la siguiente propiedad:
Un producto mixto no cambia con un reordenamiento circular (cíclico) de sus factores. Reorganizar dos factores adyacentes cambia el signo del producto.
= ==-()=-()=-().
Finalmente, la siguiente afirmación se deriva directamente del significado geométrico de un producto mixto.
Una condición necesaria y suficiente para la coplanaridad de vectores.,,es la igualdad de su producto mixto a cero:
La suma de los cuadrados de los cosenos directores es igual a uno.
Si se conocen los cosenos directores del vector, entonces sus coordenadas se pueden encontrar usando las fórmulas: Se aplican fórmulas similares en el caso tridimensional: si se conocen los cosenos directores del vector, entonces sus coordenadas se pueden encontrar usando las fórmulas:
9 Dependencia lineal e independencia lineal de vectores. Base en el avión y en el espacio.
Un conjunto de vectores se llama sistema de vectores.
linealmente dependiente, si hay números que no son todos iguales a cero al mismo tiempo, eso
Un sistema de vectores se llama independiente linealmente, si la igualdad es posible sólo para , es decir cuando la combinación lineal del lado izquierdo de la igualdad es trivial.
1. Un vector también forma un sistema: en - linealmente dependiente y en - linealmente independiente.
2. Cualquier parte de un sistema de vectores se llama subsistema.
1. Si un sistema de vectores incluye un vector cero, entonces es linealmente dependiente
2. Si un sistema de vectores tiene dos vectores iguales, entonces es linealmente dependiente.
3. Si un sistema de vectores tiene dos vectores proporcionales, entonces es linealmente dependiente.
4. Un sistema de vectores es linealmente dependiente si y sólo si al menos uno de los vectores es una combinación lineal de los demás.
5. Cualquier vector incluido en un sistema linealmente independiente forma un subsistema linealmente independiente.
6. Un sistema de vectores que contiene un subsistema linealmente dependiente es linealmente dependiente.
7. Si un sistema de vectores es linealmente independiente y, después de agregarle un vector, resulta ser linealmente dependiente, entonces el vector se puede expandir en vectores y, además, de una manera única, es decir, los coeficientes de expansión se pueden encontrar de forma única.
Base en un plano y en el espacio se llama sistema máximo de vectores que es linealmente independiente en un plano o en el espacio (agregar otro vector al sistema lo hace linealmente dependiente).
Por lo tanto, una base en un plano son dos vectores cualesquiera no colineales tomados en un orden determinado, y una base en el espacio son tres vectores cualesquiera no coplanares tomados en un orden determinado.
Sea una base en el espacio, entonces, según T.3, cualquier vector del espacio se puede descomponer de forma única en vectores base: . Los coeficientes de expansión se llaman coordenadas del vector en la base.
Escribir operaciones lineales sobre vectores a través de coordenadas:
a) suma y resta: - base
b) multiplicación por el número R:
Las fórmulas se derivan de las propiedades de las operaciones lineales.
10 Coordenadas del vector relativas a la base. orty
Base en el espacio vectorial libre V 3 es cualquier triple ordenado de vectores no coplanares.
Dejar EN :un 1,un 2,un 3– base fija en V 3.
Coordenadas vector b en relación con la base EN llamado triple ordenado de números ( x, y, z), incl. b=X· un 1 +yun 2 +z· un 3.
Designación:b={x, y, z} B Nota: Las coordenadas de un vector fijo significan las coordenadas del vector libre correspondiente.
Teorema 1: La correspondencia entre V 3 y R 3 para una base fija es uno a uno, es decir b V 3 ! {x, y, z) R 3 y ( x, y, z) R 3 ! b V 3, incluido b={x, y, z} B
La correspondencia entre un vector y sus coordenadas en una base determinada tiene las siguientes propiedades:
1. Dejar segundo 1 ={x1, y1, z1} B , segundo 2 ={x2, y2, z2} B segundo 1 + segundo 2 ={x 1 + x 2 , y 1 + y 2 , z 1 + z 2} B
2. Dejar b={x, y, z} B , λR λ b={ λ· X, λ· y, λ· z} B
3. deja segundo 1 || segundo 2 , segundo 1 = {x1, y1, z1} B
, segundo 2 ={x2, y2, z2} B
(Aquí: cualquier número).
Vector unitario, dirigido a lo largo del eje X, se denota i, vector unitario, dirigido a lo largo del eje Y, se denota j, A vector unitario, dirigido a lo largo del eje Z, se denota k. Vectores i, j, k son llamados ortos– tienen módulos individuales, es decir
yo = 1, j = 1, k = 1
11 producto escalar de vectores. Ángulo entre vectores. Condición para la ortogonalidad vectorial
Este es un número igual al producto de las longitudes de estos vectores por el coseno del ángulo entre ellos.
Producto escalar de vectores en términos de sus coordenadas.
Producto escalar de vectores X, Y, Z y:
¿Dónde está el ángulo entre los vectores y? si cualquiera, entonces
De la definición de producto escalar se deduce que donde, por ejemplo, es la magnitud de la proyección del vector sobre la dirección del vector.
Vector escalar cuadrado:
Propiedades del producto escalar:
Ángulo entre vectores
Condiciones para la ortogonalidad vectorial.
Dos vector a y B ortogonal (perpendicular), si su producto escalar es igual a cero a· b= 0
Entonces, en el caso de un problema de vector plano
a= (a x ;a y )y b= (b x ;b y )
ortogonal ifa b= a x b x + a y b y = 0
12 producto vectorial de vectores, sus propiedades. Condición de colinealidad de vectores.
El producto cruzado de un vector y un vector es un vector indicado por un símbolo y definido por las siguientes tres condiciones:
1). El módulo del vector es igual a , donde es el ángulo entre los vectores y ;
2). El vector es perpendicular a cada uno de los vectores y ;
3). La dirección del vector corresponde a la "regla de la mano derecha". Esto significa que si los vectores , y se llevan a un origen común, entonces el vector debe dirigirse de la misma manera que el dedo medio de la mano derecha, cuyo pulgar se dirige a lo largo del primer factor (es decir, a lo largo del vector), y el dedo índice, a lo largo del segundo (es decir, a lo largo del vector). El producto vectorial depende del orden de los factores, a saber: .
El módulo del producto vectorial es igual al área S de un paralelogramo construido sobre los vectores y : .
El producto vectorial en sí se puede expresar mediante la fórmula,
¿Dónde está el vector unitario del producto vectorial?
El producto vectorial desaparece si y sólo si los vectores y son colineales. En particular, .
Si el sistema de ejes de coordenadas es recto y los vectores y se especifican en este sistema por sus coordenadas:
entonces el producto vectorial de un vector y un vector está determinado por la fórmula
Un vector es colineal con un vector distinto de cero si y sólo si las coordenadas
los vectores son proporcionales a las coordenadas correspondientes del vector, es decir
Las operaciones lineales sobre vectores especificados por sus coordenadas en el espacio se realizan de manera similar.
13 producto mixto de vectores. Sus propiedades. Condición de coplanaridad de vectores.
Producto mixto de tres vectores., , es un número igual al producto escalar de un vector y un vector:
Propiedades de un producto mixto:
3° Tres vectores son coplanares si y sólo si
4° Una terna de vectores es correcta si y sólo si . Si , entonces los vectores , y forman el triplete izquierdo de vectores.
10° Identidad Jacobi:
Si los vectores , y están dados por sus coordenadas, entonces su producto mixto se calcula mediante la fórmula
Los vectores paralelos a un plano o que se encuentran en el mismo plano se llaman Vectores coplanares.
Condiciones para la coplanaridad de vectores.
Tres los vectores son coplanares si su producto mixto es cero.
Tres los vectores son coplanares si son linealmente dependientes.
15 diferentes tipos de ecuaciones lineales y planas
Cualquier línea recta en el plano se puede especificar mediante una ecuación de primer orden.
Hacha + Wu + C = 0,
Además, las constantes A y B no son iguales a cero al mismo tiempo. Esta ecuación de primer orden se llama ecuación general de una recta. Dependiendo de los valores de las constantes A, B y C, son posibles los siguientes casos especiales:
C = 0, A ≠0, B ≠ 0 – la recta pasa por el origen
A = 0, B ≠0, C ≠0 (By + C = 0) - línea recta paralela al eje Ox
B = 0, A ≠0, C ≠ 0 (Ax + C = 0) – línea recta paralela al eje Oy
B = C = 0, A ≠0 – la línea recta coincide con el eje Oy
A = C = 0, B ≠0 – la línea recta coincide con el eje Ox
La ecuación de una línea recta se puede presentar de diferentes formas dependiendo de las condiciones iniciales dadas.
Propiedad:
cos 2 α + cos 2 β + cos 2 γ = 1
b) definición de operaciones lineales
la suma de dos vectores no colineales es el vector que proviene del origen común de los vectores a lo largo de la diagonal de un paralelogramo construido sobre estos vectores
La diferencia de vectores es la suma de un vector y un vector opuesto al vector: 
. Conectemos los comienzos de los vectores y , luego el vector se dirige desde el final del vector hasta el final del vector. 
La obra un vector por un número se llama vector con módulo, y en y en. Geométricamente, multiplicar por un número significa “estirar” el vector por un factor, manteniendo la dirección en y cambiando al opuesto en .
De las reglas anteriores para sumar vectores y multiplicarlos por un número, se siguen afirmaciones obvias:
1. 
(la suma es conmutativa);
2. 
(la suma es asociativa);
3. 
(existencia de un vector cero);
4. 
(existencia de un vector opuesto);
5. 
(la suma es asociativa);
6. (la multiplicación por un número es distributiva);
7. 
(la suma de vectores es distributiva);
c) producto escalar y sus propiedades básicas
Producto escalar dos vectores distintos de cero es un número igual al producto de las longitudes de estos vectores y el coseno del ángulo entre ellos. Si al menos uno de los dos vectores es cero, entonces el ángulo entre ellos no está definido y el producto escalar se considera igual a cero. El producto escalar de vectores y se denota.
, donde y son las longitudes de los vectores y , respectivamente, y es el ángulo entre los vectores y .
El producto escalar de un vector consigo mismo se llama cuadrado escalar.
Propiedades del producto escalar.
Para cualquier vector y lo siguiente es cierto: propiedades del producto escalar:
la propiedad conmutativa de un producto escalar;
Propiedad distributiva 
o 
;
propiedad asociativa 
o 
, donde es un número real arbitrario;
el cuadrado escalar de un vector siempre es no negativo si y sólo si el vector es cero.
D) producto vectorial y sus propiedades
producto vectorial El vector a al vector b se llama vector c, cuya longitud es numéricamente igual al área del paralelogramo construido sobre los vectores a y b, perpendicular al plano de estos vectores y dirigido de manera que la rotación más pequeña de a a b alrededor del vector c está en sentido antihorario cuando se ve desde el vector final c
Fórmulas para calcular el producto vectorial de vectores.
Ilustraciones vectoriales dos vectores a = (a x; a y; a z) y b = (b x; b y; b z) en el sistema de coordenadas cartesiano es un vector cuyo valor se puede calcular mediante las siguientes fórmulas:
- El producto cruzado de dos vectores a y b distintos de cero es igual a cero si y solo si los vectores son colineales.
- El vector c, igual al producto vectorial de los vectores a y b distintos de cero, es perpendicular a estos vectores.
- a × b = -b × a
- (k una) × b = una × (k b) = k (una × b)
- (a + b) × c = a × c + b × c
Ecuación de una línea recta en un plano.
A) ecuación de una línea recta con un coeficiente de ángulo
Pendiente de una recta se llama tangente del ángulo de inclinación de esta recta.
La pendiente de una línea recta generalmente se indica con la letra k. Luego por definición.
Si la recta es paralela al eje de ordenadas, entonces la pendiente no existe (en este caso también se dice que la pendiente llega al infinito).
Una pendiente positiva de una recta indica un aumento en la gráfica de la función, una pendiente negativa indica una disminución. La ecuación de una línea recta con un coeficiente angular tiene la forma y=kx+b, donde k es el coeficiente angular de la línea, b es algún número real. Usando la ecuación de una línea recta con un coeficiente angular, puede especificar cualquier línea recta que no sea paralela al eje Oy (para una línea recta paralela al eje de ordenadas, el coeficiente angular no está definido).
B) tipos de ecuaciones en línea recta
La ecuacion 
llamado ecuación general de la recta en la superficie.
Cualquier ecuación de primer grado con dos variables. X Y y amable , Dónde A, EN Y CON– algunos números reales, y A Y EN no son iguales a cero al mismo tiempo, define una línea recta en un sistema de coordenadas rectangular oxi en el plano, y cada línea en el plano está dada por una ecuación de la forma .
Ecuación lineal de la forma , donde a Y b– algunos números reales distintos de cero se llaman ecuación de una recta en segmentos. Este nombre no es casual, ya que los valores absolutos de los números. A Y b igual a las longitudes de los segmentos que la recta corta en los ejes de coordenadas Buey Y Oye respectivamente (los segmentos se cuentan desde el origen).
Ecuación lineal de la forma , donde X Y y- variables, y k Y b– algunos números reales se llaman ecuación de una recta con pendiente (k- pendiente)
Ecuación canónica de una recta en un plano. en un sistema de coordenadas cartesiano rectangular oxi parece 
, donde y son algunos números reales y al mismo tiempo no son iguales a cero.
Evidentemente, por el punto pasa la recta definida por la ecuación canónica de la recta. A su vez, los números y en los denominadores de las fracciones representan las coordenadas del vector director de esta recta. Por tanto, la ecuación canónica de la recta en un sistema de coordenadas rectangular oxi en el plano corresponde a una recta que pasa por un punto y que tiene un vector director .
Ecuaciones paramétricas de una recta en un plano. parece 
, donde y son algunos números reales, y al mismo tiempo no son iguales a cero, y es un parámetro que toma cualquier valor real.
Las ecuaciones lineales paramétricas establecen una relación implícita entre las abscisas y las ordenadas de puntos en una línea recta mediante un parámetro (de ahí el nombre de este tipo de ecuación lineal).
Un par de números que se calculan a partir de las ecuaciones paramétricas de una recta para algún valor real del parámetro representan las coordenadas de un determinado punto de la recta. Por ejemplo, cuando tenemos 
, es decir, el punto con coordenadas se encuentra en una línea recta.
Cabe señalar que los coeficientes y para el parámetro en las ecuaciones paramétricas de una línea recta son las coordenadas del vector director de esta línea recta.
Ecuación de una recta que pasa por dos puntos.
Sean dos puntos M 1 (x 1, y 1, z 1) y M 2 (x 2, y 2, z 2) en el espacio, entonces la ecuación de la recta que pasa por estos puntos es:
Si alguno de los denominadores es igual a cero, el numerador correspondiente debe ser igual a 0. En el plano, la ecuación de la recta escrita arriba se simplifica:
si x 1 ≠ x 2 y x = x 1, si x 1 = x 2.
La fracción = k se llama pendiente derecho.
C) calcular el ángulo entre dos rectas
si se dan dos rectas y = k 1 x + b 1, y = k 2 x + b 2, entonces el ángulo agudo entre estas rectas se definirá como
.
Dos rectas son paralelas si k 1 = k 2. Dos rectas son perpendiculares si k 1 = -1/ k 2.
Teorema. Las rectas Ax + Bу + C = 0 y A 1 x + B 1 y + C 1 = 0 son paralelas cuando los coeficientes A 1 = λA, B 1 = λB son proporcionales. Si también C 1 = λC, entonces las rectas coinciden. Las coordenadas del punto de intersección de dos rectas se encuentran como solución al sistema de ecuaciones de estas rectas.
D) condiciones de paralelismo y perpendicularidad de dos rectas
Condiciones para el paralelismo de dos rectas:
a) Si las rectas están dadas por ecuaciones con coeficiente angular, entonces la condición necesaria y suficiente para su paralelismo es la igualdad de sus coeficientes angulares:
k 1 = k 2 .
b) Para el caso en que las rectas estén dadas por ecuaciones en forma general (6), una condición necesaria y suficiente para su paralelismo es que los coeficientes de las correspondientes coordenadas actuales en sus ecuaciones sean proporcionales, es decir
Condiciones de perpendicularidad de dos rectas:
a) En el caso de que las rectas estén dadas por las ecuaciones (4) con un coeficiente angular, una condición necesaria y suficiente para su perpendicularidad es que sus coeficientes angulares sean de magnitud inversa y de signo opuesto, es decir
Esta condición también se puede escribir en la forma
k 1 k 2 = -1.
b) Si las ecuaciones de las rectas se dan en la forma general (6), entonces la condición para su perpendicularidad (necesaria y suficiente) es satisfacer la igualdad
A 1 A 2 + B 1 B 2 = 0.
Límite de función
A) límite de secuencia
El concepto de límite fue utilizado por Newton en la segunda mitad del siglo XVII y por matemáticos del siglo XVIII como Euler y Lagrange, pero entendieron el límite de forma intuitiva. Las primeras definiciones rigurosas del límite de secuencia fueron dadas por Bolzano en 1816 y Cauchy en 1821.
el numero se llama límite de la secuencia numérica, si la secuencia es infinitesimal, es decir todos sus elementos, comenzando por uno determinado, son menores en valor absoluto que cualquier número positivo predeterminado.
Si una secuencia numérica tiene un límite en la forma de un número real, se llama convergente a este número. De lo contrario, la secuencia se llama divergente . Si además es ilimitado, entonces se supone que su límite es igual al infinito.
Además, si todos los elementos de una secuencia ilimitada, a partir de un cierto número, tienen un signo positivo, entonces se dice que el límite de dicha secuencia es más infinito .
Si los elementos de una secuencia ilimitada, a partir de un cierto número, tienen un signo negativo, entonces se dice que el límite de dicha secuencia es igual a menos infinito .
B) límite de la función
Límite de función (valor límite de la función) en un punto dado, limitante para el dominio de definición de una función, es el valor al que tiende el valor de la función considerada a medida que su argumento tiende a un punto dado.
Límite de función es una generalización del concepto de límite de una secuencia: inicialmente, el límite de una función en un punto se entendía como el límite de una secuencia de elementos del dominio de valores de una función compuesta por imágenes de puntos de una secuencia de elementos del dominio de definición de una función que convergen en un punto dado (cuyo límite se considera); si existe tal límite, entonces se dice que la función converge al valor especificado; si tal límite no existe, entonces se dice que la función diverge.
Límite de función- uno de los conceptos básicos del análisis matemático. El valor se llama límite (valor límite) de una función en un punto si para cualquier secuencia de puntos que convergen pero no contienen uno de sus elementos (es decir, en una vecindad perforada), la secuencia de valores de la función converge a .
El valor se llama límite (valor límite) funciona en el punto si para cualquier número positivo tomado de antemano hay un número positivo correspondiente tal que para todos los argumentos que satisfacen la condición se cumple la desigualdad.
C) dos límites destacables
· El primer límite destacable:
Consecuencias
· 
· 
· 
· El segundo límite destacable:
Consecuencias
1. 
2. 
3. 
4. 
5. 
Para ,
6. 
D) funciones infinitesimales e infinitamente grandes
Función y=f(x) llamado infinitesimal en x→a o cuando X→∞, si o , es decir una función infinitesimal es una función cuyo límite en un punto dado es cero.
si funcion y=f(x) representable con x→a como suma de un número constante b y magnitud infinitesimal α(x): f (x)=b+ α(x) Eso .
Por el contrario, si , entonces f(x)=b+α(x), Dónde hacha)– infinitesimal en x→a.
Corolario 1. Si y, entonces.
Corolario 2. Si c= constante, entonces.
Si la función f(x) es infinitamente grande en x→a, entonces función 1 /f(x) es infinitesimal en x→a.
Si la función f(x)- infinitesimal en x→a(o x→∞) y no desaparece, entonces y= 1/f(x) es una función infinitamente grande. Las propiedades más simples de funciones infinitamente pequeñas e infinitamente grandes se pueden escribir utilizando las siguientes relaciones condicionales: A≠ 0
D) divulgación de incertidumbres. La regla de L'Hopital
principales tipos de incertidumbres: cero dividido por cero ( 0 a 0), infinito dividido por infinito, cero multiplicado por infinito, infinito menos infinito, uno elevado a infinito, cero elevado a cero, infinito elevado a cero.
La regla de L'Hopital muy utilizado para cálculos de límites cuando existe una incertidumbre de la forma cero dividido por cero, infinito dividido por infinito.
Estos tipos de incertidumbres incluyen las incertidumbres cero por infinito e infinito menos infinito.
Si y si funciones f(x) Y gramo(x) son diferenciables en una vecindad del punto, entonces 
En el caso de que la incertidumbre no desaparezca tras aplicar la regla de L'Hopital, se podrá aplicar nuevamente.
Cálculo de derivadas
A) la regla para derivar una función compleja
Déjalo ser función compleja , donde la función es un argumento intermedio. Mostraremos cómo encontrar la derivada de una función compleja, conociendo la derivada de la función (la denotaremos por) y la derivada de la función.
Teorema 1. Si una función tiene derivada en un punto X, y la función tiene una derivada en el punto (), entonces la función compleja en el punto X tiene una derivada, y = .
De lo contrario, la derivada de una función compleja es igual al producto de la derivada de la función dada con respecto al argumento intermedio y la derivada del argumento intermedio.
B) derivación de una función especificada paramétricamente
Sea la función dada en forma paramétrica, es decir, en la forma:
donde las funciones y son definidas y continuas durante un cierto intervalo de variación del parámetro. Encontremos los diferenciales de los lados derecho e izquierdo de cada una de las igualdades:
Para encontrar la segunda derivada, realizamos las siguientes transformaciones:
B) el concepto de derivada logarítmica de una función
La derivada logarítmica de una función positiva se llama derivada. Dado que , entonces según la regla de derivación de una función compleja obtenemos la siguiente relación para la derivada logarítmica:
.
Utilizando la derivada logarítmica es conveniente calcular la derivada ordinaria en los casos en que el logaritmo simplifica la forma de la función.
La esencia de esta diferenciación es la siguiente: primero, se encuentra el logaritmo de una función dada y solo luego se calcula su derivada. Dejemos que se dé alguna función. Tomemos logaritmos de los lados izquierdo y derecho de esta expresión:
Y luego, expresando la derivada deseada, el resultado es:
D) derivada de la función inversa
Si y=f(x) y x=g(y) son un par de funciones mutuamente inversas, y la función y=f(x) tiene una derivada f"(x), entonces la derivada de la función inversa g"( x)=1/f” (x).
Por tanto, las derivadas de funciones mutuamente inversas son cantidades recíprocas. Fórmula para la derivada de la función inversa:
D) derivada de una función implícita
Si una función de una variable se describe mediante la ecuación y=F(X), donde la variable y está en el lado izquierdo, y el lado derecho depende sólo del argumento X, entonces dicen que la función está dada explícitamente. Por ejemplo, las siguientes funciones se especifican explícitamente:
y=pecado X,y=X 2+2X+5,y=lncos X.
Sin embargo, en muchos problemas la función se puede especificar implícitamente, es decir. como una ecuación
F(X,y)=0.
para encontrar la derivada y′( X) no es necesario convertir una función especificada implícitamente a una forma explícita. Para ello, conociendo la ecuación F(X,y)=0, simplemente haz lo siguiente:
Primero necesitas diferenciar ambos lados de la ecuación con respecto a la variable. X, asumiendo que y− es una función diferenciable X y usar la regla para calcular la derivada de una función compleja. En este caso, la derivada de cero (en el lado derecho) también será igual a cero.
Comentario: Si el lado derecho no es cero, es decir la ecuación implícita es
F(X,y)=gramo(X,y),
luego diferenciamos los lados izquierdo y derecho de la ecuación.
Resuelve la ecuación resultante para la derivada. y′( X).
Concepto de derivada
A) definición de derivada
Derivada de una función diferenciación integración.
y XX
Definición de derivada
Considere la función F(X X 0. Entonces la función F(X) es diferenciable en el punto X 0, y ella derivado está determinado por la fórmula
F′( X 0)=limΔ X→0Δ yΔ X=limΔ X→0F(X 0+Δ X)−F(X 0)Δ X.
Derivada de una función es uno de los conceptos básicos de las matemáticas, y en el análisis matemático la derivada, junto con la integral, ocupa un lugar central. El proceso de encontrar la derivada se llama diferenciación. La operación inversa (restaurar una función a partir de una derivada conocida) se llama integración.
La derivada de una función en un punto determinado caracteriza la tasa de cambio de la función en ese punto. Se puede obtener una estimación de la tasa de cambio calculando la relación del cambio en la función Δ y a un cambio correspondiente en el argumento Δ X. En la definición de derivada, dicha relación se considera límite bajo la condición Δ X→0. Pasemos a una formulación más estricta:
Definición de derivada
Considere la función F(X), cuyo dominio contiene algún intervalo abierto alrededor del punto X 0. Entonces la función F(X) es diferenciable en el punto X 0, y ella derivado está determinado por la fórmula
F′( X 0)=limΔ X→0Δ yΔ X=limΔ X→0F(X 0+Δ X)−F(X 0)Δ X.
B) significado geométrico de la derivada
La derivada de la función, calculada para un valor dado, es igual a la tangente del ángulo formado por la dirección positiva del eje y la dirección positiva de la tangente trazada a la gráfica de esta función en el punto de la abscisa:
Si una función tiene una derivada finita en un punto, entonces en la vecindad se puede aproximar mediante una función lineal.
La función se llama tangente al punto Número.
D) tabla de derivadas de las funciones elementales más simples
Sea el vector dado. Vector unitario en la misma dirección que 
(vector unitario 
) se encuentra mediante la fórmula:
.
deja que el eje 
forma ángulos con los ejes coordenados 
.Cosenos de dirección del eje. 
Los cosenos de estos ángulos se llaman:. si la dirección 
dado por un vector unitario 
, entonces los cosenos directores sirven como coordenadas, es decir:
.
Los cosenos directores están relacionados entre sí por la relación:
si la dirección 
dado por un vector arbitrario 
, luego encuentre el vector unitario de este vector y, comparándolo con la expresión del vector unitario 
, conseguir:
Producto escalar
Producto escalar
dos vectores 
Y 
es un número igual al producto de sus longitudes por el coseno del ángulo entre ellas: 
.
El producto escalar tiene las siguientes propiedades:
Por eso, 
.
Significado geométrico del producto escalar.: producto escalar de un vector y un vector unitario 
igual a la proyección del vector 
a la dirección determinada 
, es decir. 
.
La siguiente tabla de multiplicación de vectores unitarios se deriva de la definición del producto escalar: 
:
.
Si los vectores están dados por sus coordenadas. 
Y 
, es decir. 
,
, luego, multiplicando estos vectores escalarmente y usando la tabla de multiplicar de vectores unitarios, obtenemos la expresión para el producto escalar 
a través de coordenadas vectoriales:
.
Ilustraciones vectoriales
Producto cruzado de un vector
a vector 
llamado vector 
, cuya longitud y dirección están determinadas por las condiciones:
El producto vectorial tiene las siguientes propiedades:
De las tres primeras propiedades se deduce que la multiplicación vectorial de una suma de vectores por una suma de vectores obedece a las reglas habituales para la multiplicación de polinomios. Solo necesitas asegurarte de que el orden de los factores no cambie.
Los vectores básicos se multiplican de la siguiente manera:
Si 
Y 
, luego, teniendo en cuenta las propiedades del producto vectorial de vectores, podemos derivar una regla para calcular las coordenadas del producto vectorial a partir de las coordenadas de los vectores factoriales:
Si tenemos en cuenta las reglas anteriores para multiplicar vectores unitarios, entonces:
Se puede construir una forma más compacta de escribir una expresión para calcular las coordenadas del producto vectorial de dos vectores introduciendo el concepto de determinante de una matriz.
Consideremos el caso especial cuando los vectores 
Y 
pertenecer al avión 
, es decir. se pueden representar como 
Y 
.
Si las coordenadas de los vectores se escriben en forma de tabla de la siguiente manera: 
, entonces podemos decir que a partir de ellos se forma una matriz cuadrada de segundo orden, es decir tamaño 
, que consta de dos filas y dos columnas. Cada matriz cuadrada está asociada a un número, que se calcula a partir de los elementos de la matriz de acuerdo con ciertas reglas y se llama determinante. El determinante de una matriz de segundo orden es igual a la diferencia entre los productos de los elementos de la diagonal principal y la diagonal secundaria:
.
En este caso:
El valor absoluto del determinante es, por tanto, igual al área del paralelogramo construido sobre los vectores. 
Y 
, ambos a los lados.
Si comparamos esta expresión con la fórmula del producto vectorial (4.7), entonces:
|
|
Esta expresión es una fórmula para calcular el determinante de una matriz de tercer orden a partir de la primera fila.
De este modo:
Determinante de una matriz de tercer orden se calcula de la siguiente manera:
y es la suma algebraica de seis términos.
La fórmula para calcular el determinante de una matriz de tercer orden es fácil de recordar si usa reglaSarrus, que queda formulado de la siguiente manera:
Cada término es el producto de tres elementos ubicados en diferentes columnas y diferentes filas de la matriz;
Los productos de elementos que forman triángulos con un lado paralelo a la diagonal principal tienen signo más;
Los productos de elementos pertenecientes a la diagonal secundaria y dos productos de elementos que forman triángulos con un lado paralelo a la diagonal secundaria tienen signo menos.
estos son los cosenos de los ángulos que forma el vector con los semiejes de coordenadas positivos. Los cosenos directores especifican de forma única la dirección del vector. Si un vector tiene longitud 1, entonces sus cosenos directores son iguales a sus coordenadas. En general, para un vector con coordenadas ( a; b; C) los cosenos directores son iguales:
donde a, b, g son los ángulos que forma el vector con los ejes X, y, z respectivamente.
21) Descomposición de un vector en vectores unitarios. El vector unitario del eje de coordenadas se denota por , los ejes por y los ejes por (Fig. 1).
Para cualquier vector que se encuentre en el plano, se produce la siguiente expansión:
si el vector 
ubicado en el espacio, entonces la expansión en vectores unitarios de los ejes de coordenadas tiene la forma:
22)Producto escalar dos vectores distintos de cero y el número igual al producto de las longitudes de estos vectores por el coseno del ángulo entre ellos se llama:
23) Ángulo entre dos vectores
Si el ángulo entre dos vectores es agudo, entonces su producto escalar es positivo; Si el ángulo entre los vectores es obtuso, entonces el producto escalar de estos vectores es negativo. El producto escalar de dos vectores distintos de cero es igual a cero si y sólo si estos vectores son ortogonales.
24) La condición de paralelismo y perpendicularidad de dos vectores.
Condición para que los vectores sean perpendiculares
Los vectores son perpendiculares si y sólo si su producto escalar es cero, dados dos vectores a(xa;ya) y b(xb;yb). Estos vectores serán perpendiculares si la expresión xaxb + yayb = 0.
25) Producto vectorial de dos vectores.
El producto vectorial de dos vectores no colineales es un vector c=a×b que satisface las siguientes condiciones: 1) |c|=|a| |b| sin(a^b) 2) c⊥a, c⊥b 3) Los vectores a, b, c forman un triplete de vectores a la derecha.
26) Vectores colineales y coplanares.
Los vectores son colineales si la abscisa del primer vector está relacionada con la abscisa del segundo de la misma manera que la ordenada del primero está relacionada con la ordenada del segundo. Dados dos vectores a (xa;ya) Y b (xb;yb). Estos vectores son colineales si xa = xb Y ya = yb, Dónde R.
Vectores −→ a,−→b y −→ C son llamados coplanar, si hay un plano al que son paralelos.
27) Producto mixto de tres vectores. Producto mixto de vectores.- producto escalar del vector a y producto vectorial de los vectores b y c. Encuentre el producto mixto de los vectores a = (1; 2; 3), b = (1; 1; 1), c = (1; 2; 1).
Solución:
1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2
28) La distancia entre dos puntos en un plano. La distancia entre dos puntos dados es igual a la raíz cuadrada de la suma de las diferencias al cuadrado de las mismas coordenadas de estos puntos.
29) División de un segmento en esta relación. Si el punto M(x; y) se encuentra en una recta que pasa por dos puntos dados ( , ) y ( , ), y se da una relación en la que el punto M divide el segmento, entonces las coordenadas del punto M están determinadas por las fórmulas
Si el punto M es el punto medio del segmento, entonces sus coordenadas están determinadas por las fórmulas
30-31. Pendiente de una recta se llama tangente del ángulo de inclinación de esta recta. La pendiente de una línea recta generalmente se indica con la letra k. Entonces por definición
Ecuación de una recta con pendiente tiene la forma donde k- pendiente en línea recta, b– algún número real. Usando la ecuación de una línea recta con un coeficiente de ángulo, puedes especificar cualquier línea recta que no sea paralela al eje. Oye(para una línea recta paralela al eje de ordenadas, el coeficiente angular no está definido).
33. Ecuación general de una recta en un plano. Ecuación de la forma 
Hay ecuación general de una recta oxi. Dependiendo de los valores de las constantes A, B y C, son posibles los siguientes casos especiales:
C = 0, A ≠0, B ≠ 0 – la recta pasa por el origen
A = 0, B ≠0, C ≠0 (By + C = 0) - línea recta paralela al eje Ox
B = 0, A ≠0, C ≠ 0 (Ax + C = 0) – línea recta paralela al eje Oy
B = C = 0, A ≠0 – la línea recta coincide con el eje Oy
A = C = 0, B ≠0 – la línea recta coincide con el eje Ox
34.Ecuación de una recta en segmentos en un plano en un sistema de coordenadas rectangular oxi tiene la forma donde a Y b- algunos números reales distintos de cero. Este nombre no es casual, ya que los valores absolutos de los números. A Y b igual a las longitudes de los segmentos que la recta corta en los ejes de coordenadas Buey Y Oye respectivamente (los segmentos se cuentan desde el origen). Así, la ecuación de una recta en segmentos facilita la construcción de esta recta en un dibujo. Para hacer esto, debes marcar los puntos con coordenadas y en un sistema de coordenadas rectangular en el plano, y usar una regla para conectarlos con una línea recta.
35. La ecuación normal de una recta tiene la forma
¿Dónde está la distancia desde la línea recta al origen? – el ángulo entre la normal a la línea y el eje.
La ecuación normal se puede obtener a partir de la ecuación general (1) multiplicándola por el factor de normalización, el signo es opuesto al signo de modo que .
Los cosenos de los ángulos entre la recta y los ejes de coordenadas se llaman cosenos directores, – el ángulo entre la recta y el eje, – entre la recta y el eje:
Por tanto, la ecuación normal se puede escribir en la forma
Distancia desde el punto a una línea recta determinado por la fórmula 
36. La distancia entre un punto y una línea se calcula mediante la siguiente fórmula: 
donde x 0 e y 0 son las coordenadas del punto, y A, B y C son coeficientes de la ecuación general de la recta.
37. Reducir la ecuación general de una recta a normal. La ecuación y el plano en este contexto no se diferencian entre sí en nada más que en el número de términos de las ecuaciones y la dimensión del espacio. Por tanto, primero diré todo sobre el avión, y al final haré una reserva sobre la línea recta.
Sea la ecuación general del plano: Ax + By + Cz + D = 0.
;. obtenemos el sistema: g;Mc=cosb, MB=cosa Llevémoslo a su forma normal. Para ello multiplicamos ambos lados de la ecuación por el factor de normalización M. Obtenemos: Max+Mvu+MCz+MD=0. En este caso MA=cos;.g;Mc=cosb, MB=cosa obtenemos el sistema:
M2B2=cos2b
M2 C2=cos2g
Sumando todas las ecuaciones del sistema obtenemos M*(A2 +B2+C2)=1 Ahora solo queda expresar M desde aquí para saber por qué factor de normalización hay que multiplicar la ecuación general original para obtenerla a la forma normal:
M=-+1/RAÍZ KV A2 +B2 +C2
MD siempre debe ser menor que cero, por lo que el signo del número M se toma en oposición al signo del número D.
Con la ecuación de una línea recta, todo es igual, solo que de la fórmula para M simplemente debes eliminar el término C2.
| Hacha + Por + cz + D = 0, |
38.Ecuación general del avión. en el espacio se llama ecuación de la forma
Dónde A 2 + B 2 + C 2 ≠ 0 .
En el espacio tridimensional en el sistema de coordenadas cartesiano, cualquier plano se describe mediante una ecuación de primer grado (ecuación lineal). Y a la inversa, cualquier ecuación lineal define un plano.
40.Ecuación de un plano en segmentos. En un sistema de coordenadas rectangular Oxyz en el espacio tridimensional una ecuación de la forma 
, Dónde a, b Y C– los números reales distintos de cero se llaman ecuación del plano en segmentos. Valores absolutos de los números. a, b Y C igual a las longitudes de los segmentos que el plano corta en los ejes de coordenadas Buey, Oye Y Onz respectivamente, contando desde el origen. Signo de números a, b Y C muestra en qué dirección (positiva o negativa) se trazan los segmentos en los ejes de coordenadas
41) Ecuación del plano normal.
La ecuación normal de un avión es su ecuación escrita en la forma
donde , , son los cosenos directores del plano normal, e
p es la distancia desde el origen al plano. Al calcular los cosenos directores de la normal, se debe suponer que se dirige desde el origen al plano (si el plano pasa por el origen, entonces la elección de la dirección positiva de la normal es indiferente).
42) Distancia de un punto a un plano.Sea el plano dado por la ecuación 
y se da un punto. Entonces la distancia del punto al plano está determinada por la fórmula
 |
Prueba. La distancia de un punto a un plano es, por definición, la longitud de la perpendicular trazada desde el punto al plano.
Ángulo entre planos
Sean los planos y especificados por las ecuaciones y , respectivamente. Necesitas encontrar el ángulo entre estos planos.
Los planos, al cruzarse, forman cuatro ángulos diédricos: dos obtusos y dos agudos o cuatro rectos, y ambos ángulos obtusos son iguales entre sí, y ambos ángulos agudos también son iguales entre sí. Siempre buscaremos un ángulo agudo. Para determinar su valor, tomamos un punto en la línea de intersección de los planos y en este punto en cada uno de
planos, dibujamos perpendiculares a la línea de intersección.
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0
