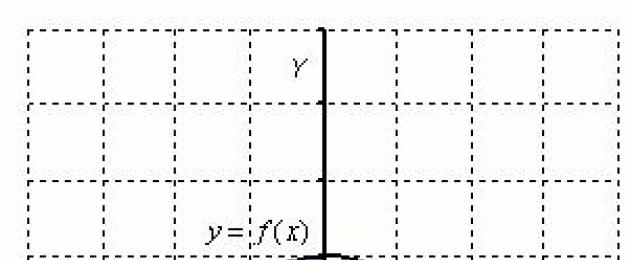Comenzamos a considerar el proceso real de cálculo de la integral doble y nos familiarizamos con su significado geométrico.

La integral doble es numéricamente igual al área de una figura plana (región de integración). Esta es la forma más simple de la integral doble, cuando la función de dos variables es igual a uno: .

Consideremos primero el problema en términos generales. ¡Ahora te sorprenderá lo simple que es en realidad! Calculemos el área de una figura plana delimitada por líneas. Por definición, suponemos que en el intervalo . El área de esta figura es numéricamente igual a:

Representemos el área en el dibujo:

Elijamos la primera forma de evitar el área:

De este modo:

E inmediatamente un truco técnico importante: las integrales iteradas se pueden considerar por separado. Primero la integral interna, luego la integral externa. Este método es muy recomendable para los que se inician en el tema de las teteras.

1) Calcular la integral interna, mientras se realiza la integración sobre la variable "y":

La integral indefinida aquí es la más simple, y luego se usa la fórmula banal de Newton-Leibniz, con la única diferencia de que los límites de integración no son números, sino funciones. Primero, sustituimos el límite superior en "y" (función antiderivada), luego el límite inferior

2) El resultado obtenido en el primer párrafo debe ser sustituido en la integral externa:

Una notación más compacta para toda la solución se ve así:

¡La fórmula resultante es exactamente la fórmula de trabajo para calcular el área de una figura plana usando la integral definida "ordinaria"! Ver lección Cálculo del área usando una integral definida, allí está ella en cada esquina!

Es decir, el problema de calcular el área usando una integral doble un poco diferente del problema de encontrar el área usando una integral definida! De hecho, ¡son uno y lo mismo!

En consecuencia, ¡no deberían surgir dificultades! No consideraré muchos ejemplos, ya que usted, de hecho, se ha encontrado repetidamente con este problema.

Ejemplo 9

Solución: Representemos el área en el dibujo:

Elijamos el siguiente orden de recorrido de la región:

Aquí y más adelante, no entraré en cómo atravesar un área porque el primer párrafo fue muy detallado.

De este modo:

Como ya señalé, es mejor que los principiantes calculen las integrales iteradas por separado, seguiré el mismo método:

1) Primero, usando la fórmula de Newton-Leibniz, tratamos con la integral interna:

2) El resultado obtenido en el primer paso se sustituye en la integral exterior:

El punto 2 en realidad es encontrar el área de una figura plana usando una integral definida.

Responder:

Aquí hay una tarea tan estúpida e ingenua.

Un ejemplo curioso para una solución independiente:

Ejemplo 10

Utilizando la integral doble, calcular el área de una figura plana delimitada por las rectas , ,

Un ejemplo de una solución final al final de la lección.

En los Ejemplos 9-10, es mucho más rentable usar la primera forma de eludir el área, los lectores curiosos, por cierto, pueden cambiar el orden del desvío y calcular las áreas de la segunda manera. Si no comete un error, entonces, naturalmente, se obtienen los mismos valores de área.

Pero en algunos casos, la segunda forma de eludir el área es más efectiva y, como conclusión del curso para jóvenes nerds, veamos un par de ejemplos más sobre este tema:

Ejemplo 11

Usando la integral doble, calcula el área de una figura plana delimitada por líneas.

Solución: estamos esperando dos parábolas con una brisa que yacen de lado. No hay necesidad de sonreír, a menudo se encuentran cosas similares en integrales múltiples.

¿Cuál es la forma más fácil de hacer un dibujo?

Representemos la parábola como dos funciones:
- rama superior y - rama inferior.

De manera similar, representamos la parábola como las ramas superior e inferior.

El área de la figura se calcula mediante la integral doble según la fórmula:

¿Qué sucede si elegimos la primera forma de evitar el área? Primero, esta área tendrá que ser dividida en dos partes. Y en segundo lugar, observaremos este triste cuadro: . Las integrales, por supuesto, no son de un nivel supercomplejo, pero... hay un viejo dicho matemático: quien es amigo de las raíces no necesita compensación.

Por tanto, del malentendido que se da en la condición, expresamos las funciones inversas:

Las funciones inversas en este ejemplo tienen la ventaja de que inmediatamente configuran toda la parábola sin hojas, bellotas, ramas y raíces.

Según el segundo método, el recorrido del área será el siguiente:

De este modo:

Como dicen, siente la diferencia.

1) Nos ocupamos de la integral interna:

Sustituimos el resultado en la integral exterior:

La integración sobre la variable "y" no debería ser embarazosa, si hubiera una letra "zyu", sería genial integrarla. Aunque quien leyó el segundo párrafo de la lección Cómo calcular el volumen de un cuerpo de revolución, ya no experimenta la más mínima vergüenza con la integración sobre "y".

También presta atención al primer paso: el integrando es par y el segmento de integración es simétrico alrededor de cero. Por lo tanto, el segmento se puede reducir a la mitad y el resultado se puede duplicar. Esta técnica se comenta en detalle en la lección. Métodos eficientes para calcular la integral definida.

Que agregar…. ¡Todo!

Responder:

Para probar su técnica de integración, puede intentar calcular . La respuesta debe ser exactamente la misma.

Ejemplo 12

Usando la integral doble, calcula el área de una figura plana delimitada por líneas

Este es un ejemplo de bricolaje. Es interesante notar que si intenta usar la primera forma de evitar el área, ¡la figura ya no se dividirá en dos, sino en tres partes! Y, en consecuencia, obtenemos tres pares de integrales iteradas. A veces ocurre.

La clase magistral ha llegado a su fin y es hora de pasar al nivel de gran maestro: ¿Cómo calcular la integral doble? Ejemplos de soluciones. Intentaré no ser tan maníaco en el segundo artículo =)

¡Le deseo éxito!

Soluciones y respuestas:

Ejemplo 2:Solución: dibujar un área en el dibujo:

Elijamos el siguiente orden de recorrido de la región:

De este modo:
Pasemos a las funciones inversas:


De este modo:
Responder:

Ejemplo 4:Solución: Pasemos a las funciones directas:


Ejecutemos el dibujo:

Cambiemos el orden de recorrido del área:

Responder:

Orden de recorrido del área:

De este modo:

1)
2)

Responder:

Integral definida. Cómo calcular el área de una figura

Pasamos ahora a la consideración de las aplicaciones del cálculo integral. En esta lección, analizaremos una tarea típica y más común. Cómo usar una integral definida para calcular el área de una figura plana. Finalmente, aquellos que buscan significado en las matemáticas superiores, que lo encuentren. Nunca sabes. En la vida real, tendrás que aproximar una casa de verano con funciones elementales y encontrar su área usando una determinada integral.

Para dominar con éxito el material, debe:

1) Comprender la integral indefinida al menos a un nivel intermedio. Por lo tanto, los tontos primero deben leer la lección. No.

2) Ser capaz de aplicar la fórmula de Newton-Leibniz y calcular la integral definida. Puede establecer cálidas relaciones amistosas con ciertos integrales en la página. Integral definida. Ejemplos de soluciones.

De hecho, para encontrar el área de una figura, no necesita tanto conocimiento de la integral indefinida y definida. La tarea "calcular el área usando una integral definida" siempre involucra la construcción de un dibujo, por lo que tus conocimientos y habilidades de dibujo serán un tema mucho más relevante. En este sentido, es útil para refrescar la memoria de las gráficas de las principales funciones elementales y, como mínimo, poder construir una recta, una parábola y una hipérbola. Esto se puede hacer (muchos lo necesitan) con la ayuda de material metodológico y un artículo sobre transformaciones geométricas de grafos.

En realidad, todos están familiarizados con el problema de encontrar el área usando una integral definida desde la escuela, y nos adelantaremos un poco al plan de estudios escolar. Puede que este artículo no exista en absoluto, pero el hecho es que el problema ocurre en 99 de cada 100 casos, cuando un estudiante es atormentado por una torre odiada con entusiasmo por dominar un curso de matemáticas superiores.

Los materiales de este taller se presentan de forma sencilla, detallada y con un mínimo de teoría.

Comencemos con un trapezoide curvilíneo.

Trapecio curvilíneo Se llama figura plana acotada por el eje , rectas , y la gráfica de una función continua en un segmento que no cambia de signo en este intervalo. Que esta figura se ubique no menos abscisa:

Luego el área de un trapezoide curvilíneo es numéricamente igual a cierta integral. Cualquier integral definida (que existe) tiene un muy buen significado geométrico. en la lección Integral definida. Ejemplos de soluciones Dije que una integral definida es un número. Y ahora es el momento de declarar otro hecho útil. Desde el punto de vista de la geometría, la integral definida es el ÁREA.

Es decir, la integral definida (si existe) corresponde geométricamente al área de alguna figura. Por ejemplo, considere la integral definida . El integrando define una curva en el plano que se encuentra arriba del eje (los que lo deseen pueden completar el dibujo), y la propia integral definida es numéricamente igual al área del trapezoide curvilíneo correspondiente.

Ejemplo 1

Esta es una declaración de tarea típica. El primer y más importante momento de la decisión es la construcción de un dibujo.. Además, el dibujo debe construirse CORRECTO.

Al construir un plano, recomiendo el siguiente orden: en primer lugar es mejor construir todas las líneas (si las hay) y solo Luego- parábolas, hipérbolas, gráficas de otras funciones. Los gráficos de funciones son más rentables para construir punto por punto, con la técnica de construcción puntual se puede encontrar en el material de referencia Gráficas y propiedades de funciones elementales. Allí también puede encontrar material que es muy útil en relación con nuestra lección: cómo construir rápidamente una parábola.

En este problema, la solución podría verse así.
Hagamos un dibujo (nótese que la ecuación define el eje):

No tramaré un trapezoide curvilíneo, es obvio de qué área estamos hablando aquí. La solución continúa así:

En el segmento se encuentra la gráfica de la función sobre el eje, es por eso:

Responder:

Que tiene dificultad para calcular la integral definida y aplicar la fórmula de Newton-Leibniz , consulte la conferencia Integral definida. Ejemplos de soluciones.

Una vez completada la tarea, siempre es útil mirar el dibujo y averiguar si la respuesta es real. En este caso, "a ojo" contamos la cantidad de celdas en el dibujo; bueno, se escribirán alrededor de 9, parece ser cierto. Está bastante claro que si tuviéramos, digamos, la respuesta: 20 unidades cuadradas, entonces, obviamente, se cometió un error en alguna parte: 20 celdas obviamente no encajan en la cifra en cuestión, como máximo una docena. Si la respuesta resultó ser negativa, entonces la tarea también se resolvió incorrectamente.

Ejemplo 2

Calcular el área de la figura delimitada por las rectas , y el eje

Este es un ejemplo de bricolaje. Solución completa y respuesta al final de la lección.

Qué hacer si se encuentra el trapezoide curvilíneo debajo del eje?

Ejemplo 3

Calcula el área de la figura delimitada por líneas y ejes de coordenadas.

Solución: Hagamos un dibujo:

Si el trapezoide curvilíneo se encuentra debajo del eje(o al menos no más alto eje dado), entonces su área se puede encontrar mediante la fórmula:
En este caso:

¡Atención! No confundas los dos tipos de tareas.:

1) Si se le pide que resuelva solo una integral definida sin ningún significado geométrico, entonces puede ser negativa.

2) Si se le pide que encuentre el área de una figura usando una integral definida, ¡entonces el área siempre es positiva! Por eso aparece el signo menos en la fórmula que acabamos de considerar.

En la práctica, la mayoría de las veces la figura se ubica tanto en el semiplano superior como en el inferior y, por lo tanto, desde los problemas escolares más simples, pasamos a ejemplos más significativos.

Ejemplo 4

Encuentra el área de una figura plana delimitada por rectas, .

Solución: Primero necesitas completar el dibujo. En términos generales, cuando construimos un dibujo en problemas de área, estamos más interesados ​​en los puntos de intersección de las líneas. Encontremos los puntos de intersección de la parábola y la recta. Esto se puede hacer de dos maneras. La primera forma es analítica. Resolvemos la ecuación:

Por lo tanto, el límite inferior de integración, el límite superior de integración.
Es mejor no usar este método si es posible..

Es mucho más rentable y rápido construir las líneas punto por punto, mientras que los límites de integración se van descubriendo como “por sí mismos”. La técnica de construcción punto por punto para varios gráficos se analiza en detalle en la ayuda Gráficas y propiedades de funciones elementales. Sin embargo, el método analítico para encontrar los límites todavía tiene que usarse a veces si, por ejemplo, el gráfico es lo suficientemente grande o la construcción enhebrada no reveló los límites de integración (pueden ser fraccionarios o irracionales). Y también consideraremos tal ejemplo.

Volvemos a nuestra tarea: es más racional construir primero una línea recta y luego una parábola. Hagamos un dibujo:

Repito que con la construcción puntual, los límites de integración se descubren con mayor frecuencia "automáticamente".

Y ahora la fórmula de trabajo: Si hay alguna función continua en el intervalo mayor que o igual alguna función continua, entonces el área de la figura delimitada por las gráficas de estas funciones y las líneas rectas, se puede encontrar mediante la fórmula:

Aquí ya no es necesario pensar dónde se encuentra la figura: sobre el eje o debajo del eje y, en términos generales, importa qué gráfico está ARRIBA(relativo a otro gráfico), y cual esta ABAJO.

En el ejemplo en consideración, es obvio que en el segmento la parábola se encuentra por encima de la línea recta y, por lo tanto, es necesario restar de

La finalización de la solución podría verse así:

La figura deseada está limitada por una parábola desde arriba y una línea recta desde abajo.
Sobre el segmento , según la fórmula correspondiente:

Responder:

De hecho, la fórmula escolar para el área de un trapezoide curvilíneo en el semiplano inferior (ver el ejemplo simple No. 3) es un caso especial de la fórmula . Como el eje viene dado por la ecuación , y la gráfica de la función se encuentra no más alto hachas, entonces

Y ahora un par de ejemplos para una decisión independiente.

Ejemplo 5

Ejemplo 6

Encuentra el área de la figura encerrada por las líneas , .

En el curso de la resolución de problemas para calcular el área utilizando una cierta integral, a veces ocurre un incidente divertido. El dibujo se hizo correctamente, los cálculos fueron correctos, pero debido a la falta de atención ... encontró el área de la figura equivocada, así la cagó varias veces tu obediente servidor. Aquí hay un caso de la vida real:

Ejemplo 7

Calcula el área de la figura delimitada por las rectas , , , .

Solución: Primero hagamos un dibujo:

…Eh, el dibujo salió una mierda, pero todo parece ser legible.

La figura cuya área necesitamos encontrar está sombreada en azul.(Mire cuidadosamente la condición, ¡cómo la figura es limitada!). Pero en la práctica, debido a la falta de atención, a menudo ocurre un "fallo", ¡que necesita encontrar el área de la figura que está sombreada en verde!

Este ejemplo también es útil porque en él el área de la figura se calcula utilizando dos integrales definidas. En realidad:

1) En el segmento sobre el eje hay un gráfico de línea recta;

2) En el segmento sobre el eje hay un gráfico de hipérbola.

Es bastante obvio que las áreas pueden (y deben) agregarse, por lo tanto:

Responder:

Pasemos a una tarea más significativa.

Ejemplo 8

Calcular el área de una figura delimitada por rectas,
Presentemos las ecuaciones en forma de "escuela" y realicemos un dibujo punto por punto:

Se puede ver en el dibujo que nuestro límite superior es "bueno": .
Pero, ¿cuál es el límite inferior? Está claro que esto no es un número entero, pero ¿qué? Quizás ? Pero, ¿dónde está la garantía de que el dibujo está hecho con perfecta precisión? Bien puede resultar eso. O raíz. ¿Qué pasa si no conseguimos el gráfico correcto en absoluto?

En tales casos, uno tiene que dedicar tiempo adicional y refinar los límites de integración analíticamente.

Encontremos los puntos de intersección de la recta y la parábola.
Para ello, resolvemos la ecuación:


,

En realidad, .

La solución adicional es trivial, lo principal es no confundirse con sustituciones y signos, los cálculos aquí no son los más fáciles.

en el segmento , según la fórmula correspondiente:

Responder:

Bueno, como conclusión de la lección, consideraremos dos tareas más difíciles.

Ejemplo 9

Calcula el área de la figura delimitada por las rectas , ,

Solución: Dibuja esta figura en el dibujo.

Joder, se me olvidó firmar el horario, y rehacer la foto, lo siento, no hotz. No es un dibujo, en fin, hoy es un día =)

Para la construcción punto por punto, es necesario conocer la apariencia de la sinusoide (y en general es útil conocer gráficas de todas las funciones elementales), así como algunos valores de seno, se pueden encontrar en tabla trigonométrica. En algunos casos (como en este caso), se permite construir un dibujo esquemático, en el que los gráficos y los límites de integración deben mostrarse en principio correctamente.

Aquí no hay problemas con los límites de integración, se siguen directamente de la condición: - "x" cambia de cero a "pi". Tomamos otra decisión:

En el segmento, la gráfica de la función se ubica arriba del eje, por lo tanto:

En esta lección aprenderemos a calcular áreas de figuras planas, que se llaman trapecios curvilíneos .

Ejemplos de tales figuras se encuentran en la siguiente figura.

Por un lado, encontrar el área de una figura plana mediante una integral definida es sumamente sencillo. Estamos hablando del área de la figura, que está limitada desde arriba por una cierta curva, desde abajo, por el eje de abscisas ( Buey), y a la izquierda y a la derecha hay algunas líneas rectas. La sencillez es que la integral definida de la función a la que se le da la curva, y ahí está el área de tal figura(trapecio curvilíneo).

Para calcular el área de una figura necesitamos:

1. Integral definida de la función que define la curva , que limita el trapezoide curvilíneo desde arriba. Y aquí viene el primer matiz significativo: un trapezoide curvilíneo puede estar limitado por una curva no solo desde arriba, sino también desde abajo . ¿Cómo actuar en este caso? Simple pero importante de recordar: la integral en este caso se toma con signo menos .
2. Límites de integración a Y B, que encontramos a partir de las ecuaciones de las rectas que limitan la figura por la izquierda y la derecha: X = a , X = B, donde a Y B- numeros

Por separado, algunos matices más..

La curva que limita el trapezoide curvilíneo desde arriba (o desde abajo) debe ser gráfico de una función continua y no negativa y = F(X) .

Los valores de X deben pertenecer al segmento [a, B] . Es decir, por ejemplo, no se tienen en cuenta las líneas como una sección de un hongo, en el que la pierna encaja perfectamente en este segmento y la tapa es mucho más ancha.

Los segmentos laterales pueden degenerar en puntos . Si viste una figura así en el dibujo, esto no debería confundirte, ya que este punto siempre tiene su propio valor en el eje x. Entonces todo está en orden con los límites de la integración.

Ahora puede pasar a fórmulas y cálculos. Entonces el área s trapezoide curvilíneo se puede calcular mediante la fórmula

Si F(X) ≤ 0 (la gráfica de la función se encuentra debajo del eje Buey), luego área de un trapezoide curvo se puede calcular con la formula

También hay casos en los que los límites superior e inferior de la figura son funciones, respectivamente y = F(X) Y y = φ (X) , entonces el área de dicha figura se calcula mediante la fórmula

. (3)

Resolvemos problemas juntos

Comencemos con los casos en los que el área de una figura se puede calcular usando la fórmula (1).

Ejemplo 1Buey) y directo X = 1 , X = 3 .

Solución. Porque y = 1/X> 0 en el segmento , entonces el área del trapezoide curvilíneo se encuentra por la fórmula (1):

.

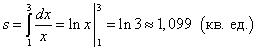Ejemplo 2 Halla el área de la figura acotada por la gráfica de la función, recta X= 1 y el eje x ( Buey ).

Solución. El resultado de aplicar la fórmula (1):

si entonces s= 1/2; si entonces s= 1/3, etc

Ejemplo 3 Encuentra el área de la figura acotada por la gráfica de la función, el eje x ( Buey) y directo X = 4 .

Solución. La figura correspondiente a la condición del problema es un trapezoide curvilíneo, en el que el segmento izquierdo ha degenerado en un punto. Los límites de integración son 0 y 4. Ya que, según la fórmula (1), encontramos el área del trapezoide curvilíneo:

.

Ejemplo 4 Halla el área de la figura delimitada por las rectas , , y ubicada en el 1er cuarto.

Solución. Para usar la fórmula (1), representamos el área de la figura dada por las condiciones del ejemplo como la suma de las áreas de un triángulo OAB y trapecio curvilíneo A B C. Al calcular el área de un triángulo. OAB los límites de integración son las abscisas de los puntos O Y A, y para la figura A B C- abscisas de puntos A Y C (A es el punto de intersección de la recta OA y parábolas, y C- punto de intersección de la parábola con el eje Buey). Resolviendo conjuntamente (como sistema) las ecuaciones de una recta y una parábola, obtenemos (la abscisa del punto A) y (la abscisa de otro punto de intersección de la recta y la parábola, que no es necesaria para la solución). Análogamente, obtenemos , (abscisas de los puntos C Y D). Ahora tenemos todo para encontrar el área de la figura. Encontramos:

Ejemplo 5 Encuentra el área de un trapezoide curvilíneo ACDB, si la ecuación de la curva discos compactos y abscisa A Y B respectivamente 1 y 2.

Solución. Esta ecuación de la curva la expresamos a través de Y: El área del trapezoide curvilíneo se encuentra mediante la fórmula (1):

.

Pasemos a los casos en los que el área de una figura se puede calcular usando la fórmula (2).

Ejemplo 6 Encuentra el área de la figura delimitada por la parábola y el eje x ( Buey ).

Solución. Esta figura se encuentra debajo del eje x. Por lo tanto, para calcular su área, usamos la fórmula (2). Los límites de integración son las abscisas y los puntos de intersección de la parábola con el eje Buey. Como consecuencia,

Ejemplo 7 Encuentre el área entre el eje x ( Buey) y dos ondas sinusoidales vecinas.

Solución. El área de esta figura se puede encontrar mediante la fórmula (2):

.

Encontremos cada término por separado:

.

.

Finalmente encontramos el área:

.

Ejemplo 8 Encuentra el área de la figura encerrada entre la parábola y la curva.

Solución. Expresemos las ecuaciones de las rectas en términos de Y:

El área según la fórmula (2) se obtendrá como

,

donde a Y B- abscisas de puntos A Y B. Los encontramos resolviendo las ecuaciones juntas:

Finalmente encontramos el área:

Y, finalmente, hay casos en que el área de una figura se puede calcular usando la fórmula (3).

Ejemplo 9 Halla el área de la figura encerrada entre las parábolas Y .

Descubrimos cómo encontrar el área de un trapezoide curvilíneo G. Estas son las fórmulas resultantes:
para una función continua y no negativa y=f(x) en el segmento ,
para una función continua y no positiva y=f(x) en el segmento .

Sin embargo, cuando se resuelven problemas para encontrar el área, a menudo hay que lidiar con figuras más complejas.

En este artículo, hablaremos sobre el cálculo del área de figuras cuyos límites están explícitamente especificados por funciones, es decir, como y=f(x) o x=g(y), y analizaremos en detalle la solución de ejemplos típicos. .

Navegación de página.

Fórmula para calcular el área de una figura delimitada por líneas y=f(x) o x=g(y) .

Teorema.

Sean las funciones y definidas y continuas en el segmento , y para cualquier valor x de . Luego área de la figura G, delimitada por líneas x=a , x=b , y se calcula mediante la fórmula .

Una fórmula similar es válida para el área de la figura delimitada por las líneas y \u003d c, y \u003d d y: .

Prueba.

Demostremos la validez de la fórmula para tres casos:

En el primer caso, cuando ambas funciones son no negativas, por la propiedad de aditividad del área, la suma del área de la figura original G y el trapezoide curvilíneo es igual al área de la figura. Como consecuencia,

Es por eso, . La última transición es posible debido a la tercera propiedad de la integral definida.

De manera similar, en el segundo caso, la igualdad es cierta. Aquí hay una ilustración gráfica:

En el tercer caso, cuando ambas funciones son no positivas, tenemos . Ilustremos esto:

Ahora podemos pasar al caso general cuando las funciones y cruzan el eje Ox.

Denotemos los puntos de intersección. Estos puntos dividen el segmento en n partes, donde . La figura G se puede representar por la unión de las figuras . Es obvio que en su intervalo cae bajo uno de los tres casos considerados anteriormente, por lo que sus áreas se encuentran como

Como consecuencia,

La última transición es válida debido a la quinta propiedad de la integral definida.

Ilustración gráfica del caso general.

Así la fórmula probado.

Es hora de pasar a resolver ejemplos para encontrar el área de figuras delimitadas por las líneas y=f(x) y x=g(y) .

Ejemplos de cálculo del área de una figura delimitada por líneas y=f(x) o x=g(y) .

Comenzaremos la solución de cada problema construyendo una figura en un plano. Esto nos permitirá representar una figura compleja como una unión de figuras más simples. En caso de dificultades con la construcción, consulte los artículos:; Y .

Ejemplo.

Calcular el área de una figura acotada por una parábola y rectas, x=1, x=4.

Solución.

Construyamos estas líneas en el plano.

En todas partes del segmento, la gráfica de una parábola arriba recto. Por lo tanto, aplicamos la fórmula obtenida anteriormente para el área y calculamos la integral definida utilizando la fórmula de Newton-Leibniz:

Vamos a complicar un poco el ejemplo.

Ejemplo.

Calcula el área de la figura delimitada por rectas.

Solución.

¿En qué se diferencia esto de los ejemplos anteriores? Anteriormente, siempre teníamos dos rectas paralelas al eje x, y ahora solo una x=7. Inmediatamente surge la pregunta: ¿dónde llevar el segundo límite de integración? Echemos un vistazo al dibujo para esto.

Quedó claro que el límite inferior de integración al encontrar el área de la figura es la abscisa del punto de intersección del gráfico de la línea recta y \u003d x y la semiparábola. Encontramos esta abscisa de la igualdad:

Por lo tanto, la abscisa del punto de intersección es x=2.

Nota.

En nuestro ejemplo y en el dibujo, se puede ver que las rectas e y=x se cortan en el punto (2;2) y los cálculos anteriores parecen redundantes. Pero en otros casos, las cosas pueden no ser tan obvias. Por lo tanto, le recomendamos que siempre calcule analíticamente las abscisas y ordenadas de los puntos de intersección de las líneas.

Obviamente, la gráfica de la función y=x se encuentra arriba de la gráfica de la función en el intervalo . Aplicamos la fórmula para calcular el área:

Compliquemos aún más la tarea.

Ejemplo.

Calcular el área de la figura acotada por las gráficas de funciones y .

Solución.

Construyamos un gráfico de proporcionalidad inversa y una parábola. .

Antes de aplicar la fórmula para encontrar el área de una figura, debemos decidir los límites de integración. Para ello, hallamos las abscisas de los puntos de intersección de las rectas igualando las expresiones y .

Para valores de x distintos de cero, la igualdad equivalente a la ecuación de tercer grado con coeficientes enteros. Puede consultar la sección para recordar el algoritmo para resolverlo.

Es fácil comprobar que x=1 es la raíz de esta ecuación: .

Dividiendo la expresión al binomio x-1 , tenemos:

Por lo tanto, las raíces restantes se encuentran a partir de la ecuación :

Ahora, del dibujo quedó claro que la figura G está encerrada sobre la línea azul y debajo de la línea roja en el intervalo . Por lo tanto, el área requerida será igual a

Veamos otro ejemplo típico.

Ejemplo.

Calcular el área de una figura delimitada por curvas y el eje de abscisas.

Solución.

Hagamos un dibujo.

Esta es una función de potencia ordinaria con un exponente de un tercio, la gráfica de la función se puede obtener del gráfico mostrándolo simétricamente con respecto al eje x y levantándolo en uno.

Encuentra los puntos de intersección de todas las rectas.

El eje x tiene la ecuación y=0 .

Las gráficas de las funciones e y=0 se cortan en el punto (0;0) ya que x=0 es la única raíz real de la ecuación.

Gráficos de funciones y y=0 se intersecan en (2;0), ya que x=2 es la única raíz de la ecuación .

Gráficas de funciones y se cortan en el punto (1;1) ya que x=1 es la única raíz de la ecuación . Este enunciado no es del todo obvio, pero es una función estrictamente creciente, y - estrictamente decreciente, por lo tanto, la ecuación tiene como máximo una raíz.

La única observación: en este caso, para encontrar el área, deberá usar una fórmula de la forma . Es decir, las líneas delimitadoras deben representarse como funciones del argumento y , pero con una línea negra .

Definamos los puntos de intersección de las rectas.

Empecemos con gráficas de funciones y :

Encontremos el punto de intersección de las gráficas de funciones y :

Queda por encontrar el punto de intersección de las rectas y :

Como puede ver, los valores coinciden.

Resumir.

Hemos analizado todos los casos más comunes de encontrar el área de una figura delimitada por líneas explícitamente dadas. Para hacer esto, debe poder construir líneas en un plano, encontrar los puntos de intersección de las líneas y aplicar la fórmula para encontrar el área, lo que implica la capacidad de calcular ciertas integrales.

Ejemplo 1 . Calcule el área de la figura delimitada por líneas: x + 2y - 4 = 0, y = 0, x = -3 y x = 2

Construyamos una figura (ver Fig.) Construimos una línea recta x + 2y - 4 \u003d 0 a lo largo de dos puntos A (4; 0) y B (0; 2). Expresando y en términos de x, obtenemos y \u003d -0.5x + 2. De acuerdo con la fórmula (1), donde f (x) \u003d -0.5x + 2, a \u003d -3, b \u003d 2, nosotros encontrar

S \u003d \u003d [-0.25 \u003d 11.25 metros cuadrados. unidades

Ejemplo 2 Calcule el área de la figura delimitada por líneas: x - 2y + 4 \u003d 0, x + y - 5 \u003d 0 e y \u003d 0.

Solución. Construyamos una figura.

Construyamos una recta x - 2y + 4 = 0: y = 0, x = - 4, A (-4; 0); x = 0, y = 2, B(0; 2).

Construyamos una línea recta x + y - 5 = 0: y = 0, x = 5, С(5; 0), x = 0, y = 5, D(0; 5).

Encuentra el punto de intersección de las rectas resolviendo el sistema de ecuaciones:

x = 2, y = 3; M(2; 3).

Para calcular el área requerida, dividimos el triángulo AMC en dos triángulos AMN y NMC, ya que cuando x cambia de A a N, el área está limitada por una línea recta, y cuando x cambia de N a C, es una línea recta

Para el triángulo AMN tenemos: ; y \u003d 0.5x + 2, es decir, f (x) \u003d 0.5x + 2, a \u003d - 4, b \u003d 2.

Para el triángulo NMC tenemos: y = - x + 5, es decir, f(x) = - x + 5, a = 2, b = 5.

Calculando el área de cada uno de los triángulos y sumando los resultados, encontramos:

cuadrados unidades

cuadrados unidades

9 + 4, 5 = 13,5 metros cuadrados unidades Verifique: = 0.5AC = 0.5 pies cuadrados unidades

Ejemplo 3 Calcular el área de una figura delimitada por rectas: y = x 2 , y = 0, x = 2, x = 3.

En este caso, se requiere calcular el área de un trapezoide curvilíneo acotado por una parábola y = x 2 , líneas rectas x \u003d 2 y x \u003d 3 y el eje Ox (ver Fig.) De acuerdo con la fórmula (1), encontramos el área de un trapezoide curvilíneo

= = 6 kv. unidades

Ejemplo 4 Calcule el área de una figura delimitada por líneas: y \u003d - x 2 + 4 y y = 0

Construyamos una figura. El área deseada está encerrada entre la parábola y \u003d - x 2 + 4 y eje Oh.

Encuentra los puntos de intersección de la parábola con el eje x. Suponiendo que y \u003d 0, encontramos x \u003d Dado que esta figura es simétrica con respecto al eje Oy, calculamos el área de la figura ubicada a la derecha del eje Oy y duplicamos el resultado: \u003d + 4x] cuadrados unidades 2 = 2 metros cuadrados unidades

Ejemplo 5 Calcular el área de una figura delimitada por rectas: y 2 = x, yx = 1, x = 4

Aquí se requiere calcular el área del trapezoide curvilíneo delimitado por la rama superior de la parábola y 2 \u003d x, el eje Ox y las líneas rectas x \u003d 1x \u003d 4 (ver Fig.)

De acuerdo con la fórmula (1), donde f(x) = a = 1 y b = 4, tenemos = (= unidades cuadradas

Ejemplo 6 . Calcula el área de la figura delimitada por líneas: y = senx, y = 0, x = 0, x=.

El área deseada está limitada por una sinusoide de media onda y el eje Ox (ver Fig.).

Tenemos - cosx \u003d - cos \u003d 1 + 1 \u003d 2 metros cuadrados. unidades

Ejemplo 7 Calcule el área de la figura delimitada por líneas: y \u003d - 6x, y \u003d 0 y x \u003d 4.

La figura está ubicada debajo del eje Ox (ver Fig.).

Por lo tanto, su área se encuentra por la fórmula (3)

= =

Ejemplo 8 Calcule el área de la figura delimitada por las líneas: y \u003d y x \u003d 2. Construiremos la curva y \u003d por puntos (ver figura). Por lo tanto, el área de la figura se encuentra mediante la fórmula (4)

Ejemplo 9 .

X 2 + y 2 = r 2 .

Aquí necesitas calcular el área delimitada por el círculo x 2 + y 2 = r 2 , es decir, el área de un círculo de radio r con centro en el origen. Encontremos la cuarta parte de esta área, tomando los límites de integración de 0

insecto; tenemos: 1 = = [

Como consecuencia, 1 =

Ejemplo 10 Calcule el área de la figura delimitada por líneas: y \u003d x 2 y y = 2x

Esta figura está limitada por la parábola y \u003d x 2 y línea recta y \u003d 2x (ver Fig.) Para determinar los puntos de intersección de las líneas dadas, resolvemos el sistema de ecuaciones: x 2 – 2x = 0 x = 0 y x = 2

Usando la fórmula (5) para encontrar el área, obtenemos

= }