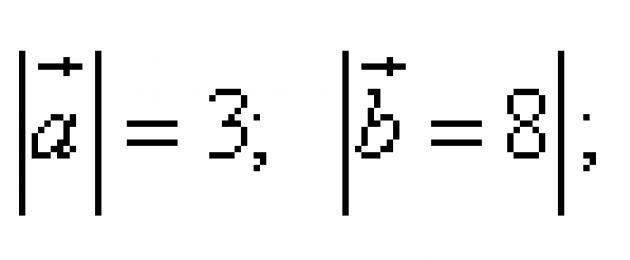Si en el problema tanto las longitudes de los vectores como el ángulo entre ellos se presentan "en bandeja de plata", entonces la condición del problema y su solución se ven así:
Ejemplo 1. Se dan vectores. Encuentra el producto escalar de vectores si sus longitudes y el ángulo entre ellos están representados por los siguientes valores:
![]()
![]()
También es válida otra definición, completamente equivalente a la definición 1.
Definición 2. El producto escalar de vectores es un número (escalar) igual al producto de la longitud de uno de estos vectores y la proyección de otro vector sobre el eje determinado por el primero de estos vectores. Fórmula según la definición 2:
Resolveremos el problema usando esta fórmula después del siguiente punto teórico importante.
Definición del producto escalar de vectores en términos de coordenadas.
Se puede obtener el mismo número si a los vectores que se multiplican se les dan sus coordenadas.
Definición 3. El producto escalar de vectores es un número igual a la suma de los productos por pares de sus coordenadas correspondientes.
En la superficie
Si dos vectores y en el plano están definidos por sus dos Coordenadas rectangulares cartesianas
entonces el producto escalar de estos vectores es igual a la suma de los productos por pares de sus coordenadas correspondientes:
![]() .
.
Ejemplo 2. Encuentre el valor numérico de la proyección del vector sobre el eje paralelo al vector.
Solución. Encontramos el producto escalar de vectores sumando los productos por pares de sus coordenadas:
Ahora necesitamos igualar el producto escalar resultante al producto de la longitud del vector y la proyección del vector sobre un eje paralelo al vector (de acuerdo con la fórmula).
Encontramos la longitud del vector como la raíz cuadrada de la suma de los cuadrados de sus coordenadas:
![]() .
.
Creamos una ecuación y la resolvemos:

Respuesta. El valor numérico requerido es menos 8.
En el espacio
Si dos vectores y en el espacio están definidos por sus tres coordenadas rectangulares cartesianas
![]()
![]() ,
,
entonces el producto escalar de estos vectores también es igual a la suma de los productos por pares de sus coordenadas correspondientes, solo que ya hay tres coordenadas:
![]() .
.
La tarea de encontrar el producto escalar utilizando el método considerado es después de analizar las propiedades del producto escalar. Porque en el problema necesitarás determinar qué ángulo forman los vectores multiplicados.
Propiedades del producto escalar de vectores.
Propiedades algebraicas
1. (propiedad conmutativa: invertir los lugares de los vectores multiplicados no cambia el valor de su producto escalar).
2. ![]() (propiedad asociativa con respecto a un factor numérico: el producto escalar de un vector multiplicado por un determinado factor y otro vector es igual al producto escalar de estos vectores multiplicado por el mismo factor).
(propiedad asociativa con respecto a un factor numérico: el producto escalar de un vector multiplicado por un determinado factor y otro vector es igual al producto escalar de estos vectores multiplicado por el mismo factor).
3. ![]() (propiedad distributiva relativa a la suma de vectores: el producto escalar de la suma de dos vectores por el tercer vector es igual a la suma de los productos escalares del primer vector por el tercer vector y del segundo vector por el tercer vector).
(propiedad distributiva relativa a la suma de vectores: el producto escalar de la suma de dos vectores por el tercer vector es igual a la suma de los productos escalares del primer vector por el tercer vector y del segundo vector por el tercer vector).
4. (cuadrado escalar de vector mayor que cero), si es un vector distinto de cero y , si es un vector cero.
Propiedades geométricas
En las definiciones de la operación en estudio ya hemos tocado el concepto de ángulo entre dos vectores. Es hora de aclarar este concepto.
En la figura de arriba puedes ver dos vectores que tienen un origen común. Y lo primero a lo que debes prestar atención es que hay dos ángulos entre estos vectores: φ 1 Y φ 2 . ¿Cuál de estos ángulos aparece en las definiciones y propiedades del producto escalar de vectores? La suma de los ángulos considerados es 2. π y por tanto los cosenos de estos ángulos son iguales. La definición de producto escalar incluye solo el coseno del ángulo y no el valor de su expresión. Pero las propiedades sólo consideran un ángulo. Y este es el de los dos ángulos que no excede π , es decir, 180 grados. En la figura este ángulo se indica como φ 1 .
1. Dos vectores se llaman ortogonal Y el ángulo entre estos vectores es recto (90 grados o π /2 ), si el producto escalar de estos vectores es cero :
![]() .
.
La ortogonalidad en álgebra vectorial es la perpendicularidad de dos vectores.
2. Dos vectores distintos de cero forman esquina filosa (de 0 a 90 grados, o lo que es lo mismo - menos π el producto escalar es positivo .
3. Dos vectores distintos de cero forman ángulo obtuso (de 90 a 180 grados, o, lo que es lo mismo, más π /2) si y sólo si el producto escalar es negativo .
Ejemplo 3. Las coordenadas están dadas por los vectores:
 .
.
Calcule los productos escalares de todos los pares de vectores dados. ¿Qué ángulo (agudo, recto, obtuso) forman estos pares de vectores?
Solución. Lo calcularemos sumando los productos de las coordenadas correspondientes.
Obtuvimos un número negativo, por lo que los vectores forman un ángulo obtuso.
Obtuvimos un número positivo, por lo que los vectores forman un ángulo agudo.
Obtuvimos cero, entonces los vectores forman un ángulo recto.
Obtuvimos un número positivo, por lo que los vectores forman un ángulo agudo.
![]() .
.
Obtuvimos un número positivo, por lo que los vectores forman un ángulo agudo.
Para la autoprueba puede utilizar calculadora en línea Producto escalar de vectores y coseno del ángulo entre ellos .
Ejemplo 4. Dadas las longitudes de dos vectores y el ángulo entre ellos:
![]() .
.
Determine a qué valor del número los vectores y son ortogonales (perpendiculares).
Solución. Multipliquemos los vectores usando la regla para multiplicar polinomios:
Ahora calculemos cada término:
![]()

![]()
![]() .
.
Creemos una ecuación (el producto es igual a cero), agreguemos términos similares y resolvamos la ecuación:

Respuesta: tenemos el valor λ = 1,8, en el que los vectores son ortogonales.
Ejemplo 5. Demuestre que el vector  ortogonal (perpendicular) al vector
ortogonal (perpendicular) al vector
Solución. Para comprobar la ortogonalidad, multiplicamos los vectores y como polinomios, sustituyendo en su lugar la expresión dada en el enunciado del problema:
 .
.
Para hacer esto, debes multiplicar cada término (término) del primer polinomio por cada término del segundo y sumar los productos resultantes:
 .
.
En el resultado resultante, la fracción se reduce en. Se obtiene el siguiente resultado:
Conclusión: como resultado de la multiplicación obtuvimos cero, por lo tanto, se prueba la ortogonalidad (perpendicularidad) de los vectores.
Resuelva el problema usted mismo y luego vea la solución.
Ejemplo 6. Las longitudes de los vectores y están dadas, y el ángulo entre estos vectores es π /4. Determinar a qué valor μ vectores y son mutuamente perpendiculares.
Para la autoprueba puede utilizar calculadora en línea Producto escalar de vectores y coseno del ángulo entre ellos .
Representación matricial del producto escalar de vectores y el producto de vectores n-dimensionales
A veces resulta ventajoso, por motivos de claridad, representar dos vectores multiplicados en forma de matrices. Luego, el primer vector se representa como una matriz de filas y el segundo como una matriz de columnas:

Entonces el producto escalar de vectores será el producto de estas matrices :

El resultado es el mismo que el obtenido por el método que ya hemos considerado. Obtuvimos un solo número, y el producto de una matriz de filas por una matriz de columnas también es un solo número.
Es conveniente representar el producto de vectores abstractos de n dimensiones en forma matricial. Así, el producto de dos vectores de cuatro dimensiones será el producto de una matriz de filas con cuatro elementos por una matriz de columnas también con cuatro elementos, el producto de dos vectores de cinco dimensiones será el producto de una matriz de filas con cinco elementos por una matriz de columnas también con cinco elementos, y así sucesivamente.
Ejemplo 7. Encuentra productos escalares de pares de vectores.
![]() ,
,
usando representación matricial.
Solución. El primer par de vectores. Representamos el primer vector como una matriz de filas y el segundo como una matriz de columnas. Encontramos el producto escalar de estos vectores como el producto de una matriz de filas y una matriz de columnas:

Representamos de manera similar el segundo par y encontramos:

Como puede ver, los resultados fueron los mismos que para los mismos pares del ejemplo 2.
Ángulo entre dos vectores
La derivación de la fórmula para el coseno del ángulo entre dos vectores es muy bonita y concisa.
Para expresar el producto escalar de vectores.
![]() (1)
(1)
en forma de coordenadas, primero encontramos el producto escalar de los vectores unitarios. El producto escalar de un vector consigo mismo por definición:
![]()
Lo que está escrito en la fórmula anterior significa: el producto escalar de un vector consigo mismo es igual al cuadrado de su longitud. El coseno de cero es igual a uno, por lo que el cuadrado de cada unidad será igual a uno:
![]()
Desde vectores
son perpendiculares por pares, entonces los productos por pares de los vectores unitarios serán iguales a cero:
![]()
Ahora realicemos la multiplicación de polinomios vectoriales:

Sustituimos los valores de los productos escalares correspondientes de los vectores unitarios en el lado derecho de la igualdad:
![]()
Obtenemos la fórmula del coseno del ángulo entre dos vectores:

Ejemplo 8. Se dan tres puntos A(1;1;1), B(2;2;1), C(2;1;2).
Encuentra el ángulo.
Solución. Encontrar las coordenadas de los vectores:
![]() ,
,
![]() .
.
Usando la fórmula del ángulo coseno obtenemos:

Por eso, .
Para la autoprueba puede utilizar calculadora en línea Producto escalar de vectores y coseno del ángulo entre ellos .
Ejemplo 9. Se dan dos vectores
Encuentra la suma, la diferencia, la longitud, el producto escalar y el ángulo entre ellos.
2.Diferencia

Definición 1
El producto escalar de vectores es un número igual al producto de las dinas de estos vectores por el coseno del ángulo entre ellos.
La notación para el producto de los vectores a → y b → tiene la forma a → , b → . Transformémoslo en la fórmula:
a → , b → = a → · b → · porque a → , b → ^ . a → y b → denotan las longitudes de los vectores, a → , b → ^ - designación del ángulo entre los vectores dados. Si al menos un vector es cero, es decir, tiene un valor de 0, entonces el resultado será igual a cero, a → , b → = 0
Al multiplicar un vector por sí mismo, obtenemos el cuadrado de su longitud:
a → , b → = a → b → porque a → , a → ^ = a → 2 porque 0 = a → 2
Definición 2
La multiplicación escalar de un vector por sí mismo se llama cuadrado escalar.
Calculado por la fórmula:
a → , b → = a → · b → · porque a → , b → ^ .
La notación a → , b → = a → · b → · cos a → , b → ^ = a → · n p a → b → = b → · n p b → a → muestra que n p b → a → es la proyección numérica de a → sobre b → , n p a → a → - proyección de b → sobre a →, respectivamente.
Formulemos la definición de un producto para dos vectores:
El producto escalar de dos vectores a → por b → se llama producto de la longitud del vector a → por la proyección b → por la dirección de a → o producto de la longitud b → por la proyección a →, respectivamente.
Producto escalar en coordenadas
El producto escalar se puede calcular a través de las coordenadas de vectores en un plano determinado o en el espacio.
El producto escalar de dos vectores en un plano, en un espacio tridimensional, se llama suma de las coordenadas de los vectores dados a → y b →.
Al calcular el producto escalar de vectores dados a → = (a x , a y) , b → = (b x , b y) en el plano del sistema cartesiano, utilice:
a → , b → = a x b x + a y b y ,
para el espacio tridimensional es aplicable la expresión:
a → , b → = a x · b x + a y · b y + a z · b z .
De hecho, ésta es la tercera definición del producto escalar.
Demostrémoslo.
Evidencia 1
Para demostrarlo, usamos a → , b → = a → · b → · cos a → , b → ^ = a x · b x + a y · b y para vectores a → = (a x , a y) , b → = (b x , b y) en el sistema cartesiano.
Los vectores deben dejarse de lado.
O A → = a → = a x , a y y O B → = b → = b x , b y .
Entonces la longitud del vector A B → será igual a A B → = O B → - O A → = b → - a → = (b x - a x , b y - a y) .
Considere el triángulo O A B .
A B 2 = O A 2 + O B 2 - 2 · O A · O B · cos (∠ A O B) es correcto según el teorema del coseno.
Según la condición, está claro que O A = a → , O B = b → , A B = b → - a → , ∠ A O B = a → , b → ^ , lo que significa que escribimos la fórmula para encontrar el ángulo entre vectores de manera diferente
b → - a → 2 = a → 2 + b → 2 - 2 · a → · b → · cos (a → , b → ^) .
Entonces de la primera definición se deduce que b → - a → 2 = a → 2 + b → 2 - 2 · (a → , b →) , lo que significa (a → , b →) = 1 2 · (a → 2 + segundo → 2 - segundo → - un → 2) .
Aplicando la fórmula para calcular la longitud de los vectores, obtenemos:
a → , b → = 1 2 · ((a 2 x + a y 2) 2 + (b 2 x + b y 2) 2 - ((b x - a x) 2 + (b y - a y) 2) 2) = = 1 2 (a 2 x + a 2 y + b 2 x + b 2 y - (b x - a x) 2 - (b y - a y) 2) = = a x b x + a y b y
Probemos las igualdades:
(a → , b →) = a → b → porque (a → , b → ^) = = a x b x + a y b y + a z b z
– respectivamente para vectores del espacio tridimensional.
El producto escalar de vectores con coordenadas dice que el cuadrado escalar de un vector es igual a la suma de los cuadrados de sus coordenadas en el espacio y en el plano, respectivamente. a → = (a x , a y , a z ), b → = (b x , b y , b z ) y (a → , a →) = a x 2 + a y 2 .
Producto escalar y sus propiedades.
Hay propiedades del producto escalar que se aplican a a → , b → y c → :
- conmutatividad (a → , b →) = (b → , a →) ;
- distributividad (a → + b → , c →) = (a → , c →) + (b → , c →) , (a → + b → , c →) = (a → , b →) + (a → , c →) ;
- propiedad combinativa (λ · a → , b →) = λ · (a → , b →), (a → , λ · b →) = λ · (a → , b →), λ - cualquier número;
- El cuadrado escalar es siempre mayor que cero (a → , a →) ≥ 0, donde (a → , a →) = 0 en el caso de que a → cero.
Las propiedades son explicables gracias a la definición del producto escalar en el plano y las propiedades de la suma y multiplicación de números reales.
Demuestre la propiedad conmutativa (a → , b →) = (b → , a →) . De la definición tenemos que (a → , b →) = a y · b y + a y · by y (b → , a →) = b x · a x + b y · a y .
Por la propiedad de conmutatividad, las igualdades a x · b x = b x · a x y a y · b y = b y · a y son verdaderas, lo que significa a x · b x + a y · b y = b x · a x + b y · a y.
Se deduce que (a → , b →) = (b → , a →) . Q.E.D.
La distributividad es válida para cualquier número:
(a (1) → + a (2) → + . . . + a (n) → , b →) = (a (1) → , b →) + (a (2) → , b →) + . . . + (a (n) → , b →)
y (a → , b (1) → + b (2) → + . . + b (n) →) = (a → , b (1) →) + (a → , b (2) →) + . . . + (a → , b → (n)) ,
por lo tanto tenemos
(a (1) → + a (2) → + . . . + a (n) → , b (1) → + b (2) → + . . . + b (m) →) = = (a ( 1) → , b (1) →) + (a (1) → , b (2) →) + . . . + (a (1) → , b (m) →) + + (a (2) → , b (1) →) + (a (2) → , b (2) →) + . . . + (a (2) → , b (m) →) + . . . + + (a (n) → , b (1) →) + (a (n) → , b (2) →) + . . . + (a (n) → , b (m) →)
Producto escalar con ejemplos y soluciones.
Cualquier problema de este tipo se resuelve utilizando las propiedades y fórmulas relativas al producto escalar:
- (a → , b →) = a → · b → · porque (a → , b → ^) ;
- (a → , b →) = a → · n p a → b → = b → · n p b → a → ;
- (a → , b →) = a x · b x + a y · b y o (a → , b →) = a x · b x + a y · b y + a z · b z ;
- (un → , un →) = un → 2 .
Veamos algunas soluciones de ejemplo.
Ejemplo 2
La longitud de a → es 3, la longitud de b → es 7. Encuentra el producto escalar si el ángulo tiene 60 grados.
Solución
Por condición, tenemos todos los datos, por lo que los calculamos mediante la fórmula:
(a → , b →) = a → b → porque (a → , b → ^) = 3 7 porque 60 ° = 3 7 1 2 = 21 2
Respuesta: (a → , b →) = 21 2 .
Ejemplo 3
Dados los vectores a → = (1, - 1, 2 - 3), b → = (0, 2, 2 + 3). ¿Cuál es el producto escalar?
Solución
Este ejemplo considera la fórmula para calcular las coordenadas, ya que se especifican en el planteamiento del problema:
(a → , b →) = a x · b x + a y · b y + a z · b z = = 1 · 0 + (- 1) · 2 + (2 + 3) · (2 + 3) = = 0 - 2 + (2 - 9) = - 9
Respuesta: (a → , b →) = - 9
Ejemplo 4
Encuentre el producto escalar de A B → y A C →. Los puntos A (1, - 3), B (5, 4), C (1, 1) se dan en el plano de coordenadas.
Solución
Para empezar se calculan las coordenadas de los vectores, ya que por condición se dan las coordenadas de los puntos:
A B → = (5 - 1, 4 - (- 3)) = (4, 7) A C → = (1 - 1, 1 - (- 3)) = (0, 4)
Sustituyendo en la fórmula usando coordenadas, obtenemos:
(A B →, A C →) = 4 0 + 7 4 = 0 + 28 = 28.
Respuesta: (A B → , A C →) = 28 .
Ejemplo 5
Dados los vectores a → = 7 · m → + 3 · n → y b → = 5 · m → + 8 · n → , encuentre su producto. m → es igual a 3 y n → es igual a 2 unidades, son perpendiculares.
Solución
(a → , b →) = (7 · m → + 3 · n → , 5 · m → + 8 · n →) . Aplicando la propiedad de distributividad obtenemos:
(7 m → + 3 n →, 5 m → + 8 n →) = = (7 m →, 5 m →) + (7 m →, 8 n →) + (3 n →, 5 m →) + ( 3 norte → , 8 norte →)
Sacamos el coeficiente del signo del producto y obtenemos:
(7 m → , 5 m →) + (7 m → , 8 n →) + (3 n → , 5 m →) + (3 n → , 8 n →) = = 7 · 5 · (m → , m →) + 7 · 8 · (m → , n →) + 3 · 5 · (n → , m →) + 3 · 8 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →)
Por la propiedad de la conmutatividad transformamos:
35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (m → , n →) + 24 · (n → , n →) = = 35 · (m → , m →) + 71 · (m → , n → ) + 24 · (n → , n →)
Como resultado obtenemos:
(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →).
Ahora aplicamos la fórmula del producto escalar con el ángulo especificado por la condición:
(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →) = = 35 · m → 2 + 71 · m → · n → · cos (m → , n → ^) + 24 · n → 2 = 35 · 3 2 + 71 · 3 · 2 · cos π 2 + 24 · 2 2 = 411 .
Respuesta: (a → , b →) = 411
Si hay una proyección numérica.
Ejemplo 6
Encuentre el producto escalar de a → y b →. El vector a → tiene coordenadas a → = (9, 3, - 3), proyección b → con coordenadas (- 3, - 1, 1).
Solución
Por condición, los vectores a → y la proyección b → están dirigidos de manera opuesta, porque a → = - 1 3 · n p a → b → → , lo que significa que la proyección b → corresponde a la longitud n p a → b → → , y con la “ -" firmar:
n p una → b → → = - n p una → b → → = - (- 3) 2 + (- 1) 2 + 1 2 = - 11 ,
Sustituyendo en la fórmula obtenemos la expresión:
(a → , b →) = a → · n p a → b → → = 9 2 + 3 2 + (- 3) 2 · (- 11) = - 33 .
Respuesta: (a → , b →) = - 33 .
Problemas con un producto escalar conocido, donde es necesario encontrar la longitud de un vector o una proyección numérica.
Ejemplo 7
¿Qué valor debe tomar λ para un producto escalar dado a → = (1, 0, λ + 1) y b → = (λ, 1, λ) será igual a -1?
Solución
De la fórmula se desprende claramente que es necesario encontrar la suma de los productos de coordenadas:
(a → , b →) = 1 λ + 0 1 + (λ + 1) λ = λ 2 + 2 λ .
Dado que tenemos (a →, b →) = - 1.
Para encontrar λ, calculamos la ecuación:
λ 2 + 2 · λ = - 1, por lo tanto λ = - 1.
Respuesta: λ = - 1.
Significado físico del producto escalar.
La mecánica considera la aplicación del producto escalar.
Cuando A trabaja con una fuerza constante F → un cuerpo en movimiento desde un punto M a N, puedes encontrar el producto de las longitudes de los vectores F → y M N → por el coseno del ángulo entre ellos, lo que significa que el trabajo es igual al producto de los vectores fuerza y desplazamiento:
A = (F → , M N →) .
Ejemplo 8
El movimiento de un punto material de 3 metros bajo la influencia de una fuerza igual a 5 Ntons se dirige en un ángulo de 45 grados con respecto al eje. Encontrar un.
Solución
Dado que el trabajo es el producto del vector fuerza y el desplazamiento, significa que con base en la condición F → = 5, S → = 3, (F →, S → ^) = 45 °, obtenemos A = (F →, S →) = F → · S → · cos (F → , S → ^) = 5 · 3 · cos (45 °) = 15 2 2 .
Respuesta: A = 15 2 2 .
Ejemplo 9
Un punto material, moviéndose de M (2, - 1, - 3) a N (5, 3 λ - 2, 4) bajo la fuerza F → = (3, 1, 2), realizó un trabajo igual a 13 J. Calcular la duración del movimiento.
Solución
Para coordenadas vectoriales dadas M N → tenemos M N → = (5 - 2, 3 λ - 2 - (- 1), 4 - (- 3)) = (3, 3 λ - 1, 7) .
Usando la fórmula para encontrar trabajo con vectores F → = (3, 1, 2) y M N → = (3, 3 λ - 1, 7), obtenemos A = (F ⇒, M N →) = 3 3 + 1 ( 3 λ - 1) + 2 7 = 22 + 3 λ.
Según la condición, se da que A = 13 J, lo que significa 22 + 3 λ = 13. Esto implica λ = - 3, lo que significa M N → = (3, 3 λ - 1, 7) = (3, - 10, 7).
Para encontrar la longitud del movimiento M N →, aplique la fórmula y sustituya los valores:
METRO norte → = 3 2 + (- 10) 2 + 7 2 = 158.
Respuesta: 158.
Si nota un error en el texto, resáltelo y presione Ctrl+Enter
Producto escalar de vectores (en adelante SP). ¡Queridos amigos! El examen de matemáticas incluye un grupo de problemas sobre resolución de vectores. Ya hemos considerado algunos problemas. Puedes verlos en la categoría “Vectores”. En general, la teoría de los vectores no es complicada, lo principal es estudiarla de forma coherente. Los cálculos y operaciones con vectores en el curso de matemáticas de la escuela son sencillos, las fórmulas no son complicadas. Echa un vistazo a. En este artículo analizaremos problemas sobre SP de vectores (incluido en el Examen Estatal Unificado). Ahora “inmersión” en la teoría:
h Para encontrar las coordenadas de un vector, debes restar de las coordenadas de su extremo.las coordenadas correspondientes de su origen
Y además:

![]()
*La longitud del vector (módulo) se determina de la siguiente manera:
![]()
¡¡¡Estas fórmulas hay que recordarlas!!!
Mostremos el ángulo entre los vectores:

Está claro que puede variar de 0 a 180 0(o en radianes de 0 a Pi).
Podemos sacar algunas conclusiones sobre el signo del producto escalar. Las longitudes de los vectores tienen un valor positivo, esto es obvio. Esto significa que el signo del producto escalar depende del valor del coseno del ángulo entre los vectores.
Posibles casos:
1. Si el ángulo entre los vectores es agudo (de 0 0 a 90 0), entonces el coseno del ángulo tendrá un valor positivo.
2. Si el ángulo entre los vectores es obtuso (de 90 0 a 180 0), entonces el coseno del ángulo tendrá un valor negativo.
*En cero grados, es decir, cuando los vectores tienen la misma dirección, el coseno es igual a uno y, en consecuencia, el resultado será positivo.
A 180 o, es decir, cuando los vectores tienen direcciones opuestas, el coseno es igual a menos uno,y en consecuencia el resultado será negativo.
¡Ahora el PUNTO IMPORTANTE!
A 90 o, es decir, cuando los vectores son perpendiculares entre sí, el coseno es igual a cero y, por tanto, el SP es igual a cero. Este hecho (consecuencia, conclusión) se utiliza para resolver muchos problemas en los que hablamos de la posición relativa de los vectores, incluso en problemas incluidos en el banco abierto de tareas matemáticas.
Formulemos el enunciado: el producto escalar es igual a cero si y sólo si estos vectores se encuentran en rectas perpendiculares.

Entonces, las fórmulas para los vectores SP:

Si se conocen las coordenadas de los vectores o las coordenadas de los puntos de su inicio y final, siempre podemos encontrar el ángulo entre los vectores:

Consideremos las tareas:
27724 Calcula el producto escalar de los vectores a y b.

Podemos encontrar el producto escalar de vectores usando una de dos fórmulas:

Se desconoce el ángulo entre los vectores, pero podemos encontrar fácilmente las coordenadas de los vectores y luego usar la primera fórmula. Dado que los orígenes de ambos vectores coinciden con el origen de coordenadas, las coordenadas de estos vectores son iguales a las coordenadas de sus extremos, es decir
![]()
En se describe cómo encontrar las coordenadas de un vector.
Calculamos:
Respuesta: 40

Encontremos las coordenadas de los vectores y usemos la fórmula:
![]()
Para encontrar las coordenadas de un vector, es necesario restar las coordenadas correspondientes de su inicio de las coordenadas del final del vector, lo que significa

Calculamos el producto escalar:
Respuesta: 40
Encuentra el ángulo entre los vectores a y b. Da tu respuesta en grados.

Sean las coordenadas de los vectores la forma:
![]()
Para encontrar el ángulo entre vectores, usamos la fórmula del producto escalar de vectores:

Coseno del ángulo entre vectores:

Por eso:

Las coordenadas de estos vectores son iguales:
![]()
Sustituyémoslos en la fórmula:

El ángulo entre los vectores es de 45 grados.
Respuesta: 45
): ⟨a | b ⟩ (\displaystyle \langle a|b\rangle )
En el caso más simple del espacio ordinario, el producto escalar de vectores distintos de cero y segundo (\displaystyle \mathbf (b) ) se define como el producto de las longitudes de estos vectores por cosenoángulo entre ellos:
(a, b) = | un | | segundo | porque (θ) (\displaystyle (\mathbf (a) ,\mathbf (b))=|\mathbf (a) ||\mathbf (b) |\cos(\theta))Definición equivalente: producto escalar es el producto de la longitud proyecciones el primer vector al segundo y la longitud del segundo vector (ver figura). Si al menos uno de los vectores es cero, entonces el producto se considera igual a cero.
El concepto de producto escalar también tiene una gran cantidad de generalizaciones para varios espacios vectoriales, es decir, para conjuntos de vectores con las operaciones de suma y multiplicación por escalares. La definición geométrica del producto escalar dada anteriormente es generalmente inadecuada, ya que no está claro qué se entiende por longitudes de los vectores y la magnitud del ángulo entre ellos. Por lo tanto, en las matemáticas modernas se utiliza el enfoque opuesto: el producto escalar se determina axiomáticamente y, a través de él, las longitudes y los ángulos. En particular, el producto escalar se define para vectores complejos , multidimensional Y espacios de dimensiones infinitas, V. álgebra tensorial.
El producto escalar y sus generalizaciones juegan un papel extremadamente importante en álgebra vectorial , teoría de la variedad, mecánica y física. Por ejemplo, trabajo de fuerza durante el movimiento mecánico es igual al producto escalar del vector fuerza y el vector desplazamiento.
Definición
Definición en el espacio euclidiano
EN norte (\ Displaystyle n)-espacio euclidiano real dimensional, los vectores se definen por sus coordenadas - conjuntos norte (\ Displaystyle n) números reales en base ortonormal. Puedes definir el producto escalar de vectores así:
(a, b) = a 1 b 1 + a 2 b 2 + a 3 b 3 + ⋯ + a n b n (\displaystyle (\mathbf (a) ,\mathbf (b))=a_(1)b_(1)+ a_(2)b_(2)+a_(3)b_(3)+\puntos +a_(n)b_(n))La verificación muestra que se cumplen los tres axiomas.
Por ejemplo, el producto escalar de vectores. ( 1 , 3 , − 5 ) (\displaystyle \(1,3,-5\)) Y ( 4 , − 2 , − 1 ) (\displaystyle \(4,-2,-1\)) se calculará así:
( 1 , 3 , − 5 ) ⋅ ( 4 , − 2 , − 1 ) = 1 ⋅ 4 + 3 ⋅ (− 2) + (− 5) ⋅ (− 1) = 4 − 6 + 5 = 3. (\ displaystyle (\begin(alineado)\ \(1,3,-5\)\cdot \(4,-2,-1\)&=1\cdot 4+3\cdot (-2)+(-5) \cdot (-1)\\&=4-6+5\\&=3.\end(alineado)))Para vectores complejos a = ( a 1 , a 2 … a n ) , b = ( b 1 , b 2 … b n ) (\displaystyle \mathbf (a) =\(a_(1),a_(2)\dots a_(n)\ ),\mathbf (b) =\(b_(1),b_(2)\dots b_(n)\)) definamos de manera similar:
(a , b) = ∑ k = 1 n a k b k ¯ = a 1 b 1 ¯ + a 2 b 2 ¯ + ⋯ + a n b n ¯ (\displaystyle (\mathbf (a) ,\mathbf (b))=\sum _( k=1)^(n)a_(k)(\overline (b_(k)))=a_(1)(\overline (b_(1)))+a_(2)(\overline (b_(2) ))+\cdots +a_(n)(\overline (b_(n)))).Ejemplo (para norte = 2 (\displaystyle n=2)): ( 1 + i , 2 ) ⋅ ( 2 + i , i ) = (1 + i) ⋅ (2 + i ¯) + 2 ⋅ i ¯ = (1 + i) ⋅ (2 − i) + 2 ⋅ (− yo) = 3 - yo. (\displaystyle \(1+i,2\)\cdot \(2+i,i\)=(1+i)\cdot ((\overline (2+i)))+2\cdot (\overline ( i))=(1+i)\cdot (2-i)+2\cdot (-i)=3-i.)
Definiciones relacionadas
En el enfoque axiomático moderno, ya sobre la base del concepto de producto escalar de vectores, se introducen los siguientes conceptos de derivada:
Longitud vector, que generalmente se entiende como su euclidiano norma :
| un | = (a , a) (\displaystyle |\mathbf (a) |=(\sqrt ((\mathbf (a) ,\mathbf (a)))))(El término "longitud" generalmente se aplica a vectores de dimensión finita, pero en el caso de calcular la longitud de una trayectoria curva, a menudo se usa en el caso de espacios de dimensión infinita).
|
Para cualquier elemento a , b (\displaystyle \mathbf (a) ,\mathbf (b) ) espacio vectorial con producto escalar se cumple la siguiente desigualdad: | (a, b) | 2 ⩽ (a , a) (b , b) (\displaystyle \vert (\mathbf (a) ,\mathbf (b))\vert ^(2)\leqslant (\mathbf (a) ,\mathbf (a) )(\mathbf (b) ,\mathbf (b))) |
En caso de que el espacio sea pseudo-euclidiano, el concepto de ángulo se define solo para vectores que no contienen líneas isotrópicas dentro del sector formado por los vectores. El ángulo en sí se ingresa como un número, coseno hiperbólico que es igual a la relación entre el módulo del producto escalar de estos vectores y el producto de sus longitudes (normas):
| (a, b) | = | un | | segundo | canal φ . (\displaystyle |(\mathbf (a) ,\mathbf (b))|=|\mathbf (a) ||\mathbf (b) |\operatorname (ch) \varphi .)- Ortogonal(perpendiculares) son vectores cuyo producto escalar es igual a cero. Esta definición se aplica a cualquier espacio con un producto escalar definido positivo. Por ejemplo, polinomios ortogonales son de hecho ortogonales (en el sentido de esta definición) entre sí en algún espacio de Hilbert.
- Un espacio (real o complejo) con un producto escalar definido positivo se llama espacio anterior a Hilbert.
- En este caso, un espacio real de dimensión finita con un producto escalar definido positivo también se llama euclidiano, y complejo - hermitiano o unitario espacio.
- El caso en el que el producto escalar no tiene signo definido conduce al llamado. espacios con métrica indefinida. El producto escalar en tales espacios ya no genera una norma (y normalmente se introduce adicionalmente). Un espacio real de dimensión finita con métrica indefinida se llama pseudo-euclidiano(el caso especial más importante de tal espacio es espacio de minkowski). Entre los espacios de dimensión infinita con métrica indefinida, los espacios de Pontryagin y los espacios de Kerin juegan un papel importante.
Propiedades
- Teorema del coseno se deriva fácilmente usando el producto escalar: | antes de Cristo | 2 = B C → 2 = (A C → − A B →) 2 = ⟨ A C → − A B → , A C → − A B → ⟩ = A C → 2 + A B → 2 − 2 ⟨ A C → , A B → ⟩ = | A B | 2 + | A C | 2-2 | A B | | A C | porque A ^ (\displaystyle |BC|^(2)=(\vec (BC))^(2)=((\vec (AC))-(\vec (AB)))^(2)=\ langle (\vec (AC))-(\vec (AB)),(\vec (AC))-(\vec (AB))\rangle =(\vec (AC))^(2)+(\vec (AB))^(2)-2\langle (\vec (AC)),(\vec (AB))\rangle =|AB|^(2)+|AC|^(2)-2|AB| |AC|\cos (\sombrero (A)))
- Estimación del ángulo entre vectores: en la fórmula (a, b) = | un | ⋅ | segundo | ⋅ porque ∠ (a , b) (\displaystyle (\mathbf (\mathbf (a) ) ,\mathbf (b))=|\mathbf (a) |\cdot |\mathbf (b) |\cdot \cos \angle ((\mathbf (a) ,\mathbf (b)))) el signo está determinado únicamente por el coseno del ángulo (las normas de los vectores son siempre positivas). Por tanto, el producto escalar > 0 si el ángulo entre los vectores es agudo, y< 0, если угол между векторами тупой.
- Proyección de un vector en la dirección definida por el vector unitario mi (\displaystyle \mathbf (e) ): un mi = (un , mi) = | un | | mi | porque ∠ (a, mi) = | un | porque ∠ (a , e) (\displaystyle a_(e)=(\mathbf (a) ,\mathbf (e))=|\mathbf (a) ||\mathbf (e) |\cos \angle (( \mathbf (a) ,\mathbf (e)))=|\mathbf (a) |\cos \angle ((\mathbf (a) ,\mathbf (e)))), porque | mi | = 1. (\displaystyle |\mathbf (e) |=1.)
- Área de un paralelogramo atravesada por dos vectores a (\displaystyle \mathbf (a)\ ) Y segundo (\displaystyle \mathbf (b)\ ), es igual
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0