Fuerza resultante. Fórmula de la fuerza resultante Resultante de todas las fuerzas que actúan sobre un cuerpo

La primera ley de Newton nos dice que en sistemas de referencia inerciales, los cuerpos pueden cambiar de velocidad sólo si están influenciados por otros cuerpos. Con la ayuda de la fuerza ($\overline(F)$) expresan la acción mutua de los cuerpos entre sí. Una fuerza puede cambiar la magnitud y dirección de la velocidad de un cuerpo. $\overline(F)$ es una cantidad vectorial, es decir, tiene módulo (magnitud) y dirección.

Definición y fórmula de la resultante de todas las fuerzas.

En dinámica clásica, la ley principal mediante la cual se encuentra la dirección y magnitud de la fuerza resultante es la segunda ley de Newton:

\[\overline(F)=m\overline(a)\ \left(1\right),\]

donde $m$ es la masa del cuerpo sobre el cual actúa la fuerza $\overline(F)$; $\overline(a)$ es la aceleración que la fuerza $\overline(F)$ imparte al cuerpo en cuestión. El significado de la segunda ley de Newton es que las fuerzas que actúan sobre un cuerpo determinan el cambio en la velocidad del cuerpo, y no solo su velocidad. Debes saber que la segunda ley de Newton es cierta para los sistemas de referencia inerciales.

Sobre un cuerpo puede actuar no una, sino una determinada combinación de fuerzas. La acción total de estas fuerzas se caracteriza utilizando el concepto de fuerza resultante. Supongamos que varias fuerzas actúan sobre un cuerpo al mismo tiempo. La aceleración del cuerpo en este caso es igual a la suma de los vectores de aceleración que surgirían en presencia de cada fuerza por separado. Las fuerzas que actúan sobre el cuerpo deben sumarse de acuerdo con la regla de la suma de vectores. La fuerza resultante ($\overline(F)$) es la suma vectorial de todas las fuerzas que actúan sobre el cuerpo en el momento considerado:

\[\overline(F)=(\overline(F))_1+(\overline(F))_2+\dots +(\overline(F))_N=\sum\limits^N_(i=1)((\ overline(F))_i)\ \left(2\right).\]

La fórmula (2) es la fórmula para la resultante de todas las fuerzas aplicadas al cuerpo. La fuerza resultante es una cantidad artificial que se introduce para facilitar los cálculos. La fuerza resultante se dirige como el vector de aceleración del cuerpo.

La ley básica de la dinámica del movimiento de traslación en presencia de varias fuerzas.

Si sobre un cuerpo actúan varias fuerzas, entonces la segunda ley de Newton se escribe como:

\[\sum\limits^N_(i=1)((\overline(F))_i)=m\overline(a)\left(3\right).\]

$\overline(F)=0$, si las fuerzas aplicadas al cuerpo se cancelan entre sí. Entonces, en el sistema de referencia inercial la velocidad del cuerpo es constante.

Al representar las fuerzas que actúan sobre un cuerpo en la figura, en el caso de un movimiento uniformemente acelerado, la fuerza resultante se representa como más larga que la suma de las fuerzas que se dirigen en dirección opuesta a él. Si el cuerpo se mueve con rapidez constante o está en reposo, las longitudes de los vectores de fuerza (la resultante y la suma de las fuerzas restantes) son iguales y se dirigen en direcciones opuestas.

Cuando se encuentra la resultante de las fuerzas, en la figura se muestran todas las fuerzas tomadas en cuenta en el problema. Estas fuerzas se suman de acuerdo con las reglas de la suma de vectores.

Ejemplos de problemas sobre fuerzas resultantes.

Ejemplo 1

Ejercicio. Sobre un punto material actúan dos fuerzas dirigidas formando un ángulo $\alpha =60()^\circ $ entre sí. ¿Cuál es la resultante de estas fuerzas si $F_1=20\ $N; $F_2=10\ $H?

Solución. Hagamos un dibujo.

Fuerzas en la Fig. Sumamos 1 según la regla del paralelogramo. La longitud de la fuerza resultante $\overline(F)$ se puede encontrar usando el teorema del coseno:

Calculemos el módulo de la fuerza resultante:

Respuesta.$F=26,5$ N

Ejemplo 2

Ejercicio. Las fuerzas actúan sobre un punto material (Fig. 2). ¿Cuál es la resultante de estas fuerzas?

Solución. La resultante de las fuerzas aplicadas al punto (Fig.2) es igual a:

\[\overline(F)=(\overline(F))_1+(\overline(F))_2+(\overline(F))_3+(\overline(F))_4\left(2.1\right).\]

Encontremos la resultante de las fuerzas $(\overline(F))_1$ y $(\overline(F))_2$. Estas fuerzas se dirigen a lo largo de la misma línea recta, pero en direcciones opuestas, por lo tanto:

Dado que $F_1>F_2$, entonces la fuerza $(\overline(F))_(12)$ se dirige en la misma dirección que la fuerza $(\overline(F))_1$.

Encontremos la resultante de las fuerzas $(\overline(F))_3$ y $(\overline(F))_4$. Estas fuerzas se dirigen a lo largo de una línea recta vertical (Fig.1), lo que significa:

La dirección de la fuerza $(\overline(F))_(34)$ coincide con la dirección del vector $(\overline(F))_3$, ya que $(\overline(F))_3>(\overline (F))_4$.

Encontramos la resultante que actúa sobre el punto material como:

\[\overline(F)=(\overline(F))_(12)+(\overline(F))_(34)\left(2.2\right).\]

Las fuerzas $(\overline(F))_(12)$ y $(\overline(F))_(34)$ son mutuamente perpendiculares. Encontremos la longitud del vector $\overline(F)$ usando el teorema de Pitágoras:

DEFINICIÓN

Fuerza es una cantidad vectorial que es una medida de la acción de otros cuerpos o campos sobre un cuerpo determinado, como resultado de lo cual se produce un cambio en el estado de este cuerpo. En este caso, un cambio de estado significa un cambio o deformación.

El concepto de fuerza hace referencia a dos cuerpos. Siempre puedes indicar el cuerpo sobre el que actúa la fuerza y ​​el cuerpo desde el que actúa.

La fuerza se caracteriza por:

• módulo;
• dirección;
• punto de aplicación.

La magnitud y dirección de la fuerza son independientes de la elección.

La unidad de fuerza en el sistema C es 1 Newton.

En la naturaleza, no existen cuerpos materiales que estén fuera de la influencia de otros cuerpos y, por tanto, todos los cuerpos están bajo la influencia de fuerzas externas o internas.

Sobre un cuerpo pueden actuar varias fuerzas al mismo tiempo. En este caso es válido el principio de independencia de acción: la acción de cada fuerza no depende de la presencia o ausencia de otras fuerzas; la acción combinada de varias fuerzas es igual a la suma de las acciones independientes de las fuerzas individuales.

Fuerza resultante

Para describir el movimiento de un cuerpo en este caso se utiliza el concepto de fuerza resultante.

DEFINICIÓN

Fuerza resultante Es una fuerza cuya acción reemplaza la acción de todas las fuerzas aplicadas al cuerpo. O, en otras palabras, la resultante de todas las fuerzas aplicadas al cuerpo es igual a la suma vectorial de estas fuerzas (Fig. 1).

Figura 1. Determinación de las fuerzas resultantes.

Dado que el movimiento de un cuerpo siempre se considera en algún sistema de coordenadas, conviene considerar no la fuerza en sí, sino sus proyecciones sobre los ejes de coordenadas (Fig. 2, a). Dependiendo de la dirección de la fuerza, sus proyecciones pueden ser positivas (Fig. 2, b) o negativas (Fig. 2, c).

Figura 2. Proyecciones de fuerza sobre ejes de coordenadas: a) en un plano; b) en línea recta (la proyección es positiva);
c) en línea recta (la proyección es negativa)

Fig. 3. Ejemplos que ilustran la suma vectorial de fuerzas.

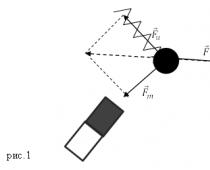
A menudo vemos ejemplos que ilustran la suma vectorial de fuerzas: una lámpara cuelga de dos cables (Fig. 3, a); en este caso, el equilibrio se logra debido al hecho de que la resultante de las fuerzas de tensión se compensa con el peso de la lámpara; el bloque se desliza a lo largo de un plano inclinado (Fig. 3, b); el movimiento se produce debido a las fuerzas resultantes de fricción, gravedad y reacción de soporte. Líneas famosas de la fábula de I.A. Krylova "¡y el carro todavía está ahí!" - también una ilustración de la igualdad de la resultante de tres fuerzas a cero (Fig. 3, c).

Ejemplos de resolución de problemas

EJEMPLO 1

Ejercicio	Sobre el cuerpo actúan dos fuerzas y . Determine el módulo y la dirección de la resultante de estas fuerzas si: a) las fuerzas están dirigidas en una dirección; b) las fuerzas se dirigen en direcciones opuestas; c) las fuerzas se dirigen perpendicularmente entre sí.
Solución	a) las fuerzas se dirigen en una dirección; Fuerza resultante: b) las fuerzas se dirigen en direcciones opuestas; Fuerza resultante: Proyectemos esta igualdad sobre el eje de coordenadas: c) las fuerzas se dirigen perpendiculares entre sí; Fuerza resultante:

Cuando hablan de la resultante, quieren decir Fuerza que es igual a la acción de dos o más fuerzas aplicadas simultáneamente a un cuerpo..

Cuando sobre un cuerpo actúan varias fuerzas, su efecto combinado puede ser diferente; depende tanto de la dirección de las distintas fuerzas como de sus valores numéricos. En cualquier caso, siempre puedes encontrar una fuerza que resulte en ellos.

Por ejemplo, se colocó un ladrillo sobre un trampolín. Hay dos fuerzas que actúan sobre el ladrillo: la gravedad y la fuerza elástica del trampolín. En el momento en que se acababa de colocar el ladrillo, la fuerza de gravedad era mayor que la fuerza de elasticidad y el ladrillo se movía hacia abajo. Tan pronto como las fuerzas se igualaron, el ladrillo se detuvo.

Si el ladrillo no se colocara sobre el trampolín, sino que se arrojara con todas sus fuerzas desde arriba, se movería hacia abajo no solo bajo la influencia de la gravedad, sino también por la fuerza de lanzamiento que se le transfiere. Bajo la influencia de estas dos fuerzas, el trampolín se doblaría más, ya que la fuerza elástica que equilibraría estas fuerzas debería ser mayor.

Cuando se logra el equilibrio de fuerzas y se detiene el movimiento, el equilibrio se alterará nuevamente, ya que sobre el ladrillo ya no actuará la fuerza de lanzamiento, sino solo las fuerzas de gravedad y elasticidad. Pero la fuerza elástica se consiguió no sólo por el peso del ladrillo, sino también por la fuerza del lanzamiento. Por tanto, la fuerza elástica será mayor que la fuerza de gravedad, y el ladrillo saltará, es decir, empezará a moverse hacia arriba.

En los casos más simples, se considera la resultante de fuerzas dirigidas en una dirección o en la dirección opuesta.

Si dos fuerzas que actúan sobre un cuerpo se dirigen en la misma dirección, entonces su resultante será igual a su suma: F 1 + F 2. Por ejemplo, si un cuerpo es empujado en una dirección por dos fuerzas de 10 N y 20 N, entonces la fuerza resultante de estas dos será igual a 30 N.

Si dos fuerzas que actúan sobre un cuerpo están dirigidas en direcciones opuestas, entonces su resultante es igual a la magnitud de la diferencia entre las fuerzas y está dirigida hacia la mayor: |F 1 – F 2 |. Por ejemplo, si una fuerza de 10 N empuja un cuerpo hacia la izquierda y otra fuerza de 15 N lo empuja hacia la derecha, entonces el cuerpo se moverá hacia la derecha bajo la influencia de una fuerza de 5 N (|10 – 15 | = 5).

Cuando las fuerzas tienen direcciones opuestas, pero son iguales en valor numérico, entonces su resultante será igual a cero. Esto significa que la fuerza resultante no tiene ningún efecto sobre el cuerpo. Si el cuerpo estaba en reposo, allí permanecerá. Si el cuerpo se movía recto y uniformemente, seguirá moviéndose. Así, aunque dos nuevas fuerzas actuaron sobre el cuerpo, se “aniquilaron mutuamente”.

Digamos que sobre un cuerpo actúan tres fuerzas, dos de las cuales se dirigen en una dirección y la tercera en la otra. En este caso, primero debes encontrar la resultante de dos fuerzas dirigidas en una dirección sumándolas. Luego compárala con la tercera fuerza para determinar en qué dirección se dirigirá la resultante de las tres fuerzas. Y encuentre el módulo de la diferencia entre la suma de los dos primeros y el tercero: |F 1 + F 2 – F 3 |.

A menudo, no una, sino varias fuerzas actúan sobre el cuerpo al mismo tiempo. Consideremos el caso en el que el cuerpo se ve afectado por dos fuerzas ( y ). Por ejemplo, un cuerpo que descansa sobre una superficie horizontal se ve afectado por la fuerza de la gravedad () y la reacción de la superficie de soporte () (Fig. 1).

Estas dos fuerzas se pueden reemplazar por una, que se llama fuerza resultante (). Encuéntrelo como una suma vectorial de fuerzas y:

Determinación de la resultante de dos fuerzas.

DEFINICIÓN

Resultante de dos fuerzas Se llama fuerza a la que produce un efecto sobre un cuerpo similar a la acción de dos fuerzas separadas.

Tenga en cuenta que la acción de cada fuerza no depende de si existen otras fuerzas o no.

Segunda ley de Newton para la resultante de dos fuerzas.

Si sobre un cuerpo actúan dos fuerzas, entonces escribimos la segunda ley de Newton como:

La dirección de la resultante siempre coincide con la dirección de aceleración del cuerpo.

Esto significa que si un cuerpo se ve afectado por dos fuerzas () al mismo tiempo, entonces la aceleración () de este cuerpo será directamente proporcional a la suma vectorial de estas fuerzas (o proporcional a las fuerzas resultantes):

M es la masa del cuerpo en cuestión. La esencia de la segunda ley de Newton es que las fuerzas que actúan sobre un cuerpo determinan cómo cambia la velocidad del cuerpo, y no solo la magnitud de la velocidad del cuerpo. Tenga en cuenta que la segunda ley de Newton se cumple exclusivamente en sistemas de referencia inerciales.

La resultante de dos fuerzas puede ser igual a cero si las fuerzas que actúan sobre el cuerpo están dirigidas en diferentes direcciones y son de igual magnitud.

Encontrar la magnitud de la resultante de dos fuerzas.

Para encontrar la resultante, debes representar en el dibujo todas las fuerzas que deben tenerse en cuenta en el problema que actúan sobre el cuerpo. Las fuerzas deben sumarse de acuerdo con las reglas de la suma de vectores.

Supongamos que sobre el cuerpo actúan dos fuerzas que se dirigen a lo largo de la misma línea recta (Fig. 1). En la figura se puede ver que están dirigidos en diferentes direcciones.

Las fuerzas resultantes () aplicadas al cuerpo serán iguales a:

Para encontrar el módulo de las fuerzas resultantes, seleccionamos un eje, lo denotamos por X y lo dirigimos a lo largo de la dirección de acción de las fuerzas. Luego, proyectando la expresión (4) sobre el eje X, obtenemos que la magnitud (módulo) de la resultante (F) es igual a:

¿Dónde están los módulos de las fuerzas correspondientes?

Imaginemos que sobre el cuerpo actúan dos fuerzas y, dirigidas en cierto ángulo entre sí (Fig. 2). Encontramos la resultante de estas fuerzas usando la regla del paralelogramo. La magnitud de la resultante será igual a la longitud de la diagonal de este paralelogramo.

Ejemplos de resolución de problemas

EJEMPLO 1

Ejercicio	Un cuerpo con una masa de 2 kg se mueve verticalmente hacia arriba mediante un hilo, mientras que su aceleración es igual a 1. ¿Cuál es la magnitud y dirección de la fuerza resultante? ¿Qué fuerzas se aplican al cuerpo?
Solución	La fuerza de la gravedad () y la fuerza de reacción del hilo () se aplican al cuerpo (Fig. 3). La resultante de las fuerzas anteriores se puede encontrar utilizando la segunda ley de Newton: En proyección sobre el eje X, la ecuación (1.1) toma la forma: Calculemos la magnitud de la fuerza resultante:
Respuesta	H, la fuerza resultante se dirige de la misma manera que la aceleración del cuerpo, es decir, verticalmente hacia arriba. Hay dos fuerzas que actúan sobre el cuerpo y .

La fuerza actúa como una medida cuantitativa de la interacción de los cuerpos. Esta es una cantidad física importante, ya que en un sistema de referencia inercial cualquier cambio en la velocidad de un cuerpo sólo puede ocurrir cuando interactúa con otros cuerpos. Es decir, cuando una fuerza actúa sobre un cuerpo.

Las interacciones de los cuerpos pueden ser de diferente naturaleza, por ejemplo, existen interacciones eléctricas, magnéticas, gravitacionales y de otro tipo. Pero al estudiar el movimiento mecánico de un cuerpo, no importa la naturaleza de las fuerzas que provocan la aceleración en el cuerpo. La mecánica no aborda el problema del origen de la interacción. Para cualquier interacción, la fuerza se convierte en una medida numérica. Las fuerzas de diferente naturaleza se miden en las mismas unidades (en el Sistema Internacional de Unidades en newtons) y se utilizan los mismos estándares. Ante esta universalidad, la mecánica se ocupa del estudio y descripción del movimiento de los cuerpos que están influenciados por fuerzas de cualquier naturaleza.

El resultado de la acción de una fuerza sobre un cuerpo es la aceleración del cuerpo (un cambio en la velocidad de su movimiento) y/o su deformación.

Suma de fuerzas

La fuerza es una cantidad vectorial. Además del módulo, tiene una dirección y punto de aplicación. Independientemente de su naturaleza, todas las fuerzas se suman como vectores.

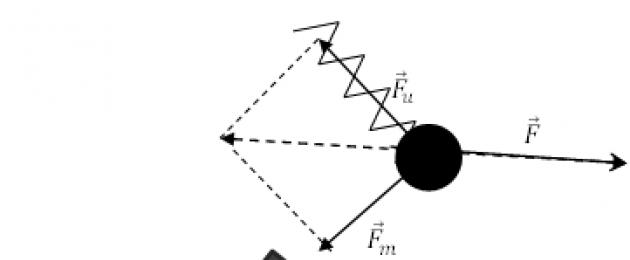
Dejemos que una bola de metal esté sostenida por un resorte elástico y atraída por un imán (Fig. 1). Entonces actúan sobre él dos fuerzas: la fuerza elástica del resorte ($(\overline(F))_u$) y la fuerza magnética ($(\overline(F))_m$) del imán. Suponemos que se conocen sus valores. Bajo la acción combinada de estas fuerzas, la pelota estará en reposo si actúa sobre ella una tercera fuerza ($\overline(F)$), que satisface la igualdad:

\[\overline(F)=-\left((\overline(F))_u+(\overline(F))_m\right)\left(1\right).\]

Esta experiencia nos permite concluir que varias fuerzas que actúan sobre un cuerpo pueden ser reemplazadas por una resultante, y la naturaleza de las fuerzas no importa. La resultante se obtiene como resultado de la suma vectorial de las fuerzas que actúan sobre el cuerpo.

Definición y fórmula de fuerza resultante.

Y así, la suma vectorial de todas las fuerzas que actúan sobre un cuerpo en el mismo momento se llama fuerza resultante ($\overline(F)$):

\[\overline(F)=(\overline(F))_1+(\overline(F))_2+\dots +(\overline(F))_N=\sum\limits^N_(i=1)((\ overline(F))_i)\ \left(2\right).\]

A veces, la fuerza resultante se denota $\overline(R)$ para dar énfasis, pero esto no es necesario.

La suma de fuerzas se puede hacer gráficamente. En este caso se utilizan las reglas del polígono, paralelogramo y triángulo. Si con esta suma de fuerzas el polígono resulta cerrado, entonces la resultante es igual a cero. Cuando la resultante es igual a cero, el sistema se llama equilibrado.

Escribir la segunda ley de Newton usando la fuerza resultante

La segunda ley de Newton es la ley fundamental de la dinámica clásica. Conecta las fuerzas que afectan al cuerpo y su aceleración y permite resolver el principal problema de la dinámica. Si un cuerpo está bajo la influencia de varias fuerzas, entonces escribo la segunda ley de Newton de la siguiente manera:

\[\overline(R)=\sum\limits^N_(i=1)((\overline(F))_i)=m\overline(a)\left(3\right).\]

La fórmula (3) significa que la resultante de todas las fuerzas aplicadas al cuerpo puede ser igual a cero si se produce una compensación mutua de fuerzas. Entonces el cuerpo se mueve a velocidad constante o está en reposo en un sistema de referencia inercial. Podemos decir lo contrario: si un cuerpo se mueve de manera uniforme y rectilínea en un sistema de referencia inercial, entonces no actúan fuerzas sobre él o su resultante es cero.

Al resolver problemas e indicar en diagramas las fuerzas que actúan sobre un cuerpo cuando el cuerpo se mueve con aceleración constante, la fuerza resultante se dirige a lo largo de la aceleración y se representa como más larga que la fuerza dirigida en sentido opuesto (suma de fuerzas). Con movimiento uniforme (o si el cuerpo está en reposo), la longitud de los vectores de fuerza que tienen direcciones opuestas es la misma (la resultante es cero).

Al examinar las condiciones del problema, es necesario determinar qué fuerzas actúan sobre el cuerpo y se tendrán en cuenta en la resultante, qué fuerzas no tienen un efecto significativo sobre el movimiento del cuerpo y pueden descartarse. En la figura se representan fuerzas importantes. Las fuerzas se suman según las reglas de la suma de vectores.

Ejemplos de problemas con soluciones.

Ejemplo 1

Ejercicio.¿En qué ángulo deben ubicarse las fuerzas en la figura? 2, de modo que su resultante sea igual en magnitud a cada una de sus fuerzas constituyentes?

Solución. Para resolver el problema utilizamos el teorema del coseno:

Ya que según las condiciones del problema:

luego transformamos la expresión (1.1) a la forma: $\ $

La solución a la ecuación trigonométrica resultante son los ángulos:

\[\alpha =\frac(2\pi )(3)+\pi n\ ;;\ \alpha =\frac(4\pi )(3)+\pi n\ \left(donde\ n es un número entero \ número\derecha).\ \]

Según la figura (Fig. 2), la respuesta es $\alpha =\frac(2\pi )(3)$.

Respuesta.$\alfa =\frac(2\pi )(3)$

Ejemplo 2

Ejercicio.¿Cuál es la fuerza resultante si las fuerzas presentadas en la figura 3 actúan sobre el cuerpo?

Solución. Encontramos la fuerza resultante mediante suma de vectores usando la regla del polígono. Secuencialmente, cada vector de fuerza posterior se aparta del final del anterior. Como resultado, el vector de la resultante de todas las fuerzas tendrá su inicio en el punto de donde sale el primer vector (tenemos el vector $(\overline(F))_1$), su final llegará al punto donde termina el último vector ($(\overline(F) ))_4$). Como resultado, obtenemos la Fig. 4.

Como resultado de la construcción se obtiene un polígono cerrado, lo que significa que la resultante de las fuerzas aplicadas al cuerpo es igual a cero.

Respuesta.$\sobrelínea(R)=0$