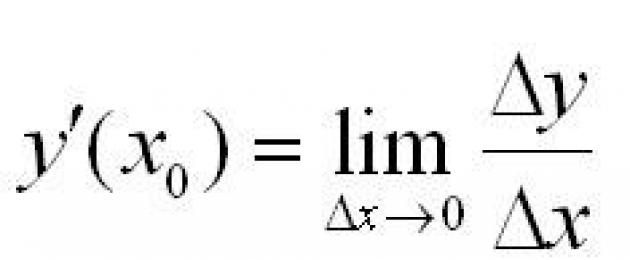Resolver problemas físicos o ejemplos en matemáticas es completamente imposible sin el conocimiento de la derivada y los métodos para calcularla. La derivada es uno de los conceptos más importantes del análisis matemático. Decidimos dedicar el artículo de hoy a este tema fundamental. ¿Qué es una derivada, cuál es su significado físico y geométrico, cómo calcular la derivada de una función? Todas estas preguntas se pueden combinar en una: ¿cómo entender la derivada?

Significado geométrico y físico de derivada.

Que haya una función f(x) , especificado en un intervalo determinado (a,b) . Los puntos x y x0 pertenecen a este intervalo. Cuando x cambia, la función misma cambia. Cambiar el argumento: la diferencia en sus valores. x-x0 . Esta diferencia se escribe como deltax y se llama incremento de argumento. Un cambio o incremento de una función es la diferencia entre los valores de una función en dos puntos. Definición de derivada:

La derivada de una función en un punto es el límite de la relación entre el incremento de la función en un punto dado y el incremento del argumento cuando este último tiende a cero.

De lo contrario se puede escribir así:

¿Cuál es el punto de encontrar tal límite? Y esto es lo que es:

la derivada de una función en un punto es igual a la tangente del ángulo entre el eje OX y la tangente a la gráfica de la función en un punto dado.

Significado físico de la derivada: la derivada de la trayectoria con respecto al tiempo es igual a la velocidad del movimiento rectilíneo.

De hecho, desde la época escolar todo el mundo sabe que la velocidad es un camino particular. x=f(t) y tiempo t . Velocidad media durante un período de tiempo determinado:

Para conocer la velocidad del movimiento en un momento dado. t0 necesitas calcular el límite:

Regla uno: establezca una constante

La constante se puede sacar del signo de la derivada. Es más, esto debe hacerse. Al resolver ejemplos de matemáticas, tómelo como regla: Si puedes simplificar una expresión, asegúrate de simplificarla. .

Ejemplo. Calculemos la derivada:

Regla dos: derivada de la suma de funciones

La derivada de la suma de dos funciones es igual a la suma de las derivadas de estas funciones. Lo mismo ocurre con la derivada de la diferencia de funciones.

No daremos una demostración de este teorema, sino que consideraremos un ejemplo práctico.

Encuentra la derivada de la función:

Regla tres: derivada del producto de funciones

La derivada del producto de dos funciones diferenciables se calcula mediante la fórmula:

Ejemplo: encontrar la derivada de una función:

Solución:

Es importante hablar aquí sobre el cálculo de derivadas de funciones complejas. La derivada de una función compleja es igual al producto de la derivada de esta función con respecto al argumento intermedio y la derivada del argumento intermedio con respecto a la variable independiente.

En el ejemplo anterior nos encontramos con la expresión:

En este caso, el argumento intermedio es 8x elevado a la quinta potencia. Para calcular la derivada de dicha expresión, primero calculamos la derivada de la función externa con respecto al argumento intermedio y luego multiplicamos por la derivada del propio argumento intermedio con respecto a la variable independiente.

Regla cuatro: derivada del cociente de dos funciones

Fórmula para determinar la derivada del cociente de dos funciones:

Intentamos hablar de derivados para tontos desde cero. Este tema no es tan simple como parece, así que tenga cuidado: a menudo hay errores en los ejemplos, así que tenga cuidado al calcular las derivadas.

Ante cualquier duda sobre este y otros temas, puedes contactar con el servicio de atención al estudiante. En poco tiempo, le ayudaremos a resolver las pruebas más difíciles y a comprender las tareas, incluso si nunca antes ha realizado cálculos de derivadas.

Las derivadas parciales de una función de varias variables son funciones de las mismas variables. Estas funciones, a su vez, pueden tener derivadas parciales, a las que llamaremos segundas derivadas parciales (o derivadas parciales de segundo orden) de la función original.

Por ejemplo, una función de dos variables tiene cuatro derivadas parciales de segundo orden, que se definen y denotan de la siguiente manera:

Una función de tres variables tiene nueve derivadas parciales de segundo orden:

Las derivadas parciales de tercer y superior orden de una función de varias variables se definen y denotan de manera similar: la derivada parcial de orden de una función de varias variables es la derivada parcial de primer orden de la derivada parcial del orden de la misma función.

Por ejemplo, la derivada parcial de tercer orden de una función es la derivada parcial de primer orden con respecto a y de la derivada parcial de segundo orden.

Una derivada parcial de segundo orden o superior tomada con respecto a varias variables diferentes se denomina derivada parcial mixta.

Por ejemplo, derivadas parciales

son derivadas parciales mixtas de una función de dos variables.

Ejemplo. Encuentra derivadas parciales mixtas de segundo orden de una función

Solución. Encontrar derivadas parciales de primer orden

Luego encontramos las derivadas parciales mixtas de segundo orden.

Vemos que las derivadas parciales mixtas que difieren entre sí solo en el orden de diferenciación, es decir, la secuencia en la que se lleva a cabo la diferenciación con respecto a varias variables, resultaron ser idénticamente iguales. Este resultado no es casual. Respecto a las derivadas parciales mixtas, se cumple el siguiente teorema, que aceptamos sin demostración.

Derivadas parciales de una función de dos variables.
Concepto y ejemplos de soluciones.

En esta lección continuaremos familiarizándonos con la función de dos variables y consideraremos quizás la tarea temática más común: encontrar derivadas parciales de primer y segundo orden, así como el diferencial total de la función. Los estudiantes a tiempo parcial, por regla general, encuentran derivadas parciales en el primer año del segundo semestre. Además, según mis observaciones, en el examen casi siempre aparece la tarea de encontrar derivadas parciales.

Para estudiar eficazmente el material siguiente, usted necesario Ser capaz de encontrar con mayor o menor confianza derivadas "ordinarias" de funciones de una variable. Puedes aprender a manejar correctamente los derivados en las lecciones. ¿Cómo encontrar la derivada? Y Derivada de una función compleja. También necesitaremos una tabla de derivadas de funciones elementales y reglas de diferenciación; lo más conveniente es si está disponible en forma impresa. Puedes conseguir material de referencia en la página. Fórmulas y tablas matemáticas..

Repitamos rápidamente el concepto de función de dos variables, intentaré limitarme al mínimo indispensable. Una función de dos variables generalmente se escribe como , y las variables se llaman variables independientes o argumentos.

Ejemplo: – función de dos variables.

A veces se utiliza la notación. También hay tareas en las que se utiliza la letra en lugar de una letra.

Desde un punto de vista geométrico, una función de dos variables suele representar una superficie en un espacio tridimensional (plano, cilindro, esfera, paraboloide, hiperboloide, etc.). Pero, de hecho, esto es más geometría analítica, y en nuestra agenda está el análisis matemático, que mi profesor universitario nunca me dejó descartar y es mi "punto fuerte".

Pasemos a la cuestión de encontrar derivadas parciales de primer y segundo orden. Tengo buenas noticias para aquellos que han tomado unas cuantas tazas de café y están sintonizando algún material increíblemente difícil: Las derivadas parciales son casi lo mismo que las derivadas "ordinarias" de una función de una variable..

Para derivadas parciales, son válidas todas las reglas de diferenciación y la tabla de derivadas de funciones elementales. Sólo hay un par de pequeñas diferencias, que conoceremos ahora mismo:

...si, por cierto, para este tema que creé pequeño libro pdf, que te permitirá “meterle el diente” en tan solo un par de horas. Pero al utilizar el sitio, seguramente obtendrá el mismo resultado, aunque tal vez un poco más lento:

Ejemplo 1

Encuentra las derivadas parciales de primer y segundo orden de la función.

Primero, encontremos las derivadas parciales de primer orden. Hay dos de ellos.

Designaciones:
o – derivada parcial con respecto a “x”
o – derivada parcial con respecto a “y”

Empecemos con . Cuando encontramos la derivada parcial con respecto a “x”, la variable se considera una constante (número constante).

Comentarios sobre las acciones realizadas:

(1) Lo primero que hacemos al encontrar la derivada parcial es concluir todo función entre paréntesis debajo del número primo con subíndice.

¡Atención, importante! NO PERDEMOS subíndices durante el proceso de solución. En este caso, si dibuja un "trazo" en algún lugar sin , entonces el maestro, como mínimo, puede colocarlo al lado de la tarea (inmediatamente muerde parte del punto por falta de atención).

(2) Usamos las reglas de diferenciación. , . Para un ejemplo sencillo como este, ambas reglas se pueden aplicar fácilmente en un solo paso. Presta atención al primer término: desde se considera una constante, y cualquier constante se puede sacar del signo de la derivada, luego lo sacamos de paréntesis. Es decir, en esta situación no es mejor que un número normal. Pasemos ahora al tercer término: aquí, por el contrario, no hay nada que sacar. Como es una constante, también lo es y en este sentido no es mejor que el último término: "siete".

(3) Usamos derivadas tabulares y .

(4) Simplifiquemos o, como me gusta decir, "modifiquemos" la respuesta.

Ahora . Cuando encontramos la derivada parcial con respecto a “y”, entonces la variableconsiderado una constante (número constante).

(1) Usamos las mismas reglas de diferenciación. , . En el primer término le quitamos la constante al signo de la derivada, en el segundo término no le podemos quitar nada porque ya es una constante.

(2) Usamos la tabla de derivadas de funciones elementales. Cambiemos mentalmente todas las “X” de la tabla por “I”. Es decir, esta tabla es igualmente válida para (y de hecho para casi cualquier letra). En particular, las fórmulas que utilizamos se ven así: y .

¿Cuál es el significado de derivadas parciales?

En esencia, las derivadas parciales de primer orden se parecen derivado "ordinario":

- Este funciones, que caracterizan tasa de cambio funciona en la dirección de los ejes y, respectivamente. Así, por ejemplo, la función caracteriza la pendiente de las “subidas” y “pendientes” superficies en la dirección del eje de abscisas, y la función nos habla del “relieve” de la misma superficie en la dirección del eje de ordenadas.

! Nota : Esto se refiere a direcciones que paralelo ejes de coordenadas.

Para una mejor comprensión, consideremos un punto específico en el plano y calculemos el valor de la función (“altura”) en él:
– y ahora imagina que estás aquí (EN LA superficie).

Calculemos la derivada parcial con respecto a "x" en un punto dado:

El signo negativo de la derivada “X” nos indica acerca de decreciente funciona en un punto en la dirección del eje de abscisas. En otras palabras, si hacemos un pequeño, pequeño (infinitesimal) paso hacia la punta del eje (paralelo a este eje), luego bajaremos por la pendiente de la superficie.

Ahora descubrimos la naturaleza del "terreno" en la dirección del eje de ordenadas:

La derivada con respecto a la “y” es positiva, por lo tanto, en un punto en la dirección del eje la función aumenta. En pocas palabras, aquí nos espera una subida cuesta arriba.

Además, la derivada parcial en un punto caracteriza tasa de cambio funciona en la dirección correspondiente. Cuanto mayor sea el valor resultante módulo– cuanto más inclinada sea la superficie, y viceversa, cuanto más cerca esté de cero, más plana será la superficie. Entonces, en nuestro ejemplo, la “pendiente” en la dirección del eje de abscisas es más pronunciada que la “montaña” en la dirección del eje de ordenadas.

Pero esos eran dos caminos privados. Está bastante claro que desde el punto en el que nos encontramos, (y en general desde cualquier punto de una superficie determinada) podemos avanzar en otra dirección. Así, existe interés en crear un "mapa de navegación" general que nos informe sobre el "paisaje" de la superficie. si es posible en cada punto dominio de definición de esta función por todos los caminos disponibles. Hablaré de esto y otras cosas interesantes en una de las siguientes lecciones, pero por ahora volvamos al aspecto técnico del tema.

Sistematicemos las reglas elementales aplicadas:

1) Cuando derivamos con respecto a , la variable se considera constante.

2) Cuando la diferenciación se realiza según, entonces se considera una constante.

3) Las reglas y tabla de derivadas de funciones elementales son válidas y aplicables para cualquier variable (o cualquier otra) mediante la cual se realiza la diferenciación.

Segundo paso. Encontramos derivadas parciales de segundo orden. Hay cuatro de ellos.

Designaciones:
o – segunda derivada con respecto a “x”
o – segunda derivada con respecto a “Y”
o - mezclado derivada de “x por igr”
o - mezclado derivada de "Y"

No hay problemas con la segunda derivada. En lenguaje sencillo, la segunda derivada es la derivada de la primera derivada.

Por conveniencia, reescribiré las derivadas parciales de primer orden ya encontradas:

Primero, encontremos derivadas mixtas:

Como puedes ver, todo es simple: tomamos la derivada parcial y la diferenciamos nuevamente, pero en este caso, esta vez según la “Y”.

Asimismo:

En ejemplos prácticos, puede centrarse en la siguiente igualdad.:

Así, mediante derivadas mixtas de segundo orden es muy conveniente comprobar si hemos encontrado correctamente las derivadas parciales de primer orden.

Encuentra la segunda derivada con respecto a “x”.
Sin inventos, vamos a tomarlo. y diferenciarlo por “x” nuevamente:

Asimismo:

Cabe señalar que al encontrar, es necesario mostrar. mayor atención, ya que no existen igualdades milagrosas que las verifiquen.

Las segundas derivadas también encuentran amplias aplicaciones prácticas, en particular, se utilizan en el problema de encontrar extremos de una función de dos variables. Pero todo tiene su tiempo:

Ejemplo 2

Calcula las derivadas parciales de primer orden de la función en el punto. Encuentra derivadas de segundo orden.

Este es un ejemplo para que lo resuelvas por tu cuenta (respuestas al final de la lección). Si tienes dificultad para diferenciar raíces, regresa a la lección. ¿Cómo encontrar la derivada? En general, muy pronto aprenderá a encontrar estos derivados "sobre la marcha".

Mejoremos en ejemplos más complejos:

Ejemplo 3

Mira esto . Escriba el diferencial total de primer orden.

Solución: Encuentre las derivadas parciales de primer orden:

Presta atención al subíndice: , al lado de la “X” no está prohibido escribir entre paréntesis que es una constante. Esta nota puede resultar muy útil para los principiantes para facilitar la navegación por la solución.

Más comentarios:

(1) Movemos todas las constantes más allá del signo de la derivada. En este caso, y , y, por tanto, su producto se considera un número constante.

(2) No olvides cómo diferenciar correctamente las raíces.

(1) Eliminamos todas las constantes del signo de la derivada; en este caso, la constante es .

(2) Bajo el primo nos queda el producto de dos funciones, por lo tanto, necesitamos usar la regla para derivar el producto .

(3) No olvide que se trata de una función compleja (aunque la más simple de las complejas). Usamos la regla correspondiente: .

Ahora encontramos derivadas mixtas de segundo orden:

Esto significa que todos los cálculos se realizaron correctamente.

Anotemos el diferencial total. En el contexto de la tarea que estamos considerando, no tiene sentido decir cuál es el diferencial total de una función de dos variables. Es importante que muy a menudo sea necesario plasmar esta diferencia en problemas prácticos.

Diferencial total de primer orden función de dos variables tiene la forma:

En este caso:

Es decir, simplemente es necesario sustituir estúpidamente en la fórmula las derivadas parciales de primer orden ya encontradas. En esta y otras situaciones similares, es mejor escribir signos diferenciales en los numeradores:

Y según repetidas peticiones de los lectores, diferencial completo de segundo orden.

Se parece a esto:

Busquemos CUIDADOSAMENTE las derivadas de “una letra” de segundo orden:

y anotamos el “monstruo”, “uniendo” con cuidado los cuadrados, el producto y sin olvidar duplicar la derivada mixta:

Está bien si algo parece difícil; siempre puedes volver a las derivadas más tarde, una vez que hayas dominado la técnica de diferenciación:

Ejemplo 4

Encuentra derivadas parciales de primer orden de una función. . Mira esto . Escriba el diferencial total de primer orden.

Veamos una serie de ejemplos con funciones complejas:

Ejemplo 5

Encuentra las derivadas parciales de primer orden de la función.

Solución:

Ejemplo 6

Encuentra derivadas parciales de primer orden de una función. .
Escriba el diferencial total.

Este es un ejemplo para que lo resuelvas por tu cuenta (respuesta al final de la lección). No te daré una solución completa porque es bastante simple.

Muy a menudo, todas las reglas anteriores se aplican en combinación.

Ejemplo 7

Encuentra derivadas parciales de primer orden de una función. .

(1) Usamos la regla para derivar la suma

(2) El primer término en este caso se considera constante, ya que no hay nada en la expresión que dependa de "x", solo "y". Ya sabes, siempre es agradable cuando una fracción se puede convertir en cero). Para el segundo término aplicamos la regla de diferenciación de productos. Por cierto, en este sentido, nada habría cambiado si en su lugar se hubiera dado una función; lo importante es que aquí producto de dos funciones, CADA uno de los cuales depende de "X" y, por lo tanto, es necesario utilizar la regla de diferenciación de productos. Para el tercer término aplicamos la regla de derivación de una función compleja.

(1) El primer término tanto en el numerador como en el denominador contiene una “Y”, por lo tanto, debes usar la regla para diferenciar cocientes: . El segundo término depende SÓLO de “x”, lo que significa que se considera una constante y se vuelve cero. Para el tercer término usamos la regla para derivar una función compleja.

Para aquellos lectores que valientemente llegaron casi hasta el final de la lección, les contaré un viejo chiste de Mekhmatov para aliviarlos:

Un día, apareció un derivado maligno en el espacio de funciones y comenzó a diferenciar a todos. Todas las funciones están dispersas en todas direcciones, ¡nadie quiere transformarse! Y sólo una función no se escapa. El derivado se acerca a ella y le pregunta:

- ¿Por qué no huyes de mí?

- Ja. Pero no me importa, porque soy “e elevado a X”, ¡y no me harás nada!

A lo que el malvado derivado con una sonrisa insidiosa responde:

- Aquí es donde te equivocas, te diferenciaré por “Y”, por lo que deberías ser un cero.

Quien entendió el chiste domina los derivados, al menos hasta el nivel “C”).

Ejemplo 8

Encuentra derivadas parciales de primer orden de una función. .

Este es un ejemplo para que lo resuelvas por tu cuenta. La solución completa y el ejemplo del problema se encuentran al final de la lección.

Bueno, eso es casi todo. Finalmente, no puedo evitar complacer a los amantes de las matemáticas con un ejemplo más. Ni siquiera se trata de aficionados, cada uno tiene un nivel diferente de preparación matemática: hay personas (y no tan raras) a las que les gusta competir con tareas más difíciles. Aunque el último ejemplo de esta lección no es tan complejo sino engorroso desde un punto de vista computacional.

En esta lección nos familiarizaremos con el concepto de función de dos variables y también consideraremos en detalle la tarea más común: encontrar Derivadas parciales primer y segundo orden, diferencial completo de una función.

Para estudiar eficazmente el material siguiente, usted necesario Ser capaz de encontrar con mayor o menor confianza derivadas "ordinarias" de funciones de una variable. Puedes aprender a manejar correctamente los derivados en las lecciones. ¿Cómo encontrar la derivada? y Derivada de una función compleja. También necesitaremos una tabla de derivadas de funciones elementales y reglas de diferenciación; lo más conveniente es si está disponible en forma impresa.

Empecemos por el concepto mismo de función de dos variables, intentaremos limitarnos al mínimo de teoría, ya que el sitio tiene una orientación práctica. Una función de dos variables generalmente se escribe como , y las variables se llaman variables independientes o argumentos.

Ejemplo: - función de dos variables.

A veces se utiliza la notación. También hay tareas en las que se utiliza la letra en lugar de una letra.

Es útil conocer el significado geométrico de las funciones. Una función de una variable corresponde a una determinada recta en un plano, por ejemplo, la conocida parábola escolar. Cualquier función de dos variables desde el punto de vista geométrico representa una superficie en el espacio tridimensional (planos, cilindros, bolas, paraboloides, etc.). Pero, de hecho, esto ya es geometría analítica y el análisis matemático está en nuestra agenda.

Para derivadas parciales, son válidas todas las reglas de diferenciación y la tabla de derivadas de funciones elementales. Sólo hay un par de pequeñas diferencias, a las que llegaremos en un momento.

Ejemplo 1

Encuentra las derivadas parciales de primer y segundo orden de la función.

Primero, encontremos las derivadas parciales de primer orden. Hay dos de ellos.

Designaciones:

O – derivada parcial con respecto a “x”

O – derivada parcial con respecto a “y”

Empecemos con .

¡Importante! Cuando encontramos la derivada parcial con respecto a “x”, entonces la variable se considera una constante (número constante).

Vamos a decidir. En esta lección, proporcionaremos inmediatamente la solución completa y proporcionaremos los comentarios a continuación.

Comentarios sobre las acciones realizadas:

(1) Lo primero que hacemos al encontrar la derivada parcial es concluir todo función entre paréntesis debajo del número primo con subíndice.

(2) Usamos las reglas de diferenciación. ; . Para un ejemplo sencillo como este, ambas reglas se pueden aplicar fácilmente en un solo paso. Presta atención al primer término: desde se considera una constante, y cualquier constante se puede sacar del signo de la derivada, luego lo sacamos de paréntesis. Es decir, en esta situación no es mejor que un número normal. Pasemos ahora al tercer término: aquí, por el contrario, no hay nada que sacar. Como es una constante, también lo es y en este sentido no es mejor que el último término: "siete".

(2) Usamos la tabla de derivadas de funciones elementales. Cambiemos mentalmente todas las “X” de la tabla por “I”. Es decir, esta tabla es igualmente válida para (y para cualquier letra en general). En este caso, las fórmulas que utilizamos son: y .

Entonces, se encuentran las derivadas parciales de primer orden.

Las derivadas parciales se utilizan en problemas que involucran funciones de varias variables. Las reglas para encontrar son exactamente las mismas que para funciones de una variable, con la única diferencia de que una de las variables debe considerarse constante (número constante) en el momento de la diferenciación.

Fórmula

Las derivadas parciales de una función de dos variables $ z(x,y) $ se escriben de la siguiente forma $ z"_x, z"_y $ y se encuentran usando las fórmulas:

Derivadas parciales de primer orden

$$ z"_x = \frac(\partial z)(\partial x) $$

$$ z"_y = \frac(\partial z)(\partial y) $$

Derivadas parciales de segundo orden

$$ z""_(xx) = \frac(\partial^2 z)(\partial x \partial x) $$

$$ z""_(yy) = \frac(\partial^2 z)(\partial y \partial y) $$

Derivado mixto

$$ z""_(xy) = \frac(\partial^2 z)(\partial x \partial y) $$

$$ z""_(yx) = \frac(\partial^2 z)(\partial y \partial x) $$

Derivada parcial de una función compleja

a) Sea $ z (t) = f(x(t), y(t)) $, entonces la derivada de una función compleja está determinada por la fórmula:

$$ \frac(dz)(dt) = \frac(\partial z)(\partial x) \cdot \frac(dx)(dt) + \frac(\partial z)(\partial y) \cdot \frac (día)(dt)$$

b) Sea $ z (u,v) = z(x(u,v),y(u,v)) $, entonces las derivadas parciales de la función se encuentran mediante la fórmula:

$$ \frac(\partial z)(\partial u) = \frac(\partial z)(\partial x) \cdot \frac(\partial x)(\partial u) + \frac(\partial z)( \partial y) \cdot \frac(\partial y)(\partial u) $$

$$ \frac(\partial z)(\partial v) = \frac(\partial z)(\partial x) \cdot \frac(\partial x)(\partial v) + \frac(\partial z)( \partial y) \cdot \frac(\partial y)(\partial v) $$

Derivadas parciales de una función implícita

a) Sea $ F(x,y(x)) = 0 $, entonces $$ \frac(dy)(dx) = -\frac(f"_x)(f"_y) $$

b) Sea $ F(x,y,z)=0 $, entonces $$ z"_x = - \frac(F"_x)(F"_z); z"_y = - \frac(F"_y)( F"_z) $$

Ejemplos de soluciones

Ejemplo 1
Encuentre derivadas parciales de primer orden $ z (x,y) = x^2 - y^2 + 4xy + 10 $
Solución
Para encontrar la derivada parcial con respecto a $ x $, consideraremos que $ y $ es un valor constante (número): $$ z"_x = (x^2-y^2+4xy+10)"_x = 2x - 0 + 4y + 0 = 2x+4y $$ Para encontrar la derivada parcial de una función con respecto a $y$, definimos $y$ mediante una constante: $$ z"_y = (x^2-y^2+4xy+10)"_y = -2y+4x $$ Si no puede resolver su problema, envíenoslo. Proporcionaremos una solución detallada. Podrás ver el progreso del cálculo y obtener información. ¡Esto te ayudará a obtener tu calificación de tu maestro de manera oportuna!
Respuesta
$$ z"_x = 2x+4y; z"_y = -2y+4x $$

Ejemplo 2
Encuentre las derivadas parciales de la función de segundo orden $ z = e^(xy) $
Solución
Primero necesitas encontrar las derivadas de primer orden y luego, conociéndolas, puedes encontrar las derivadas de segundo orden. Sea $y$ una constante: $$ z"_x = (e^(xy))"_x = e^(xy) \cdot (xy)"_x = ye^(xy) $$ Ahora establezcamos que $ x $ sea un valor constante: $$ z"_y = (e^(xy))"_y = e^(xy) \cdot (xy)"_y = xe^(xy) $$ Conociendo las primeras derivadas, encontramos de manera similar la segunda. Establezca $y$ como una constante: $$ z""_(xx) = (z"_x)"_x = (ye^(xy))"_x = (y)"_x e^(xy) + y(e^(xy))"_x = 0 + ye^(xy)\cdot (xy)"_x = y^2e^(xy) $$ Establecemos $ x $ como una constante: $$ z""_(yy) = (z"_y)"_y = (xe^(xy))"_y = (x)"_y e^(xy) + x(e^(xy))"_y = 0 + x^2e^(xy) = x^2e^(xy) $$ Ahora sólo queda encontrar la derivada mixta. Puedes diferenciar $ z"_x $ por $ y $, y puedes diferenciar $ z"_y $ por $ x $, ya que según el teorema $ z""_(xy) = z""_(yx) $ $$ z""_(xy) = (z"_x)"_y = (ye^(xy))"_y = (y)"_y e^(xy) + y (e^(xy))"_y = ye^(xy)\cdot (xy)"_y = yxe^(xy) $$
Respuesta
$$ z"_x = ye^(xy); z"_y = xe^(xy); z""_(xy) = yxe^(xy) $$

Ejemplo 4
Dejemos que $ 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ defina la función implícita $ F(x,y,z) = 0 $. Encuentre derivadas parciales de primer orden.
Solución
Escribimos la función en el formato: $ F(x,y,z) = 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ y encontramos las derivadas: $$ z"_x (y,z - const) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_x = 3 x^2 z - 4 $$ $$ z"_y (x,y - const) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_y = 3z^2 $$
Respuesta
$$ z"_x = 3x^2 z - 4; z"_y = 3z^2; $$