Encontrar la proyección de un vector sobre un eje dado. Proyección vectorial

Una descripción vectorial del movimiento es útil, ya que en un dibujo siempre puedes representar muchos vectores diferentes y obtener una "imagen" visual del movimiento ante tus ojos. Sin embargo, utilizar una regla y un transportador cada vez para realizar operaciones con vectores requiere mucha mano de obra. Por lo tanto, estas acciones se reducen a acciones con números positivos y negativos: proyecciones de vectores.

Proyección del vector sobre el eje. Se llama cantidad escalar igual al producto del módulo del vector proyectado y el coseno del ángulo entre las direcciones del vector y el eje de coordenadas seleccionado.

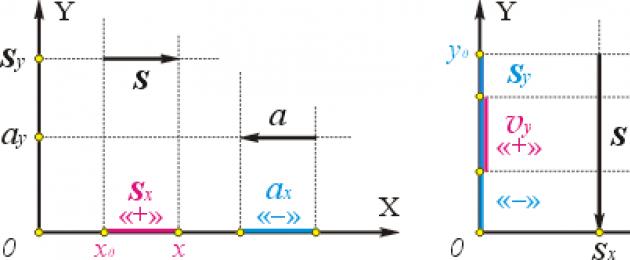
El dibujo de la izquierda muestra un vector de desplazamiento, cuyo módulo es de 50 km, y su dirección forma ángulo obtuso 150° con la dirección del eje X. Usando la definición, encontramos la proyección del desplazamiento en el eje X:

sx = s cos(α) = 50 km cos(150°) = –43 km

Dado que el ángulo entre los ejes es de 90°, es fácil calcular que la dirección del movimiento forma un ángulo agudo de 60° con la dirección del eje Y. Usando la definición, encontramos la proyección del desplazamiento en el eje Y:

sy = s cos(β) = 50 km cos(60°) = +25 km

Como puedes ver, si la dirección del vector forma un ángulo agudo con la dirección del eje, la proyección es positiva; si la dirección del vector forma un ángulo obtuso con la dirección del eje, la proyección es negativa.

El dibujo de la derecha muestra un vector de velocidad, cuyo módulo es de 5 m/s, y la dirección forma un ángulo de 30° con la dirección del eje X. Encontremos las proyecciones:

υx = υ · cos(α) = 5 m/s · cos( 30°) = +4,3 m/s
υy = υ · cos(β) = 5 m/s · cos( 120°) = –2,5 m/s

Es mucho más fácil encontrar proyecciones de vectores sobre ejes si los vectores proyectados son paralelos o perpendiculares a los ejes seleccionados. Tenga en cuenta que para el caso de paralelismo, son posibles dos opciones: el vector es codireccional al eje y el vector es opuesto al eje, y para el caso de perpendicularidad solo hay una opción.

La proyección de un vector perpendicular al eje es siempre cero (ver sy y ay en el dibujo de la izquierda, y sx y υx en el dibujo de la derecha). De hecho, para un vector perpendicular al eje, el ángulo entre él y el eje es de 90°, por lo que el coseno es cero, lo que significa que la proyección es cero.

La proyección de un vector codireccional con el eje es positiva e igual a su valor absoluto, por ejemplo, sx = +s (ver dibujo de la izquierda). En efecto, para un vector codireccional con el eje, el ángulo entre éste y el eje es cero, y su coseno es “+1”, es decir, la proyección es igual a la longitud del vector: sx = x – xo = + s .

La proyección del vector opuesto al eje es negativa e igual a su módulo tomado con signo menos, por ejemplo, sy = –s (ver el dibujo de la derecha). En efecto, para un vector opuesto al eje, el ángulo entre éste y el eje es de 180°, y su coseno es “–1”, es decir, la proyección es igual a la longitud del vector tomado con signo negativo: sy = y – yo = –s .

Los lados derechos de ambos dibujos muestran otros casos en los que los vectores son paralelos a uno de los ejes de coordenadas y perpendiculares al otro. Le invitamos a asegurarse de que también en estos casos se siguen las reglas formuladas en los párrafos anteriores.

§ 3. Proyecciones de un vector sobre los ejes de coordenadas.

1. Encontrar proyecciones geométricamente.

Vector
- proyección del vector sobre el eje BUEY
- proyección del vector sobre el eje oy

Definición 1. Proyección vectorial en cualquier eje de coordenadas hay un número tomado con un signo más o menos, correspondiente a la longitud del segmento ubicado entre las bases de las perpendiculares caídas desde el principio y el final del vector hasta el eje de coordenadas.

El signo de proyección se define de la siguiente manera. Si, al moverse a lo largo del eje de coordenadas, hay un movimiento desde el punto de proyección del comienzo del vector hasta el punto de proyección del final del vector en la dirección positiva del eje, entonces la proyección del vector se considera positiva. . Si es opuesto al eje, entonces la proyección se considera negativa.

La figura muestra que si el vector está orientado de alguna manera en dirección opuesta al eje de coordenadas, entonces su proyección sobre este eje es negativa. Si un vector está orientado de alguna manera en la dirección positiva del eje de coordenadas, entonces su proyección sobre este eje es positiva.

Si un vector es perpendicular al eje de coordenadas, entonces su proyección sobre este eje es cero.
Si un vector es codireccional con un eje, entonces su proyección sobre este eje es igual al valor absoluto del vector.
Si un vector se dirige en dirección opuesta al eje de coordenadas, entonces su proyección sobre este eje es igual en valor absoluto al valor absoluto del vector tomado con un signo menos.

2. La definición más general de proyección.

De un triángulo rectángulo ABD: .

Definición 2. Proyección vectorial en cualquier eje de coordenadas hay un número igual al producto del módulo del vector por el coseno del ángulo formado por el vector con la dirección positiva del eje de coordenadas.

El signo de la proyección está determinado por el signo del coseno del ángulo formado por el vector con la dirección positiva del eje.
Si el ángulo es agudo, entonces el coseno tiene signo positivo y las proyecciones son positivas. Para ángulos obtusos, el coseno tiene signo negativo, por lo que en tales casos las proyecciones sobre el eje son negativas.
- por tanto, para vectores perpendiculares al eje, la proyección es cero.

Sean dos vectores y se dan en el espacio. Pospongamos desde un punto arbitrario. oh vectores y . Ángulo entre vectores se llama el más pequeño de los ángulos. Designada .

Considere el eje yo y trazar un vector unitario sobre él (es decir, un vector cuya longitud sea igual a uno).

En un ángulo entre el vector y el eje. yo entender el ángulo entre los vectores y .

Entonces deja yo es algún eje y es un vector.

Denotemos por un 1 Y B 1 proyecciones sobre el eje yo respectivamente puntos A Y B. pretendamos que un 1 tiene una coordenada x1, A B 1– coordinar x2 en el eje yo.

Entonces proyección vector por eje yo llamada diferencia x1 – x2 entre las coordenadas de las proyecciones del final y el comienzo del vector sobre este eje.

Proyección del vector sobre el eje. yo denotaremos.

Está claro que si el ángulo entre el vector y el eje yo picante entonces x2> x1 y proyección x2 – x1> 0; si este ángulo es obtuso, entonces x2< x1 y proyección x2 – x1< 0. Наконец, если вектор перпендикулярен оси yo, Eso x2= x1 Y x2– x1=0.

Por tanto, la proyección del vector sobre el eje. yo es la longitud del segmento A 1 B 1, tomado con cierto signo. Por tanto, la proyección del vector sobre el eje es un número o un escalar.

La proyección de un vector sobre otro se determina de manera similar. En este caso, se encuentran las proyecciones de los extremos de este vector sobre la recta en la que se encuentra el segundo vector.

Veamos algunos básicos propiedades de las proyecciones.

SISTEMAS VECTORIALES LINEALMENTE DEPENDIENTES Y LINEALMENTE INDEPENDIENTES

Consideremos varios vectores.

Combinación lineal de estos vectores es cualquier vector de la forma , donde hay algunos números. Los números se llaman coeficientes de combinación lineal. También dicen que en este caso se expresa linealmente a través de estos vectores, es decir se obtiene de ellos mediante acciones lineales.

Por ejemplo, si se dan tres vectores, entonces los siguientes vectores pueden considerarse como su combinación lineal:

Si un vector se representa como una combinación lineal de algunos vectores, entonces se dice que es Dispuesto a lo largo de estos vectores.

Los vectores se llaman linealmente dependiente, si hay números, no todos iguales a cero, tales que . Está claro que los vectores dados serán linealmente dependientes si cualquiera de estos vectores se expresa linealmente en términos de los demás.

De lo contrario, es decir cuando la proporción realizado sólo cuando , estos vectores se llaman independiente linealmente.

Teorema 1. Dos vectores cualesquiera son linealmente dependientes si y sólo si son colineales.

Prueba:

El siguiente teorema se puede demostrar de manera similar.

Teorema 2. Tres vectores son linealmente dependientes si y sólo si son coplanares.

Prueba.

BASE

Base es una colección de vectores linealmente independientes distintos de cero. Denotaremos los elementos de la base por .

En el párrafo anterior vimos que dos vectores no colineales en un plano son linealmente independientes. Por tanto, según el teorema 1 del párrafo anterior, una base en un plano son dos vectores cualesquiera no colineales en este plano.

De manera similar, tres vectores cualesquiera no coplanares son linealmente independientes en el espacio. En consecuencia, llamamos base en el espacio a tres vectores no coplanares.

La siguiente afirmación es cierta.

Teorema. Sea una base dada en el espacio. Entonces cualquier vector se puede representar como una combinación lineal. , Dónde X, y, z- algunos números. Ésta es la única descomposición.

Prueba.

Por lo tanto, la base permite que cada vector esté asociado de forma única con un triple de números: los coeficientes de expansión de este vector en los vectores de la base: . Lo contrario también es cierto, por cada tres números x, y, z usando la base, puedes comparar el vector si haces una combinación lineal .

Si la base y , entonces los números x, y, z son llamados coordenadas vector en una base dada. Las coordenadas vectoriales se indican con .

SISTEMA DE COORDENADAS CARTESIANAS

Sea un punto dado en el espacio. oh y tres vectores no coplanares.

sistema de coordenadas Cartesianas en el espacio (en el plano) es el conjunto de un punto y una base, es decir un conjunto de un punto y tres vectores no coplanares (2 vectores no colineales) que emanan de este punto.

Punto oh llamado el origen; Las líneas rectas que pasan por el origen de coordenadas en la dirección de los vectores base se denominan ejes de coordenadas: abscisas, ordenadas y ejes aplicados. Los planos que pasan por los ejes de coordenadas se llaman planos de coordenadas.

Considere un punto arbitrario en el sistema de coordenadas seleccionado. METRO. Introduzcamos el concepto de coordenadas puntuales. METRO. Vector que conecta el origen con un punto. METRO. llamado vector de radio puntos METRO.

Un vector en la base seleccionada se puede asociar con un triple de números – sus coordenadas: .

Coordenadas del vector de radio del punto. METRO. son llamados coordenadas del punto M. en el sistema de coordenadas considerado. M(x,y,z). La primera coordenada se llama abscisa, la segunda ordenada y la tercera aplicación.

Las coordenadas cartesianas en el plano se determinan de manera similar. Aquí el punto tiene sólo dos coordenadas: abscisa y ordenada.

Es fácil ver que para un sistema de coordenadas dado, cada punto tiene ciertas coordenadas. Por otro lado, para cada tripleta de números existe un único punto que tiene como coordenadas estos números.

Si los vectores tomados como base en el sistema de coordenadas seleccionado tienen una longitud unitaria y son perpendiculares por pares, entonces el sistema de coordenadas se llama rectangular cartesiano.

Es fácil demostrarlo.

Los cosenos directores de un vector determinan completamente su dirección, pero no dicen nada sobre su longitud.

Antes de aprender todo sobre los vectores y sus operaciones, prepárese para resolver un problema simple. Hay un vector de tu emprendimiento y un vector de tus habilidades innovadoras. El vector del emprendimiento te lleva al Objetivo 1 y el vector de las habilidades innovadoras te lleva al Objetivo 2. Las reglas del juego son tales que no puedes moverte en las direcciones de estos dos vectores a la vez y lograr dos objetivos a la vez. Los vectores interactúan o, hablando en lenguaje matemático, se realiza alguna operación sobre los vectores. El resultado de esta operación es el vector “Resultado”, que le lleva al Objetivo 3.

Ahora dígame: ¿el resultado de qué operación sobre los vectores “Emprendimiento” y “Habilidades innovadoras” es el vector “Resultado”? Si no puede saberlo de inmediato, no se desanime. A medida que avance en esta lección, podrá responder esta pregunta.

Como ya hemos visto anteriormente, el vector necesariamente proviene de un punto determinado. A en línea recta hasta algún punto B. En consecuencia, cada vector no sólo tiene un valor numérico (longitud), sino también un valor físico y geométrico: dirección. De aquí surge la primera y más simple definición de vector. Entonces, un vector es un segmento dirigido que viene de un punto. A al punto B. Se designa de la siguiente manera: .

Y para empezar varios operaciones con vectores , necesitamos familiarizarnos con otra definición de vector.

Un vector es un tipo de representación de un punto al que se debe llegar desde algún punto de partida. Por ejemplo, un vector tridimensional generalmente se escribe como (x, y, z) . En términos muy simples, estos números significan qué tan lejos debes caminar en tres direcciones diferentes para llegar a un punto.

Sea un vector dado. Donde X = 3 (la mano derecha apunta a la derecha), y = 1 (la mano izquierda apunta hacia adelante) z = 5 (debajo del punto hay una escalera que conduce hacia arriba). Con estos datos encontrarás un punto caminando 3 metros en la dirección que indica tu mano derecha, luego 1 metro en la dirección que indica tu mano izquierda, luego te espera una escalera y subiendo 5 metros finalmente encontrarás usted mismo en el punto final.

Todos los demás términos son aclaraciones de la explicación presentada anteriormente, necesarias para diversas operaciones con vectores, es decir, para resolver problemas prácticos. Repasemos estas definiciones más rigurosas, centrándonos en los problemas vectoriales típicos.

Ejemplos fisicos Las cantidades vectoriales pueden ser el desplazamiento de un punto material que se mueve en el espacio, la velocidad y aceleración de este punto, así como la fuerza que actúa sobre él.

vector geométrico presentado en un espacio bidimensional y tridimensional en la forma segmento direccional. Este es un segmento que tiene un principio y un final.

Si A- el comienzo del vector, y B- su final, entonces el vector se indica con el símbolo o una letra minúscula . En la figura, el final del vector está indicado por una flecha (Fig.1)

Longitud(o módulo) de un vector geométrico es la longitud del segmento que lo genera

Los dos vectores se llaman igual , si se pueden combinar (si las direcciones coinciden) mediante transferencia paralela, es decir si son paralelos, están dirigidos en la misma dirección y tienen longitudes iguales.

En física a menudo se considera vectores pinned, especificado por el punto de aplicación, longitud y dirección. Si el punto de aplicación del vector no importa, entonces se puede transferir, manteniendo su longitud y dirección, a cualquier punto del espacio. En este caso, el vector se llama gratis. Aceptaremos considerar sólo vectores gratis.

Operaciones lineales sobre vectores geométricos.

Multiplicar un vector por un número

Producto de un vector por numero es un vector que se obtiene de un vector estirando (en) o comprimiendo (en) por un factor, y la dirección del vector sigue siendo la misma si, y cambia a la opuesta si. (Figura 2)

De la definición se deduce que los vectores y = siempre están ubicados en una o líneas paralelas. Estos vectores se llaman colineal. (También podemos decir que estos vectores son paralelos, pero en álgebra vectorial se acostumbra decir “colineales”.) Lo contrario también es cierto: si los vectores son colineales, entonces están relacionados por la relación

En consecuencia, la igualdad (1) expresa la condición de colinealidad de dos vectores.

Suma y resta de vectores.

Al sumar vectores necesitas saber que cantidad vectores y se llama vector, cuyo comienzo coincide con el comienzo del vector y el final con el final del vector, siempre que el comienzo del vector esté unido al final del vector. (Fig. 3)

Esta definición se puede distribuir sobre cualquier número finito de vectores. Que se den en el espacio. norte vectores gratis. Al sumar varios vectores, su suma se toma como el vector de cierre, cuyo comienzo coincide con el comienzo del primer vector y el final con el final del último vector. Es decir, si adjunta el comienzo del vector al final del vector y el comienzo del vector al final del vector, etc. y, finalmente, hasta el final del vector, el comienzo del vector, luego la suma de estos vectores es el vector de cierre , cuyo comienzo coincide con el comienzo del primer vector y el final, con el final del último vector. (Figura 4)

Los términos se llaman componentes del vector y la regla formulada es regla del polígono. Es posible que este polígono no sea plano.

Cuando se multiplica un vector por el número -1, se obtiene el vector opuesto. Los vectores y tienen las mismas longitudes y direcciones opuestas. Su suma da vector cero, cuya longitud es cero. La dirección del vector cero no está definida.

En álgebra vectorial, no es necesario considerar la operación de resta por separado: restar un vector de un vector significa sumar el vector opuesto al vector, es decir,

Ejemplo 1. Simplifica la expresión:

.

,

es decir, los vectores se pueden sumar y multiplicar por números de la misma forma que los polinomios (en particular, también problemas de simplificación de expresiones). Normalmente, surge la necesidad de simplificar expresiones linealmente similares con vectores antes de calcular los productos de los vectores.

Ejemplo 2. Los vectores y sirven como diagonales del paralelogramo ABCD (Fig. 4a). Expresa mediante y los vectores , , y , que son los lados de este paralelogramo.

Solución. El punto de intersección de las diagonales de un paralelogramo biseca cada diagonal. Encontramos las longitudes de los vectores requeridos en el planteamiento del problema como la mitad de las sumas de los vectores que forman un triángulo con los requeridos, o como la mitad de las diferencias (dependiendo de la dirección del vector que sirve como diagonal), o, como en el último caso, la mitad de la suma se toma con un signo menos. El resultado son los vectores requeridos en el planteamiento del problema:

Hay muchas razones para creer que ya ha respondido correctamente a la pregunta sobre los vectores "Emprendimiento" y "Habilidades innovadoras" al comienzo de esta lección. Respuesta correcta: se realiza una operación de suma sobre estos vectores.

Resuelva problemas vectoriales usted mismo y luego observe las soluciones.

¿Cómo encontrar la longitud de la suma de vectores?

Este problema ocupa un lugar especial en las operaciones con vectores, ya que implica el uso de propiedades trigonométricas. Digamos que te encuentras con una tarea como la siguiente:

Las longitudes de los vectores están dadas. y la longitud de la suma de estos vectores. Encuentra la longitud de la diferencia entre estos vectores.

Las soluciones a este y otros problemas similares y las explicaciones de cómo resolverlos se encuentran en la lección " Suma de vectores: longitud de la suma de vectores y teorema del coseno ".

Y puedes consultar la solución a este tipo de problemas en Calculadora en línea "Lado desconocido de un triángulo (suma de vectores y teorema del coseno)" .

¿Dónde están los productos de los vectores?

Los productos vector-vector no son operaciones lineales y se consideran por separado. Y tenemos las lecciones "Producto escalar de vectores" y "Productos vectoriales y mixtos de vectores".

Proyección de un vector sobre un eje

La proyección de un vector sobre un eje es igual al producto de la longitud del vector proyectado por el coseno del ángulo entre el vector y el eje:

Como es sabido, la proyección de un punto A en la línea recta (plano) es la base de la perpendicular que cae desde este punto sobre la línea recta (plano).

Sea un vector arbitrario (Fig.5) y sean las proyecciones de su origen (puntos A) y final (puntos B) por eje yo. (Para construir una proyección de un punto A) dibuja una línea recta que pasa por el punto A un plano perpendicular a una recta. La intersección de la línea y el plano determinará la proyección requerida.

Componente vectorial en el eje l Se llama un vector que se encuentra en este eje, cuyo comienzo coincide con la proyección del principio y el final con la proyección del final del vector.

Proyección del vector sobre el eje. yo número llamado

,

igual a la longitud del vector componente en este eje, tomado con un signo más si la dirección de los componentes coincide con la dirección del eje yo, y con signo menos si estas direcciones son opuestas.

Propiedades básicas de las proyecciones vectoriales sobre un eje:

1. Las proyecciones de vectores iguales sobre el mismo eje son iguales entre sí.

2. Cuando un vector se multiplica por un número, su proyección se multiplica por el mismo número.

3. La proyección de la suma de los vectores sobre cualquier eje es igual a la suma de las proyecciones de los sumandos de los vectores sobre el mismo eje.

4. La proyección del vector sobre el eje es igual al producto de la longitud del vector proyectado por el coseno del ángulo entre el vector y el eje:

.

Solución. Proyectamos vectores sobre el eje. yo como se define en los antecedentes teóricos anteriores. De la Fig. 5a se desprende claramente que la proyección de la suma de vectores es igual a la suma de las proyecciones de vectores. Calculamos estas proyecciones:

Encontramos la proyección final de la suma de vectores:

Relación entre un vector y un sistema de coordenadas cartesiano rectangular en el espacio

Conociendo El sistema de coordenadas cartesianas rectangulares en el espacio tuvo lugar en la lección correspondiente., es recomendable abrirlo en una nueva ventana.

En un sistema ordenado de ejes de coordenadas. 0xyz eje Buey llamado eje x, eje 0 años – eje y y eje 0z – aplicar eje.

Con un punto arbitrario METRO vector de conexión espacial

llamado vector de radio puntos METRO y proyectarlo sobre cada uno de los ejes de coordenadas. Denotemos las magnitudes de las proyecciones correspondientes:

Números x, y, z son llamados coordenadas del punto M, respectivamente abscisa, ordenada Y aplicar, y se escriben como un punto ordenado de números: M(x;y;z)(Figura 6).

Un vector de longitud unitaria cuya dirección coincide con la dirección del eje se llama vector unitario(o ortom) ejes. Denotemos por

En consecuencia, los vectores unitarios de los ejes de coordenadas. Buey, Oye, Onz

Teorema. Cualquier vector se puede expandir en vectores unitarios de ejes de coordenadas:

(2)

La igualdad (2) se llama expansión del vector a lo largo de los ejes de coordenadas. Los coeficientes de esta expansión son las proyecciones del vector sobre los ejes de coordenadas. Por tanto, los coeficientes de expansión (2) del vector a lo largo de los ejes de coordenadas son las coordenadas del vector.

Después de elegir un determinado sistema de coordenadas en el espacio, el vector y el triplete de sus coordenadas se determinan entre sí de forma única, por lo que el vector se puede escribir en la forma

Las representaciones del vector en la forma (2) y (3) son idénticas.

Condición de colinealidad de vectores en coordenadas.

Como ya hemos señalado, los vectores se llaman colineales si están relacionados por la relación

Se dan los vectores. . Estos vectores son colineales si las coordenadas de los vectores están relacionadas por la relación

,

es decir, las coordenadas de los vectores son proporcionales.

Ejemplo 6. Se dan vectores . ¿Son estos vectores colineales?

Solución. Averigüemos la relación entre las coordenadas de estos vectores:

.

Las coordenadas de los vectores son proporcionales, por tanto, los vectores son colineales, o lo que es lo mismo, paralelos.

Cosenos de longitud y dirección del vector

Debido a la perpendicularidad mutua de los ejes de coordenadas, la longitud del vector

igual a la longitud de la diagonal de un paralelepípedo rectangular construido sobre vectores

y se expresa por la igualdad

(4)

Un vector se define completamente especificando dos puntos (inicio y final), por lo que las coordenadas del vector se pueden expresar en términos de las coordenadas de estos puntos.

Sea, en un sistema de coordenadas dado, el origen del vector en el punto

y el final está en el punto

Desde la igualdad

sigue eso

o en forma de coordenadas

Por eso, Las coordenadas del vector son iguales a las diferencias entre las mismas coordenadas del final y el comienzo del vector. . La fórmula (4) en este caso tomará la forma

La dirección del vector está determinada. cosenos de dirección . Estos son los cosenos de los ángulos que forma el vector con los ejes Buey, Oye Y Onz. Denotemos estos ángulos en consecuencia. α , β Y γ . Entonces los cosenos de estos ángulos se pueden encontrar usando las fórmulas

Los cosenos directores de un vector también son las coordenadas del vector de ese vector y, por tanto, del vector del vector.

.

Considerando que la longitud del vector unitario es igual a una unidad, es decir

,

obtenemos la siguiente igualdad para los cosenos directores:

Ejemplo 7. Encuentra la longitud del vector. X = (3; 0; 4).

Solución. La longitud del vector es

Ejemplo 8. Puntos otorgados:

Descubre si el triángulo construido sobre estos puntos es isósceles.

Solución. Usando la fórmula de longitud del vector (6), encontramos las longitudes de los lados y determinamos si hay dos iguales entre ellos:

Se han encontrado dos lados iguales, por lo tanto no es necesario buscar la longitud del tercer lado, y el triángulo dado es isósceles.

Ejemplo 9. Encuentre la longitud del vector y sus cosenos directores si .

Solución. Las coordenadas vectoriales están dadas:

.

La longitud del vector es igual a la raíz cuadrada de la suma de los cuadrados de las coordenadas del vector:

.

Encontrar cosenos directores:

Resuelva el problema del vector usted mismo y luego mire la solución.

Operaciones con vectores dados en forma de coordenadas.

Sean dos vectores y estén dados, definidos por sus proyecciones:

Indiquemos acciones sobre estos vectores.

1.Adición:

o lo que es lo mismo

(al sumar dos vectores, se suman las coordenadas del mismo nombre).

Primero, recordemos qué es. eje de coordenadas, proyección de un punto sobre un eje Y coordenadas de un punto sobre el eje.

Eje de coordenadas- Esta es una línea recta a la que se le da alguna dirección. Puedes considerarlo como un vector con un módulo infinitamente grande.

Eje de coordenadas denotado por alguna letra: X, Y, Z, s, t... Por lo general, se selecciona (arbitrariamente) un punto en el eje, que se llama origen y, por regla general, se denota con la letra O. A partir de este punto el Se miden las distancias a otros puntos de interés para nosotros.

Proyección de un punto sobre un eje.- esta es la base de la perpendicular bajada desde este punto hasta este eje (Fig. 8). Es decir, la proyección de un punto sobre el eje es un punto.

Coordenada del punto en el eje.- es un número cuyo valor absoluto es igual a la longitud del segmento del eje (en la escala seleccionada) contenido entre el origen del eje y la proyección del punto sobre este eje. Este número se toma con signo más si la proyección del punto se ubica en la dirección del eje desde su origen y con signo menos si es en sentido contrario.

Proyección escalar de un vector sobre un eje- Este número, cuyo valor absoluto es igual a la longitud del segmento del eje (en la escala seleccionada) encerrado entre las proyecciones del punto inicial y el punto final del vector. ¡Importante! Generalmente en lugar de la expresión proyección escalar de un vector sobre un eje simplemente dicen - proyección del vector sobre el eje, es decir, la palabra escalar bajado. Proyección vectorial se denota con la misma letra que el vector proyectado (en escritura normal, sin negrita), con un índice más bajo (como regla general) del nombre del eje sobre el cual se proyecta este vector. Por ejemplo, si un vector se proyecta sobre el eje X A, entonces su proyección se denota por una x. Al proyectar el mismo vector sobre otro eje, digamos, el eje Y, su proyección se denotará como y (Fig. 9).

Calcular proyección del vector sobre el eje(por ejemplo, el eje X), es necesario restar la coordenada del punto inicial de la coordenada de su punto final, es decir

una x = x k - x norte.

Debemos recordar: ¡la proyección escalar de un vector sobre un eje (o, simplemente, la proyección de un vector sobre un eje) es un número (no un vector)! Además, la proyección puede ser positiva si el valor x k es mayor que el valor x n, negativa si el valor x k es menor que el valor x n e igual a cero si x k es igual a x n (Fig. 10).

La proyección de un vector sobre un eje también se puede encontrar conociendo el módulo del vector y el ángulo que forma con este eje.

De la Figura 11 queda claro que a x = a Cos α

Es decir, la proyección del vector sobre el eje es igual al producto del módulo del vector por el coseno del ángulo. entre la dirección del eje y la dirección del vector. Si el ángulo es agudo, entonces Cos α > 0 y a x > 0, y si es obtuso, entonces el coseno del ángulo obtuso es negativo y la proyección del vector sobre el eje también será negativa.

Los ángulos medidos desde el eje en sentido antihorario se consideran positivos y los ángulos medidos a lo largo del eje son negativos. Sin embargo, dado que el coseno es una función par, es decir, Cos α = Cos (− α), al calcular las proyecciones, los ángulos se pueden contar tanto en el sentido de las agujas del reloj como en el sentido contrario a las agujas del reloj.

Al resolver problemas, a menudo se utilizarán las siguientes propiedades de las proyecciones: si

A = b + C +…+ d, entonces a x = b x + c x +…+ d x (similar a otros ejes),

a= metro b, entonces a x = mb x (de manera similar para otros ejes).

La fórmula a x = a Cos α será A menudo ocurren al resolver problemas, por lo que definitivamente necesitas saberlo. Necesita conocer la regla para determinar la proyección. ¡de memoria!

¡Recordar!

Para encontrar la proyección de un vector sobre un eje, el módulo de este vector debe multiplicarse por el coseno del ángulo entre la dirección del eje y la dirección del vector.

Una vez más, ¡de memoria!