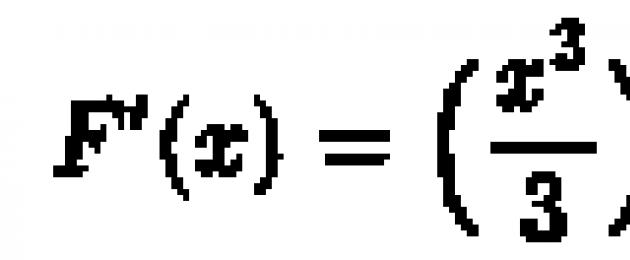Las propiedades más simples de las integrales. Las propiedades más simples de las integrales 2 definición de una integral indefinida y sus propiedades

Estas propiedades se utilizan para realizar transformaciones de la integral con el fin de reducirla a una de las integrales elementales y realizar cálculos posteriores.

1. La derivada de la integral indefinida es igual al integrando:

2. El diferencial de la integral indefinida es igual al integrando:

3. La integral indefinida del diferencial de una determinada función es igual a la suma de esta función y una constante arbitraria:

4. El factor constante se puede sacar del signo integral:

Además, a ≠ 0

5. La integral de la suma (diferencia) es igual a la suma (diferencia) de las integrales:

6. La propiedad es una combinación de las propiedades 4 y 5:

Además, a ≠ 0 ˄ b ≠ 0

7. Propiedad de invariancia de la integral indefinida:

Si entonces

8. Propiedad:

Si entonces

De hecho, esta propiedad es caso especial integración utilizando el método de cambio de variable, que se analiza con más detalle en la siguiente sección.

Veamos un ejemplo:

Primero aplicamos la propiedad 5, luego la propiedad 4, luego usamos la tabla de antiderivadas y obtuvimos el resultado.

El algoritmo de nuestra calculadora integral en línea admite todas las propiedades enumeradas anteriormente y puede encontrar fácilmente solución detallada para tu integral.

En cálculo diferencial el problema se resuelve: bajo esta función ƒ(x) encuentre su derivada(o diferencial). El cálculo integral resuelve el problema inverso: encontrar la función F(x), conociendo su derivada F "(x)=ƒ(x) (o diferencial). La función buscada F(x) se llama antiderivada de la función ƒ(x) ).

La función F(x) se llama antiderivada función ƒ(x) en el intervalo (a; b), si para cualquier x є (a; b) la igualdad

F " (x)=ƒ(x) (o dF(x)=ƒ(x)dx).

Por ejemplo, la primitiva de la función y = x 2, x є R, es la función, ya que

Obviamente, cualquier función también será antiderivada.

donde C es una constante, ya que

Teorema 29. 1. Si la función F(x) es una antiderivada de la función ƒ(x) en (a;b), entonces el conjunto de todas las antiderivadas de ƒ(x) viene dado por la fórmula F(x)+ C, donde C es un número constante.

▲ La función F(x)+C es una antiderivada de ƒ(x).

De hecho, (F(x)+C) " =F " (x)=ƒ(x).

Sea Ф(x) alguna otra, diferente de F(x), antiderivada de la función ƒ(x), es decir, Ф "(x)=ƒ(х). Entonces, para cualquier x є (а;b) tenemos

Y esto significa (ver Corolario 25.1) que

donde C es un número constante. Por lo tanto, Ф(x)=F(x)+С.▼

El conjunto de todas las funciones primitivas F(x)+С para ƒ(x) se llama integral indefinida de la función ƒ(x) y se denota con el símbolo ∫ ƒ(x) dx.

Así, por definición

∫ ƒ(x)dx= F(x)+C.

Aquí ƒ(x) se llama función integrando, ƒ(x)dx — expresión integrando, X - variable de integración, ∫ -signo de la integral indefinida.

La operación de encontrar la integral indefinida de una función se llama integrar esta función.

Geométricamente, la integral indefinida es una familia de curvas “paralelas” y=F(x)+C (cada valor numérico de C corresponde a una curva específica de la familia) (ver Fig. 166). La gráfica de cada antiderivada (curva) se llama curva integral.

¿Toda función tiene una integral indefinida?

Hay un teorema que establece que “toda función continua en (a;b) tiene una primitiva en este intervalo” y, en consecuencia, una integral indefinida.

Observemos una serie de propiedades de la integral indefinida que se derivan de su definición.

1. El diferencial de la integral indefinida es igual al integrando y la derivada de la integral indefinida es igual al integrando:

d(∫ ƒ(x)dx)=ƒ(x)dх, (∫ ƒ(x)dx) " =ƒ(x).

De hecho, d(∫ ƒ(x) dx)=d(F(x)+C)=dF(x)+d(C)=F " (x) dx =ƒ(x) dx

(∫ ƒ (x) dx) " =(F(x)+C)"=F"(x)+0 =ƒ (x).

Gracias a esta propiedad, la exactitud de la integración se comprueba mediante diferenciación. Por ejemplo, la igualdad

∫(3x 2 + 4) dx=х з +4х+С

cierto, ya que (x 3 +4x+C)"=3x 2 +4.

2. La integral indefinida del diferencial de una determinada función es igual a la suma de esta función y una constante arbitraria:

∫dF(x)= F(x)+C.

En realidad,

3. El factor constante se puede sacar del signo integral:

α ≠ 0 es una constante.

En realidad,

(ponga C 1 / a = C.)

4. La integral indefinida de la suma algebraica de un número finito de funciones continuas es igual a la suma algebraica de las integrales de las sumandos de las funciones:

Sean F"(x)=ƒ(x) y G"(x)=g(x). Entonces

donde C 1 ±C 2 =C.

5. (Invariancia de la fórmula de integración).

Si , donde u=φ(x) es una función arbitraria con una derivada continua.

▲ Sea x una variable independiente, ƒ(x) una función continua y F(x) su primitiva. Entonces

Establezcamos ahora u=φ(x), donde φ(x) es una función continuamente diferenciable. Considere la función compleja F(u)=F(φ(x)). Debido a la invariancia de la forma del primer diferencial de la función (ver pág. 160), tenemos

Desde aquí▼

Así, la fórmula de la integral indefinida sigue siendo válida independientemente de si la variable de integración es la variable independiente o cualquier función de ella que tenga una derivada continua.

Entonces, de la fórmula reemplazando x con u (u=φ(x)) obtenemos

En particular,

Ejemplo 29.1. Encuentra la integral

donde C=C1+C 2 +C 3 +C 4.

Ejemplo 29.2. Encuentra la solución integral:

• 29.3. Tabla de integrales indefinidas básicas

Aprovechando que la integración es la acción inversa de la diferenciación, se puede obtener una tabla de integrales básicas invirtiendo las fórmulas correspondientes del cálculo diferencial (tabla de diferenciales) y utilizando las propiedades de la integral indefinida.

Por ejemplo, porque

d(sen tu)=cos tu . du

La derivación de una serie de fórmulas en la tabla se dará al considerar los métodos básicos de integración.

Las integrales en la siguiente tabla se llaman tabulares. Deben saberse de memoria. En el cálculo integral no existen reglas simples y universales para encontrar antiderivadas de funciones elementales, como en el cálculo diferencial. Los métodos para encontrar antiderivadas (es decir, integrar una función) se reducen a indicar técnicas que convierten una integral dada (buscada) en una integral tabular. Por tanto, es necesario conocer las integrales de tablas y poder reconocerlas.

Tenga en cuenta que en la tabla de integrales básicas, la variable de integración puede indicar tanto una variable independiente como una función de la variable independiente (de acuerdo con la propiedad de invariancia de la fórmula de integración).

La validez de las fórmulas siguientes se puede verificar tomando el diferencial del lado derecho, que será igual al integrando del lado izquierdo de la fórmula.

Probemos, por ejemplo, la validez de la fórmula 2. La función 1/u está definida y es continua para todos los valores de y distintos de cero.

Si u > 0, entonces ln|u|=lnu, entonces Es por eso

Si tu<0, то ln|u|=ln(-u). НоMedio

Entonces, la fórmula 2 es correcta. De manera similar, revisemos la fórmula 15:

Tabla de integrales principales

¡Amigos! Te invitamos a discutir. Si tienes tu propia opinión, escríbenos en los comentarios.

En este artículo enumeraremos las principales propiedades de la integral definida. La mayoría de estas propiedades se prueban con base en los conceptos de integral definida de Riemann y Darboux.

El cálculo de la integral definida suele realizarse utilizando las cinco primeras propiedades, por lo que nos referiremos a ellas cuando sea necesario. Las propiedades restantes de la integral definida se utilizan principalmente para evaluar varias expresiones.

Antes de seguir adelante propiedades básicas de la integral definida, acordemos que a no excede a b.

Para la función y = f(x) definida en x = a, la igualdad es verdadera.

Es decir, el valor de una integral definida con los mismos límites de integración es igual a cero. Esta propiedad es consecuencia de la definición de la integral de Riemann, ya que en este caso cada suma integral para cualquier partición del intervalo y cualquier elección de puntos es igual a cero, ya que, por tanto, el límite de sumas integrales es cero.

Para una función integrable en un intervalo, .

En otras palabras, cuando los límites superior e inferior de integración cambian de lugar, el valor de la integral definida cambia al opuesto. Esta propiedad de una integral definida también se deriva del concepto de integral de Riemann, solo la numeración de la partición del segmento debe comenzar desde el punto x = b.

para funciones integrables en un intervalo y = f(x) y y = g(x) .

Prueba.

Escribamos la suma integral de la función. para una partición dada de un segmento y una elección dada de puntos:

donde y son las sumas integrales de las funciones y = f(x) e y = g(x) para una partición dada del segmento, respectivamente.

Llegando al límite en obtenemos que, por definición de la integral de Riemann, es equivalente al enunciado de la propiedad que se está demostrando.

El factor constante se puede sacar del signo de la integral definida. Es decir, para una función y = f(x) integrable en un intervalo y un número arbitrario k, se cumple la siguiente igualdad: .

La demostración de esta propiedad de la integral definida es absolutamente similar a la anterior:


Sea la función y = f(x) integrable en el intervalo X, y y luego .

Esta propiedad es cierta tanto para , como para o .

La demostración se puede realizar basándose en las propiedades anteriores de la integral definida.

Si una función es integrable en un intervalo, entonces es integrable en cualquier intervalo interno.

La prueba se basa en la propiedad de las sumas de Darboux: si se agregan nuevos puntos a una partición existente de un segmento, entonces la suma de Darboux inferior no disminuirá y la superior no aumentará.

Si la función y = f(x) es integrable en el intervalo y para cualquier valor del argumento, entonces .

Esta propiedad se demuestra mediante la definición de la integral de Riemann: cualquier suma integral para cualquier elección de puntos de partición del segmento y puntos en no será negativa (no positiva).

Consecuencia.

Para funciones y = f(x) e y = g(x) integrables en un intervalo, se cumplen las siguientes desigualdades:


Esta afirmación significa que la integración de las desigualdades es permisible. Usaremos este corolario para demostrar las siguientes propiedades.

Sea la función y = f(x) integrable en el intervalo , entonces se cumple la desigualdad .

Prueba.

Es obvio que . En la propiedad anterior encontramos que la desigualdad se puede integrar término a término, por lo tanto, es cierta . Esta doble desigualdad se puede escribir como .

Sean las funciones y = f(x) e y = g(x) integrables en el intervalo y para cualquier valor del argumento, entonces , Dónde Y .

La prueba se realiza de manera similar. Dado que m y M son los valores más pequeño y más grande de la función y = f(x) en el segmento, entonces . Multiplicar la doble desigualdad por una función no negativa y = g(x) nos lleva a la siguiente doble desigualdad. Integrandolo en el intervalo , llegamos al enunciado que se demuestra.

Función antiderivada e integral indefinida

Hecho 1. La integración es la acción inversa de la diferenciación, es decir, restaurar una función a partir de la derivada conocida de esta función. La función así restablecida F(X) se llama antiderivada para función F(X).

Definición 1. Función F(X F(X) en algún intervalo X, si para todos los valores X a partir de este intervalo se cumple la igualdad F "(X)=F(X), es decir, esta función F(X) es la derivada de la función antiderivada F(X). .

Por ejemplo, la función F(X) = pecado X es una antiderivada de la función F(X) = porque X en toda la recta numérica, ya que para cualquier valor de x (pecado X)" = (porque X) .

Definición 2. Integral indefinida de una función F(X) es el conjunto de todas sus antiderivadas. En este caso se utiliza la notación

∫

F(X)dx

,

donde esta la señal ∫ llamada signo integral, la función F(X) – función integrando, y F(X)dx – expresión integrando.

Así, si F(X) – alguna antiderivada para F(X) , Eso

∫

F(X)dx = F(X) +C

Dónde C - constante arbitraria (constante).

Para comprender el significado del conjunto de primitivas de una función como integral indefinida, resulta apropiada la siguiente analogía. Que haya una puerta (puerta tradicional de madera). Su función es “ser una puerta”. ¿De qué está hecha la puerta? Hecho de madera. Esto significa que el conjunto de primitivas del integrando de la función “ser una puerta”, es decir, su integral indefinida, es la función “ser un árbol + C”, donde C es una constante, que en este contexto puede denota, por ejemplo, el tipo de árbol. Así como una puerta se hace de madera usando algunas herramientas, una derivada de una función se “hace” a partir de una función antiderivada usando fórmulas que aprendimos mientras estudiamos la derivada .

Entonces la tabla de funciones de los objetos comunes y sus correspondientes antiderivadas (“ser una puerta” - “ser un árbol”, “ser una cuchara” - “ser metal”, etc.) es similar a la tabla de funciones básicas integrales indefinidas, que se darán a continuación. La tabla de integrales indefinidas enumera funciones comunes con una indicación de las antiderivadas a partir de las cuales se “hacen” estas funciones. En parte de los problemas para encontrar la integral indefinida se dan integrandos que se pueden integrar directamente sin mucho esfuerzo, es decir, usando la tabla de integrales indefinidas. En problemas más complejos, primero se debe transformar el integrando para poder utilizar integrales de tabla.

Hecho 2. Al restaurar una función como antiderivada, debemos tener en cuenta una constante arbitraria (constante) C, y para no escribir una lista de antiderivadas con varias constantes del 1 al infinito, es necesario escribir un conjunto de antiderivadas con una constante arbitraria C, por ejemplo, así: 5 X³+C. Entonces, se incluye una constante arbitraria (constante) en la expresión de la antiderivada, ya que la antiderivada puede ser una función, por ejemplo, 5 X³+4 o 5 X³+3 y cuando se diferencia, 4 o 3, o cualquier otra constante va a cero.

Planteemos el problema de integración: para esta función F(X) encontrar tal función F(X), cuyo derivado igual a F(X).

Ejemplo 1. Encuentra el conjunto de primitivas de una función.

Solución. Para esta función, la antiderivada es la función

Función F(X) se llama antiderivada de la función F(X), si la derivada F(X) es igual a F(X), o, lo que es lo mismo, diferencial F(X) es igual F(X) dx, es decir.

(2)

Por tanto, la función es una primitiva de la función. Sin embargo, no es la única antiderivada de . También cumplen funciones

Dónde CON- Constante arbitraria. Esto se puede verificar mediante diferenciación.

Por lo tanto, si hay una primitiva para una función, entonces para ella hay un número infinito de primitivas que difieren en un término constante. Todas las primitivas de una función se escriben en la forma anterior. Esto se desprende del siguiente teorema.

Teorema (declaración formal de hecho 2). Si F(X) – antiderivada de la función F(X) en algún intervalo X, entonces cualquier otra antiderivada para F(X) en el mismo intervalo se puede representar en la forma F(X) + C, Dónde CON- Constante arbitraria.

En el siguiente ejemplo, pasamos a la tabla de integrales, que se dará en el párrafo 3, después de las propiedades de la integral indefinida. Hacemos esto antes de leer toda la tabla para que quede clara la esencia de lo anterior. Y después de la tabla y las propiedades, las usaremos en su totalidad durante la integración.

Ejemplo 2. Encuentre conjuntos de funciones antiderivadas:

Solución. Encontramos conjuntos de funciones antiderivadas a partir de las cuales se “hacen” estas funciones. Cuando mencione fórmulas de la tabla de integrales, por ahora simplemente acepte que existen tales fórmulas y estudiaremos la tabla de integrales indefinidas un poco más.

1) Aplicando la fórmula (7) de la tabla de integrales para norte= 3, obtenemos

2) Usando la fórmula (10) de la tabla de integrales para norte= 1/3, tenemos

3) Desde

luego de acuerdo con la fórmula (7) con norte= -1/4 encontramos

No es la función en sí la que está escrita bajo el signo integral. F, y su producto por el diferencial dx. Esto se hace principalmente para indicar con qué variable se busca la antiderivada. Por ejemplo,

, ;

aquí en ambos casos el integrando es igual a , pero sus integrales indefinidas en los casos considerados resultan diferentes. En el primer caso, esta función se considera como función de la variable X, y en el segundo - en función de z .

El proceso de encontrar la integral indefinida de una función se llama integrar esa función.

Significado geométrico de la integral indefinida.

Supongamos que necesitamos encontrar una curva y=F(x) y ya sabemos que la tangente del ángulo tangente en cada uno de sus puntos es una función dada f(x) abscisa de este punto.

Según el significado geométrico de la derivada, la tangente del ángulo de inclinación de la tangente en un punto dado de la curva. y=F(x) igual al valor de la derivada F"(x). Entonces necesitamos encontrar tal función. F(x), para cual F"(x)=f(x). Función requerida en la tarea. F(x) es una antiderivada de f(x). Las condiciones del problema no se satisfacen con una curva, sino con una familia de curvas. y=F(x)- una de estas curvas, y cualquier otra curva se puede obtener a partir de ella mediante traslación paralela a lo largo del eje Oye.

Llamemos a la gráfica de la función antiderivada de f(x) curva integral. Si F"(x)=f(x), entonces la gráfica de la función y=F(x) hay una curva integral.

Hecho 3. La integral indefinida está representada geométricamente por la familia de todas las curvas integrales. , como en la imagen de abajo. La distancia de cada curva desde el origen de coordenadas está determinada por una constante de integración arbitraria. C.

Propiedades de la integral indefinida

Hecho 4. Teorema 1. La derivada de una integral indefinida es igual al integrando y su diferencial es igual al integrando.

Hecho 5. Teorema 2. Integral indefinida del diferencial de una función F(X) es igual a la función F(X) hasta un término constante , es decir.

(3)

Los teoremas 1 y 2 muestran que la diferenciación y la integración son operaciones mutuamente inversas.

Hecho 6. Teorema 3. El factor constante en el integrando se puede sacar del signo de la integral indefinida , es decir.

Deja que la función y = F(X) se define en el intervalo [ a, b ], a < b. Realicemos las siguientes operaciones:

1) dividamos [ a, b] puntos a = X 0 < X 1 < ... < X i- 1 < X i < ... < X norte = b en norte segmentos parciales [ X 0 , X 1 ], [X 1 , X 2 ], ..., [X i- 1 , X i ], ..., [X norte- 1 , X norte ];

2) en cada uno de los segmentos parciales [ X i- 1 , X i ], i = 1, 2, ... norte, elige un punto arbitrario y calcula el valor de la función en este punto: F(z yo ) ;

3) encontrar las obras F(z yo ) · Δ X i , donde es la longitud del segmento parcial [ X i- 1 , X i ], i = 1, 2, ... norte;

4) vamos a hacer las paces suma integral funciones y = F(X) en el segmento [ a, b ]:

Desde un punto de vista geométrico, esta suma σ es la suma de las áreas de rectángulos cuyas bases son segmentos parciales [ X 0 , X 1 ], [X 1 , X 2 ], ..., [X i- 1 , X i ], ..., [X norte- 1 , X norte ], y las alturas son iguales F(z 1 ) , F(z 2 ), ..., F(zn) en consecuencia (Fig. 1). Denotemos por λ longitud del segmento parcial más largo:

5) encontrar el límite de la suma integral cuando λ → 0.

Definición. Si existe un límite finito de la suma integral (1) y no depende del método de partición del segmento [ a, b] a segmentos parciales, ni de la selección de puntos z yo en ellos, entonces este límite se llama integral definida de la función y = F(X) en el segmento [ a, b] y se denota

De este modo,

En este caso la función F(X) se llama integrable en [ a, b]. Números a Y b se denominan límites inferior y superior de integración, respectivamente, F(X) – función integrando, F(X ) dx– expresión integrando, X– variable de integración; segmento de línea [ a, b] se llama intervalo de integración.

Teorema 1. Si la función y = F(X) es continua en el intervalo [ a, b], entonces es integrable en este intervalo.

La integral definida con los mismos límites de integración es igual a cero:

Si a > b, entonces, por definición, asumimos

2. Significado geométrico de la integral definida

Dejemos en el segmento [ a, b] se especifica una función continua no negativa y = F(X ) . trapezoide curvilíneo es una figura acotada arriba por la gráfica de una función y = F(X), desde abajo - a lo largo del eje Buey, hacia la izquierda y hacia la derecha - líneas rectas x = un Y x = segundo(Figura 2).

Integral definida de una función no negativa y = F(X) desde un punto de vista geométrico es igual al área de un trapecio curvilíneo acotado arriba por la gráfica de la función y = F(X), izquierda y derecha – segmentos de línea x = un Y x = segundo, desde abajo: un segmento del eje Buey.

3. Propiedades básicas de la integral definida

1. El valor de la integral definida no depende de la designación de la variable de integración:

2. El factor constante se puede sacar del signo de la integral definida:

3. La integral definida de la suma algebraica de dos funciones es igual a la suma algebraica de las integrales definidas de estas funciones:

4.Si funciona y = F(X) es integrable en [ a, b] Y a < b < C, Eso

5. (teorema del valor medio). Si la función y = F(X) es continua en el intervalo [ a, b], entonces en este segmento hay un punto tal que

4. Fórmula de Newton-Leibniz

Teorema 2. Si la función y = F(X) es continua en el intervalo [ a, b] Y F(X) es cualquiera de sus antiderivadas en este segmento, entonces es válida la siguiente fórmula:

Lo que es llamado Fórmula de Newton-Leibniz. Diferencia F(b) - F(a) generalmente se escribe de la siguiente manera:

donde el símbolo se llama doble comodín.

Por tanto, la fórmula (2) se puede escribir como:

Ejemplo 1. calcular integrales

Solución. Para el integrando F(X ) = X 2 una antiderivada arbitraria tiene la forma

Dado que en la fórmula de Newton-Leibniz se puede utilizar cualquier antiderivada, para calcular la integral tomamos la antiderivada que tenga la forma más simple:

5. Cambio de variable en una integral definida

Teorema 3. Deja que la función y = F(X) es continua en el intervalo [ a, b]. Si:

1) función X = φ ( t) y su derivada φ "( t) son continuos para ;

2) un conjunto de valores de función X = φ ( t) para es el segmento [ a, b ];

3) φ ( a) = a, φ ( b) = b, entonces la fórmula es válida

Lo que es llamado fórmula para cambiar una variable en una integral definida .

A diferencia de la integral indefinida, en este caso no es necesario para volver a la variable de integración original, basta con encontrar nuevos límites de integración α y β (para ello es necesario resolver la variable t ecuaciones φ ( t) = a y φ ( t) = b).

En lugar de sustitución X = φ ( t) puedes usar la sustitución t = gramo(X). En este caso, encontrar nuevos límites de integración sobre una variable t simplifica: α = gramo(a) , β = gramo(b) .

Ejemplo 2. calcular integrales

Solución. Introduzcamos una nueva variable usando la fórmula. Al elevar al cuadrado ambos lados de la igualdad obtenemos 1 + x = t 2 , dónde x = t 2 - 1, dx = (t 2 - 1)"dt= 2tdt. Encontramos nuevos límites de integración. Para hacer esto, sustituyamos los viejos límites en la fórmula x = 3 y x = 8. Obtenemos: , de donde t= 2 y α = 2; , dónde t= 3 y β = 3. Entonces,

Ejemplo 3. Calcular

Solución. Dejar tu= iniciar sesión X, Entonces , v = X. Según la fórmula (4)