Cómo entender la proporción 1 a 3. Razones

base La investigación matemática es la capacidad de obtener conocimiento sobre ciertas cantidades comparándolas con otras cantidades que son igual, o más o menos que los que son objeto de estudio. Esto generalmente se hace con una serie ecuaciones Y dimensiones. Cuando usamos ecuaciones, determinamos la cantidad que buscamos encontrándola igualdad con alguna otra cantidad o cantidades ya familiares.

Sin embargo, a menudo sucede que estamos comparando una cantidad desconocida con otras que no es igual ella, pero más o menos de ella. Aquí necesitamos un enfoque diferente para el procesamiento de datos. Es posible que necesitemos saber, por ejemplo, cuánto un valor es mayor que el otro, o cuantas veces uno contiene al otro. Para encontrar respuestas a estas preguntas, averiguaremos qué es proporción dos tamaños Una proporción se llama aritmética, y otro geométrico. Aunque vale la pena señalar que ambos términos no fueron adoptados por casualidad o solo por el bien de la distinción. Tanto las relaciones aritméticas como las geométricas se aplican tanto a la aritmética como a la geometría.

Al ser un componente de un tema amplio e importante, la proporción depende de razones, por lo que es necesaria una comprensión clara y completa de estos conceptos.

338. proporción aritmética esta diferenciaentre dos cantidades o una serie de cantidades. Las cantidades mismas se llaman miembros razones, es decir, términos entre los cuales existe una razón. Así, 2 es la razón aritmética de 5 y 3. Esto se expresa colocando un signo menos entre los dos valores, es decir, 5 - 3. Por supuesto, el término razón aritmética y su desglose es prácticamente inútil, ya que solo se reemplaza la palabra diferencia al signo menos en la expresión.

339. Si ambos miembros de una relación aritmética multiplicar o dividir por la misma cantidad entonces proporción, eventualmente se multiplicará o dividirá por esa cantidad.
Así, si tenemos a - b = r
Luego multiplique ambos lados por h , (Ax. 3.) ha - hb = hr
Y dividiendo por h, (Ax. 4.) $\frac(a)(h)-\frac(b)(h)=\frac(r)(h)$

340. Si los términos de una razón aritmética se suman o restan a los términos correspondientes de otra, entonces la razón de la suma o diferencia será igual a la suma o diferencia de las dos razones.
Si a-b
Y dh
son dos proporciones,
Entonces (a + d) - (b + h) = (a - b) + (d - h). Que en cada caso = a + d - b - h.
Y (a - d) - (b - h) = (a - b) - (d - h). Que en cada caso = a - d - b + h.
Entonces la razón aritmética de 11 - 4 es 7
Y la razón aritmética 5 - 2 es 3
La razón de la suma de los términos 16 - 6 es 10, - la suma de las razones.
La relación de la diferencia de los miembros 6 - 2 es 4, - la diferencia de proporciones.

341. proporción geométrica es la relación entre cantidades, que se expresa PRIVADO si un valor se divide por otro.
Entonces, la razón de 8 a 4 se puede escribir como 8/4 o 2. Es decir, el cociente de 8 dividido por 4. En otras palabras, muestra cuántas veces 4 está contenido en 8.

Del mismo modo, la razón de cualquier cantidad a otra puede determinarse dividiendo la primera por la segunda, o, lo que es básicamente lo mismo, haciendo que la primera sea el numerador de la fracción y la segunda el denominador.
Entonces la razón de a a b es $\frac(a)(b)$
La razón de d + h a b + c es $\frac(d+h)(b+c)$.

342. La razón geométrica también se escribe colocando dos puntos uno encima del otro entre los valores comparados.
Así a:b es la razón de a a b, y 12:4 es la razón de 12 a 4. Las dos cantidades juntas forman Pareja, en el que el primer término se llama antecedente, y el último es consecuente.

343. Esta notación punteada y la otra, en forma de fracción, son intercambiables según sea necesario, siendo el antecedente el numerador de la fracción y el consecuente el denominador.
Entonces 10:5 es lo mismo que $\frac(10)(5)$ y b:d es lo mismo que $\frac(b)(d)$.

344. Si cualquiera de estos tres significados: antecedente, consecuente y relación se les da alguna dos, entonces se puede encontrar el tercero.

Sea a= antecedente, c= consecuente, r= relación.
Por definición, $r=\frac(a)(c)$, es decir, la razón es igual al antecedente dividido por el consecuente.
Multiplicando por c, a = cr, es decir, el antecedente es igual al consecuente por la razón.
Divide por r, $c=\frac(a)(r)$, es decir, el consecuente es igual al antecedente dividido por la razón.

resp. 1. Si dos pares tienen antecedentes y consecuentes iguales, entonces sus proporciones también son iguales.

resp. 2. Si las razones y los antecedentes de dos pares son iguales, entonces las consecuencias son iguales, y si las razones y las consecuencias son iguales, entonces los antecedentes son iguales.

345. Si dos cantidades comparadas igual, entonces su razón es igual a la unidad o la igualdad. La razón 3 * 6:18 es igual a uno, ya que el cociente de cualquier valor dividido por sí mismo es igual a 1.

Si el antecedente de la pareja más, que el consecuente, entonces la razón es mayor que uno. Como el dividendo es mayor que el divisor, el cociente es mayor que uno. Así que la razón de 18:6 es 3. Esto se llama la razón mayor desigualdad.

Por el contrario, si el antecedente menos que el consecuente, entonces la razón es menor que uno, y esto se llama la razón menos desigualdad. Entonces la razón 2:3 es menor que uno, porque el dividendo es menor que el divisor.

346. Contrarrestar razón es la razón de dos recíprocos.
Entonces la razón del inverso de 6 a 3 es a, es decir:.
La relación directa de a con b es $\frac(a)(b)$, es decir, el antecedente dividido por el consecuente.
La relación inversa es $\frac(1)(a)$:$\frac(1)(b)$ o $\frac(1)(a).\frac(b)(1)=\frac(b) (a)$.
es decir, la cosecuencia b dividida por el antecedente a.

Por lo tanto, la relación inversa se expresa invirtiendo una fracción, que muestra una relación directa, o, cuando la notación se hace usando puntos, invertir el orden de los miembros de escritura.
Así, a se relaciona con b de manera opuesta a como b se relaciona con a.

347. Relación compleja esta proporción obras términos correspondientes con dos o más relaciones simples.
Entonces la razón es 6:3, igual a 2
y proporción 12:4 es igual a 3
La razón formada por ellos es 72:12 = 6.

Aquí se obtiene una relación compleja multiplicando dos antecedentes y también dos consecuentes de relaciones simples.
Entonces la razón está compuesta
De la relación a:b
Y proporciones c:d
y la relación h:y
Esta es la razón $ach:bdy=\frac(ach)(bdy)$.
Una relación compleja no difiere en su naturaleza de cualquier otra proporción. Este término se usa para mostrar el origen de una relación en ciertos casos.

resp. Una razón compleja es igual al producto de razones simples.
La razón a:b es igual a $\frac(a)(b)$
La razón c:d es igual a $\frac(c)(d)$
La razón h:y es igual a $\frac(h)(y)$
Y la razón sumada de estos tres será ach/bdy, que es el producto de fracciones que expresan razones simples.

348. Si en la sucesión de relaciones en cada par anterior el consecuente es el antecedente en el siguiente, entonces la razón del primer antecedente y el último consecuente es igual a la que se obtiene de las razones intermedias.
Así que en varias proporciones
a:b
antes de Cristo
discos compactos
d: h
la relación a:h es igual a la relación sumada de las relaciones a:b y b:c y c:d y d:h. Así que la relación compleja del último artículo es $\frac(abcd)(bcdh)=\frac(a)(h)$, o a:h.

De la misma manera, todas las cantidades que son a la vez antecedentes y consecuentes desaparecer, cuando el producto de fracciones se simplificará a sus términos inferiores y en el resto la relación compleja se expresará por el primer antecedente y el último consecuente.

349. Una clase especial de relaciones complejas se obtiene multiplicando una relación simple por él mismo o a otro igual proporción. Estas proporciones se llaman doble, triple, cuadruplicar, y así sucesivamente, según el número de multiplicaciones.

proporción compuesta por dos proporciones iguales, es decir, cuadrado doble proporción.

Compuestos de Tres, es decir, cubo razón simple se llama triple, etc

Del mismo modo, la proporción raíces cuadradas dos cantidades se llama razón raíz cuadrada, y la relación raíces cúbicas- proporción raíz cúbica, etc
Entonces la razón simple de a a b es a:b
La doble razón de a a b es a 2:b 2
La razón triple de a a b es a 3:b 3
La razón de la raíz cuadrada de a a b es √a :√b
La razón de la raíz cúbica de a a b es 3 √a : 3 √b , y así sucesivamente.
Condiciones doble, triple, y así sucesivamente no necesitan ser mezclados con duplicado, triplicado, etc
La razón de 6 a 2 es 6:2 = 3
Si duplicamos esta razón, es decir, la razón dos veces, obtenemos 12:2 = 6
Triplicamos esta razón, es decir, esta razón tres veces, obtenemos 18: 2 = 9
PERO doble proporción, es decir cuadrado la razón es 6 2:2 2 = 9
Y triple la razón, es decir, el cubo de la razón, es 6 3:2 3 = 27

Art. 350. Para que las cantidades sean correlativas entre sí, deben ser de la misma especie, de manera que se pueda afirmar con certeza si son iguales entre sí, o si una de ellas es mayor o menor. Un pie es a una pulgada como 12 a 1: es 12 veces más grande que una pulgada. Pero uno no puede, por ejemplo, decir que una hora es más larga o más corta que un palo, o que un acre es más o menos que un grado. Sin embargo, si estos valores se expresan en números, entonces puede haber una relación entre estos números. Es decir, puede haber una relación entre la cantidad de minutos en una hora y la cantidad de pasos en una milla.

351. Dirigiéndose a naturaleza proporciones, el siguiente paso que debemos tener en cuenta es cómo el cambio en uno o dos términos que se comparan entre sí afectará la proporción misma. Recuerda que una razón directa se expresa como una fracción, donde antecedente las parejas son siempre numerador, pero consiguiente - denominador. Entonces será fácil obtener de la propiedad de las fracciones que los cambios en la razón ocurren al variar las cantidades comparadas. La razón de las dos cantidades es la misma que sentido fracciones, cada una de las cuales representa privado: el numerador dividido por el denominador. (Art. 341.) Ahora se ha demostrado que multiplicar el numerador de una fracción por cualquier valor es lo mismo que multiplicar sentido por la misma cantidad y que dividir el numerador es lo mismo que dividir los valores de una fracción. Es por eso,

352. Multiplicar el antecedente de un par por cualquier valor significa multiplicar las razones por este valor, y dividir el antecedente es dividir esta razón.
Entonces la relación 6:2 es 3
Y la relación 24:2 es 12.
Aquí el antecedente y la razón en el último par son 4 veces mayores que en el primero.
La relación a:b es igual a $\frac(a)(b)$
Y la relación na:b es igual a $\frac(na)(b)$.

resp. Con un consecuente conocido, cuanto más antecedente, cuanto más proporción, y viceversa, cuanto mayor sea la razón, mayor será el antecedente.

353. Multiplicando el consecuente de un par por cualquier valor, como resultado, obtenemos la división de la razón por este valor, y dividiendo el consecuente, multiplicamos la razón. Al multiplicar el denominador de una fracción, dividimos el valor, y al dividir el denominador, el valor se multiplica.
Entonces la razón de 12:2 es 6
Y la relación 12:4 es 3.
Aquí está el consecuente del segundo par en dos veces más, pero la proporción dos veces menos que el primero.
La razón a:b es $\frac(a)(b)$
Y la razón a:nb es igual a $\frac(a)(nb)$.

resp. Para un antecedente dado, cuanto mayor sea el consecuente, menor será la razón. Por el contrario, cuanto mayor sea la relación, menor será el consecuente.

354. De los dos últimos artículos se sigue que antecedente de multiplicación pares por cualquier valor tendrá el mismo efecto en la razón que división del consecuente por esta cantidad y división antecedente, tendrá el mismo efecto que multiplicación consecuente.
Entonces la relación 8:4 es 2
Multiplicando el antecedente por 2, la relación 16:4 es 4
Dividiendo el antecedente por 2, la razón 8:2 es 4.

resp. Ninguna factor o divisor puede transferirse del antecedente de un par al consecuente, o del consecuente al antecedente, sin cambiar la relación.

Vale la pena señalar que cuando un factor se transfiere de un término a otro, se convierte en un divisor y el divisor transferido se convierte en un factor.
Entonces la relación es 3.6:9 = 2
Cambiando el factor 3, $6:\frac(9)(3)=2$
la misma proporción.

La relación $\frac(ma)(y):b=\frac(ma)(by)$
Moviendo y $ma:by=\frac(ma)(by)$
Moviendo m, a:$a:\frac(m)(by)=\frac(ma)(by)$.

355. Como se desprende de los artículos. 352 y 353, si el antecedente y el consecuente se multiplican o se dividen por la misma cantidad, entonces la razón no cambia.

resp. 1. La razón de dos fracciones, que tienen un denominador común, igual a la razón de sus numeradores.
Por lo tanto, la relación a/n:b/n es la misma que a:b.

resp. 2. directo la razón de dos fracciones que tienen un numerador común es igual a su razón recíproca denominadores.

356. Es fácil determinar la proporción de dos fracciones cualesquiera del artículo. Si cada término se multiplica por dos denominadores, entonces la razón estará dada por expresiones integrales. Así, multiplicando los términos del par a/b:c/d por bd, obtenemos $\frac(abd)(b)$:$\frac(bcd)(d)$, que se convierte en ad:bc, al reducir los valores totales de los numeradores y denominadores.

356 b. Proporción mayor desigualdad aumenta su
Deje que la mayor relación de desigualdad se dé como 1 + n: 1
y cualquier proporción a:b
Una razón compleja será (Art. 347,) a + na:b
¿Qué es mayor que la relación a:b (Art. 351 resp.)
Pero la proporción menos desigualdad, sumado con otra proporción, reduce su.
Sea la razón de la diferencia más pequeña 1-n:1
Cualquier proporción dada a:b
Razón compleja a - na:b
Cuanto es menor que a:b.

357. Si hacia o desde miembros de cualquier parejaagregar o restar otras dos cantidades que están en la misma razón, entonces las sumas o residuos tendrán la misma razón.
Sea la razón a:b
Será lo mismo que c:d
Entonces la relación montos antecedentes a la suma de los consecuentes, es decir, a + c a b + d, es también lo mismo.
Es decir, $\frac(a+c)(b+d)$ = $\frac(c)(d)$ = $\frac(a)(b)$.

Prueba.

1. Por suposición, $\frac(a)(b)$ = $\frac(c)(d)$
2. Multiplicar por b y por d, ad = bc
3. Agregue cd a ambos lados, ad + cd = bc + cd
4. Divida por d, $a+c=\frac(bc+cd)(d)$
5. Divide entre b + d, $\frac(a+c)(b+d)$ = $\frac(c)(d)$ = $\frac(a)(b)$.

Proporción diferencia los antecedentes a la diferencia de los consecuentes son también lo mismo.

358. Si las proporciones en varios pares son iguales, entonces la suma de todos los antecedentes es a la suma de todos los consecuentes como cualquier antecedente es a su consecuente.
Así la proporción
|12:6 = 2
|10:5 = 2
|8:4 = 2
|6:3 = 2
Así la razón (12 + 10 + 8 + 6): (6 + 5 + 4 + 3) = 2.

358b. Proporción mayor desigualdaddisminuye, agregando la misma cantidad a ambos miembros.
Sea una relación dada a+b:a o $\frac(a+b)(a)$
Al sumar x a ambos términos, obtenemos a+b+x:a+x o $\frac(a+b)(a)$.

El primero se convierte en $\frac(a^2+ab+ax+bx)(a(a+x))$
Y el último es $\frac(a^2+ab+ax)(a(a+x))$.
Como el último numerador es obviamente menor que el otro, entonces proporción debería ser menos. (Art. 351 resp.)

Pero la proporción menos desigualdad aumenta, sumando el mismo valor a ambos términos.
Sea la relación dada (a-b):a, o $\frac(a-b)(a)$.
Al sumar x a ambos términos, se convierte en (a-b+x):(a+x) o $\frac(a-b+x)(a+x)$
Llevándolos a un denominador común,
El primero se convierte en $\frac(a^2-ab+ax-bx)(a(a+x))$
Y el último, $\frac(a^2-ab+ax)(a(a+x)).\frac((a^2-ab+ax))(a(a+x))$.

Como el último numerador es mayor que el otro, entonces proporción más.
Si en lugar de sumar el mismo valor quitar a partir de dos términos, es obvio que el efecto sobre la razón será el contrario.

Ejemplos.

1. ¿Cuál es más grande: una proporción de 11:9 o una proporción de 44:35?

2. ¿Cuál es mayor: la razón $(a+3):\frac(a)(6)$, o la razón $(2a+7):\frac(a)(3)$?

3. Si el antecedente de un par es 65 y la razón es 13, ¿cuál es el consecuente?

4. Si el consecuente de un par es 7 y la razón es 18, ¿cuál es el antecedente?

5. ¿Cómo se ve una razón compleja formada por 8:7 y 2a:5b, y también (7x+1):(3y-2)?

6. ¿Cómo es una razón compleja compuesta por (x + y): b, y (x-y): (a + b), y también (a + b): h? Reps. (x 2 - y 2):bh.

7. Si las relaciones (5x+7):(2x-3), y $(x+2):\left(\frac(x)(2)+3\right)$ forman una relación compleja, entonces, ¿qué relación obtendrá: más o menos desigualdad? Reps. La razón de mayor desigualdad.

8. ¿Cuál es la razón formada por (x + y):ay (x - y):b, y $b:\frac(x^2-y^2)(a)$? Reps. Relación de igualdad.

9. ¿Cuál es la razón de 7:5 y el doble de 4:9 y el triple de 3:2?
Reps. 14:15.

10. ¿Cuál es la razón formada por 3:7, y el triple de la razón x:y, y sacando la raíz de la razón 49:9?
Reps. x3:y3.

Fórmula de proporción

La proporción es la igualdad de dos razones cuando a:b=c:d

relación 1 : 10 es igual a la razón de 7 : 70, que también se puede escribir como una fracción: 1 10 = 7 70 dice: "uno es a diez como siete es a setenta"

Propiedades básicas de la proporción

El producto de los términos extremos es igual al producto de los términos medios (en cruz): si a:b=c:d , entonces a⋅d=b⋅c

1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7

Inversión de proporciones: si a:b=c:d , entonces b:a=d:c

1 10 7 70 10 1 = 70 7

Permutación de miembros intermedios: si a:b=c:d , entonces a:c=b:d

1 10 7 70 1 7 = 10 70

Permutación de miembros extremos: si a:b=c:d , entonces d:b=c:a

1 10 7 70 70 10 = 7 1

Resolver una proporción con una incógnita | La ecuacion

1 : 10 = X : 70 o 1 10 = X 70

Para encontrar x, necesitas multiplicar dos números conocidos en forma cruzada y dividir por el valor opuesto

X = 1 ⋅ 70 10 = 7

Cómo calcular la proporción

Una tarea: necesitas beber 1 tableta de carbón activado por cada 10 kilogramos de peso. ¿Cuántas tabletas se deben tomar si una persona pesa 70 kg?

Hagamos una proporción: 1 tableta - 10 kg X tabletas - 70 kg Para encontrar x, debe multiplicar dos números conocidos en forma cruzada y dividir por el valor opuesto: 1 tableta X tabletas✕ 10kg 70 kg X = 1 ⋅ 70 : 10 = 7 Responder: 7 tabletas

Una tarea: Vasya escribe dos artículos en cinco horas. ¿Cuántos artículos escribirá en 20 horas?

Hagamos una proporción: 2 artículos - 5 horas X artículos - 20 horas X = 2 ⋅ 20 : 5 = 8 Responder: 8 artículos

Puedo decirles a los futuros graduados de la escuela que la capacidad de hacer proporciones me fue útil tanto para reducir proporcionalmente las imágenes como en el diseño HTML de una página web y en situaciones cotidianas.

Una relación es una cierta relación entre las entidades de nuestro mundo. Estos pueden ser números, cantidades físicas, objetos, productos, fenómenos, acciones e incluso personas.

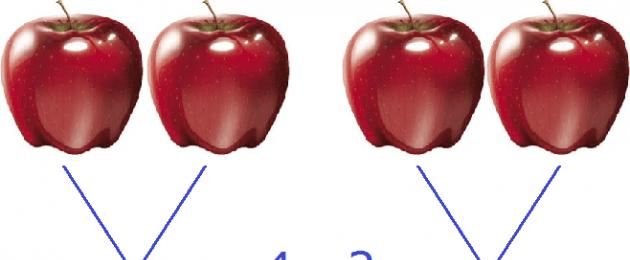
En la vida cotidiana, cuando se trata de proporciones, decimos "proporción de esto y aquello". Por ejemplo, si hay 4 manzanas y 2 peras en un florero, entonces decimos proporción de manzana a pera proporción de pera a manzana.

En matemáticas, la razón se usa a menudo como "la relación de algo con algo". Por ejemplo, la proporción de cuatro manzanas y dos peras, que consideramos anteriormente, en matemáticas se leerá como "la proporción de cuatro manzanas a dos peras" o si intercambias manzanas y peras, entonces "la proporción de dos peras a cuatro manzanas".

La relación se expresa como a para B(donde en lugar de a Y B cualquier número), pero más a menudo puede encontrar una entrada que se compone usando dos puntos como a:b. Puedes leer esta entrada de varias formas:

a para B
a se refiere a B
actitud a para B

Escribimos la razón de cuatro manzanas y dos peras usando el símbolo de razón:

4: 2

Si intercambiamos manzanas y peras, tendremos una proporción de 2: 4. Esta relación se puede leer como "dos a cuatro" o cualquiera "Dos peras equivalen a cuatro manzanas" .

En lo que sigue, nos referiremos a la relación como una relación.

Contenido de la lección

¿Qué es una actitud?

La relación, como se mencionó anteriormente, se escribe como a:b. También se puede escribir como una fracción. Y sabemos que tal registro en matemáticas significa división. Entonces el resultado de la relación será el cociente de números a Y B.

En matemáticas, una razón es el cociente de dos números.

La razón te permite averiguar cuánto de una entidad hay por unidad de otra. Volvamos a la proporción de cuatro manzanas por dos peras (4:2). Esta razón nos permitirá saber cuántas manzanas hay por unidad de pera. Una unidad significa una pera. Primero, escribamos la razón 4:2 como una fracción:

Esta razón es la división del número 4 por el número 2. Si realizamos esta división, obtendremos la respuesta a la pregunta de cuántas manzanas hay por unidad de pera.

Obtuvimos 2. Entonces, cuatro manzanas y dos peras (4: 2) están correlacionadas (interconectadas entre sí) de modo que hay dos manzanas por pera.

La figura muestra cómo cuatro manzanas y dos peras se relacionan entre sí. Se puede ver que hay dos manzanas por cada pera.

La relación se puede invertir escribiendo como . Luego obtenemos la proporción de dos peras y cuatro manzanas, o "la proporción de dos peras a cuatro manzanas". Esta razón mostrará cuántas peras hay por unidad de manzana. La unidad de una manzana significa una manzana.

Para encontrar el valor de una fracción, debes recordar cómo dividir un número más pequeño por uno más grande.

Obtuve 0.5. Convirtamos esta fracción decimal en una ordinaria:

Reducir la fracción ordinaria resultante por 5

Obtuve una respuesta (media pera). Entonces, dos peras y cuatro manzanas (2: 4) están correlacionadas (interrelacionadas entre sí) de modo que una manzana representa la mitad de una pera.

La figura muestra cómo se relacionan entre sí dos peras y cuatro manzanas. Se puede ver que por cada manzana hay media pera.

Los números que forman una relación se llaman miembros de la relación. Por ejemplo, en la relación 4:2, los miembros son los números 4 y 2.

Considere otros ejemplos de relaciones. Una receta se hace para preparar algo. La receta se construye a partir de las proporciones entre los productos. Por ejemplo, hacer avena generalmente requiere un vaso de cereal por dos vasos de leche o agua. Esto da como resultado una proporción de 1:2 ("uno a dos" o "un vaso de cereal por dos vasos de leche").

Convirtamos la razón 1:2 en una fracción, obtenemos. Calculando esta fracción, obtenemos 0,5. Entonces, un vaso de cereal y dos vasos de leche están correlacionados (correlacionados) de modo que hay medio vaso de cereal para un vaso de leche.

Si cambias la proporción 1:2, obtienes una proporción 2:1 ("dos a uno" o "dos vasos de leche por un vaso de cereal"). Convirtiendo la relación 2:1 a una fracción, obtenemos. Calculando esta fracción, obtenemos 2. Entonces, dos vasos de leche y un vaso de cereal están relacionados (correlacionados entre sí) de modo que hay dos vasos de leche por un vaso de cereal.

Ejemplo 2 Hay 15 estudiantes en la clase. De estos, 5 son niños, 10 son niñas. Es posible escribir una proporción de niñas a niños de 10:5 y convertir esta proporción en una fracción. Calculando esta fracción, obtenemos 2. Es decir, las niñas y los niños están relacionados entre sí de modo que por cada niño hay dos niñas.

La figura muestra cómo diez niñas y cinco niños se relacionan entre sí. Se puede ver que por cada niño hay dos niñas.

No siempre es posible convertir una razón en una fracción y encontrar un cociente. En algunos casos será ilógico.

Entonces, si le das la vuelta a la proporción, esta es la proporción entre niños y niñas. Si calculas esta fracción, obtienes 0,5. Resulta que cinco niños están relacionados con diez niñas de tal manera que por cada niña hay medio niño. Matemáticamente, esto es cierto, por supuesto, pero desde el punto de vista de la realidad, no es del todo razonable, porque un niño es una persona viva y no se puede tomar y dividir como una pera o una manzana.

La capacidad de construir la actitud correcta es una habilidad importante en la resolución de problemas. Entonces, en física, la relación entre la distancia recorrida y el tiempo es la velocidad del movimiento.

La distancia se denota por la variable S, tiempo - a través de una variable t, velocidad - a través de la variable v. Entonces la frase "la relación entre la distancia recorrida y el tiempo es la velocidad del movimiento" será descrita por la siguiente expresión:

Supongamos que un automóvil recorre 100 kilómetros en 2 horas. Entonces la razón de 100 kilómetros recorridos a 2 horas será la velocidad del carro:

La velocidad es la distancia recorrida por un cuerpo por unidad de tiempo. La unidad de tiempo es 1 hora, 1 minuto o 1 segundo. Y la razón, como se mencionó anteriormente, te permite saber cuánto hay de una entidad por unidad de otra. En nuestro ejemplo, la relación de cien kilómetros a dos horas muestra cuántos kilómetros hay para una hora de movimiento. Vemos que por cada hora de movimiento hay 50 kilómetros

Entonces la velocidad se mide en km/h, m/min, m/s. El símbolo de fracción (/) indica la relación entre la distancia y el tiempo: Kilómetros por hora , metros por minuto Y metros por segundo respectivamente.

Ejemplo 2. La relación entre el valor de una mercancía y su cantidad es el precio de una unidad de la mercancía.

Si tomamos 5 barras de chocolate en la tienda y su costo total fue de 100 rublos, entonces podemos determinar el precio de una barra. Para hacer esto, debe encontrar la proporción de cien rublos por la cantidad de barras. Entonces obtenemos que una barra representa 20 rublos.

Comparación de valores

Anteriormente aprendimos que la razón entre cantidades de distinta naturaleza forman una nueva cantidad. Por lo tanto, la relación entre la distancia recorrida y el tiempo es la velocidad de movimiento. La relación entre el valor de una mercancía y su cantidad es el precio de una unidad de la mercancía.

Pero la razón también se puede usar para comparar valores. El resultado de tal relación es un número que muestra cuántas veces el primer valor es mayor que el segundo, o qué parte del segundo es el primer valor.

Para saber cuántas veces el primer valor es mayor que el segundo, debes escribir un valor mayor en el numerador de la razón y un valor menor en el denominador.

Para saber qué parte es el primer valor del segundo, debes escribir un valor más pequeño en el numerador de la razón y un valor más grande en el denominador.

Considera los números 20 y 2. Averigüemos cuántas veces el número 20 es mayor que el número 2. Para hacer esto, encontramos la razón del número 20 al número 2. Escribe el número 20 en el numerador de la razón. , y el número 2 en el denominador

El valor de esta razón es diez

La razón del número 20 al número 2 es el número 10. Este número muestra cuántas veces el número 20 es mayor que el número 2. Entonces, el número 20 es diez veces mayor que el número 2.

Ejemplo 2 Hay 15 estudiantes en la clase. 5 de ellos son niños, 10 son niñas. Determina cuántas veces hay más niñas que niños.

Escriba la actitud de las niñas hacia los niños. En el numerador de la razón escribimos el número de niñas, en el denominador de la razón, el número de niños:

El valor de esta razón es 2. Significa que en una clase de 15 hay el doble de niñas que de niños.

Ya no existe la cuestión de cuántas niñas hay para un niño. En este caso, la razón se usa para comparar el número de niñas con el número de niños.

Ejemplo 3. ¿Qué parte del número 2 es del número 20?

Encontramos la relación del número 2 al número 20. En el numerador de la relación escribimos el número 2, y en el denominador, el número 20

Para encontrar el significado de esta relación, es necesario recordar,

El valor de la razón del número 2 al número 20 es el número 0.1

En este caso, la fracción decimal 0.1 se puede convertir en una ordinaria. Esta respuesta será más fácil de entender:

Entonces el número 2 del número 20 es una décima.

Puedes hacer un cheque. Para hacer esto, encontraremos desde el número 20. Si hicimos todo correctamente, deberíamos obtener el número 2

20: 10 = 2

2x1 = 2

Obtuvimos el número 2. Entonces, una décima parte del número 20 es el número 2. De esto concluimos que el problema se resolvió correctamente.

Ejemplo 4 Hay 15 personas en la clase. 5 de ellos son niños, 10 son niñas. Determine qué proporción del número total de estudiantes son niños.

Anotamos la proporción de niños entre el número total de estudiantes. Escribimos cinco niños en el numerador de la razón y el número total de escolares en el denominador. El número total de escolares es de 5 niños más 10 niñas, por lo que escribimos el número 15 en el denominador de la razón

Para encontrar el valor de esta razón, debes recordar cómo dividir un número más pequeño por uno más grande. En este caso, el número 5 debe dividirse por el número 15

Cuando divides 5 por 15, obtienes una fracción periódica. Convirtamos esta fracción en ordinaria

Obtuve la respuesta final. Así que los chicos constituyen un tercio de toda la clase.

La figura muestra que en una clase de 15 estudiantes, un tercio de la clase son 5 niños.

Si para la verificación encontramos de 15 escolares, obtendremos 5 niños

15: 3 = 5

5x1 = 5

Ejemplo 5¿Cuántas veces el número 35 es mayor que el número 5?

Escribimos la relación del número 35 al número 5. En el numerador de la relación, debe escribir el número 35, en el denominador, el número 5, pero no al revés.

El valor de esta razón es 7. Entonces el número 35 es siete veces mayor que el número 5.

Ejemplo 6 Hay 15 personas en la clase. 5 de ellos son niños, 10 son niñas. Determine qué proporción del número total son niñas.

Anotamos la proporción de niñas con respecto al número total de estudiantes. Escribimos diez niñas en el numerador de la razón, y el número total de escolares en el denominador. El número total de escolares es de 5 niños más 10 niñas, por lo que escribimos el número 15 en el denominador de la razón

Para encontrar el valor de esta razón, debes recordar cómo dividir un número más pequeño por uno más grande. En este caso, el número 10 debe dividirse por el número 15

Cuando divides 10 por 15, obtienes una fracción periódica. Convirtamos esta fracción en ordinaria

Reduzcamos la fracción resultante en 3

Obtuve la respuesta final. Entonces, las niñas constituyen dos tercios de toda la clase.

La figura muestra que en una clase de 15 estudiantes, dos tercios de la clase son 10 niñas.

Si para la verificación encontramos de 15 escolares, entonces obtenemos 10 niñas.

15: 3 = 5

5x2 = 10

Ejemplo 7 que parte de 10 cm son 25 cm

Escribe la razón de diez centímetros a veinticinco centímetros. En el numerador de la razón escribimos 10 cm, en el denominador - 25 cm

Para encontrar el valor de esta razón, debes recordar cómo dividir un número más pequeño por uno más grande. En este caso, el número 10 debe dividirse por el número 25

Convirtamos la fracción decimal resultante a una ordinaria

Reduzcamos la fracción resultante en 2

Obtuve la respuesta final. Entonces 10 cm son 25 cm.

Ejemplo 8 Cuantas veces es 25 cm mayor que 10 cm

Escribe la razón de veinticinco centímetros a diez centímetros. En el numerador de la razón escribimos 25 cm, en el denominador - 10 cm

Tengo la respuesta 2.5. Así que 25 cm es 2,5 veces más que 10 cm (dos veces y media)

Nota IMPORTANTE. Al encontrar la razón de las mismas cantidades físicas, estas cantidades deben expresarse en una unidad de medida, de lo contrario, la respuesta será incorrecta.

Por ejemplo, si estamos tratando con dos longitudes y queremos saber cuántas veces la primera longitud es mayor que la segunda, o qué parte de la primera longitud es de la segunda, entonces ambas longitudes deben expresarse primero en una unidad de medida.

Ejemplo 9¿Cuántas veces es 150 cm más que 1 metro?

Primero, asegurémonos de que ambas longitudes estén expresadas en la misma unidad. Para hacer esto, convierte 1 metro a centímetros. un metro son cien centimetros

1 metro = 100 cm

Ahora encontramos la razón de ciento cincuenta centímetros a cien centímetros. En el numerador de la razón escribimos 150 centímetros, en el denominador - 100 centímetros

Encontremos el valor de esta relación.

Tengo la respuesta 1.5. Así que 150 cm es más que 100 cm por 1,5 veces (una vez y media).

Y si no empezáramos a convertir metros en centímetros e inmediatamente tratáramos de encontrar la razón de 150 cm a un metro, obtendríamos lo siguiente:

Resultaría que 150 cm es ciento cincuenta veces más que un metro, pero esto no es cierto. Por lo tanto, es imperativo prestar atención a las unidades de medida de las cantidades físicas que intervienen en la relación. Si estas cantidades se expresan en diferentes unidades de medida, entonces para encontrar la relación de estas cantidades, debe ir a una unidad de medida.

Ejemplo 10 El mes pasado, el salario de una persona era de 25 000 rublos, y este mes el salario aumentó a 27 000 rublos. Determinar cuánto ha aumentado el salario.

Anotamos la razón de veintisiete mil a veinticinco mil. En el numerador de la razón escribimos 27000, en el denominador - 25000

Encontremos el valor de esta relación.

Tengo la respuesta 1.08. Por lo que el salario aumentó en 1,08 veces. En el futuro, cuando nos familiaricemos con los porcentajes, expresaremos indicadores como el salario como porcentaje.

Ejemplo 11. El edificio de apartamentos tiene 80 metros de ancho y 16 metros de alto. ¿Cuántas veces es mayor el ancho de la casa que su altura?

Escribimos la relación entre el ancho de la casa y su altura:

El valor de esta razón es 5. Esto significa que el ancho de la casa es cinco veces su altura.

propiedad de relación

La razón no cambiará si sus términos se multiplican o dividen por el mismo número.

Esta una de las propiedades más importantes de una relación se deriva de la propiedad del cociente. Sabemos que si el dividendo y el divisor se multiplican o dividen por el mismo número, entonces el cociente no cambiará. Y como la razón no es más que una división, la propiedad del cociente también funciona.

Volvamos a la actitud de las niñas hacia los niños (10:5). Esta proporción mostró que por cada niño hay dos niñas. Veamos cómo funciona la propiedad de la relación, es decir, intentemos multiplicar o dividir sus miembros por el mismo número.

En nuestro ejemplo, es más conveniente dividir los términos de la relación por su máximo común divisor (MCD).

MCD de los miembros 10 y 5 es el número 5. Por lo tanto, puedes dividir los términos de la relación por el número 5

Tengo una nueva actitud. Es una proporción de dos a uno (2:1). Esta proporción, como la proporción anterior de 10:5, muestra que hay dos niñas por cada niño.

La figura muestra una proporción de 2:1 (dos a uno). Como en la proporción anterior de 10:5, hay dos niñas por niño. En otras palabras, la actitud no ha cambiado.

Ejemplo 2. Hay 10 niñas y 5 niños en una clase. Hay 20 niñas y 10 niños en otra clase. ¿Cuántas veces hay más niñas que niños en primer grado? ¿Cuántas veces hay más niñas que niños en segundo grado?

Hay el doble de niñas que de niños en ambas clases, ya que las proporciones de y son iguales al mismo número.

La propiedad de relación le permite construir varios modelos que tienen parámetros similares al objeto real. Supongamos que un edificio de apartamentos tiene 30 metros de ancho y 10 metros de alto.

Para dibujar una casa similar en papel, debe dibujarla en la misma proporción de 30:10.

Divide ambos términos de esta razón por el número 10. Entonces obtenemos la razón 3:1. Esta razón es 3, al igual que la razón anterior es 3

Convertir metros a centímetros. 3 metros son 300 centímetros y 1 metro son 100 centímetros.

3 metros = 300 cm

1 metro = 100 cm

Tenemos una razón de 300 cm: 100 cm. Divida los términos de esta razón por 100. Obtenemos una razón de 3 cm: 1 cm. Ahora podemos dibujar una casa con un ancho de 3 cm y una altura de 1 cm.

Por supuesto, la casa dibujada es mucho más pequeña que la casa real, pero la proporción de ancho y alto permanece sin cambios. Esto nos permitió dibujar una casa lo más cerca posible de la real.

La actitud se puede entender de otra manera. Inicialmente se decía que una casa real tiene un ancho de 30 metros y una altura de 10 metros. El total es 30 + 10, es decir, 40 metros.

Estos 40 metros pueden entenderse como 40 partes. Una proporción de 30:10 significa 30 partes de ancho y 10 partes de alto.

Además, los miembros de la proporción 30: 10 se dividieron por 10. El resultado fue una proporción de 3: 1. Esta proporción se puede entender como 4 partes, tres de las cuales caen en el ancho y una en la altura. En este caso, generalmente necesita averiguar exactamente cuántos metros por ancho y alto.

En otras palabras, necesitas averiguar cuántos metros se dividen en 3 partes y cuántos metros se dividen en 1 parte. Primero debe averiguar cuántos metros caen en una parte. Para ello hay que dividir los 40 metros totales entre 4, ya que son solo cuatro partes en una proporción de 3:1

Determinemos de cuántos metros es el ancho:

10m × 3 = 30m

Determinemos cuántos metros caen en la altura:

10 metros × 1 = 10 metros

Múltiples miembros de una relación

Si se dan varios miembros en una relación, entonces pueden entenderse como partes de algo.

Ejemplo 1. Compró 18 manzanas. Estas manzanas se repartieron entre mamá, papá e hija en una proporción de 2:1:3. ¿Cuántas manzanas recibió cada uno?

La proporción de 2: 1: 3 indica que la madre recibió 2 partes, el padre - 1 parte, la hija - 3 partes. En otras palabras, cada miembro de la proporción 2:1:3 es una determinada fracción de 18 manzanas:

Si sumas los términos de la razón 2: 1: 3, entonces puedes averiguar cuántas partes hay en total:

2 + 1 + 3 = 6 (partes)

Averigüe cuántas manzanas caen en una parte. Para ello, divide 18 manzanas entre 6

18:6 = 3 (manzanas por parte)

Ahora determinemos cuántas manzanas recibió cada uno. Al multiplicar tres manzanas por cada miembro de la proporción 2:1:3, puedes determinar cuántas manzanas recibió mamá, cuántas recibió papá y cuántas recibió hija.

Averigua cuántas manzanas recibió mamá:

3 × 2 = 6 (manzanas)

Averigua cuántas manzanas recibió papá:

3 × 1 = 3 (manzanas)

Averigüe cuántas manzanas recibió la hija:

3 × 3 = 9 (manzanas)

Ejemplo 2. La plata nueva (alpaca) es una aleación de níquel, zinc y cobre en una proporción de 3:4:13. ¿Cuántos kilogramos de cada metal se deben tomar para obtener 4 kg de plata nueva?

4 kilogramos de plata nueva contendrán 3 partes de níquel, 4 partes de zinc y 13 partes de cobre. Primero, averiguamos cuántas partes habrá en cuatro kilogramos de plata:

3 + 4 + 13 = 20 (partes)

Determine cuántos kilogramos caerán en una parte:

4 kg: 20 = 0,2 kg

Determinemos cuántos kilogramos de níquel habrá en 4 kg de plata nueva. En la proporción 3:4:13, se dice que tres partes de la aleación contienen níquel. Entonces multiplicamos 0.2 por 3:

0,2 kg × 3 = 0,6 kg de níquel

Ahora determinemos cuántos kilogramos de zinc estarán contenidos en 4 kg de plata nueva. En la proporción 3:4:13, se dice que cuatro partes de la aleación contienen zinc. Así que multiplicamos 0,2 por 4:

0,2 kg × 4 = 0,8 kg de zinc

Ahora determinemos cuántos kilogramos de cobre estarán contenidos en 4 kg de plata nueva. En la proporción 3:4:13, se dice que trece partes de la aleación contienen cobre. Por lo tanto, multiplicamos 0,2 por 13:

0,2 kg × 13 = 2,6 kg cobre

Entonces, para obtener 4 kg de plata nueva, debe tomar 0,6 kg de níquel, 0,8 kg de zinc y 2,6 kg de cobre.

Ejemplo 3. El latón es una aleación de cobre y zinc cuya relación de masa es de 3:2. Se necesitan 120 g de cobre para hacer una pieza de latón. ¿Cuánto zinc se requiere para hacer esta pieza de latón?

Determinemos cuántos gramos de la aleación caen en una parte. La condición dice que se requieren 120 g de cobre para hacer una pieza de latón. También se dice que tres partes de la aleación contienen cobre. Si dividimos 120 por 3, encontramos cuántos gramos de la aleación hay en una parte:

120: 3 = 40 gramos por pieza

Ahora determinemos cuánto zinc se requiere para hacer una pieza de latón. Para ello, multiplicamos 40 gramos por 2, ya que en una proporción de 3:2 se indica que dos partes contienen zinc:

40 g × 2 = 80 gramos de zinc

Ejemplo 4. Tomaron dos aleaciones de oro y plata. En uno la relación de estos metales es 1:9, y en el otro 2:3. ¿Cuánto de cada aleación se debe tomar para obtener 15 kg de una nueva aleación en la que el oro y la plata estarían relacionados 1:4?

Solución

15 kg de una nueva aleación deben estar en una proporción de 1: 4. Esta proporción indica que una parte de la aleación tendrá oro y cuatro partes tendrán plata. Hay cinco partes en total. Esquemáticamente, esto se puede representar de la siguiente manera

Determinemos la masa de una parte. Para hacer esto, primero agregue todas las partes (1 y 4), luego divida la masa de la aleación por el número de estas partes

1 + 4 = 5
15 kg: 5 = 3 kg

Una parte de la aleación tendrá una masa de 3 kg. Entonces 15 kg de la nueva aleación contendrán 3 × 1 = 3 kg de oro y 3 × 4 = 12 kg de plata.

Por tanto, para obtener una aleación de 15 kg de peso, necesitamos 3 kg de oro y 12 kg de plata.

Ahora respondamos la pregunta de la tarea: " ¿Cuánto tomar cada aleación? »

Tomaremos 10 kg de la primera aleación, ya que la proporción de oro y plata en ella es de 1:9. Es decir, esta primera aleación nos dará 1 kg de oro y 9 kg de plata.

Tomaremos 5 kg de la segunda aleación, ya que en ella hay oro y plata en una proporción de 2:3. Es decir, esta segunda aleación nos dará 2 kg de oro y 3 kg de plata.

¿Te gustó la lección?
Únase a nuestro nuevo grupo Vkontakte y comience a recibir notificaciones de nuevas lecciones

Para resolver la mayoría de los problemas de matemáticas de la escuela secundaria, se requiere conocimiento de proporciones. Esta habilidad simple ayudará no solo a realizar ejercicios complejos del libro de texto, sino también a profundizar en la esencia misma de la ciencia matemática. ¿Cómo hacer una proporción? Ahora vamos a averiguarlo.

El ejemplo más simple es un problema donde se conocen tres parámetros y se debe encontrar el cuarto. Las proporciones son, por supuesto, diferentes, pero a menudo necesitas encontrar algún número por porcentaje. Por ejemplo, el niño tenía diez manzanas en total. Le dio la cuarta parte a su madre. ¿Cuántas manzanas le quedan al niño? Este es el ejemplo más simple que te permitirá hacer una proporción. Lo principal es hacerlo. Originalmente había diez manzanas. Que sea al 100%. Esto marcamos todas sus manzanas. Dio un cuarto. 1/4=25/100. Entonces, se fue: 100% (fue originalmente) - 25% (dio) = 75%. Esta figura muestra el porcentaje de la cantidad de fruta sobrante sobre la cantidad de fruta que estaba disponible primero. Ahora tenemos tres números por los cuales ya podemos resolver la proporción. 10 manzanas - 100%, X manzanas - 75%, donde x es la cantidad deseada de fruta. ¿Cómo hacer una proporción? Es necesario entender qué es. Matemáticamente se parece a esto. El signo igual es para su comprensión.

10 manzanas = 100%;

x manzanas = 75%.

Resulta que 10/x = 100%/75. Esta es la principal propiedad de las proporciones. Después de todo, cuanto más x, más porcentaje es este número del original. Resolvemos esta proporción y obtenemos que x=7.5 manzanas. Por qué el niño decidió dar una cantidad no entera, no lo sabemos. Ahora ya sabes cómo hacer una proporción. Lo principal es encontrar dos proporciones, una de las cuales contiene la incógnita deseada.

Resolver una proporción a menudo se reduce a una simple multiplicación y luego a una división. A los niños no se les enseña en las escuelas por qué esto es así. Si bien es importante entender que las relaciones proporcionales son clásicos matemáticos, la esencia misma de la ciencia. Para resolver proporciones, necesitas poder manejar fracciones. Por ejemplo, a menudo es necesario convertir porcentajes en fracciones ordinarias. Es decir, un registro del 95% no funcionará. Y si escribe inmediatamente 95/100, entonces puede hacer reducciones sólidas sin comenzar el conteo principal. Vale la pena decir de inmediato que si tu proporción resultó con dos incógnitas, entonces no se puede resolver. Ningún profesor puede ayudarte aquí. Y lo más probable es que su tarea tenga un algoritmo más complejo para las acciones correctas.

Considere otro ejemplo donde no hay porcentajes. El automovilista compró 5 litros de gasolina por 150 rublos. Pensó en cuánto pagaría por 30 litros de combustible. Para resolver este problema, denotamos por x la cantidad de dinero requerida. Puede resolver este problema usted mismo y luego verificar la respuesta. Si aún no ha descubierto cómo hacer una proporción, entonces mire. 5 litros de gasolina son 150 rublos. Como en el primer ejemplo, escribamos 5l - 150r. Ahora encontremos el tercer número. Por supuesto, son 30 litros. De acuerdo en que un par de 30 l - x rublos es apropiado en esta situación. Pasemos al lenguaje matemático.

5 litros - 150 rublos;

30 litros - x rublos;

Resolvemos esta proporción:

x = 900 rublos.

Eso es lo que decidimos. En su tarea, no olvide comprobar la adecuación de la respuesta. Sucede que con la decisión equivocada, los automóviles alcanzan velocidades poco realistas de 5000 kilómetros por hora, etc. Ahora ya sabes cómo hacer una proporción. También puedes resolverlo. Como puede ver, no hay nada complicado en esto.

Una razón (en matemáticas) es una relación entre dos o más números del mismo tipo. Las razones comparan valores absolutos o partes de un todo. Las razones se calculan y escriben de diferentes maneras, pero los principios básicos son los mismos para todas las razones.

Pasos

Parte 1

Definición de proporciones

Uso de proporciones. Las proporciones se usan tanto en la ciencia como en la vida cotidiana para comparar cantidades. Las razones más simples relacionan solo dos números, pero hay razones que comparan tres o más valores. En cualquier situación en la que esté presente más de una cantidad, se puede escribir una razón. Al vincular algunos valores, las proporciones pueden, por ejemplo, sugerir cómo aumentar la cantidad de ingredientes en una receta o sustancias en una reacción química.

Definición de proporciones. Una relación es una relación entre dos (o más) valores del mismo tipo. Por ejemplo, si un pastel requiere 2 tazas de harina y 1 taza de azúcar, entonces la proporción de harina y azúcar es de 2 a 1.
- Las proporciones también se pueden usar cuando dos cantidades no están relacionadas entre sí (como en el ejemplo del pastel). Por ejemplo, si hay 5 niñas y 10 niños en una clase, entonces la razón de niñas a niños es de 5 a 10. Estas cantidades (la cantidad de niños y la cantidad de niñas) no dependen entre sí, es decir, sus valores cambiarán si alguien abandona la clase o si llega un nuevo alumno a la clase. Las razones simplemente comparan valores de cantidades.
Fíjate en las diferentes formas en que se representan las razones. Las relaciones se pueden representar con palabras o con símbolos matemáticos.
- Muy a menudo, las proporciones se expresan en palabras (como se muestra arriba). Especialmente esta forma de representación de proporciones se usa en la vida cotidiana, lejos de la ciencia.
- Además, las proporciones se pueden expresar a través de dos puntos. Al comparar dos números en una razón, usará dos puntos (por ejemplo, 7:13); al comparar tres o más valores, coloque dos puntos entre cada par de números (por ejemplo, 10:2:23). En nuestro ejemplo de clase, podrías expresar la proporción de niñas a niños de esta manera: 5 niñas: 10 niños. O así: 5:10.
- Con menos frecuencia, las proporciones se expresan mediante una barra oblicua. En el ejemplo de la clase, podría escribirse así: 5/10. Sin embargo, esto no es una fracción y tal razón no se lee como una fracción; además, recuerda que en una razón, los números no son parte de un solo todo.
Parte 2
Uso de proporciones
1. Simplifica la razón. La razón se puede simplificar (similar a las fracciones) dividiendo cada término (número) de la razón por . Sin embargo, no pierda de vista los valores de relación originales.
  - En nuestro ejemplo, hay 5 niñas y 10 niños en la clase; la proporción es 5:10. El máximo común divisor de los términos de la razón es 5 (ya que tanto 5 como 10 son divisibles por 5). Divide cada número de proporción entre 5 para obtener una proporción de 1 niña por 2 niños (o 1:2). Sin embargo, al simplificar la relación, tenga en cuenta los valores originales. En nuestro ejemplo, no hay 3 estudiantes en la clase, sino 15. La razón simplificada compara el número de niños y el número de niñas. Es decir, por cada niña hay 2 niños, pero no hay 2 niños y 1 niña en la clase.
  - Algunas relaciones no se simplifican. Por ejemplo, la razón 3:56 no está simplificada porque estos números no tienen divisores comunes (3 es un número primo y 56 no es divisible por 3).
2. Usa la multiplicación o la división para aumentar o disminuir la razón. Un problema común es aumentar o disminuir dos valores que son proporcionales entre sí. Si te dan una razón y necesitas encontrar una razón más grande o más pequeña que coincida con ella, multiplica o divide la razón original por algún número dado.
  - Por ejemplo, un panadero necesita triplicar la cantidad de ingredientes de una receta. Si la receta dice que la proporción de harina a azúcar es 2:1 (2:1), entonces el panadero multiplicará cada término por 3 para obtener una proporción de 6:3 (6 tazas de harina por 3 tazas de azúcar).
  - Por otro lado, si el panadero necesita reducir a la mitad la cantidad de ingredientes que se dan en la receta, entonces el panadero dividirá cada término de proporción por 2 y obtendrá una proporción de 1:½ (1 taza de harina por 1/2 taza de azúcar).
3. Buscar un valor desconocido cuando se dan dos razones equivalentes. Este es un problema en el que necesitas encontrar una variable desconocida en una relación usando una segunda relación que es equivalente a la primera. Para resolver tales problemas, utilice . Escribe cada razón como una fracción, coloca un signo igual entre ellas y multiplica sus términos en cruz.
  - Por ejemplo, dado un grupo de alumnos, en el que hay 2 chicos y 5 chicas. ¿Cuál será el número de niños si el número de niñas aumenta a 20 (se conserva la proporción)? Primero, escribe dos proporciones: 2 niños: 5 niñas y X chicos: 20 chicas. Ahora escribe estas razones como fracciones: 2/5 y x/20. Multiplique los términos de las fracciones en forma de cruz y obtenga 5x = 40; por lo tanto x = 40/5 = 8.
parte 3
Errores comunes
1. Evite sumas y restas en problemas de proporciones de texto. Muchos problemas verbales se parecen a esto: “La receta requiere 4 tubérculos de papa y 5 zanahorias de raíz. Si quieres agregar 8 papas, ¿cuántas zanahorias necesitas para mantener la misma proporción? Al resolver tales problemas, los estudiantes a menudo cometen el error de agregar la misma cantidad de ingredientes al número original. Sin embargo, para mantener la proporción, necesitas usar la multiplicación. Aquí hay ejemplos de soluciones correctas e incorrectas:
  - Incorrecto: “8 - 4 = 4 - entonces agregamos 4 tubérculos de papa. Entonces, debes tomar 5 raíces de zanahoria y agregarles 4 más ... ¡Detente! Las proporciones no funcionan de esa manera. Vale la pena volver a intentarlo".
  - Correcto: "8 ÷ 4 = 2, por lo que multiplicamos la cantidad de papas por 2. En consecuencia, también se deben multiplicar 5 raíces de zanahoria por 2. 5 x 2 = 10: se deben agregar 10 raíces de zanahoria a la receta".

total:0
En contacto con 0
Google+ 0
OK 0
Facebook 0