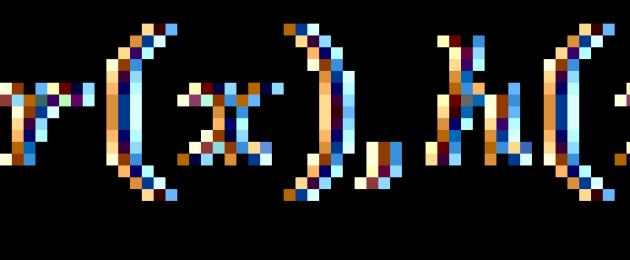Ejemplos de ecuaciones racionales para entrenamiento. Lección en video "Ecuaciones racionales

Las ecuaciones racionales son ecuaciones que contienen expresiones racionales.

Definición 1

En este caso, las expresiones racionales son expresiones que se pueden escribir como una fracción ordinaria de la forma $\frac(m)(n)$, mientras que $m$ y $n$ son números enteros y $n$ no puede ser igual a cero. Las expresiones racionales incluyen no solo expresiones que contienen fracciones de la forma $\frac(2)(3)$, sino también expresiones que contienen solo números enteros, ya que cualquier número entero puede representarse como una fracción impropia.

Ahora echemos un vistazo más de cerca a lo que son las ecuaciones racionales.

Como mencionamos anteriormente, las ecuaciones racionales son ecuaciones que contienen expresiones y variables racionales.

Según la posición de la variable en una ecuación racional, puede ser una ecuación racional fraccionaria o una ecuación racional entera.

Las ecuaciones fraccionarias pueden contener una fracción con una variable en solo una parte de la ecuación, mientras que las ecuaciones completas no contienen expresiones fraccionarias con una variable.

Ejemplos de ecuaciones racionales completas: $5x+2= 12$; $3y=-7(-4y + 5)$; $7a-14=256$.

Ejemplos de ecuaciones fraccionarias-racionales: $\frac(3x-2)(x+3)+\frac(1)(2)=\frac(5)(x)$; $\frac(7)(2y-3)=5$;

Vale la pena señalar que solo las ecuaciones que contienen una fracción en el denominador se denominan ecuaciones racionales fraccionarias, ya que las ecuaciones que contienen expresiones fraccionarias sin variables pueden reducirse fácilmente a ecuaciones enteras lineales.

¿Cómo resolver ecuaciones racionales?

Dependiendo de si se trata de una ecuación racional entera o fraccionaria, se utilizan algoritmos ligeramente diferentes para resolverla.

Algoritmo para resolver ecuaciones racionales enteras

1. Primero, necesitas determinar el mínimo común denominador para toda la igualdad.
2. Luego, debe determinar los factores por los que necesita multiplicar cada término de la igualdad.
3. La siguiente etapa es la reducción a un común denominador de toda igualdad.
4. Finalmente, la implementación de la búsqueda de las raíces de la igualdad racional entera obtenida.

Ejemplo 1

Resuelve la ecuación: $\frac(5x+9)(2)=\frac(x)(4)$

Primero, encontremos el factor común, en este caso, el número $4$. Para deshacernos del denominador, multiplicamos el lado izquierdo por $\frac(2)(2)$, obtenemos:

$10x+18=x$ - la ecuación resultante es lineal, su raíz es $x=-2$.

¿Cómo resolver ecuaciones racionales fraccionarias?

En el caso de ecuaciones racionales fraccionarias, el orden de solución es similar al algoritmo para resolver ecuaciones racionales enteras, es decir, se conservan los puntos 1-4, pero después de encontrar las raíces esperadas, en el caso de usar transformaciones no equivalentes, las raíces deben comprobarse sustituyéndolas en la ecuación.

Ejemplo 2

Resuelve la ecuación racional fraccionaria: $\frac(x-3)(x-5)+\frac(1)(x)=\frac(x+5)(x \cdot (x-5))$

Para reducir la fracción a común denominador, aquí es $x \cdot (x-5)$, multiplicamos cada fracción por uno, representado como el factor necesario para reducir a común denominador:

$\frac((x-3) \cdot x)((x-5)\cdot x)+\frac(1 \cdot (x-5))(x \cdot (x-5))=\frac( x+5)(x \cdot (x-5))$

Ahora que toda la fracción tiene un denominador común, puedes deshacerte de él:

$(x-3) \cdot x+(x-5)=x+5$

$x^2 ​​​​- 3x+x-5 = x+5$

Usemos el teorema de Vieta para resolver la ecuación cuadrática resultante:

$\begin(casos) x_1 + x_2 = 3 \\ x_1 \cdot x_2 = -10 \\ \end(casos)$

$\begin(casos) x_1=5 \\ x_2=-2 \\ \end(casos)$

Como la transformación utilizada para simplificar la ecuación no es equivalente, las raíces obtenidas se deben comprobar en la ecuación original, para ello las sustituimos:

$\frac(-2-3)(-2-5) +\frac(1)(-2)=\frac(-2+5)((-2) \cdot (-2-5))$

$\frac(5)(7)-\frac(1)(2)=\frac(3)(14)$

$\frac(3)(14)=\frac(3)(14)$ - por lo tanto, la raíz $x_2=-2$ es correcta.

$\frac(5-3)(5-5) +\frac(1)(5)=\frac(5+5)((-2) \cdot (5-5))$

Aquí queda inmediatamente claro que el cero se forma en el denominador, por lo tanto, la raíz $x_1=5$ es una extraña.

Debe recordarse que si una ecuación que contiene una expresión de la forma $\frac(m)(n)$ en el lado izquierdo o derecho es igual a cero, solo el numerador de la fracción puede ser igual a cero. Esto se debe al hecho de que si se forma un cero en algún lugar del denominador, la raíz que se verifica no es la raíz de la ecuación, ya que toda la igualdad pierde su significado en este caso. Las raíces que llevan el denominador a cero se llaman extrañas.

Si la ecuación fraccionaria-racional tiene una forma bastante compleja, para su mayor simplificación y solución es posible usar el reemplazo de parte de la ecuación con una nueva variable, probablemente ya haya visto ejemplos de tales ecuaciones fraccionarias-racionales:

Ejemplo 3

Resuelve la ecuación:

$\frac(1)(x^2+3x-3)+\frac(2)(x^2+3x+1)=\frac(7)(5)$

Para simplificar la solución, introducimos la variable $t= x^2+3x$:

$\frac(1)(t-3)+\frac(2)(t+1)=\frac(7)(5)$

El denominador común aquí es $5 \cdot (t-3)(t+1)$, multiplicamos todas las partes de la ecuación por los factores necesarios para eliminarlo:

$\frac(5(t+1))(5(t-3)(t+1))+\frac(2 \cdot 5(t-3))(5(t+1)(t-3) )=\frac(7(t+1)(t-3))(5(t-3)(t+1))$

$5(t+1)+10(t-3)=7(t+1)(t-3)$

$5t+5+10t-30=7(t^2-3t+t-3)$

$15t-25=7t^2-14t-21$

A través del discriminante, calculamos las raíces:

$t_1=4;t_2=\frac(1)(7)$

Como usamos transformaciones no equivalentes, es necesario verificar las raíces obtenidas en el denominador, deben cumplir la condición $5(t-3)(t+1)≠0$. Ambas raíces cumplen esta condición.

Ahora sustituimos las raíces obtenidas por $t$ y obtenemos dos ecuaciones:

$x^2+3x=4$ y $x^2+3x=\frac(1)(7)$.

Por el teorema de Vieta, las raíces de la primera ecuación $x_1=-4; x_2=1$, calculamos las raíces de la segunda en términos del discriminante y tenemos $x_(1,2)=\frac(-3±\sqrt(\frac(67)(7)))(2) PS

Todas las raíces de la ecuación serán: $x_1=-4; x_2=1, x_(3,4)=\frac(-3±\sqrt(\frac(67)(7)))(2)$.

Transformaciones para simplificar la forma de la ecuación

Como puede ver arriba, se utilizan varias transformaciones para resolver ecuaciones racionales.

Hay dos tipos de transformaciones de ecuaciones: equivalentes (idénticas) y desiguales.

Las transformaciones se denominan equivalentes si conducen a un nuevo tipo de ecuación, cuyas raíces son las mismas que las de la original.

Las transformaciones de identidad que se pueden usar para cambiar la forma de la ecuación original sin más controles son las siguientes:

• Multiplicar o dividir la ecuación completa por algún número distinto de cero;
• Transferir partes de una ecuación del lado izquierdo al lado derecho y viceversa.

Las transformaciones no equivalentes son transformaciones en el curso de las cuales pueden aparecer raíces extrañas. Las transformaciones no equivalentes incluyen:

• Elevar al cuadrado ambos lados de la ecuación;
• Deshacerse de los denominadores que contienen la variable;

Las raíces de las ecuaciones racionales resueltas usando transformaciones no equivalentes deben verificarse por sustitución en la ecuación original, ya que pueden aparecer raíces extrañas durante las transformaciones no equivalentes. Las transformaciones no equivalentes no siempre conducen a la aparición de raíces extrañas, pero, sin embargo, es necesario tener esto en cuenta.

Solución de ecuaciones racionales con potencias mayores que dos

Los métodos más utilizados para resolver ecuaciones con potencias mayores que dos son el método de cambio de variable, que discutimos anteriormente usando el ejemplo de una ecuación racional fraccionaria, así como el método de factorización.

Consideremos el método de factorización con más detalle.

Sea dada una ecuación de la forma $P(x)= 0$, donde $P(x)$ es un polinomio de grado mayor que dos. Si esta ecuación se puede factorizar para que tome la forma $P_1(x)P_2(x)P_3(x)..\cdot P_n(x)=0$, entonces la solución a esta ecuación es el conjunto de soluciones de ecuaciones $P_1(x)=0, P_2(x)=0, P_3(x)=0...P_n(x)=0$.

Para quien no lo recuerde: un término libre de una ecuación es un término de ecuaciones que no contiene una variable como factor. Al mismo tiempo, habiendo encontrado una de las raíces de dicha ecuación, se puede usar para factorizar aún más la ecuación.

Ejemplo 5

Resuelve la ecuación:

Los divisores del término libre serán los números $±1, ±2, ±3, ±4, ±6, ±8, ±12$ y $±24$. Cuando se verificaron, $x=2$ resultó ser una raíz adecuada. Esto significa que este polinomio se puede expandir usando esta raíz: $(x-2)(x^2+6+12)=0$.

El polinomio en el segundo par de paréntesis de raíces no tiene raíces, lo que significa que la única raíz de esta ecuación será $x=2$.

Otro tipo de ecuaciones con grado mayor que dos son ecuaciones bicuadráticas de la forma $ax^4+bx^2+ c=0$. Tales ecuaciones se resuelven reemplazando $x^2$ por $y$, aplicándolo obtenemos una ecuación de la forma $ay^2+y+c=0$, y luego el valor resultante de la nueva variable se usa para calcular la variable original.

También hay otro tipo de ecuación llamada retornable. Tales ecuaciones se ven así: $ax^4+bx^3+cx^2+bx+a=0$. Tienen ese nombre debido a la repetición de coeficientes en grados más altos y más bajos.

Una expresión entera es una expresión matemática formada por números y variables literales que utilizan las operaciones de suma, resta y multiplicación. Los números enteros también incluyen expresiones que incluyen la división por algún número distinto de cero.

El concepto de una expresión racional fraccionaria

Una expresión fraccionaria es una expresión matemática que, además de las operaciones de suma, resta y multiplicación realizadas con números y variables literales, así como la división por un número distinto de cero, también contiene la división en expresiones con variables literales.

Las expresiones racionales son todas expresiones enteras y fraccionarias. Las ecuaciones racionales son ecuaciones cuyos lados izquierdo y derecho son expresiones racionales. Si en una ecuación racional las partes izquierda y derecha son expresiones enteras, entonces tal ecuación racional se llama un número entero.

Si en una ecuación racional las partes izquierda o derecha son expresiones fraccionarias, entonces tal ecuación racional se llama fraccionaria.

Ejemplos de expresiones racionales fraccionarias

1.x-3/x=-6*x+19

2. (x-4)/(2*x+5) = (x+7)/(x-2)

3. (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5))

Esquema para resolver una ecuación racional fraccionaria

1. Encuentra el denominador común de todas las fracciones que están incluidas en la ecuación.

2. Multiplica ambos lados de la ecuación por un denominador común.

3. Resuelva la ecuación completa resultante.

4. Verifique las raíces y excluya aquellas que conviertan el denominador común en cero.

Como estamos resolviendo ecuaciones racionales fraccionarias, habrá variables en los denominadores de las fracciones. Entonces, estarán en un denominador común. Y en el segundo párrafo del algoritmo, multiplicamos por un denominador común, luego pueden aparecer raíces extrañas. En el cual el denominador común será igual a cero, lo que significa que la multiplicación por él no tendrá sentido. Por lo tanto, al final, asegúrese de verificar las raíces obtenidas.

Considere un ejemplo:

Resolver una ecuación racional fraccionaria: (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5)).

Nos adherimos al esquema general: primero encontramos el denominador común de todas las fracciones. Obtenemos x*(x-5).

Multiplica cada fracción por un denominador común y escribe la ecuación completa resultante.

(x-3)/(x-5) * (x*(x-5))= x*(x+3);
1/x * (x*(x-5)) = (x-5);
(x+5)/(x*(x-5)) * (x*(x-5)) = (x+5);
x*(x+3) + (x-5) = (x+5);

Simplifiquemos la ecuación resultante. Obtenemos:

x^2+3*x + x-5 - x - 5 =0;
x^2+3*x-10=0;

Obtuvimos una ecuación cuadrática reducida simple. Lo resolvemos por cualquiera de los métodos conocidos, obtenemos las raíces x=-2 yx=5.

Ahora comprobamos las soluciones obtenidas:

Sustituimos los números -2 y 5 en el común denominador. En x=-2, el común denominador x*(x-5) no desaparece, -2*(-2-5)=14. Entonces el número -2 será la raíz de la ecuación racional fraccionaria original.

En x=5, el denominador común x*(x-5) se convierte en cero. Por lo tanto, este número no es la raíz de la ecuación racional fraccionaria original, ya que habrá división por cero.

Ya hemos aprendido a resolver ecuaciones cuadráticas. Extendamos ahora los métodos estudiados a ecuaciones racionales.

¿Qué es una expresión racional? Ya nos hemos encontrado con este concepto. Expresiones racionales llamadas expresiones formadas por números, variables, sus grados y signos de operaciones matemáticas.

En consecuencia, las ecuaciones racionales son ecuaciones de la forma: , donde - expresiones racionales.

Previamente, consideramos solo aquellas ecuaciones racionales que se reducen a lineales. Ahora consideremos aquellas ecuaciones racionales que pueden reducirse a ecuaciones cuadráticas.

Ejemplo 1

Resuelve la ecuación: .

Solución:

Una fracción es 0 si y solo si su numerador es 0 y su denominador no es 0.

Obtenemos el siguiente sistema:

La primera ecuación del sistema es una ecuación cuadrática. Antes de resolverlo, dividimos todos sus coeficientes por 3. Obtenemos:

Obtenemos dos raíces: ; .

Dado que 2 nunca es igual a 0, se deben cumplir dos condiciones: . Dado que ninguna de las raíces de la ecuación obtenida anteriormente coincide con los valores inválidos de la variable que se obtuvieron al resolver la segunda desigualdad, ambas son soluciones de esta ecuación.

Responder:.

Entonces, formulemos un algoritmo para resolver ecuaciones racionales:

1. Mover todos los términos al lado izquierdo para que se obtenga 0 en el lado derecho.

2. Transforme y simplifique el lado izquierdo, lleve todas las fracciones a un denominador común.

3. Igualar la fracción resultante a 0, según el siguiente algoritmo: .

4. Anota aquellas raíces que se obtienen en la primera ecuación y satisface la segunda desigualdad en respuesta.

Veamos otro ejemplo.

Ejemplo 2

Resuelve la ecuación: .

Solución

Al principio, transferimos todos los términos al lado izquierdo para que el 0 permanezca a la derecha.

Ahora llevamos el lado izquierdo de la ecuación a un denominador común:

Esta ecuación es equivalente al sistema:

La primera ecuación del sistema es una ecuación cuadrática.

Los coeficientes de esta ecuación: . Calculamos el discriminante:

Obtenemos dos raíces: ; .

Ahora resolvemos la segunda desigualdad: el producto de factores no es igual a 0 si y solo si ninguno de los factores es igual a 0.

Se deben cumplir dos condiciones: . Obtenemos que de las dos raíces de la primera ecuación, solo una es adecuada: 3.

Responder:.

En esta lección, recordamos qué es una expresión racional y también aprendimos cómo resolver ecuaciones racionales, que se reducen a ecuaciones cuadráticas.

En la siguiente lección, consideraremos ecuaciones racionales como modelos de situaciones reales y también consideraremos problemas de movimiento.

Bibliografía

1. Bashmakov M. I. Álgebra, 8vo grado. - M.: Ilustración, 2004.
2. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. et al.Álgebra, 8. 5ª ed. - M.: Educación, 2010.
3. Nikolsky S.M., Potapov M.A., Reshetnikov N.N., Shevkin A.V. Álgebra, 8vo grado. Libro de texto para instituciones educativas. - M.: Educación, 2006.

1. Festival de ideas pedagógicas "Lección Abierta" ().
2. Escuela.xvatit.com().
3. Rudocs.exdat.com().

Tarea

El mínimo común denominador se usa para simplificar esta ecuación. Este método es aplicable en el caso de que sea imposible escribir esta ecuación con una expresión racional en cada lado de la ecuación (y usar el método de multiplicación cruzada). Este método se usa cuando se da una ecuación racional con tres o más fracciones (en el caso de dos fracciones es mejor usar la multiplicación cruzada).

Encuentra el mínimo común denominador de fracciones (o mínimo común múltiplo). NOZ es el número más pequeño que es divisible por cada denominador.

• A veces NOZ es un número obvio. Por ejemplo, si se da la ecuación: x/3 + 1/2 = (3x + 1)/6, entonces es obvio que el mínimo común múltiplo de los números 3, 2 y 6 será 6.
• Si el NOD no es obvio, anota los múltiplos del mayor denominador y encuentra entre ellos uno que también sea múltiplo de los otros denominadores. A menudo puedes encontrar el NOD simplemente multiplicando dos denominadores. Por ejemplo, si se da la ecuación x/8 + 2/6 = (x - 3)/9, entonces NOZ = 8*9 = 72.
• Si uno o más denominadores contienen una variable, entonces el proceso es algo más complicado (pero no imposible). En este caso, la NOZ es una expresión (que contiene una variable) que es divisible por cada denominador. Por ejemplo, en la ecuación 5/(x-1) = 1/x + 2/(3x) NOZ = 3x(x-1), porque esta expresión es divisible por cada denominador: 3x(x-1)/(x -1 ) = 3x; 3x(x-1)/3x = (x-1); 3x(x-1)/x = 3(x-1).

Multiplica tanto el numerador como el denominador de cada fracción por un número igual al resultado de dividir la NOZ por el denominador correspondiente de cada fracción. Como estás multiplicando tanto el numerador como el denominador por el mismo número, estás multiplicando efectivamente una fracción por 1 (por ejemplo, 2/2 = 1 o 3/3 = 1).

• Entonces, en nuestro ejemplo, multiplica x/3 por 2/2 para obtener 2x/6, y multiplica 1/2 por 3/3 para obtener 3/6 (no es necesario multiplicar 3x + 1/6 porque el denominador es 6).
• Procede de manera similar cuando la variable está en el denominador. En nuestro segundo ejemplo NOZ = 3x(x-1), entonces 5/(x-1) por (3x)/(3x) es 5(3x)/(3x)(x-1); 1/x por 3(x-1)/3(x-1) para obtener 3(x-1)/3x(x-1); 2/(3x) multiplica por (x-1)/(x-1) y obtienes 2(x-1)/3x(x-1).

Busque "x". Ahora que has reducido las fracciones a un denominador común, puedes deshacerte del denominador. Para ello, multiplica cada lado de la ecuación por un denominador común. Luego resuelve la ecuación resultante, es decir, encuentra "x". Para hacer esto, aísle la variable en un lado de la ecuación.

• En nuestro ejemplo: 2x/6 + 3/6 = (3x +1)/6. Puedes sumar dos fracciones con el mismo denominador, así que escribe la ecuación como: (2x+3)/6=(3x+1)/6. Multiplica ambos lados de la ecuación por 6 y elimina los denominadores: 2x+3 = 3x +1. Resuelva y obtenga x = 2.
• En nuestro segundo ejemplo (con una variable en el denominador), la ecuación se ve así (después de reducirla a un denominador común): 5(3x)/(3x)(x-1) = 3(x-1)/3x(x -1) + 2 (x-1)/3x(x-1). Al multiplicar ambos lados de la ecuación por NOZ, te deshaces del denominador y obtienes: 5(3x) = 3(x-1) + 2(x-1), o 15x = 3x - 3 + 2x -2, o 15x = x - 5 Resuelve y obtiene: x = -5/14.

Su privacidad es importante para nosotros. Por esta razón, hemos desarrollado una Política de privacidad que describe cómo usamos y almacenamos su información. Lea nuestra política de privacidad y háganos saber si tiene alguna pregunta.

Recopilación y uso de información personal

La información personal se refiere a los datos que se pueden utilizar para identificar o contactar a una persona específica.

Es posible que se le solicite que proporcione su información personal en cualquier momento cuando se comunique con nosotros.

Los siguientes son algunos ejemplos de los tipos de información personal que podemos recopilar y cómo podemos usar dicha información.

Qué información personal recopilamos:

• Cuando envía una solicitud en el sitio, podemos recopilar información diversa, incluido su nombre, número de teléfono, dirección de correo electrónico, etc.

Cómo usamos tu información personal:

• La información personal que recopilamos nos permite comunicarnos con usted e informarle sobre ofertas únicas, promociones y otros eventos y próximos eventos.
• De vez en cuando, podemos usar su información personal para enviarle avisos y mensajes importantes.
• También podemos utilizar la información personal para fines internos, como realizar auditorías, análisis de datos y diversas investigaciones para mejorar los servicios que brindamos y brindarle recomendaciones sobre nuestros servicios.
• Si participa en un sorteo, concurso o incentivo similar, podemos utilizar la información que proporcione para administrar dichos programas.

Divulgación a terceros

No divulgamos la información que recibimos de usted a terceros.

Excepciones:

• En caso de que sea necesario, de conformidad con la ley, orden judicial, en procedimientos judiciales y/o en base a solicitudes públicas o solicitudes de organismos estatales en el territorio de la Federación Rusa, divulgar su información personal. También podemos divulgar información sobre usted si determinamos que dicha divulgación es necesaria o apropiada por razones de seguridad, aplicación de la ley u otras razones de interés público.
• En el caso de una reorganización, fusión o venta, podemos transferir la información personal que recopilamos al tercero sucesor correspondiente.

Protección de datos personales

Tomamos precauciones, incluidas las administrativas, técnicas y físicas, para proteger su información personal de pérdida, robo y uso indebido, así como del acceso, divulgación, alteración y destrucción no autorizados.

Mantener su privacidad a nivel de empresa

Para garantizar que su información personal esté segura, comunicamos las prácticas de privacidad y seguridad a nuestros empleados y hacemos cumplir estrictamente las prácticas de privacidad.