Dibuja un diagrama del sistema y marca el centro de gravedad en él. Si el centro de gravedad encontrado está fuera del sistema de objetos, recibió una respuesta incorrecta. Es posible que haya medido distancias desde diferentes puntos de referencia. Repetir las medidas.
- Por ejemplo, si los niños están sentados en un columpio, el centro de gravedad estará en algún lugar entre los niños y no a la derecha o izquierda del columpio. Además, el centro de gravedad nunca coincidirá con el punto donde está sentado el niño.
- Estos argumentos son válidos en un espacio bidimensional. Dibuja un cuadrado que contendrá todos los objetos del sistema. El centro de gravedad debe estar dentro de este cuadrado.
Revisa tus cálculos si obtienes un resultado pequeño. Si el punto de referencia está en un extremo del sistema, un resultado pequeño ubica el centro de gravedad cerca del final del sistema. Esta puede ser la respuesta correcta, pero en la gran mayoría de los casos este resultado indica un error. Cuando calculaste los momentos, ¿multiplicaste los pesos y distancias correspondientes? Si en lugar de multiplicar sumaras los pesos y las distancias, obtendrías un resultado mucho menor.
Corrija el error si encontró múltiples centros de gravedad. Cada sistema tiene un solo centro de gravedad. Si encontró múltiples centros de gravedad, lo más probable es que no haya sumado todos los momentos. El centro de gravedad es igual a la relación entre el momento "total" y el peso "total". No es necesario dividir “cada” momento entre “cada” peso: así encontrarás la posición de cada objeto.
Verifique el punto de referencia si la respuesta difiere en algún valor entero. En nuestro ejemplo, la respuesta es 3,4 m. Digamos que obtuvo la respuesta 0,4 mo 1,4 m, u otro número que termine en ".4". Esto se debe a que no elegiste el extremo izquierdo del tablero como punto de partida, sino un punto que se encuentra completamente a la derecha. De hecho, tu respuesta es correcta sin importar el punto de referencia que elijas. Sólo recuerda: el punto de referencia siempre está en la posición x = 0. Aquí tienes un ejemplo:
- En nuestro ejemplo, el punto de referencia estaba en el extremo izquierdo del tablero y encontramos que el centro de gravedad estaba a 3,4 m de este punto de referencia.
- Si eliges como punto de referencia un punto que se encuentra a 1 m a la derecha del extremo izquierdo del tablero, obtendrás como respuesta 2,4 m, es decir, el centro de gravedad está a 2,4 m del nuevo punto de referencia, lo que , a su vez, se ubica a 1 m del extremo izquierdo del tablero. Por tanto, el centro de gravedad está a una distancia de 2,4 + 1 = 3,4 m del extremo izquierdo del tablero. ¡Resultó ser una respuesta antigua!
- Nota: al medir distancias, recuerde que las distancias al punto de referencia "izquierdo" son negativas y al punto de referencia "derecho" son positivas.
Mide distancias en línea recta. Supongamos que hay dos niños en un columpio, pero uno es mucho más alto que el otro, o un niño está colgado debajo de la tabla en lugar de sentado en ella. Ignore esta diferencia y mida las distancias a lo largo de la línea recta del tablero. Medir distancias en ángulos dará resultados cercanos pero no del todo precisos.
- Para el problema del balancín, recuerde que el centro de gravedad está entre los extremos derecho e izquierdo del tablero. Posteriormente aprenderás a calcular el centro de gravedad de sistemas bidimensionales más complejos.
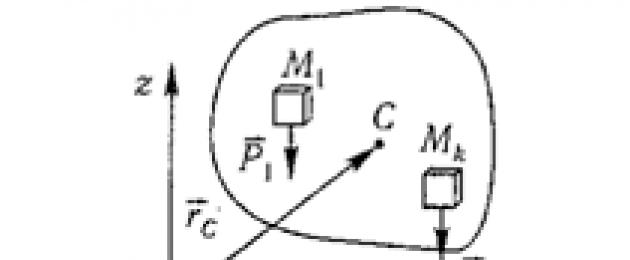
Centro de gravedad de un cuerpo sólido es un punto geométrico que está rígidamente conectado a este cuerpo y es el centro de fuerzas gravitacionales paralelas aplicadas a partículas elementales individuales del cuerpo (Figura 1.6).
Vector de radio de este punto.

Figura 1.6
Para un cuerpo homogéneo, la posición del centro de gravedad del cuerpo no depende del material, sino que está determinada por la forma geométrica del cuerpo.
Si el peso específico de un cuerpo homogéneo γ , peso de una partícula elemental del cuerpo
PAG k = γΔV k (PAG = γV ) sustituir en la fórmula para determinar r C , tenemos
De donde, proyectando sobre los ejes y pasando al límite, obtenemos las coordenadas del centro de gravedad de un volumen homogéneo.

Lo mismo ocurre con las coordenadas del centro de gravedad de una superficie homogénea con área S (Figura 1.7, a)


Figura 1.7
Para las coordenadas del centro de gravedad de una línea homogénea de longitud. l (Figura 1.7, b)

Métodos para determinar las coordenadas del centro de gravedad.
Con base en las fórmulas generales obtenidas anteriormente, podemos indicar métodos para determinar las coordenadas de los centros de gravedad de cuerpos sólidos:
1 Analítico(por integración).
2 Método de simetría. Si un cuerpo tiene un plano, un eje o un centro de simetría, entonces su centro de gravedad se encuentra, respectivamente, en el plano de simetría, el eje de simetría o el centro de simetría.
3 Experimental(método de colgar el cuerpo).
4 Terrible. El cuerpo está dividido en un número finito de partes, para cada una de las cuales la posición del centro de gravedad es C y área S conocido. Por ejemplo, la proyección de un cuerpo sobre un plano. xoy (Figura 1.8) se puede representar como dos figuras planas con áreas S 1 Y S 2 (S=S 1 +S 2 ). Los centros de gravedad de estas figuras están ubicados en puntos C 1 (X 1 , y 1 ) Y C 2 (X 2 , y 2 ) . Entonces las coordenadas del centro de gravedad del cuerpo son iguales.


Figura 1.8
5Suma(método de áreas o volúmenes negativos). Un caso especial del método de partición. Se aplica a cuerpos que tienen recortes si se conocen los centros de gravedad del cuerpo sin el recorte y la parte recortada. Por ejemplo, necesitas encontrar las coordenadas del centro de gravedad de una figura plana (Figura 1.9):


Figura 1.9
Centros de gravedad de las figuras más simples.

Figura 1.10
1 triángulo
El centro de gravedad del área del triángulo coincide con el punto de intersección de sus medianas (Figura 1.10, a).
DM = MB , cm= (1/3)SOY. .
2 arco circular
El arco tiene un eje de simetría (Figura 1.10, b). El centro de gravedad se encuentra sobre este eje, es decir y C = 0 .

dl – elemento de arco, dl = Rdφ , R – radio del círculo, x = Rcosφ , l= 2αR ,
Por eso:
X C = R(senα/α) .
3 sectores circulares
sector radio R con ángulo central 2 α tiene un eje de simetría Buey , en el que se encuentra el centro de gravedad (Figura 1.10, c).
Dividimos el sector en sectores elementales, que pueden considerarse triángulos. Los centros de gravedad de los sectores elementales están ubicados en un arco circular de radio (2/3) R .
El centro de gravedad del sector coincide con el centro de gravedad del arco. AB :

14. Métodos para especificar el movimiento de un punto.
Con el método vectorial para especificar el movimiento, la posición de un punto se determina mediante un vector de radio dibujado desde un punto fijo en el sistema de referencia seleccionado.
Con el método de coordenadas para especificar el movimiento, las coordenadas de un punto se especifican en función del tiempo:

Se trata de ecuaciones paramétricas de la trayectoria de un punto en movimiento, en las que el tiempo juega el papel de parámetro. t . Para escribir su ecuación en forma explícita, es necesario excluir de ellas t .
Con el método natural de especificar el movimiento, se especifican la trayectoria del punto, el origen de la referencia en la trayectoria que indica la dirección positiva de la referencia y la ley de cambio en la coordenada del arco: s=s(t) . Este método es conveniente de utilizar si la trayectoria del punto se conoce de antemano.
15. Velocidad de 1,2 puntos
Considere el movimiento de un punto durante un corto período de tiempo. Δt :
![]()
velocidad promedio de un punto durante un período de tiempo DT . Velocidad de un punto en un momento dado


Velocidad puntual es una medida cinemática de su movimiento, igual a la derivada temporal del radio vector de este punto en el sistema de referencia considerado. El vector de velocidad se dirige tangencialmente a la trayectoria del punto en la dirección del movimiento.
Instrucciones
Intenta encontrar el centro. gravedad departamento cifras empíricamente. Tome un lápiz nuevo sin punta y colóquelo verticalmente. Coloca una figura plana encima. Marca en el lápiz el punto de la figura donde queda estable. este sera el centro gravedad tuyo cifras. En lugar de un lápiz, simplemente use el dedo índice extendido hacia arriba. Pero esto se debe a que es necesario asegurarse de que el dedo esté derecho, no se balancee ni tiemble.
Para demostrar que el punto resultante es el centro de masa, haz un agujero con una aguja. Pasar un hilo por el agujero y hacer un nudo en un extremo para que el hilo no se salga. Sosteniendo el otro extremo del hilo, cuelga tu cuerpo de él. si el centro gravedad Así es, la figura quedará colocada exactamente, paralela al suelo. Sus costados no se moverán.
encontrar el centro gravedad cifras geométricamente. Si te dan un triángulo, construye . Estos segmentos conectan los vértices del triángulo con la mitad del lado opuesto. El punto se convertirá centro masas triangulares. Para encontrar el punto medio de un lado, puedes incluso doblar la figura por la mitad, pero ten en cuenta que esto alterará la uniformidad. cifras.
Comparar los resultados obtenidos geométrica y experimentalmente. Informar el progreso del experimento. Los pequeños errores se consideran normales. Se explican por la imperfección. cifras, inexactitud de los instrumentos, factor humano (pequeños defectos en el trabajo, imperfección del ojo humano, etc.).
Fuentes:
- Calcular las coordenadas del centro de gravedad de una figura plana.
En un campo gravitacional uniforme, el centro de gravedad coincide con el centro de masa. En geometría, los conceptos de “centro de gravedad” y “centro de masa” también son equivalentes, ya que no se considera la existencia de un campo gravitacional. El centro de masa también se llama centro de inercia y baricentro (del griego barus - pesado, kentron - centro). Caracteriza el movimiento de un cuerpo o sistema de partículas. Así, durante la caída libre, un cuerpo gira alrededor de su centro de inercia.
Instrucciones
Sea el sistema formado por dos puntos idénticos. Luego, obviamente, se sitúa en el medio entre ellos. Si los puntos con coordenadas x1 y x2 tienen masas diferentes m1 y m2, entonces la coordenada del centro de masa es x(c)=(m1 x1+m2 x2)/(m1+m2). Dependiendo del “cero” elegido del sistema de referencia, las coordenadas también pueden ser negativas.
Los puntos en un plano tienen dos coordenadas: xey. Cuando se especifica en el espacio, se agrega una tercera coordenada z. Para no describir cada coordenada por separado, conviene considerar el vector radio del punto: r=x i+y j+z· k, Dónde i,j,k− vectores unitarios de ejes coordenados.
Supongamos ahora que el sistema consta de tres puntos con masas m1, m2 y m3. Sus vectores de radio, respectivamente, r1, r2 Y r3. Entonces el radio vector de su centro de gravedad. r(c)=(m1· r1+m2· r2+m3· r3)/(m1+m2+m3).
Si el sistema consta de puntos arbitrarios, entonces el vector de radio, por definición, se encuentra mediante la fórmula:
r(c)=∑metro(yo) Rhode Island)/∑m(i). La suma se realiza utilizando el índice i (escrito debajo del signo de suma ∑). Aquí m(i) es algún sistema i-ésimo, Rhode Island)− su vector de radio.
Si el cuerpo es homogéneo en masa, la suma se convierte en integral. Rompe mentalmente el cuerpo en trozos infinitamente pequeños de masa dm. Como el cuerpo es homogéneo, la masa de cada pieza se puede escribir como dm=ρ·dV, donde dV es el volumen elemental de esta pieza, ρ es la densidad (la misma en todo el volumen de un cuerpo homogéneo).
La suma integral de la masa de todas las piezas dará la masa de todo el cuerpo: ∑m(i)=∫dm=M. Entonces resulta r(c)=1/M·∫ρ·dV· dr.. La densidad, un valor constante, se puede sacar del signo integral: r(c)=ρ/M·∫dV· dr.. Para la integración directa necesitará configurar una función específica entre dV y dr., que depende de los parámetros de la figura.
Por ejemplo, el centro de gravedad de un segmento (una barra larga y homogénea) está en el medio. El centro de masa de la esfera y la bola se encuentra en el centro. El baricentro del cono se sitúa a la altura del segmento axial, contando desde la base.
El centro también se puede determinar experimentalmente. Recorta cualquier forma de una hoja de papel grueso o cartón (por ejemplo, el mismo triángulo). Intente colocarlo en la punta de un dedo extendido verticalmente. El lugar donde se puede hacer esto será el centro de inercia del cuerpo.
Fuentes:
- "Mecánica", D.V. Sivukhin, 2006.
- Determinar las coordenadas del centro de gravedad del barco.
En el sentido habitual, el centro de gravedad se percibe como el punto al que se puede aplicar la resultante de todas las fuerzas que actúan sobre el cuerpo. El ejemplo más sencillo es un columpio para niños en forma de tabla normal. Sin ningún cálculo, cualquier niño seleccionará el soporte de la tabla de tal manera que equilibre (y tal vez incluso supere) a un hombre pesado en un columpio. En el caso de cuerpos y secciones complejos, son indispensables cálculos precisos y las fórmulas correspondientes. Incluso si obtienes expresiones engorrosas, lo principal es no tenerles miedo, sino recordar que inicialmente estamos hablando de una tarea casi elemental.

Instrucciones
Considere la palanca más simple (ver Figura 1) en la posición de equilibrio. Coloque x₁₂ en el eje horizontal con la abscisa y coloque puntos materiales de masas m₁ y m₂ en los bordes. Considere sus coordenadas a lo largo del eje 0x como conocidas e iguales a x₁ y x₂. La palanca está en la posición de equilibrio si los momentos de las fuerzas de peso Р₁=m₁g y P₂=m₂g son iguales. El momento es igual al producto de la fuerza por su brazo, que se puede encontrar como la longitud de la perpendicular que desciende desde el punto de aplicación de la fuerza a la vertical x=x₁₂. Por lo tanto, de acuerdo con la Figura 1, m₁gℓ₁= m₂gℓ₂, ℓ₁=х₁₂-х₁, ℓ₂=х₂-х₁₂. Entonces m₁(х₁₂-х₁)=m₂(х₂-х₁₂). Resuelve esta ecuación y obtén x₁₂=(m₁x₁+m₂x₂)/(m₁+m₂).

Para encontrar la ordenada y₁₂, aplique el mismo razonamiento y cálculos que en el paso 1. Siga aún la ilustración que se muestra en la Figura 1, donde m₁gh₁= m₂gh₂, h₁=y₁₂-y₁, h₂=y₂-y₁₂. Entonces m₁(y₁₂-y₁)=m₂(y₂-y₁₂). El resultado es y₁₂=(m₁у₁+m₂у₂)/(m₁+m₂). A continuación, considere que en lugar de un sistema de dos puntos hay un punto M₁₂(x12,у12) de la masa total (m₁+m₂).
Al sistema de dos puntos, suma otra masa (m₃) con coordenadas (x₃, y₃). Al calcular, aún debes asumir que estás tratando con dos puntos, donde el segundo de ellos tiene masa (m₁+m₂) y coordenadas (x12,y12). Repitiendo todas las acciones de los pasos 1 y 2 para estos dos puntos, llegarás al centro de los tres puntos x₁x₁+m₂x₂+m₃x₃)/(m₁+m₂+m₃), y₁₂₃=(m₁у₁+m₂у₂+m₃y₃)/( m₁+ m₂ +m₃). A continuación, agregue los puntos cuarto, quinto, etc. Después de repetir el mismo procedimiento muchas veces, asegúrese de que para un sistema de n puntos las coordenadas del centro de gravedad se calculen mediante la fórmula (ver Fig. 2). Observe usted mismo el hecho de que durante el trabajo la aceleración de la gravedad g disminuyó. Por tanto, las coordenadas del centro de masa y de gravedad coinciden.

Imaginemos que en la sección considerada hay una determinada región D, cuya densidad superficial es ρ=1. Desde arriba y desde abajo, la figura está limitada por las gráficas de las curvas y=φ(x) y y=ψ(x), x є [a,b]. Divida el área D con verticales x=x₍i-1₎, x=x₍i₎ (i=1,2,…,n) en tiras delgadas, de modo que puedan considerarse aproximadamente rectángulos con bases ∆хi (ver Fig. .3). En este caso, considere que la mitad del segmento ∆хi coincide con la abscisa del centro de masa ξi=(1/2). Considere que la altura del rectángulo es aproximadamente igual a [φ(ξi)-ψ(ξi)]. Entonces la ordenada del centro de masa del área elemental es ηi=(1/2)[φ(ξi)+ψ(ξi)].

Debido a la distribución uniforme de la densidad, considere que el centro de masa de la tira coincidirá con su centro geométrico. La masa elemental correspondiente ∆mi=ρ[φ(ξi)-ψ(ξi)]∆хi=[φ(ξi)-ψ(ξi)]∆хi se concentra en el punto (ξi,ηi). Ha llegado el momento de la transición inversa de la masa presentada en forma discreta a la continua. De acuerdo con las fórmulas para calcular las coordenadas (ver Fig. 2) del centro de gravedad, se forman sumas integrales, ilustradas en la Fig. 4a. Al pasar al límite en ∆xi→0 (ξi→xi) de sumas a integrales definidas, obtenga la respuesta final (Fig. 4b). No hay masa en la respuesta. La igualdad S=M debe entenderse sólo como cuantitativa. Las dimensiones aquí son diferentes entre sí.

Con base en las fórmulas generales obtenidas anteriormente, es posible indicar métodos específicos para determinar las coordenadas de los centros de gravedad de los cuerpos.
1. Simetría. Si un cuerpo homogéneo tiene un plano, eje o centro de simetría (Fig. 7), entonces su centro de gravedad se encuentra, respectivamente, en el plano de simetría, eje de simetría o en el centro de simetría.
Fig.7
2. Terrible. El cuerpo se divide en un número finito de partes (Fig. 8), de cada una de las cuales se conocen la posición del centro de gravedad y el área.

Fig.8
3.Método del área negativa. Un caso especial del método de partición (Fig. 9). Se aplica a cuerpos que tienen recortes si se conocen los centros de gravedad del cuerpo sin el recorte y la parte recortada. Un cuerpo en forma de placa con un recorte está representado por una combinación de una placa sólida (sin un recorte) con un área S 1 y un área de la parte recortada S 2 .

Fig.9
4.Método de agrupación. Es un buen complemento a los dos últimos métodos. Después de dividir una figura en sus elementos componentes, conviene volver a combinar algunos de ellos para luego simplificar la solución teniendo en cuenta la simetría de este grupo.
Centros de gravedad de algunos cuerpos homogéneos.
1) Centro de gravedad de un arco circular. Considere el arco AB radio R con un ángulo central. Debido a la simetría, el centro de gravedad de este arco se encuentra en el eje Buey(Figura 10).

Fig.10
Encontremos la coordenada usando la fórmula. Para hacer esto, seleccione en el arco. AB elemento mm' longitud, cuya posición está determinada por el ángulo. Coordinar X elemento mm' voluntad . Sustituyendo estos valores X y d yo y teniendo en cuenta que la integral debe extenderse a toda la longitud del arco, obtenemos:

Dónde l- longitud de arco AB, igual a .
De aquí finalmente encontramos que el centro de gravedad de un arco circular se encuentra sobre su eje de simetría a una distancia del centro. ACERCA DE, igual
donde el ángulo se mide en radianes.
2) Centro de gravedad del área del triángulo. Considere un triángulo que se encuentra en el plano. oxi, cuyas coordenadas de vértices se conocen: yo(xyo,y yo), (i= 1,2,3). Rompiendo el triángulo en tiras estrechas paralelas al lado A 1 A 2, llegamos a la conclusión de que el centro de gravedad del triángulo debe pertenecer a la mediana A 3 METRO 3 (figura 11).

Fig.11
Romper un triángulo en tiras paralelas al lado A 2 A 3, podemos verificar que debe estar en la mediana A 1 METRO 1 . De este modo, el centro de gravedad de un triángulo se encuentra en el punto de intersección de sus medianas, que, como se sabe, separa una tercera parte de cada mediana, contando desde el lado correspondiente.
En particular, para la mediana A 1 METRO 1 obtenemos, teniendo en cuenta que las coordenadas del punto METRO 1 es la media aritmética de las coordenadas de los vértices A 2 y A 3:
xc = X 1 + (2/3)∙(xm 1 - X 1) = X 1 + (2/3)∙[(X 2 + X 3)/2-X 1 ] = (X 1 +X 2 +X 3)/3.
Así, las coordenadas del centro de gravedad del triángulo son la media aritmética de las coordenadas de sus vértices:
X C =(1/3)Σ xyo ; y C =(1/3)Σ y yo.
3) Centro de gravedad del área de un sector circular. Considere un sector de un círculo con radio. R con un ángulo central de 2α, ubicado simétricamente con respecto al eje Buey(Figura 12).
Es obvio que y C = 0, y la distancia desde el centro del círculo desde el cual se corta este sector hasta su centro de gravedad se puede determinar mediante la fórmula:


Fig.12
La forma más sencilla de calcular esta integral es dividiendo el dominio de integración en sectores elementales con un ángulo dφ. Preciso para infinitesimales de primer orden, dicho sector puede ser reemplazado por un triángulo con una base igual a R× dφ y altura R. El área de tal triángulo. dF=(1/2)R 2 ∙dφ, y su centro de gravedad está a una distancia de 2/3 R desde el vértice, por lo tanto en (5) ponemos X = (2/3)R∙cosφ. Sustituyendo en (5) F= α R 2, obtenemos:

Utilizando la última fórmula, calculamos, en particular, la distancia al centro de gravedad. semicírculo.
Sustituyendo α = π/2 en (2), obtenemos: X C = (4R)/(3π) ≅ 0,4 R .
Ejemplo 1. Determinemos el centro de gravedad del cuerpo homogéneo que se muestra en la figura. 13.

Fig.13
El cuerpo es homogéneo y consta de dos partes con forma simétrica. Coordenadas de sus centros de gravedad:
Sus volúmenes:
Por tanto, las coordenadas del centro de gravedad del cuerpo.
Ejemplo 2. Encontremos el centro de gravedad de una placa doblada en ángulo recto. Las dimensiones están en el dibujo (Fig. 14).

Fig.14
Coordenadas de los centros de gravedad:
Áreas:
![]()
|

Fig.15
En este problema, es más conveniente dividir el cuerpo en dos partes: un cuadrado grande y un agujero cuadrado. Sólo el área del agujero debe considerarse negativa. Luego las coordenadas del centro de gravedad de la lámina con el agujero:
coordinar ![]() ya que el cuerpo tiene un eje de simetría (diagonal).
ya que el cuerpo tiene un eje de simetría (diagonal).
Ejemplo 4. El soporte de alambre (Fig. 16) consta de tres secciones de igual longitud. yo.

Fig.16
Coordenadas de los centros de gravedad de los tramos:
Por tanto, las coordenadas del centro de gravedad de todo el soporte son:
Ejemplo 5. Determine la posición del centro de gravedad de la armadura, cuyas varillas tienen la misma densidad lineal (Fig. 17).
Recordemos que en física la densidad de un cuerpo ρ y su gravedad específica g están relacionadas por la relación: γ= ρ gramo, Dónde gramo- aceleración de la gravedad. Para encontrar la masa de un cuerpo tan homogéneo, debes multiplicar la densidad por su volumen.

Fig.17
El término densidad “lineal” o “lineal” significa que para determinar la masa de un alma, la densidad lineal debe multiplicarse por la longitud de esta varilla.
Para resolver el problema, puede utilizar el método de partición. Representando una armadura dada como la suma de 6 varillas individuales, obtenemos:
Dónde yo longitud i el alma, y xyo, y yo- coordenadas de su centro de gravedad.
La solución a este problema se puede simplificar agrupando las últimas 5 barras de la armadura. Es fácil ver que forman una figura con un centro de simetría ubicado en el medio de la cuarta varilla, donde se ubica el centro de gravedad de este grupo de varillas.
Por tanto, una armadura determinada puede representarse mediante una combinación de sólo dos grupos de varillas.
El primer grupo está formado por la primera varilla, para ello l 1 = 4 metros, X 1 = 0 metros, y 1 = 2 m El segundo grupo de varillas consta de cinco varillas, para ello l 2 = 20 metros, X 2 = 3 metros, y 2 = 2 metros.
Las coordenadas del centro de gravedad de la armadura se encuentran mediante la fórmula:
X C = (l 1 ∙X 1 +l 2 ∙X 2)/(l 1 + l 2) = (4∙0 + 20∙3)/24 = 5/2 m;
y C = (l 1 ∙y 1 +l 2 ∙y 2)/(l 1 + l 2) = (4∙2 + 20∙2)/24 = 2m.
Tenga en cuenta que el centro CON se encuentra en la línea recta que une CON 1 y CON 2 y divide el segmento CON 1 CON 2 respecto a: CON 1 CON/SS 2 = (X C - X 1)/(X 2 - X C ) = l 2 /l 1 = 2,5/0,5.
Preguntas de autoevaluación
¿Cómo se llama el centro de fuerzas paralelas?
¿Cómo se determinan las coordenadas del centro de fuerzas paralelas?
¿Cómo determinar el centro de fuerzas paralelas cuya resultante es cero?
¿Qué propiedades tiene el centro de fuerzas paralelas?
¿Qué fórmulas se utilizan para calcular las coordenadas del centro de fuerzas paralelas?
¿Cuál es el centro de gravedad de un cuerpo?
¿Por qué las fuerzas gravitacionales de la Tierra que actúan sobre un punto de un cuerpo pueden considerarse como un sistema de fuerzas paralelas?
¿Escriba la fórmula para determinar la posición del centro de gravedad de cuerpos heterogéneos y homogéneos, la fórmula para determinar la posición del centro de gravedad de secciones planas?
Escriba la fórmula para determinar la posición del centro de gravedad de formas geométricas simples: ¿rectángulo, triángulo, trapezoide y semicírculo?
¿Cuál es el momento estático del área?
Dé un ejemplo de un cuerpo cuyo centro de gravedad se encuentre fuera del cuerpo.
¿Cómo se utilizan las propiedades de simetría para determinar los centros de gravedad de los cuerpos?
¿Cuál es la esencia del método de pesos negativos?
¿Dónde está el centro de gravedad de un arco circular?
¿Qué construcción gráfica se puede utilizar para encontrar el centro de gravedad de un triángulo?
Escribe la fórmula que determina el centro de gravedad de un sector circular.
Usando fórmulas que determinan los centros de gravedad de un triángulo y un sector circular, deriva una fórmula similar para un segmento circular.
¿Qué fórmulas se utilizan para calcular las coordenadas de los centros de gravedad de cuerpos homogéneos, figuras planas y líneas?
¿Cómo se llama el momento estático del área de una figura plana con respecto al eje, cómo se calcula y qué dimensión tiene?
¿Cómo determinar la posición del centro de gravedad de un área si se conoce la posición de los centros de gravedad de sus partes individuales?
¿Qué teoremas auxiliares se utilizan para determinar la posición del centro de gravedad?
En la práctica de la ingeniería, sucede que existe la necesidad de calcular las coordenadas del centro de gravedad de una figura plana compleja que consta de elementos simples para los cuales se conoce la ubicación del centro de gravedad. Esta tarea es parte de la tarea de determinar...
Características geométricas de secciones compuestas de vigas y varillas. A menudo, los ingenieros de diseño de matrices de corte tienen que enfrentarse a preguntas similares al determinar las coordenadas del centro de presión, los desarrolladores de esquemas de carga para varios vehículos al colocar la carga, los diseñadores de estructuras metálicas de construcción al seleccionar las secciones transversales de los elementos y, por supuesto, estudiantes al cursar las disciplinas “Mecánica Teórica” y “Resistencia de Materiales”.
Biblioteca de figuras elementales.

Para figuras planas simétricas, el centro de gravedad coincide con el centro de simetría. El grupo simétrico de objetos elementales incluye: círculo, rectángulo (incluido el cuadrado), paralelogramo (incluido el rombo), polígono regular.
De las diez figuras presentadas en la figura anterior, sólo dos son básicas. Es decir, utilizando triángulos y sectores de círculos, puedes combinar casi cualquier figura de interés práctico. Cualquier curva arbitraria se puede dividir en secciones y reemplazar con arcos circulares.
Las ocho figuras restantes son las más comunes, por lo que se incluyeron en esta biblioteca única. En nuestra clasificación, estos elementos no son básicos. A partir de dos triángulos se puede formar un rectángulo, un paralelogramo y un trapezoide. Un hexágono es la suma de cuatro triángulos. Un segmento de círculo es la diferencia entre un sector de un círculo y un triángulo. El sector anular de un círculo es la diferencia entre dos sectores. Un círculo es un sector de un círculo con un ángulo α=2*π=360˚. Un semicírculo es, por tanto, un sector de un círculo con un ángulo α=π=180˚.
Cálculo en Excel de las coordenadas del centro de gravedad de una figura compuesta.
Siempre es más fácil transmitir y percibir información considerando un ejemplo que estudiar el tema mediante cálculos puramente teóricos. Consideremos la solución al problema "¿Cómo encontrar el centro de gravedad?" usando el ejemplo de la figura compuesta que se muestra en la figura debajo de este texto.

La sección compuesta es un rectángulo (con dimensiones a1 =80 milímetros, b1 =40 mm), al que se le añadió un triángulo isósceles en la parte superior izquierda (con el tamaño de la base a2 =24 mm y altura h2 =42 mm) y del cual se recortó un semicírculo arriba a la derecha (con el centro en el punto con coordenadas X03 =50 mm y y03 =40 mm, radio r3 = 26 mm).
Usaremos un programa para ayudarle a realizar los cálculos. Excel o programa OOo cálculo . ¡Cualquiera de ellos hará frente fácilmente a nuestra tarea!
En celdas con amarillo lo llenaremos preliminar auxiliar cálculos .
Calculamos los resultados en celdas con un relleno de color amarillo claro.
Azul la fuente es datos iniciales .
Negro la fuente es intermedio resultados del cálculo .
Rojo la fuente es final resultados del cálculo .
Comenzamos a resolver el problema: comenzamos a buscar las coordenadas del centro de gravedad de la sección.
Datos iniciales:
1. Escribiremos en consecuencia los nombres de las figuras elementales que forman una sección compuesta.
a la celda D3: Rectángulo
a la celda E3: Triángulo
a la celda F3: Semicírculo
2. Utilizando la "Biblioteca de figuras elementales" presentada en este artículo, determinaremos las coordenadas de los centros de gravedad de los elementos de la sección compuesta. xci Y yci en mm en relación con los ejes 0x y 0y seleccionados arbitrariamente y escriba
a la celda D4: =80/2 = 40,000
xc 1 = a 1 /2
a la celda D5: =40/2 =20,000
yc 1 = b 1 /2
a la celda E4: =24/2 =12,000
xc 2 = a 2 /2
a la celda E5: =40+42/3 =54,000
yc 2 = b 1 + h 2 /3
a la celda F4: =50 =50,000
xc 3 = X03
a la celda F5: =40-4*26/3/PI() =28,965
yc 3 = y 03 -4* r3 /3/ π
3. Calculemos las áreas de los elementos. F 1 , F 2 , F3 en mm2, utilizando nuevamente las fórmulas de la sección “Biblioteca de figuras elementales”
en la celda D6: =40*80 =3200
F1 = a 1 * b1
en la celda E6: =24*42/2 =504
F2 = a2 *h2 /2
en la celda F6: =-PI()/2*26^2 =-1062
F3 =-π/2*r3 ^2
El área del tercer elemento, el semicírculo, es negativa porque es un recorte, ¡un espacio vacío!

Cálculo de las coordenadas del centro de gravedad:
4. Determina el área total de la figura final. F0 en mm2
en la celda combinada D8E8F8: =D6+E6+F6 =2642
F0 = F 1 + F 2 + F3
5. Calculemos los momentos estáticos de una figura compuesta. Sx Y si en mm3 respecto a los ejes seleccionados 0x y 0y
en la celda combinada D9E9F9: =D5*D6+E5*E6+F5*F6 =60459
Sx = yc1 * F1 + yc2 *F2 + yc3 *F3
en la celda combinada D10E10F10: =D4*D6+E4*E6+F4*F6 =80955
si = xc1 * F1 + xc2 *F2 + xc3 *F3
6. Y finalmente, calculemos las coordenadas del centro de gravedad de la sección compuesta. xc Y yc en mm en el sistema de coordenadas seleccionado 0x - 0y
en la celda combinada D11E11F11: =D10/D8 =30,640
xc = si / F0
en la celda combinada D12E12F12: =D9/D8 =22,883
Yc=Sx/F0
El problema se resolvió, se completó el cálculo en Excel: ¡se encontraron las coordenadas del centro de gravedad de la sección, compiladas utilizando tres elementos simples!
Conclusión.
Se eligió el ejemplo del artículo por ser muy simple para facilitar la comprensión de la metodología para calcular el centro de gravedad de una sección compleja. El método consiste en dividir cualquier figura compleja en elementos simples con ubicaciones conocidas de los centros de gravedad y realizar cálculos finales para toda la sección.
Si la sección se compone de perfiles laminados, esquinas y canales, entonces no es necesario dividirlos en rectángulos y cuadrados con sectores circulares recortados “π/2”. Las coordenadas de los centros de gravedad de estos perfiles se dan en las tablas GOST, es decir, tanto el ángulo como el canal serán los elementos elementales básicos en sus cálculos de secciones compuestas (no tiene sentido hablar de vigas en I, tubos, varillas y hexágonos: son secciones centralmente simétricas).
¡La ubicación de los ejes de coordenadas, por supuesto, no afecta la posición del centro de gravedad de la figura! Por lo tanto, elija un sistema de coordenadas que simplifique sus cálculos. Si, por ejemplo, en nuestro ejemplo tuviera que girar el sistema de coordenadas 45˚ en el sentido de las agujas del reloj, calcular las coordenadas de los centros de gravedad de un rectángulo, triángulo y semicírculo se convertiría en otra etapa de cálculo separada y engorrosa que no se puede realizar " en la cabeza".
El archivo de cálculo de Excel que se presenta a continuación no es un programa en este caso. Más bien, es un boceto de una calculadora, un algoritmo, una plantilla que se sigue en cada caso concreto. crea tu propia secuencia de fórmulas para celdas con un relleno amarillo brillante.
¡Ahora ya sabes cómo encontrar el centro de gravedad de cualquier sección! El cálculo completo de todas las características geométricas de secciones compuestas complejas arbitrarias se considerará en uno de los próximos artículos de la sección "". Sigue las novedades en el blog.
Para recepción información sobre el lanzamiento de nuevos artículos y para descargar archivos de programa de trabajo Le pido que se suscriba a los anuncios en la ventana ubicada al final del artículo o en la ventana en la parte superior de la página.
Después de ingresar su dirección de correo electrónico y hacer clic en el botón "Recibir anuncios de artículos" NO LO OLVIDE CONFIRMA TU SUSCRIPCIÓN haciendo clic en el enlace en una carta que le llegará inmediatamente a la dirección de correo electrónico especificada (a veces en la carpeta « Correo basura » )!
Unas pocas palabras sobre el vaso, la moneda y los dos tenedores, que se muestran en el "icono de ilustración" al principio del artículo. Seguramente muchos de vosotros conocéis este “truco” que provoca miradas de admiración en niños y adultos no iniciados. El tema de este artículo es el centro de gravedad. ¡Son él y el punto de apoyo, jugando con nuestra conciencia y experiencia, quienes simplemente están engañando a nuestra mente!
El centro de gravedad del sistema “tenedor+moneda” siempre está situado en fijado distancia verticalmente hacia abajo desde el borde de la moneda, que a su vez es el punto de apoyo. ¡Esta es una posición de equilibrio estable! Si sacude las horquillas, inmediatamente se hace evidente que el sistema se esfuerza por recuperar su posición estable anterior. Imaginemos un péndulo: un punto de fijación (= el punto de apoyo de una moneda en el borde de un vaso), una varilla-eje del péndulo (= en nuestro caso, el eje es virtual, ya que la masa de las dos horquillas es repartidos en diferentes direcciones del espacio) y una carga en la parte inferior del eje (= el centro de gravedad de todo el sistema “horquilla” + moneda"). Si comienza a desviar el péndulo de la vertical en cualquier dirección (hacia adelante, atrás, izquierda, derecha), inevitablemente volverá a su posición original bajo la influencia de la gravedad. estado estacionario de equilibrio(con nuestros tenedores y monedas pasa lo mismo)!
Si no entiendes pero quieres entenderlo, descúbrelo tú mismo. ¡Es muy interesante “llegar allí” usted mismo! Agregaré que el mismo principio de utilizar el equilibrio estable también se implementa en el juguete Vanka-stand-up. Sólo el centro de gravedad de este juguete se encuentra por encima del punto de apoyo, pero por debajo del centro del hemisferio de la superficie de soporte.
¡¡¡Siempre me alegra ver sus comentarios, queridos lectores!!!
Preguntar, RESPECTO A trabajo del autor, descargar archivo DESPUÉS DE SUSCRIBIRSE para anuncios de artículos.
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0