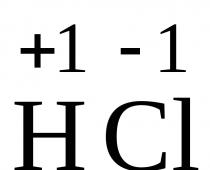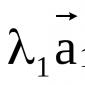Ecuación diferencial de movimiento punto material bajo fuerza F se puede representar en la siguiente forma vectorial:

Dado que la masa de un punto metro se acepta como constante, entonces se puede ingresar bajo el signo de derivada. Entonces

La fórmula (1) expresa el teorema sobre el cambio en el momento de un punto en forma diferencial: la primera derivada con respecto al tiempo del momento de un punto es igual a la fuerza que actúa sobre el punto.

En proyecciones sobre ejes de coordenadas (1) se puede representar como

Si ambos lados (1) se multiplican por dt, luego obtenemos otra forma del mismo teorema: el teorema del momento en forma diferencial:

aquellos. el diferencial del momento de un punto es igual al impulso elemental de la fuerza que actúa sobre el punto.

Proyectando ambas partes de (2) sobre los ejes de coordenadas, obtenemos

Integrando ambas partes de (2) desde cero hasta t (Fig. 1), tenemos

¿Dónde está la velocidad del punto en este momento? t; - velocidad a t = 0;

S- impulso de fuerza en el tiempo t.

Una expresión en la forma (3) a menudo se denomina teorema del momento en forma finita (o integral): el cambio en el impulso de un punto durante cualquier período de tiempo es igual al impulso de la fuerza durante el mismo período de tiempo.

En proyecciones sobre ejes de coordenadas, este teorema se puede representar de la siguiente forma:

Para un punto material, el teorema sobre el cambio de impulso en cualquiera de sus formas no difiere esencialmente de las ecuaciones diferenciales de movimiento de un punto.

Teorema sobre el cambio de impulso de un sistema

La cantidad de movimiento del sistema se llamará cantidad vectorial. q, igual a la suma geométrica (vector principal) de las cantidades de movimiento de todos los puntos del sistema.

Considere un sistema que consta de norte puntos materiales. Compongamos ecuaciones diferenciales de movimiento para este sistema y sumémoslas término por término. Entonces obtenemos:

La última suma, debido a la propiedad de las fuerzas internas, es igual a cero. Además,

Finalmente encontramos:

La ecuación (4) expresa el teorema sobre el cambio de momento del sistema en forma diferencial: la derivada temporal del impulso del sistema es igual a la suma geométrica de todas las fuerzas externas que actúan sobre el sistema.

Encontremos otra expresión para el teorema. Deja entrar el momento t= 0 la cantidad de movimiento del sistema es P 0, y en el momento del tiempo t 1 se vuelve igual Pregunta 1. Luego, multiplicando ambos lados de la igualdad (4) por dt e integrando obtenemos:

O donde:

(S-impulso de fuerza)

dado que las integrales de la derecha dan impulsos de fuerzas externas,

La ecuación (5) expresa el teorema sobre el cambio en el momento del sistema en forma integral: el cambio en el impulso del sistema durante un cierto período de tiempo es igual a la suma de los impulsos de las fuerzas externas que actúan sobre el sistema durante el mismo período de tiempo.

En proyecciones sobre los ejes de coordenadas tendremos:

Ley de conservación del impulso.

Del teorema sobre el cambio de momento de un sistema, se pueden obtener los siguientes corolarios importantes:

1. Sea la suma de todas las fuerzas externas que actúan sobre el sistema igual a cero:

Entonces de la ecuación (4) se deduce que en este caso Q = constante.

De este modo, Si la suma de todas las fuerzas externas que actúan sobre el sistema es igual a cero, entonces el vector del momento del sistema será constante en magnitud y dirección.

2. 01Deja Fuerzas externas, que actúan sobre el sistema, son tales que la suma de sus proyecciones sobre algún eje (por ejemplo, Ox) es igual a cero:

Entonces de las ecuaciones (4`) se deduce que en este caso Q = constante.

De este modo, Si la suma de las proyecciones de todas las fuerzas externas que actúan sobre cualquier eje es igual a cero, entonces la proyección de la cantidad de movimiento del sistema sobre este eje es un valor constante.

Estos resultados expresan Ley de conservación del momento de un sistema. De ellos se deduce que las fuerzas internas no pueden cambiar la cantidad total de movimiento del sistema.

Veamos algunos ejemplos:

· Fenómeno de devolución del rollo. Si consideramos el rifle y la bala como un solo sistema, entonces la presión de los gases de la pólvora durante el disparo será una fuerza interna. Esta fuerza no puede cambiar el impulso total del sistema. Pero dado que los gases de pólvora, al actuar sobre la bala, le imparten una cierta cantidad de movimiento hacia adelante, al mismo tiempo deben impartir al rifle la misma cantidad de movimiento en dirección hacia adelante. direccion contraria. Esto hará que el rifle se mueva hacia atrás, es decir. el llamado retorno. Un fenómeno similar ocurre al disparar un arma (retroceso).

· Funcionamiento de la hélice (hélice). La hélice imparte movimiento a una determinada masa de aire (o agua) a lo largo del eje de la hélice, devolviendo esta masa hacia atrás. Si consideramos la masa lanzada y el avión (o barco) como un solo sistema, entonces las fuerzas de interacción entre la hélice y el medio ambiente, como internas, no pueden cambiar la cantidad total de movimiento de este sistema. Por lo tanto, cuando se devuelve una masa de aire (agua), el avión (o el barco) recibe una velocidad de avance correspondiente tal que la cantidad total de movimiento del sistema considerado sigue siendo igual a cero, ya que era cero antes de que comenzara el movimiento. .

Un efecto similar se consigue mediante la acción de remos o ruedas de paletas.

· Propulsión R e c t i v e. En un cohete (cohete), los productos gaseosos de la combustión del combustible son expulsados ​​a gran velocidad por el orificio situado en la cola del cohete (desde la tobera del motor a reacción). Las fuerzas de presión que actúan en este caso serán fuerzas internas y no pueden cambiar el momento total del sistema de gases de pólvora del cohete. Pero como los gases que se escapan tienen un cierto movimiento dirigido hacia atrás, el cohete recibe una velocidad de avance correspondiente.

Teorema de los momentos respecto de un eje.

Considere el punto de masa material. metro, moviéndose bajo la influencia de la fuerza. F. Encontremos para ello la relación entre el momento de los vectores. mV Y F en relación con algún eje Z fijo.

m z (F) = xF - yF (7)

Lo mismo ocurre con el valor metro(mV), si se saca metro Estará fuera de paréntesis

metro z (mV) = m(xV - yV)(7`)

Tomando las derivadas con respecto al tiempo de ambos lados de esta igualdad, encontramos

En el lado derecho de la expresión resultante, el primer paréntesis es igual a 0, ya que dx/dt=V y dу/dt = V, el segundo paréntesis según la fórmula (7) es igual a

mz(F), ya que según la ley básica de la dinámica:

Finalmente tendremos (8)

La ecuación resultante expresa el teorema de los momentos con respecto al eje: la derivada temporal del momento de impulso de un punto con respecto a cualquier eje es igual al momento de la fuerza actuante con respecto al mismo eje. Un teorema similar se cumple para momentos con respecto a cualquier centro O.

Dado que la masa del punto es constante y su aceleración, la ecuación (2), que expresa la ley básica de la dinámica, se puede representar en la forma

La ecuación (32) expresa simultáneamente el teorema sobre el cambio en el momento de un punto en forma diferencial: la derivada temporal del momento de un punto es igual a la suma de las fuerzas que actúan sobre el punto.

Supongamos que un punto en movimiento tiene una velocidad en el momento del tiempo y una velocidad en el momento. Luego multiplicamos ambos lados de la igualdad (32) por y les tomamos integrales definidas. En este caso, a la derecha, donde se produce la integración en el tiempo, los límites de la integral serán y a la izquierda, donde se integra la velocidad, los límites de la integral serán los valores de velocidad correspondientes.

Como la integral de es igual, el resultado es

Las integrales de la derecha, como se desprende de la fórmula (30), representan impulsos fuerzas activas. Por lo tanto finalmente será

La ecuación (33) expresa el teorema sobre el cambio en el momento de un punto en su forma final: el cambio en el momento de un punto durante un cierto período de tiempo es igual a la suma de los impulsos de todas las fuerzas que actúan sobre el punto sobre el mismo periodo de tiempo.

Al resolver problemas, en lugar de la ecuación vectorial (33), a menudo se utilizan ecuaciones en proyecciones. Proyectando ambos lados de la igualdad (33) sobre los ejes de coordenadas, obtenemos

En el caso de un movimiento rectilíneo que se produce a lo largo del eje, el teorema se expresa mediante la primera de estas ecuaciones.

Resolución de problemas. Las ecuaciones (33) o (34) permiten, sabiendo cómo cambia la velocidad de un punto cuando un punto se mueve, determinar el impulso de las fuerzas actuantes (el primer problema de la dinámica) o, conociendo los impulsos de las fuerzas actuantes, determinar cómo cambia la velocidad de un punto cuando se mueve (el segundo problema de la dinámica). Al resolver el segundo problema, cuando se dan fuerzas, es necesario calcular sus impulsos, como se puede ver en las igualdades (30) o (31), esto sólo se puede hacer cuando las fuerzas son constantes o dependen únicamente del tiempo.

Por lo tanto, las ecuaciones (33), (34) se pueden usar directamente para resolver el segundo problema de dinámica, cuando los datos y cantidades requeridas en el problema incluyen: fuerzas actuantes, tiempo de movimiento del punto y sus velocidades inicial y final (es decir, cantidades), y las fuerzas deben ser constantes o dependientes sólo del tiempo.

Problema 95. Un punto con una masa de kg se mueve en un círculo con una velocidad numéricamente constante. Determine el impulso de la fuerza que actúa sobre el punto durante el tiempo durante el cual el punto pasa un cuarto del círculo.

Solución. Según el teorema sobre el cambio de impulso, construyendo geométricamente la diferencia entre estas cantidades de movimiento (Fig.222), encontramos en el triángulo rectángulo resultante

Pero de acuerdo con las condiciones del problema, por lo tanto,

Para el cálculo analítico, utilizando las dos primeras ecuaciones (34), podemos encontrar

Problema 96. A una carga que tiene una masa y se encuentra en un plano horizontal se le da (mediante un empujón) una velocidad inicial. El movimiento posterior de la carga se frena mediante una fuerza constante F. Determine cuánto tiempo tardará la carga para detener,

Solución. De los datos del problema, está claro que para determinar el tiempo de movimiento se puede utilizar el teorema probado. Representamos la carga en una posición arbitraria (Fig. 223). Sobre él actúa la fuerza de gravedad P, la reacción del plano N y la fuerza de frenado F. Dirigiendo el eje en la dirección del movimiento, componemos la primera de las ecuaciones (34)

En este caso, la velocidad en el momento de detenerse), a. De las fuerzas, sólo la fuerza F da proyección sobre el eje, ya que es constante, ¿dónde está el tiempo de frenado? Sustituyendo todos estos datos en la ecuación (a), obtenemos el tiempo requerido

El sistema discutido en el teorema puede ser cualquier sistema mecánico formado por cualquier cuerpo.

Declaración del teorema

La cantidad de movimiento (impulso) de un sistema mecánico es una cantidad igual a la suma de las cantidades de movimiento (impulsos) de todos los cuerpos incluidos en el sistema. El impulso de las fuerzas externas que actúan sobre los cuerpos del sistema es la suma de los impulsos de todas las fuerzas externas que actúan sobre los cuerpos del sistema.

( kgm/s)

El teorema sobre el cambio de impulso de un sistema establece

El cambio en el impulso del sistema durante un cierto período de tiempo es igual al impulso de las fuerzas externas que actúan sobre el sistema durante el mismo período de tiempo.

Ley de conservación del impulso de un sistema.

Si la suma de todas las fuerzas externas que actúan sobre el sistema es cero, entonces la cantidad de movimiento (momento) del sistema es una cantidad constante.

, obtenemos la expresión del teorema sobre el cambio en el momento del sistema en forma diferencial:

Habiendo integrado ambos lados de la igualdad resultante durante un período de tiempo arbitrariamente tomado entre algunos y , obtenemos la expresión del teorema sobre el cambio en el momento del sistema en forma integral:

Ley de conservación del impulso. (Ley de conservación del impulso.) afirma que la suma vectorial de los impulsos de todos los cuerpos del sistema es un valor constante si la suma vectorial de las fuerzas externas que actúan sobre el sistema es igual a cero.

(momento de impulso m 2 kg s −1)

Teorema sobre el cambio del momento angular con respecto al centro.

derivada con respecto al tiempo del impulso ( momento cinético) de un punto material con respecto a cualquier centro fijo es igual al momento de la fuerza que actúa sobre el punto con respecto al mismo centro.

dk 0 /dt = M 0 (F ) .

Teorema sobre el cambio del momento angular con respecto a un eje

la derivada temporal del momento de impulso (momento cinético) de un punto material con respecto a cualquier eje fijo es igual al momento de la fuerza que actúa sobre este punto con respecto al mismo eje.

dk X /dt = M X (F ); dk y /dt = M y (F ); dk z /dt = M z (F ) .

Considere un punto material METRO masa metro , moviéndose bajo la influencia de la fuerza. F (Figura 3.1). Anotemos y construyamos el vector del momento angular (momento cinético) METRO 0 punto material relativo al centro oh :

Diferenciamos la expresión del momento angular (momento cinético k 0) por tiempo:

Porque dr. /dt = V , entonces el producto vectorial V ⊗ metro ⋅ V (vectores colineales V Y metro ⋅ V ) es igual a cero. Al mismo tiempo re(m) ⋅ V) /dt = F según el teorema del impulso de un punto material. Por lo tanto entendemos que

dk 0 /dt = r ⊗F , (3.3)

Dónde r ⊗F = METRO 0 (F ) – vector-momento de fuerza F relativo a un centro fijo oh . Vector k 0 ⊥ plano ( r , metro ⊗V ), y el vector METRO 0 (F ) ⊥ avión ( r ,F ), finalmente tenemos

dk 0 /dt = M 0 (F ) . (3.4)

La ecuación (3.4) expresa el teorema sobre el cambio en el momento angular (momento angular) de un punto material con respecto al centro: la derivada temporal del momento de impulso (momento cinético) de un punto material con respecto a cualquier centro fijo es igual al momento de fuerza que actúa sobre el punto con respecto al mismo centro.

Proyectando la igualdad (3.4) sobre los ejes de coordenadas cartesianas, obtenemos

dk X /dt = M X (F ); dk y /dt = M y (F ); dk z /dt = M z (F ) . (3.5)

Las igualdades (3.5) expresan el teorema sobre el cambio en el momento angular (momento cinético) de un punto material con respecto al eje: la derivada temporal del momento de impulso (momento cinético) de un punto material con respecto a cualquier eje fijo es igual al momento de la fuerza que actúa sobre este punto con respecto al mismo eje.

Consideremos las consecuencias que se derivan de los teoremas (3.4) y (3.5).

Corolario 1. Considere el caso cuando la fuerza F durante todo el movimiento el punto pasa por el centro estacionario oh (caso de fuerza central), es decir Cuando METRO 0 (F ) = 0. Entonces del teorema (3.4) se deduce que k 0 = constante ,

aquellos. en el caso de una fuerza central, el momento angular (momento cinético) de un punto material con respecto al centro de esta fuerza permanece constante en magnitud y dirección (Figura 3.2).

Figura 3.2

De la condición k 0 = constante de ello se deduce que la trayectoria de un punto en movimiento es una curva plana, cuyo plano pasa por el centro de esta fuerza.

Corolario 2. Dejar METRO z (F ) = 0, es decir fuerza cruza el eje z o paralelo a él. En este caso, como se puede ver en la tercera de las ecuaciones (3.5), k z = constante ,

aquellos. Si el momento de fuerza que actúa sobre un punto con respecto a cualquier eje fijo es siempre cero, entonces el momento angular (momento cinético) del punto con respecto a este eje permanece constante.

Prueba del teorema sobre el cambio de impulso.

Sea el sistema formado por puntos materiales con masas y aceleraciones. Dividimos todas las fuerzas que actúan sobre los cuerpos del sistema en dos tipos:

Las fuerzas externas son fuerzas que actúan desde cuerpos no incluidos en el sistema considerado. La resultante de fuerzas externas que actúan sobre un punto material con número i vamos a denotar

Las fuerzas internas son aquellas fuerzas con las que los cuerpos del propio sistema interactúan entre sí. La fuerza con la que sobre el punto con el número. i el punto con el número es válido k, denotaremos , y la fuerza de influencia i punto en kº punto - . Obviamente, cuando, entonces

Usando la notación introducida, escribimos la segunda ley de Newton para cada uno de los puntos materiales considerados en la forma

Teniendo en cuenta que y sumando todas las ecuaciones de la segunda ley de Newton, obtenemos:

La expresión representa la suma de todas las fuerzas internas que actúan en el sistema. Según la tercera ley de Newton, en esta suma, a cada fuerza le corresponde una fuerza tal que, por tanto, se cumple Dado que toda la suma consta de esos pares, la suma misma es cero. Así, podemos escribir

Usando la notación para el momento del sistema, obtenemos

Al introducir en consideración el cambio en el impulso de las fuerzas externas , obtenemos la expresión del teorema sobre el cambio en el momento del sistema en forma diferencial:

Así, cada una de las últimas ecuaciones obtenidas nos permite afirmar: un cambio en el impulso del sistema se produce sólo como resultado de la acción de fuerzas externas, y las fuerzas internas no pueden tener ninguna influencia sobre este valor.

Habiendo integrado ambos lados de la igualdad resultante en un intervalo de tiempo arbitrariamente tomado entre algunos y , obtenemos la expresión del teorema sobre el cambio en el impulso del sistema en forma integral:

donde y son los valores de la cantidad de movimiento del sistema en momentos de tiempo y, respectivamente, y es el impulso de fuerzas externas durante un período de tiempo. De acuerdo con lo dicho anteriormente y las notaciones introducidas,

Teorema sobre el cambio de impulso de un punto

Dado que la masa de un punto es constante y su aceleración, la ecuación que expresa la ley básica de la dinámica se puede representar en la forma

La ecuación expresa simultáneamente el teorema sobre el cambio en el momento de un punto en forma diferencial: derivada del tiempo del momento de un punto es igual a la suma geométrica de las fuerzas que actúan sobre el punto.

Integramos esta ecuación. Deja que la masa apunte metro, moviéndose bajo la influencia de la fuerza (Fig. 15), tiene en este momento t=0 velocidad, y en este momento t 1 velocidad.

Fig.15

Luego multiplicamos ambos lados de la igualdad por y les tomamos integrales definidas. En este caso, a la derecha, donde la integración ocurre en el tiempo, los límites de las integrales serán 0 y t 1, y a la izquierda, donde se integra la velocidad, los límites de la integral serán los valores correspondientes de velocidad y . Desde la integral de es igual , entonces como resultado obtenemos:

.

Las integrales de la derecha representan los impulsos de las fuerzas actuantes. Por tanto, finalmente tendremos:

.

La ecuación expresa el teorema sobre el cambio en el momento de un punto en su forma final: el cambio en el impulso de un punto durante un cierto período de tiempo es igual a la suma geométrica de los impulsos de todas las fuerzas que actúan sobre el punto durante el mismo período de tiempo ( arroz. 15).

Al resolver problemas, a menudo se utilizan ecuaciones en proyecciones en lugar de ecuaciones vectoriales.

En el caso de un movimiento rectilíneo que se produce a lo largo del eje Oh el teorema se expresa mediante la primera de estas ecuaciones.

Ejemplo 9. Encuentra la ley del movimiento de un punto material de masa. metro, moviéndose a lo largo del eje X bajo la influencia de una fuerza constante en módulo F(Fig. 16) en condiciones iniciales: , en .

Fig.16

Solución. vamos a componer ecuación diferencial movimiento de un punto en proyección sobre un eje X: . Integrando esta ecuación encontramos: . La constante se determina a partir de la condición inicial para la velocidad y es igual a . Finalmente

.

Además, teniendo en cuenta que v = dx/dt, llegamos a la ecuación diferencial: , integrando lo cual obtenemos

La constante se determina a partir de la condición inicial de la coordenada del punto. Es igual. En consecuencia, la ley del movimiento de un punto tiene la forma

Ejemplo 10. Carga de peso R(Fig.17) comienza a moverse desde el reposo a lo largo de un plano horizontal suave bajo la influencia de una fuerza. F = nudos. Encuentre la ley del movimiento de la carga.

Fig.17

Solución. Elijamos el origen del sistema de coordenadas. ACERCA DE en la posición inicial de la carga y dirigir el eje X en la dirección del movimiento (Fig. 17). Entonces las condiciones iniciales tienen la forma: X(t= 0) = 0,v( t= 0) = 0. Las fuerzas actúan sobre la carga. F,PAG y fuerza de reacción plana norte. Proyecciones de estas fuerzas sobre el eje. X tener significados FX = F = kt, RX = 0, nx= 0, por lo que la ecuación de movimiento correspondiente se puede escribir de la siguiente manera: . Separando las variables en esta ecuación diferencial y luego integrando, obtenemos: v = gramokt 2 /2PAG + C 1 . Sustituyendo los datos iniciales ( v(0) = 0), encontramos que C 1 = 0, y obtenemos la ley del cambio de velocidad. .

La última expresión, a su vez, es una ecuación diferencial, integrando la cual encontramos la ley del movimiento de un punto material: . La constante incluida aquí se determina a partir de la segunda condición inicial. X(0) = 0. Es fácil comprobarlo. Finalmente

Ejemplo 11. Sobre una carga en reposo sobre un plano horizontal liso (ver Fig. 17) a una distancia a desde el origen, comienza a actuar en la dirección positiva del eje. X fuerza F = k 2 (PAG/gramo)X, Dónde R - peso de la carga. Encuentre la ley del movimiento de la carga.

Solución. Ecuación de movimiento de la carga considerada (punto material) en proyección sobre el eje X

Las condiciones iniciales de la ecuación (1) tienen la forma: X(t= 0) = a, v( t= 0) = 0.

Representemos la derivada temporal de la velocidad incluida en la ecuación (1) de la siguiente manera:

.

Sustituyendo esta expresión en la ecuación (1) y reduciendo por ( PAG/gramo), obtenemos

Separando las variables en la última ecuación, encontramos que. Integrando este último, tenemos: . Usando condiciones iniciales , obtenemos , y, por lo tanto,

, . (2)

Dado que la fuerza actúa sobre la carga en la dirección positiva del eje. X, entonces está claro que debería moverse en la misma dirección. Por lo tanto, en la solución (2) se debe elegir el signo más. Reemplazando aún más en la segunda expresión (2) con , obtenemos una ecuación diferencial para determinar la ley de movimiento de la carga. De donde, separando las variables, tenemos

.

Integrando este último encontramos: . Después de encontrar la constante finalmente obtenemos

Ejemplo 12. Pelota METRO masas metro(Fig. 18) cae sin velocidad inicial bajo la influencia de la gravedad. Cuando la pelota cae, experimenta resistencia, donde – coeficiente de resistencia constante. Encuentra la ley del movimiento de la pelota.

Fig.18

Solución. Introduzcamos un sistema de coordenadas con el origen en el punto de ubicación de la pelota en t= 0, dirigiendo el eje en verticalmente hacia abajo (Fig. 18). Ecuación diferencial del movimiento de una bola en proyección sobre el eje. en entonces tiene la forma

Las condiciones iniciales de la pelota se escriben de la siguiente manera: y(t= 0) = 0, v( t= 0) = 0.

Separando las variables en la ecuación (1)

e integrando encontramos: , donde . O después de encontrar una constante

o . (2)

De ello se deduce que la velocidad máxima, es decir la velocidad en , es igual a .

Para encontrar la ley del movimiento, reemplace v en la ecuación (2) por dy/dt. Luego, integrando la ecuación resultante teniendo en cuenta la condición inicial, finalmente encontramos

.

Ejemplo 13. Submarino de investigación de forma y masa esférica. metro= = 1,5×10 5 kg comienza a descender con los motores apagados, teniendo una velocidad horizontal v X 0 = 30 EM y flotabilidad negativa R 1 = 0.01mg, Dónde – suma vectorial de la fuerza de flotabilidad de Arquímedes q y gravedad mg, actuando sobre el barco (Fig. 20). Fuerza de resistencia al agua , kg/s. Determine las ecuaciones de movimiento del barco y su trayectoria.

La cantidad de movimiento de un punto material. llamada cantidad vectorial mV, igual al producto de la masa de un punto por su vector velocidad. Vector mV aplicado a un punto en movimiento.

La cantidad de movimiento del sistema. llamada cantidad vectorial q, igual a la suma geométrica (vector principal) de las cantidades de movimiento de todos los puntos del sistema:

Vector q es un vector libre. En el sistema de unidades SI, el módulo de momento se mide en kg m/s o N s.

Como regla general, las velocidades de todos los puntos del sistema son diferentes (ver, por ejemplo, la distribución de velocidades de los puntos de una rueda en movimiento, que se muestra en la figura 6.21) y, por lo tanto, la suma directa de vectores en el lado derecho de la igualdad (17.2) es difícil. Encontremos una fórmula con la ayuda de la cual la cantidad q mucho más fácil de calcular. De la igualdad (16.4) se deduce que

Tomando la derivada temporal de ambos lados, obtenemos Por tanto, teniendo en cuenta la igualdad (17.2), encontramos que

es decir, el momento del sistema es igual al producto de la masa de todo el sistema por la velocidad de su centro de masa.

Tenga en cuenta que el vector P, Al igual que el principal vector de fuerzas en estática, es una especie de vector generalizado característico del movimiento de todo el sistema mecánico. En el caso general del movimiento de un sistema, su momento es q Puede considerarse como una característica de la parte traslacional del movimiento del sistema junto con su centro de masa. Si, cuando el sistema (cuerpo) se mueve, el centro de masa está estacionario, entonces la cantidad de movimiento del sistema será igual a cero. Éste es, por ejemplo, el impulso de un cuerpo que gira alrededor de un eje fijo que pasa por su centro de masa.

Ejemplo. Determine la cantidad de movimiento del sistema mecánico (Fig. 17.1, A), compuesto por carga A masa t un - 2 kg, bloque homogéneo EN peso 1 kg y ruedas D masa metro re - 4 kg. Carga A se mueve a velocidad VA- 2 m/s, rueda D Rueda sin deslizarse, el hilo es inextensible y ingrávido. Solución. Cantidad de movimiento de un sistema de cuerpos.

Cuerpo A avanza y Q A = m A V A(numéricamente Preguntas y respuestas= 4 kg m/s, dirección del vector Preguntas y respuestas coincide con la dirección V A). Bloquear EN se compromete movimiento rotacional alrededor de un eje fijo que pasa por su centro de masa; por eso, QB- 0. Rueda D hace un plano paralelo

movimiento; su centro de velocidad instantánea está en el punto A, por lo tanto la velocidad de su centro de masa (punto MI) igual a V E = V A /2= 1m/s. Cantidad de movimiento de la rueda Q D - m D V E - 4 kg m/s; vector QD dirigido horizontalmente hacia la izquierda.

Representando los vectores Preguntas y respuestas Y QD en la Fig. 17.1, b, encuentra la cantidad de movimiento q sistemas según la fórmula (a). Teniendo en cuenta las direcciones y valores numéricos de las cantidades, obtenemos Q ~^Q A +Q E=4l/2~ kg m/s, dirección del vector q mostrado en la Fig. 17.1, b.

Teniendo en cuenta que -dV/dt, La ecuación (13.4) de la ley básica de la dinámica se puede representar como

La ecuación (17.4) expresa el teorema sobre el cambio en el momento de un punto en forma diferencial: en cada instante de tiempo, la derivada temporal del momento de un punto es igual a la fuerza que actúa sobre el punto. (Esencialmente, esta es otra formulación de la ley fundamental de la dinámica, cercana a la dada por Newton). Si varias fuerzas actúan sobre un punto, entonces en el lado derecho de la igualdad (17.4) habrá una resultante de las fuerzas aplicadas. al punto material.

Si ambos lados de la igualdad se multiplican por dt, entonces obtenemos

La cantidad vectorial del lado derecho de esta igualdad caracteriza la acción ejercida sobre el cuerpo por una fuerza en un período de tiempo elemental. dt este valor se denota dS y llama elemental impulso de fuerza, es decir.

Legumbres S fortaleza F durante un período de tiempo finito /, - / 0 se define como el límite de la suma integral de los impulsos elementales correspondientes, es decir,

En el caso especial, si la fuerza F es constante en magnitud y dirección, entonces S = F(t| -/ 0) y S-F(tl-/ 0). En el caso general, la magnitud del impulso de fuerza se puede calcular a partir de sus proyecciones sobre los ejes de coordenadas:

Ahora, integrando ambos lados de la igualdad (17.5) con t= constante, obtenemos

La ecuación (17.9) expresa el teorema sobre el cambio de momento de un punto en forma finita (integral): el cambio en el impulso de un punto durante un cierto período de tiempo es igual al impulso de la fuerza que actúa sobre el punto (o el impulso de la resultante de todas las fuerzas que se le aplican) durante el mismo período de tiempo.

Al resolver problemas, utilice las ecuaciones de este teorema en proyecciones sobre los ejes de coordenadas.

Ahora consideremos sistema mecánico, que consiste en PAG puntos materiales. Luego, para cada punto podemos aplicar el teorema sobre el cambio de momento en la forma (17.4), teniendo en cuenta las fuerzas externas e internas aplicadas a los puntos:

Sumando estas igualdades y teniendo en cuenta que la suma de las derivadas es igual a la derivada de la suma, obtenemos

Dado que por la naturaleza de las fuerzas internas. HFk=0 y por definición de impulso ^fn kV/ c = q, entonces finalmente encontramos

La ecuación (17.11) expresa el teorema sobre el cambio de momento del sistema en forma diferencial: en cada momento, la derivada temporal del impulso del sistema es igual a la suma geométrica de todas las fuerzas externas que actúan sobre el sistema.

Proyectando la igualdad (17.11) sobre los ejes de coordenadas, obtenemos

Multiplicando ambos lados (17.11) por dt e integrando obtenemos

donde 0, P 0 - la cantidad de movimiento del sistema en momentos de tiempo respectivamente y / 0.

La ecuación (17.13) expresa el teorema sobre el cambio de momento del sistema en forma integral: el cambio en el impulso del sistema en cualquier tiempo es igual a la suma de los impulsos de todas las fuerzas externas que actúan sobre el sistema durante el mismo tiempo.

En proyecciones sobre los ejes de coordenadas obtenemos

Del teorema sobre el cambio en el momento de un sistema se pueden obtener las siguientes consecuencias importantes, que expresan Ley de conservación del momento de un sistema.

• 1. Si la suma geométrica de todas las fuerzas externas que actúan sobre el sistema es cero (LF k=0), entonces de la ecuación (17.11) se deduce que en este caso q= constante, es decir, el vector de impulso del sistema será constante en magnitud y dirección.
• 2. Si las fuerzas externas que actúan sobre el sistema son tales que la suma de sus proyecciones sobre cualquier eje es cero (por ejemplo, yo e kx = 0), entonces de las ecuaciones (17.12) se deduce que en este caso Q x = constante, es decir, la proyección del impulso del sistema sobre este eje permanece sin cambios.

Tenga en cuenta que las fuerzas internas del sistema no participan en la ecuación del teorema sobre el cambio en el momento del sistema. Estas fuerzas, aunque influyen en el impulso de puntos individuales del sistema, no pueden cambiar el impulso del sistema en su conjunto. Teniendo en cuenta esta circunstancia, a la hora de resolver problemas, es recomendable elegir el sistema considerado de tal forma que las fuerzas desconocidas (todas o parte de ellas) se hagan internas.

Es conveniente aplicar la ley de conservación del impulso en los casos en que, al cambiar la velocidad de una parte del sistema, es necesario determinar la velocidad de su otra parte.

Problema 17.1. A pesaje de carro tx- 12 kg moviéndose a lo largo de un plano horizontal liso en un punto A se fija una varilla ingrávida mediante una bisagra cilíndrica ANUNCIO longitud /= 0,6 m con carga D masa t2- 6 kg al final (Fig. 17.2). En el momento / 0 = 0, cuando la velocidad del carro Y () - 0,5 m/s, varilla ANUNCIO comienza a girar alrededor de un eje A, perpendicular al plano de dibujo, según la ley f = (tg/6)(3^2 - 1) rad (/-en segundos). Definir: u=f.

§ 17.3. Teorema sobre el movimiento del centro de masa.

El teorema sobre el cambio en el momento de un sistema mecánico se puede expresar de otra forma, llamada teorema sobre el movimiento del centro de masa.

Sustituyendo en la ecuación (17.11) la igualdad Q = VM C, obtenemos

si la masa METRO el sistema es constante, obtenemos

Dónde y con - aceleración del centro de masa del sistema.

La ecuación (17.15) expresa el teorema sobre el movimiento del centro de masa del sistema: el producto de la masa de un sistema por la aceleración de su centro de masa es igual a la suma geométrica de todas las fuerzas externas que actúan sobre el sistema.

Proyectando la igualdad (17.15) sobre los ejes de coordenadas, obtenemos

Dónde xc, yc, zc- coordenadas del centro de masa del sistema.

Estas ecuaciones son ecuaciones diferenciales de movimiento del centro de masa en proyecciones sobre los ejes del sistema de coordenadas cartesiano.

Analicemos los resultados obtenidos. Primero recordemos que el centro de masa de un sistema es un punto geométrico, a veces ubicado fuera de los límites geométricos del cuerpo. Las fuerzas que actúan sobre el sistema mecánico (externas e internas) se aplican a todos los puntos materiales del sistema. Las ecuaciones (17.15) permiten determinar el movimiento del centro de masa del sistema sin determinar el movimiento de sus puntos individuales. Comparando las ecuaciones (17.15) del teorema sobre el movimiento del centro de masa y las ecuaciones (13.5) de la segunda ley de Newton para un punto material, llegamos a la conclusión: El centro de masa de un sistema mecánico se mueve como un punto material, cuya masa es igual a la masa de todo el sistema, y ​​como si todas las fuerzas externas que actúan sobre el sistema se aplicaran a este punto. Así, las soluciones que obtenemos al considerar cuerpo dado como punto material, determinan la ley de movimiento del centro de masa de este cuerpo.

En particular, si un cuerpo se mueve traslacionalmente, entonces las características cinemáticas de todos los puntos del cuerpo y su centro de masa son las mismas. Es por eso un cuerpo en movimiento traslacional siempre puede considerarse como un punto material con una masa igual a la masa de todo el cuerpo.

Como puede verse en (17.15), las fuerzas internas que actúan sobre los puntos del sistema no afectan el movimiento del centro de masa del sistema. Las fuerzas internas pueden influir en el movimiento del centro de masa en los casos en que las fuerzas externas cambian bajo su influencia. A continuación se darán ejemplos de esto.

Del teorema sobre el movimiento del centro de masa se pueden obtener las siguientes consecuencias importantes, que expresan la ley de conservación del movimiento del centro de masa del sistema.

1. Si suma geométrica de todas las fuerzas externas que actúan sobre el sistema es cero (LF k=0), entonces de la ecuación (17.15) se deduce,

¿Qué pasa con esto? a c = 0 o V c = constante, es decir, el centro de masa de este sistema

se mueve con una velocidad constante en magnitud y dirección (en otras palabras, de manera uniforme y rectilínea). En un caso particular, si al principio el centro de masa estaba en reposo ( vc=0), entonces permanecerá en reposo; dónde

pista Sabes que su posición en el espacio no cambiará, es decir. rc = constante

2. Si las fuerzas externas que actúan sobre el sistema son tales que la suma de sus proyecciones sobre algún eje (por ejemplo, el eje X) igual a cero (?F y kx= 0), entonces de la ecuación (17.16) se deduce que en este caso xs=0 o V Cx =x c = const, es decir la proyección de la velocidad del centro de masa del sistema sobre este eje es un valor constante. En el caso especial, si en el momento inicial Vejar= 0, entonces en cualquier momento posterior este valor seguirá siendo el mismo, y se deduce que la coordenada xs el centro de masa del sistema no cambiará, es decir xc- constante

Consideremos ejemplos que ilustran la ley del movimiento del centro de masa.

Ejemplos. 1. Como se señaló, el movimiento del centro de masa depende únicamente de fuerzas externas; las fuerzas internas no pueden cambiar la posición del centro de masa. Pero las fuerzas internas del sistema pueden provocar influencias externas. Así, el movimiento de una persona sobre una superficie horizontal se produce bajo la influencia de fuerzas de fricción entre las suelas de sus zapatos y la superficie de la carretera. Con la fuerza de sus músculos (fuerzas internas), una persona empuja la superficie de la carretera con los pies, por lo que surge una fuerza de fricción (externa a la persona) en los puntos de contacto con la carretera, dirigida en la dirección de su movimiento.

• 2. El coche se mueve de forma similar. Las fuerzas de presión interna en su motor obligan a las ruedas a girar, pero como estas últimas tienen tracción con la carretera, las fuerzas de fricción resultantes "empujan" el automóvil hacia adelante (como resultado, las ruedas no giran, sino que se mueven en un plano paralelo). . Si la carretera es absolutamente plana, entonces el centro de masa del automóvil estará estacionario (con velocidad inicial cero) y las ruedas, en ausencia de fricción, patinarán, es decir, realizarán un movimiento de rotación.
• 3. El movimiento con ayuda de hélice, hélice o remos se produce debido al rechazo de una determinada masa de aire (o agua). Si consideramos la masa lanzada y el cuerpo en movimiento como un solo sistema, entonces las fuerzas de interacción entre ellos, como internas, no pueden cambiar la cantidad total de movimiento de este sistema. Sin embargo, cada parte de este sistema moverá, por ejemplo, la embarcación hacia adelante y el agua que los remos arrojan hacia atrás.
• 4. En el espacio sin aire, cuando un cohete se mueve, la "masa arrojada" debe "llevarse consigo": el motor a reacción imparte movimiento al cohete arrojando hacia atrás los productos de combustión del combustible con el que está lleno el cohete.
• 5. Al descender en paracaídas, puedes controlar el movimiento del centro de masa del sistema hombre-paracaídas. Si, mediante esfuerzos musculares, una persona aprieta las líneas del paracaídas de modo que cambie la forma de su cúpula o el ángulo de ataque del flujo de aire, esto provocará un cambio en la influencia externa del flujo de aire y, por lo tanto, influirá en el movimiento. de todo el sistema.

Problema 17.2. EN El problema 17.1 (ver Fig. 17.2) determina: 1) ley del movimiento del carro X (= /)(/), si se sabe que en el momento inicial del tiempo t 0 = O el sistema estaba en reposo y la coordenada x 10 = 0; 2) la ley del cambio en el tiempo del valor total de la reacción normal norte(norte = norte" + norte") plano horizontal, es decir N=f2(t).

Solución. Aquí, como en el problema 17.1, consideramos un sistema que consta de un carro y una carga. D, en una posición arbitraria bajo la influencia de fuerzas externas que se le aplican (ver Fig. 17.2). Ejes de coordenadas Ohhh dibújelo de modo que el eje x sea horizontal y el eje en pasó por el punto Un 0, es decir, la ubicación del punto A en un momento dado tt 0 - 0.

1. Determinación de la ley de movimiento del carro. Para determinar x, = /,(0, usamos el teorema sobre el movimiento del centro de masa del sistema. Creemos una ecuación diferencial de su movimiento en proyección sobre el eje x:

Como todas las fuerzas externas son verticales, entonces T,F y kx = 0, y por lo tanto

Integrando esta ecuación encontramos que Mx s = B, es decir, la proyección de la velocidad del centro de masa del sistema sobre el eje x es un valor constante. Desde el momento inicial del tiempo

Integrando la ecuación. mx= 0, obtenemos

es decir coordinar xs el centro de masa del sistema es constante.

Escribamos la expresión. mx para una posición arbitraria del sistema (ver Fig. 17.2), teniendo en cuenta que xA-x { , x D - x 2 Y x 2 - x ( - I pecado f. De acuerdo con la fórmula (16.5), que determina la coordenada del centro de masa del sistema, en este caso Mx s - t ( x ( + 2 x 2".

por un momento arbitrario en el tiempo

por el momento de tiempo / () = 0, X (= 0 y

De acuerdo con la igualdad (b), la coordenada xs el centro de masa de todo el sistema permanece sin cambios, es decir xD^,) = xc(t). En consecuencia, igualando las expresiones (c) y (d), obtenemos la dependencia de la coordenada x con el tiempo.

Respuesta: X - 0,2 m, donde t- en segundos.

2. Definición de reacción NORTE. Para determinar norte=f 2 (t) compongamos una ecuación diferencial de movimiento del centro de masa del sistema en proyección sobre el eje vertical en(ver figura 17.2):

Por lo tanto, denotando N=N+N", obtenemos

Según la fórmula que determina la ordenada. y s centro de masa del sistema, mus = t ( yx + t 2 y 2, donde y, = en C1,a las 2= yD = Ud.A ~ 1 porque Ф" obtenemos

Diferenciando esta igualdad dos veces en el tiempo (teniendo en cuenta que en C1 Y en A cantidades son constantes y, por tanto, sus derivadas son iguales a cero), encontramos

Sustituyendo esta expresión en la ecuación (e), determinamos la dependencia deseada norte de t.

Respuesta: NORTE- 176,4 + 1,13,

donde f = (i/6)(3/ -1), t- en segundos, NORTE- en newtons.

Problema 17.3. Peso del motor eléctrico tx unido a la superficie horizontal de la base con pernos (Fig. 17.3). Una varilla ingrávida de longitud l se fija en un extremo al eje del motor en ángulo recto con respecto al eje de rotación, y se monta un peso puntual en el otro extremo de la varilla. A masa t2. El eje gira uniformemente con una velocidad angular c. Encuentre la presión horizontal del motor sobre los pernos. Solución. Considere un sistema mecánico que consta de un motor y un peso puntual. A, en cualquier posición. Representemos las fuerzas externas que actúan sobre el sistema: la gravedad. R x, R 2, Reacción de la base en forma de fuerza vertical. norte y fuerza horizontal r. llevemos a cabo eje de coordenadas xhorizontal.

Para determinar la presión horizontal del motor sobre los pernos (y será numéricamente igual a la reacción R y dirigido opuesto al vector R ), componeremos la ecuación del teorema sobre el cambio en el momento del sistema en proyección sobre el eje x horizontal:

Para el sistema considerado en su posición arbitraria, teniendo en cuenta que la cantidad de movimiento del cuerpo motor es cero, obtenemos Qx = - t 2 UA soc. Teniendo en cuenta que VA = a z/, f = co/ (la rotación del motor es uniforme), obtenemos Qx - - m 2 co/cos co/. diferenciando Qx en el tiempo y sustituyendo en la igualdad (a), encontramos R- m 2 co 2 /sin co/.

Tenga en cuenta que son precisamente estas fuerzas las que fuerzan (ver § 14.3); cuando actúan, surgen vibraciones forzadas de las estructuras.

Ejercicios para Trabajo independiente

• 1. ¿Cómo se llama impulso de un punto y de un sistema mecánico?
• 2. ¿Cómo cambia el impulso de un punto que se mueve uniformemente alrededor de un círculo?
• 3. ¿Qué caracteriza a un impulso de fuerza?
• 4. ¿Las fuerzas internas de un sistema afectan su momento? ¿Sobre el movimiento de su centro de masa?
• 5. ¿Cómo afectan los pares de fuerzas que se le aplican al movimiento del centro de masa del sistema?
• 6. ¿En qué condiciones está en reposo el centro de masa del sistema? ¿Se mueve uniformemente y en línea recta?

7. En un barco parado sin flujo de agua, un adulto se sienta en la popa y un niño en la proa del barco. ¿En qué dirección se moverá el barco si cambian de lugar?

¿En qué caso el módulo de movimiento del barco será grande: 1) si el niño se mueve hacia la popa del adulto; 2) ¿si un adulto se acerca al niño en la proa del barco? ¿Cuál será el desplazamiento del centro de masa del sistema “barco y dos personas” durante estos movimientos?