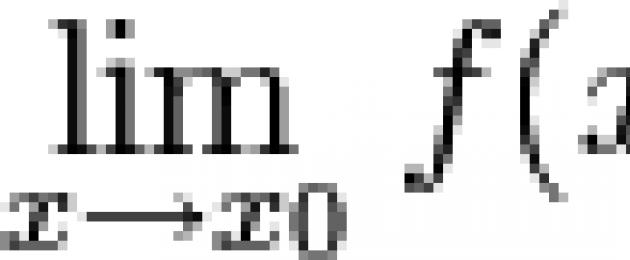Función y=f(x) llamado infinitesimal en x→a o cuando X→∞, si o , es decir una función infinitesimal es una función cuyo límite en un punto dado es cero.
Ejemplos.
1. Función f(x)=(X-1) 2 es infinitesimal en X→1, ya que (ver figura).
2. Función f(x)= tg X– infinitesimal en X→0.
3. f(x)= iniciar sesión(1+ X) – infinitesimal en X→0.
4. f(x) = 1/X– infinitesimal en X→∞.
Establezcamos la siguiente relación importante:
Teorema. Si la función y=f(x) representable con x→a como suma de un número constante b y magnitud infinitesimal α(x): f (x)=b+ α(x) Eso .
Por el contrario, si , entonces f(x)=b+α(x), Dónde hacha)– infinitesimal en x→a.
Prueba.
1. Probemos la primera parte del enunciado. Desde la igualdad f(x)=b+a(x) debería |f(x) – b|=| α|. Pero desde hacha) es infinitesimal, entonces para ε arbitrario hay δ – una vecindad del punto a, en frente de todos X de donde, valores hacha) satisfacer la relación |α(x)|< ε. Entonces |f(x) – b|< ε. Y esto significa que.
2. Si , entonces para cualquier ε >0 para todos X desde algún δ - vecindad de un punto a voluntad |f(x) – b|< ε. Pero si denotamos f(x) – b= α, Eso |α(x)|< ε, lo que significa que a– infinitesimal.
Consideremos las propiedades básicas de las funciones infinitesimales.
Teorema 1. La suma algebraica de dos, tres y en general cualquier número finito de infinitesimales es una función infinitesimal.
Prueba. Demos una prueba para dos términos. Dejar f(x)=α(x)+β(x), dónde y . Necesitamos demostrar que para cualquier ε pequeño y arbitrario > 0 encontrado δ> 0, tal que para X, satisfaciendo la desigualdad |x – a|<δ , realizado |f(x)|< ε.
Entonces, arreglemos un número arbitrario ε > 0. Dado que según las condiciones del teorema a(x) es una función infinitesimal, entonces existe tal δ 1 > 0, que es |x – a|< δ 1 tenemos |α(x)|< ε / 2. Asimismo, desde β(x) es infinitesimal, entonces existe tal δ 2 > 0, que es |x – a|< δ 2 tenemos | β(x)|< ε / 2.
Echemos δ=mín(δ 1 , δ2 } .Luego en las cercanías del punto a radio δ cada una de las desigualdades será satisfecha |α(x)|< ε / 2 y | β(x)|< ε / 2. Por lo tanto, en este barrio habrá
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
aquellos. |f(x)|< ε, que es lo que había que demostrar.
Teorema 2. Producto de una función infinitesimal hacha) para una función limitada f(x) en x→a(o cuando x→∞) es una función infinitesimal.
Prueba. Desde la función f(x) es limitado, entonces hay un número METRO tal que para todos los valores X desde algún barrio de un punto a|f(x)|≤M. Es más, desde hacha) es una función infinitesimal en x→a, entonces para un ε arbitrario > 0 hay una vecindad del punto a, en el que se mantendrá la desigualdad |α(x)|< ε /METRO. Luego, en el más pequeño de estos barrios tenemos | αf|< ε /METRO= ε. Y esto significa que af– infinitesimal. Para la ocasión x→∞ la prueba se realiza de manera similar.
Del teorema probado se sigue:
Corolario 1. Si y, entonces.
Corolario 2. Si c= constante, entonces.
Teorema 3. Razón de una función infinitesimal a(x) por función f(x), cuyo límite es distinto de cero, es una función infinitesimal.
Prueba. Dejar . Entonces 1 /f(x) hay una función limitada. Por tanto, una fracción es el producto de una función infinitesimal y una función limitada, es decir la función es infinitesimal.
Cálculo de infinitesimales y grandes.
Cálculo infinitesimal- cálculos realizados con cantidades infinitesimales, en los que el resultado obtenido se considera como una suma infinita de infinitesimales. El cálculo de infinitesimales es un concepto general del cálculo diferencial e integral, que forma la base de las matemáticas superiores modernas. El concepto de cantidad infinitesimal está estrechamente relacionado con el concepto de límite.
Infinitesimal
Subsecuencia a norte llamado infinitesimal, Si . Por ejemplo, una secuencia de números es infinitesimal.
La función se llama infinitesimal en la proximidad de un punto X 0 si ![]() .
.
La función se llama infinitesimal en el infinito, Si ![]() o
o ![]() .
.
También infinitesimal es una función que es la diferencia entre una función y su límite, es decir, si ![]() , Eso F(X) − a = α( X)
, .
, Eso F(X) − a = α( X)
, .
Cantidad infinitamente grande
En todas las fórmulas siguientes, se supone que el infinito a la derecha de la igualdad tiene un signo determinado (ya sea “más” o “menos”). Esta es, por ejemplo, la función X pecado X, ilimitado en ambos lados, no es infinitamente grande en .
Subsecuencia a norte llamado infinitamente grande, Si ![]() .
.
La función se llama infinitamente grande en las proximidades de un punto X 0 si ![]() .
.
La función se llama infinitamente grande en el infinito, Si ![]() o
o ![]() .
.
Propiedades de infinitamente pequeño e infinitamente grande.
Comparación de cantidades infinitesimales
¿Cómo comparar cantidades infinitesimales?
La proporción de cantidades infinitesimales forma la llamada incertidumbre.
Definiciones
Supongamos que tenemos valores infinitesimales α( X) y β( X) (o, lo que no es importante para la definición, secuencias infinitesimales).
Para calcular dichos límites es conveniente utilizar la regla de L'Hopital.
Ejemplos de comparación
Usando ACERCA DE-simbolismo, los resultados obtenidos se pueden escribir de la siguiente forma X 5 = oh(X 3). En este caso, las siguientes entradas son verdaderas: 2X 2 + 6X = oh(X) Y X = oh(2X 2 + 6X).Valores equivalentes
Definición
Si , entonces las cantidades infinitesimales α y β se llaman equivalente ().
Es obvio que las cantidades equivalentes son un caso especial de cantidades infinitesimales del mismo orden de pequeñez.
Cuando sean válidas las siguientes relaciones de equivalencia (como consecuencia de los llamados límites notables):
Teorema
El límite del cociente (ratio) de dos cantidades infinitesimales no cambiará si una de ellas (o ambas) se reemplaza por una cantidad equivalente..Este teorema tiene importancia práctica a la hora de encontrar límites (ver ejemplo).
Ejemplo de uso
Reemplazo sinorte 2X valor equivalente 2 X, obtenemosBosquejo histórico
El concepto de "infinitesimal" se discutió en la antigüedad en relación con el concepto de átomos indivisibles, pero no se incluyó en las matemáticas clásicas. Revivió nuevamente con la llegada del "método de los indivisibles" en el siglo XVI, dividiendo la figura en estudio en secciones infinitesimales.
En el siglo XVII se produjo la algebraización del cálculo infinitesimal. Comenzaron a definirse como cantidades numéricas que son menores que cualquier cantidad finita (distinta de cero) y, sin embargo, no iguales a cero. El arte del análisis consistía en trazar una relación que contuviera infinitesimales (diferenciales) y luego integrarla.
Los matemáticos de la vieja escuela ponen a prueba el concepto infinitesimal duras críticas. Michel Rolle escribió que el nuevo cálculo es “ conjunto de errores ingeniosos"; Voltaire señaló cáusticamente que el cálculo es el arte de calcular y medir con precisión cosas cuya existencia no se puede probar. Incluso Huygens admitió que no entendía el significado de los diferenciales de órdenes superiores.
Como una ironía del destino, se puede considerar el surgimiento a mediados de siglo de un análisis no estándar, que demostró que el punto de vista original, los infinitesimales reales, también era consistente y podía usarse como base para el análisis.
ver también
Fundación Wikimedia. 2010.
Vea qué es “Cantidad infinitesimal” en otros diccionarios:
CANTIDAD INFINITAMENTE PEQUEÑA- una cantidad variable en un determinado proceso, si en este proceso se acerca (tiende) infinitamente a cero... Gran Enciclopedia Politécnica
Infinitesimal- ■ Algo desconocido, pero relacionado con la homeopatía... Léxico de verdades comunes
Se da la definición de una secuencia infinitamente grande. Se consideran los conceptos de vecindad de puntos en el infinito. Se da una definición universal del límite de una secuencia, que se aplica tanto a límites finitos como infinitos. Se consideran ejemplos de aplicación de la definición de secuencia infinitamente grande.
ContenidoVer también: Determinar el límite de secuencia
Definición
Subsecuencia (βn) llamada secuencia infinitamente grande, si para cualquier número M, por grande que sea, existe un número natural N M que depende de M tal que para todos los números naturales n > N M se cumple la desigualdad
|βn | >M.
En este caso escriben
.
O en .
Dicen que tiende al infinito, o converge al infinito.
Si, a partir de algún número N 0
, Eso
( converge a más infinito).
si entonces
( converge a menos infinito).
Escribamos estas definiciones usando los símbolos lógicos de existencia y universalidad:
(1)
.
(2)
.
(3)
.
Las secuencias con límites (2) y (3) son casos especiales de una secuencia infinitamente grande (1). De estas definiciones se deduce que si el límite de una secuencia es igual a más o menos infinito, entonces también es igual a infinito:
.
Lo contrario, por supuesto, no es cierto. Los miembros de una secuencia pueden tener signos alternos. En este caso, el límite puede ser igual al infinito, pero sin un signo específico.
Tenga en cuenta también que si alguna propiedad se cumple para una secuencia arbitraria con un límite igual al infinito, entonces la misma propiedad se cumple para una secuencia cuyo límite es igual a más o menos infinito.
En muchos libros de texto de cálculo, la definición de secuencia infinitamente grande establece que el número M es positivo: M > 0 . Sin embargo, este requisito es innecesario. Si se cancela, no surgen contradicciones. Lo que pasa es que los valores pequeños o negativos no nos interesan. Estamos interesados en el comportamiento de la secuencia para valores positivos arbitrariamente grandes de M. Por lo tanto, si surge la necesidad, entonces M puede limitarse desde abajo por cualquier número predeterminado a, es decir, podemos suponer que M > a.
Cuando definimos ε - la vecindad del punto final, entonces el requisito ε > 0 es una importante. Para valores negativos, la desigualdad no puede satisfacerse en absoluto.
Barrios de puntos en el infinito.
Cuando consideramos límites finitos, introdujimos el concepto de vecindad de un punto. Recuerde que una vecindad de un punto final es un intervalo abierto que contiene este punto. También podemos introducir el concepto de vecindades de puntos en el infinito.
Sea M un número arbitrario.
Barrio del punto "infinito", , se llama conjunto.
Barrio del punto "más infinito", , se llama conjunto.
En las proximidades del punto "menos infinito", , se llama conjunto.
Estrictamente hablando, la vecindad del punto "infinito" es el conjunto
(4)
,
donde m 1
y M 2
- números positivos arbitrarios. Usaremos la primera definición, ya que es más sencilla. Aunque todo lo que se dice a continuación también es cierto cuando se utiliza la definición (4).
Ahora podemos dar una definición unificada del límite de una secuencia que se aplica tanto a límites finitos como a infinitos.
Definición universal de límite de secuencia..
Un punto a (finito o en el infinito) es el límite de una secuencia si para cualquier vecindad de este punto existe un número natural N tal que todos los elementos de la secuencia con números pertenecen a esa vecindad.
Por tanto, si existe un límite, entonces fuera de la vecindad del punto a sólo puede haber un número finito de miembros de la secuencia, o un conjunto vacío. Esta condición es necesaria y suficiente. La demostración de esta propiedad es exactamente la misma que para los límites finitos.
Propiedad de vecindad de una secuencia convergente
Para que un punto a (finito o en el infinito) sea límite de la secuencia, es necesario y suficiente que fuera de cualquier vecindad de este punto haya un número finito de términos de la secuencia o un conjunto vacío.
Prueba .
También a veces se introducen los conceptos de ε - vecindades de puntos en el infinito.
Recuerde que la ε-vecindad de un punto finito a es el conjunto.
Introduzcamos la siguiente notación. Sea ε la vecindad del punto a. Luego, para el punto final,
.
Para puntos en el infinito:
;
;
.
Usando los conceptos de ε-vecindades, podemos dar otra definición universal del límite de una secuencia:
Un punto a (finito o en el infinito) es el límite de la secuencia si para cualquier número positivo ε > 0
existe un número natural N ε que depende de ε tal que para todos los números n > N ε los términos x n pertenecen a la ε-vecindad del punto a:
.
Utilizando los símbolos lógicos de existencia y universalidad, esta definición se escribirá de la siguiente manera:
.
Ejemplos de secuencias infinitamente grandes.
Ejemplo 1
.
.
Anotemos la definición de una secuencia infinitamente grande:
(1)
.
En nuestro caso
.
Introducimos números y , conectándolos con desigualdades:
.
Según las propiedades de las desigualdades, si y , entonces
.
Tenga en cuenta que esta desigualdad es válida para cualquier n. Por lo tanto, puedes elegir así:
en ;
en .
Entonces, para cualquiera podemos encontrar un número natural que satisfaga la desigualdad. Entonces para todos,
.
Esto significa que . Es decir, la secuencia es infinitamente grande.
Ejemplo 2
Usando la definición de una secuencia infinitamente grande, demuestre que
.
(2)
.
El término general de la secuencia dada tiene la forma:
.
Ingrese los números y:
.
.
Entonces, para cualquiera se puede encontrar un número natural que satisfaga la desigualdad, por lo que para todos,
.
Esto significa que .
.
Ejemplo 3
Usando la definición de una secuencia infinitamente grande, demuestre que
.
Anotemos la definición del límite de una secuencia igual a menos infinito:
(3)
.
El término general de la secuencia dada tiene la forma:
.
Ingrese los números y:
.
De esto queda claro que si y , entonces
.
Dado que para cualquiera es posible encontrar un número natural que satisfaga la desigualdad, entonces
.
Dado , como N podemos tomar cualquier número natural que satisfaga la siguiente desigualdad:
.
Ejemplo 4
Usando la definición de una secuencia infinitamente grande, demuestre que
.
Anotamos el término general de la sucesión:
.
Anotemos la definición del límite de una secuencia igual a más infinito:
(2)
.
Como n es un número natural, n = 1, 2, 3, ...
, Eso
;
;
.
Introducimos números y M, conectándolos con desigualdades:
.
De esto queda claro que si y , entonces
.
Entonces, para cualquier número M podemos encontrar un número natural que satisfaga la desigualdad. Entonces para todos,
.
Esto significa que .
Referencias:
L.D. Kudryavtsev. Curso de análisis matemático. Volumen 1. Moscú, 2003.
CM. Nikolski. Curso de análisis matemático. Volumen 1. Moscú, 1983.
INFINITAS PEQUEÑAS FUNCIONES Y SUS PROPIEDADES BÁSICAS
Función y=f(x) llamado infinitesimal en x→a o cuando X→∞, si o , es decir una función infinitesimal es una función cuyo límite en un punto dado es cero.
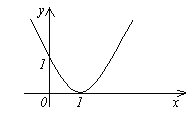
Ejemplos.
Establezcamos la siguiente relación importante:
Teorema. Si la función y=f(x) representable con x→a como suma de un número constante b y magnitud infinitesimal α(x): f (x)=b+ α(x) Eso .
Por el contrario, si , entonces f(x)=b+α(x), Dónde hacha)– infinitesimal en x→a.
Prueba.
Consideremos las propiedades básicas de las funciones infinitesimales.
Teorema 1. La suma algebraica de dos, tres y en general cualquier número finito de infinitesimales es una función infinitesimal.
Prueba. Demos una prueba para dos términos. Dejar f(x)=α(x)+β(x), dónde y . Necesitamos demostrar que para cualquier ε pequeño y arbitrario > 0 encontrado δ> 0, tal que para X, satisfaciendo la desigualdad |x – a|<δ , realizado |f(x)|< ε.
Entonces, arreglemos un número arbitrario ε > 0. Dado que según las condiciones del teorema a(x) es una función infinitesimal, entonces existe tal δ 1 > 0, que es |x – a|< δ 1 tenemos |α(x)|< ε / 2. Asimismo, desde β(x) es infinitesimal, entonces existe tal δ 2 > 0, que es |x – a|< δ 2 tenemos | β(x)|< ε / 2.
Echemos δ=mín(δ 1 , δ2 } .Luego en las cercanías del punto a radio δ cada una de las desigualdades será satisfecha |α(x)|< ε / 2 y | β(x)|< ε / 2. Por lo tanto, en este barrio habrá
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
aquellos. |f(x)|< ε, que es lo que había que demostrar.
Teorema 2. Producto de una función infinitesimal hacha) para una función limitada f(x) en x→a(o cuando x→∞) es una función infinitesimal.
Prueba. Desde la función f(x) es limitado, entonces hay un número METRO tal que para todos los valores X desde algún barrio de un punto a|f(x)|≤M. Es más, desde hacha) es una función infinitesimal en x→a, entonces para un ε arbitrario > 0 hay una vecindad del punto a, en el que se mantendrá la desigualdad |α(x)|< ε /METRO. Luego, en el más pequeño de estos barrios tenemos | αf|< ε /METRO= ε. Y esto significa que af– infinitesimal. Para la ocasión x→∞ la prueba se realiza de manera similar.
Del teorema probado se sigue:
Corolario 1. Si y, entonces.
Corolario 2. Si c= constante, entonces.
Teorema 3. Razón de una función infinitesimal a(x) por función f(x), cuyo límite es distinto de cero, es una función infinitesimal.
Prueba. Dejar ![]() . Entonces 1 /f(x) hay una función limitada. Por lo tanto la fracción
. Entonces 1 /f(x) hay una función limitada. Por lo tanto la fracción ![]() es el producto de una función infinitesimal y una función acotada, es decir la función es infinitesimal.
es el producto de una función infinitesimal y una función acotada, es decir la función es infinitesimal.
RELACIÓN ENTRE FUNCIONES INFINITAMENTE PEQUEÑAS E INFINITAMENTE GRANDES
Teorema 1. Si la función f(x) es infinitamente grande en x→a, entonces función 1 /f(x) es infinitesimal en x→a.
Prueba. Tomemos un número arbitrario ε >0 y mostrar eso para algunos δ>0 (dependiendo de ε) para todos X, para cual |x – a|<δ , la desigualdad se satisface, y esto significará que 1/f(x) es una función infinitesimal. De hecho, desde f(x) es una función infinitamente grande en x→a, entonces habrá δ>0 tal que tan pronto como |x – a|<δ , entonces | f(x)|> 1/ ε. Pero luego por lo mismo X.
Ejemplos.
También se puede demostrar el teorema inverso.
Teorema 2. Si la función f(x)- infinitesimal en x→a(o x→∞) y no desaparece, entonces y= 1/f(x) es una función infinitamente grande.
Realice usted mismo la prueba del teorema.
Ejemplos.
Por tanto, las propiedades más simples de funciones infinitesimales e infinitamente grandes se pueden escribir utilizando las siguientes relaciones condicionales: A≠ 0
TEOREMAS DE LÍMITE
Teorema 1. El límite de la suma algebraica de dos, tres y, en general, un cierto número de funciones es igual a la suma algebraica de los límites de estas funciones, es decir
Prueba. Realicemos la prueba para dos términos, ya que se puede hacer de la misma forma para cualquier número de términos. Dejar ![]() .Entonces f(x)=b+a(x) Y g(x)=c+β(x), Dónde α
Y β
– funciones infinitesimales. Por eso,
.Entonces f(x)=b+a(x) Y g(x)=c+β(x), Dónde α
Y β
– funciones infinitesimales. Por eso,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Porque b+c es una constante y α(x) + β(x) es una función infinitesimal, entonces
Ejemplo. .
Teorema 2. El límite del producto de dos, tres y, en general, un número finito de funciones es igual al producto de los límites de estas funciones:
Prueba. Dejar ![]() . Por eso, f(x)=b+a(x) Y g(x)=c+β(x) Y
. Por eso, f(x)=b+a(x) Y g(x)=c+β(x) Y
fg = (b + α)(c + β) = antes de Cristo + (bβ + cα + αβ).
Trabajar antes de Cristo hay un valor constante. Función bβ + c α + αβ Según las propiedades de las funciones infinitesimales, existe una cantidad infinitesimal. Es por eso .
Corolario 1. El factor constante se puede llevar más allá del signo límite:
![]() .
.
Corolario 2. El límite de grado es igual al grado límite:
![]() .
.
Ejemplo.![]() .
.
Teorema 3. El límite del cociente de dos funciones es igual al cociente de los límites de estas funciones si el límite del denominador es distinto de cero, es decir
 .
.
Prueba. Dejar . Por eso, f(x)=b+a(x) Y g(x)=c+β(x), Dónde α, β – infinitesimal. Consideremos el cociente
Una fracción es una función infinitesimal porque el numerador es una función infinitesimal y el denominador tiene un límite. c 2 ≠0.
Ejemplos.
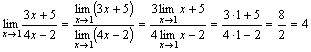

Teorema 4. Sean tres funciones f(x), u(x) Y v(x), satisfaciendo las desigualdades u (x)≤f(x)≤v(x). Si las funciones tu(x) Y v(x) tener el mismo límite en x→a(o x→∞), entonces la función f(x) tiende al mismo límite, es decir Si
![]() , Eso .
, Eso .
El significado de este teorema se desprende claramente de la figura.
La demostración del teorema 4 se puede encontrar, por ejemplo, en el libro de texto: Piskunov N. S. Cálculo diferencial e integral, volumen 1 - M.: Nauka, 1985.
Teorema 5. Estoy gordo x→a(o x→∞) función y=f(x) acepta valores no negativos y≥0 y al mismo tiempo tiende al límite b, entonces este límite no puede ser negativo: b≥0.
Prueba. Realizaremos la prueba por contradicción. pretendamos que b<0 , Entonces |y – b|≥|b| y, por lo tanto, el módulo de diferencia no tiende a cero cuando x→a. Pero entonces y no llega al limite b en x→a, lo que contradice las condiciones del teorema.
Teorema 6. Si dos funciones f(x) Y gramo(x) para todos los valores del argumento X satisfacer la desigualdad f(x)≥ g(x) y tienen límites, entonces la desigualdad se cumple b≥c.
Prueba. Según las condiciones del teorema. f(x)-g(x) ≥0, por lo tanto, por el Teorema 5 ![]() , o
, o ![]() .
.
LÍMITES UNILATERALES

Hasta ahora hemos considerado determinar el límite de una función cuando x→a de manera arbitraria, es decir el límite de la función no dependía de cómo se ubicara X hacia a, a la izquierda o a la derecha de a. Sin embargo, es bastante común encontrar funciones que no tienen límite bajo esta condición, pero sí tienen límite si x→a, quedando a un lado de A, izquierda o derecha (ver figura). Por tanto, se introducen los conceptos de límites unilaterales.
Si f(x) tiende al límite b en X tendiendo a un cierto número a Entonces X acepta solo valores menores que a, luego escriben y llaman blímite de la función f(x) en el punto a de la izquierda.
Definiciones y propiedades de funciones infinitesimales e infinitamente grandes en un punto. Pruebas de propiedades y teoremas. Relación entre funciones infinitesimales e infinitamente grandes.
ContenidoVer también: Secuencias infinitesimales: definición y propiedades
Propiedades de secuencias infinitamente grandes.
Definición de funciones infinitesimales y infinitesimales
sea x 0 es un punto finito o infinito: ∞, -∞ o +∞.
Definición de una función infinitesimal
Función α (X) llamado infinitesimal cuando x tiende a x 0
0
, y es igual a cero:
.
Definición de una función infinitamente grande
Función f (X) llamado infinitamente grande cuando x tiende a x 0
, si la función tiene un límite como x → x 0
, y es igual a infinito:
.
Propiedades de funciones infinitesimales
Propiedad de la suma, diferencia y producto de funciones infinitesimales
Suma, diferencia y producto número finito de funciones infinitesimales cuando x → x 0 es una función infinitesimal como x → x 0 .
Esta propiedad es una consecuencia directa de las propiedades aritméticas de los límites de una función.
Teorema sobre el producto de una función acotada y un infinitesimal
Producto de una función acotada en alguna vecindad perforada del punto x 0 , a infinitesimal, como x → x 0 , es una función infinitesimal como x → x 0 .
La propiedad de representar una función como la suma de una constante y una función infinitesimal.
Para que la función f (X) tenía un límite finito, es necesario y suficiente que
,
donde es una función infinitesimal cuando x → x 0
.
Propiedades de funciones infinitamente grandes
Teorema sobre la suma de una función acotada y una función infinitamente grande
La suma o diferencia de una función acotada en alguna vecindad perforada del punto x 0
, y una función infinitamente grande, como x → x 0
, es una función infinitamente grande cuando x → x 0
.
Teorema sobre la división de una función acotada por una infinitamente grande
Si la función f (X) es infinitamente grande como x → x 0
, y la función g (X)- está limitado por alguna vecindad perforada del punto x 0
, Eso
.
Teorema sobre la división de una función acotada inferiormente por una infinitesimal
Si la función , en alguna vecindad perforada del punto , está limitada desde abajo por un número positivo en valor absoluto:
,
y la función es infinitesimal cuando x → x 0
:
,
y hay una vecindad perforada del punto en el que, entonces
.
Propiedad de desigualdades de funciones infinitamente grandes.
Si la función es infinitamente grande en:
,
y las funciones y , en alguna vecindad perforada del punto satisfacen la desigualdad:
,
entonces la función también es infinitamente grande en:
.
Esta propiedad tiene dos casos especiales.
Sean, en alguna vecindad perforada del punto , las funciones y satisfacen la desigualdad:
.
Entonces si, entonces y.
Si, entonces y.
Relación entre funciones infinitamente grandes e infinitesimales
De las dos propiedades anteriores se desprende la conexión entre funciones infinitamente grandes e infinitesimales.
Si una función es infinitamente grande en , entonces la función es infinitesimal en .
Si una función es infinitesimal para , y , entonces la función es infinitamente grande para .
La relación entre una función infinitesimal y una función infinitamente grande se puede expresar simbólicamente:
,
.
Si una función infinitesimal tiene cierto signo en , es decir, es positiva (o negativa) en alguna vecindad perforada del punto , entonces podemos escribirla así:
.
De la misma manera, si una función infinitamente grande tiene un cierto signo en , entonces escriben:
, o .
Entonces, la conexión simbólica entre funciones infinitamente pequeñas e infinitamente grandes se puede complementar con las siguientes relaciones:
,
,
,
.
Se pueden encontrar fórmulas adicionales relacionadas con los símbolos de infinito en la página
"Puntos al infinito y sus propiedades".
Prueba de propiedades y teoremas.
Demostración del teorema sobre el producto de una función acotada y una infinitesimal
Para demostrar este teorema usaremos . También usamos la propiedad de las sucesiones infinitesimales, según la cual
Sea la función infinitesimal en y esté acotada en alguna vecindad perforada del punto:
en .
Como hay un límite, hay una vecindad perforada del punto en el que se define la función. Que haya una intersección de barrios y . Luego las funciones y están definidas en él.
.
,
una secuencia es infinitesimal:
.
Aprovechemos que el producto de una secuencia acotada y una secuencia infinitesimal es una secuencia infinitesimal:
.
.
El teorema ha sido demostrado.
Prueba de la propiedad de representar una función como la suma de una constante y una función infinitesimal
Necesidad. Sea la función un límite finito en un punto
.
Considere la función:
.
Usando la propiedad del límite de la diferencia de funciones, tenemos:
.
Es decir, existe una función infinitesimal en .
Adecuación. Déjalo ser. Apliquemos la propiedad del límite de la suma de funciones:
.
La propiedad ha sido probada.
Demostración del teorema sobre la suma de una función acotada y una función infinitamente grande
Para demostrar el teorema, usaremos la definición de Heine del límite de una función.
en .
Como hay un límite, hay una vecindad perforada del punto en el que se define la función. Que haya una intersección de barrios y . Luego las funciones y están definidas en él.
Sea una secuencia arbitraria convergente a , cuyos elementos pertenecen a la vecindad:
.
Luego se definen las secuencias y. Además, la secuencia es limitada:
,
una secuencia es infinitamente grande:
.
Dado que la suma o diferencia de una secuencia limitada y una infinitamente grande
.
Entonces, según la definición del límite de una secuencia según Heine,
.
El teorema ha sido demostrado.
Prueba del teorema sobre el cociente de división de una función acotada por una infinitamente grande
Para demostrar esto, usaremos la definición de Heine del límite de una función. También utilizamos la propiedad de las sucesiones infinitamente grandes, según la cual es una sucesión infinitesimal.
Sea la función infinitamente grande en y esté acotada en alguna vecindad perforada del punto:
en .
Dado que la función es infinitamente grande, existe una vecindad perforada del punto donde está definida y no desaparece:
en .
Que haya una intersección de barrios y . Luego las funciones y están definidas en él.
Sea una secuencia arbitraria convergente a , cuyos elementos pertenecen a la vecindad:
.
Luego se definen las secuencias y. Además, la secuencia es limitada:
,
una secuencia es infinitamente grande con términos distintos de cero:
,
.
Dado que el cociente de dividir una secuencia limitada por una infinitamente grande es una secuencia infinitesimal, entonces
.
Entonces, según la definición del límite de una secuencia según Heine,
.
El teorema ha sido demostrado.
Prueba del teorema del cociente para dividir una función acotada inferiormente por una infinitesimal
Para demostrar esta propiedad, usaremos la definición de Heine del límite de una función. También utilizamos la propiedad de las secuencias infinitamente grandes, según la cual es una secuencia infinitamente grande.
Sea la función infinitesimal para , y dejemos que la función esté limitada en valor absoluto desde abajo por un número positivo, en alguna vecindad perforada del punto:
en .
Por condición, existe una vecindad perforada del punto en el que se define la función y no desaparece:
en .
Que haya una intersección de barrios y . Luego las funciones y están definidas en él. Además, y .
Sea una secuencia arbitraria convergente a , cuyos elementos pertenecen a la vecindad:
.
Luego se definen las secuencias y. Además, la secuencia está limitada a continuación:
,
y la secuencia es infinitesimal con términos distintos de cero:
,
.
Dado que el cociente de dividir una secuencia acotada debajo por una infinitesimal es una secuencia infinitamente grande, entonces
.
Y que haya una vecindad perforada del punto en el que
en .
Tomemos una secuencia arbitraria que converge a . Entonces, a partir de algún número N, los elementos de la secuencia pertenecerán a esta vecindad:
en .
Entonces
en .
Según la definición del límite de una función según Heine,
.
Entonces, por la propiedad de las desigualdades de secuencias infinitamente grandes,
.
Dado que la secuencia es arbitraria y converge a , entonces, por la definición del límite de una función según Heine,
.
La propiedad ha sido probada.
Referencias:
L.D. Kudryavtsev. Curso de análisis matemático. Volumen 1. Moscú, 2003.
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0