Será útil para todo estudiante que se esté preparando para el Examen Estatal Unificado de Matemáticas repetir el tema "Encontrar un ángulo entre líneas rectas". Como muestran las estadísticas, al aprobar el examen de certificación, las tareas de esta sección de estereometría causan dificultades a un gran número de estudiantes. Al mismo tiempo, las tareas que requieren encontrar el ángulo entre líneas rectas se encuentran en el Examen Estatal Unificado tanto en el nivel básico como en el especializado. Esto significa que todos deberían poder resolverlos.
Momentos básicos
Hay 4 tipos de posiciones relativas de líneas en el espacio. Pueden coincidir, cruzarse, ser paralelos o cruzarse. El ángulo entre ellos puede ser agudo o recto.
Para encontrar el ángulo entre líneas en el Examen Estatal Unificado o, por ejemplo, al resolverlo, los escolares de Moscú y otras ciudades pueden utilizar varias formas de resolver problemas en esta sección de estereometría. Puedes completar la tarea utilizando construcciones clásicas. Para ello, conviene aprender los axiomas y teoremas básicos de la estereometría. El estudiante necesita ser capaz de razonar lógicamente y crear dibujos para poder llevar la tarea a un problema planimétrico.
También puede utilizar el método del vector de coordenadas utilizando fórmulas, reglas y algoritmos simples. Lo principal en este caso es realizar todos los cálculos correctamente. El proyecto educativo de Shkolkovo le ayudará a perfeccionar sus habilidades para resolver problemas en estereometría y otras secciones del curso escolar.
Ángulo entre rectas en el espacio llamaremos a cualquiera de los ángulos adyacentes formados por dos rectas trazadas por un punto arbitrario paralelo al dato.
Sean dos líneas en el espacio:
Obviamente, el ángulo φ entre líneas rectas se puede tomar como el ángulo entre sus vectores directores y . Desde entonces, usando la fórmula para el coseno del ángulo entre vectores obtenemos
Las condiciones de paralelismo y perpendicularidad de dos rectas son equivalentes a las condiciones de paralelismo y perpendicularidad de sus vectores directores y:
dos seguidos paralelo si y sólo si sus coeficientes correspondientes son proporcionales, es decir yo 1 paralelo yo 2 si y sólo si es paralelo a .
dos seguidos perpendicular si y sólo si la suma de los productos de los coeficientes correspondientes es igual a cero: .
Ud. meta entre linea y plano
Déjalo ser recto d- no perpendicular al plano θ;
d′− proyección de una recta d al plano θ;
El ángulo más pequeño entre líneas rectas. d Y d' llamaremos ángulo entre una recta y un plano.
Denotémoslo como φ=( d,θ)
Si d⊥θ, entonces ( d,θ)=π/2
Oye→j→k→− sistema de coordenadas rectangulares.
Ecuación plana:
θ: Hacha+Por+cz+D=0
Suponemos que la recta está definida por un punto y un vector director: d[METRO 0,pag→]
Vector norte→(A,B,C)⊥θ
Entonces queda por descubrir el ángulo entre los vectores. norte→ y pag→, denotémoslo como γ=( norte→,pag→).
Si el ángulo γ<π/2 , то искомый угол φ=π/2−γ .
Si el ángulo es γ>π/2, entonces el ángulo deseado es φ=γ−π/2
sinφ=sin(2π−γ)=cosγ
sinφ=sin(γ−2π)=−cosγ
Entonces, ángulo entre la recta y el plano se puede calcular usando la fórmula:
sinφ=∣cosγ∣=∣ ∣ AP 1+pb 2+CP 3∣ ∣ √A 2+B 2+C 2√pag 21+pag 22+pag 23
Pregunta 29. El concepto de forma cuadrática. Definitividad de signos de formas cuadráticas.
Forma cuadrática j (x 1, x 2, …, x n) n variables reales x 1, x 2, …, x n se llama suma de la forma , (1)
Dónde un ij – algunos números llamados coeficientes. Sin pérdida de generalidad, podemos suponer que un ij = un ji.
La forma cuadrática se llama válido, Si un ij Î GR. Matriz de forma cuadrática se llama matriz formada por sus coeficientes. La forma cuadrática (1) corresponde a una única matriz simétrica, es decir A T = A. En consecuencia, la forma cuadrática (1) se puede escribir en forma matricial j ( X) = x T Ah, Dónde xt = (X 1 X 2 … xn). (2)
Y, a la inversa, toda matriz simétrica (2) corresponde a una única forma cuadrática hasta la notación de variables.
Rango de forma cuadrática se llama rango de su matriz. La forma cuadrática se llama no degenerado, si su matriz es no singular A. (recordemos que la matriz A se llama no degenerado si su determinante no es igual a cero). De lo contrario, la forma cuadrática es degenerada.
positivo definitivo(o estrictamente positivo) si
j ( X) > 0 , para cualquiera X = (X 1 , X 2 , …, xn), excepto X = (0, 0, …, 0).
Matriz A forma cuadrática definida positiva j ( X) también se llama definida positiva. Por lo tanto, una forma cuadrática definida positiva corresponde a una matriz definida positiva única y viceversa.
La forma cuadrática (1) se llama definido negativamente(o estrictamente negativo) si
j ( X) < 0, для любого X = (X 1 , X 2 , …, xn), excepto X = (0, 0, …, 0).
De manera similar a lo anterior, una matriz de forma cuadrática definida negativa también se llama definida negativa.
En consecuencia, la forma cuadrática definida positiva (negativa) j ( X) alcanza el valor mínimo (máximo) j ( X*) = 0 en X* = (0, 0, …, 0).
Tenga en cuenta que la mayoría de las formas cuadráticas no tienen signos definidos, es decir, no son ni positivas ni negativas. Estas formas cuadráticas llegan a 0 no sólo en el origen del sistema de coordenadas, sino también en otros puntos.
Cuando norte> 2, se requieren criterios especiales para comprobar el signo de una forma cuadrática. Mirémoslos.
menores mayores forma cuadrática se llaman menores:
es decir, se trata de menores del orden de 1, 2,..., norte matrices A, ubicado en la esquina superior izquierda, el último de ellos coincide con el determinante de la matriz A.
Criterio de certeza positiva (criterio de Sylvester)
X) = x T Ah fue positivo definitivo, es necesario y suficiente que todos los menores mayores de la matriz A fueron positivos, es decir: METRO 1 > 0, METRO 2 > 0, …, Minnesota > 0. Criterio de certeza negativo Para que la forma cuadrática j ( X) = x T Ah era negativo definido, es necesario y suficiente que sus menores principales de orden par sean positivos, y de orden impar, negativos, es decir: METRO 1 < 0, METRO 2 > 0, METRO 3 < 0, …, (–1)norte
Este material está dedicado a un concepto como el ángulo entre dos líneas que se cruzan. En el primer párrafo explicaremos qué es y lo mostraremos en ilustraciones. Luego veremos las formas en que se puede encontrar el seno, el coseno de un ángulo dado y el ángulo mismo (consideraremos por separado los casos con un plano y un espacio tridimensional), daremos las fórmulas necesarias y mostraremos con ejemplos exactamente cómo se utilizan en la práctica.
Para entender cuál es el ángulo que se forma cuando dos rectas se cruzan, debemos recordar la definición misma de ángulo, perpendicularidad y punto de intersección.
Definición 1
Llamamos a dos rectas que se cruzan si tienen un punto en común. Este punto se llama punto de intersección de dos rectas.
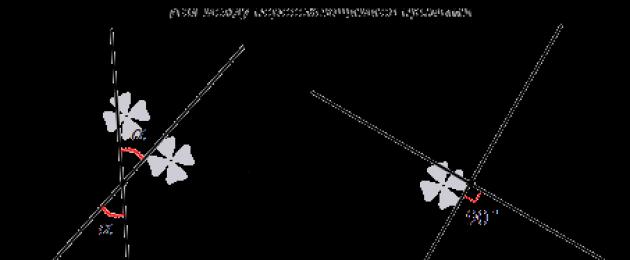
Cada línea recta se divide por un punto de intersección en rayos. Ambas rectas forman 4 ángulos, dos de los cuales son verticales y dos adyacentes. Si conocemos la medida de uno de ellos, entonces podremos determinar los restantes.
Digamos que sabemos que uno de los ángulos es igual a α. En este caso, el ángulo que forma vertical respecto a él también será igual a α. Para encontrar los ángulos restantes, necesitamos calcular la diferencia 180 ° - α. Si α es igual a 90 grados, entonces todos los ángulos serán rectos. Las líneas que se cruzan en ángulos rectos se llaman perpendiculares (se dedica un artículo aparte al concepto de perpendicularidad).
Echa un vistazo a la imagen:
Pasemos a formular la definición principal.
Definición 2
El ángulo formado por dos rectas que se cruzan es la medida del menor de los 4 ángulos que forman estas dos rectas.
De la definición se debe sacar una conclusión importante: el tamaño del ángulo en este caso se expresará mediante cualquier número real en el intervalo (0, 90). Si las líneas son perpendiculares, entonces el ángulo entre ellas será en cualquier caso igual a 90 grados.

La capacidad de encontrar la medida del ángulo entre dos líneas que se cruzan es útil para resolver muchos problemas prácticos. El método de solución se puede elegir entre varias opciones.
Para empezar, podemos utilizar métodos geométricos. Si sabemos algo sobre ángulos suplementarios, entonces podemos relacionarlos con el ángulo que necesitamos usando las propiedades de figuras iguales o similares. Por ejemplo, si conocemos los lados de un triángulo y necesitamos calcular el ángulo entre las rectas en las que se encuentran estos lados, entonces el teorema del coseno es adecuado para nuestra solución. Si tenemos un triángulo rectángulo en nuestra condición, para los cálculos también necesitaremos saber el seno, el coseno y la tangente del ángulo.
El método de coordenadas también es muy conveniente para resolver problemas de este tipo. Te explicamos cómo utilizarlo correctamente.
Tenemos un sistema de coordenadas rectangular (cartesiano) O x y, en el que se dan dos líneas rectas. Denotémoslos con las letras a y b. Las líneas rectas se pueden describir usando algunas ecuaciones. Las líneas originales tienen un punto de intersección M. ¿Cómo determinar el ángulo requerido (llamémoslo α) entre estas líneas rectas?
Comencemos formulando el principio básico de encontrar un ángulo en determinadas condiciones.
Sabemos que el concepto de línea recta está estrechamente relacionado con conceptos como vector de dirección y vector normal. Si tenemos una ecuación de una recta determinada, podemos tomar de ella las coordenadas de estos vectores. Podemos hacer esto para dos líneas que se cruzan a la vez.
El ángulo subtendido por dos líneas que se cruzan se puede encontrar usando:
- ángulo entre vectores de dirección;
- ángulo entre vectores normales;
- el ángulo entre el vector normal de una recta y el vector director de la otra.
Ahora veamos cada método por separado.
1. Supongamos que tenemos una recta a con un vector director a → = (a x, a y) y una recta b con un vector director b → (b x, b y). Ahora tracemos dos vectores a → y b → desde el punto de intersección. Luego de esto veremos que cada uno estará ubicado en su propia línea recta. Entonces tenemos cuatro opciones para su disposición relativa. Ver ilustración:

Si el ángulo entre dos vectores no es obtuso, entonces será el ángulo que necesitamos entre las líneas que se cruzan a y b. Si es obtuso, entonces el ángulo deseado será igual al ángulo adyacente al ángulo a →, b → ^. Así, α = a → , b → ^ si a → , b → ^ ≤ 90 ° , y α = 180 ° - a → , b → ^ si a → , b → ^ > 90 ° .
Partiendo del hecho de que los cosenos de ángulos iguales son iguales, podemos reescribir las igualdades resultantes de la siguiente manera: cos α = cos a →, b → ^, si a →, b → ^ ≤ 90 °; cos α = cos 180 ° - a →, b → ^ = - cos a →, b → ^, si a →, b → ^ > 90 °.
En el segundo caso se utilizaron fórmulas de reducción. De este modo,
cos α cos a → , b → ^ , cos a → , b → ^ ≥ 0 - cos a → , b → ^ , cos a → , b → ^< 0 ⇔ cos α = cos a → , b → ^
Escribamos la última fórmula en palabras:
Definición 3
El coseno del ángulo formado por dos rectas que se cruzan será igual al módulo del coseno del ángulo entre sus vectores directores.
La forma general de la fórmula para el coseno del ángulo entre dos vectores a → = (a x , a y) y b → = (b x , b y) se ve así:
porque a → , b → ^ = a → , b → ^ a → b → = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
De ahí podemos derivar la fórmula del coseno del ángulo entre dos rectas dadas:
cos α = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2 = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Entonces el ángulo en sí se puede encontrar usando la siguiente fórmula:
α = a r c cos a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Aquí a → = (a x , a y) y b → = (b x , b y) son los vectores directores de las rectas dadas.
Pongamos un ejemplo de cómo resolver el problema.
Ejemplo 1
En un sistema de coordenadas rectangular en un plano, se dan dos líneas que se cruzan a y b. Pueden describirse mediante las ecuaciones paramétricas x = 1 + 4 · λ y = 2 + λ λ ∈ R y x 5 = y - 6 - 3. Calcula el ángulo entre estas líneas.
Solución
Tenemos una ecuación paramétrica en nuestra condición, lo que significa que para esta línea podemos escribir inmediatamente las coordenadas de su vector director. Para hacer esto, necesitamos tomar los valores de los coeficientes del parámetro, es decir, la recta x = 1 + 4 · λ y = 2 + λ λ ∈ R tendrá un vector director a → = (4, 1).
La segunda línea se describe usando la ecuación canónica x 5 = y - 6 - 3. Aquí podemos tomar las coordenadas de los denominadores. Por tanto, esta recta tiene un vector director b → = (5, - 3).
A continuación, pasamos directamente a encontrar el ángulo. Para hacer esto, simplemente sustituya las coordenadas existentes de los dos vectores en la fórmula anterior α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2. Obtenemos lo siguiente:
α = a r c cos 4 5 + 1 (- 3) 4 2 + 1 2 5 2 + (- 3) 2 = a r c cos 17 17 34 = a r c cos 1 2 = 45 °
Respuesta: Estas líneas rectas forman un ángulo de 45 grados.
Podemos resolver un problema similar encontrando el ángulo entre vectores normales. Si tenemos una recta a con un vector normal n a → = (n a x , n a y) y una recta b con un vector normal n b → = (n b x , n b y), entonces el ángulo entre ellas será igual al ángulo entre n a → y n b → o el ángulo que será adyacente a n a → , n b → ^ . Este método se muestra en la imagen:

Las fórmulas para calcular el coseno del ángulo entre líneas que se cruzan y este ángulo mismo usando las coordenadas de vectores normales se ven así:
cos α = cos n a → , n b → ^ = n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2 α = a r c cos n a x n b x + n a y + n by n a x 2 + n a y 2 n b x 2 + n by 2
Aquí n a → y n b → denotan los vectores normales de dos rectas dadas.
Ejemplo 2
En un sistema de coordenadas rectangular, se dan dos líneas rectas usando las ecuaciones 3 x + 5 y - 30 = 0 y x + 4 y - 17 = 0. Encuentra el seno y el coseno del ángulo entre ellos y la magnitud de este ángulo mismo.
Solución
Las líneas originales se especifican usando ecuaciones de líneas normales de la forma A x + B y + C = 0. Denotamos el vector normal como n → = (A, B). Encontremos las coordenadas del primer vector normal para una línea y escríbalas: n a → = (3, 5) . Para la segunda recta x + 4 y - 17 = 0, el vector normal tendrá coordenadas n b → = (1, 4). Ahora sumemos los valores obtenidos a la fórmula y calculemos el total:
cos α = cos n a → , n b → ^ = 3 1 + 5 4 3 2 + 5 2 1 2 + 4 2 = 23 34 17 = 23 2 34
Si conocemos el coseno de un ángulo, entonces podemos calcular su seno usando la identidad trigonométrica básica. Dado que el ángulo α formado por rectas no es obtuso, entonces sen α = 1 - cos 2 α = 1 - 23 2 34 2 = 7 2 34.
En este caso, α = a r c cos 23 2 34 = a r c sen 7 2 34.
Respuesta: cos α = 23 2 34, sen α = 7 2 34, α = a r c cos 23 2 34 = a r c sen 7 2 34
Analicemos el último caso: encontrar el ángulo entre rectas si conocemos las coordenadas del vector director de una recta y el vector normal de otra.
Supongamos que la recta a tiene un vector director a → = (a x , a y) , y la recta b tiene un vector normal n b → = (n b x , n b y) . Necesitamos apartar estos vectores del punto de intersección y considerar todas las opciones para sus posiciones relativas. Ver en la imagen:

Si el ángulo entre los vectores dados no supera los 90 grados, resulta que complementará el ángulo entre ayb con un ángulo recto.
a → , n b → ^ = 90 ° - α si a → , n b → ^ ≤ 90 ° .
Si es inferior a 90 grados, obtenemos lo siguiente:
a → , n b → ^ > 90 ° , entonces a → , n b → ^ = 90 ° + α
Usando la regla de igualdad de cosenos de ángulos iguales, escribimos:
cos a → , n b → ^ = cos (90 ° - α) = sen α para a → , n b → ^ ≤ 90 ° .
cos a → , n b → ^ = cos 90 ° + α = - sen α para a → , n b → ^ > 90 ° .
De este modo,
sin α = cos a → , n b → ^ , a → , n b → ^ ≤ 90 ° - cos a → , n b → ^ , a → , n b → ^ > 90 ° ⇔ sin α = cos a → , n b → ^ , a → , n b → ^ > 0 - porque a → , n b → ^ , a → , n b → ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^
Formulemos una conclusión.
Definición 4
Para encontrar el seno del ángulo entre dos rectas que se cruzan en un plano, debes calcular el módulo del coseno del ángulo entre el vector director de la primera recta y el vector normal de la segunda.
Anotemos las fórmulas necesarias. Encontrar el seno de un ángulo:
pecado α = cos a → , n b → ^ = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Encontrar el ángulo en sí:
α = a r c pecado = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Aquí a → es el vector dirección de la primera línea y n b → es el vector normal de la segunda.
Ejemplo 3
Dos líneas que se cruzan están dadas por las ecuaciones x - 5 = y - 6 3 y x + 4 y - 17 = 0. Encuentra el ángulo de intersección.
Solución
Tomamos las coordenadas del vector guía y normal de las ecuaciones dadas. Resulta a → = (- 5, 3) y n → b = (1, 4). Tomamos la fórmula α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2 y calculamos:
α = a r c sen = - 5 1 + 3 4 (- 5) 2 + 3 2 1 2 + 4 2 = a r c sen 7 2 34
Tenga en cuenta que tomamos las ecuaciones del problema anterior y obtuvimos exactamente el mismo resultado, pero de manera diferente.
Respuesta:α = a r c sen 7 2 34
Presentemos otra forma de encontrar el ángulo deseado utilizando los coeficientes angulares de líneas rectas dadas.
Tenemos una recta a, que se define en un sistema de coordenadas rectangular usando la ecuación y = k 1 x + b 1, y una recta b, definida como y = k 2 x + b 2. Estas son ecuaciones de rectas con pendiente. Para encontrar el ángulo de intersección usamos la fórmula:
α = a r c cos k 1 · k 2 + 1 k 1 2 + 1 · k 2 2 + 1, donde k 1 y k 2 son las pendientes de las rectas dadas. Para obtener este registro se utilizaron fórmulas para determinar el ángulo a través de las coordenadas de vectores normales.
Ejemplo 4
Hay dos rectas que se cruzan en un plano, dadas por las ecuaciones y = - 3 5 x + 6 e y = - 1 4 x + 17 4. Calcula el valor del ángulo de intersección.
Solución
Los coeficientes angulares de nuestras líneas son iguales a k 1 = - 3 5 y k 2 = - 1 4. Sumémoslos a la fórmula α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1 y calculemos:
α = a r c cos - 3 5 · - 1 4 + 1 - 3 5 2 + 1 · - 1 4 2 + 1 = a r c cos 23 20 34 24 · 17 16 = a r c cos 23 2 34
Respuesta:α = ar c cos 23 2 34
En las conclusiones de este párrafo, cabe señalar que las fórmulas para encontrar el ángulo que se dan aquí no es necesario aprenderlas de memoria. Para ello basta con conocer las coordenadas de las guías y/o vectores normales de unas rectas dadas y poder determinarlas mediante distintos tipos de ecuaciones. Pero es mejor recordar o anotar las fórmulas para calcular el coseno de un ángulo.
Cómo calcular el ángulo entre líneas que se cruzan en el espacio
El cálculo de tal ángulo se puede reducir a calcular las coordenadas de los vectores directores y determinar la magnitud del ángulo formado por estos vectores. Para tales ejemplos, se utiliza el mismo razonamiento que dimos antes.
Supongamos que tenemos un sistema de coordenadas rectangular ubicado en un espacio tridimensional. Contiene dos rectas a y b con un punto de intersección M. Para calcular las coordenadas de los vectores directores, necesitamos conocer las ecuaciones de estas rectas. Denotemos los vectores directores a → = (a x , a y , a z ) y b → = (b x , b y , b z ) . Para calcular el coseno del ángulo entre ellos utilizamos la fórmula:
cos α = cos a → , b → ^ = a → , b → a → b → = a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
Para encontrar el ángulo en sí, necesitamos esta fórmula:
α = a r c porque a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
Ejemplo 5
Tenemos una recta definida en el espacio tridimensional usando la ecuación x 1 = y - 3 = z + 3 - 2. Se sabe que se cruza con el eje O z. Calcula el ángulo de intersección y el coseno de ese ángulo.
Solución
Denotemos el ángulo que debe calcularse con la letra α. Anotemos las coordenadas del vector director de la primera línea recta – a → = (1, - 3, - 2) . Para el eje aplicado, podemos tomar el vector de coordenadas k → = (0, 0, 1) como guía. Hemos recibido los datos necesarios y podemos agregarlos a la fórmula deseada:
cos α = cos a → , k → ^ = a → , k → a → k → = 1 0 - 3 0 - 2 1 1 2 + (- 3) 2 + (- 2) 2 0 2 + 0 2 + 1 2 = 2 8 = 1 2
Como resultado, encontramos que el ángulo que necesitamos será igual a a r c cos 1 2 = 45 °.
Respuesta: porque α = 1 2 , α = 45 ° .
Si nota un error en el texto, resáltelo y presione Ctrl+Enter
Sean dos rectas l y m en un plano en un sistema de coordenadas cartesianas dadas por ecuaciones generales: l: A 1 x + B 1 y + C 1 = 0, m: A 2 x + B 2 y + C 2 = 0
Vectores normales a estas líneas: = (A 1, B 1) – a la línea l,
= (A 2 , B 2) – a la línea m.
Sea j el ángulo entre las líneas l y m.


Dado que los ángulos con lados mutuamente perpendiculares son iguales o suman p, entonces ![]() , es decir, cos j = .
, es decir, cos j = .
Entonces, hemos demostrado el siguiente teorema.
Teorema. Sea j el ángulo entre dos líneas en el plano, y sean estas líneas especificadas en el sistema de coordenadas cartesianas mediante las ecuaciones generales A 1 x + B 1 y + C 1 = 0 y A 2 x + B 2 y + C 2 = 0. Entonces cos j =  .
.
Ejercicios.
1) Derive una fórmula para calcular el ángulo entre líneas rectas si:
(1) ambas líneas se especifican paramétricamente; (2) ambas líneas están dadas por ecuaciones canónicas; (3) una línea se especifica paramétricamente y la otra línea se especifica mediante una ecuación general; (4) ambas líneas están dadas por una ecuación con un coeficiente angular.
2) Sea j el ángulo entre dos líneas rectas en un plano, y definamos estas líneas rectas en un sistema de coordenadas cartesiano mediante las ecuaciones y = k 1 x + b 1 y y = k 2 x + b 2 .
Entonces tan j = .
3) Explore la posición relativa de dos líneas rectas, dada por ecuaciones generales en el sistema de coordenadas cartesiano, y complete la tabla:
La distancia de un punto a una línea recta en un plano.
Sea la recta l sobre un plano en el sistema de coordenadas cartesiano viene dada por la ecuación general Ax + By + C = 0. Encontremos la distancia desde el punto M(x 0 , y 0) a la recta l.
La distancia desde el punto M a la recta l es la longitud de la perpendicular HM (H О l, HM ^ l).

El vector y el vector normal a la recta l son colineales, por lo que | | = | | | | y | | = .
Sean las coordenadas del punto H (x,y).
Dado que el punto H pertenece a la línea l, entonces Ax + By + C = 0 (*).
Coordenadas de vectores y: = (x 0 - x, y 0 - y), = (A, B).
| | = ![]() =
= ![]() =
=
(C = -Ax - Por, ver (*))
Teorema. Deje que la línea recta l se especifique en el sistema de coordenadas cartesiano mediante la ecuación general Ax + By + C = 0. Luego, la distancia desde el punto M(x 0 , y 0) a esta línea recta se calcula mediante la fórmula: r ( M; l) = .
Ejercicios.
1) Derive una fórmula para calcular la distancia desde un punto a una línea si: (1) la línea se da de manera paramétrica; (2) se da la línea a las ecuaciones canónicas; (3) la línea recta viene dada por una ecuación con un coeficiente angular.
2) Escribe la ecuación de una circunferencia tangente a la recta 3x – y = 0, con centro en el punto Q(-2,4).
3) Escribe las ecuaciones de las rectas que dividen los ángulos formados por la intersección de las rectas 2x + y - 1 = 0 y x + y + 1 = 0, por la mitad.
§ 27. Definición analítica de un plano en el espacio.
Definición. El vector normal al avión. Llamaremos vector distinto de cero a cualquier representante del cual sea perpendicular a un plano dado.
Comentario. Está claro que si al menos un representante del vector es perpendicular al plano, entonces todos los demás representantes del vector son perpendiculares a este plano.
Sea un sistema de coordenadas cartesiano en el espacio.
Sea un plano dado, = (A, B, C) – el vector normal a este plano, el punto M (x 0, y 0, z 0) pertenece al plano a.

Para cualquier punto N(x, y, z) del plano a, los vectores y son ortogonales, es decir, su producto escalar es igual a cero: = 0. Escribamos la última igualdad en coordenadas: A(x - x 0 ) + B(y - y 0) + C(z - z 0) = 0.
Sea -Ax 0 - By 0 - Cz 0 = D, luego Ax + By + Cz + D = 0.
Tomemos un punto K (x, y) tal que Ax + By + Cz + D = 0. Dado que D = -Ax 0 - By 0 - Cz 0, entonces A(x - x 0) + B(y - y 0) + C(z - z 0) = 0. Dado que las coordenadas del segmento dirigido = (x - x 0, y - y 0, z - z 0), la última igualdad significa que ^ y, por tanto, K О a.
Entonces, hemos demostrado el siguiente teorema:
Teorema. Cualquier plano en el espacio en un sistema de coordenadas cartesiano se puede especificar mediante una ecuación de la forma Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0), donde (A, B, C) son los coordenadas del vector normal a este plano.
Lo opuesto también es cierto.
Teorema. Cualquier ecuación de la forma Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) en el sistema de coordenadas cartesiano especifica un determinado plano, y (A, B, C) son las coordenadas de la normal. vector a este plano.
Prueba.
Tome un punto M (x 0, y 0, z 0) tal que Ax 0 + By 0 + Cz 0 + D = 0 y vector = (A, B, C) ( ≠ q).
Un plano (y sólo uno) pasa por el punto M perpendicular al vector. Según el teorema anterior, este plano viene dado por la ecuación Ax + By + Cz + D = 0.
Definición. Una ecuación de la forma Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) se llama ecuación del plano general.
Ejemplo.
Escribamos la ecuación del plano que pasa por los puntos M (0,2,4), N (1,-1,0) y K (-1,0,5).
1. Encuentra las coordenadas del vector normal al plano (MNK). Dado que el producto vectorial ´ es ortogonal a los vectores no colineales y , entonces el vector es colineal ´ .
= (1, -3, -4), = (-1, -2, 1);
´ = (-11, 3, -5).
Entonces, como vector normal tomamos el vector = (-11, 3, -5).
2. Usemos ahora los resultados del primer teorema:
ecuación de este plano A(x - x 0) + B(y - y 0) + C(z - z 0) = 0, donde (A, B, C) son las coordenadas del vector normal, (x 0, y 0 , z 0) – coordenadas de un punto que se encuentra en el plano (por ejemplo, el punto M).
11(x - 0) + 3(y - 2) - 5(z - 4) = 0
11x + 3y – 5z + 14 = 0
Respuesta: -11x + 3y - 5z + 14 = 0.
Ejercicios.
1) Escribe la ecuación del avión si
(1) el plano pasa por el punto M (-2,3,0) paralelo al plano 3x + y + z = 0;
(2) el plano contiene el eje (Ox) y es perpendicular al plano x + 2y – 5z + 7 = 0.
2) Escribe la ecuación del avión que pasa por los tres puntos dados.
§ 28. Definición analítica de un semiespacio*
Comentario*. Que se arregle algún avión. Bajo medio espacio entenderemos el conjunto de puntos que se encuentran a un lado de un plano dado, es decir, dos puntos se encuentran en el mismo semiespacio si el segmento que los conecta no corta el plano dado. Este avión se llama borde de este medio espacio. La unión de este plano y el semiespacio se llamará medio espacio cerrado.
Sea un sistema de coordenadas cartesiano fijo en el espacio.
Teorema. Sea el plano a dado por la ecuación general Ax + By + Cz + D = 0. Entonces uno de los dos semiespacios en que el plano a divide el espacio viene dado por la desigualdad Ax + By + Cz + D > 0 , y el segundo semiespacio viene dado por la desigualdad Ax + By + Cz + D< 0.
Prueba.
Tracemos el vector normal = (A, B, C) al plano a desde el punto M (x 0 , y 0 , z 0) que se encuentra en este plano: = , M О a, MN ^ a. El plano divide el espacio en dos semiespacios: b 1 y b 2. Está claro que el punto N pertenece a uno de estos semiespacios. Sin pérdida de generalidad, asumiremos que N О b 1 .

Demostremos que el semiespacio b 1 está definido por la desigualdad Ax + By + Cz + D > 0.
1) Tome un punto K(x,y,z) en el semiespacio b 1. El ángulo Ð NMK es el ángulo entre los vectores y - agudo, por lo tanto el producto escalar de estos vectores es positivo: > 0. Escribamos esta desigualdad en coordenadas: A(x - x 0) + B(y - y 0) + C(z - z 0) > 0, es decir, Ax + By + Cy - Ax 0 - By 0 - C z 0 > 0.
Dado que M О b 1, entonces Ax 0 + By 0 + C z 0 + D = 0, por lo tanto -Ax 0 - By 0 - C z 0 = D. Por tanto, la última desigualdad se puede escribir de la siguiente manera: Ax + By + Cz + D > 0.
2) Tome un punto L(x,y) tal que Ax + By + Cz + D > 0.
Reescribamos la desigualdad, reemplazando D con (-Ax 0 - By 0 - C z 0) (ya que M О b 1, entonces Ax 0 + By 0 + C z 0 + D = 0): A(x - x 0) + B(y - y 0) + C(z - z 0) > 0.
Un vector con coordenadas (x - x 0,y - y 0, z - z 0) es un vector, por lo que la expresión A(x - x 0) + B(y - y 0) + C(z - z 0) puede entenderse como un producto escalar de vectores y . Dado que el producto escalar de los vectores y es positivo, el ángulo entre ellos es agudo y el punto L О b 1 .
De manera similar, podemos demostrar que el semiespacio b 2 está dado por la desigualdad Ax + By + Cz + D< 0.
Notas.
1) Está claro que la demostración dada anteriormente no depende de la elección del punto M en el plano a.
2) Está claro que el mismo semiespacio puede definirse mediante diferentes desigualdades.
Lo opuesto también es cierto.
Teorema. Cualquier desigualdad lineal de la forma Ax + By + Cz + D > 0 (o Ax + By + Cz + D< 0) (A 2 + B 2 + C 2 ≠ 0) задает в пространстве в декартовой системе координат полупространство с границей Ax + By + Cz + D = 0.
Prueba.
La ecuación Ax + By + Cz + D = 0 (A 2 + B 2 + C 2 ≠ 0) en el espacio define un determinado plano a (ver § ...). Como quedó demostrado en el teorema anterior, uno de los dos semiespacios en que el plano divide el espacio viene dado por la desigualdad Ax Ax + By + Cz + D > 0.
Notas.
1) Está claro que un semiespacio cerrado puede definirse mediante una desigualdad lineal no estricta, y cualquier desigualdad lineal no estricta en el sistema de coordenadas cartesiano define un semiespacio cerrado.
2) Cualquier poliedro convexo se puede definir como la intersección de semiespacios cerrados (cuyos límites son planos que contienen las caras del poliedro), es decir, analíticamente, mediante un sistema de desigualdades lineales no estrictas.
Ejercicios.
1) Demuestre los dos teoremas presentados para un sistema de coordenadas afín arbitrario.
2) ¿Es cierto lo contrario, que cualquier sistema de desigualdades lineales no estrictas define un polígono convexo?
Ejercicio.1) Explora las posiciones relativas de dos planos definidos por ecuaciones generales en el sistema de coordenadas cartesiano y completa la tabla.
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0