Este es un cuadrilátero cuyos lados opuestos son paralelos en pares.
Propiedad 1. Cualquier diagonal de un paralelogramo lo divide en dos triángulos iguales.
Prueba . Según la característica II (ángulos transversales y lado común).
El teorema está demostrado..
Propiedad 2. En un paralelogramo, los lados opuestos son iguales y los ángulos opuestos son iguales.
Prueba .
Asimismo,
El teorema está demostrado..

Propiedad 3. En un paralelogramo, las diagonales son bisecadas por el punto de intersección.
Prueba .
El teorema está demostrado..

Propiedad 4. La bisectriz del ángulo de un paralelogramo, que corta al lado opuesto, lo divide en triángulo isósceles y trapezoide. (Cap. palabras - vértice - ¿dos isósceles? -ka).
Prueba .

El teorema está demostrado..
Propiedad 5. En un paralelogramo, un segmento de recta con extremos en lados opuestos que pasa por el punto de intersección de las diagonales es bisecado por este punto.
Prueba .
El teorema está demostrado..

Propiedad 6. El ángulo entre las altitudes que caen desde el vértice de un ángulo obtuso de un paralelogramo es igual a un ángulo agudo de un paralelogramo.
Prueba .

El teorema está demostrado..
Propiedad 7. La suma de los ángulos de un paralelogramo adyacente a un lado es 180°.
Prueba .
El teorema está demostrado..

Construir la bisectriz de un ángulo. Propiedades de la bisectriz de un triángulo.
1) Construir un rayo arbitrario DE.
2) En un rayo dado, construye un círculo arbitrario con centro en el vértice y el mismo
con el centro al inicio del rayo construido.
3) F y G - puntos de intersección del círculo con los lados de un ángulo dado, H - punto de intersección del círculo con el rayo construido

Construya un círculo con centro en el punto H y radio igual a FG.
5) I es el punto de intersección de los círculos de la viga construida.
6) Dibuja una línea recta que pase por el vértice y I.
IDH es el ángulo requerido.
)
Propiedad 1. La bisectriz de un ángulo de un triángulo divide al lado opuesto en proporción a los lados adyacentes.

Prueba . Sean x, y segmentos del lado c. Continuamos el rayo BC. En el rayo BC trazamos desde C un segmento CK igual a AC.
Un paralelogramo es un cuadrilátero cuyos lados opuestos son paralelos, es decir se encuentran en líneas paralelas
Propiedades de un paralelogramo: 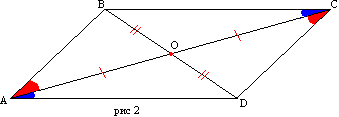 Teorema 22.
Los lados opuestos de un paralelogramo son iguales.
Teorema 22.
Los lados opuestos de un paralelogramo son iguales.
Prueba. En el paralelogramo ABCD dibujamos una diagonal AC. Los triángulos ACD y ACB son iguales porque tienen un lado común AC y dos pares. ángulos iguales. adyacente a él: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (como ángulos transversales con líneas paralelas AD y BC). Esto significa que AB = CD y BC = AD, como los lados correspondientes de triángulos iguales, etc. De la igualdad de estos triángulos también se deduce que los ángulos correspondientes de los triángulos son iguales:
Teorema 23.
Los ángulos opuestos del paralelogramo son iguales: ∠ A=∠ C y ∠ B=∠ D.
La igualdad del primer par proviene de la igualdad de los triángulos ABD y CBD, y del segundo, ABC y ACD.
Teorema 24.
Ángulos adyacentes de un paralelogramo, es decir Los ángulos adyacentes a un lado suman 180 grados.
Esto es así porque son ángulos interiores unilaterales.
Teorema 25.
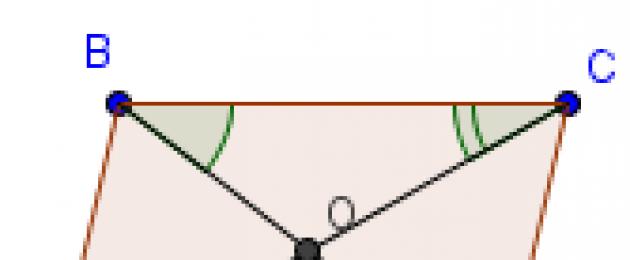
Las diagonales de un paralelogramo se bisecan en su punto de intersección.
Prueba. Considere los triángulos BOC y AOD. Según la primera propiedad AD=BC ∠ OAD=∠ OCB y ∠ ODA=∠ OBC transversales para las rectas paralelas AD y BC. Por tanto, los triángulos BOC y AOD son iguales en ángulos laterales y adyacentes. Esto significa BO=OD y AO=OS, como los lados correspondientes de triángulos iguales, etc.
Signos de un paralelogramo
Teorema 26.
Si los lados opuestos de un cuadrilátero son iguales en pares, entonces es un paralelogramo.
Prueba. Sea el cuadrilátero ABCD los lados AD y BC, AB y CD respectivamente iguales (Fig. 2). Dibujemos la diagonal AC. Los triángulos ABC y ACD son iguales en tres lados. Entonces los ángulos BAC y DCA son iguales y, por tanto, AB es paralelo a CD. El paralelismo de los lados BC y AD se deriva de la igualdad de los ángulos CAD y ACB.
Teorema 27.
Si los ángulos opuestos de un cuadrilátero son iguales en pares, entonces es un paralelogramo.
Sean ∠ A=∠ C y ∠ B=∠ D. Porque ∠ A+∠ B+∠ C+∠ D=360 o, entonces ∠ A+∠ B=180 o y los lados AD y BC son paralelos (basado en el paralelismo de rectas). También demostraremos el paralelismo de los lados AB y CD y concluiremos que ABCD es un paralelogramo por definición.
Teorema 28.
Si las esquinas adyacentes de un cuadrilátero, es decir Los ángulos adyacentes a un lado suman 180 grados, entonces es un paralelogramo.
Si los ángulos interiores de un lado suman 180 grados, entonces las rectas son paralelas. Entonces AB es paralelo a CD y BC es paralelo a AD. Un cuadrilátero resulta ser un paralelogramo por definición.
Teorema 29.
Si las diagonales de un cuadrilátero se bisecan en el punto de intersección, entonces el cuadrilátero es un paralelogramo.
Prueba. Si AO = OC, BO = OD, entonces los triángulos AOD y BOC son iguales, ya que tienen ángulos iguales (verticales) en el vértice O, encerrado entre los pares. lados iguales. De la igualdad de los triángulos concluimos que AD y BC son iguales. Los lados AB y CD también son iguales y el cuadrilátero resulta ser un paralelogramo según el criterio 1.
Teorema 30.
Si un cuadrilátero tiene un par de lados iguales y paralelos, entonces es un paralelogramo.
Sean los lados AB y CD del cuadrilátero ABCD paralelos e iguales. Dibujemos las diagonales AC y BD. Del paralelismo de estas rectas se deduce que los ángulos transversales ABO = CDO y BAO = OCD son iguales. Los triángulos ABO y CDO son iguales en ángulos laterales y adyacentes. Por lo tanto AO=OS, VO=ОD, es decir Las diagonales se dividen por la mitad por el punto de intersección y el cuadrilátero resulta ser un paralelogramo según el criterio 4.
En geometría se consideran casos especiales de paralelogramos.
Al resolver problemas sobre este tema, excepto propiedades básicas paralelogramo y las fórmulas correspondientes, puedes recordar y aplicar lo siguiente:
- La bisectriz de un ángulo interior de un paralelogramo corta un triángulo isósceles.
- Las bisectrices de ángulos interiores adyacentes a uno de los lados de un paralelogramo son mutuamente perpendiculares.
- Las bisectrices que provienen de esquinas interiores opuestas de un paralelogramo son paralelas entre sí o se encuentran en la misma línea recta.
- La suma de los cuadrados de las diagonales de un paralelogramo es igual a la suma de los cuadrados de sus lados.
- El área de un paralelogramo es igual a la mitad del producto de las diagonales por el seno del ángulo entre ellas
Consideremos problemas en los que se utilizan estas propiedades.
Tarea 1.
La bisectriz del ángulo C del paralelogramo ABCD corta el lado AD en el punto M y la continuación del lado AB más allá del punto A en el punto E. Calcula el perímetro del paralelogramo si AE = 4, DM = 3.
Solución.
1. El triángulo CMD es isósceles. (Propiedad 1). Por tanto, CD = MD = 3 cm.
2. El triángulo EAM es isósceles.
Por tanto, AE = AM = 4 cm.
3. AD = AM + MD = 7 cm.
4. Perímetro ABCD = 20 cm.
Respuesta. 20 centímetros.
Tarea 2.
Las diagonales se dibujan en un cuadrilátero convexo ABCD. Se sabe que las áreas de los triángulos ABD, ACD, BCD son iguales. Demuestra que este cuadrilátero es un paralelogramo.

Solución.
1. Sea BE la altura del triángulo ABD, CF la altura del triángulo ACD. Dado que, según las condiciones del problema, las áreas de los triángulos son iguales y tienen una base común AD, entonces las alturas de estos triángulos son iguales. SER = CF.
2. BE, CF son perpendiculares a AD. Los puntos B y C están ubicados en el mismo lado con respecto a la línea recta AD. SER = CF. Por tanto, la recta BC || ANUNCIO. (*)
3. Sea AL la altura del triángulo ACD y BK la altura del triángulo BCD. Dado que, según las condiciones del problema, las áreas de los triángulos son iguales y tienen una base común CD, entonces las alturas de estos triángulos son iguales. AL = BK.
4. AL y BK son perpendiculares a CD. Los puntos B y A están ubicados en el mismo lado con respecto a la línea recta CD. AL = BK. Por tanto, la recta AB || CD (**)
5. De las condiciones (*), (**) se deduce que ABCD es un paralelogramo.
Respuesta. Probado. ABCD es un paralelogramo.
Tarea 3.
En los lados BC y CD del paralelogramo ABCD, los puntos M y H están marcados, respectivamente, de modo que los segmentos BM y HD se cruzan en el punto O;<ВМD = 95 о,
 Solución.
Solución.
1. En el triángulo DOM<МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.
2. En un triángulo rectángulo DHC Entonces<НСD = 30 о. СD: НD = 2: 1 Pero CD = AB. Entonces AB:HD = 2:1. 3. <С = 30 о, 4. <А = <С = 30 о, <В = Respuesta: AB: HD = 2: 1,<А = <С = 30 о, <В = Tarea 4. Una de las diagonales de un paralelogramo de longitud 4√6 forma un ángulo de 60° con la base y la segunda diagonal forma un ángulo de 45° con la misma base. Encuentra la segunda diagonal. Solución.
1. AO = 2√6. 2. Aplicamos el teorema del seno al triángulo AOD. AO/sen D = OD/sen A. 2√6/sen 45 o = OD/sen 60 o. ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6. Respuesta: 12.
Tarea 5. Para un paralelogramo con lados 5√2 y 7√2, el ángulo menor entre las diagonales es igual al ángulo menor del paralelogramo. Encuentra la suma de las longitudes de las diagonales. Solución.
Sean d 1, d 2 las diagonales del paralelogramo, y el ángulo entre las diagonales y el ángulo más pequeño del paralelogramo es igual a φ. 1. Contemos dos diferentes S ABCD = AB AD sen A = 5√2 7√2 sen f, S ABCD = 1/2 AC ВD sen AOB = 1/2 d 1 d 2 sen f. Obtenemos la igualdad 5√2 · 7√2 · sen f = 1/2d 1 d 2 sen f o 2 · 5√2 · 7√2 = re 1 re 2 ; 2. Usando la relación entre los lados y las diagonales del paralelogramo, escribimos la igualdad (AB 2 + AD 2) 2 = AC 2 + BD 2. ((5√2) 2 + (7√2) 2) 2 = re 1 2 + re 2 2. re 1 2 + re 2 2 = 296. 3. Creemos un sistema: (re 1 2 + re 2 2 = 296, Multipliquemos la segunda ecuación del sistema por 2 y sumémosla a la primera. Obtenemos (d 1 + d 2) 2 = 576. Por tanto, Id 1 + d 2 I = 24. Dado que d 1, d 2 son las longitudes de las diagonales del paralelogramo, entonces d 1 + d 2 = 24. Respuesta: 24.
Tarea 6. Los lados del paralelogramo son 4 y 6. El ángulo agudo entre las diagonales es de 45 grados. Encuentra el área del paralelogramo. Solución.
1. Del triángulo AOB, usando el teorema del coseno, escribimos la relación entre el lado del paralelogramo y las diagonales. AB 2 = AO 2 + VO 2 2 · AO · VO · cos AOB. 4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1/2) · (d 2 /2)cos 45 o; d 1 2 /4 + d 2 2 /4 – 2 · (d 1/2) · (d 2 /2)√2/2 = 16. re 1 2 + re 2 2 – re 1 · re 2 √2 = 64. 2. De manera similar, escribimos la relación para el triángulo AOD. tomemos en cuenta que<АОD = 135 о и cos 135 о = -cos 45 о = -√2/2. Obtenemos la ecuación d 1 2 + d 2 2 + d 1 · d 2 √2 = 144. 3. Tenemos un sistema Restando la primera de la segunda ecuación, obtenemos 2d 1 · d 2 √2 = 80 o re 1 re 2 = 80/(2√2) = 20√2 4. S ABCD = 1/2 AC ВD sen AOB = 1/2 d 1 d 2 sen α = 1/2 20√2 √2/2 = 10. Nota: En este problema y en el anterior no es necesario resolver el sistema por completo, anticipando que en este problema necesitamos el producto de diagonales para calcular el área. Respuesta: 10. Tarea 7. El área del paralelogramo es 96 y sus lados son 8 y 15. Encuentra el cuadrado de la diagonal más pequeña. Solución.
1. S ABCD = AB · AD · sen ВAD. Hagamos una sustitución en la fórmula. Obtenemos 96 = 8 · 15 · sin ВAD. Por tanto sen ВAD = 4/5. 2. Busquemos cos VAD. sen 2 VAD + cos 2 VAD = 1. (4/5) 2 + cos 2 VAD = 1. cos 2 VAD = 9/25. Según las condiciones del problema, encontramos la longitud de la diagonal menor. La diagonal ВАD será menor si el ángulo ВАD es agudo. Entonces cos VAD = 3/5. 3. Del triángulo ABD, usando el teorema del coseno, encontramos el cuadrado de la diagonal BD. ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВAD. ВD 2 = 8 2 + 15 2 – 2 8 15 3 / 5 = 145. Respuesta: 145.
¿Aún tienes preguntas? ¿No sabes cómo resolver un problema de geometría? sitio web, al copiar material total o parcialmente, se requiere un enlace a la fuente. Así como en la geometría euclidiana un punto y una línea recta son los elementos principales de la teoría de los planos, el paralelogramo es una de las figuras clave de los cuadriláteros convexos. De él, como hilos de una bola, fluyen los conceptos de "rectángulo", "cuadrado", "rombo" y otras cantidades geométricas. En contacto con cuadrilátero convexo, formado por segmentos, cada par de los cuales es paralelo, se conoce en geometría como paralelogramo. El aspecto de un paralelogramo clásico se representa mediante un cuadrilátero ABCD. Los lados se llaman bases (AB, BC, CD y AD), la perpendicular trazada desde cualquier vértice al lado opuesto a este vértice se llama altura (BE y BF), las rectas AC y BD se llaman diagonales. ¡Atención! El cuadrado, el rombo y el rectángulo son casos especiales de paralelogramo. Propiedades clave, en general, predeterminado por la propia designación, están demostrados por el teorema. Estas características son las siguientes: Prueba: Consideremos ∆ABC y ∆ADC, que se obtienen dividiendo el cuadrilátero ABCD por la recta AC. ∠BCA=∠CAD y ∠BAC=∠ACD, ya que AC es común para ellos (ángulos verticales para BC||AD y AB||CD, respectivamente). De esto se deduce: ∆ABC = ∆ADC (el segundo signo de igualdad de los triángulos). Los segmentos AB y BC en ∆ABC corresponden en pares a las rectas CD y AD en ∆ADC, lo que significa que son idénticos: AB = CD, BC = AD. Así, ∠B corresponde a ∠D y son iguales. Dado que ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, que también son idénticos por pares, entonces ∠A = ∠C. La propiedad ha sido probada. Caracteristica principal de estas rectas de un paralelogramo: el punto de intersección las divide por la mitad. Prueba: Sea el punto de intersección de las diagonales AC y BD de la figura ABCD. Forman dos triángulos proporcionales: ∆ABE y ∆CDE. AB=CD ya que son opuestos. Según rectas y secantes, ∠ABE = ∠CDE y ∠BAE = ∠DCE. Según el segundo criterio de igualdad, ∆ABE = ∆CDE. Esto significa que los elementos ∆ABE y ∆CDE: AE = CE, BE = DE y a la vez son partes proporcionales de AC y BD. La propiedad ha sido probada. Los lados adyacentes tienen una suma de ángulos igual a 180°, ya que se encuentran en el mismo lado de rectas paralelas y una transversal. Para el cuadrilátero ABCD: ∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º Propiedades de la bisectriz: Las características de esta figura se derivan de su teorema principal, que establece lo siguiente: un cuadrilátero se considera un paralelogramo en el caso de que sus diagonales se crucen, y este punto las divida en segmentos iguales. Prueba: dejemos que las líneas AC y BD del cuadrilátero ABCD se crucen en, es decir, Dado que ∠AED = ∠BEC, y AE+CE=AC BE+DE=BD, entonces ∆AED = ∆BEC (según el primer criterio para la igualdad de triángulos). Es decir, ∠EAD = ∠BCE. También son los ángulos transversales internos de la secante AC para las rectas AD y BC. Así, por definición de paralelismo - AD || ANTES DE CRISTO. También se deriva una propiedad similar de las líneas BC y CD. El teorema ha sido demostrado. Área de esta figura encontrado por varios métodos una de las más sencillas: multiplicar la altura y la base a la que se dibuja. Prueba: trazar las perpendiculares BE y CF desde los vértices B y C. ∆ABE y ∆DCF son iguales, ya que AB = CD y BE = CF. ABCD tiene el mismo tamaño que el rectángulo EBCF, ya que se compone de figuras conmensurables: S ABE y S EBCD, así como S DCF y S EBCD. De esto se deduce que el área de esta figura geométrica es la misma que la de un rectángulo: S ABCD = S EBCF = BE×BC=BE×AD. Para determinar la fórmula general para el área de un paralelogramo, denotamos la altura como media pensión, y el lado - b. Respectivamente: Cálculos de área a través de los lados del paralelogramo y el ángulo, que forman, es el segundo método conocido. Spr-ma - área; a y b son sus lados α es el ángulo entre los segmentos a y b. Este método se basa prácticamente en el primero, pero por si se desconoce. siempre corta un triángulo rectángulo cuyos parámetros se encuentran mediante identidades trigonométricas, es decir. Transformando la relación, obtenemos . En la ecuación del primer método reemplazamos la altura con este producto y obtenemos una prueba de la validez de esta fórmula. A través de las diagonales de un paralelogramo y el ángulo, que crean cuando se cruzan, también puedes encontrar el área. Prueba: AC y BD se cruzan para formar cuatro triángulos: ABE, BEC, CDE y AED. Su suma es igual al área de este cuadrilátero. El área de cada uno de estos ∆ se puede encontrar mediante la expresión , donde a=BE, b=AE, ∠γ =∠AEB. Desde , los cálculos utilizan un único valor de seno. Eso es . Dado que AE+CE=AC= d 1 y BE+DE=BD= d 2, la fórmula del área se reduce a: Las características de las partes constituyentes de este cuadrilátero han encontrado aplicación en álgebra vectorial, es decir, la suma de dos vectores. La regla del paralelogramo establece que si se dan vectoresYNoson colineales, entonces su suma será igual a la diagonal de esta figura, cuyas bases corresponden a estos vectores. Prueba: desde un comienzo elegido arbitrariamente, es decir. - construir vectores y . A continuación, construimos un paralelogramo OASV, donde los segmentos OA y OB son lados. Por tanto, el sistema operativo se encuentra en el vector o suma. Las identidades se dan bajo las siguientes condiciones: Un paralelogramo es un cuadrilátero cuyos lados opuestos son paralelos en pares. La siguiente figura muestra el paralelogramo ABCD. Tiene el lado AB paralelo al lado CD y el lado BC paralelo al lado AD. Como habrás adivinado, un paralelogramo es un cuadrilátero convexo. Consideremos las propiedades básicas de un paralelogramo. 1. En un paralelogramo, los ángulos opuestos y los lados opuestos son iguales. Demostremos esta propiedad: considere el paralelogramo presentado en la siguiente figura. La diagonal BD lo divide en dos triángulos iguales: ABD y CBD. Son iguales a lo largo del lado BD y los dos ángulos adyacentes a él, ya que los ángulos que se encuentran transversalmente en la secante BD de las líneas paralelas BC y AD y AB y CD, respectivamente. Por lo tanto AB = CD y 2. Las diagonales de un paralelogramo se dividen por la mitad por el punto de intersección. Sea el punto O el punto de intersección de las diagonales AC y BD del paralelogramo ABCD. Entonces el triángulo AOB y el triángulo COD son iguales entre sí, en el lado y en dos ángulos adyacentes. (AB = CD ya que estos son lados opuestos del paralelogramo. Y ángulo1 = ángulo2 y ángulo3 = ángulo4 son como ángulos transversales cuando las líneas AB y CD se cruzan con las secantes AC y BD, respectivamente.) De esto se deduce que AO = OC y OB = OD, que necesitaba ser probado. Todas las propiedades principales se ilustran en las tres figuras siguientes.
(
(Ya que en un triángulo rectángulo el cateto opuesto al ángulo de 30° es igual a la mitad de la hipotenusa).
 maneras su área.
maneras su área.
(d 1 + d 2 = 140.
(re 1 2 + re 2 2 – re 1 · re 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Para obtener ayuda de un tutor, regístrese.
¡La primera lección es gratis!
Definición de paralelogramo
Lados y ángulos: características de la relación.
Características de las diagonales de una figura.
Características de las esquinas adyacentes.
Determinación de los rasgos característicos de un paralelogramo mediante el teorema.
Calcular el área de una figura

Otras formas de encontrar el área
![]() ,
,![]() .
.Aplicación en álgebra vectorial

Fórmulas para calcular los parámetros de un paralelogramo.
Parámetro
Fórmula
Encontrar los lados
a lo largo de las diagonales y el coseno del ángulo entre ellas
![]()
![]()
a lo largo de diagonales y lados
![]()
![]()
a través de la altura y el vértice opuesto
Encontrar la longitud de las diagonales
en los lados y el tamaño del ápice entre ellos.
Propiedades de un paralelogramo

antes de Cristo = d.C. Y de la igualdad de los ángulos 1, 2, 3 y 4 se deduce que ángulo A = ángulo1 + ángulo3 = ángulo2 + ángulo4 = ángulo C.