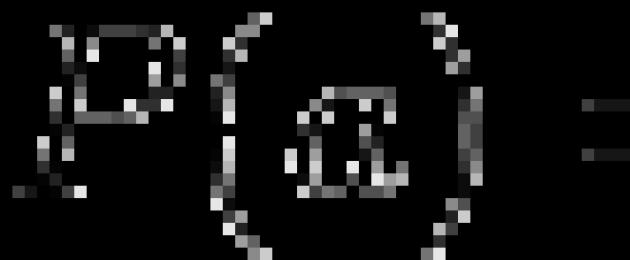Bezoutov teorem, unatoč prividnoj jednostavnosti i očitosti, jedan je od osnovnih teorema teorije polinoma. U ovom teoremu, algebarske karakteristike polinoma (one vam omogućuju rad s polinomima kao cijelim brojevima) povezane su s njihovim funkcionalnim karakteristikama (koje vam omogućuju da polinome smatrate funkcijama).

Bezoutov teorem navodi da je ostatak pri dijeljenju polinoma polinomom .

Koeficijenti polinoma leže u nekom komutativnom prstenu s jedinicom (na primjer, u polju realnih ili kompleksnih brojeva).

Bezoutov teorem – dokaz.

Podijeli polinom s ostatkom P(x) na polinom (x-a):

Na temelju činjenice da stupanj R(x)< deg (x-a) = 1 - polinom stupnja ne višeg od nule. Zamjenjujemo, budući da dobijemo .

Ali nije teorem najvažniji, već korolar Bezoutovog teorema:

1. Broj je korijen polinoma P(x) tada i samo kada P(x) djeljiv binomom bez ostatka x-a.

Na temelju toga, skup korijena polinoma P(x) identičan je skupu korijena odgovarajuće jednadžbe x-a.

2. Slobodni član polinoma dijeli se bilo kojim cjelobrojnim korijenom polinoma s cjelobrojnim koeficijentima (kada je vodeći koeficijent jednak jedinici, svi racionalni korijeni su cijeli brojevi).

3. Pretpostavimo da je to cjelobrojni korijen reduciranog polinoma P(x) s cjelobrojnim koeficijentima. To znači da je za svaki cijeli broj broj djeljiv s .

Bezoutov teorem omogućuje da se, nakon pronalaska jednog korijena polinoma, dalje traže korijeni polinoma čiji je stupanj već za 1 manji: ako je , tada je ovaj polinom P(x) izgledat će ovako:

Primjeri Bezoutovog teorema:

Odredite ostatak pri dijeljenju polinoma binomom.

Primjeri rješenja Bezoutovog teorema:

Na temelju Bezoutovog teorema, traženi ostatak odgovara vrijednosti polinoma u točki. Tada ćemo pronaći , za ovo smo zamijeniti vrijednost u izraz za polinom umjesto . Dobivamo:

Odgovor: Ostatak = 5.

Hornerova shema.

Hornerova shema je algoritam za dijeljenje (dijeljenje po Hornerovoj shemi) polinoma, napisan za poseban slučaj ako je kvocijent jednak binomu.

Napravimo ovaj algoritam:

Pretpostavimo da je to dividenda

Kvocijent (njegov stupanj će vjerojatno biti jedan manji), r- ostatak (budući da se dijeljenje provodi polinomom 1 stupnja, tada će stupanj ostatka biti za jedan manji, tj. nula, pa je ostatak konstanta).

Po definiciji dijeljenja s ostatkom P(x) = Q(x) (x-a) + r. Nakon zamjene polinomskih izraza dobivamo:

Otvorimo zagrade i izjednačimo koeficijente pri istim potencijama, nakon čega koeficijente količnika izrazimo kroz koeficijente djeljenika i djelitelja:

Prikladno je sažeti izračune u sljedećoj tablici:

Ističe one ćelije čiji je sadržaj uključen u izračune u sljedećem koraku.

Primjeri Hornerovih shema:

Pretpostavimo da trebamo podijeliti polinom s binomom x-2.

Izrađujemo tablicu s dva retka. U 1 retku ispisujemo koeficijente našeg polinoma. U drugom retku ćemo dobiti koeficijente nepotpunog kvocijenta prema sljedećoj shemi: prvo prepišemo vodeći koeficijent ovog polinoma, zatim, da bismo dobili sljedeći koeficijent, pomnožimo posljednji pronađeni s a=2 i zbroji s pripadajućim koeficijentom polinoma F(x). Najnoviji koeficijent bit će ostatak, a svi prethodni koeficijenti nepunog količnika.

znanstveni rad

Primjena teorema

Zadržat ću se na razmatranju nekih primjera primjene Bezoutovog teorema na rješavanje praktičnih problema.

Treba napomenuti da je kod rješavanja jednadžbi pomoću Bezoutovog teorema potrebno:

· pronaći sve cjelobrojne djelitelje slobodnog člana;

· iz ovih djelitelja pronaći barem jedan korijen jednadžbe (a);

· lijevu stranu jednadžbe podijeliti s (x-a);

· umnožak djelitelja i količnika zapisati na lijevu stranu jednadžbe;

· riješiti dobivenu jednadžbu.

Pronađite ostatak polinoma x 3 -3x 2 +6x-5

binomom x-2.

Prema Bezoutovom teoremu:

R=f(2)=2 3 -3*2 2 +6*2-5=3.

Odgovor: R=3.

Pri kojoj se vrijednosti a polinom x 4 +ax 3 +3x 2 -4x-4 dijeli bez ostatka binomom x-2?

Prema Bezoutovom teoremu: R=f(2)=16+8a+12-8- 4=8a+16.

Ali prema uvjetu, R=0, što znači 8a+16=0, dakle a=-2.

Odgovor: a=-2.

Pri kojim vrijednostima a i b je polinom ax 3 +bx 2 -73x+102 djeljiv trinomom x 2 -5x+6 bez ostatka?

Rastavimo djelitelj na faktore: x 2 -5x+6=(x-2)(x-3).

Budući da su binomi x-2 i x-3 međusobno prosti, ovaj polinom je djeljiv s x-2 i x-3, što znači da prema Bezoutovom teoremu:

R 1 =f(2)=8a+4b-146+102=8a+4b-44=0

R 2 =f(3)=27a+9b-219+102=27a+9b-117=0

Riješit ću sustav jednadžbi:

8a+4b-44=0 2a+b=11

27a+9b-117=0 3a+b=13

Odavde dobivamo: a=2, b=7.

Odgovor: a=2, b=7.

Za koje vrijednosti a i b vrijedi polinom x 4 +ax 3 -9x 2 +11x+b

je djeljiv bez ostatka trinomom x 2 -2x+1?

Zamislimo djelitelj ovako: x 2 - 2x + 1 = (x - 1) 2

Ovaj polinom je djeljiv s x-1 bez ostatka ako, prema Bezoutovom teoremu:

R 1 =f(1)=1+a-9+11+b=a+b+3=0.

Nađimo kvocijent dijeljenja ovog polinoma s x-1:

X 4 +ax 3 -9x 2 +11x-a-3 x-1

x 4 -x 3 x 3 +(a+1)x 2 +(a-8)x+(a+3)

(a+1)x 3 -(a + 1)x 2

(a-8)x 2 -(a-8)x

Kvocijent x 3 +(a+1)x 2 +(a-8)x+(a+3) dijeli se sa (x-1) bez ostatka, odakle

R 2 =f(1)=1+(a+1)*1+(a-8)*1+a+3=3a-3=0.

Riješit ću sustav jednadžbi:

a + b + 3 = 0 a + b =-3

3a - 3 = 0 a = 1

Iz sustava: a=1, b=-4

Odgovor: a=1, b=-4.

Faktorirajte polinom f(x)=x 4 +4x 2 -5.

Među djeliteljima slobodnog člana, broj 1 je korijen zadanog polinoma f(x), što znači da je prema korolariji 2 Bezoutovog teorema, f(x) djeljiv s (x-1) bez ostatka:

f(x)/(x-1)=x 3 +x 2 +5x+5, što znači f(x)=(x-1)(x 3 +x 2 +5x+5).

Među djeliteljima slobodnog člana polinoma x 3 +x 2 +5x+5 x=-1 nalazi se njegov korijen, što znači da je prema korolariji 2 Bezoutovog teorema x 3 +x 2 +5x+5 djeljiv s (x +1) bez ravnoteže:

X 4 +4x 2 -5 x-1 _x 3 +x 2 +5x+5 x+1

x 4 -x 3 x 3 +x 2 +5x+5 x 3 +x 2 x 2 +5

X 3 +4x 2 _5x+5

(x 3 +x 2 +5x+5)/(x+1)=x 2 +5, što znači x 3 +x 2 +5x+5=(x+1)(x 2 +5).

Stoga je f(x)=(x-1)(x+1)(x 2 +5).

Posljedicom 7 (x 2 +5) ne može se faktorizirati, jer nema pravih korijena, pa se f(x) ne može dalje faktorizirati.

Odgovor: x 4 +4x 2 -5=(x-1)(x+1)(x 2 +5).

Faktorirajte polinom f(x)=x 4 +324.

f(x) nema korijena, jer x 4 ne može biti jednako -324, što znači da se prema korolariji 7 f(x) ne može faktorizirati.

Odgovor: polinom se ne može faktorizirati.

Konstruirajte kubni polinom s korijenom 4 iz višekratnika 2 i korijenom -2.

Prema korolariji 3, ako polinom f(x) ima korijen iz 4 iz višekratnika 2 i korijen iz -2, tada je djeljiv bez ostatka s (x-4) 2 (x+2), što znači:

f(x)/(x-4) 2 (x+2)=q(x), tj.

f(x)=(x-4) 2 (x+2)q(x),

f(x)=(x 2 -8x+16)(x+2)q(x),

f(x)=(x 3 -8x 2 +16x+2x 2 -16x+32)q(x),

f(x)=(x 3 -6x 2 +32)q(x).

(x 3 -6x 2 +32) je kubni polinom, ali po uvjetu f(x) je također kubni polinom, stoga je Q(x) neki realni broj. Neka je Q(x)=1, tada je f(x)=x 3 -6x 2 +32.

Odgovor: x 3 -6x 2 +32.

Riješite jednadžbu x 4 +3x 3 -13x 2 -9x+30=0.

301; 2, 3, 5, 6, 10.

(x-2)(x 3 +5x 2 -3x-15)=0

(x-2)(x+5)(x 2 -3)=0

X 4 +3x 3 -13x 2 -9x+30 x-2

x 4 -2x 3 x 3 +5x 2 -3x-15

Odgovor: x 1 =2, x 2 =-5, x 3,4 =.

Riješite jednadžbu x 6 +x 5 -7x 4 -5x 3 +16x 2 +6x-12=0.

Gledajući jednadžbu, možemo odmah reći da prema korolariji 4 ona nema više od 6 korijena jednadžbe.

12 1; 2; 3; 4; 6; 12.

X 6 +x 5 -7x 4 -5x 3 +16x 2 +6x-12 x-1

x 6 -x 5 x 5 +2x 4 -5x 3 -10x 2 +6x+12

10x 3 +16x 2 _x 5 +2x 4 -5x 3 -10x 2 +6x+12 x+2

10x 3 -10x 2 x 5 +2x 4 x 4 -5x 2 +6

6x 2 +6x _ -5x 3 -10x 2

6x 2 -6x -5x 3 -10x 2

x 6 +x 5 -7x 4 -5x 3 +16x 2 +6x-12=(x-1)(x 5 +2x 4 -5x 3 -10x 2 +6x+12)=0

x 6 +x 5 -7x 4 -5x 3 +16x 2 +6x-12=(x-1)(x+2)(x 4 -5x 2 +6)=0

x 4 -5x 2 +6=0 - bikvadratna jednadžba, x 1,2 =, x 3,4 =.

Odgovor: x 1,2 =, x 3,4 =, x 5 =1, x 6 =-2.

Riješite jednadžbu x 3 -5x 2 +8x-6=0.

X 3 -5x 2 +8x-6 x-3

x 3 -3x 2 x 2 -2x+2

x 3 -5x 2 +8x-6=(x 2 -2x+2)(x-3)=0

x 2 -2x+2=0 je kvadratna jednadžba, nema korijena, jer D<0.

Odgovor: x=3.

Riješite jednadžbu 6x 3 +11x 2 -3x-2=0.

6x 3 +11x 2 -3x-2 x+2

6x 3 +12x 2 6x 2 -x-1

6x 3 +11x 2 -3x-2=(6x 2 -x-1)(x+2)=0

6x 2 -x-1=0 - kvadratna jednadžba, x 1 =S, x 2 =-?.

Odgovor: x 1 =S, x 2 =-?, x 3 =-2.

Biografija i djela A. N. Kolmogorova

Kolmogorovljevi teoremi: 1. Teorem o normiranim prostorima (1934.); 2. Teorem o primjenjivosti zakona velikih brojeva (1928.); 3. Teorem o primjenjivosti velikih brojeva jakog zakona (1930., 1933.). 2,8...

Biprimarne grupe

Pretpostavimo da je teorem netočan i da je grupa protuprimjer minimalnog reda. Neka --- bude ciklička Sylowska -podgrupa u, i, gdje je --- Sylowska 2-podgrupa u, --- njen invarijantni komplement u. Na temelju leme, uvjet teoreme je zadovoljen za...

Proučavanje Bezoutovog teorema za rješavanje jednadžbi n-tog stupnja za n>2

Stanični prostori

Posljedica 1. Neka je X stanični prostor i A njegov stanični potprostor. Ako je A kontraktibilan u sebi do točke, tada je X/A ~ X. Dokaz. Označimo s projekcijom X X/A. Budući da je A kontraktibilan, postoji homotopija ft: AA, kao što je...

Maksimalne faktorizacije simplektičkih grupa

Teorem Za bilo koji paran broj i bilo koje polje, grupa je jednostavna osim grupe, koja nije jednostavna. Dokaz. 1) Izuzetno ponašanje grupe proizlazi iz. Stoga ćemo pretpostaviti da u općem slučaju i...

Znanstvena dostignuća Pitagore

1. zadatak Rješenje: D ABC je pravokutnik s hipotenuzom AB, prema Pitagorinom poučku: AB2 = AC2 + BC2, AB2 = 82 + 62, AB2 = 64 + 36, AB2 = 100, AB = 10. Odgovor: AB = 10 Zadatak broj 2 Rješenje: D DCE - pravokutnik s hipotenuzom DE, prema Pitagorinom poučku: DE2 = DC2 + CE2,DC2 = DE2 - CE2,DC2 = 52 - 32...

Primjena izvoda u rješavanju nekih problema

Primjer 1. Dokažite teorem: ako jednadžba (1) ima pozitivan korijen, onda i jednadžba (2) ima pozitivan korijen i još k tome manji...

Sustavi ekvivalentni sustavima s poznatom vrstom točaka mirovanja

Dobivamo gdje je bilo koja neparna kontinuirana funkcija. Uz diferencijalni sustav (1) razmatramo perturbirani sustav (2), gdje je bilo koja kontinuirana neparna funkcija. Poznat po...

Graf spektra

Niz temeljnih svojstava spektra grafova (ili, općenito, multidigrafa) može se utvrditi na temelju određenih teorema teorije matrica. Ovaj odjeljak predstavlja samo najvažnije matrične teoreme...

Sylowljev teorem

Neka je G grupa, a P druga grupa. Neka je svakom elementu aG pridružen neki element iz S, tj. dano mu je preslikavanje G i S. Preslikavanje μ nazivamo homomorfnim ili homomorfizmom G u S...

Teorija eliptičkih integrala i eliptičkih funkcija

Teorem 1. Derivacija eliptične funkcije također je eliptička funkcija. Zapravo, diferencirajućom relacijom (1), koja vrijedi za bilo koji z, dobivamo Dakle, derivacija f(z) ima iste periode 2 i 2 kao izvorna funkcija...

Jednadžbe i nejednadžbe s modulom o centraliziranom testiranju

Formulirajmo teorem prikladan za rješavanje nejednakosti u umnošcima ili kvocijentima razlike modula: Teorem Predznak razlike modula dvaju izraza podudara se s predznakom razlike kvadrata tih izraza...

Funkcionalni prikazi ograničenih distributivnih rešetki

Lema1. Kongruencije tvore otvorenu obitelj. Dokaz. Potrebno je pokazati da je za bilo koji element skup otvoren. Neka bude, dakle, za neke. Ako je proizvoljni primarni ideal od, tada, i stoga...

Cilindrične funkcije

Koristeći Cauchyjev teorem o integralima funkcija kompleksne varijable, može se iz Poissonovog integrala dobiti još jedan integralni prikaz, koji je vrlo važan za teoriju Besselovih funkcija...

Ekstremni problem kod indeksiranja klasa

U ovom slučaju, izjava teorema je očita. Neka bude. Lema 3. Za svaki DF i bilo koju točku, postoji DF takav da je v(t)(t) (v(t)(t)) u nekoj okolini točke. Dokaz. Ako ne postoji i, 0in+2 tako da je n-1 paran i Yi(0)...

Dokaz Bezoutovog teorema

Neka f(x) označava proizvoljni polinom n-tog stupnja s obzirom na varijablu x i neka kada se podijeli s binomom (x-a) rezultat je q(x) u kvocijentu i R u ostatku. Očito, q (x) će biti neki polinom ( n-1)-tog stupnja u odnosu na x, a ostatak R će biti konstantna vrijednost, tj. neovisno o x.

Kad bi ostatak R bio polinom barem prvog stupnja u odnosu na x, tada bi to značilo da dijeljenje nije uspjelo. Dakle, R ne ovisi o x.

Po definiciji dijeljenja (dividenda je jednaka umnošku djelitelja i količnika plus ostatak), dobivam identitet

f(x) =(x-a)q(x)+R.

Ova jednakost vrijedi za bilo koju vrijednost x, što znači da vrijedi i za x=a.

Zamjenom broja a u lijevu i desnu stranu jednakosti umjesto varijable x dobivam:

f(a)=(a-a)q(a)+R. (1)

Ovdje simbol f(a) više ne označava f(x), tj. nije polinom za x, već vrijednost ovog polinoma pri x=a. q(a) označava vrijednost q(x) pri x=a.

Ostatak R ostaje isti kao i prije, jer R ne ovisi o x.

Umnožak (a-a)q(a) jednak je nuli, jer je faktor (a-a) jednak nuli, a faktor q(a) je određeni broj. (Polinom q(x) ne gubi svoje značenje ni za jednu određenu vrijednost x.)

Stoga iz jednakosti (1) dobivamo:

Q.E.D.

Korolari iz teoreme

Korolar 1.

Ostatak dijeljenja polinoma f(x) binomom (ax+b) jednak je vrijednosti

ovaj polinom na x=-b/a, tj. R=f(-b/a).

Dokaz:

Prema pravilu za dijeljenje polinoma:

f(x)= (ax+b)*q(x)+R.

f(-b/a)=(a(-b/a)+b)q(-b/a)+R=R. Dakle, R=f(-b/a),

Q.E.D.

Korolar 2:

Ako je broj a korijen polinoma f(x), tada je taj polinom djeljiv s (x-a) bez ostatka.

Dokaz:

Prema Bezoutovom teoremu, ostatak dijeljenja polinoma f(x) s (x-a) jednak je f(a), a prema uvjetu, a je korijen od f(x), što znači da je f(a) = 0, što je i trebalo dokazati.

Iz ovog korolara Bezoutovog teorema jasno je da je problem rješavanja jednadžbe f(x) = 0 ekvivalentan problemu identifikacije djelitelja polinoma f koji imaju prvi stupanj (linearni djelitelji).

Korolar 3:

Ako polinom f(x) ima po paru različite korijene a 1 , a 2 ,… ,a n , tada se dijeli umnoškom (x-a 1)…(x-a n) bez ostatka.

Dokaz:

Provedimo dokaz matematičkom indukcijom o broju korijena. Za n=1 tvrdnja je dokazana u korolariji 2. Neka je već dokazana za slučaj kada je broj korijena jednak k, to znači da je f(x) djeljiv bez ostatka s

(x-a 1)(x-a 2)…(x-a k), gdje su a 1, a 2,…, a k njegovi korijeni.

Neka f(x) ima (k+1) po paru različitih korijena. Prema hipotezi indukcije, a 1, a 2, a k,…, (a k+1) su korijeni polinoma, što znači da je polinom podijeljen umnoškom (x-a 1)…(x-a k), što znači da

f(x)=(x-a 1)…(x-a k)q(x).

U ovom slučaju (a k+1) je korijen polinoma f(x), tj.

To znači da zamjenom x (a k+1) dobivamo ispravnu jednakost:

f(a k+1)=(a k+1 -a 1)…(a k+1 -a k)q(a k+1)=0.

Ali (a k+1) se razlikuje od brojeva a 1 ,…, a k, pa stoga niti jedan od brojeva (a k+1 -a 1),…, (a k+1 -a k) nije jednak 0. Prema tome, nula je jednaka q(a k+1), tj. (a k+1) je korijen polinoma q(x). A iz korolara 2 ispada da je q(x) djeljiv s (x-a k+1) bez ostatka.

q(x)=(x-a k+1)q 1 (x), i prema tome

f(x)=(x-a 1)...(x-a k)q(x)=(x-a 1)...(x-a k)(x-a k+1)q 1 (x).

To znači da je f(x) podijeljeno s (x-a 1)…(x-a k+1) bez ostatka.

Dakle, dokazano je da je teorem točan za k=1, a iz njegove valjanosti za n=k slijedi da je točan i za n=k+1. Dakle, teorem je istinit za bilo koji broj korijena, što je trebalo dokazati.

Korolar 4:

Polinom stupnja n ima najviše n različitih korijena.

Dokaz:

Upotrijebimo metodu kontradiktorno: ako polinom f(x) stupnja n ima više od n korijena - n+k (a 1 , a 2 ,..., a n+k su njegovi korijeni), tada prema prethodno dokazani korolar 3 podijelio bi se na produkt (x-a 1)...(x-a n+k), koji ima stupanj (n+k), što je nemoguće.

Došli smo do kontradikcije, što znači da je naša pretpostavka netočna i da polinom stupnja n ne može imati više od n korijena, što smo i trebali dokazati.

Korolar 5:

Za bilo koji polinom f(x) i broj a, razlika (f(x)-f(a)) dijeli se bez ostatka s binomom (x-a).

Dokaz:

Neka je f(x) zadani polinom stupnja n, a neka je bilo koji broj.

Polinom f(x) može se predstaviti kao: f(x)=(x-a)q(x)+R, gdje je q(x) kvocijent polinoma pri dijeljenju f(x) s (x-a), R je ostatak podjele f(x) do (x-a).

Štoviše, prema Bezoutovom teoremu:

f(x)=(x-a)q(x)+f(a).

f(x)-f(a)=(x-a)q(x),

a to znači djeljivost bez ostatka (f(x)-f(a))

na (x-a), što je i trebalo dokazati.

Korolar 6:

Broj a je korijen polinoma f(x) barem prvog stupnja samo ako je f(x) djeljiv s (x-a) bez ostatka.

Dokaz:

Za dokaz ovog teorema potrebno je razmotriti nužnost i dostatnost formuliranog uvjeta.

1. Nužnost.

Neka je a korijen polinoma f(x), tada je prema korolariji 2 f(x) djeljiv s (x-a) bez ostatka.

Dakle, djeljivost f(x) sa (x-a) je nužan uvjet da a bude korijen od f(x), jer je posljedica ovoga.

2. Dostatnost.

Neka je polinom f(x) podijeljen bez ostatka sa (x-a),

onda je R=0, gdje je R ostatak dijeljenja f(x) sa (x-a), ali prema Bezoutovom teoremu R=f(a), što znači da je f(a)=0, što znači da je a korijen f (x).

Dakle, djeljivost f(x) sa (x-a) također je dovoljan uvjet da a bude korijen od f(x).

Djeljivost f(x) sa (x-a) je nužan i dovoljan uvjet da a bude korijen od f(x), što smo i trebali dokazati.

Korolar 7:

Polinom koji nema realne korijene ne sadrži linearne faktore kada se faktorizira.

Dokaz:

Upotrijebimo metodu kontradiktorno: pretpostavimo da neukorijenjeni polinom f(x) kad je faktoriziran sadrži linearni faktor

tada bi bio djeljiv s (x-a), ali bi prema korolariji 6 a bio korijen od f(x), a prema uvjetu ne sadrži prave korijene. Došli smo do kontradikcije, što znači da je naša pretpostavka netočna i da polinom koji nema realne korijene ne sadrži linearne faktore u svojoj faktorizaciji, što smo trebali dokazati.

Nađimo ostatak dijeljenja polinoma P(x) na linearni binom oblika ( x ‑ a), Gdje a– određeni broj. Budući da polinom djelitelja ima prvi stupanj, ostatak mora imati nulti stupanj, odnosno mora biti određeni broj r. Onda ako Q(x) kvocijentni polinom, tada vrijedi jednakost: P(x) = Q(x)·( x ‑ a) + r. Umjesto toga zamjenjujući u dobivenu jednakost x broj a, dobivamo: P(a) = Q(a)·( a ‑ a) + r = Q(a)·0 + r = r. Dakle, ispada da je ostatak od dijeljenja polinoma P(x) binomom ( x ‑ a) može se pronaći bez izvođenja dijeljenja zamjenom u polinom dividende a umjesto x. Dokazana tvrdnja, uspješno korištena u rješavanju mnogih nestandardnih problema, bit je Bezoutovog teorema (Etienne Bezout, 1730. - 1783., francuski matematičar, član Pariške akademije znanosti).

Bezoutov teorem: Ostatak r od dijeljenja polinoma P(x) binomom ( x ‑ a) jednaka je vrijednosti ovog polinoma u točki a, tj. r = P(a).

Napomena 1: Polinom nazvao dano, ako je njegov vodeći koeficijent (tj. koeficijent člana najvišeg stupnja) jednak 1. Na primjer, polinomi , su reducirani, ali , nisu.

Napomena 2: Kod dijeljenja polinoma s cijelim koeficijentima s reduciranim polinomom s cijelim koeficijentima, svi koeficijenti kvocijentnog polinoma i ostatka polinoma također ispadaju cijeli brojevi (ovo je lako razumjeti ako se prisjetite kako se polinom dijeli s "kutnim" polinomom ). Konkretno, kada se polinom s cjelobrojnim koeficijentima dijeli binomom ( x ‑ a), Gdje a– cijeli broj, svi koeficijenti kvocijentnog polinoma ispadaju cijeli brojevi.

Broj a nazvao korijen polinoma P(x), Ako P(a) = 0 (drugim riječima, ako je broj a- korijen jednadžbe P(x) = 0). Na primjer, brojevi 1 i -1 su korijeni polinoma, brojevi -2 i 5 su korijeni polinoma, a polinom nema korijena jer je jednakost nemoguća. Iz Bezoutovog teorema slijedi da ako broj a je korijen polinoma P(x), zatim ostatak od dijeljenja polinoma P(x) binomom ( x ‑ a) je jednako P(a) = 0, odnosno polinom P(x) podjeljeno sa ( x ‑ a) bez ostatka. Drugim riječima, ako a– korijen polinoma P(x), To P(x) bit će predstavljen u obliku: P(x) = (x ‑ a)· Q(x). Ova izjava je bit korolara Bezoutovog teorema.

Korolar Bezoutovog teorema: Broj a je korijen polinoma P(x) ako i samo ako P(x) podjeljeno sa ( x ‑ a) bez ostatka.

Zadaci:

1. Nađi ostatak pri dijeljenju polinoma s .

2. Nađi polinom trećeg stupnja koji kada se podijeli sa x daje ostatak 1, na x- 2 – ostatak 3, a djeljiv je sa bez ostatka.

3. Dokažite da je polinom djeljiv s .

4. Na koje vrijednosti a I b polinom djeljiv je bez ostatka na sljedeće polinome:

5. Pri dijeljenju polinoma sa x- 1 ostavlja ostatak 2, a kada se podijeli sa x- 2 - 1. Koliki je ostatak kada se ovaj polinom podijeli s ?

6. Nađi ostatak pri dijeljenju polinoma s .

7. Poznato je da je ostatak pri dijeljenju polinoma s jednak 2 x+ 1. Nađi ostatak pri dijeljenju ovog polinoma sa:

A) x – 1;

b) 3 x + 2;

8. Nađi reducirani polinom četvrtog stupnja ako je poznato da je djeljiv s , a kada se podijeli s ostavlja ostatak .

9. Kakvi mogu biti ostaci od dijeljenja polinoma? P(x) uključeno x– 1, i polinom Q(x) - uključeno x+ 1 ako pri dijeljenju sa x 2 – 1 polinom ostavlja ostatak od -6?

10. Dokaži da je broj djeljiv sa 7.

11. Dokažite da su ostaci dijeljenja s 11 brojeva 100.000 i 1.000.000.000 jednaki.

12. Nađi ostatak pri dijeljenju broja sa 26.

13. Jedan od korijena jednadžbe jednaka je 3. Pronađite vrijednost parametra a i riješite jednadžbu.

Gal.: stranica 111, br. 9.10 (b).

Domaća zadaća:

14. Bez dijeljenja pronaći ostatak pri dijeljenju polinoma sa x + 2.

Etienne Bezout–

Francuski matematičar, član Pariške akademije znanosti (od 1758.), rođen u Nemoursu 31. ožujka 1730., a umro 27. rujna 1783. godine.

Od 1763. Bezu je predavao matematiku u školi za veziste, a od 1768. u Kraljevskom topničkom korpusu.

Glavni radovi Etiennea Bezouta odnose se na višu algebru, a posvećeni su stvaranju teorije za rješavanje algebarskih jednadžbi. U teoriji rješavanja sustava linearnih jednadžbi pridonio je nastanku teorije determinanti, razvio teoriju uklanjanja nepoznanica iz sustava jednadžbi viših stupnjeva i dokazao teorem (prvi ga je formulirao K. Maclaurin) da dvije krivulje reda m i n sijeku se u najviše mn točaka. U Francuskoj i inozemstvu, do 1848., njegov "Tečaj matematike" u šest tomova, koji je napisao 1764.-69., bio je vrlo popularan. Bezou je razvio metodu neodređenih množitelja, po njemu je u elementarnoj algebri nazvana metoda za rješavanje sustava jednadžbi koja se temelji na ovoj metodi. Dio Bezoutovih radova posvećen je vanjskoj balistici. Po znanstveniku je nazvan jedan od osnovnih teorema algebre.

Bezoutov teorem.

Ostatak dijeljenja polinoma P n ( x )

prema binomu ( x - a ) jednaka je vrijednosti

ovaj polinom na x = a .

Pn(x) – zadani polinom stupnja n ,

binomni (x- a) - njegov djelitelj,

Qn-1 (x) – kvocijent dijeljenja Pn(x) na x- a(polinom stupnja n-1) ,

R- ostatak dijeljenja ( R ne sadrži varijablu x kao djelitelj prvog stupnja s obzirom na x).

Dokaz:

Prema pravilu dijeljenja polinoma s ostatkom možemo napisati:

Pn(x) = (x-a)Qn-1(x)+R .

Stoga, na x = a :

Pn(a) = (a-a)Qn-1(a) + R =0*Qn-1(a)+R=

=0+ R= R .

Sredstva, R = Pn(a) , tj. ostatak pri dijeljenju polinoma sa (x- a) jednaka vrijednosti ovoga

polinom pri x= a, što je i trebalo dokazati.

Korolari iz teoreme .

S posljedica 1 :

Ostatak dijeljenja polinoma P n ( x )

binomom sjekira + b jednaka vrijednosti

ovaj polinom na x = - b / a ,

T . e . R=P n (-b/a) .

Dokaz:

Prema pravilu za dijeljenje polinoma:

Pn(x)= (ax + b)* Qn-1(x)+R.

Pn (-b/a) = (a(-b/a) + b)Qn-1(-b/a) + R = R. To znači da je R = Pn (-b/a) , što je ono što je potrebno da se dokaže.

Korolar 2 :

Ako broj a je korijen

polinom P ( x ) , To ovaj

polinom je djeljiv sa ( x - a ) bez

ostatak.

Dokaz:

Prema Bezoutovom teoremu, ostatak polinoma je P (x) na x- a jednaki P (a) , i po stanju a je korijen P (x) , što znači da P (a) = 0 , što je i trebalo dokazati .

Iz ove posljedice Bezoutovog teorema jasno je da problem rješavanja jednadžbe P (x) = 0 je ekvivalentan problemu identifikacije djelitelja polinoma P koji imaju prvi stupanj (linearni djelitelji).

Korolar 3 :

Ako polinom P ( x ) Ima

u paru različiti korijeni

a 1 , a 2 , … , a n , zatim se dijeli sa

posao ( x - a 1 ) … ( x - a n )

bez traga .

Dokaz:

Provedimo dokaz matematičkom indukcijom o broju korijena. Na n=1 tvrdnja je dokazana u korolaru 2. Pretpostavimo da je već dokazano za slučaj kada je broj korijena jednak k, to znači da P(x) djeljiv bez ostatka sa (x- a1 )(x- a2 ) … (x- ak) , Gdje

a1 , a2 , … , ak- svoje korijene.

Neka P(x) Ima k+1 po paru različiti korijeni.Po hipotezi indukcije a1 , a2 , ak , … , ak+1 su korijeni polinoma, što znači da je polinom djeljiv umnoškom (x- a1 ) … (x- ak) , odakle to dolazi

P(x) = (x-a1 ) … (x-ak)Q(x).

pri čemu ak+1 – korijen polinoma P(x) , tj. . P(ak+1 ) = 0 .

Dakle, zamjena umjesto toga xak+1 , dobivamo ispravnu jednakost:

Godišnjek+1) = (ak+1-a1 ) ... (ak+1-ak)Q(ak+1) =

Ali ak+1 različito od brojeva a1 , … , ak, pa stoga ni jedan od brojeva ak+1 - a1 , … , ak+1 - ak nije jednako 0. Prema tome, nula je jednaka Q(ak+1 ) , tj. ak+1 – korijen polinoma Q(x) . A iz korolara 2 ispada da Q(x) podjeljeno sa x- ak+ 1 bez traga.

Q(x) = (x- ak+1 ) Q1 (x) , i zato

P(x) = (x-a1) … (x-ak)Q(x) =

=(x- a1 ) … (x- ak)(x- ak+1 ) Q1 (x) .

Ovo znači to P(x) podjeljeno sa (x- a1 ) … (x- ak+1 ) bez traga.

Dakle, dokazano je da je teorem točan za k =1 , a od njegove valjanosti kod n = k slijedi da je istina i kada n = k+1 . Dakle, teorem je istinit za bilo koji broj korijena, što itrebalo dokazati .

Korolar 4 :

Polinom stupnja n nema više

n različiti korijeni.

Dokaz:

Poslužimo se metodom kontradikcije: ako polinom Pn(x) stupnjeva n imao bi više n korijenje - n+ k (a1 , a2 , … , an+ k- njegovi korijeni), tada, prema prethodno dokazanom Korolaru 3, to

bi se podijelio s umnoškom (x- a1 ) … (x- an+ k) , s diplomom n+ k, što je nemoguće.

Došli smo do kontradikcije, što znači da je naša pretpostavka netočna i da polinom stupnja n ne može imati više od n korijenje, Q.E.D.

Korolar 5 :

Za bilo koji polinom P ( x )

i brojevima a razlika

( P ( x )- P ( a )) dijeli se bez

ostatak prema binomu ( x - a ) .

Dokaz:

Neka P(x) – zadani polinom stupnja n , a- bilo koji broj.

Polinom Pn(x) može se predstaviti kao: Pn(x)=(x- a) Qn-1 (x)+ R ,

Gdje Qn-1 (x) – polinom, količnik pri dijeljenju Pn(x) na (x- a) ,

R- ostatak dijeljenja Pn(x) na (x- a) .

Štoviše, prema Bezoutovom teoremu:

R = Pn(a), tj.

Pn(x)=(x-a)Qn-1(x)+Pn(a) .

Pn(x) - Pn(a) = (x-a)Qn-1(x) ,

a to znači djeljivost bez ostatka (Pn(x) – Pn(a))

na (x- a) , što je i trebalo dokazati .

Korolar 6 :

Broj a je korijen

polinom P ( x ) stupnjeva

ne niži od prvog tada i

samo kada

P ( x ) podjeljeno sa ( x - a )

bez traga .

Dokaz:

Za dokaz ovog teorema potrebno je razmotriti nužnost i dostatnost formuliranog uvjeta.

1. Nužnost .

Neka a– korijen polinoma P(x) , zatim korolarom 2 P(x) podjeljeno sa (x- a) bez traga.

Tako djeljivost P(x) na (x- a) nužan je uvjet za a bio korijen P(x) , jer je posljedica ovoga.

2. Adekvatnost .

Neka polinom P(x) djeljiv bez ostatka sa (x- a) ,

Zatim R = 0 , Gdje R- ostatak dijeljenja P(x) na (x- a) , ali prema Bezoutovom teoremu R = P(a) , odakle to dolazi P(a) = 0 , što znači da a je korijen P(x) .

Tako djeljivost P(x) na (x- a) također je dovoljan uvjet za a bio korijen P(x) .

Djeljivost P(x) na (x- a) je potrebno i dovoljno uvjet za a bio korijen P(x) , Q.E.D.

Polinom koji nema real

čvrsto korijenje, u raspadanju

na faktore linearnih faktora

ne sadrži.

Dokaz:

Upotrijebimo metodu kontradiktorno: pretpostavimo da je polinom bez korijena P(x) kada se faktorira, sadrži linearni faktor (x – a) :

P(x) = (x – a)Q(x),

onda bi se podijelio po (x – a) , ali prema korolariji 6 a bio bi korijen P(x) , ali po stanju ne sadrži korijene. Došli smo do kontradikcije, što znači da je naša pretpostavka netočna i polinom