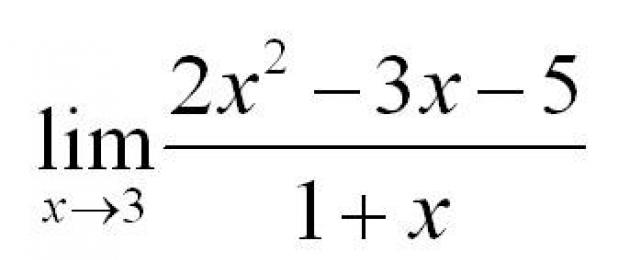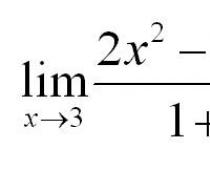Prvo značajno ograničenje je sljedeća jednakost:

\begin(equation)\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1 \end(equation)

Budući da za $\alpha\to(0)$ imamo $\sin\alpha\to(0)$, kažu da prva značajna granica otkriva nesigurnost oblika $\frac(0)(0)$. Općenito govoreći, u formuli (1) umjesto varijable $\alpha$ ispod znaka sinusa i nazivnika može se staviti bilo koji izraz, ako su ispunjena dva uvjeta:

Izrazi pod znakom sinusa i u nazivniku istovremeno teže nuli, tj. postoji nesigurnost oblika $\frac(0)(0)$.
Izrazi pod znakom sinusa i u nazivniku su isti.

Korolari iz prve izvanredne granice također se često koriste:

\begin(jednadžba) \lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0) )\frac(\arcsin\alpha)(\alpha)=1 \end(equation) \begin(equation) \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1 \kraj(jednadžba)

Na ovoj stranici riješeno je jedanaest primjera. Primjer br. 1 posvećen je dokazu formula (2)-(4). Primjeri br. 2, br. 3, br. 4 i br. 5 sadrže rješenja s detaljnim komentarima. Primjeri br. 6-10 sadrže rješenja praktički bez komentara, jer su detaljna objašnjenja data u prethodnim primjerima. Rješenje koristi neke trigonometrijske formule koje se mogu pronaći.

Dopustite mi da primijetim da prisutnost trigonometrijskih funkcija zajedno s nesigurnošću $\frac (0) (0)$ ne znači nužno primjenu prve značajne granice. Ponekad su dovoljne jednostavne trigonometrijske transformacije - na primjer, vidi.

Primjer br. 1

Dokažite da je $\lim_(\alpha\to(0))\frac(\tg\alpha)(\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arcsin\alpha ) (\alpha)=1$, $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.

a) Budući da je $\tg\alpha=\frac(\sin\alpha)(\cos\alpha)$, tada:

$$ \lim_(\alpha\to(0))\frac(\tg(\alpha))(\alpha)=\lijevo|\frac(0)(0)\desno| =\lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) $$

Budući da $\lim_(\alpha\to(0))\cos(0)=1$ i $\lim_(\alpha\to(0))\frac(\sin\alpha)(\alpha)=1$, Da:

$$ \lim_(\alpha\to(0))\frac(\sin(\alpha))(\alpha\cos(\alpha)) =\frac(\displaystyle\lim_(\alpha\to(0)) \frac(\sin(\alpha))(\alpha))(\displaystyle\lim_(\alpha\to(0))\cos(\alpha)) =\frac(1)(1) =1. $$

b) Napravimo promjenu $\alpha=\sin(y)$. Budući da je $\sin(0)=0$, tada iz uvjeta $\alpha\to(0)$ imamo $y\to(0)$. Osim toga, postoji okolina nule u kojoj je $\arcsin\alpha=\arcsin(\sin(y))=y$, pa je:

$$ \lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=\lijevo|\frac(0)(0)\desno| =\lim_(y\to(0))\frac(y)(\sin(y)) =\lim_(y\to(0))\frac(1)(\frac(\sin(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\sin(y))(y)) =\frac(1)(1) =1. $$

Dokazana je jednakost $\lim_(\alpha\to(0))\frac(\arcsin\alpha)(\alpha)=1$.

c) Napravimo zamjenu $\alpha=\tg(y)$. Budući da je $\tg(0)=0$, tada su uvjeti $\alpha\to(0)$ i $y\to(0)$ ekvivalentni. Osim toga, postoji okolina nule u kojoj $\arctg\alpha=\arctg\tg(y))=y$, prema tome, na temelju rezultata točke a), imat ćemo:

$$ \lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=\lijevo|\frac(0)(0)\desno| =\lim_(y\to(0))\frac(y)(\tg(y)) =\lim_(y\to(0))\frac(1)(\frac(\tg(y))( y)) =\frac(1)(\displaystyle\lim_(y\to(0))\frac(\tg(y))(y)) =\frac(1)(1) =1. $$

Dokazana je jednakost $\lim_(\alpha\to(0))\frac(\arctg\alpha)(\alpha)=1$.

Jednakosti a), b), c) često se koriste uz prvu značajnu granicu.

Primjer br. 2

Izračunajte granicu $\lim_(x\to(2))\frac(\sin\left(\frac(x^2-4)(x+7)\right))(\frac(x^2-4) (x+7))$.

Budući da $\lim_(x\to(2))\frac(x^2-4)(x+7)=\frac(2^2-4)(2+7)=0$ i $\lim_( x \to(2))\sin\lijevo(\frac(x^2-4)(x+7)\desno)=\sin(0)=0$, tj. a i brojnik i nazivnik razlomka istovremeno teže nuli, onda ovdje imamo posla s nesigurnošću oblika $\frac(0)(0)$, tj. učinjeno. Osim toga, jasno je da se izrazi pod znakom sinusa i u nazivniku podudaraju (tj. i da je zadovoljeno):

Dakle, ispunjena su oba uvjeta navedena na početku stranice. Iz ovoga slijedi da je formula primjenjiva, tj. $\lim_(x\to(2)) \frac(\sin\lijevo(\frac(x^2-4)(x+7)\desno))(\frac(x^2-4)(x+ 7 ))=1$.

Odgovor: $\lim_(x\to(2))\frac(\sin\lijevo(\frac(x^2-4)(x+7)\desno))(\frac(x^2-4)(x +7))=1$.

Primjer br. 3

Pronađite $\lim_(x\to(0))\frac(\sin(9x))(x)$.

Budući da $\lim_(x\to(0))\sin(9x)=0$ i $\lim_(x\to(0))x=0$, tada imamo posla s nesigurnošću oblika $\frac (0 )(0)$, tj. učinjeno. Međutim, izrazi pod znakom sinusa i u nazivniku se ne podudaraju. Ovdje je potrebno prilagoditi izraz u nazivniku željenom obliku. Trebamo izraz $9x$ da bude u nazivniku, tada će postati istina. U biti, nedostaje nam faktor od 9$ u nazivniku, koji nije tako teško unijeti—samo pomnožite izraz u nazivniku s 9$. Naravno, da biste kompenzirali množenje s 9$, morat ćete odmah podijeliti s 9$:

$$ \lim_(x\to(0))\frac(\sin(9x))(x)=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(\sin(9x))(9x\cdot\frac(1)(9)) =9\lim_(x\to(0))\frac(\sin (9x))(9x)$$

Sada se izrazi u nazivniku i pod znakom sinusa podudaraju. Oba uvjeta za granicu $\lim_(x\to(0))\frac(\sin(9x))(9x)$ su zadovoljena. Prema tome, $\lim_(x\to(0))\frac(\sin(9x))(9x)=1$. A to znači da:

$$ 9\lim_(x\to(0))\frac(\sin(9x))(9x)=9\cdot(1)=9. $$

Odgovor: $\lim_(x\to(0))\frac(\sin(9x))(x)=9$.

Primjer br. 4

Pronađite $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))$.

Budući da $\lim_(x\to(0))\sin(5x)=0$ i $\lim_(x\to(0))\tg(8x)=0$, ovdje se radi o nesigurnosti oblika $\frac(0)(0)$. Međutim, forma prve izvanredne granice je prekršena. Brojnik koji sadrži $\sin(5x)$ zahtijeva nazivnik $5x$. U ovoj situaciji, najlakši način je podijeliti brojnik s $5x$ i odmah pomnožiti s $5x$. Osim toga, izvršit ćemo sličnu operaciju s nazivnikom, množenjem i dijeljenjem $\tg(8x)$ s $8x$:

$$\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x) )$$

Smanjujući za $x$ i uzimajući konstantu $\frac(5)(8)$ izvan graničnog znaka, dobivamo:

$$ \lim_(x\to(0))\frac(\frac(\sin(5x))(5x)\cdot(5x))(\frac(\tg(8x))(8x)\cdot(8x )) =\frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))( 8x)) $$

Imajte na umu da $\lim_(x\to(0))\frac(\sin(5x))(5x)$ u potpunosti zadovoljava zahtjeve za prvu značajnu granicu. Za pronalaženje $\lim_(x\to(0))\frac(\tg(8x))(8x)$ primjenjiva je sljedeća formula:

$$ \frac(5)(8)\cdot\lim_(x\to(0))\frac(\frac(\sin(5x))(5x))(\frac(\tg(8x))(8x )) =\frac(5)(8)\cdot\frac(\displaystyle\lim_(x\to(0))\frac(\sin(5x))(5x))(\displaystyle\lim_(x\to (0))\frac(\tg(8x))(8x)) =\frac(5)(8)\cdot\frac(1)(1) =\frac(5)(8). $$

Odgovor: $\lim_(x\to(0))\frac(\sin(5x))(\tg(8x))=\frac(5)(8)$.

Primjer br. 5

Pronađite $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)$.

Budući da je $\lim_(x\to(0))(\cos(5x)-\cos^3(5x))=1-1=0$ (zapamtite da $\cos(0)=1$) i $\ lim_(x\to(0))x^2=0$, tada imamo posla s nesigurnošću oblika $\frac(0)(0)$. Međutim, kako biste primijenili prvu značajnu granicu, trebali biste se riješiti kosinusa u brojniku i prijeći na sinuse (kako biste zatim primijenili formulu) ili tangente (kako biste zatim primijenili formulu). To se može učiniti sljedećom transformacijom:

$$\cos(5x)-\cos^3(5x)=\cos(5x)\cdot\lijevo(1-\cos^2(5x)\desno)$$ $$\cos(5x)-\cos ^3(5x)=\cos(5x)\cdot\lijevo(1-\cos^2(5x)\desno)=\cos(5x)\cdot\sin^2(5x).$$

Vratimo se na limit:

$$ \lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(\cos(5x)\cdot\sin^2(5x))(x^2) =\lim_(x\to(0))\lijevo(\cos (5x)\cdot\frac(\sin^2(5x))(x^2)\desno) $$

Razlomak $\frac(\sin^2(5x))(x^2)$ već je blizu oblika potrebnog za prvu značajnu granicu. Poradimo malo s razlomkom $\frac(\sin^2(5x))(x^2)$, prilagođavajući ga prvoj značajnoj granici (imajte na umu da se izrazi u brojniku i ispod sinusa moraju podudarati):

$$\frac(\sin^2(5x))(x^2)=\frac(\sin^2(5x))(25x^2\cdot\frac(1)(25))=25\cdot\ frac(\sin^2(5x))(25x^2)=25\cdot\lijevo(\frac(\sin(5x))(5x)\desno)^2$$

Vratimo se na limit o kojem je riječ:

$$ \lim_(x\to(0))\lijevo(\cos(5x)\cdot\frac(\sin^2(5x))(x^2)\desno) =\lim_(x\to(0) ))\lijevo(25\cos(5x)\cdot\lijevo(\frac(\sin(5x))(5x)\desno)^2\desno)=\\ =25\cdot\lim_(x\to( 0))\cos(5x)\cdot\lim_(x\to(0))\lijevo(\frac(\sin(5x))(5x)\desno)^2 =25\cdot(1)\cdot( 1^2) =25. $$

Odgovor: $\lim_(x\to(0))\frac(\cos(5x)-\cos^3(5x))(x^2)=25$.

Primjer br. 6

Pronađite granicu $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))$.

Budući da $\lim_(x\to(0))(1-\cos(6x))=0$ i $\lim_(x\to(0))(1-\cos(2x))=0$, tada imamo posla s neizvjesnošću $\frac(0)(0)$. Otkrijmo to uz pomoć prve značajne granice. Da bismo to učinili, prijeđimo s kosinusa na sinuse. Budući da je $1-\cos(2\alpha)=2\sin^2(\alpha)$, tada:

$$1-\cos(6x)=2\sin^2(3x);\;1-\cos(2x)=2\sin^2(x).$$

Prelazeći na sinuse u zadanoj granici, imat ćemo:

$$ \lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(2\sin^2(3x))(2\sin^2(x)) =\lim_(x\to(0))\frac(\sin^ 2(3x))(\sin^2(x))=\\ =\lim_(x\to(0))\frac(\frac(\sin^2(3x))((3x)^2)\ cdot(3x)^2)(\frac(\sin^2(x))(x^2)\cdot(x^2)) =\lim_(x\to(0))\frac(\lijevo(\ frac(\sin(3x))(3x)\desno)^2\cdot(9x^2))(\lijevo(\frac(\sin(x))(x)\desno)^2\cdot(x^ 2)) =9\cdot\frac(\displaystyle\lim_(x\to(0))\lijevo(\frac(\sin(3x))(3x)\desno)^2)(\displaystyle\lim_(x \to(0))\lijevo(\frac(\sin(x))(x)\desno)^2) =9\cdot\frac(1^2)(1^2) =9. $$

Odgovor: $\lim_(x\to(0))\frac(1-\cos(6x))(1-\cos(2x))=9$.

Primjer br. 7

Izračunajte granicu $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)$ podložno $\alpha\neq \ beta$.

Detaljna objašnjenja dana su ranije, ali ovdje jednostavno napominjemo da ponovno postoji nesigurnost $\frac(0)(0)$. Prijeđimo s kosinusa na sinuse pomoću formule

$$\cos\alpha-\cos\beta=-2\sin\frac(\alpha+\beta)(2)\cdot\sin\frac(\alpha-\beta)(2).$$

Pomoću ove formule dobivamo:

$$ \lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\lijevo|\frac(0)( 0)\desno| =\lim_(x\to(0))\frac(-2\sin\frac(\alpha(x)+\beta(x))(2)\cdot\sin\frac(\alpha(x)-\ beta(x))(2))(x^2)=\\ =-2\cdot\lim_(x\to(0))\frac(\sin\lijevo(x\cdot\frac(\alpha+\beta )(2)\desno)\cdot\sin\lijevo(x\cdot\frac(\alpha-\beta)(2)\desno))(x^2) =-2\cdot\lim_(x\to( 0))\lijevo(\frac(\sin\lijevo(x\cdot\frac(\alpha+\beta)(2)\desno))(x)\cdot\frac(\sin\lijevo(x\cdot\frac (\alpha-\beta)(2)\desno))(x)\desno)=\\ =-2\cdot\lim_(x\to(0))\lijevo(\frac(\sin\lijevo(x) \cdot\frac(\alpha+\beta)(2)\desno))(x\cdot\frac(\alpha+\beta)(2))\cdot\frac(\alpha+\beta)(2)\cdot\frac (\sin\lijevo(x\cdot\frac(\alpha-\beta)(2)\desno))(x\cdot\frac(\alpha-\beta)(2))\cdot\frac(\alpha- \beta)(2)\desno)=\\ =-\frac((\alpha+\beta)\cdot(\alpha-\beta))(2)\lim_(x\to(0))\frac(\ sin\lijevo(x\cdot\frac(\alpha+\beta)(2)\desno))(x\cdot\frac(\alpha+\beta)(2))\cdot\lim_(x\to(0)) \frac(\sin\lijevo(x\cdot\frac(\alpha-\beta)(2)\desno))(x\cdot\frac(\alpha-\beta)(2)) =-\frac(\ alfa^2-\beta^2)(2)\cdot(1)\cdot(1) =\frac(\beta^2-\alfa^2)(2). $$

Odgovor: $\lim_(x\to(0))\frac(\cos(\alpha(x))-\cos(\beta(x)))(x^2)=\frac(\beta^2-\ alfa^2)(2)$.

Primjer br. 8

Pronađite granicu $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)$.

Budući da je $\lim_(x\to(0))(\tg(x)-\sin(x))=0$ (zapamtite da je $\sin(0)=\tg(0)=0$) i $\ lim_(x\to(0))x^3=0$, onda se ovdje radi o nesigurnosti oblika $\frac(0)(0)$. Raščlanimo to na sljedeći način:

$$ \lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\lijevo|\frac(0)(0)\desno| =\lim_(x\to(0))\frac(\frac(\sin(x))(\cos(x))-\sin(x))(x^3) =\lim_(x\to( 0))\frac(\sin(x)\cdot\lijevo(\frac(1)(\cos(x))-1\desno))(x^3) =\lim_(x\to(0)) \frac(\sin(x)\cdot\lijevo(1-\cos(x)\desno))(x^3\cdot\cos(x))=\\ =\lim_(x\to(0)) \frac(\sin(x)\cdot(2)\sin^2\frac(x)(2))(x^3\cdot\cos(x)) =\frac(1)(2)\cdot\ lim_(x\to(0))\lijevo(\frac(\sin(x))(x)\cdot\lijevo(\frac(\sin\frac(x)(2))(\frac(x)( 2))\desno)^2\cdot\frac(1)(\cos(x))\desno) =\frac(1)(2)\cdot(1)\cdot(1^2)\cdot(1 ) =\frac(1)(2). $$

Odgovor: $\lim_(x\to(0))\frac(\tg(x)-\sin(x))(x^3)=\frac(1)(2)$.

Primjer br. 9

Pronađite granicu $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))$.

Budući da je $\lim_(x\to(3))(1-\cos(x-3))=0$ i $\lim_(x\to(3))(x-3)\tg\frac(x - 3)(2)=0$, tada postoji nesigurnost oblika $\frac(0)(0)$. Prije nego što prijeđete na njezino širenje, zgodno je napraviti promjenu varijable na takav način da nova varijabla teži nuli (imajte na umu da je u formulama varijabla $\alpha \to 0$). Najlakši način je uvesti varijablu $t=x-3$. Međutim, radi pogodnosti daljnjih transformacija (ova se korist može vidjeti u tijeku rješenja u nastavku), vrijedi napraviti sljedeću zamjenu: $t=\frac(x-3)(2)$. Napominjem da su obje zamjene primjenjive u ovom slučaju, samo što će vam druga zamjena omogućiti manje rada s razlomcima. Budući da je $x\to(3)$, onda $t\to(0)$.

$$ \lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=\lijevo|\frac (0)(0)\desno| =\lijevo|\početak(poravnano)&t=\frac(x-3)(2);\\&t\to(0)\kraj(poravnano)\desno| =\lim_(t\to(0))\frac(1-\cos(2t))(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(2\sin^ 2t)(2t\cdot\tg(t)) =\lim_(t\to(0))\frac(\sin^2t)(t\cdot\tg(t))=\\ =\lim_(t\ to(0))\frac(\sin^2t)(t\cdot\frac(\sin(t))(\cos(t))) =\lim_(t\to(0))\frac(\sin (t)\cos(t))(t) =\lim_(t\to(0))\lijevo(\frac(\sin(t))(t)\cdot\cos(t)\desno) =\ lim_(t\to(0))\frac(\sin(t))(t)\cdot\lim_(t\to(0))\cos(t) =1\cdot(1) =1. $$

Odgovor: $\lim_(x\to(3))\frac(1-\cos(x-3))((x-3)\tg\frac(x-3)(2))=1$.

Primjer br. 10

Pronađite granicu $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\lijevo(\frac(\pi)(2)-x\desno)^ 2 )$.

Opet imamo posla s neizvjesnošću $\frac(0)(0)$. Prije nego što prijeđete na njezino širenje, zgodno je napraviti promjenu varijable na takav način da nova varijabla teži nuli (imajte na umu da je u formulama varijabla $\alpha\to(0)$). Najlakši način je uvesti varijablu $t=\frac(\pi)(2)-x$. Budući da $x\to\frac(\pi)(2)$, onda $t\to(0)$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\lijevo(\frac(\pi)(2)-x\desno)^2) =\lijevo|\frac(0)(0)\desno| =\lijevo|\početak(poravnano)&t=\frac(\pi)(2)-x;\\&t\to(0)\kraj(poravnano)\desno| =\lim_(t\to(0))\frac(1-\sin\lijevo(\frac(\pi)(2)-t\desno))(t^2) =\lim_(t\to(0) ))\frac(1-\cos(t))(t^2)=\\ =\lim_(t\to(0))\frac(2\sin^2\frac(t)(2))( t^2) =2\lim_(t\to(0))\frac(\sin^2\frac(t)(2))(t^2) =2\lim_(t\to(0))\ frac(\sin^2\frac(t)(2))(\frac(t^2)(4)\cdot(4)) =\frac(1)(2)\cdot\lim_(t\to( 0))\lijevo(\frac(\sin\frac(t)(2))(\frac(t)(2))\desno)^2 =\frac(1)(2)\cdot(1^2 ) =\frac(1)(2). $$

Odgovor: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\lijevo(\frac(\pi)(2)-x\desno)^2) =\frac(1)(2)$.

Primjer br. 11

Pronađite granice $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)$, $\lim_(x\to\frac(2) \ pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)$.

U ovom slučaju ne moramo koristiti prvu divnu granicu. Imajte na umu da i prva i druga granica sadrže samo trigonometrijske funkcije i brojeve. Često je u primjerima ove vrste moguće pojednostaviti izraz koji se nalazi ispod znaka granice. Štoviše, nakon spomenutog pojednostavljenja i smanjenja nekih faktora, nesigurnost nestaje. Dao sam ovaj primjer samo s jednom svrhom: da pokažem da prisutnost trigonometrijskih funkcija ispod znaka granice ne znači nužno korištenje prve značajne granice.

Budući da je $\lim_(x\to\frac(\pi)(2))(1-\sin(x))=0$ (zapamtite da $\sin\frac(\pi)(2)=1$ ) i $\lim_(x\to\frac(\pi)(2))\cos^2x=0$ (da vas podsjetim da $\cos\frac(\pi)(2)=0$), tada imamo koji se bave nesigurnošću oblika $\frac(0)(0)$. Međutim, to ne znači da ćemo morati koristiti prvu divnu granicu. Da bi se otkrila nesigurnost, dovoljno je uzeti u obzir da je $\cos^2x=1-\sin^2x$:

$$ \lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x) =\lijevo|\frac(0)(0)\desno| =\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(1-\sin^2x) =\lim_(x\to\frac(\pi)( 2))\frac(1-\sin(x))((1-\sin(x))(1+\sin(x))) =\lim_(x\to\frac(\pi)(2) )\frac(1)(1+\sin(x)) =\frac(1)(1+1) =\frac(1)(2). $$

Slično rješenje nalazi se u Demidovičevu rješeniku (br. 475). Što se tiče druge granice, kao u prethodnim primjerima u ovom odjeljku, imamo nesigurnost oblika $\frac(0)(0)$. Zašto nastaje? Nastaje jer $\tg\frac(2\pi)(3)=-\sqrt(3)$ i $2\cos\frac(2\pi)(3)=-1$. Koristimo ove vrijednosti za transformaciju izraza u brojniku i nazivniku. Cilj našeg djelovanja je da zbroj u brojniku i nazivniku zapišemo kao umnožak. Usput, često je unutar sličnog tipa zgodno promijeniti varijablu, napravljenu na takav način da nova varijabla teži nuli (vidi, na primjer, primjere br. 9 ili br. 10 na ovoj stranici). Međutim, u ovom primjeru nema smisla zamjenjivati, iako po želji zamjenu varijable $t=x-\frac(2\pi)(3)$ nije teško implementirati.

$$ \lim_(x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1) =\lim_(x\ do\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cdot\lijevo(\cos(x)+\frac(1)(2)\desno )) =\lim_(x\to\frac(2\pi)(3))\frac(\tg(x)-\tg\frac(2\pi)(3))(2\cdot\lijevo(\ cos(x)-\cos\frac(2\pi)(3)\desno))=\\ =\lim_(x\to\frac(2\pi)(3))\frac(\frac(\sin \lijevo(x-\frac(2\pi)(3)\desno))(\cos(x)\cos\frac(2\pi)(3)))(-4\sin\frac(x+\frac (2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)) =\lim_(x\to\frac(2\pi)(3 ))\frac(\sin\lijevo(x-\frac(2\pi)(3)\desno))(-4\sin\frac(x+\frac(2\pi)(3))(2)\ sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3))=\\ =\lim_(x\to\frac (2\pi)(3))\frac(2\sin\frac(x-\frac(2\pi)(3))(2)\cos\frac(x-\frac(2\pi)(3 ))(2))(-4\sin\frac(x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2) \cos(x)\cos\frac(2\pi)(3)) =\lim_(x\to\frac(2\pi)(3))\frac(\cos\frac(x-\frac(2) \pi)(3))(2))(-2\sin\frac(x+\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi)(3 ))=\\ =\frac(1)(-2\cdot\frac(\sqrt(3))(2)\cdot\lijevo(-\frac(1)(2)\desno)\cdot\lijevo( -\frac(1)(2)\desno)) =-\frac(4)(\sqrt(3)). $$

Kao što vidite, nismo morali primijeniti prvo divno ograničenje. Naravno, možete to učiniti ako želite (vidi napomenu ispod), ali nije nužno.

Koje je rješenje korištenjem prve značajne granice? Pokaži sakrij

Korištenjem prve značajne granice dobivamo:

$$ \lim_(x\to\frac(2\pi)(3))\frac(\sin\lijevo(x-\frac(2\pi)(3)\desno))(-4\sin\frac (x+\frac(2\pi)(3))(2)\sin\frac(x-\frac(2\pi)(3))(2)\cos(x)\cos\frac(2\pi )(3))=\\ =\lim_(x\to\frac(2\pi)(3))\lijevo(\frac(\sin\lijevo(x-\frac(2\pi)(3)\ desno))(x-\frac(2\pi)(3))\cdot\frac(1)(\frac(\sin\frac(x-\frac(2\pi)(3))(2)) (\frac(x-\frac(2\pi)(3))(2)))\cdot\frac(1)(-2\sin\frac(x+\frac(2\pi)(3))( 2)\cos(x)\cos\frac(2\pi)(3))\desno) =1\cdot(1)\cdot\frac(1)(-2\cdot\frac(\sqrt(3) )(2)\cdot\lijevo(-\frac(1)(2)\desno)\cdot\lijevo(-\frac(1)(2)\desno)) =-\frac(4)(\sqrt( 3)). $$

Odgovor: $\lim_(x\to\frac(\pi)(2))\frac(1-\sin(x))(\cos^2x)=\frac(1)(2)$, $\lim_( x\to\frac(2\pi)(3))\frac(\tg(x)+\sqrt(3))(2\cos(x)+1)=-\frac(4)(\sqrt( 3))$.

Ograničenja svim studentima matematike zadaju mnogo problema. Da biste riješili ograničenje, ponekad morate upotrijebiti mnogo trikova i odabrati iz niza metoda rješenja upravo onu koja je prikladna za određeni primjer.

U ovom članku nećemo vam pomoći da shvatite granice svojih mogućnosti ili shvatite granice kontrole, već ćemo pokušati odgovoriti na pitanje: kako razumjeti granice u višoj matematici? Razumijevanje dolazi s iskustvom, pa ćemo ujedno dati nekoliko detaljnih primjera rješavanja granica s objašnjenjima.

Pojam limita u matematici

Prvo pitanje je: koja je to granica i granica čega? Možemo govoriti o granicama numeričkih nizova i funkcija. Zanima nas pojam limesa funkcije jer se s njim učenici najčešće susreću. Ali prvo, najopćenitija definicija ograničenja:

Recimo da postoji neka promjenjiva vrijednost. Ako se ta vrijednost u procesu promjene neograničeno približava određenom broju a , To a – granica ove vrijednosti.

Za funkciju definiranu u određenom intervalu f(x)=y takav se broj naziva limitom A , kojoj funkcija teži kada x , težeći određenoj točki A . Točka A pripada intervalu na kojem je funkcija definirana.

Zvuči glomazno, ali je napisano vrlo jednostavno:

Lim- s engleskog ograničiti- granica.

Postoji i geometrijsko objašnjenje za određivanje granice, ali ovdje nećemo ulaziti u teoriju, jer nas više zanima praktična nego teorijska strana problema. Kad to kažemo x teži nekoj vrijednosti, to znači da varijabla ne poprima vrijednost broja, već mu se približava beskonačno blizu.

Navedimo konkretan primjer. Zadatak je pronaći granicu.

Da bismo riješili ovaj primjer, zamijenit ćemo vrijednost x=3 u funkciju. Dobivamo:

Usput, ako ste zainteresirani, pročitajte poseban članak o ovoj temi.

U primjerima x može težiti bilo kojoj vrijednosti. To može biti bilo koji broj ili beskonačnost. Evo primjera kada x teži beskonačnosti:

Intuitivno, što je veći broj u nazivniku, to će funkcija imati manju vrijednost. Dakle, s neograničenim rastom x značenje 1/x smanjit će se i približiti nuli.

Kao što vidite, da biste riješili granicu, samo trebate zamijeniti vrijednost kojoj želite težiti u funkciju x . Međutim, ovo je najjednostavniji slučaj. Pronalaženje granice često nije tako očito. Unutar granica postoje neizvjesnosti tipa 0/0 ili beskonačnosti/beskonačnosti . Što učiniti u takvim slučajevima? Pribjegavajte trikovima!

Neizvjesnosti unutar

Neodređenost oblika beskonačnost/beskonačnost

Neka postoji granica:

Pokušamo li u funkciju zamijeniti beskonačnost, dobit ćemo beskonačnost i u brojniku i u nazivniku. Općenito, vrijedi reći da postoji određeni element umjetnosti u rješavanju takvih nesigurnosti: morate primijetiti kako možete transformirati funkciju na takav način da nesigurnost nestane. U našem slučaju, brojnik i nazivnik dijelimo s x u višem stupnju. Što će se dogoditi?

Iz primjera o kojem smo već raspravljali, znamo da će članovi koji sadrže x u nazivniku težiti nuli. Tada je rješenje granice:

Za rješavanje nesigurnosti tipa beskonačnosti/beskonačnosti podijeliti brojnik i nazivnik sa x do najvišeg stupnja.

Usput! Za naše čitatelje sada postoji popust od 10% na

Druga vrsta nesigurnosti: 0/0

Kao i uvijek, zamjena vrijednosti u funkciju x=-1 daje 0 u brojniku i nazivniku. Pogledajte malo pažljivije i primijetit ćete da imamo kvadratnu jednadžbu u brojniku. Pronađimo korijene i napišimo:

Smanjimo i dobijemo:

Dakle, ako ste suočeni s nesigurnošću tipa 0/0 – rastavljaju brojnik i nazivnik.

Kako bismo vam olakšali rješavanje primjera, donosimo tablicu s ograničenjima nekih funkcija:

L'Hopitalova vladavina unutar

Još jedan moćan način za uklanjanje obje vrste neizvjesnosti. Što je bit metode?

Ako postoji nesigurnost u granici, uzimajte derivaciju brojnika i nazivnika dok nesigurnost ne nestane.

L'Hopitalovo pravilo izgleda ovako:

Važna točka : granica u kojoj umjesto brojnika i nazivnika moraju postojati izvedenice brojnika i nazivnika.

A sada - pravi primjer:

Postoji tipična neizvjesnost 0/0 . Uzmimo izvodnice brojnika i nazivnika:

Voila, neizvjesnost se rješava brzo i elegantno.

Nadamo se da ćete ove informacije moći korisno primijeniti u praksi i pronaći odgovor na pitanje “kako riješiti granice u višoj matematici”. Ukoliko trebate izračunati limes niza ili limes funkcije u točki, a nemate baš vremena za taj posao, obratite se stručnoj studentskoj službi za brzo i detaljno rješenje.

Ograničenje funkcije- broj a bit će granica neke varijabilne veličine ako se u procesu svoje promjene ta varijabilna veličina neograničeno približava a.

Ili drugim riječima, broj A je granica funkcije y = f(x) u točki x 0, ako za bilo koji niz točaka iz domene definicije funkcije , nisu jednaki x 0, a koja konvergira u točku x 0 (lim x n = x0), niz odgovarajućih vrijednosti funkcije konvergira u broj A.

Graf funkcije čija je granica, s obzirom na argument koji teži beskonačnosti, jednaka L:

Značenje A je granica (granična vrijednost) funkcije f(x) u točki x 0 u slučaju za bilo koji niz točaka , koji konvergira u x 0, ali koji ne sadrži x 0 kao jedan od njegovih elemenata (tj. u probušenoj blizini x 0), niz vrijednosti funkcije konvergira u A.

Limit Cauchyjeve funkcije.

Značenje A bit će granica funkcije f(x) u točki x 0 ako za bilo koji unaprijed uzet nenegativan broj ε pronaći će se odgovarajući nenegativan broj δ = δ(ε) tako da za svaki argument x, zadovoljavajući uvjet 0 < | x - x0 | < δ , nejednakost će biti zadovoljena | f(x)A |< ε .

Bit će vrlo jednostavno ako razumijete bit granice i osnovna pravila za njezino pronalaženje. Što je granica funkcije f (x) na x težeći za a jednaki A, piše se ovako:

Štoviše, vrijednost kojoj varijabla teži x, može biti ne samo broj, već i beskonačnost (∞), ponekad +∞ ili -∞, ili možda uopće ne postoji ograničenje.

Da shvatim kako pronaći limite funkcije, najbolje je pogledati primjere rješenja.

Potrebno je pronaći limite funkcije f (x) = 1/x na:

x→ 2, x→ 0, x→ ∞.

Pronađimo rješenje prve granice. Da biste to učinili, možete jednostavno zamijeniti x broj kojem teži, tj. 2, dobivamo:

Nađimo drugu granicu funkcije. Ovdje umjesto toga zamijenite čistu 0 x to je nemoguće, jer Ne možete dijeliti s 0. Ali možemo uzeti vrijednosti blizu nule, na primjer, 0,01; 0,001; 0,0001; 0,00001 i tako dalje, te vrijednost funkcije f (x) povećat će se: 100; 1000; 10000; 100 000 i tako dalje. Dakle, može se razumjeti da kada x→ 0 vrijednost funkcije koja je ispod granice raste neograničeno, tj. stremi ka beskonačnosti. Što znači:

Što se tiče treće granice. Ista situacija kao u prethodnom slučaju, nemoguće je zamijeniti ∞ u svom najčišćem obliku. Moramo razmotriti slučaj neograničenog povećanja x. Zamjenjujemo 1000 jedan po jedan; 10000; 100 000 i tako dalje, imamo tu vrijednost funkcije f (x) = 1/x smanjit će se: 0,001; 0,0001; 0,00001; i tako dalje, težeći nuli. Zato:

Potrebno je izračunati limit funkcije

Počinjući rješavati drugi primjer, vidimo nesigurnost. Odavde nalazimo najviši stupanj brojnika i nazivnika - ovo je x 3, izvadimo ga iz zagrada u brojniku i nazivniku i zatim smanjimo za:

Odgovor

Prvi korak u pronalaženje ove granice, umjesto toga zamijenite vrijednost 1 x, što dovodi do neizvjesnosti. Da bismo ga riješili, faktorizirajmo brojnik i učinimo to pomoću metode pronalaženja korijena kvadratne jednadžbe x 2 + 2x - 3:

D = 2 2 - 4*1*(-3) = 4 +12 = 16→ √ D=√16 = 4

x 1,2 = (-2±4)/2→ x 1 = -3;x 2= 1.

Dakle, brojnik će biti:

Odgovor

Ovo je definicija njezine specifične vrijednosti ili određenog područja u koje funkcija spada, a koje je ograničeno limitom.

Za rješavanje ograničenja slijedite pravila:

Shvativši bit i glavno pravila za rješavanje granice, dobit ćete osnovno razumijevanje kako ih riješiti.

Metode rješavanja granica. Neizvjesnosti.
Redoslijed rasta funkcije. Metoda zamjene

Primjer 4

Pronađite granicu

Ovo je jednostavniji primjer za samostalno rješavanje. U predloženom primjeru opet postoji nesigurnost (višeg reda rasta od korijena).

Ako "x" teži "minus beskonačno"

Bauk "minus beskonačnosti" već dugo lebdi u ovom članku. Razmotrimo granice s polinomima u kojima . Principi i metode rješenja bit će potpuno isti kao u prvom dijelu lekcije, s izuzetkom niza nijansi.

Pogledajmo 4 trika koji će biti potrebni za rješavanje praktičnih zadataka:

1) Izračunajte granicu

Vrijednost limita ovisi samo o terminu jer on ima najviši red rasta. Ako tada beskonačno velik po modulu negativan broj na PARNU potenciju, u ovom slučaju – u četvrtom, jednako je “plus beskonačno”: . Konstanta ("dva") pozitivan, Zato:

2) Izračunajte granicu

Evo opet visoke diplome čak, Zato: . Ali ispred njega stoji "minus" ( negativan konstanta –1), dakle:

3) Izračunajte granicu

Granična vrijednost ovisi samo o . Kao što se sjećate iz škole, "minus" "iskače" ispod neparnog stupnja, dakle beskonačno velik po modulu negativan broj na neparnu potenciju jednako je "minus beskonačno", u ovom slučaju: .
Konstanta ("četiri") pozitivan, Sredstva:

4) Izračunajte granicu

Opet ima prvi momak u selu neparan stupanj, osim toga, u njedrima negativan konstanta, što znači: Dakle:
.

Primjer 5

Pronađite granicu

Koristeći gore navedene točke, dolazimo do zaključka da ovdje postoji neizvjesnost. Brojnik i nazivnik su istog reda rasta, što znači da će u limitu rezultat biti konačan broj. Saznajmo odgovor tako što ćemo odbaciti sve pomfrite:

Rješenje je trivijalno:

Primjer 6

Pronađite granicu

Ovo je primjer koji trebate sami riješiti. Potpuno rješenje i odgovor na kraju lekcije.

A sada, možda, najsuptilniji slučajevi:

Primjer 7

Pronađite granicu

Razmatrajući vodeće termine, dolazimo do zaključka da ovdje postoji neizvjesnost. Brojnik je višeg reda rasta od nazivnika, pa odmah možemo reći da je granica jednaka beskonačnosti. Ali kakva beskonačnost, "plus" ili "minus"? Tehnika je ista - riješimo se sitnica u brojniku i nazivniku:

Mi odlučujemo:

Podijelite brojnik i nazivnik s

Primjer 15

Pronađite granicu

Ovo je primjer koji trebate sami riješiti. Približan uzorak konačnog dizajna na kraju lekcije.

Još par zanimljivih primjera na temu zamjene varijabli:

Primjer 16

Pronađite granicu

Zamjenom jedinice u granicu dobiva se nesigurnost. Promjena varijable se već nameće sama od sebe, ali prvo transformiramo tangentu pomoću formule. Doista, zašto nam je potrebna tangenta?

Imajte na umu da, dakle. Ako nije sasvim jasno, pogledajte vrijednosti sinusa trigonometrijska tablica. Time se odmah rješavamo množitelja, osim toga dobivamo već poznatu neizvjesnost od 0:0. Bilo bi lijepo kada bi naš limit težio nuli.

Zamijenimo:

Ako tada

Pod kosinusom imamo “x”, koji također treba izraziti kroz “te”.
Iz zamjene izražavamo: .

Dovršavamo rješenje:

(1) Izvodimo zamjenu

(2) Otvorite zagrade ispod kosinusa.

(4) Organizirati prva divna granica, umjetno pomnožite brojnik s i recipročnim brojem.

Zadatak za samostalno rješavanje:

Primjer 17

Pronađite granicu

Potpuno rješenje i odgovor na kraju lekcije.

To su bili jednostavni zadaci u njihovom razredu, u praksi sve može biti i gore, a, k tome redukcijske formule, morate koristiti razne trigonometrijske formule, kao i druge trikove. U članku Complex Limits pogledao sam nekoliko stvarnih primjera =)

Uoči blagdana konačno ćemo razjasniti situaciju s još jednom uobičajenom neizvjesnošću:

Uklanjanje neizvjesnosti “jedan na potenciju beskonačnosti”

Ova neizvjesnost se "servira" druga divna granica, au drugom dijelu te lekcije vrlo smo detaljno pogledali standardne primjere rješenja koja se u većini slučajeva nalaze u praksi. Sada će slika s eksponentima biti zaokružena, osim toga, završni zadaci lekcije bit će posvećeni "lažnim" granicama, u kojima se ČINI da je potrebno primijeniti 2. divnu granicu, iako to uopće nije slučaj.

Nedostatak dviju radnih formula za 2. izvanrednu granicu je da argument mora težiti "plus beskonačnosti" ili nuli. Ali što ako argument teži drugom broju?

U pomoć dolazi univerzalna formula (koja je zapravo posljedica drugog izvanrednog ograničenja):

Nesigurnost se može eliminirati pomoću formule:

Negdje mislim da sam već objasnio što znače uglate zagrade. Ništa posebno, zagrade su samo zagrade. Obično se koriste za jasnije isticanje matematičkih zapisa.

Istaknimo bitne točke formule:

1) Radi se o samo o neizvjesnosti i ničemu drugom.

2) Argument “x” može težiti proizvoljna vrijednost(a ne samo na nulu ili), posebice, na "minus beskonačno" ili na bilo tko konačan broj.

Pomoću ove formule možete riješiti sve primjere u lekciji. Divna ograničenja, koji spadaju u 2. izvanrednu granicu. Na primjer, izračunajmo granicu:

U ovom slučaju , a prema formuli :

Istina, ne preporučujem da to radite; tradicija je da se i dalje koristi "uobičajeni" dizajn rješenja, ako se može primijeniti. Međutim pomoću formule vrlo je zgodno provjeriti"klasičnih" primjera do 2. izuzetna granica.

Elementarne funkcije i njihovi grafovi.

Glavne elementarne funkcije su: potencijska funkcija, eksponencijalna funkcija, logaritamska funkcija, trigonometrijske funkcije i inverzne trigonometrijske funkcije, te polinom i racionalna funkcija, koja je omjer dvaju polinoma.

U elementarne funkcije ubrajaju se i one funkcije koje se dobivaju iz elementarnih primjenom osnovne četiri računske operacije i formiranjem složene funkcije.

Grafovi elementarnih funkcija

	Ravna crta- graf linearne funkcije y = sjekira + b. Funkcija y monotono raste za a > 0 i opada za a< 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)
	Parabola- graf kvadratne trinomske funkcije y = ax 2 + bx + c. Ima okomitu os simetrije. Ako je a > 0, ima minimum ako je a< 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax 2 + bx +c =0
	Hiperbola- graf funkcije. Kada je a > O nalazi se u I i III četvrtini, kada je a< 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а >0) ili y - - x(a< 0).
	Eksponencijalna funkcija. Izlagač(eksponencijalna funkcija prema bazi e) y = e x. (Drugi pravopis y = exp(x)). Asimptota je apscisna os.
	Logaritamska funkcija y = log a x(a > 0)
	y = sinx. Sinusni val- periodička funkcija s periodom T = 2π

Ograničenje funkcije.

Funkcija y=f(x) ima broj A kao limit dok x teži a, ako za bilo koji broj ε › 0 postoji broj δ › 0 takav da je | y – A | ‹ ε ako je |x - a| ‹ δ,

ili lim y = A

Kontinuitet funkcije.

Funkcija y=f(x) je neprekidna u točki x = a ako je lim f(x) = f(a), tj.

limit funkcije u točki x = a jednak je vrijednosti funkcije u danoj točki.

Pronalaženje limita funkcija.

Osnovni teoremi o granicama funkcija.

1. Granica konstantne vrijednosti jednaka je ovoj konstantnoj vrijednosti:

2. Limes algebarskog zbroja jednak je algebarskom zbroju limesa ovih funkcija:

lim (f + g - h) = lim f + lim g - lim h

3. Limes umnoška više funkcija jednak je umnošku limesa tih funkcija:

lim (f * g* h) = lim f * lim g * lim h

4. Limes kvocijenta dviju funkcija jednak je kvocijentu limesa tih funkcija ako limes nazivnika nije jednak 0:

lim------- = ----------

Prva značajna granica: lim --------- = 1

Druga značajna granica: lim (1 + 1/x) x = e (e = 2, 718281..)

Primjeri nalaženja limesa funkcija.

5.1. Primjer:

Svaki limit sastoji se od tri dijela:

1) Dobro poznata ikona ograničenja.

2) Unosi ispod ikone ograničenja. Unos glasi "X ima tendenciju na jedan." Najčešće je to x, iako umjesto “x” može biti bilo koja druga varijabla. Umjesto jedan može biti apsolutno bilo koji broj, kao i beskonačno 0 ili .

3) Funkcije pod znakom granice, u ovom slučaju .

Sama snimka glasi ovako: "granica funkcije dok x teži jedinici."

Vrlo važno pitanje - što znači izraz "x"? nastoji do jednog"? Izraz "x" nastoji do jedan” treba shvatiti na sljedeći način: “x” dosljedno poprima vrijednosti koji se jedinstvu približavaju beskrajno blizu i praktički koincidiraju s njim.

Kako riješiti gornji primjer? Na temelju gore navedenog, trebate samo zamijeniti jedan u funkciju ispod znaka granice:

Dakle, prvo pravilo : Kada dobijete ograničenje, prvo jednostavno uključite broj u funkciju.

5.2. Primjer s beskonačnošću:

Hajdemo shvatiti što je to? To je slučaj kada raste bez ograničenja.

Dakle: ako , zatim funkcija teži minus beskonačno:

Prema našem prvom pravilu, umjesto "X" zamijenimo funkciju beskonačnost i dobivamo odgovor.

5.3. Još jedan primjer s beskonačnošću:

Opet počinjemo povećavati do beskonačnosti i promatramo ponašanje funkcije.
Zaključak: funkcija se neograničeno povećava

5.4. Niz primjera:

Pokušajte sami mentalno analizirati sljedeće primjere i riješiti najjednostavnije vrste granica:

, , , , , , , , ,

Što trebate zapamtiti i razumjeti od navedenog?

Kada dobijete bilo kakvo ograničenje, prvo jednostavno uključite broj u funkciju. U isto vrijeme, morate razumjeti i odmah riješiti najjednostavnije granice, kao što su , , itd.

6. Granice s nesigurnošću tipa i metoda za njihovo rješavanje.

Sada ćemo razmotriti grupu granica kada je , a funkcija je razlomak čiji brojnik i nazivnik sadrže polinome.

6.1. Primjer:

Izračunajte granicu

Prema našem pravilu, pokušavamo zamijeniti beskonačnost u funkciju. Što dobivamo na vrhu? Beskonačnost. I što se događa ispod? Također beskonačnost. Dakle, imamo ono što se zove neizvjesnost vrste. Moglo bi se pomisliti da je = 1 i odgovor je spreman, ali u općem slučaju to uopće nije slučaj i potrebno je primijeniti neku tehniku rješenja koju ćemo sada razmotriti.

Kako riješiti limite ove vrste?

Prvo pogledamo brojnik i nađemo najveću snagu:

Vodeći stepen u brojniku je dvojka.

Sada gledamo nazivnik i također ga nalazimo na najveću potenciju:

Najviši stupanj nazivnika je dva.

Zatim biramo najveću potenciju brojnika i nazivnika: u ovom primjeru oni su isti i jednaki su dva.

Dakle, metoda rješenja je sljedeća: otkriti neizvjesnost morate brojnik i nazivnik podijeliti sa u višem stupnju.

Dakle, odgovor nije 1.

Primjer

Pronađite granicu

Opet u brojniku i nazivniku nalazimo u najvišem stupnju:

Maksimalni stupanj u brojniku: 3

Maksimalni stupanj u nazivniku: 4

Odaberite najveći vrijednost, u ovom slučaju četiri.
Prema našem algoritmu, da bismo otkrili nesigurnost, dijelimo brojnik i nazivnik s .

Primjer

Pronađite granicu

Maksimalni stupanj "X" u brojniku: 2

Maksimalni stupanj "X" u nazivniku: 1 (može se napisati kao)
Da bi se otkrila nesigurnost, potrebno je brojnik i nazivnik podijeliti s . Konačno rješenje može izgledati ovako: