Praksa prošlogodišnjeg jedinstvenog državnog ispita i državnog ispita pokazuje da geometrijski problemi stvaraju poteškoće mnogim školarcima. Lako ćete se nositi s njima ako zapamtite sve potrebne formule i vježbate rješavanje problema.
U ovom ćete članku vidjeti formule za pronalaženje površine trapeza, kao i primjere problema s rješenjima. Na iste možete naići u KIM-ovima tijekom certifikacijskih ispita ili na olimpijadama. Stoga ih pažljivo tretirajte.
Što trebate znati o trapezu?
Za početak, podsjetimo se toga trapez naziva se četverokut u kojem su dvije suprotne stranice, koje se nazivaju i osnovice, paralelne, a druge dvije nisu.
U trapezu se visina (okomito na osnovicu) može i spustiti. Nacrtana je srednja linija - to je ravna linija koja je paralelna s bazama i jednaka je polovici njihovog zbroja. Kao i dijagonale koje se mogu presijecati, tvoreći oštre i tupe kutove. Ili, u nekim slučajevima, pod pravim kutom. Osim toga, ako je trapez jednakokračan, u njega se može upisati kružnica. I opišite krug oko njega.
Formule površine trapeza
Prvo, pogledajmo standardne formule za pronalaženje površine trapeza. U nastavku ćemo razmotriti načine za izračunavanje površine jednakokračnih i krivuljastih trapeza.
Dakle, zamislite da imate trapez s bazama a i b, u kojem je visina h spuštena na veću osnovicu. Izračunavanje površine figure u ovom slučaju jednostavno je poput guljenja krušaka. Samo trebate podijeliti zbroj duljina baza s dva i rezultat pomnožiti s visinom: S = 1/2(a + b)*h.
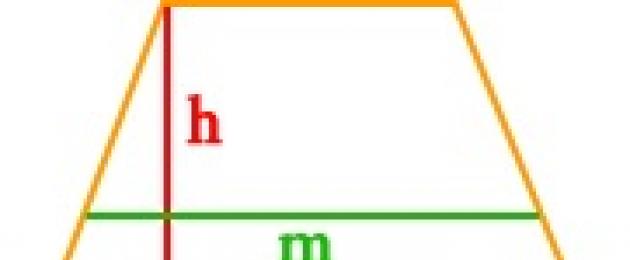
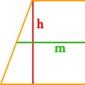
Uzmimo drugi slučaj: pretpostavimo da u trapezu, osim visine, postoji središnja linija m. Poznata nam je formula za određivanje duljine središnje crte: m = 1/2(a + b). Stoga s pravom možemo pojednostaviti formulu za područje trapeza na sljedeći oblik: S = m*h. Drugim riječima, da biste pronašli područje trapeza, trebate pomnožiti središnju liniju s visinom.

Razmotrimo drugu opciju: trapez sadrži dijagonale d 1 i d 2 koje se ne sijeku pod pravim kutom α. Da biste izračunali površinu takvog trapeza, trebate podijeliti proizvod dijagonala s dva i pomnožiti rezultat s grijehom kuta između njih: S= 1/2d 1 d 2 *sinα.

Sada razmotrite formulu za pronalaženje područja trapeza ako se o njemu ne zna ništa osim duljina svih njegovih stranica: a, b, c i d. Ovo je glomazna i složena formula, ali bit će korisno zapamtiti je za svaki slučaj: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2.
Usput, gornji primjeri vrijede i za slučaj kada vam je potrebna formula za područje pravokutnog trapeza. Ovo je trapez, čija strana graniči s bazama pod pravim kutom.
Jednakokračni trapez
Trapez čije su stranice jednake naziva se jednakokračan. Razmotrit ćemo nekoliko opcija za formulu za područje jednakokračnog trapeza.
Prva opcija: za slučaj kada je unutar jednakokračnog trapeza upisana kružnica polumjera r, a stranica i veća osnovica čine šiljasti kut α. U trapez se može upisati kružnica pod uvjetom da je zbroj duljina njegovih osnovica jednak zbroju duljina stranica.

Površina jednakokračnog trapeza izračunava se na sljedeći način: pomnožite kvadrat polumjera upisane kružnice s četiri i sve podijelite s sinα: S = 4r 2 /sinα. Druga formula površine poseban je slučaj za opciju kada je kut između velike baze i stranice 30 0: S = 8r2.
Druga opcija: ovaj put uzimamo jednakokračni trapez, u kojem su dodatno nacrtane dijagonale d 1 i d 2, te visina h. Ako su dijagonale trapeza međusobno okomite, visina je polovica zbroja osnovica: h = 1/2(a + b). Znajući ovo, lako je transformirati formulu za područje trapeza koji vam je već poznat u ovaj oblik: S = h 2.
Formula za površinu zakrivljenog trapeza
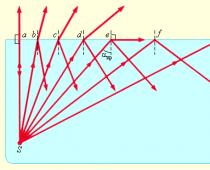
Započnimo s otkrivanjem što je zakrivljeni trapez. Zamislimo koordinatnu os i graf kontinuirane i nenegativne funkcije f koja ne mijenja predznak unutar zadanog segmenta na x-osi. Krivocrtni trapez tvori graf funkcije y = f(x) - na vrhu, x os je na dnu (odsječak), a sa strane - ravne linije povučene između točaka a i b i grafa funkcija.
Nemoguće je izračunati površinu takve nestandardne figure pomoću gore navedenih metoda. Ovdje trebate primijeniti matematičku analizu i koristiti integral. Naime: Newton-Leibnizova formula - S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a). U ovoj formuli F je antiderivacija naše funkcije na odabranom segmentu. A površina krivocrtnog trapeza odgovara prirastu antiderivacije na danom segmentu.

Uzorak problema
Da biste sve ove formule lakše razumjeli u glavi, evo nekoliko primjera problema za pronalaženje površine trapeza. Najbolje bi bilo da prvo sami pokušate riješiti probleme, a tek onda usporedite dobiveni odgovor s gotovim rješenjem.
Zadatak #1: Zadan je trapez. Njegova veća baza je 11 cm, a manja 4 cm. Trapez ima dijagonale od kojih je jedna duga 12 cm, a druga 9 cm.
Rješenje: Konstruirajte trapez AMRS. Povuci ravnu liniju RH kroz vrh P tako da bude paralelna s dijagonalom MC i siječe pravac AC u točki X. Dobit ćeš trokut APH.
Razmotrit ćemo dvije figure dobivene kao rezultat ovih manipulacija: trokut APX i paralelogram CMRX.
Zahvaljujući paralelogramu saznajemo da je PX = MC = 12 cm i CX = MR = 4 cm. Odakle možemo izračunati stranicu AX trokuta ARX: AX = AC + CX = 11 + 4 = 15 cm.
Također možemo dokazati da je trokut APX pravokutan (za to primijenimo Pitagorin poučak - AX 2 = AP 2 + PX 2). I izračunajte njegovu površinu: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 cm 2.
Zatim ćete morati dokazati da su trokuti AMP i PCX jednake površine. Osnova će biti ravnopravnost stranaka MR i CX (već gore dokazano). A također i visine koje spuštate na te strane - jednake su visini AMRS trapeza.
Sve ovo će vam omogućiti da kažete da je S AMPC = S APX = 54 cm 2.
Zadatak #2: Zadan je trapez KRMS. Na njegovim bočnim stranicama nalaze se točke O i E, dok su OE i KS paralelne. Također je poznato da su površine trapeza ORME i OKSE u omjeru 1:5. RM = a i KS = b. Morate pronaći OE.
Rješenje: Kroz točku M povucite pravac paralelan s RK, a točku njegovog sjecišta s OE označite kao T. A je sjecište pravca povučenog kroz točku E paralelnog s RK s osnovicom KS.
Uvedimo još jednu oznaku - OE = x. I također visinu h 1 za trokut TME i visinu h 2 za trokut AEC (možete nezavisno dokazati sličnost ovih trokuta).
Pretpostavit ćemo da je b > a. Površine trapeza ORME i OKSE su u omjeru 1:5, što nam daje za pravo sastaviti sljedeću jednadžbu: (x + a) * h 1 = 1/5(b + x) * h 2. Transformirajmo i dobijemo: h 1 / h 2 = 1/5 * ((b + x)/(x + a)).
Budući da su trokuti TME i AEC slični, imamo h 1 / h 2 = (x – a)/(b – x). Kombinirajmo oba unosa i dobijemo: (x – a)/(b – x) = 1/5 * ((b + x)/(x + a)) ↔ 5(x – a)(x + a) = ( b + x)(b – x) ↔ 5(x 2 – a 2) = (b 2 – x 2) ↔ 6x 2 = b 2 + 5a 2 ↔ x = √(5a 2 + b 2)/6.
Dakle, OE = x = √(5a 2 + b 2)/6.
Zaključak
Geometrija nije najlakša znanost, ali sigurno se možete nositi s ispitnim pitanjima. Dovoljno je pokazati malo upornosti u pripremi. I, naravno, zapamtite sve potrebne formule.
Pokušali smo prikupiti sve formule za izračunavanje površine trapeza na jednom mjestu kako biste ih mogli koristiti prilikom priprema za ispite i obnavljanja gradiva.
Obavezno obavijestite svoje kolege i prijatelje na društvenim mrežama o ovom članku. Neka bude više dobrih ocjena za jedinstveni državni ispit i državne ispite!
web stranice, pri kopiranju materijala u cijelosti ili djelomično, poveznica na izvor je obavezna.
Problemi s trapezom ne čine se teškima u brojnim oblicima koji su prethodno proučavani. Pravokutni trapez smatra se posebnim slučajem. A kada tražite njegovo područje, ponekad je prikladnije podijeliti ga na dva već poznata: pravokutnik i trokut. Treba samo malo razmisliti i sigurno ćete pronaći rješenje.
Definicija pravokutnog trapeza i njegova svojstva
Proizvoljni trapez ima paralelne osnovice, a stranice mogu imati proizvoljne kutove s njima. Ako uzmemo u obzir pravokutni trapez, tada je jedna od njegovih stranica uvijek okomita na baze. Odnosno, dva kuta u njemu bit će jednaka 90 stupnjeva. Štoviše, oni uvijek pripadaju susjednim vrhovima ili, drugim riječima, istoj strani.
Ostali kutovi u pravokutnom trapezu uvijek su šiljasti i tupi. Štoviše, njihov će zbroj uvijek biti jednak 180 stupnjeva.
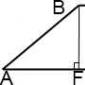
Svaka dijagonala sa svojom manjom stranicom čini pravokutni trokut. A visina, koja je izvučena iz vrha s tupim kutom, dijeli lik na dva dijela. Jedan od njih je pravokutnik, a drugi pravokutni trokut. Usput, ova strana je uvijek jednaka visini trapeza.
Koje oznake se koriste u prikazanim formulama?
Prikladno je odmah navesti sve veličine koje se koriste u različitim izrazima koji opisuju trapez i prikazati ih u tablici:
Formule koje opisuju elemente pravokutnog trapeza
Najjednostavniji od njih odnosi se na visinu i manju stranu:
Još nekoliko formula za ovu stranicu pravokutnog trapeza:
s = d *sinα;
c = (a - b) * tan α;
c = √ (d 2 - (a - b) 2).
Prvi slijedi iz pravokutnog trokuta. I kaže da kateta hipotenuze daje sinus suprotnog kuta.
U istom trokutu druga je kateta jednaka razlici dviju baza. Stoga je istinita tvrdnja da se tangens kuta izjednačuje s omjerom kateta.
Iz istog trokuta može se izvesti formula na temelju poznavanja Pitagorinog teorema. Ovo je treći zabilježeni izraz.

Možete zapisati formule za drugu stranu. Ima ih i tri:
d = (a - b) /cosα;
d = c / sin α;
d = √ (c 2 + (a - b) 2).
Prva dva su opet dobivena iz omjera stranica u istom pravokutnom trokutu, a druga je izvedena iz Pitagorinog teorema.
Koju formulu možete koristiti za izračunavanje površine?
Onaj koji je dan za slobodni trapez. Samo trebate uzeti u obzir da je visina strana okomita na baze.
S = (a + b) * h / 2.
Ove količine nisu uvijek eksplicitno navedene. Stoga, da biste izračunali površinu pravokutnog trapeza, morat ćete izvršiti neke matematičke izračune.

Što ako trebate izračunati dijagonale?
U ovom slučaju morate vidjeti da tvore dva pravokutna trokuta. To znači da uvijek možete koristiti Pitagorin teorem. Tada će prva dijagonala biti izražena na sljedeći način:
d1 = √ (c 2 + b 2)
ili na drugi način, zamjenom "c" sa "h":
d1 = √ (h 2 + b 2).
Formule za drugu dijagonalu dobivaju se na sličan način:
d2 = √ (c 2 + b 2) ili d 2 = √ (h 2 + a 2).
Zadatak br. 1
Stanje. Površina pravokutnog trapeza je poznata i jednaka je 120 dm 2. Njegova visina je dužina 8 cm. Potrebno je izračunati sve stranice trapeza. Dodatni uvjet je da jedna baza bude za 6 dm manja od druge.
Riješenje. Kako nam je zadan pravokutni trapez kojemu je poznata visina, odmah možemo reći da je jedna stranica 8 dm, odnosno manja stranica.
Sada možete računati drugi: d = √ (c 2 + (a - b) 2). Štoviše, ovdje su i stranica c i razlika baza dane odjednom. Potonji je jednak 6 dm, to je poznato iz uvjeta. Tada će d biti jednako kvadratnom korijenu od (64 + 36), odnosno od 100. Tako se nalazi druga stranica jednaka 10 dm.
Zbroj baza može se pronaći iz formule za površinu. To će biti jednako dvostrukoj površini podijeljenoj s visinom. Ako računate, ispada 240 / 8. To znači da je zbroj osnovica 30 dm. S druge strane, razlika im je 6 dm. Kombinacijom ovih jednadžbi možete računati obje baze:
a + b = 30 i a - b = 6.
Možete izraziti a kao (b + 6), zamijeniti ga u prvu jednakost. Tada se ispostavlja da će 2b biti jednako 24. Prema tome, jednostavno b će ispasti 12 dm.
Tada je zadnja stranica a 18 dm.
Odgovor. Stranice pravokutnog trapeza: a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.

Zadatak br. 2
Stanje. Zadan je pravokutni trapez. Njegova glavna stranica jednaka je zbroju baza. Visina mu je duga 12 cm.Konstruiran je pravokutnik čije su stranice jednake osnovicama trapeza. Potrebno je izračunati površinu ovog pravokutnika.
Riješenje. Morate početi s onim što tražite. Tražena površina se određuje kao umnožak a i b. Obje ove količine su nepoznate.
Bit će potrebno koristiti dodatne jednakosti. Jedan od njih temelji se na tvrdnji iz uvjeta: d = a + b. Potrebno je koristiti treću formulu za ovu stranu, koja je navedena gore. Ispada: d 2 = c 2 + (a - b) 2 ili (a + b) 2 = c 2 + (a - b) 2.
Potrebno je izvršiti transformacije zamjenom umjesto c njegove vrijednosti iz uvjeta - 12. Nakon otvaranja zagrada i dovođenja sličnih članova, ispada da je 144 = 4 ab.
Na početku rješenja je rečeno da a*b daje traženu površinu. Stoga, u zadnjem izrazu možete zamijeniti ovaj umnožak sa S. Jednostavan izračun će dati vrijednost površine. S = 36 cm 2.
Odgovor. Tražena površina je 36 cm 2.

Zadatak br. 3
Stanje. Površina pravokutnog trapeza je 150√3 cm². Oštri kut je 60 stupnjeva. Kut između male baze i manje dijagonale ima isto značenje. Moramo izračunati manju dijagonalu.
Riješenje. Iz svojstava kutova trapeza ispada da je njegov tupi kut 120º. Zatim ga dijagonala dijeli na jednake dijelove, jer jedan dio već ima 60 stupnjeva. Tada je kut između ove dijagonale i druge baze također 60 stupnjeva. To jest, trokut koji čine velika baza, nagnuta stranica i manja dijagonala je jednakostraničan. Tako će željena dijagonala biti jednaka a, kao i bočna stranica d = a.
Sada trebamo razmotriti pravokutni trokut. Treći kut u njemu je 30 stupnjeva. To znači da je kateta nasuprot njoj jednaka polovici hipotenuze. Odnosno, manja osnovica trapeza jednaka je polovici željene dijagonale: b = a/2. Iz nje morate pronaći visinu jednaku strani okomitoj na baze. Strana s nogom ovdje. Iz Pitagorine teoreme:
c = (a/2) * √3.
Sada sve što preostaje je zamijeniti sve količine u formulu površine:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Rješavanje ove jednadžbe daje korijen 20
Odgovor. Manja dijagonala ima duljinu 20 cm.
Bit će korisno za sve maturante koji se pripremaju za polaganje Jedinstvenog državnog ispita iz matematike da osvježe pamćenje na temu "Slobodni trapez". Kao što je dugogodišnja praksa pokazala, planimetrijski zadaci iz ovog odjeljka stvaraju određene poteškoće mnogim srednjoškolcima. Istodobno, rješavanje problema Jedinstvenog državnog ispita na temu "Slobodni trapez" potrebno je prilikom polaganja i osnovne i profilne razine certifikacijskog testa. Stoga bi se svi maturanti trebali moći nositi s takvim vježbama.
Kako se pripremiti za ispit?
Većina planimetrijskih problema rješava se klasičnim konstrukcijama. Ako u problemu Jedinstvenog državnog ispita trebate pronaći, na primjer, područje trapeza prikazanog na slici, vrijedi označiti sve poznate parametre na crtežu. Nakon toga zapamtite glavne teoreme vezane uz njih. Njihovom primjenom moći ćete pronaći točan odgovor.
Kako bi vaša priprema za ispit bila uistinu učinkovita, posjetite obrazovni portal Shkolkovo. Ovdje ćete pronaći sve osnovne materijale o temama „Slobodni trapez ili koji će vam pomoći da uspješno položite Jedinstveni državni ispit. Glavna svojstva slike, formule i teoremi prikupljeni su u odjeljku "Teoretske informacije".
Svoje vještine rješavanja problema maturanti će moći usavršiti i na našem matematičkom portalu. Odjeljak "Katalog" predstavlja velik izbor relevantnih vježbi različitih razina težine. Naši stručnjaci redovito ažuriraju i dopunjuju popis zadataka.
Studenti iz Moskve i drugih gradova mogu dosljedno izvoditi vježbe online. Ako je potrebno, bilo koji zadatak može se spremiti u odjeljak "Favoriti" i kasnije se vratiti na njega za raspravu s nastavnikom.
U ovom članku za vas je napravljen još jedan izbor zadataka s trapezom. Uvjeti su nekako povezani s njegovom srednjom linijom. Tipovi zadataka preuzeti su iz otvorene banke tipičnih zadataka. Ako želite, možete obnoviti teoretsko znanje. Blog je već raspravljao o zadacima čiji su uvjeti povezani, kao i. Ukratko o srednjoj liniji:

Sredina trapeza spaja središta bočnih stranica. Paralelan je s bazama i jednak je njihovom poluzbroju.
Prije rješavanja problema, pogledajmo teorijski primjer.
Zadan je trapez ABCD. Dijagonala AC koja se siječe sa središnjicom čini točku K, dijagonala BD točku L. Dokažite da je dužina KL jednaka polovici razlike osnovica.

Prvo zapazimo činjenicu da srednja crta trapeza raspolavlja svaki segment čiji krajevi leže na njegovim bazama. Ovaj se zaključak nameće sam po sebi. Zamislite segment koji povezuje dvije točke baza; on će podijeliti ovaj trapez na dva druga. Ispada da će segment koji je paralelan s bazama trapeza i prolazi kroz sredinu stranice proći kroz sredinu druge strane.
Ovo se također temelji na Thalesovom teoremu:
Ako je nekoliko jednakih segmenata položeno jedan za drugim na jednoj od dvije crte i kroz njihove krajeve su povučene paralelne crte koje sijeku drugu crtu, tada će oni odrezati jednake segmente na drugoj liniji.
To jest, u ovom slučaju, K je sredina AC, a L je sredina BD. Dakle, EK je središnja crta trokuta ABC, LF je središnja crta trokuta DCB. Prema svojstvu srednje crte trokuta:

Sada možemo izraziti segment KL u terminima baza:
dokazano!
Ovaj primjer je dat s razlogom. U zadacima za samostalno rješavanje nalazi se upravo takav zadatak. Samo što ne kaže da segment koji povezuje središta dijagonala leži na središnjoj liniji. Razmotrimo zadatke:
27819. Odredite središnju trapeza ako su mu osnovice 30 i 16.

Računamo pomoću formule:

27820. Srednja crta trapeza je 28, a manja osnovica 18. Nađite veću osnovicu trapeza.

Izrazimo veću bazu:
Tako:
27836. Okomica spuštena iz vrha tupog kuta na veću osnovicu jednakokračnog trapeza dijeli ga na dijelove koji imaju duljine 10 i 4. Odredite središnju crtu tog trapeza.

Da biste pronašli srednju liniju morate znati baze. Bazu AB je lako pronaći: 10+4=14. Pronađimo DC.
Konstruirajmo drugu okomicu DF:

Segmenti AF, FE i EB bit će jednaki redom 4, 6 i 4. Zašto?
U jednakokračnom trapezu okomice spuštene na veću osnovicu dijele ga na tri segmenta. Dvije od njih, koje su kraci odsječenih pravokutnih trokuta, međusobno su jednake. Treći segment jednak je manjoj osnovici, jer se kod konstruiranja navedenih visina formira pravokutnik, au pravokutniku su suprotne strane jednake. U ovom zadatku:

Stoga je DC=6. Računamo:

27839. Osnovice trapeza su u omjeru 2:3, a srednica je 5. Nađite manju osnovicu.

Uvedimo koeficijent proporcionalnosti x. Tada je AB=3x, DC=2x. Možemo napisati:
Prema tome, manja baza je 2∙2=4.
27840. Opseg jednakokračnog trapeza je 80, njegova središnja linija jednaka je bočnoj stranici. Pronađite stranicu trapeza.

Na temelju uvjeta možemo napisati:
Ako srednju liniju označimo kroz vrijednost x, dobivamo:

Druga se jednadžba već može napisati kao:

27841. Srednjica trapeza je 7, a jedna mu je osnovica veća od druge za 4. Nađite veću osnovicu trapeza.

Označimo manju bazu (DC) kao x, tada će veća (AB) biti jednaka x+4. Možemo to zapisati
Otkrili smo da je manja baza rano pet, što znači da je veća jednaka 9.
27842. Srednjica trapeza je 12. Jedna od dijagonala ga dijeli na dva segmenta čija je razlika 2. Nađite veću osnovicu trapeza.

Veću osnovicu trapeza lako ćemo pronaći ako izračunamo odsječak EO. To je središnja linija u trokutu ADB, a AB=2∙EO.
Što imamo? Kaže se da je srednja linija jednaka 12, a razlika odsječaka EO i OF jednaka 2. Možemo napisati dvije jednadžbe i riješiti sustav:
![]()
Jasno je da u ovom slučaju možete odabrati par brojeva bez izračuna, to su 5 i 7. No, ipak, riješimo sustav:

Dakle, EO=12–5=7. Dakle, veća baza je jednaka AB=2∙EO=14.
27844. U jednakokračnom trapezu dijagonale su okomite. Visina trapeza je 12. Nađite njegovu središnju liniju.

Napomenimo odmah da visina povučena kroz sjecište dijagonala u jednakokračnom trapezu leži na osi simetrije i dijeli trapez na dva jednaka pravokutna trapeza, odnosno osnovice te visine dijele se popola.
Čini se da za izračunavanje srednje linije moramo pronaći razloge. Ovdje nastaje mala slijepa ulica... Kako, znajući visinu, u ovom slučaju izračunati baze? Nema šanse! Postoji mnogo takvih trapeza s fiksnom visinom i dijagonalama koje se sijeku pod kutom od 90 stupnjeva. Što da napravim?
Pogledajte formulu za središnju crtu trapeza. Uostalom, ne moramo znati same razloge, dovoljno je znati njihov zbroj (ili poluzbroj). Mi to možemo.
Budući da se dijagonale sijeku pod pravim kutom, formiraju se jednakokračni pravokutni trokuti visine EF:
Iz navedenog slijedi da je FO=DF=FC, a OE=AE=EB. Zapišimo sada čemu je jednaka visina izražena kroz segmente DF i AE:

Dakle, srednja linija je 12.
*Općenito, ovo je problem, kao što razumijete, za mentalno računanje. Ali siguran sam da je navedeno detaljno objašnjenje potrebno. I tako... Pogledate li sliku (pod uvjetom da se pri konstrukciji poštuje kut između dijagonala) odmah upada u oči jednakost FO=DF=FC, te OE=AE=EB.
Prototipovi također uključuju tipove zadataka s trapezom. Izgrađen je na listu papira u kvadratu i trebate pronaći srednju liniju; strana ćelije obično je jednaka 1, ali može biti drugačija vrijednost.
27848. Odredite središnju crtu trapeza ABCD, ako su stranice kvadratnih ćelija jednake 1.

Jednostavno je, izračunavamo baze po ćelijama i koristimo formulu: (2+4)/2=3
Ako su baze izgrađene pod kutom prema ćelijskoj mreži, tada postoje dva načina. Na primjer!
Trapez- četverokut čije su dvije stranice paralelne. Paralelne stranice su osnovke, a neparalelne stranice su stranice.
Postoji nekoliko glavnih tipova: krivocrtni, jednakokračni, proizvoljni, pravokutni. Izračun površine trapeza pomoću formule varira ovisno o specifičnoj vrsti geometrijske figure.
Što je trapezoid: vrste i razlike
Ukupno postoje četiri vrste, koje se razlikuju ne samo u varijabilnosti kutova, već iu mogućoj prisutnosti zakrivljenih segmenata.

Površina proizvoljnog trapeza
Varijabilnost u izračunavanju površine proizvoljnog trapeza je mala. Može se izračunati u odnosu na zadane dimenzije i visinu baze; brojati kroz naznačene četiri strane figure; riješiti primjer, znajući duljinu središnje crte i visinu; duž naznačenih dijagonala i kuta između njih; izračunaj kroz osnovice i dva kuta.
Osnovna formula za izračun ove metode: 
Gdje su a i b paralelne stranice, a h je visina četverokuta.
Primjer zadatka: Zadan je ravni geometrijski lik čije paralelne stranice odgovaraju duljinama od 12 i 20 cm, a visina je 10 cm.Kako pronaći površinu?
Riješenje: Valjano rješenje prema gornjoj formuli S = (a + b)/2 x h: S = (12 + 20)/2 x 10 = 160 cm².
Znajući duljinu srednje linije i visinu ravne figure, uvijek možete pronaći područje trapeza doslovno izvodeći jednu radnju:

Gdje je h visina četverokuta, a m središnja linija (ravna linija koja povezuje središta stranica).
Primjer rješavanja problema: Zadan je trapez u kojem je duljina središnje crte 28 cm, a visina lika 19 cm. Kolika je površina ravnog četverokuta?
Riješenje: Koristeći formulu S = hm, umjesto slova zamjenjujemo digitalne vrijednosti iz uvjeta problema. Dobivamo S = 28 x 19 = 532 cm².
Ova metoda nije tako jednostavna kao prethodne. Ovdje se kao osnova uzimaju osnovni teoremi geometrije, pa je stoga princip izračuna površine trapeza sljedeći:

Gdje su a, b, c, d četiri strane figure, a stranica b nužno mora biti duža od a.
Primjer izračuna: Zadane su stranice - a = 2 cm, b = 4 cm, c = 8 cm, d = 7 cm Kako pronaći površinu trapeza?
Izračun:
Također možete izračunati površinu trapeza znajući dimenzije obiju dijagonala i kut između njih. 
Oznake: d₁ i d₂ su prva i druga dijagonala, α je kut između dijagonala.
Primjer: Izračunajte površinu figure za sljedeće poznate vrijednosti - d₁ = 17 cm, d₂ = 25 cm, α = 35⁰.
Prava odluka: S = ½ x 17 x 25 x sin35 = 212,5 x 0,57 = 121,125 cm².
Još jedna opcija izračuna koja se temelji na izračunavanju površine trapeza pomoću duljina dviju baza i dva kuta.

Značenja slova: b, a – duljine osnovica, α i β – kutovi.
Riješenje:
Video za obuku
Izvrsna pomoć u učenju osnovnih tipova izračuna površina su videozapisi s pristupačnim, razumljivim jezikom, detaljnim objašnjenjima i primjerima rješavanja problema.
Video "Trapezoid: rješavanje problema"
Videozapis za početnike - jasno prikazane informacije koje sadrže osnovne formule za izračunavanje površine trapeza.
Video "Površina trapeza"
Videozapis sadrži najpotpunije informacije o vrstama trapeza, ispravnim oznakama slova i mogućnostima rješavanja raznih problema koristeći sve poznate metode i načela izračuna.
Sve navedene formule i metode izračuna široko su primjenjive pri učenju geometrije u školama i na sveučilištima. Studentima, školarcima i pristupnicima ponuđene informacije bit će korisne kao internetska varalica u razdoblju intenzivnih priprema za ispite, kolokvije, pisanje eseja, seminarskih radova i sličnih radova.
- U kontaktu s 0
- Google+ 0
- u redu 0
- Facebook 0