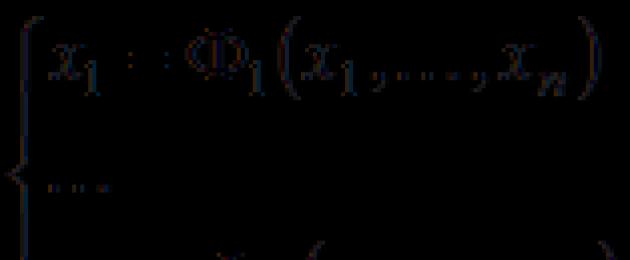Լուծել ոչ գծային հավասարումների համակարգ՝ օգտագործելով պարզ կրկնությունների մեթոդը: Ոչ գծային հավասարումների համակարգերի լուծում

Ոչ գծային հավասարումների համակարգը ունի ձև.

Ահա անհայտ փոփոխականներ, և (7) համակարգը կոչվում է նորմալ կարգի համակարգ, եթե ֆունկցիաներից գոնե մեկը ոչ գծային է:

Ոչ գծային հավասարումների համակարգերի լուծումը հաշվողական մաթեմատիկայի բարդ խնդիրներից է։ Դժվարությունը կայանում է նրանում, որ որոշելը, թե արդյոք համակարգը լուծում ունի, և եթե այո, ապա քանիսը: Տվյալ տարածքում լուծումների մշակումն ավելի պարզ խնդիր է:

Թող գործառույթները սահմանվեն ոլորտներում: Այդ ժամանակ տարածքը կլինի այն տարածքը, որտեղ կարելի է լուծում գտնել։ Լուծումը զտելու ամենատարածված մեթոդներն են պարզ կրկնման մեթոդը և Նյուտոնի մեթոդը:

Ոչ գծային հավասարումների համակարգերի լուծման պարզ կրկնման մեթոդ

Սկզբնական համակարգից (7) համարժեք փոխակերպումների միջոցով մենք անցնում ենք ձևի համակարգի.

Բանաձևերով սահմանված կրկնվող գործընթաց

կարող եք սկսել՝ նշելով նախնական մոտավորությունը: Կրկնվող գործընթացի մերձեցման համար բավարար պայման երկու պայմաններից մեկն է.

Գրենք առաջին պայմանը.

Գրենք երկրորդ պայմանը.

Եկեք դիտարկենք (7) համակարգը (8) ձևի վերածելու եղանակներից մեկը, որը թույլ է տալիս կոնվերգենտ կրկնություններ:

Թողեք ձևի երկրորդ կարգի համակարգ.

Դուք պետք է այն բերեք այս ձևին.

Եկեք համակարգի առաջին հավասարումը բազմապատկենք անհայտ հաստատունով, երկրորդը՝ անհայտ հաստատունով, ապա գումարենք դրանք և գումարենք հավասարման երկու կողմերին։ Մենք ստանում ենք փոխակերպված համակարգի առաջին հավասարումը

Մենք որոշում ենք անհայտ հաստատունները բավարար պայմաններկոնվերգենցիա

Ավելի մանրամասն գրենք այս պայմանները.

Ենթադրելով, որ մոդուլի նշանի տակ արտահայտությունները հավասար են զրոյի, հաստատունները որոշելու համար ստանում ենք չորս հավասարումների համակարգ՝ չորս անհայտով.

Պարամետրերի այս ընտրությամբ կոնվերգենցիայի պայմանները կբավարարվեն, եթե ֆունկցիաների մասնակի ածանցյալները և շատ արագ չփոխվեն կետի մոտակայքում:

Համակարգը լուծելու համար դուք պետք է նշեք նախնական գուշակություն և հաշվարկեք ածանցյալների արժեքները և այս պահին: Հաշվարկն իրականացվում է կրկնության յուրաքանչյուր քայլում, մինչդեռ

Պարզ կրկնությունների մեթոդը ինքնաշտկվող է, ունիվերսալ և հեշտ է իրականացնել համակարգչում: Եթե ​​համակարգն ունի մեծ պատվեր, ապա հավելվածը այս մեթոդը, որն ունի դանդաղ կոնվերգենցիայի արագություն, խորհուրդ չի տրվում: Այս դեպքում կիրառվում է Նյուտոնի մեթոդը, որն ունի ավելի արագ կոնվերգենցիա։

Նյուտոնի մեթոդը ոչ գծային հավասարումների համակարգերի լուծման համար

Թող անհրաժեշտ լինի լուծել (7) ձևի ոչ գծային հավասարումների համակարգը: Ենթադրենք, որ լուծումը գոյություն ունի ինչ-որ տիրույթում, որտեղ բոլոր գործառույթները շարունակական են և ունեն, ըստ գոնե, առաջին ածանցյալը։ Նյուտոնի մեթոդը կրկնվող գործընթաց է, որն իրականացվում է հետևյալ ձևի որոշակի բանաձևի համաձայն.

Նյուտոնի մեթոդի օգտագործման դժվարությունները.

կա՞ հակադարձ մատրիցա։

Դա տարածաշրջանից այն կողմ չի՞ դուրս գալիս։

Փոփոխված Նյուտոնի մեթոդը հեշտացնում է առաջին առաջադրանքը: Փոփոխությունն այն է, որ մատրիցը հաշվարկվում է ոչ թե յուրաքանչյուր կետում, այլ միայն սկզբնականում: Այսպիսով, փոփոխված Նյուտոնի մեթոդն ունի հետևյալ բանաձևը.

Բայց փոփոխված Նյուտոնի մեթոդը չի պատասխանում երկրորդ հարցին։

(8) կամ (10) բանաձևերի համաձայն կրկնվող գործընթացը ավարտվում է, եթե բավարարվում է հետևյալ պայմանը

Նյուտոնի մեթոդի առավելությունը նրա արագ կոնվերգենցիան է՝ համեմատած պարզ կրկնման մեթոդի հետ։

Հաշվարկի բանաձև Նյուտոնի մեթոդըունի ձև.

Որտեղ n=0,1,2,..

Երկրաչափական առումով Նյուտոնի մեթոդընշանակում է, որ արմատին հաջորդ մոտեցումը OX առանցքի հետ հատման կետն է: ֆունկցիայի գրաֆիկին շոշափող y=f(x)կետում.

Թեորեմ Նյուտոնի մեթոդի կոնվերգենցիայի մասին։

Թող լինի պարզ արմատ մի հավասարման որոշ հարևանությամբ, որի ֆունկցիան երկու անգամ շարունակաբար տարբերվում է:

Այնուհետև կա արմատի այնքան փոքր հարևանություն, որ այս հարևանությունից նախնական մոտարկման կամայական ընտրությամբ Նյուտոնի մեթոդի կրկնվող հաջորդականությունը չի անցնում հարևանությունից այն կողմ, և գնահատումը վավեր է:

Նյուտոնի մեթոդը(1) զգայուն նախնական մոտարկման ընտրության նկատմամբ x 0 .

Գործնականում մեթոդի միատոն կոնվերգենցիայի համար անհրաժեշտ է:

1-ին ածանցյալ f(x)

2-րդ ածանցյալ f(x) պետք է ունենա մշտական ​​նշան մեկուսացված արմատի տեղայնացման [a, b] միջակայքում.

սկզբնական մոտեցման համար x 0 ընտրվում է տեղայնացման միջակայքի սահմանը, որի դեպքում ֆունկցիայի արտադրյալն իր 2-րդ ածանցյալով զրոյից մեծ է (f(c)f '' (c) > 0, որտեղ c-ն միջակայքի սահմաններից մեկն է):

. Տրված ճշգրտության համար >

Ինչպես նշված է թեորեմում, Նյուտոնի մեթոդն ունի տեղային կոնվերգենցիա, այսինքն՝ նրա կոնվերգենցիայի շրջանը արմատի փոքր հարևանությունն է։ .

Վատ ընտրությունը կարող է հանգեցնել տարբեր կրկնությունների հաջորդականության:

Կրկնման պարզ մեթոդ (հաջորդական կրկնությունների մեթոդ):

Պարզ կրկնման մեթոդը կիրառելու համար հետևում է նախնական հավասարումը վերածել կրկնման համար հարմար ձևի .

Այս փոխակերպումը կարող է իրականացվել տարբեր ձևերով:

Ֆունկցիան կոչվում է կրկնվող ֆունկցիա։

Պարզ կրկնման մեթոդի հաշվարկման բանաձևը հետևյալն է.

Որտեղ n=0,1,2,..

Թեորեմ պարզ կրկնման մեթոդի կոնվերգենցիայի վրա։

Թող ֆունկցիան լինի շարունակական տարբերակելի արմատի ինչ-որ հարևանությամբ և բավարարի անհավասարությունը

Որտեղ 0 < q < 1 - մշտական.

Այնուհետև, անկախ նշված հարևանությունից նախնական մոտարկման ընտրությունից, կրկնությունների հաջորդականությունը չի լքում այս հարևանությունը, մեթոդը համընկնում է.

երկրաչափական հաջորդականության արագությամբ և սխալի գնահատումը վավեր է :

Կրկնվող գործընթացն ավարտելու չափանիշ .

Տրված >0 ճշտության համար հաշվարկները պետք է կատարվեն այնքան ժամանակ, քանի դեռ անհավասարությունը չի բավարարվել

Եթե ​​արժեքը , ապա կարող է օգտագործվել կրկնությունների ավարտի ավելի պարզ չափանիշ.

Եթե ​​անհավասարության մեջ (5) q > 1, ապա կրկնվող մեթոդը (4) տարբերվում է։

Եթե ​​անհավասարության մեջ (5) ք= 1 , ապա կրկնվող մեթոդը (4) կարող է կամ համընկնել կամ շեղվել:

Այն դեպքում, եթե ք > = 1 , ապա կրկնվող մեթոդը (4) շեղվում է և

կիրառվում է կրկնության պարզ մեթոդ՝ կրկնության պարամետրով.

Կիրառման հիմնական կետը հավասարումը համարժեք փոխակերպումն է.

αf(x) = 0

x = x+αf(x), (9)

Որտեղ α - կրկնության պարամետր (իրական հաստատուն):

Հաշվարկի բանաձև կրկնության պարզ մեթոդ՝ կրկնության պարամետրովունի ձև.

x (n+1) = x (n) + αf(x (n) ) , (10)

Որտեղ n=0,1,2,..

(10) ձևի համաձայն կառուցված կրկնվող գործընթացը համընկնում է, Եթե:

Ֆունկցիայի 1-ին ածանցյալ f(x)նշանով հաստատուն է և սահմանափակված է մեկուսացված արմատի տեղայնացման միջակայքում.

կրկնվող պարամետրի նշան α ֆունկցիայի 1-ին ածանցյալի հակառակ նշանը f(x)մեկուսացված արմատի տեղայնացման միջակայքի վրա.

կրկնվող պարամետրի արժեքի մոդուլ α գնահատվում է անհավասարությունից

| α | < 2/M , (11)

որտեղ M-ը ֆունկցիայի 1-ին ածանցյալի առավելագույն մոդուլն է f(x)

Այնուհետև,  կրկնության պարամետրի նման ընտրությամբ, մեթոդը (10) զուգակցվում է ինտերվալին պատկանող սկզբնական մոտարկման ցանկացած արժեքի համար երկրաչափական պրոգրեսիայի արագությամբ, q հայտարարով հավասար է.

որտեղ m-ը ֆունկցիայի 1-ին ածանցյալի նվազագույն մոդուլն է f(x)մեկուսացված արմատի տեղայնացման միջակայքի վրա:

ՈՒԿՐԱԻՆԱՅԻ ԿՐԹՈՒԹՅԱՆ ԵՎ ԳԻՏՈՒԹՅԱՆ ՆԱԽԱՐԱՐՈՒԹՅՈՒՆ

ՍՈՒՄԻ ՊԵՏԱԿԱՆ ՀԱՄԱԼՍԱՐԱՆ

Համակարգչային գիտության բաժին

ԴԱՍԸՆԹԱՑ ԱՇԽԱՏԱՆՔ

ԸՆԴՀԱՆՈՒՐ ԸՆԴՀԱՆՈՒՐ:

Թվային մեթոդներ

«Ոչ գծային հավասարումների համակարգերի լուծման կրկնվող մեթոդներ»

1. Ոչ գծային հավասարումների համակարգերի լուծման մեթոդներ. ընդհանուր տեղեկություն

2.1 Կրկնման պարզ մեթոդ

2.2 Aitken փոխակերպում

2.3 Նյուտոնի մեթոդ

2.3.1 Նյուտոնի մեթոդի փոփոխություններ

2.3.2 Քվազի-Նյուտոն մեթոդներ

2.4 Ոչ գծային հավասարումների համակարգերի լուծման այլ կրկնվող մեթոդներ

2.4.1 Պիկարդ մեթոդ

2.4.2 Գրադիենտ վայրէջքի մեթոդ

2.4.3 Ռելաքսացիոն մեթոդ

3. Իտերատիվ մեթոդների իրականացում ծրագրային եղանակով և Maple մաթեմատիկական փաթեթի կիրառմամբ

3.1 Կրկնման պարզ մեթոդ

3.2 Գրադիենտ վայրէջքի մեթոդ

3.3 Նյուտոնի մեթոդ

3.4 Փոփոխված Նյուտոնի մեթոդ

Օգտագործված գրականության ցանկ

1. Ոչ գծային հավասարումների լուծման մեթոդներ. Ընդհանուր տեղեկություն։

Մեզ տրվի հավասարումների համակարգ, որտեղ

- որոշ ոչ գծային օպերատորներ. (1.1)

Այն կարող է ներկայացվել նաև մատրիցային ձևով.

(1.1)

Դրա լուծումը կոչվում է այս արժեք

, ինչի համար

Շատ տարածված հաշվողական խնդիր է (1.1) համակարգի որոշ կամ բոլոր լուծումները գտնելը nոչ գծային հանրահաշվական կամ տրանսցենդենտալ հավասարումների հետ nանհայտ.

Նշենք ըստ Xսյունակի վեկտոր ( X 1 , X 2 ,..., x n)Տև հավասարումների համակարգը գրի՛ր (1.2) բանաձևի տեսքով. Ֆ(X) = 0, որտեղ F=(զ 1 , զ 2 ,..., f n)Տ.

Հավասարումների նմանատիպ համակարգեր կարող են ուղղակիորեն առաջանալ, օրինակ, կառուցելիս ֆիզիկական համակարգեր, կամ անուղղակիորեն։ Այսպիսով, օրինակ, որոշակի գործառույթի նվազագույնի հասցնելու խնդիրը լուծելիս Գ(Xհաճախ անհրաժեշտ է որոշել այն կետերը, որոնցում այս ֆունկցիայի գրադիենտը զրո է: Հավատալով F= grad Գ,մենք ստանում ենք ոչ գծային համակարգ:

Ի տարբերություն գծային համակարգերի հանրահաշվական հավասարումներ, որի լուծման համար կարող են օգտագործվել որպես ուղիղ(կամ ճշգրիտ), և կրկնվող(կամ փակել) մեթոդները, ոչ գծային հավասարումների համակարգերի լուծումը կարելի է ստանալ միայն մոտավոր, կրկնվող մեթոդներով։ Նրանք թույլ են տալիս ստանալ մոտավորությունների հաջորդականություն

. Եթե ​​կրկնվող գործընթացը համընկնում է, ապա սահմանային արժեքը տվյալ հավասարումների համակարգի լուծումն է:

Համակարգի համար լուծում գտնելու մեթոդների ըմբռնումն ավարտելու համար անհրաժեշտ է պարզաբանել այնպիսի հասկացություն, ինչպիսին է «կոնվերգենցիայի դրույքաչափը»: Եթե ​​հետևողականության համար x n, համընկնում է սահմանին X *, բանաձեւը ճիշտ է

(կդրական իրական թիվ է), ապա կկոչվում է այս հաջորդականության կոնվերգենցիայի արագություն:

2. Ոչ գծային հավասարումների համակարգերի լուծման կրկնվող մեթոդներ

2.1 Կրկնման պարզ մեթոդ

Պարզ կրկնությունների մեթոդը (հաջորդական մոտարկումներ) հաշվողական մաթեմատիկայի հիմնականներից է և օգտագործվում է հավասարումների լայն դասի լուծման համար։ Եկեք այս մեթոդի նկարագրությունը և հիմնավորումը տանք ձևի ոչ գծային հավասարումների համակարգերի համար

f i (x 1 , x 2 ,...x n) = 0, ես=1,2,..n;

Եկեք հավասարումների համակարգը բերենք հատուկ ձևի.

(2.1)

Կամ վեկտորի տեսքով

. (2.2)

Ընդ որում, այս համակարգին անցումը պետք է լինի միայն այն պայմանով, որ

կծկման քարտեզ է:

Օգտագործելով որոշ նախնական մոտարկում X (0) = (x 1 (0) , x 2 (0) ,...x n (0))

Կառուցենք X (k+1) =  (X (k)) կրկնվող պրոցես։ Հաշվարկները շարունակվում են այնքան ժամանակ, քանի դեռ պայմանը չի կատարվել

. Այնուհետև հավասարումների համակարգի լուծումը քարտեզագրման ֆիքսված կետն է:

Մեթոդը հիմնավորենք որոշակի նորմով

տարածություն.

Ներկայացնենք կոնվերգենցիայի թեորեմ, որի պայմանների կատարումը հանգեցնում է համակարգի լուծում գտնելուն։

Թեորեմ (կոնվերգենցիայի մասին):Թող

1). Վեկտորային ֆունկցիան Ф(х) սահմանվում է տարածաշրջանում

; պայմանը բավարարված է

3). Անհավասարությունն արդար է

Այնուհետև կրկնվող գործընթացում.

, – հավասարումների համակարգի լուծում. ,

Մեկնաբանություն. 2) պայմանի անհավասարությունը Lipschitz պայմանն է տիրույթում Ф(х) վեկտորային ֆունկցիայի համար։ Սհաստատունով

(սեղմման վիճակ): Դա ցույց է տալիս Ֆտարածաշրջանում սեղմման օպերատորն է Ս, այսինքն (2.2) հավասարման համար կիրառվում է սկզբունքը սեղմված քարտեզագրումներ. Թեորեմի պնդումները նշանակում են, որ (2.2) հավասարումը լուծում ունի տարածաշրջանում Ս, և հաջորդական մոտարկումները համընկնում են այս լուծմանը հայտարարով երկրաչափական հաջորդականության արագությամբ ք.

Ապացույց. Քանի որ

, ապա 3) ենթադրությամբ պայմանավորված մոտարկման համար ունենք . Դա նշանակում է որ ։ Ցույց տանք, որ k=2,3,... և հարևան մոտարկումների համար բավարարված է անհավասարությունը (2.3):

Մենք կվիճարկենք ինդուկցիայի միջոցով. ժամը

հայտարարությունը ճշմարիտ է, քանի որ Եվ . Ենթադրենք, որ մոտարկումները պատկանում են S-ին, և անհավասարությունը (2.3) գործում է . Քանի որ , ուրեմն թեորեմի 2) պայմանը հաշվի առնելու համար ունենք .

Ինդուկտիվ վարկածով

ԼԱԲՈՐԱՏՈՐԱԿԱՆ ԱՇԽԱՏԱՆՔ թիվ 3-4.

Տարբերակ թիվ 5.

Աշխատանքի նպատակը.սովորել լուծել ոչ գծային հավասարումների համակարգեր (SNE)՝ օգտագործելով պարզ կրկնման մեթոդը (SI) և Նյուտոնի մեթոդը՝ օգտագործելով համակարգիչը:

1. Ուսումնասիրեք MPI-ի և Նյուտոնի մեթոդը ոչ գծային հավասարումների համակարգերի լուծման համար:

2. Միացված կոնկրետ օրինակսովորել MPI-ի և Նյուտոնի մեթոդով ոչ գծային հավասարումների համակարգերի լուծման կարգը համակարգչի միջոցով:

3. Ստեղծեք ծրագիր և օգտագործեք այն լուծելու համար ճշգրտությամբ հավասարումների համակարգ:

ԱՇԽԱՏԱՆՔԻ ԿԱՏԱՐՄԱՆ ՕՐԻՆԱԿ

Զորավարժություններ.

1. Լուծել SNE վերլուծական:

2. Նախնական մոտարկումով համակարգի թվային լուծման համար MPI-ի և Նյուտոնի մեթոդի աշխատանքային բանաձևերը.

3. Կազմել ծրագիր ցանկացած ծրագրավորման լեզվով, որն իրականացնում է կառուցված կրկնվող գործընթացը:

Լուծում.

Վերլուծական մեթոդ.

SDE-ի վերլուծական լուծումը կետերն են և .

Պարզ կրկնությունների մեթոդ (SIM):

Համակարգի թվային լուծման համար աշխատանքային MPI բանաձևեր կառուցելու համար նախ անհրաժեշտ է այն բերել ձևի.

Դա անելու համար համակարգի առաջին հավասարումը բազմապատկեք անհայտ հաստատունով, երկրորդը՝ , ապա գումարեք դրանք և ավելացրեք հավասարման երկու կողմերում: Մենք ստանում ենք փոխակերպված համակարգի առաջին հավասարումը.

Մենք անհայտ հաստատունները որոշում ենք կրկնվող գործընթացի կոնվերգենցիայի համար բավարար պայմաններից.

Ավելի մանրամասն գրենք այս պայմանները.

Ենթադրելով, որ մոդուլի նշանի տակ արտահայտությունները հավասար են զրոյի, մենք ստանում ենք 4-րդ կարգի գծային հանրահաշվական հավասարումների համակարգ (SLAE)՝ 4 անհայտներով.

Համակարգը լուծելու համար անհրաժեշտ է հաշվարկել մասնակի ածանցյալները.

Այնուհետև SLAE-ն կգրվի այսպես.

Նկատի ունեցեք, որ եթե մասնակի ածանցյալները քիչ են փոխվում նախնական մոտավորության մոտակայքում, ապա.

Այնուհետև SLAE-ն կգրվի այսպես.

Այս համակարգի լուծումը կետերն են , , , : Այնուհետև SNL-ի լուծման MPI-ի աշխատանքային բանաձևերը կունենան հետևյալ ձևը.

Համակարգչում իրականացման համար աշխատանքային բանաձևերը կարող են վերաշարադրվել հետևյալ կերպ.

Կրկնվող գործընթացը կարելի է սկսել՝ նախնական մոտարկումը դնելով x 0 =-2, y 0 =-4: Գործընթացն ավարտվում է, երբ միաժամանակ երկու պայման է կատարվում՝ և . Այս դեպքում արժեքները և SNL-ի լուծումներից մեկի մոտավոր արժեքն են:

Նյուտոնի մեթոդը.

Կառուցել Նյուտոնի մեթոդի աշխատանքային բանաձևերը ձևով

որտեղ անհրաժեշտ է.

1. Գտե՛ք մասնակի ածանցյալների մատրիցը.

2. Գտե՛ք այս մատրիցայի որոշիչը.

3. Սահմանել հակադարձ մատրիցա:

Փոխակերպումը կատարելուց հետո.

Մենք ստանում ենք Նյուտոնի մեթոդի աշխատանքային բանաձևը համակարգչի վրա իրականացման համար.

Բլոկ սխեմա SLE-ի լուծման MPI-ն և Նյուտոնի մեթոդը ներկայացված են Նկար 1-ում:

Նկ.1 MPI-ի և Նյուտոնի մեթոդի սխեմաները:

Ծրագրի տեքստեր.

Ծրագիր P3_4; (կրկնություններ)

օգտագործում է Crt;

var n՝ ամբողջ թիվ;

clrscr;

xn:=x-(x-y+2)+(1/2)*(x*y-3);

yn:=y+(2/3)*(x-y+2)+(1/6)*(x*y-3);

գրել (n:3, x:9:5, xn:9:5, (xn-x):9:5, y:9:5, yn:9:5, (yn-y):9:5) ;

n:=n+1;

մինչև (abs(x-zx)<=eps) and (abs(y-zy)<=eps);

readln;

2) Նյուտոնի մեթոդ.

Ծրագիր P3_4; (Նյուտոն)

օգտագործում է Crt;

var n՝ ամբողջ թիվ;

x0,x,xn,y0,y,yn,eps,zx,zy:real;

clrscr;

n:=0; x0:=-2; x: = x0; y0:=-4; y:=y0; eps:=0.001;

writeln("n x(i) x(i+1) x(i+1)-x(i) y(i) y(i+1) y(i+1)-y(i)");

xn:=x-(1/(x+y))*(x*x-x*y+2*x+x-y+2);

yn:=y-(1/(x+y))*(x*y*(-y)-3*(-y)+x*y-3);

գրել (n:3, x:9:5, xn:9:5, abs(xn-x):9:5, y:9:5, yn:9:5, abs(yn-y):9: 5);

n:=n+1;

մինչև (abs(x-zx)<=eps) and (abs(y-zy)<=eps);

Ծրագրի գործարկման արդյունքները.

· Նկար 2 – պարզ կրկնումների մեթոդով աշխատող ծրագիր;

· Նկար 3 – ծրագիր, որն աշխատում է Նյուտոնի մեթոդով:

Նկ.2 Պատասխան՝ x(16)≈-3.00023, y(16)≈-1.00001

Նկ.3 Պատասխան՝ x(8)≈-3.00000, y(8)≈-1.00000

Պարզ կրկնման մեթոդը, որը նաև կոչվում է հաջորդական մոտարկման մեթոդ, մաթեմատիկական ալգորիթմ է անհայտ մեծության արժեքը աստիճանաբար զտելու միջոցով գտնելու համար։ Այս մեթոդի էությունն այն է, որ, ինչպես հուշում է անունից, նախնական մոտարկումից աստիճանաբար արտահայտելով հետագաները, ստացվում են ավելի ու ավելի հստակ արդյունքներ: Այս մեթոդը օգտագործվում է տվյալ ֆունկցիայի փոփոխականի արժեքը գտնելու համար, ինչպես նաև գծային և ոչ գծային հավասարումների համակարգեր լուծելիս։

Եկեք նայենք, թե ինչպես է այս մեթոդն իրականացվում SLAE-ների լուծման ժամանակ: Կրկնման պարզ մեթոդն ունի հետևյալ ալգորիթմը.

1. Կոնվերգենցիայի պայմանի կատարման ստուգում սկզբնական մատրիցում: Կոնվերգենցիայի թեորեմ. եթե համակարգի սկզբնական մատրիցն ունի անկյունագծային գերակայություն (այսինքն՝ յուրաքանչյուր տողում հիմնական անկյունագծի տարրերը բացարձակ արժեքով պետք է ավելի մեծ լինեն, քան երկրորդական անկյունագծերի տարրերի գումարը բացարձակ արժեքով), ապա պարզ կրկնության մեթոդը կոնվերգենտ է:

2. Բնօրինակ համակարգի մատրիցը միշտ չէ, որ ունի անկյունագծային գերակշռություն: Նման դեպքերում համակարգը կարող է փոխակերպվել: Կոնվերգենցիայի պայմանը բավարարող հավասարումները մնում են անձեռնմխելի, իսկ գծային համակցություններ են արվում նրանց հետ, որոնք չեն, այսինքն. բազմապատկել, հանել, իրար ավելացնել հավասարումներ, մինչև ստացվի ցանկալի արդյունք:

Եթե ​​ստացված համակարգում կան անհարմար գործակիցներ հիմնական անկյունագծի վրա, ապա i * x i ձևի տերմինները ավելացվում են նման հավասարման երկու կողմերին, որոնց նշանները պետք է համընկնեն անկյունագծային տարրերի նշանների հետ:

3. Ստացված համակարգի փոխակերպումը նորմալ ձևի.

x - =β - +α*x -

Դա կարելի է անել բազմաթիվ ձևերով, օրինակ՝ այսպես՝ առաջին հավասարումից արտահայտեք x 1-ը այլ անհայտների առումով, երկրորդից՝ x 2, երրորդից՝ x 3 և այլն։ Այս դեպքում մենք օգտագործում ենք բանաձևերը.

α ij = -(a ij / a ii)

i = b i /a ii
Կրկին պետք է համոզվեք, որ ստացված նորմալ ձևի համակարգը համապատասխանում է կոնվերգենցիայի պայմանին.

∑ (j=1) |α ij |≤ 1, մինչդեռ i= 1,2,...n

4. Մենք սկսում ենք կիրառել, փաստորեն, ինքնին հաջորդական մոտարկումների մեթոդը։

x (0) սկզբնական մոտարկումն է, մենք դրա միջոցով կարտահայտենք x (1), այնուհետև x (2)-ը x (1) միջոցով: Ընդհանուր բանաձևը մատրիցային ձևով ունի հետևյալ տեսքը.

x (n) = β - +α*x (n-1)

Մենք հաշվարկում ենք այնքան ժամանակ, մինչև հասնենք պահանջվող ճշգրտությանը.

max |x i (k)-x i (k+1) ≤ ε

Այսպիսով, եկեք կիրառենք պարզ կրկնման մեթոդը: Օրինակ:
Լուծել SLAE:

4.5x1-1.7x2+3.5x3=2
3.1x1+2.3x2-1.1x3=1
1.8x1+2.5x2+4.7x3=4 ճշտությամբ ε=10 -3

Տեսնենք, թե արդյոք մոդուլում գերակշռում են անկյունագծային տարրերը։

Մենք տեսնում ենք, որ միայն երրորդ հավասարումը բավարարում է կոնվերգենցիայի պայմանը։ Եկեք փոխակերպենք առաջինը և երկրորդը, իսկ երկրորդը ավելացնենք առաջին հավասարմանը.

7.6x1+0.6x2+2.4x3=3

Երրորդից հանում ենք առաջինը.

2.7x1+4.2x2+1.2x3=2

Մենք սկզբնական համակարգը վերածեցինք համարժեքի.

7.6x1+0.6x2+2.4x3=3
-2.7x1+4.2x2+1.2x3=2
1.8x1+2.5x2+4.7x3=4

Հիմա եկեք համակարգը բերենք իր սովորական ձևի.

x1=0,3947-0,0789x2-0,3158x3
x2=0.4762+0.6429x1-0.2857x3
x3= 0,8511-0,383x1-0,5319x2

Մենք ստուգում ենք կրկնվող գործընթացի կոնվերգենցիան.

0.0789+0.3158=0,3947 ≤ 1
0.6429+0.2857=0.9286 ≤ 1
0,383+ 0,5319= 0,9149 ≤ 1, այսինքն. պայմանը բավարարված է.

0,3947
Սկզբնական ենթադրություն x(0) = 0,4762
0,8511

Այս արժեքները փոխարինելով նորմալ ձևի հավասարման մեջ՝ մենք ստանում ենք հետևյալ արժեքները.

0,08835
x (1) = 0,486793
0,446639

Փոխարինելով նոր արժեքները՝ մենք ստանում ենք.

0,215243
x (2) = 0,405396
0,558336

Մենք շարունակում ենք հաշվարկները, մինչև մոտենանք տվյալ պայմանին բավարարող արժեքներին։

x (7) = 0,441091

Ստուգենք ստացված արդյունքների ճիշտությունը.

4,5*0,1880 -1.7*0,441+3.5*0,544=2,0003
3.1*0.1880+2.3*0.441-1.1x*0.544=0.9987
1.8*0,1880+2.5*0,441+4.7*0,544=3,9977

Գտնված արժեքները սկզբնական հավասարումների մեջ փոխարինելով ստացված արդյունքները լիովին բավարարում են հավասարման պայմանները:

Ինչպես տեսնում ենք, պարզ կրկնման մեթոդը բավականին ճշգրիտ արդյունքներ է տալիս, բայց այս հավասարումը լուծելու համար մենք պետք է շատ ժամանակ ծախսեինք և ծանր հաշվարկներ անեինք: